1 Introduction

Accurate forecasting of rainfall plays an important role in flood control and disaster relief and has attracted the attention of hydrology researchers in this field who realize that no one modeling method is superior to another because each modeling technique has its own merits and drawbacks. There are several serious drawbacks of using previous rainfall forecasting applications. These include (1) the necessity of accurate stochastic modelling, which may not be possible in the case of rainfall; (2) the non-linearity features of input/output mapping may not be possible to examine; (3) the requirement for a priori information of the system measurement and development of covariance matrices for each new pattern and (4) the weak observation ability of some temporal pattern states that may lead to unstable estimates for the forecasted values.

The most commonly encountered and probably the most challenging work in any data-driving modeling such as rainfall modeling involves analysis of the studied problems, data collection, data pre-processing, input selection, model recognition and evaluation of model performance. Determining input variables is a fundamental and vital task. Without appropriate model inputs, any advanced model structure and parameter optimization algorithm can be useless for model recognition. However, mostly, model recognition depends on the training data.

In recent years scientists have endeavored to minimize the error in rainfall processing over time for rainfall forecasting purposes. For this goal, different categories of statistical (e.g., moving average) model; and time domain transform intelligent models, such as Fourier Transform (FT) and Wavelet Transform (WT) have been applied. There are some weaknesses in statistical methods of which the moving average is no exception. In addition, there are also some problems with time domain transform such as FT. Notably; the FT methods require the data under investigation to be stationary. Focusing on hydrology, signal fluctuations are highly non-stationary and physical processes often operate under a large range of scales varying from one day to several decades both for rainfall rates (DeLima and Grasman 1999) and river discharges (Labat et al. 2002). Therefore, to be able to cover those weaknesses in the statistical and Fourier methods there is a need for methods which are able to provide an improved knowledge of the mechanisms that produces a series, their seasonal variations, internal correlations, and possible trends and wavelet could be favorable and maybe appropriate for the elimination of the errors. Mathematically, the wavelets are identified as one of the new findings of absolute mathematics, which, nowadays, have myriad applications in network traffic (Syed et al. 2010), biomedical engineering (Fu and Serrai 2011), energy conversion and management (Shafiekhah et al. 2011), computer science (Genovese et al. 2011), magnetic resonance imaging (Serrai and Senhadji 2005), signal process (Zhao and Ye 2010), image compression (Yang et al. 2008), voice code (Fonseca et al. 2007), pattern recognition (Chen et al. 2009), earthquake investigation (Haigh et al. 2002) and many other non-linear engineering fields.

In hydrology, Nourani et al. (2009) examined combining the wavelet analysis with the artificial neural network (ANN) concept for monthly prediction of Ligvanchai watershed precipitation in Iran, Wang et al. (2009) proposed a new hybrid model between wavelet analysis and ANN to predict the short and long term inflows of the Three Gorges Dam in the Yangtze River, China, Rezaeian Zadeh et al. (2010) applied wavelet-ANN for predicting daily flows, Singh and Singh (2010) proposed a model to estimate the mean annual flood, Adamowski and Chan (2011) presented a new method based on coupling discrete wavelet transforms (WT) and ANN for the groundwater level modeling, Quebec, Canada; and Rajaee et al. (2011) proposed daily suspended sediment load (SSL) prediction in rivers by wavelet-ANN model.

In addition to the application of wavelet-ANN; Partal and Kisi (2007) proposed a new conjunction method (wavelet-neuro-fuzzy) for precipitation forecast in Turkey. The wavelet-neuro-fuzzy model provided a good fit to the observed data, especially for time series which have zero precipitation values in the summer months and for the peaks in the testing period. Ozger (2010) presented a wavelet-neuro fuzzy model for significant wave height forecasting; Dastorani et al. (2010) proposed hybrid adaptive neuro-fuzzy inference system (ANFIS) and wavelet to predict the missing data of stream flow for gauging stations using data from neighboring sites; and Shiri and Kisi (2010) proposed short-term and long-term stream flow forecasting using a wavelet and neuro-fuzzy conjunction model.

This paper presents two scenarios; firstly, monthly rainfall is used solely as inputs in different time lags from the time (t) to the time (t-4) without pre-processing to ANN and ANFIS. Second scenario uses the wavelet decomposition transfer to eliminate the error and then wavelet-based sub-signals are used as inputs in different lag times to see its applicability for rainfall forecasting of the Klang River basin in Malaysia. Although hydrological implications of wavelet and ANFIS have been already addressed by several studies, their conjunction as a hybrid model is quite a new issue in precipitation modeling. Due to the uncertainty involved in the precipitation process in one hand and the capability of Fuzzy theory and ANFIS (ANN+Fuzzy) to handle such uncertainties in the other hand, the hybrid wavelet-ANFIS model is proposed in this study for precipitation modeling and the results are compared with the previously presented models; e.g., ad hoc ANN and ANFIS models as well as wavelet-ANN model presented by Nourani et al. (2009).

2 Materials and Methods

2.1 Feed ForwardBack Propagation Neural Network (FFNN)

This class of networks consists of multiple layers of computational units, usually interconnected in a feed- forward way. Each neuron in one layer has directed connections to the neurons of the subsequent layer. In many applications the units of these networks apply a sigmoid function. Basically, the MLP consists of three layers: the input layer, where the data are introduced to the network; the hidden layer, where the data are processed (that can be one or more) and the output layer, where the results for given inputs are produced (Junsawang et al. 2007). Each layer is made up of several nodes, and layers are interconnected by sets of correlation weights. Each input node in input layer broadcasts the activation function (Fig. 1). Multi-layer networks use a variety of learning techniques. Back-propagation is the most commonly used supervised training algorithm in the multilayer feed-forward networks. The objective of a back propagation network is to find the weights that approximate target values of output with a selected accuracy. The network weights are modified by minimizing the error between target and computed outputs. The error between the outputs of the network and the target outputs are computed at the end of each forward pass. If an error is higher than a selected value, the procedure continuous with a reverse pass, otherwise, training is stopped (Kisi 2003).

Fig. 1
figure 1

Three layer feed forward perceptron ANN

Full size image

2.2 ANFIS Model

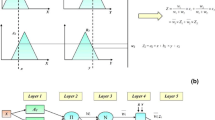
Neuro-fuzzy simulation refers to the algorithm of applying different learning techniques in the neural network literature to fuzzy modeling or a fuzzy inference system (FIS) (Chen and Lin 2006). A particular approach in neuro-fuzzy development is the adaptive neuro-fuzzy inference system (ANFIS). ANFIS first introduced by Jang (1993) that employs a neural network learning algorithm. It is a network representation of Sugeno-type fuzzy systems endowed by neural learning abilities.

In Fig. 2 the construction of an ANFIS is shown. According to the Fig. 2a, x and y are inputs; z is output (calculated monthly rainfall in this paper); A 1,2,  B 1,2 are fuzzy sets described by the shape of the membership function (μ) that is continuous and piecewise differentiable such as a Gaussian function; p 1,2,  q 1,2 are coefficients of linear equations z i (x,  y) and they are referred to as consequent parameters and w i is defined as:

$$ {w}_i={\mu}_{A_i}(x)\times {\mu}_{B_i}(y) $$
(1)

The membership functions for A and B are usually expressed by generalized bell functions, e.g.:

$$ {\mu}_{A_i}(x)=\frac{1}{1+{\left(\left(x-{c}_i\right)/{a}_i\right)}^{2{b}_i}} $$
(2)

Where [a i ,  b i ,  c i ] is the parameter set and is determined through five layers of ANFIS as Fig. 2b.

Fig. 2
figure 2

Construction of ANFIS system a Fuzzy inference system; b Equivalent ANFIS architecture

Full size image

2.3 Wavelet

Various mathematical transforms have been developed to determine some information which cannot be achieved from raw signals easily. The basic aim of wavelet analysis is both to determine the frequency (or scale) content of a signal and to assess the temporal variation of this frequency content. This property is in complete contrast to the Fourier analysis, which allows for the determination of the frequency content of a signal but fails to determine the frequency time—dependence. Therefore, the wavelet transform is the tool of choice when signals are characterized by localized high frequency events or when signals are characterized by a large number of scale-variable processes. In other words, wavelet analysis is a multi-resolution analysis in time and frequency domain.

Scientifically, the wavelet theory is a mathematical model in terms of smoothing of a signal, system, or process with a set of special signals-signals, which are small waves or wavelets. The waves must be oscillatory and have amplitudes, which quickly decay to zero in both the positive and negative directions. The required oscillatory condition leads to sinusoids as the building blocks. The quick decay condition is a tapering or windowing operation. These two conditions must be simultaneously met for the function to shrink the wavelets as small as possible called acceptability and expressed by:

$$ {\displaystyle \int \varphi (t)d(t)=0} $$
(3)

Where, φ(t) is the wavelet function.

Wavelet transforms are broadly divided into two classes: continuous, discrete.

Continuous Wavelet Transform (CWT) can be expressed as:

$$ \mathrm{CWT}\left(\mathrm{scale},\mathrm{position}\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f(t)\varphi \left( scale, position\right)d(t)} $$
(4)

Or

$$ CW{T}_s^{\varphi}\left(s,\tau \right)=\frac{1}{\sqrt{\left|s\right|}}{\displaystyle \int S(t){\varphi}_{s,\tau }*(t)d(t)} $$
(5)

This equation is a two variable (s, τ) function in which τ is the translation and S is the scale and * shows the complex conjugate. τ and S are real numbers and S is always positive. In continuous wavelet transforms, τ and S have continuous values, while in discrete transform they have discrete values.

φ(t) is called mother wavelet which is a resource for other window functions. All window functions φ s,τ (t) which are produced by the mother wavelet, are called daughter wavelets and expressed as below:

$$ {\varphi}_{s,\tau }(t)=\varphi \left[\frac{t-z}{s}\right] $$
(6)

The following properties make it difficult to apply continuous wavelet transform (CWT) in practice:

  1. i)

    Redundancy of CWT

The basic functions of the continuous wavelet transform are shifted and scaled versions of each other. It is obvious that these scaled functions do not make an orthogonal basis.

  1. ii)

    Infinite solution space

An infinite number of wavelets result from continuous wavelet transform. This makes it even harder to solve and also makes it difficult to identify the desired results from the transformed data.

  1. iii)

    Efficiency

Most of the transforms cannot be solved analytically. Either the solutions have to be calculated numerically, which takes an incredible amount of time, or by a computer. In order to use the wavelet transform for anything rational, we must find very efficient algorithms, that is the purpose of the DWT discussed earlier.

The DWT is more accurate than CWT because the transformed data though DWT has no extra details and the reverse function can be used in different ranks of time-frequency data.

From the signal processing point of view, the DWT is a filter bank algorithm iterated on the low-pass output. The low-pass filtering produces an approximation of the signal while the high pass filtering reveals the detail coefficient. The DWT is also related to a multi resolution framework. The idea is to represent a signal as a series of approximations (low-pass version) to the signal and details (high-pass version) at different resolution levels.

Such a discrete wavelet has the form:

$$ {g}_{m,n}(t)=\frac{1}{\sqrt{a_0^m}}g\left(\frac{t-n{b}_0{a}_0^m}{a_0^m}\right) $$
(7)

Where m and n are integers, which control the wavelet dilation and translation, respectively; a 0 is a specified-fined dilation step greater than 1; and b 0 is the location parameter and must be greater than zero. The most common and simplest choice for parameters are a 0 = 2 and b 0 = 1.

This power-of-two logarithmic scaling of the translation and dilation is known as the dyadic grid arrangement. The dyadic wavelet can be written in a more compact notation as:

$$ {g}_{m,n}={2}^{\raisebox{1ex}{$-m$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}g\left({2}^{-m}i-n\right) $$
(8)

This allows for the complete regeneration of the original signal as an expansion of a linear combination of translates and dilates orthonormal wavelets. For a discrete time series, x i the dyadic wavelet transform becomes:

$$ {T}_{m.n}={2}^{\raisebox{1ex}{$-m$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\displaystyle \sum_{I=0}^{N-1}g\left({2}^{-m}i-n\right){x}_i} $$
(9)

Where T m,n is the wavelet coefficients for the discrete wavelet of scale a = 2m and location b = 2m n. Thus, DWT provides information about the variation in a time series at different scales and locations.

2.4 Case Study

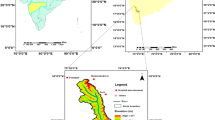
The Klang River flows through Kuala Lumpur and Selangor in Malaysia and eventually flows into the Straits of Malacca. It is approximately 120 km in length and drains a basin of about 1,288 km2, about 35 % of which is developed for residential, commercial, industrial, and institutional use. The Klang River has 11 major tributaries. These include Gombak River, Batu River, Kerayong River, Damansara River, Keruh River, Kuyoh River, Penchala River and Ampang River. Klang is geographically located at latitude (3.233°) 3° 13′ 58″ North of the equator and longitude (101.75°) 101° 45′ 0″ East of the Prime Meridian on the Map of Kuala Lumpur. Given the fact that the river flows through Klang Valley which is a heavily populated area of more than with an estimated population of over 7.56 million (about 25 % of the national population 29.6 million in 2012), and growing at almost 5 % per year, the Basin has experienced the highest economic growth in the country.

Rapid and uncontrolled development projects aggravate the problem. Heavy development has narrowed certain stretches of the river until it resembles a large storm drain. This contributes to flash floods in Kuala Lumpur, especially after heavy rain. The Klang River was used to be called Sungai Seleh. There are two major dams upstream of the river; Batu Dam and Klang Gates Dam, which provide water supply to the people of Klang Valley and mitigate floods. The study location map is shown in Fig. 3.

Fig. 3
figure 3

Location map of the Klang River Basin

Full size image

2.5 Data Pre-Processing and Analysis

2.5.1 Data Description

Descriptive statistics play an important role in data analysis. The descriptive statistics crystallizes the importance of data in creating the noble ideas about data analysis. All information and used data are based on the Klang Gates Dam data from 1997 to 2008. Table 1 presents pertinent information about the Klang River and some descriptive statistics of the original data, including mean (μ), variance (σ 2), standard deviation (S x ), skewness coefficient (C s ), minimum (X min) and maximum (X max).

Table 1 The statistical parameters for the monthly dataset
Full size table

The data indicate that the heaviest rainfall occurs in September with a mean of 17.87 cm in 2001 and the lowest rainfall pours in October with a mean of 0.31 cm in 2005. According to Table 1, rainfall variation shows higher variance in 2001 and the smoothness of rainfall in 2006.

The used data observed in the Klang gates dam from 1997 to 2008 are shown in Fig. 4.

Fig. 4
figure 4

Monthly time series of rainfall

Full size image

2.5.2 Data Reliability and Validity

One of the most important parts in any data-driving modeling such as rainfall modeling is data pre-processing. There are different methods to assess the reliability and validity of the collected data. One of the methods is called Double Mass method (Searcy and Hardison 1960). The basic of this method is obtained by plotting the cumulative annual amounts. The data are arranged in Table 2.

Table 2 Homogeneity test performance
Full size table

In Table 2, first, the means of annual rainfall and runoff are shown. So, the amounts higher than the mean data are represented by the letter ‘a’ and the amounts lower than the mean data are represented by the letter ‘b’ and accordingly, the table are formed.

Following that, the number of ‘a’ and ‘b’ that are repeated more than once, are denoted. Then, Table 3 is formed. In the last column (column 6), the sum of ‘a’ and ‘b’ has been calculated. These two numbers acquired are used as the input of the double mass method.

Table 3 Double mass test feature
Full size table

According to Table 3, if the sum of ‘a’ and ‘b’ is between 2 < a + b < 9, data are homogeneous. Since this number is equal to three, it can be safely claimed that the gained data are significant with 95 % confidence.

2.5.3 Data Normalization

One of the steps of data pre-processing is data normalization. The need to make harmony and balance between network data range and used activation function causes the data to be normal in activation function range. Sigmoid logarithm (Logsig) function is used for all layers in this study. By considering Sigmoid, it can be seen that its range is between 0 and 1, so data must be normalized between [0, 1]:

$$ {x}_n=\frac{x-{x}_{\min }}{x_{\max }-{x}_{\min }} $$
(10)

Where x is actual data and x min is minimum value of original series and x max is maximum value of original series.

The Logsig activation function (Fig. 5) was selected among Tansig, Sigmoid and Logsig activation functions through a trial-error process in the form of:

$$ y=\frac{1}{1+{e}^{- \log (x)}} $$
(11)
Fig. 5
figure 5

Logsig activation function

Full size image

2.5.4 Performance Criteria

Four different criteria are used in order to evaluate the effectiveness of each model and its ability to make precise predictions. Beside, two criteria called Correlation Coefficient (R 2), and Nash Sutcliffe coefficient (NE) are used to achieve the optimal input pattern in order to enhance the forecasting capabilities for the output. The four criteria are Root Mean Square Error (RMSE), Correlation Coefficient (R 2), Gamma Test (G), Spearman Correlation Coefficient (ρ) as:

$$ \mathrm{Nash}-\mathrm{Sutcliffe}: NE=1-\frac{{\displaystyle \sum {\left({X}_t-\overline{X_t}\right)}^2}}{{\displaystyle \sum {\left({X}_0-\overline{X_0}\right)}^2}} $$
(12)
$$ \mathrm{Spearman}\;\mathrm{rank}\;\mathrm{correlation}:\rho =1-\frac{6{\displaystyle \sum {d}_i^2}}{n\left({n}^2-1\right)} $$
(13)
$$ \mathrm{Correlation}\;\mathrm{Coefficient}\left({R}^2\right):{R}^2=\frac{{\displaystyle \sum_{i=1}^n\left({X}_t-{\overline{X}}_t\right)\left({X}_0-\overline{X_0}\right)}}{\sqrt{{\displaystyle \sum_{i=1}^n{\left({X}_t-\overline{X_t}\right)}^2{\left({X}_0-\overline{X_0}\right)}^2}}} $$
(14)
$$ \mathrm{Root}\;\mathrm{Mean}\;\mathrm{Square}\;\mathrm{Error}\left(\mathrm{RMSE}\right): RMSE=\sqrt{{\displaystyle \sum_{i=1}^n\frac{{\left({X}_t-{X}_0\right)}^2}{n}}} $$
(15)

Gamma test: Basically, the Gamma test is able to provide the best mean square error that can possibly be achieved using any nonlinear smooth models.

$$ G=\frac{N_s-{N}_d}{N_s+{N}_d} $$
(16)

Where Nsthe number of pairs of cases ranked in the same order on both variables Nd the number of pairs of cases ranked differently on the variables d i is the difference in the ranks given to the two variable values for each item of data.

Where X t is the observation data and X 0 computed data and n is the number of data. \( \overline{X_t} \) is the mean of actual data and \( \overline{X_0} \) is the mean of the computed data. Due to implication of normalized data in the modeling all criteria are dimensionless.

3 Results and Discussion

ANN and ANFIS models are introduced into rainfall modelling as a powerful, flexible, and statistical modelling techniques to address complex pattern recognition problems.

Figure 6 illustrates the implementation framework of rainfall forecasting where prediction models can be conducted in two modes: without/with data pre-processing methods. The acronyms in the box “methods for model inputs” represent LCA (linear correlation analysis).

Fig. 6
figure 6

Implementation framework of rainfall forecasting with data pre-processing

Full size image

One of the most important tasks in developing a satisfactory ANN or ANFIS forecasting model is the selection of optimal input pattern in order to enhance the forecasting capabilities for the output. Therefore, the correlation coefficient and Nash coefficient between the initial data should be considered first (Chen and Lin 2006). In this study, different combinations of input data were explored to assess their influence on the rainfall estimation modeling. Table 4 demonstrates the linear relationship between the input and target rainfall.

Table 4 Linear relationship between the input and target rainfall
Full size table

Table 4 shows the persistent effect of current rainfall versus several previous rainfall values at the rainfall gauging station of the basin.

As can be seen, the rainfall movement forward to 3 month, the pattern of the rainfall seems well matched. Consequently, several previous average rainfalls over the watershed (R (t-5), R (t-6), R (t-7) and R (t-8)) are used as inputs; however, as shown in Table 4, the correlation coefficient is varying and not stable. Nevertheless, if we only have a limited number of datasets, the model structure might only be good for the training sets due to overtraining and could not be used for future events (Chen and Lin 2006).

The available dataset for catchment (144 patterns) was divided into three groups: training set (calibration), testing set (validation), and checking set (checking). The data for training and testing patterns are randomly selected to 100 and 44 and 30 (these 30 values are selected among 100 calibration values) input patterns, respectively. Different combinations of the rainfall were used to construct the appropriate input structure. The general structures of the rainfall forecasting models are given in Table 5.

Table 5 Model structures for estimation of rainfall
Full size table

In the first scenario, monthly rainfall is imposed solely as an input in different time delays from the time (t) to the time (t-4) to ANN and ANFIS models. As a three layer perceptron is adopted, the identification of ANN’s structure is to optimize the number of hidden nodes in the hidden layer since the model inputs have been determined by LCA. For this purpose, a model based on a feed forward neural network with a single hidden layer is used for monthly rainfall. The back propagation algorithm and Logsig activation function are used to train the network. For the ANFIS method the hybrid algorithm was also used in order to determine the nonlinear input and linear output parameters. In the training and testing of ANN and ANFIS models the same dataset was used and the performance of models are also evaluated and compared based on the mentioned criteria. The qualities of the results produced by ANN and ANFIS models are shown in Tables 6 and 7 respectively.

Table 6 Performance of ANN model
Full size table
Table 7 Performance of ANFIS model
Full size table

The structure parameters selected by trial and error method during the ANFIS training process is shown in Table 8.

Table 8 The training parameters of the ANFIS model
Full size table

According to the tabulated results in Tables 6 and 7, it is obvious that the highest correlation between observed with computed data for different inputs is obtained by ANFIS. Figure 7a, b, c, d show the scatter plots of different sub-models of ANFIS model.

Fig. 7
figure 7

ANFIS output scatter plots sub-model of a 1, b 2, c 3, d 4

Full size image

In the second scenario, the wavelet transfer is used to eliminate the error and then the smoothed signals are used as inputs in different time delays for ANN and ANFIS models. Wavelet Analysis (WA) decomposes a rainfall time series into many linearly independent components at different scales (or periods). A low-frequency component generally reflects identification of the signal (such as, trend and periodic signals) whereas a high-frequency component uncovers details. Many different wavelet filters exist, each of them being particularly suitable for specific purposes of analysis. Wavelet filters differ in their properties and in their ability to match with the features of the time-series under study. Because of boundary conditions, longer filters are well adapted for long time-series. In fact, the wavelet and the scaling coefficients contain different information. This is an important feature as it ensures that the wavelet decomposition will preserve variance of the original series. The other important point in choosing the correct wavelet is its length. In fact, the most crucial point is probably not to choose the “right” filter but to choose a filter with an appropriate length. Increasing the filter length permits a better fit to the data.

According to the shape of data, there are some similarities between the time series and Dmey wavelet (Mallat 1998) which is shown in Fig. 8. The data for period of 1978–1988 are shown in Fig. 8.

Fig. 8
figure 8

The Dmey wavelet and rainfall data of “1978–1988”

Full size image

The “MATLAB” code was programmed using the Demy wavelet transform to decompose the signal into sub-series of approximation and detail sub-signals at level 10 according to the principle of wavelet decomposition as shown in Fig. 9. As can see in Fig. 9, there is a trend in level 4 which means that there is not much frequency variation after level 4 and the decomposition reaches to a trend which there is no need higher decomposition.

Fig. 9
figure 9

The decomposed time series in different levels

Full size image

Basically, one of the main purposes of this paper is to smooth out the rainfall fluctuation of the Klang River basin in Malaysia to obtain a clear view of the long term trend and true underlying behavior of the series and to increase the interpreter of a time series by picking out its main features. One of these main features is the trend component. The key property of the wavelet transform that makes it useful for studying possible non-stationary is providing useful information and new insights into the datasets.

Wavelet transform at final stage, has reverse process which is called the inverse wavelet transform or signal reconstruction. The decomposed data could reconstruct and used as an input in different time delays for ANN and ANFIS by:

$$ S={\displaystyle \sum_{i=1}^n{d}_n}+{a}_n $$
(17)

Where S is the original de-noised signal; d n is detail a n is approximation sub-signals and n is the last decomposition level.

After determination of suitable decomposition level (L) and mother wavelet within calibration and verification processes using the available (observed) data, the wavelet transform is only applied to the last part of the time series (including the new forecasted value at each step, t + 1) with the decomposition length of 2L (from t-L + 1 to t + 1) like a sliding window with a freezed dilation of transform (without dilation over time series). Such methodology is also employed by sliding window Fast Fourier Transform (Mallat 1998).

The pre-processed data were entered to the ANN model in order to improve the model accuracy. The used wavelet decomposes the main rainfall signal (X t ) into one approximation sub- signal, a 4 and 4 detailed sub-signals, (d 1, d 2, d 3,, d 4) (Fig. 10). To continue, for each of the five cases mentioned, the rainfall values of a distinct month from each sub-signal of calibration data set were considered as input layer neurons to predict the precipitation 1 month ahead (as output layer neuron) using ANN and ANFIS models.

Fig. 10
figure 10

a Approximation and details at level b 1, c 2, d 3 and e 4 decomposed by Dmey

Full size image

The qualities of the results produced by ANN and ANFIS using wavelet transform are shown in Tables 9 and 10, respectively.

Table 9 Performance of ANN using wavelet transform
Full size table
Table 10 Performance of ANFIS using wavelet transforms
Full size table

According to presented results on Tables 9 and 10, it is obvious that the highest correlation between observed and computed data for different inputs are obtained by ANFIS as shown in Fig. 11a, b, c, d. Table 11 shows the structures and parameters of the best ANN, ANFIS, ANN-wavelet and ANFIS-wavelet models.

Fig. 11
figure 11

ANFIS outputs scatter plots pre-processed by wavelet, sub-model of a 1, b 2, c 3, d 4

Full size image
Table 11 Parameters of the best ANN, ANFIS models
Full size table

The comparison of obtained results by proposed wavelet-ANFIS model with the results of ANN, ANFIS and previously presented wavelet-ANN model by Nourani et al. (2009) denotes to the capability of wavelet analysis to deal with the non-stationary of the time series by detecting the dominant seasonalities and periodicities involved in the process; so that the ANN and ANFIS apply larger weights to the dominant components of the process in the training process. The wavelet-based seasonal models (i.e., hybrid wavelet-ANN and wavelet-ANFIS models) are more efficient than the autoregressive models (i.e., ANN and ANFIS) in monitoring peak values of precipitation (see Fig. 11). It is evident that extreme or peak values in the rainfall time series, which occur in a periodic pattern, can be detected by the seasonal models accurately. On the other hand, the results show a bit (about 10 %) improvement in the modelling performance when using hybrid wavelet-ANFIS with regard to wavelet-ANN model. Such superiority may be due to the ability of Fuzzy set theory and ANFIS technique in dealing with the uncertainties of the precipitation process. As an example of such uncertainties, an averaged value of the pointy measured rainfalls by the rain gauges over a watershed is usually assigned to the whole of the watershed. Using this constant real number as the watershed rainfall in the ANN input layer can be a source of uncertainty. In such uncertain situations, the implication of ANFIS could lead to better outcomes.

In the presented research by Partal and Kisi (2007), the linear correlation coefficients between sub-series and the original precipitation series provided information for the selection of the neuro-fuzzy model inputs and for the determination of the effective wavelet components to be used for predicting precipitation values; but as criticized by Nourani et al. (2011), there may be a strong non-linear relationship in absence of a linear regression. Therefore, the presented methodology in this paper which considers the imposition of decomposed sub-series into the ANFIS model may be more reliable methodology.

4 Conclusions

In this study, two scenarios were introduced; in the first scenario, monthly rainfall was used solely as an input in different time delays from the time (t) to the time (t-4) to the ANN and ANFIS models. In second scenario, the wavelet transfer was also used to eliminate the noise and then imposed as an input in different lag time to ANN and ANFIS models. The four criteria as Root Mean Square Error (RMSE), Correlation Coefficient (R 2), Gamma coefficient (G), and Spearman Correlation Coefficient (ρ) were used to evaluate the proposed models. The results showed that the model based on wavelet decomposition performed higher forecasting accuracy and lower error in compared to ANN and ANFIS models. R + 4 ANFIS model, which consists four antecedent rainfall values as inputs, showed the highest correlation and the minimum RMSE and was selected as the best-fit model for modelling of rainfall flow for the Klang River.

Table 12 summarizes the results obtained by the ANFIS model and the wavelet-ANFIS models, during the calibration and the verification periods. Comparing the performances of the ANFIS and wavelet-ANFIS models, RMSE values of wavelet-ANFIS model is lower than ANFIS model. In addition, values of Spearman (ρ), correlation coefficient (R 2) and Gamma (G) of wavelet-ANFIS model are also higher than conventional ANFIS models. It can be said that, the performance of wavelet-ANFIS method is better than conventional ANFIS method according to criteria and Wavelet-ANFIS method is superior to the conventional ANFIS method in forecasting monthly rainfall values.

Table 12 The comparing of the performances of the ANFIS and wavelet-ANFIS models
Full size table