1 Introduction

Monitoring and assessment of surface water reservoirs that provide municipal water are necessary to reduce the impact of pollution. Of importance are the amount and the type of pollution and the reaction of the reservoir system to various decisions. To forecast system reactions, it is necessary to use a simulation model as a part of the decision support system (DSS).

Fontane et al. (1981) developed a quantitative–qualitative reservoir operation model by integrating a water quality simulator and dynamic programming (DP) to assess the water temperature profile at different reservoir depths. Loftis et al. (1985) presented a deterministic quantitative–qualitative multi-reservoir operation model that used an optimization method for extracting an operation policy. However, to reduce calculation efforts, they extracted outflow quality in some scenarios and used them in the optimization model as an offline water quality simulation. Dandy and Crawley (1992) developed a reservoir operation policy for meeting demand that used a complete mixing concept for quality simulation and optimization. The objective function consisted of minimization of system costs taking into account salinity damages.

Lence and Takyi (1992) used goal programming to extract upstream reservoir operation policies that reduce the environmental adverse impact of a thermal power plant for controlling downstream river temperature. Hayes et al. (1998) studied reservoir operation with hydropower generation considering the quantity and quality of the allocated water for controlling downstream dissolved oxygen (DO). Power production was used as an objective and downstream DO used as a constraint in the optimization model. The most important drawbacks in the aforementioned works were the inefficient simulators employed, which used simple quality assessment assumptions such as complete mixing. However, because of improvements in computing facilities and methods, recent reservoir quality assessment have employed more robust assessment models. Those robust models, however, are time-consuming and cannot be used as part of the optimization process in order to extract optimal strategies. As discussed next, some studies have been done in an attempt to overcome the aforementioned drawbacks.

Chaves et al. (2004) developed an integrated stochastic dynamic programming (SDP) model linked with two water quality simulators. The simulators were carried out through a physical model and an artificial neural network (ANN). They assumed that the water quality variables are independent of monthly time steps. They indicated that if the water quality variables are considered dependent, the number of state variables increases and the SDP may no longer be applicable due to the curse of dimensionality. Besides the problem of dimensionality, the backward-moving calculation which is required for SDP models, may be the main bottleneck for the combination of SDP with water quality simulation models.

Kerachian and Karamouz (2006) presented a method for extracting operation policies that considers water salinity by using a one-dimensional water quality model and a stochastic conflict resolution model based on Nash’s theory (Nash 1950). They used a varying chromosome length genetic algorithm (VLGA) as an optimization tool and concluded that although the proposed method reduces the computational burden, it still has a considerable run-time. Kerachian and Karamouz (2007) also proposed a method for extracting operation policies for water salinity management in a river-reservoir system. They used conflict resolution models to address conflicts in downstream water quality and meeting demands and upstream pollution load allocation.

Chen et al. (2007) extracted reservoir operation policies for quantitative-qualitative objectives, indicating the optimal Pareto set of policies and discussing the advantages of multi-objective operation policies. Shirangi et al. (2008) combined an evolutionary multi-objective method and a surface water salinity simulator to extract Pareto policies for quantitative-qualitative objectives and to reduce the run-time of GA-based optimization models. The main problem was divided into long-term and annual optimization models with water supply as the objective function in the long-term optimization and quantity and quality of allocated water as the objective functions in the annual optimization. One of the solutions of the Pareto set of policies was chosen by using Nash’s theory (Nash 1950). Hakimi-Asiabar et al. (2010) used self learning GA (SLGA) as a multi-objective optimization method to extract a Pareto set of operation policies for a reservoir. Their method was developed to decrease the optimization run-time. Dhar and Datta (2006) and Dhar and Datta (2008) developed a methodology for short-term operation of reservoir systems to control the released water quality considering inflow uncertainty. They used a single objective GA to minimize the deviation of the storage from a target level and considered water quality as a constraint. Belayneh and Bhallamudi (2012) tried to manage outflows from an upstream reservoir to control tidal water quality. Specifically, they proposed a simulation-optimization model based on simulated annealing (SA) to investigate the effect of tidal variation on the minimum stream discharge that is required to maintain the water quality constant, for a given pollutant loading.

Overall, the aforementioned investigations are mostly concerned with long-term input pollution, disregarding the sudden input of pollutants into a reservoir, whereas nowadays, the possibility of such pollutants’ occurrence is so high that it is considered in this study. Some investigations have addressed the pollution of volatile organic compounds (VOC) such as methyl tert-butyl ether (MTBE), benzene, toluene, ethylbenzene, and xylenes (BTEX) in reservoirs, which is considered herein. However, very little research exists in the management of VOC in reservoirs as well as in the modeling of VOCs in surface water. In this paper, an MTBE simulator is developed by adding a volatilization calculation capability to the CE-QUAL-W2 simulation model (Cole and Wells 2006). Thus, in the present study, the reservoir simulation is two-dimensional, taking into account reservoir depth, longitudinal dispersion, and the pollutant’s decay factor.

Because water quality problems involve both quality and quantity assessment, investigators are faced with meeting qualitative and quantitative objectives. Usually, to determine the best solution, a multi-objective optimization problem is transformed into a single-objective problem by using a conflict resolution method or traditional methods (e.g. weighted sum or ε-constraint) whereby one optimal solution is obtained instead of a set of optimal solutions. By following this approach, several optimal solutions may be lost because in multi-objective problems, there is a set of optimal non-dominated solutions. Determination of these solutions, allows the system manager to choose one of the relevant solutions by employing techniques such as Young’s (1993) bargaining method.

Many popular and important single- and multi-objective optimization methods employed in water resources management are meta-heuristic (e.g. Bozorg Haddad et al. 2008a; Fallah-Mehdipour et al. 2012; Soltanjalili et al. 2013), which suffer from a long-time analysis of the problem for requiring a very large number of time-consuming simulations, especially in surface water qualitative simulators such as CE-QUAL-W2. Moreover, many optimization techniques have been developed and applied for optimization in all aspects of water resources systems such as reservoir operation (Bozorg Haddad et al. 2008b, c, 2009, 2011a; Afshar et al. 2011), optimal cultivation rules (Moradi-Jalal et al. 2007; Noory et al. 2012), optimal pumping schedules (Bozorg Haddad and Mariño 2007; Bozorg Haddad et al. 2011b; Rasoulzadeh-Gharibdousti et al. 2011), optimal design of water distribution networks (Soltanjalili et al. 2010; Fallah-Mehdipour et al. 2011; Ghajarnia et al. 2011; Sabbaghpour et al. 2012;). Various complexities have been addressed in each of the aforementioned studies but only a few have taken into account the sudden entering of a pollutant in a hydrosystem.

One of the methods used to decrease the run-time of meta-heuristic optimization faced with a time-consuming simulator is surrogate-modeling. Jin (2011) reviewed the state-of-the-art of surrogate-assisted evolutionary computation. In surrogate-modeling, an alternate and fast simulator is used. These alternate simulators are mostly approximating methods (e.g., regression analysis or artificial neural networks).

Solomatine and Torres (1996) used ANN as an alternative simulator in a three-reservoir basin, with two criteria: hydropower and navigability. The main and time-consuming simulator which they used to model hydrodynamics and hydrology of the basin was MIKE-11. Thus, they trained ANN using a time-consuming model output and then solved the problem using ANN as a quick simulator. The ANN inputs included 21 sub-catchment run-offs, three releases from reservoirs, and previous week water levels, while the ANN outputs consisted of three water levels from each reservoir in each week. Aly and Peralta (1999) presented a methodology to determine an optimal strategy for pump and injection rates in a pump-and-treat aquifer clean-up problem. Because of the time-consuming simulation model, they trained a particular form of a feed-forward ANN with one hidden layer by using only 250–300 simulations carried out by the time-consuming model. After that, the prepared ANN was used instead as the main time-consuming model for calculating the proportion of maximum remaining contamination concentration in the aquifer as part of the optimization model. Johnson and Rogers (2000) examined the impact of ANN and linear approximation (LA) as an approximating method on the solution of two ground-water remediation problems using simulated annealing (SA) optimization. In their study, ANN and LA trained with 400 pre-generated patterns using a SUTRA model, and then used ANN, LA, and SUTRA separately for optimization. They concluded that the quality of the optimal solution from ANN was near that of SUTRA’s. Neeklakantan and Pundarikanthan (2000) used ANN as approximation for optimizing a large-scale reservoir operation problem. They trained an initial ANN using a time-consuming model and determined the near-optimal solution of the ANN model with a nonlinear optimization method. The near-optimal solution was used as an initial solution for an optimization with the time-consuming model for reaching a global-optimum point. They asserted that although the ANN-based simulation-optimization method needed less time for the optimization, the accuracy of the results was almost the same as with a conventional simulation-optimization method.

A significant drawback in the above-mentioned studies is the fact that all decision space parts were trained with equal accuracy. However, there is a wide range of decision space which is not important in the optimization. Thus, the approach would be more efficient if only the spaces surrounding an optimal solution were trained.

Castelletti et al. (2010) used three different approximating functions to increase the multi-objective optimization speed. They applied the proposed method in the optimization of a quality improvement plan in the Googong reservoir. They used a method called learning and planning optimization based on a response surface (LPRS). The two separate parts of the optimization, learning and planning, were carried out jointly and thus the approximating function was trained more efficiently.

Shokri et al. (2013) developed an adaptive learning ANN (ALANN) method to speed up optimization algorithms for time-consuming simulation models. The ALANN model has the capability to train an ANN for nominated parts of the decision space. In this paper, the trained ANN is used for quality simulation during the optimization process. Thus, the entire multi-objective optimization algorithm is a non-dominated sorting genetic algorithm with adaptive learning ANN (NSGAII-ALANN). This paper uses an expanded version of the simulation model CE-QUAL-W2 as a two-dimensional pollution movement model, now embedded with the capability of VOCs modeling, and a multi-objective optimization (NSGAII-ALANN) method to develop a set of non-dominated reservoir operation policies when a pollutant (MTBE) suddenly enters the Karaj reservoir.

2 MTBE Simulation

Because there is no simulation model for VOCs in surface water, we have added that capability to the existing CE-QUAL-W2 model for two-dimensional simulation of MTBE. Use of the CE-QUAL-W2 is advantageous because it is an open-source model capable of considering two-dimensional hydrodynamic simulation. Despite the advantages of CE-QUAL-W2, for generic pollution simulation only the decay factor is supported, while for VOC, volatilization plays a major role in eliminating the pollution. For this purpose, a two-film diffusion theory proposed by Lewis and Whitman (1924), that was recently applied by Heald et al. (2005), was formulated and embedded in CE-QUAL-W2. Thus, the volatilization rate can be added as a new elimination factor in the model. The volatilization rate is calculated using the equation (Heald et al. 2005):

$$ \frac{ d\varPhi}{ d t}=\frac{K_{OL}\left({\varPhi}_s-{\varPhi}_t\right)}{h} $$
(1)

in which Φ s  = saturated pollution concentration in water (10−6 g/l); Φ t  = pollution concentration in water surface (10−6 g/l) at time t; h = surface water layer thickness (m); and K OL  = total transfer velocity of VOC (cm/s), computed with the equation (Rathbun 2000):

$$ \frac{1}{K_{OL}}=\frac{1}{K_L}+\frac{R\times {T}_W}{H\times {K}_G} $$
(2)

where K L  = transfer velocity in liquid phase (cm/s) ; K G  = transfer velocity in air (cm/s); R = universal gas constant, equal to 8.2 × 10−5 (atm × m3 /mol × K); T W  = water temperature (Kelvin degrees); and H = Henry’s gas law coefficient, equal to 4 × 10−4 (atm × m3/mol). To calculate K G , four other equations are used (Hyduk and Laudie 1974; Bender et al. 2003):

$$ {K}_G={\left(\frac{D_a(VOC)}{D_a\left({H}_2O\right)}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\left(0.15{U}_w\right) $$
(3)
$$ \left(\frac{D_a(VOC)}{D_a\left({H}_2O\right)}\right)=\sqrt{\frac{M_{H_2O}}{M_{VOC}}}{\left(\frac{T_a}{293.16}\right)}^{3/2} $$
(4)
$$ {K}_L=0.45\sqrt{\frac{600{D}_L}{\nu }}{U}_W^{1.64} $$
(5)
$$ {D}_L=\frac{7.48\times {10}^{-8}\sqrt{2.26{M}_{H_{2^O}}{T}_W}}{\mu {V}_m^{0.6}} $$
(6)

where U w  = wind speed (m/s); D a (VOC), D a (H 2 O) = diffusivities of the VOC in air and water (cm2/s), respectively; \( {M}_{VOC},{M}_{H_2O}= \) molecular weight of the VOC and water (g/mol), respectively; T a  = air temperature (Kelvin degrees); ν = kinematic viscosity of water (cm/s); D L  = molecular diffusivity of the VOC in water; μ = absolute viscosity of water (g/(m.s)); and V m  = molar volume of the VOC, which for MTBE it is equal to 119 / (cm × mol).

3 Development of Optimization-Simulation Method, NSGAII-ALANN

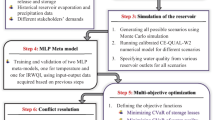
This study uses a coupled non-dominated sorting genetic algorithm (NSGAII) (Deb et al. 2002), which is a multi-objective optimization method, with MLP to form a new method called NSGAII-ALANN (Shokri et al. 2013). The latter is advantageous when solving optimization problems with a time-consuming simulator. Figure 1 shows a flowchart of the NSGAII-ALANN method. It can be seen that a hybrid simulation is used instead of a single simulator. The hybrid simulator is composed of a control part and an ANN simulator in addition to the time-consuming simulator. In this approach, whenever a solution is going to be simulated, the control part estimates the accuracy of the ANN simulation. If the accuracy of the ANN is estimated to be in an acceptable range, then the ANN is used as a quick simulator. Otherwise, the time-consuming simulator is used and simulation results are employed for retraining the ANN. In this manner, at the beginning of the optimization period, the accuracy of the ANN for the whole decision domain is less than an acceptable threshold but after a while enough solutions are simulated, and the ANN is trained in the high-use part of the decision space. Subsequently, some solutions are simulated by ANN because of the latter’s suitable accuracy. Because of the convergence of evolutionary methods toward optimal solutions, the ANN is trained near the optimal solutions, in the high-use part of the decision area, and after producing some generation, the algorithm will use ANN for simulating most of the solutions instead of the time-consuming simulator. It should be noted that, in some cases, the optimal solutions may be far apart from each other and the optimal solutions contain some discontinuous parts in the decision space. However, in those cases, the ANN can be trained appropriately for every high-used part of the decision space.

Fig. 1
figure 1

Flowchart of NSGAII-ALANN algorithm

Full size image

Because the accuracy of the ANN cannot be calculated directly, without having the main output of an input set in the control part, an index is defined to estimate the accuracy of the output only when the input set is known. This estimation should only recognize if the accuracy of the ANN is appropriate enough or not so this estimation should only answer the question as a yes or no. This index is the Euclidean distance of the solution under examination from the nth nearest solution in the ANN training data set. Thus, if the density index is less than a constant threshold, then the ANN simulation is of low accuracy. Otherwise, the ANN is recognized as an accurate simulator for the solution under examination and it can be used for the simulation of the problem under consideration. Equation (7) shows the density index used in this paper:

$$ {D}_n=\sqrt{\frac{{\displaystyle \sum_{i=1}^m{\left({x}_i-{z}_i^n\right)}^2}}{m}} $$
(7)

in which D n  = density index, which is the Euclidean distance of the n th nearest training solution that the less value shows more density; m = number of decision variables; x i  = i th decision variable; and z n i  = i th decision variable of the n th nearest training solution. It should be noted that this index does not measure the accuracy directly using the outputs (because it consumes some simulation time) and it estimates the range of accuracy (if it is good enough or not) using inputs with no simulation cost. Also, in this index n is a parameter that can be a small positive integer number. A larger n parameter needs more training points around it to exceed the threshold.

Output of all multi-objective optimization methods (including NSGAII-ALANN) is a Pareto set which contains several optimal options. All of these optimal solutions are potentially the final choice and the decision maker should choose one of them as a final solution. There are several methods that can be employed to select a final solution among the Pareto set. Young’s (1993) theory can be easily used to resolve conflicts of multi-objectives in optimal reservoir operation considering water quality issues (Shirangi et al. 2008). Karamouz et al. (2003) presented more detail about applications of multiple-criterion decision-making techniques in water quality management.

In this study, the employed ANN is a feedforward ANN and contains three hidden-layers in which every layer has 15 perceptrons. The sigmoid function (Han and Moraga 1995) is used as the perceptron activation function for all perceptrons. The employed NSGAII population is 50, maximum generation is equal to 51, selection function is tournament with size 2, and crossover function is intermediate.

4 Case Study

The Karaj dam in Iran is used to illustrate the capability of the NSGAII-ALANN algorithm. The dam, which was constructed for flood control and water supply for the cities of Tehran and Karaj and for generating hydropower on the Karaj River, is located 63 km northeast of Tehran. The area of the Karaj dam basin is about 846 km2 with an annual average inflow of 400 × 106 m3. Karaj is a two-arch dam, 180 m elevation from its foundation. The maximum area of the water in the Karaj Lake is 4 km2. The dam has two Ogee spillways (a special type of spillway with as ogee shape) with a bottom elevation of 1,757 m above sea level and one bottom outlet at 1,660 m elevation from sea level. Values of MTBE simulation parameters used in this study are: molecular weight of the MTBE (M voc ) = 88.15 g, molar, volume of the MTBE (V m ) = 119 / (cm × mol), and coefficients for degradation of MTBE (k 1 ) = 2 × 10−3 / (day).

It is assumed that an MTBE carrier with a volume of 30 m3 enters the Karaj reservoir. Based on the availability of data needed, including hygrometric and meteorological data in 2006–07, simulation and optimization are performed for those years. Four entering pollution scenarios are considered, each occurring in the first day of each season. Figure 2 shows 2006–07 water input data and the average of historical data.

Fig. 2
figure 2

Monthly variation of maximum, minimum, average and 2006–07 inflow

Full size image

Because Karaj dam is one of the most important sources of water supply for Tehran, pollution of this source will produce a crisis. Thus, it is important to develop optimal management decisions for controlling any ensuing pollution. In this study, the best reservoir operation policy will be extracted so as to control the sudden pollution entering the Karaj reservoir. Sudden-pollution damages are divided into two groups: (1) damage from unmet demands because of the low quality of the water and (2) damage from meeting demand with low-quality water, i.e., damage due to usage of low-quality water and its corresponding adverse environmental and agricultural effects or the cost of polluted water treatment. These two groups of damages are not independent of each other. Thus, for simplicity, two different objective functions are considered: quantitative and qualitative.

5 Optimization Model

Equations (8)–(14) comprise the mathematical optimization model for this problem:

$$ \begin{array}{ll} Min\hfill & {f}_1\left(X,Y\right)=a{{\displaystyle \sum_{i=1}^n\left(\frac{X_i-D{e}_i}{X_i}\right)}}^2+\left(1-a\right)\left(\frac{S_{\max }-{S}_L}{S_{\max }}\right)\hfill \end{array} $$
(8)
$$ \begin{array}{ll} Min\hfill & {f}_2\left(X,Y\right)={\displaystyle \sum_{j=1}^m{\left({M}_j\right)}^2}\hfill \end{array} $$
(9)
$$ M=h\left(X,Y\right) $$
(10)
$$ {S}_{j+1}={S}_j+{Q}_j-{X}_j^{\prime }-{Y}_j^{\prime }-S{p}_j,\kern0.5em j=1,2,\dots, m $$
(11)
$$ S{p}_j=\left\{\begin{array}{cc}\hfill 0\hfill & \hfill, \kern1em {S}_j-{X}_j^{\prime }-{Y}_j^{\prime }+{Q}_j<{S}_{max}\hfill \\ {}\hfill {S}_j-{X}_j^{\prime }-{Y}_j^{\prime }+{Q}_j-{S}_{max}\hfill & \hfill, \kern1em {S}_j-{X}_j^{\prime }-{Y}_j^{\prime }+{Q}_j\ge {S}_{max}\hfill \end{array}\right. $$
(12)
$$ {X}_i,{Y}_i\ge 0,i=1,2,\dots, n $$
(13)
$$ \begin{array}{cc}\hfill {S}_j\ge {S}_{\min}\hfill & \hfill, \kern1em j=1,2,\dots, m\hfill \end{array} $$
(14)

in which X and Y = vectors of decision variables, where X = amount of released water from the reservoir for meeting the demand and Y = amount of water used only for discharging the pollution and not used for meeting demand; X i and Y i  = members of the X and Y vectors, respectively, that show the amount of releases during i th period including several days; De i  = water demand in i th period; S n  = remaining water storage in the reservoir; f 1 and f 2 = objective functions; a = weighting ratio of first part and second parts of f 1; X ′ and Y ′ = daily water output vector corresponding to X and Y, respectively (the difference between (X , Y) and (X ′, Y ′) is in their length, the length of X and Y is equal to the number of decision variables and the length of X ′ and Y ′ is equal to the number of crisis period days, i.e., each variable may show the release in more than one day); M j  = outflow pollution mass in j th day; m = number of days in the simulation period; h(X,Y) = function used to simulate the output contamination mass vector, and in this study the CE-QUAL-W2 (Cole and Wells 2006) that is developed for simulating MTBE is used; S j  = reservoir water storage in j th day; Q j  = inflow volume in j th day; S max and S min = maximum and minimum reservoir storage capacities; and SP j  = spill volume in j th day; i, j = subscripts for decision variable and day, respectively.

6 Objective Functions

Objective functions (8) and (9) are a necessary part of optimization models which estimate the performance of each set of decision variables. Equation (8) is composed of two parts: the first part is for unmet demand in the crisis period and the second part is for the remaining water storage at the end of the crisis period. In the first part of the quantitative objective function, the summation of square unmet demand ratio is used, so severe shortages will cause more increase in the objective function. The second part of the quantitative objective function is for storing more water in the reservoir. By using these two objective functions with the aid of the developed NSGAII-ALANN, a set of non-dominated solutions (namely, Pareto solutions) will be obtained. Each point in such Pareto curves yields a solution for the multi-objective optimization problem which can be useful in a specified condition where the decision-makers’ goals or constraints need to be satisfied with a predefined value.

The qualitative objective function is equal to the summation of square pollution weight in output water in each day. In this objective function, as in the first part of the quantitative objective function, an increase in the output weight of pollution in a day will cause the gradient of the objective function to decrease. On the other hand, MTBE is a dangerous pollutant and using domestic water with a high concentration of MTBE is not permissible, so the output pollution should be treated by aeration and volatilization. Because MTBE elimination from water is expensive, an outflow pollution variable has been used in the quantitative objective function.

7 Decision Variables

Recall that a set of decision variables is composed of two parts: (1) amount of water released from the reservoir to meet demand and (2) amount of water used only for discharging the pollution and not used for meeting demand, which are separated after the release from the reservoir to channels Thus, in each interval two decision variables are available: one of them depends on the water which is allocated for meeting demands and the other is for the amount of water to discharge. The separation of variables allows the optimization model to discharge water to eliminate pollution without allocating polluted water.

The crisis period in the optimization problem is divided into eight intervals. Because of the crisis specification of this problem, the initial interval is considered shorter than other intervals. The interval duration is shown in Fig. 3. A typical change in the outlet pollution is also shown. According to this figure, the early part of the crisis period shows more varying pollution concentration than in later parts of the crisis period, so a smaller time step is needed for the early crisis period. However, the simulation time step is definitely shorter than the optimization interval. A short time step is needed for numerical simulator models to converge and the simulation steps are less than 10 min.

Fig. 3
figure 3

Optimization model interval durations

Full size image

8 Constraint and Boundary Conditions

As shown in Eq. (10), the release pollution mass vector is simulated with a developed version of the CE-QUAL-W2 or ANN simulator for simulating MTBE in the reservoir; the upstream and downstream are not taken into account. As mentioned earlier, the developed version of the CE-QUAL-W2 can simulate VOC in surface water. The inputs of the ANN which may be used instead of the CE-QUAL-W2 simulator are decision variables and the outputs are the release pollution mass vectors. Equation (11) is the continuity equation for consecutive intervals. Spill volume is calculated with Eq. (12).

9 Results

Because initial reservoir storage, demands, inputs, and meteorological parameters vary during the year, entrance of MTBE is considered in four scenarios the first day of each season and labeled S1 to S4 respectively from spring to winter. Water input and initial stored water for each scenario are depicted in Fig. 4. For all scenarios except S1, input water is less than output water. Notice that during the spring, water is stored while in other times the stored water is used. According to Fig. 4a, in S1 scenario the difference between summation of input water and output water is 132 × 106 m3. However, initial storage capacity in S1 scenario is only 107 × 106 m3 less than the maximum capacity of the reservoir. Thus, in this scenario, 25 × 106 m3 extra water is available, which will overflow after filling the dam.

Fig. 4
figure 4

Daily inflow variation and initial water storage in scenarios a S1, b S2, c S3, and d S4

Full size image

The a factor that is used in the quantitative objective function [Eq. (8)] is important in the optimization and the extracted Pareto sets. This factor shows the importance of the first part of the objective function compared to the second part. Thus, each scenario is solved with three different states with different a factors which are 75 %, 50 %, and 25 % referred to as 75, 50, and 25 states, respectively. That is, the optimization model is solved by considering four scenarios and each scenario in three states, giving a total of 12 different optimization problems.

The optimizations are done with the NSGAII-ALANN method, with various thresholds for the density index in four different scenarios. The NSGAIIs are implemented using 51 generations and a population number of 50. Table 1 shows the run-time, number of CE-QUAL-W2 simulations, number of ANN simulations, and number of retraining for each scenario for different thresholds. According to Table 1, an increase in the threshold leads to more ANN simulations, less retraining processes, and thus less run-time. For instance, for threshold 3 and scenario S1 only about ¼ of simulations are performed with the time-consuming simulator (CE-QUAL-W2) and the remaining ¾ simulations are performed with ANN. Finally, for further assessment, only the optimization with threshold 3 is discussed next.

Table 1 Run-time, number of CE-QUAL-W2 simulations, number of ANN simulations, and number of retraining
Full size table

The extracted Pareto front includes many decision variable sets and the best choice could be chosen by the reservoir manager. In this paper, the set of optimal decision variables is chosen using Young’s conflict resolution method (Young 1993). The selected point contains a complete set of all decision variables which can be presented as the optimal solution and it is referred to as the “selected policy” herein. In this regard, output concentration, water release, and output pollution rate for the selected policy are depicted in Fig. 5 in addition to the Pareto front for Scenario S1.

Fig. 5
figure 5

1st row the extracted Pareto fronts and selected solutions, 2nd row the MTBE concentration variation for the different policies, 3rd row releases from the reservoir and allocated water for the “selected policy” and demand variation during the crisis period, 4th row the output pollution rate corresponding to each release. Columns from left to right show states 25, 50, and 75, respectively

Full size image

First-row diagrams in Fig. 5a, b and c show the extracted Pareto fronts for various a factors and solutions specified with a circle are the selected solutions, chosen with Young’s (1993) method, where each point in each Pareto is a non-dominated solution. The second row in Fig. 5d, e and f show the MTBE concentration variation for the following three policies: (1) no management policy, in which there is no attention to the pollution and the water is released only for meeting demands completely. In most of the extracted Pareto fronts this policy is the top left point, the only exception is state 25 of Scenario S3. In this case, because of the low importance of meeting demand and the high amount of unfilled storage capacity, all the solutions recommend storing water and not releasing it; (2) selected policy, which is selected from the Pareto specified via a circle and chosen with Young’s method; and (3) no release policy, in which the gate is closed and there is no water released downstream. In all the optimizations, this policy is indicated by the bottom right point of the Pareto.

In Fig. 5g, h and i, releases from the reservoir and allocated water are shown for the “selected policy,” depicting demand variation during the crisis period and the final reservoir storage. In this study, the water released from the reservoir includes (1) the allocated water and (2) the water that is released for discharging the pollution and not allocated to any demand. Thus, in these figures, the difference between allocated and released water shows the amount of water that is released but does not meet any part of demand and it is released to discharge water and pollution. Figure 5j, k and l depict the output pollution rate corresponding to each release. Columns in Fig. 5 from left to right show states 25, 50, and 75, respectively.

In Fig. 5d, e and f, the variation in concentration shows that after a decrease in the reservoir pollution, the pollutant concentration in the released water increases in a short period and decreases after reaching the peak concentration. The duration of the increase in pollution concentration is an important factor in reservoir management because the longer the period of pollution concentration increases (reaching the peak pollution), the more alert time for the reservoir operator to improve the operation of the reservoir. Also, the value of the peak pollution concentration is another important factor for decision-makers to be ready if such a condition occurs and try to supply non-polluted water from other sources or even neighboring basins. As it is apparent in Fig. 5d, e and f, although the ascending part of the diagram is similar in different operational policies, in various scenarios presented in different diagrams, differences between maximum concentrations and ascending period lengths are observed. Table 2 shows specification of the ascending part of different scenarios. It should be noted that because of the similarity among states (25, 50, and 75) and also among different policies, the content of this table compares the maximum concentration and ascending period lengths for various scenarios.

Table 2 Duration and maximum concentration of various scenarios
Full size table

According to Table 2, Scenario S1, the duration of the pollution increase is about 12 days and the maximum pollutant concentration is between 90 and 106 mg/l (this slight variation is due to the assumption of different policies). However, in other scenarios the duration of the pollution increase is about 2–6 days, with a concentration higher than in Scenario S1. As a result, Scenario S1 is less hazardous than other scenarios in terms of pollutant duration and maximum concentration. For example, in Scenario S1, an increase in water release causes a decrease in the descending duration in concentration. In Scenario S4, the descending graph is similar to that of other scenarios. The extra available water in Scenario S1 causes the pollution washout but in other scenarios there is less release compared to S1 and this causes the similar pollution concentration output. Another considerable point in the descending part of the concentration graphs is the duration of descending time. In the S2 and S3 scenarios, the descending speeds are very high and in the S1 and S4 scenarios descending speeds are low.

Figure 5g, h and i depict water releases from the reservoir for various policies. Because of the availability of extra stored water in Scenario S1, a high amount of water is released for washout of the pollution. However, in the “selected policy” of other scenarios, less water is released for pollution washout. It should be noted that by decreasing the importance of meeting demand (a factor), water releases decrease and water stored at the end of the crisis period increases.

In the “selected policy” for all scenarios, allocated percentage of demands at the beginning and end of crisis periods in more than in the middle of those periods. In other words, in middle intervals because of high pollution concentration, less water is allocated to meet municipal demand. As depicted in the “selected policy” of Fig. 5j, k and l, the rate output pollution is distributed uniformly. Generally, the released pollution can be considered in terms of: (1) the total mass of allocated pollution which is costly to treat it before use, and (2) the peak of released pollution, because of the limited maximum capacity of treatment plants. A discussion on these two terms is presented next.

Table 3 illustrates further assessment of the weight of released, allocated, and maximum rate of pollution for various states and scenarios. For the “selected policy” shown in the table, the pollution release weight and maximum output pollution rates are considerably less than in the “no management policy,” but a decrease in the pollution causes a decrease in the demand water allocation.

Table 3 Weight of released, allocated, and maximum rate of pollution for various states of various scenarios
Full size table

There are four factors that play a fundamental role in decreasing the pollutant concentration in outlets: (1) volatilization, (2) decay, (3) pollution release, and (4) mixing. According to Table 3, it is clear that from 30 m3 of input MTBE, less than half of that input is released and no MTBE remains in the reservoir. Most of the entering MTBE is decayed or volatilized.

Table 4 shows the percentage of decrease in allocated water, released pollution mass, and the peak of allocated pollution. For example, in state 75 of Scenario S2, using the “selected policy” yields a 36 % decrease in water allocation, 60 % allocated pollution, and 76 % maximum output rate compared to the “no management policy.” In other states and scenarios, similar results are achieved except in state 25 of Scenario S3 in which the released water volume in all extracted policies is nearly zero and water preservation is proposed because of the high unfilled reservoir storage capacity and low importance of meeting demand compared to storing water.

Table 4 Percentage of decrease in allocated water and pollution and the maximum of allocated pollution
Full size table

10 Discussion

Input of abrupt pollution into water resources in general and into surface reservoirs in particular is possible and creates a serious crisis for water-supplying systems. In such conditions, decision-makers and reservoir operators should be concerned with reservoir operation policies that would prevent the crisis. Because operation policies should be designed for a particular condition and there is a huge number of possible conditions for a crisis to occur, it is not possible to make a policy for every possible condition. Thus, application of the proposed method for a real-world problem should yield policies for conditions covering a wide range of important parameters such as size and type of pollution, place and season of pollution entrance, reservoir storage and input discharge, and so forth. If in the future any similar event occurs, then the type of policy that should be used could be extracted from a previously prepared data base. Also, these conditions may not occur in the future but in a crisis condition, an optimal policy for a similar condition may be useful to reduce the vulnerability of the system. Those policies can be obtained by preliminary studies with the aim of multi-objective optimization analysis.

For the aforementioned analysis, water quality simulators are needed that simulate the pollution and solve the governing quality equations with analytical solvers. Because such governing equations are mostly differential equations, the execution time of such simulators is high. CE-QUAL-W2 is one of the simulation packages in this field that can consider almost all aspects of water quality decay processes except volatilization, which is an important process in MTBE pollution and a probable occurrence in a surface reservoir.

Moreover, addressing water quality issues with evolutionary optimization techniques requires extensive running of simulation models. To overcome the weakness of such models, a new algorithm is needed that makes possible the analysis in a shorter time. In this paper, a multi-objective optimization algorithm (NSGAII) was linked to the CE-QUAL-W2 simulation package. To facilitate the MTBE simulation by this package, volatilization equations were inserted into the CE-QUAL-W2. However, the combination of NSGAII and CE-QUAL-W2 needed considerable time to converge to an optimal solution. Thus, an ANN model was linked to the aforementioned combination to be activated for some simulation alternatives instead of CE-QUAL-W2. The process of training the ANN was planned to be conducted in each new simulation after CE-QUAL-W2 simulations and by an adaptive learning process. Thus the whole algorithm was named NSGAII-ALANN.

The NSGAII-ALANN algorithm was developed and applied to the Karaj Dam in Iran due to the latter’s importance and its key role in meeting Tehran and Karaj domestic water demands. It was necessary to obtain the best operation policy so as to achieve minimum damages in the abrupt crisis of VOCs, and especially MTBE. The multi-objective optimization, denoting the importance of quantity and quality issues, was conducted by considering four scenarios consisting of entering pollution at the beginning of each season, and for three states in each season. Thus 12 different multi-objective optimizations were conducted.

As it is noted in the results section, three different states show different weights for the final remaining water after a critical situation. Since the range of these weights can be between 0 and 1, weights 0.25, 0.5, and 0.75 are chosen to create state 25, state 50, and state75 respectively.

By comparing the results for different scenarios (Table 4), it can be concluded that the efficiency of the management strategies (the ratio of decrease in meeting demands and decrease in allocation pollution and maximum pollution rate) in different scenarios are similar, but in the 3rd scenario it is slightly higher.

The resulting solutions formed a set of solutions named Pareto. Each point in a Pareto denotes a set of decision operation valuables (operational policy) that can be used or applied in a specific situation. To compare decisions in all 12 runs, a point among Pareto fronts was selected and nominated by the Young (1993) conflict resolution method and named “selected policy.” As shown in Fig. 5, the objective functions of left extreme solutions are almost (0,7) respectively for first and second objectives for all states and the objective functions of the right extreme solutions are (0.25,0), (0.5,0), and (0.75,0) respectively for state 25, state 50, and state 75. The Pareto shape in all Paretos is partly linear, meaning that by decreasing the value of one objective function, the rate of increase of the other objective function is constant, indicating that the decision-making procedure is not highly sensitive to the selected objective.

11 Concluding Remarks

Based on results obtained, if MTBE enters the reservoir in the spring, an increase in concentration takes longer time than in other scenarios. Thus, crisis management in the summer, fall, and winter should be done more quickly than in the spring. On the other hand, the maximum outputs when MTBE enters the reservoir in the spring are less than in other seasons so the crisis in the other seasons will be more severe.

Table 4 showed how the use of the “selected policy” in different states of various scenarios affected the percentage of meeting demand, summation of allocated pollution, and maximum rate. For example, use of the “selected policy” in state 75 in Scenario S2 had a 36 % decrease in meeting demand while summation of allocated pollution and maximum rate decreased 60 % and 76 %, respectively. Other states of other scenarios showed similar performances. Thus, by decreasing a smaller percentage of met demand, a larger decrease was observed in the summation of allocated and maximum rate of pollution. Only in state 25 of Scenario S3 the released water volume in all extracted policies was nearly zero and water preservation was proposed because of the high unfilled reservoir storage capacity and the low importance of meeting demand compared to storing water.