1 Introduction

Irrigation planning problem is constructed in the form of Linear Programming model, with a number of objective functions and set of constraints. Dealing with a single objective, does not fulfill the different needs of farmers of the region. In irrigation planning problem some of the multiple objectives may conflict with one another (Vedula and Mujumdar 2005). In case of multiple objective analysis, single optimal solutions do not yield, but which are more useful for the determination of the trade-offs among noncommensurable objectives. The crop production study, which provides the maximum net benefits, is not likely to create the highest employment of labour, nor may it produce the maximum yield or returns in terms of foreign exchange from agricultural exports. Focusing on the case of developing countries these objectives may be more important than maximization of net benefits only (Loucks et al. 1981). Decisions relating to most of the irrigation planning problems need to be made in the face of hydrologic uncertainty. The uncertainty makes the irrigation planning problem more complex. The irrigation production planning generally depends on different parameters such as weather, rainfall, temperature, market situation and availability of resources. These parameters cannot be easily quantified and most of the times are not fully controllable. These parameters can be recognized as common source of uncertainty. While dealing with the irrigation planning and development, the input data and other parameters such as resources, cost and demand are also imprecise because some information is incomplete or unobtainable such as inflows, crop yield, crop prices, labour demand, manure utilization etc. The concept of fuzzy set is considered as an alternative to deal with vagueness with multiple objectives and imprecision involved in the parameter values. Labadie (2004) presented a review of the computer modeling tools in order to decide policies on operations of reservoirs especially under conditions of uncertainty occurring due to the randomness observed in natural phenomena. Suresh and Mujumdar (2004) have developed a model for fuzzy risk of low yield of a crop, that serves as a performance indicator for developing a reservoir operating policy and have successfully applied it to the case of Malaprabha reservoir project in Krishna basin in the State of Karnataka, India. There have been researches and studies wherein the fuzzy programming has been successfully applied in the development of reservoir operating policies to the optimal operation of single reservoir as well as to the operation of multi reservoirs (Shrestha et al. 1996; Fontane et al. 1997; Panigrahi and Mujumdar 2000; Dubrovin et al. 2002; Timant et al. 2002; Mousavi et al. 2004; Mohan and Prasad 2006; Abolpour and Javan 2007). Anand Raj and Nagesh Kumar (1998, 1999) successfully developed and employed the new method of ranking in order to rank fuzzy alternatives along with their total utility value. Raju and Nagesh Kumar (2000a) have given forth through their study a FLP for three conflicting objectives in case of Sri Ram Sagar project in Andhra Pradesh, India. Raju and Nagesh Kumar (2000b) have developed Linear Programming (LP) irrigation planning model for evaluation of irrigation development strategy for the case study of Sri Ram Sagar project, in Andhra Pradesh of India.

On the other hand, Mujumdar (2002) took up review of some noted mathematical tools and techniques of fuzzy optimization and fuzzy inference system for irrigation system operation, crop water allocation, and performance evaluation. Gasimov and Yenilmez (2002) have succeeded in developing a methodology for dealing with problems encountered in fuzzy linear programming and effectively used the same to solve the numerical example with fuzzy numbers. Sethi et al. (2002) have developed an optimization model to find out the optimal cropping pattern and area allocation in relation with availability of water resources for different seasons. Raju and Duckstein (2003) attempted to develop the MOFLP model for planning sustainable irrigation considering fuzzy objectives and have pointed out many advantages of the FLP compared with other methods of multi-objective optimization such as Constraint and Weighting methods. For planning irrigation, Raju and Nagesh Kumar (2005) have come out with Fuzzy Decision System that is based on two fuzzy logic based MCDM Methods viz. Similarity Analysis (SA) and Decision Analysis (DA).

Tsakiris and Spiliotis (2006) came out with a Goal Programming (GP) approach using the fuzzy set theory to find out the cropping pattern for Thessaly Plain in Greece. Sahoo et al. (2006) have brought out their linear programming and fuzzy optimization models for three conflicting objectives for planning irrigation in the Mahanadi-Kathajodi delta in eastern India wherein a compromised solution was worked out for the objectives viz. Maximization of Net Return, Crop Production and Minimization of Labour. Arikan and Gungor (2007) developed two-phase approach with the involvement of DM for solving the MOFLP problems by using the advantages and at the same time overcoming the disadvantages of FLP. Jimenez et al. (2007) dealt with LP problems with various parameters as fuzzy numbers but whose decision variables are crisp and developed an interactive method for solving linear programming with fuzzy numbers. Regulwar and Anand Raj (2008, 2009) developed a monthly Multi Objective Genetic Algorithm Fuzzy Optimization model, which was applied to a multi-reservoir system in Godavari river sub-basin in the State of Maharashtra, India. 3-D optimal surface was proposed for determining operation polices. Regulwar and Gurav (2010) presented the MOFLP model for taking decisions with regard to planning of irrigation under conflicting situations with fuzzy objectives.

From the literature, it shows that fuzzy logic has invariably been made use of whether or not the objectives were fuzzy or were with resources and so far no one has reported the formulation and application of MOFLP for the planning of irrigation made with the help of fuzzy objective function coefficients, fuzzy technological coefficients, and fuzzy resources. The present MOFLP approach takes into consideration all these coefficients in a mathematical model as fuzzy as one finds in a real life. Five strategies are considered in the present study. Considering one or more fuzzy decision parameters in the irrigation planning model, it is classified as strategy-I to V. The objective of this paper is to develop and apply Fuzzy Parametric Programming (FPP) based MOFLP model in sustainable irrigation planning for Jayakwadi Project Stage-I, Maharashtra State, India. The developed MOFLP model (Strategy-V) includes the fuzzy objective function coefficients, fuzzy technological coefficients and fuzzy resources/stipulations simultaneously. The objective of the present MOFLP irrigation planning model is to find out an optimal cropping pattern that maximizes simultaneously the Net Benefits (NB), Crop Production (CP), Employment Generation (EG) and Manure Utilization (MU). All four objectives are to be maximized and the last three are related to sustainability.

2 Model Development and Methodology

The objective of the present study is to find optimal cropping pattern for the 75 % dependable inflow. The problem has been formulated as an optimization model based on deterministic inflows. In the formulation of the problem, various assumptions have been made: Crops are considered to be grown throughout the year. The irrigation intensity adopted is 22 % in Kharif season, 45 % in Rabi season and 28 % in Two Seasonal, Hot Weather crop 3 %; Perennial 4.5 % of the total command area and that becomes a total irrigation intensity of 102.5 %. Ground water usage is not considered in the command area. Only surface water has been considered for irrigation. The soil of the study area is considered homogeneous in nature. Various relationships within the models are based on the framework of linearity. Same management practice has been applied for a particular crop event under each land and hence, the CP, NB, EG and MU under particular crop activity is treated as constant. The duration and timings of the cropping activity are considered as constant and do not vary over the years. There are three seasons for growing crops (viz. Kharif, Rabi, and Two Seasonal). Under certain overlapping situations, care is taken of by adding specific constraints. The input cost for each crop is considered as 20 percent of the total gross benefits to be gained.

2.1 Description of the Study Area

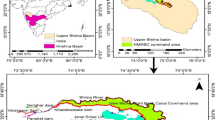
The lower Godavari River Basin, Maharashtra State, India is taken for present study. The Jayakwadi Project Stage-I is located across the eastward flowing river Godavari. The salient features of the Jayakwadi Project Stage-I are presented in Table 1. From the soil survey report, it is seen that near the canal alignment, the soils are shallow, consisting of a thin mantle of soil over the murum stratum. The area adjoining the Godavari River and its major tributaries are deep silt and black soils. The condition of remaining areas lies in between the above two kinds of soil. Figure 1 shows index map of Jayakwadi Project, Maharashtra State, India.

Table 1 Salient features of the Jayakwadi project stage-I
Full size table
Fig. 1
figure 1

Index map of Maharashtra State, India

Full size image

2.2 Model Development

The four objectives are considered in the present study.

2.2.1 Maximization of Net Benefits (NB)

The decision maker will try to maximize the net benefits. The net benefits coefficients from the irrigated area under various crops are obtained by subtracting the input cost (20 % of gross benefit) from gross benefit for different crops. The Gross benefits are calculated by multiplying the average yield of a crop per ha and current market price of that crop. The objective function for maximization of net benefits can be expressed as

$$ \matrix{ {Maximize\;NB = \left[ {\left( {\sum\limits_{{i = 1}}^2 {A_i^KBC_i^K + \sum\limits_{{i = 1}}^3 {A_i^RBC_i^R + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}BC_i^{{TS}} + \sum\limits_{{i = 1}}^2 {A_i^PBC_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}BC_i^{{HW}}} } } } } } \right)} \right.} \\ {\left. { - \left( {\sum\limits_{{i = 1}}^2 {A_i^KIC_i^K + \sum\limits_{{i = 1}}^3 {A_i^RIC_i^R + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}IC_i^{{TS}} + \sum\limits_{{i = 1}}^2 {A_i^PIC_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}IC_i^{{HW}}} } } } } } \right)} \right]} \\ }<!end array> $$
(1)

[In which i = crop index. 1 = Sugarcane (Perennial), 2 = Banana (Perennial), 3 = Chillies (Two Seasonal), 4 = L S Cotton (Two Seasonal), 5 = Sorghum (Kharif), 6 = Paddy (Kharif), 7 = Sorghum (Rabi), 8 = Wheat (Rabi), 9 = Gram (Rabi) and 10 = Groundnut (Hot Weather)]

$$ \matrix{ {A_i^K = {\text{Area}}\;{\text{of}}\;{{\text{i}}^{\text{th}}}\;{\text{crop}}\;{\text{in}}\;{\text{Kharif}}\;{\text{season}}\;{\text{in}}\;{\text{ha}};} \hfill &{A_i^R = {\text{Area}}\;{\text{of}}\;{i^{{th}}}\;{\text{crop}}\;{\text{in}}\;{\text{Rabi}}\;{\text{season}}\;{\text{in}}\;{\text{ha}};} \hfill \\ {A_i^{{HW}}{\text{ = Area}}\;{\text{under}}\;{\text{Hot}}\;{\text{Weather}}\;{\text{crop}}\;{\text{in}}\;{\text{ha}};} \hfill &{A_i^P = {\text{Area}}\;{\text{under}}\;{\text{Perennial}}\;{\text{crop\,in}}\;{\text{ha}};} \hfill \\ {A_i^{{TS}} = {\text{Area\,under}}\;{\text{Two}}\;{\text{Seasonal}}\;{\text{crop}}\;{\text{in}}\;{\text{ha}};} \hfill &{B{C_i} = {\text{Benefit}}\;{\text{coefficient}}\;{\text{for}}\;{i^{{th}}}\;{\text{crop}};} \hfill \\ {I{C_i} = {\text{Input}}\;{\text{cost}}\;{\text{for}}\;{i^{{th}}}\;{\text{crop}};} \hfill &{K = {\text{Kharif}};} \hfill \\ {P = {\text{Perennial}};} \hfill &{R = {\text{Rabi}};} \hfill \\ {TS = {\text{Two}}\;{\text{Seasonal}};} \hfill &{HW = {\text{Hot}}\;{\text{Weather}};} \hfill \\ }<!end array> $$

2.2.2 Maximization of Crop Production (CP)

The decision maker will try to maximize the crop production. The crop production coefficients are taken as the average yield of a crop per ha. (Commissionerate of Agriculture Maharashtra State, Agricultural Statistical Information Maharashtra State, India part-II 2006). The objective function for maximization of crop production can be written as

$$ Maximize\;\left( {CP} \right) = \left[ {\left( {\sum\limits_{{i = 1}}^2 {A_i^KAY_i^K + \sum\limits_{{i = 1}}^3 {A_i^RAY_i^R + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}AY_i^{{TS}} + \sum\limits_{{i = 1}}^2 {A_i^PAY_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}AY_i^{{HW}}} } } } } } \right)} \right] $$
(2)

AY i = Average yield of i th crop (Tons per ha);

In case of second objective i.e. Maximization of Crop Production is thought of from keeping the food sufficiency in the region. At least survival of people of region can only be thought of if sufficient food is available. By considering this aspect, the second objective is sustainability related.

2.2.3 Maximization of Employment Generation (EG)

Keeping in mind the socio-economic development, the decision maker (DM) has to concentrate on the maximization of employment generation.

$$ Maximize\;\left( {EG} \right) = \left[ {\left( {\sum\limits_{{i = 1}}^2 {A_i^KRMD_i^K + \sum\limits_{{i = 1}}^3 {A_i^RRMD_i^R + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}RMD_i^{{TS}} + \sum\limits_{{i = 1}}^2 {A_i^PRMD_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}RMD_i^{{HW}}} } } } } } \right)} \right] $$
(3)

RMD i = Requirement of Man Days for i th crop per ha;

The labour requirement or number of Man Days (MD) for a particular crop per ha are arrived at by discussions with farmers and experts from agricultural field.

In case of third objective i.e. Maximization of Employment Generation is thought from the socio-economic point of view. In developing country like India, the distribution of agricultural land is uneven. Most of people they do not have their own land to cultivate and they can think of themselves in the form of labour to avail bread and butter for their survival. The irrigation policy maker has to think from employment generation point of view for sustainability in case social and economical aspects. Due to these reasons, the third objective is related to sustainability.

2.2.4 Maximization of Manure Utilization (MU)

In order to maintain the fertility and nutrient sufficiency of soil in proper manner, decision maker should concentrate on maximization of utilization of manures.

$$ Maximize\;\left( {MU} \right) = \left[ {\left( {\sum\limits_{{i = 1}}^2 {A_i^KRMU_i^K + \sum\limits_{{i = 1}}^3 {A_i^RRMU_i^R + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}RMU_i^{{TS}} + \sum\limits_{{i = 1}}^2 {A_i^PRMU_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}RMU_I^{{HW}}} } } } } } \right)} \right] $$
(4)

RMU i = Requirement of Manure Utilization in tons for i th crop per ha;

The Requirement of Manure Utilization (RMU) for a crop per ha is arrived by discussion with farmers and experts from agricultural field.

In case of the fourth objective i.e. maximization of Manure Utilization, green manure is prepared by the farmer by decomposing the waste from the farming activity and waste from the live stock activities. This does not include any harmful chemicals, fertilizers and pesticides. This kind of manure will help to maintain nutrients sufficiency of soil for various crops. Now a day due to excessive use of fertilizers and chemicals, the soil is loosing its own ability to supply nutrients. Hence, it is tried to incorporate the Manure Utilization as related to sustainability.

2.3 Constraints

2.3.1 Total Sowing Area Constraint

The total area constraint, for various crops, for the present study, is considered in order to take care of the total area available for cultivation in command area during different crop seasons. The total sowing area constraint is given by the equation,

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^K + \sum\limits_{{i = 1}}^3 {A_i^R + \sum\limits_{{i = 1}}^2 {A_i^{{TS}} + \sum\limits_{{i = 1}}^2 {A_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}} } } } } } \right) \leqslant CA $$
(5)

CA = Total command area;

Maximum Sowing Area Constraint (According to the existing cropping Pattern)

The maximum sowing area constraint for various crops is defined, to account for maximum sowing area available for cultivation during various crop seasons according to existing cropping pattern of the project. The maximum sowing area constraint is given by,

Kharif

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^P} + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}} + \sum\limits_{{i = 1}}^2 {A_i^K} } \right) \leqslant CA_i^P + CA_i^{{TS}} + CA_i^K $$
(6)

Rabi

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^P} + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}} + \sum\limits_{{i = 1}}^3 {A_i^R} } \right) \leqslant CA_i^P + CA_i^{{TS}} + CA_i^R $$
(7)

Hot Weather and Perennial

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}} } } \right) \leqslant CA_i^P + CA_i^{{HW}} $$
(8)

\( CA_i^K \) = Command area for kharif season for i th crop in ha;

\( CA_i^R \) = Command area for rabi season for i th crop in ha;

\( CA_i^{{HW}} \) = Command area under hot weather crop in ha;

\( CA_i^P \) = Command area under perennial crop in ha;

2.3.2 Affinity Constraint

The farmers of the region have a tendency to grow cash crops and other crops according to their interest and benefits. To safeguard the interest of the food requirement of the region according to the storage capacity of the reservoir, the following limitation (upper limit using the existing cropping pattern) for various crops are incorporated as constraints,

Perennial

$$ \matrix{ {A_1^P \leqslant CA_i^P} \hfill \\ {A_1^P{\text{ = Area}}\;{\text{under}}\;{\text{perennial}}\;{\text{crop}}\;{\text{Sugarcane}}} \hfill \\ }<!end array> $$
(9a)
$$ \matrix{ {A_2^P \leqslant CA_i^P} \hfill \\ {A_2^P{\text{ = Area}}\;{\text{under}}\;{\text{perennial}}\;{\text{crop}}\;{\text{Banana}}} \hfill \\ }<!end array> $$
(9b)

Two Seasonal

$$ \matrix{ {A_3^{{TS}} \leqslant CA_i^{{TS}}} \hfill \\ {A_3^{{TS}}{\text{ = Area}}\;{\text{under}}\;{\text{two}}\;{\text{seasonal}}\;{\text{crop}}\;{\text{Chillies}}} \hfill \\ }<!end array> $$
(9c)
$$ \matrix{ {A_4^{{TS}} \leqslant CA_i^{{TS}}} \hfill \\ {A_4^{{TS}}{\text{ = Area}}\;{\text{under}}\;{\text{two}}\;{\text{seasonal}}\;{\text{crop}}\;{\text{L}}\;{\text{S}}\;{\text{Cotton}}} \hfill \\ }<!end array> $$
(9d)

Kharif

$$ \matrix{ {A_5^K \leqslant CA_i^K} \hfill \\ {A_5^K{\text{ = Area}}\;{\text{under}}\;{\text{kharif}}\;{\text{crop}}\;{\text{Sorghum}}} \hfill \\ }<!end array> $$
(9e)
$$ \matrix{ {A_6^K \leqslant CA_i^K} \hfill \\ {A_6^K{\text{ = Area}}\;{\text{under}}\;{\text{kharif}}\;{\text{crop}}\;{\text{Paddy}}} \hfill \\ }<!end array> $$
(9f)

Rabi

$$ \matrix{ {A_7^R \leqslant CA_i^R} \hfill \\ {A_7^R = {\text{Area under}}\;{\text{rabi}}\;{\text{crop}}\;{\text{Sorghum}}} \hfill \\ }<!end array> $$
(9g)
$$ \matrix{ {A_8^R \leqslant CA_i^R} \hfill \\ {A_8^R = {\text{Area}}\;{\text{under}}\;{\text{rabi}}\;{\text{crop}}\;{\text{Wheat}}} \hfill \\ }<!end array> $$
(9h)
$$ \matrix{ {A_9^R \leqslant CA_i^R} \hfill \\ {A_9^R = {\text{Area}}\;{\text{under}}\;{\text{rabi}}\;{\text{crop}}\;{\text{Gram}}} \hfill \\ }<!end array> $$
(9i)

Hot Weather

$$ \matrix{ {A_{{10}}^{{HW}} \leqslant CA_i^{{HW}}} \hfill \\ {A_{{10}}^{{HW}} = {\text{Area}}\;{\text{under}}\;{\text{hot}}\;{\text{weather}}\;{\text{crop}}\;{\text{Groundnut}}} \hfill \\ }<!end array> $$
(9j)

2.3.3 Labour Availability Constraint

Refereeing to the problem of unavailability of labour during farming season it is suggested that to tackle the problem of uncertainty of availability of labour, the labour requirement should not exceed the total labour availability during that interval,

Kharif

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^PRMD}_i^P + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}RMD_i^{{TS}}} + \sum\limits_{{i = 1}}^2 {A_i^KRMD_i^K} } \right) \leqslant \sum\limits_{{i = 1}}^2 {LA_i^P + } \sum\limits_{{i = 1}}^2 {LA_i^{{TS}} + } \sum\limits_{{i = 1}}^2 {LA_i^K} $$
(10)

Rabi

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^PRMD}_i^P + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}RMD_i^{{TS}}} + \sum\limits_{{i = 1}}^3 {A_i^RRMD_i^R} } \right) \leqslant \sum\limits_{{i = 1}}^2 {LA_i^P + } \sum\limits_{{i = 1}}^2 {LA_i^{{TS}} + } \sum\limits_{{i = 1}}^3 {LA_i^R} $$
(11)

Perennial and Hot Weather

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^PRMD}_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}RMD_i^{{HW}}} } \right) \leqslant \sum\limits_{{i = 1}}^2 {LA_i^P + } \sum\limits_{{i = 1}}^1 {LA_i^{{HW}}} $$
(12)

LA i = Labour availability for i th crop;

RMD i = Requirement of Man Days for i th crop per ha;

2.3.4 Manure Availability Constraint

Referring to the scarcity of manure, which is needed to ensure the fertility of soil, it is suggested that in order to maintain fertility of the soil, the total manure requirement should not exceed the total availability of the manure in that season.

Kharif

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^PRMU}_i^P + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}RMU_i^{{TS}}} + \sum\limits_{{i = 1}}^2 {A_i^KRMU_i^K} } \right) \leqslant \sum\limits_{{i = 1}}^2 {MA_i^P + } \sum\limits_{{i = 1}}^2 {MA_i^{{TS}} + } \sum\limits_{{i = 1}}^2 {MA_i^K} $$
(13)

Rabi

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^PRMU}_i^P + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}RMU_i^{{TS}}} + \sum\limits_{{i = 1}}^3 {A_i^RRMU_i^R} } \right) \leqslant \sum\limits_{{i = 1}}^2 {MA_i^P + } \sum\limits_{{i = 1}}^2 {MA_i^{{TS}} + } \sum\limits_{{i = 1}}^3 {MA_i^R} $$
(14)

Perennial and Hot Weather

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^PRMU}_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}RMU_i^{{HW}}} } \right) \leqslant \sum\limits_{{i = 1}}^2 {MA_i^P + } \sum\limits_{{i = 1}}^1 {MA_i^{{HW}}} $$
(15)

MA i = Manure availability for i th crop;

RMU i = Requirement of Manure Utilization for i th crop per ha;

2.3.5 Water Availability Constraint

The total water requirement of different crops should not exceed the total water availability in the reservoir,

$$ \left( {\sum\limits_{{i = 1}}^2 {A_i^KIWR_i^K + \sum\limits_{{i = 1}}^3 {A_i^RIWR_i^R + \sum\limits_{{i = 1}}^2 {A_i^{{TS}}IWR_i^{{TS}} + \sum\limits_{{i = 1}}^2 {A_i^PIWR_i^P + \sum\limits_{{i = 1}}^1 {A_i^{{HW}}IWR_i^{{HW}}} } } } } } \right) \leqslant TWA_i^j $$
(16)

j = 1,2,3,4,5. (No of crop Seasons)

IWR i = Irrigation water requirement (m) for i th crop;

\( TWA_i^j \) = Total water availability for i th crop (all crops) for j th interval (all seasons);

2.3.6 Non Negativity Constraint

$$ \begin{array}{*{20}{c}} {A_{i}^{K},A_{i}^{R},A_{i}^{{TS}},A_{i}^{P},A_{i}^{{HW}},A{{Y}_{i}},M{{D}_{i}},M{{U}_{i}},CA,CA_{i}^{K},CA_{i}^{R},CA_{i}^{P},CA_{i}^{{TS}},CA_{i}^{{HW}},LA_{i}^{P},LA_{i}^{{TS}},LA_{i}^{K},LA_{i}^{R},LA_{i}^{{HW}},MA_{i}^{P},MA_{i}^{{TS}},MA_{i}^{K},MA_{i}^{R},MA_{i}^{{HW}},} \hfill \\ {RMD_{i}^{P},RMD_{i}^{{TS}},RMD_{i}^{K},RMD_{i}^{R},RMD_{i}^{{HW}},LA_{i}^{P},LA_{i}^{{TS}},LA_{i}^{K},LA_{i}^{R},LA_{i}^{{HW}},RMU_{i}^{P},RMU_{i}^{{TS}},RMU_{i}^{K},RMU_{i}^{R},RMU_{i}^{{HW}},MA_{i}^{P},MA_{i}^{{TS}},MA_{i}^{K},MA_{i}^{R},} \hfill \\ {MA_{i}^{{HW}},IWR_{i}^{P},IWR_{i}^{{TS}},IWR_{i}^{K},IWR_{i}^{R},IWR_{i}^{{HW}},TWA_{i}^{j} \geqslant 0\quad \forall i,j} \hfill \\ \end{array} $$
(17)

2.4 Fuzzy Linear Programming Problem with all Parameters Fuzzy

Brief description of fuzzy objective function coefficients, fuzzy technological coefficients and fuzzy resources of the proposed FLP model is as given below:

$$ \begin{array}{*{20}{c}} {\max = \sum\limits_{{j = 1}}^{n} {{{{\widetilde{c}}}_{j}}{{x}_{j}}} } \hfill \\ {s.t.\quad \:\:\sum\limits_{{j = 1}}^{n} {{{{\widetilde{a}}}_{{ij}}}{{x}_{j}} \leqslant {{{\widetilde{b}}}_{i}},\:\left( {i \in {{\mathbb{N}}_{m}}} \right)} } \hfill \\ {\quad \quad \quad {{x}_{j}} \geqslant 0\left( {j \in {{\mathbb{N}}_{n}}} \right)} \hfill \\ \end{array} $$
(18)

\( {\tilde{c}_j} \),\( {\tilde{a}_{{ij}}} \) and \( {\tilde{b}_i} \)are fuzzy numbers having linear membership functions and x j are variables whose states are fuzzy numbers\( \left( {i \in {\mathbb{N}_m},j \in {\mathbb{N}_n}} \right) \); the operations of addition and multiplication are operations of fuzzy arithmetic, and ≤ denotes the ordering of fuzzy numbers.

The FLP approach be used to solve the above problem formulation. However, this FLP uses the ideal solutions to construct intervals of linear membership functions and hence it does not reflect the fuzziness derived from the decision-makers (DM). To overcome this, in the present study, first the FPP approach is used to develop multiple objective decision problems for each different grade of precision according to the preferences of the DM. So the fuzziness is reflected in each model. Then MOFLP model is used to reach simultaneous optimal solutions for all objective functions.

2.5 The FPP Based MOFLP Approach Model Algorithm

The FPP-MOFLP approach algorithm is divided into following steps,

  1. 1.

    Development of multi objective mathematical programming model focusing on the number of competing objectives and constraints.

  2. 2.

    Decision-makers opinion about fuzzy parameters (Decision-maker finalizes which parameters are fuzzy in nature, whether all parameters a, b and c or only a and c or a and b are fuzzy).

  3. 3.

    Finalization and development of membership function. For the imprecise parameters decided in the step 2, using the FPP approach the trade-off membership functions are developed in any form (linear/nonlinear and/or piece-wise linear). It is assumed that the intervals for possible values of fuzzy parameters are denoted by the DM as [c 0,c 1), [a 0,a 1), [b 0,b 1). c 0 Represent “risk free” value and c 1 as “unimplementable” value similarly for b 0and b 1. a 0 Represent “unimplementable” value and a 1 as “risk free” value. The lower bounds represent “risk free” values, which indicate that the solution is implementable. On the other hand, the upper bounds indicate that the solution is unimplementable because upper bounds represent parameter values, which are most certainly unrealistic, “impossible”. Formulation of multi objective decision problem for each membership precision level (μ). With the help of constructed membership functions, FPP model are formulated for each precision level for fully trade off membership \( \left( {\mu = \left( {{\mu_{{ck}}}or{\mu_{{zk}}}} \right) = {\mu_A} = {\mu_b}} \right) \). Assuming that all membership functions are linear in form, FPP for each model is as given below,

    $$ \matrix{ {\quad Max {Z_k} = \left[ {C_{{kj}}^1 - \mu {c_{{kj}}}\left( {C_{{kj}}^1 - C_{{kj}}^0} \right)} \right]{x_j}} \hfill \\ {{\text{s}}.{\text{t}}.\left[ {A_{{ij}}^1 + \mu {A_{{ij}}}\left( {A_{{ij}}^0 - A_{{ij}}^1} \right)} \right]{x_j} \leqslant b_i^1 - \mu {b_i}\left( {b_i^1 - b_i^0} \right),} \hfill \\ {\quad {x_j} \geqslant 0.} \hfill \\ }<!end array> \quad \forall i,j\;{\text{and}}\;\mu \;{\text{level}} $$
    (19)
  1. 4.

    Comparing the values of objective functions obtained in step 3; construct the pay-off table and work out the upper/best (Z u ) and lower/worst (Z l ) values for each objective under consideration.

  2. 5.

    Keeping in view the upper/best (Z u ) and lower/worst (Z l ) values for each objective; establish the linear membership function.

  3. 6.

    Introducing the dummy variable (λ), the new objective function is to maximize the dummy variable (λ) for each precision level (μ) =0, 0.1… 1.0 subjected to the additional constraints due to the fuzziness in the value of the objective functions and original fuzzy constraints. MOFLP models are constructed as below:

    $$ \begin{array}{*{20}{c}} {Max\:\lambda } \hfill \\ {s.t.\left( {{{Z}_{k}} - {{Z}_{{lk}}}} \right)/\left( {{{Z}_{{uk}}} - {{Z}_{{lk}}}} \right)2 \geqslant \lambda } \hfill \\ {\left[ {A_{{ij}}^{1} + \mu {{A}_{{ij}}}\left( {A_{{ij}}^{0} - A_{{ij}}^{1}} \right)} \right]{{x}_{j}} \leqslant b_{i}^{1} - \mu {{b}_{i}}\left( {b_{i}^{1} - b_{i}^{0}} \right),} \hfill \\ {0 \leqslant \lambda \leqslant 1,} \hfill \\ {{{x}_{j}} \geqslant 0.} \hfill \\ \end{array} $$
    (20)

    Where \( \lambda = {\mu_k}(x) = {{{\left( {{Z_k} - {Z_{{lk}}}} \right)}} \left/ {{\left( {{Z_{{uk}}} - {Z_{{lk}}}} \right)}} \right.} \), \( \mu = {\mu_s} = {\mu_A} = {\mu_b} = {\mu_c} \) and \( {Z_k} = \left[ {C_{{kj}}^1 - \mu {c_{{kj}}}\left( {C_{{kj}}^1 - C_{{kj}}^0} \right)} \right]{x_j} \)

  1. 7.

    Solve the problem for each precision level (μ).

  2. 8.

    Presentation of solutions to the DM. Incase if the DM is unsatisfied, then reverting to step 2 or 3 and repeat the procedure.

Schematic representation of FPP based MOFLP approach model for all fuzzy parameters is shown in Fig. 2.

Fig. 2
figure 2

Schematic representation of algorithm for the FPP based MOFLP approach model for all fuzzy parameters (a, b, c)

Full size image

3 Results and Discussion

As the multi-objective optimization problem with imprecise parameters is difficult to solve by traditional approaches, Fuzzy set theory has been applied to tackle this difficulty. In the present study, first the FPP approach is used to find the optimal compromise between the “risk free” and “impossible” parameter values (a, b, c) as a function of grades of imprecision in parameters. Then MOFLP model is developed and applied to find the optimal cropping pattern plan for the Jayakwadi Project Stage-I, Maharashtra State, India. The four objectives under considerations are NB, CP, EG and MU respectively. All parameters (a, b, c) of the model are considered as fuzzy.

In the present study five strategies have been considered, the fuzziness has been considered only in the objective function and the constraints are to be crisp in nature (Strategy-I). These objective functions have been maximized separately, subject to constraints (Eqs. 5–17) using the LINGO (Language for INteractive General Optimization). The results of this individual maximization of the four different objectives have been used to construct the membership function for each objective taking the help of the upper/best Z u and lower/worst Z l values of the same. From this solution, it is observed that the area to be irrigated is constant in case of Chillies (TS) and Sorghum (K) under LP model and MOFLP model solution. (The table of LP model results has not been presented due to space limitation). In case of individual optimization for four objectives, the irrigation intensity has been 54.04 %, 54.86 %, 79.54 % and 68.81 % respectively, while in case of MOFLP it is 70.02 %. In case of MOFLP, the irrigation intensity has been found to be more by 15.97 %, 15.15 %, 1.21 % if we compare with individual optimization for Net Benefits, Crop Production and Manure Utilization respectively and less by 9.52 % if we compare with individual optimization for Employment Generation. The results of MOFLP model are presented in Table 3. The level of satisfaction for compromised solution for four conflicting objectives under the fuzzy environment, worked out to be λ = 0.58. MOFLP compromised solution provides Net Benefits 1503.73 (Million Rupees), Crop Production 319,563.50 (Tons), Employment Generation 29.74 (Million Man Days) and Manure Utilization 154,506.50 (Tons) respectively.

For the Strategy-II, the MOFLP model which represents the fuzzification of resources/stipulations (\( {\tilde{b}_i} \)) only; considers the uncertainty involved in the various resources such as water availability, labour availability, manure utilization and land availability. Comparing the values of the Z1 to Z4 from strict constraint solution and loose constraint solution, the best and worst values of Z1 to Z4 are picked up. These values are represented in form of Table 2 as Payoff Matrix. The results of Strategy-II are presented in Table 3.

Table 2 Upper/best and lower/worst values of the objective function after comparison (i. e., Payoff Matrix)
Full size table
Table 3 Salient parameters of optimal cropping pattern planning for \( \tilde{Z} \),\( {\tilde{b}_i} \), \( {\tilde{a}_{{ij}}} \), \( {\tilde{a}_{{ij}}} \)and \( {\tilde{b}_i} \)
Full size table

The level of satisfaction for compromised solution for four conflicting objectives under fuzzy environment worked out to be λ = 0.50. The MOFLP compromised solution provides Net Benefits 1314.87 (Million Rupees), Crop Production 278,042.50 (Tons), Employment Generation 25.99 (Million Man Days) and Manure Utilization 134,365.30 (Tons) respectively. The irrigation intensity is 61.15 %. The MOFLP model along with the fuzzification of technological coefficients (\( {\tilde{a}_{{ij}}} \)) is treated as Strategy-III in which the benefit coefficients and input cost for i th crop, average yield, labour requirement, irrigation water requirement and manure requirement for i th crop are considered as fuzzy in nature and the resources as crisp in nature. The results for the Strategy III have been presented in Table 3. The level of satisfaction for compromised solution for four conflicting objectives under fuzzy environment works out to λ = 0.50. MOFLP compromised solution provides Net Benefits 1617.66 (Million Rupees), Crop Production 312,941.30 (Tons), Employment Generation 34.03 (Million Man Days) and Manure Utilization 163,647.90 (Tons) respectively. The irrigation intensity is 78.48 %. The MOFLP model along with fuzzification of technological coefficients (\( {\tilde{a}_{{ij}}} \)) and resources/stipulations (\( {\tilde{b}_i} \)) are considered simultaneously as Strategy-IV. The results for the same are presented in Table 3. The level of satisfaction for compromised solution for four conflicting objectives under fuzzy environment worked out to λ = 0.28. MOFLP compromised solution provides Net Benefits 1602.43 (Million Rupees), Crop Production 308,066.20 (Tons), Employment Generation 32.60 (Million Man Days) and Manure Utilization 131,783 (Tons) respectively. The irrigation intensity is 72.94 %. The results for Strategy I to IV have been represented graphically in Fig. 3. Regulwar and Gurav (2011) have given the detailed description of Strategy-I to IV.

Fig. 3
figure 3

Optimal cropping pattern for fuzzification of Z, bi, aij, aij and bi

Full size image

The MOFLP model involving the fuzziness in all parameters (a, b, c) has been considered and treated as Strategy-V. The solution for this Strategy has been obtained as per the procedure given in the methodology. The membership functions for each fuzzy parameter (a, b, c) have been constructed (Figs. 4, 5 and 6). It has been assumed that linear monotonously increasing, linear concave/convex membership functions are associated with a ij, b i, and c kj parameters where A = [aij], b = [bi ], c k = [ckj], i = 1… 17 and j = 1…10, k = 1…4.

Fig. 4
figure 4

Membership function (monotonously increasing) for technological coefficients a1-risk free value and a0-Unimplementable value

Full size image
Fig. 5
figure 5

Membership function (linear concave) for cost Coefficients c1-Unimplementable and c0- risk free value

Full size image
Fig. 6
figure 6

Membership function (linear convex) for stipulations/resources b0-risk free value and b1-Unimplementable value

Full size image
$$ \matrix{ {\mu {a_{{ij}}} = {{{\left( {{a_{{ij}}} - a_{{ij}}^1} \right)}} \left/ {{\left( {a_{{ij}}^0 - a_{{ij}}^1} \right),}} \right.}} \hfill \\ {\mu {b_i} = {{1} \left/ {{\left( {1 - \exp \left( { - 0.8} \right)} \right)}} \right.}\left[ {1 - \exp \left( { - 0.8{{{\left( {{b_i} - b_i^1} \right)}} \left/ {{\left( {b_i^0 - b_i^1} \right)}} \right.}} \right)} \right],} \hfill \\ {\mu {c_{{kj}}} = {{1} \left/ {{\left( {1 - \exp (3)} \right)}} \right.}\left[ {1 - \exp \left( {3{{{\left( {{c_{{kj}}} - c_{{kj}}^1} \right)}} \left/ {{\left( {c_{{kj}}^0 - c_{{kj}}^1} \right)}} \right.}} \right)} \right],} \hfill \\ }<!end array> $$

The model parameters are derived from the membership functions as follows:

$$ \matrix{ {{a_{{ij}}} = a_{{ij}}^1 + \mu {a_{{ij}}}\left( {a_{{ij}}^0 - a_{{ij}}^1} \right),} \hfill \\ {{b_i} = b_i^1 - \left( {{{1} \left/ {{0.8}} \right.}} \right)\ln \left[ {1 - \mu {b_i}\left( {1 - \exp \left( { - 0.8} \right)} \right)} \right]\left( {b_i^0 - b_i^1} \right),} \hfill \\ {{c_{{kj}}} = c_{{kj}}^1 + \left( {{{1} \left/ {3} \right.}} \right)\ln \left[ {1 - \mu {c_{{kj}}}\left( {1 - \exp (3)} \right)} \right]\left( {c_{{kj}}^0 - c_{{kj}}^1} \right),} \hfill \\ }<!end array> $$

Then all the coefficients have been parameterized according to their membership functions. The parametric multiple objective linear programming problem (MOLP) is formulated as:

$$ \matrix{ {Max{Z_k} = \left[ {c_{{kj}}^1 + \left( {{{1} \left/ {3} \right.}} \right)\ln \left[ {1 - \mu {c_{{kj}}}\left( {1 - \exp (3)} \right)} \right]\left( {C_{{kj}}^1 - C_{{kj}}^0} \right)} \right]{x_j},} \hfill \\ {\left[ {A_{{ij}}^1 + \mu {A_{{ij}}}\left( {A_{{ij}}^0 - A_{{ij}}^1} \right)} \right]{x_j} \leqslant b_i^1 - \left( {{{1} \left/ {{0.8}} \right.}} \right)\ln \left[ {1 - \mu {b_i}\left( {1 - \exp \left( { - 0.8} \right)} \right)} \right]\left( {b_i^0 - b_i^1} \right),\quad \quad \forall i,\;j\;{\text{and}}\;{\text{level}}} \hfill \\ {{x_j} \geqslant 0.} \hfill \\ }<!end array> $$

As each membership function shows the degree of precision and the precision worked out from the optimal solution equals the precision of the most risky of the parameters(μs = min (μa, μb, μc)), the best value for the objective function is yielded when μs = μa = μb = μc for all i, j, k. In other words the best value of the objective function, at fixed level of precision, can be found out, by using parameter values of the same level of precision. Since the membership functions are different in nature, it is therefore suggested that the above parametric MOLP problem should not be used as it is for the optimal solution. For which a series of model run have to be carried out with various membership values ranging from μs = μa = μb = μc = 0, 0.1, 0.2…1.0. The MOLP problems have been solved by considering only one objective at a time and ignoring remaining three objectives. The ideal solution for each precision level is found out. The Pay-off table (Table 4) is then constructed with help of ideal solution derived for each precision level. From the Pay-off table (bold figures) for each objective upper/best value (Z u ) and lower/worst value (Z l ) are worked out. Using these values and focusing on the precision level (μ) the linear membership function of each objective function has been constructed according to the FLP. For μ = 0, membership functions are shown in Eqs. (21)–(24). The precision level μ is related with how much precision a decision maker wants for fuzzy decision parameters in the irrigation policy planning.

Table 4 Pay-off table
Full size table
(21)
(22)
(23)
(24)

The λ is introduced as the fuzzy achievement function (λ = min [μZ 1(x), μZ 2(x), μZ 3(x), μZ 4(x)]), finally the modified form of the optimization problem as a MOFLP model becomes such that the objective is to:

Maximize λ

Subject to,

(Z1−1606.95 × 106)/(1976.02 × 106−1606.95 × 106) ≥ λ

(Z2−177,867.20)/(517,825.50−177,867.20) ≥ λ

(Z3−31.47 × 106)/(37.43 × 106−31.47 × 106) ≥ λ

(Z4−82,930.79)/(119,208.40−82,930.79) ≥ λ

And all other fuzzy constraint (Eqs. (5)–(17)) in the model;

0 ≥ λ ≥ 1.

The solution of the above model according to the precision level (μ) is presented in Table 5. The results for the Strategy-V have been shown graphically in the form of Fig. 7. The solution provides the alternative decision plans to the DM for the optimal cropping pattern planning for the Jayakwadi Project Stage-I. The aggregated satisfaction levels of the optimal cropping pattern planning problem with all fuzzy parameters are over 68 % for each precision level (μ = 0, 0.1, 0.2…1.0). The numerical value of λ represents that four objectives are optimized simultaneously and out of which one is satisfied at λ level and the others are satisfied at least at λ level. With this solution, DM has a number of alternative plans for optimal cropping pattern planning. The numerical value of the λ is maximum (0.727) when the precision level (μ) is minimum (zero) and λ is minimum (0.682) when precision level is maximum (1.0). DM may take competent decisions based on the precision level required as per the need and time. From Table 5 it is seen that when μ is zero, four objectives are to be satisfied, which are Net Benefits = 1875.27 Million Rupees, Crop Production =381,720.70 Tons, Employment Generation = 35.80 Million Man Days and Manure Utilization = 109,306 Tons respectively. These objectives have minimum values when μ =1.0. Similarly, all ten crops have maximum area allotment when the precision level (μ) is minimum (zero) and having minimum area allotment for maximum precision level (1.0). Groundnut (HW) is having zero area allotment for cultivation. Also Sorghum (R) has zero area allotment for cultivation when μ is greater than or equal to 0.6.

Table 5 The MOFLP optimization model solutions for μ = 0.0.1, 0.2… 1.0
Full size table
Fig. 7
figure 7

Optimal cropping pattern for all fuzzy parameters (A, b, c)

Full size image

4 Conclusion

The FPP based MOFLP model is developed and applied to the Jayakwadi Project Stage-I in Godavari River sub basin in Maharashtra State, India. The Proposed MOFLP model considers the uncertainty incorporated in the objective functions, resources/stipulations, technological coefficients and technological coefficients along with resources (Strategy-I to IV). In addition, Strategy-V represents the fuzziness in all parameters (objective function coefficients, resources and technological coefficients). The observations from the study are given below.

  1. 1.

    The decision maker’s satisfaction level (λ) works out to be in the range of 0.58–0.50 (for Strategy-I to III) except for the Strategy-IV for which the level of satisfaction (λ) is 0.28. This may be because of the uncertainty treated as fuzziness in technological coefficients and resources simultaneously.

  2. 2.

    In Strategy-I to IV the area allotment for Sorghum(R) and Groundnut (HW) is zero because their coefficient value is less. The net cropped areas are 99,183.36, 86,617.26, 111,164.42 and 103,320.11 (ha) for different strategies along with irrigation intensities of 70.02, 61.15, 78.48 and 72.94 % respectively as evident from Table 3.

  3. 3.

    It is observed from Table 3 that net benefit in Strategy-III is 7.04 % greater than that of Strategy-I, 18.72 % greater than that of Strategy-II and almost same in Strategy-IV. The crop production in Strategy-I is 12.99 % greater than that of Strategy-II, 2.07 % greater than that of Strategy-III and 3.6 % greater than that of Strategy-IV. The employment generation in Strategy-III is 12.62 % greater than that of Strategy-I, 23.65 % greater than that of Strategy-II and 4.21 % greater than that of Strategy-IV. Similarly, the manure utilization in Strategy-III is 5.58 % increment that of Strategy-I, 17.80 % greater than that of Strategy-II and 19.48 % greater than that of Strategy-IV.

  4. 4.

    In Strategy-I area allotment for Sugarcane (P) is more as compared to the other strategies. The area allotment for various crops except Sugarcane (P) is more in Strategy-III as compared to the strategies-I, II and IV.

  5. 5.

    From Table 5, in case of Strategy-V, it is seen that the irrigation intensity is 82.52 % at λ = 0.727 and it is 45.30 % at λ =0.682. The area allotment for Groundnut (HW) for each precision level is zero because its coefficients value is less and hence is not allowed in optimal cropping pattern plan. For precision level μ = 0.6 and onwards the area allotment for the Sorghum (R) is zero as its coefficient value is less.

  6. 6.

    The Decision Maker may select any one optimal cropping pattern as per the level of precision.

  7. 7.

    All solutions presented in Table 5 for each precision level are optimal and efficient solutions. Among the results of the Strategy-I to V, the results of the Strategy-V, presented in this paper, have the best adaptation to deal with real world situations of sustainable irrigation planning problem.

  8. 8.

    The proposed FPP based MOFLP model (Strategy-V) is general-purpose model. Its application can be extended to the entire Godavari river basin and to the other basin with a little modification related to the basin characteristics under consideration.

  9. 9.

    The developed model tackles the uncertainty/vagueness involved in the parameters such as objective function coefficients, technological coefficients and resources by fuzzifying these parameters simultaneously which is more close to real life than till the date the models available for optimal cropping pattern/planning which have been dealt with only fuzzification of objective function and/or resources.

  10. 10.

    The analysis of present model gives the series of optimal solutions according to the level of precision in the form of optimal cropping pattern instead of single optimal solution approach of conventional model.

  11. 11.

    The Strategy-V procedure includes DM’s experience, information and expectations at each and every stage of model formulation and analysis.

  12. 12.

    The limitation of the present model is that the DM has to decide the risk free value and unimplementable values of the parameters based on experience, information and expectations.

Considering the study carried out through different strategies the fuzzification of decision parameters are feasible for sustainable irrigation planning as multiobjective analysis. Based on the uncertainty/vagueness that arises in the field, a proper model and its analysis can be used judiciously by the Decision Maker.