1 Introduction

Short-term urban water forecasting can be of use for the efficient operation and maintenance of pumps, wells, reservoirs and mains, whereas medium and long term forecasting may be required for infrastructure investments and regional policy making (Herrera et al. 2010). In this context, modeling and scenario-building becomes critical, especially when conditions experienced in the past are not expected to repeat themselves in the future. This may be the case with fast demographic growth, climate changes and over-pumping from aquifers, which are likely to impact not only the amount but also the quality and the patterns of future water supply and demand (Issar and Zohar 2009; Oron et al. 1999).

According to Jain and Ormsbee (2002), perhaps the most frequently used forecasting models for water demand are based on linear regression and time series analysis. In the 1980s, Maidment and Miaou (1986) used Box and Jenkins models to forecast daily municipal water use as a function of rainfall and air temperature in nine US cities, and Smith (1988) included day-of-week effects among the predictors and randomly varying means as a regression method. An et al. (1996) revisited rough set methodologies describing the relationships between water factors and water consumption. On the other hand, in the field of deterministic prediction, important research has been conducted in developing models of water budgeting according to different foundations such as classical hydrology (Grubbs 1994) and environmental isotopes (Adar et al. 1988).

Since the introduction of the back propagation algorithm by Rumelhart et al. (1986), Artificial Neural Networks (ANNs) have been used in a large variety of forecasting applications. This method has been frequently used because it can tackle problems where the underlying relationships in the time series are complex or unknown, but there is enough data (i.e. observations) to train a network (Zhang et al. 1998). A number of ANN configurations have been used for hydrological forecasting with good results. In this respect, Jain and Ormsbee (2002), Bougadis et al. (2005), Adamowski (2008), Adamowski and Karapataki (2010), Güldal and Tongal (2010) and Shirsath and Singh (2010) used ANNs to forecast various aspects of water resources demand. In all these instances, it was concluded that ANN-based methods provide better results than conventional autoregressive methods. Zhang et al. (1998), in a state-of-the-art survey, observed that although some contradicting reports exist in the literature, ANN is a useful method for non-linear modeling while autoregressive approaches may be more suitable for linear relationships in the data.

When comparing ANNs to newer methods mixed results were found. Msiza et al. (2007) compared ANNs to support vector machines (SVM) for urban water demand, concluding that ANNs were more precise; on the other hand, Herrera et al. (2010) used ANN, SVM, projection pursuit regression and multivariate adaptive regression splines, and found that SVMs were more precise for urban water demand forecasting.

With regards to spectral analysis of time series, the discovery of wavelet functions has shed new light onto the analysis of non-stationary and/or noisy phenomena (Rioul and Vetterli 1991). In geophysics it is not uncommon to find time series that include a trend in the mean, non-constant variance, and discontinuities as well as background noise (Jowitt and Xu 1992). Foufoula-Georgiou and Kumar (1994) described the basic properties that make wavelet analysis a powerful tool for geophysical applications. It was noted that the multi-resolution approach may be useful for the analysis of multi-scale features, detection of singularities, analysis of transient phenomena, non-stationary series, and fractal processes.

With specific attention to hydrology, Labat (2005) noted that the application of wavelets may lead to several improvements in the analysis of global hydrological fluctuations and their mutual time varying relationships. It was also suggested that wavelets should be used more systematically, notably in hydrology as a preferable alternative to classical Fourier analysis. For example, Chou (2011) used wavelet-denoising instead of Fourier thresholding in order to eliminate the effect of high-tide low-tide variations at gauge level from the relation between rainfall and run-off. Adamowski et al. (2009) developed a wavelet-aided technique for trend detection in monthly streamflow and water resource forecasting and Labat (2008) used wavelets for multi-scale analysis of the world’s largest river discharges.

In recent years, several authors noted that coupling wavelet transforms with ANNs could provide highly accurate hydrological forecasts. Partal and Cigizoglu (2008) used wavelets in conjunction with ANNs for the forecasting of evapotranspiration; Zhou et al. (2007) and Kisi (2008, 2009) used wavelet-decomposition in order to improve ANN forecasting of river stream-flow; Wang et al. (2009) analyzed time series by means of wavelet-transforms in order to forecast “xunly” mean discharge of the Three Gorges Dam (where “xun” is the Chinese term indicating a 10-day period); Adamowski and Sun (2010) used coupled wavelet-neural network models in flow forecasting; Adamowski and Chan (2011) used wavelets and ANN for the forecasting of ground-water levels; and Adamowski et al. (2012) used wavelets and neural networks to forecast urban water demand for the city of Montreal, Canada. These studies found that coupled wavelet-neural network models generally provided more accurate forecasts than other models (such as ARIMA, ANN, MLR, etc.). With specific regard to denoising methods based on wavelets, Nourani et al. (2009) and Cannas et al. (2006) both explored the multi-scaling property of wavelets for maximization of ANN forecasting accuracy (in the context of flow forecasting). Empirical results show that networks trained with pre-processed data performed better than networks trained on un-decomposed, noisy raw signals.

In this study, we tackle the problem of forecasting urban water demand by means of back-propagation artificial neural networks coupled with wavelet-denoising. In addition, non-coupled ANN and Linear Multiple Regression methods were used as comparison models. We considered the case of the municipality of Syracuse, Italy. For this purpose, we used a 7 year-long time series of monthly urban water demand; no additional predictors such as demographic, economic or environmental variables were used. ANN tuning is fully described in a step by step procedure. Six forecasting horizons, from 1 to 6 months ahead, were considered. The main objective of the study was to calibrate a forecasting model for operational applications (i.e. monthly water budgeting for the municipality of Syracuse, Italy). Moreover, we measured the impact of different filter-banks (namely, Haar and Daubechies of type db2, db3, db4, and db5) on a single back-propagation multi layered neural network for the prediction of monthly water demand. Thus, an additional objective was to explore the impact of different wavelets on ANN generalization.

2 Data

The dataset is a time series consisting of 84 measurements (from January 2002 to December 2008) of monthly water consumption of the municipality of Syracuse, Italy (Fig. 1a). It cumulates monthly water flow measured at the outlet of several urban water tanks. Syracuse is located in the South-East coast of Sicily at 37°5’0” North and 15°17’0” East, according to the World Geodetic System 84. The Mediterranean climate is characterized by mild, wet winters and warm to hot, dry summers (Koppen climate classification: Csa). The time series in Fig. 1a shows seasonal oscillation around the mean; it reaches a local maximum approximately every 12 months during the summer and a local minimum during the winter. The mean of the year-maximum values is 1.92 million m3/month, the mean of the year-minimum is 1.60 million m3/month. The mean monthly water consumption is 1.78 million m3/month with a standard deviation of 0.086 million m3/month. Mean and standard deviation are not constant; a decreasing trend is also detectable. The samples come from an underlying sinusoidal model and they have a high degree of autocorrelation at 6 and 12 lagged observations (Fig. 1c). The Lilliefors test (Conover 1980) rejects the null hypothesis at the 5 % significance level that the sample in our time series comes from a distribution in the normal family (against the alternative that it does not come from a normal distribution). Thus, the distribution is not likely to be normally distributed (Fig. 1b).

Fig. 1
figure 1

Monthly water demand of the municipality of Syracuse, Italy. In (a) 84 measurements in blue; the central dotted line (in green) represents the overall mean; the external dotted lines (in violet) represent the control limits, one standard deviation above and below the mean; the continuous line (red) represents the trend line. In (b) the histogram of water demand versus the normal fit; in (c) the autocorrelation coefficients are included

Full size image

3 Methodology

3.1 Multiple Linear Regression

Multiple linear regression (MLR) models are capable of making predictions based on multiple inputs. The analytical expression (Holder 1985) is defined by:

$$ {y_t} = {a_0} + {a_1}{x_1}(t) + \ldots + {a_n}{x_n}(t) + \varepsilon (t) $$
(1)

where y t is the output, a 0 is a constant, a 1 …a n are regression coefficients computed via the least squares method, x 1 (t)…x n (t) are the inputs into the model, and ε(t) is a random variable with zero mean and constant variance.

3.2 Artificial Neural Networks

An artificial neural network (ANN) is an interconnected group of simple processing units mimicking the function of biological neurons first discovered in physiology. According to the prevalent terminology, we call neurons or nodes the processing units of an artificial neural network. Neurons are arranged in layers; neurons between layers are connected by links called weights. Error-back propagation includes an additional set of feed-back connections from the output to the input layer (Rumelhart et al. 1986). Back propagation networks are a generalization of the Widrow-Hoff learning rule (Widrow and Lehr 1990), in which the network weights are adapted along the negative gradient of the performance function (Rumelhart et al. 1986). Back-propagation multi-layered fully connected neural networks are among the most popular and proven (Hagan et al. 1996). Complete derivation of the model and the learning algorithm can be found in Rumelhart et al. (1986) and Haykin (1994). A single-output multilayer feed forward back propagation network performs the following mapping from the input to the output data (Zhang et al. 2001):

$$ \widehat{y}_{t} = f\left( {{y_{{t - 1}}},{y_{{t - 2}}}, \ldots, {y_{{t - n}}}} \right) $$
(2)

where \( \widehat{y}_{t} \) is the output at time t, n is the dimension of the input vector or the number of past observations used to predict future observations, and f is a nonlinear function determined both by the network and the data at hand. From Eq. 2 the feed-forward function can be viewed as a general nonlinear, autoregressive model (Zhang et al. 2001). In a trained network, the relation between outputs and inputs has the following expression (Zhang 2003):

$$ {y_t} = {\alpha_0} + \sum\limits_{{j = 1}}^q {{\alpha_j}g\left( {{\beta_{{0j}}} + \sum\limits_{{i = 1}}^p {{\beta_{{ij}}}{y_{{t - i}}}} } \right) + {\varepsilon_t}} $$
(3)

where α j for (j = 0,1,2,…q) and β ij for (i = 0,1,2,…p; j = 0,1,2,…q) are the model parameters, also referred to as weights in the connectionist literature; p is the number of input nodes and q is the number of hidden nodes; the function g is a logistic function, in our case we used a log-sigmoid function:

$$ g(x) = \frac{1}{{1 + {e^{{\left( { - x} \right)}}}}} $$
(4)

Neural networks operate on the basis of learning rules which define exactly how the network weights should be adjusted (updated) between successive training cycles (epochs). Thus, training is the process of featuring the function f in Eq. 2 which eventually is uniquely determined by the linking weights of the network. We used a supervised learning method. In practice the network learned the mapping from the input data space to the output, by means of a set of correct solutions used for supervising the training process. We used a Levenberg-Marquardt (LM) training algorithm. LM is often the fastest back propagation algorithm, and is highly recommended as a first-choice for supervised learning (Hagan et al. 1996). The mean squared error (MSE) was used as a performance function. We used a log-sigmoid activation function (Eq. 4) for all the hidden layers, and a linear activation for the output layer. Training was terminated when any of the following conditions occurred: a) the maximum number of epochs (repetitions) was reached, in this case maximum(epoch) = 100; b) the maximum amount of time had been exceeded, in this case maximum(time) = infinite; c) performance had been minimized to the goal, in this case no goal was pre-determined, goal = null; d) the performance gradient fell below a threshold, minimum(gradient) = 1e−10; e) “mu” exceeded maximum(mu) = 1e10; f) validation performance increased more than 5 times since the last time it decreased (over the validation dataset).

At each ANN iteration, the training set was randomly partitioned into three subsets: training, validation, and testing. The training-subset was used to update the weights of the network. The validation-subset was used to set a rule to interrupt training (as described above). The test-subsets were used to measure ANN performances on a portion of data that had not been used for training, also referred to as off-set data. There are several heuristics for partitioning: we used 60 % of the dataset for training, 20 % for validation and 20 % for testing (Haykin 1994). In practice, at each ANN iteration, we forecasted only 14 months out of 72 dates comprising the forecasting domain (from January 2003 to December 2008). By means of several hundred repetitions we managed to cover the entire forecasting domain with at least 30 off-set forecasts for each single month.

The next steps of ANN configuration consisted of choosing: a) the dimension of the input vectors; b) the number of layers; c) the number of neurons per layer. Regarding the optimal length of the input vectors, the objective was to determine the optimal number of lagged observations, which is n in Eq. 2. This is among the tasks with the largest impact on convergence (Haykin 1994). There is no theoretical support that can be used to guide the selection of n (Zhang et al. 2001). We tested 3, 6 and 12-dimensional input-vectors on a number of networks having hidden layers ranging from 1 to 8 and neurons per layer ranging from 1 to 8, for a total of 8 × 8 = 64 network configurations. We evaluated the performance of each configuration over 100 numerical experiments, for a total of 3 × 64 × 100 = 19,200 numerical experiments. Figure 2 shows three correlation surfaces corresponding to our 64 configurations trained respectively by 3, 6, and 12-dimensional input vectors. In all cases, other than two exceptions, a 12-dimensinal input vector showed higher correlations than any other ANN trained with 6d and 3d input vectors. Hence, we selected a 12d input vector (n = 12).

Fig. 2
figure 2

Correlation surface of different ANNs. On the horizontal grid the combination of neurons and layers are presented; on the vertical axis the correlation coefficient corresponding to each combination is presented. Each stratum of the figure corresponds to 3, 6, and 12 dimensional input vectors, respectively

Full size image

In the remaining sections we will refer to a number of variables defined as follows: (Yt) is the forecasted value for the month t; [Yr] is the output vector consisting of the scalars (Yt), where r = 1, 2, .. z is the ordinal number of the experiment; and [Ym] is the vector of final forecasts of the model m, defined as the average of the set {Yr}. The model performances are measured by a number of indexes based on the benchmarking of [Ym] against targets [T], where [T] is the vector of measured monthly water demand.

Regarding the optimal number of layers and neurons, in most function approximation tasks, one layer (with several neurons) is sufficient to approximate continuous functions; generally, two hidden layers may be necessary for learning functions with discontinuities (Hagan et al. 1996). Nevertheless, these general considerations may not necessarily be optimal for the data set at hand. Several approaches are suggested to define neural architecture (Widrow and Lehr 1990). Guidelines may be either heuristic or derived from empirical experiments. The methodological “freedom” in the choice of layers and neurons has been mentioned by Zhang et al. (1998) as one of the reasons for inconsistent reports about ANN performances in the scientific literature. Having fixed the length of the input vector equal to 12, we systematically evaluated all the configurations comprising a number of layers ranging from 1 to 14 consisting respectively of a number of neurons ranging from 1 to 14 per layer, for a total of 14 × 14 = 196 configurations. We tested each configuration 100 times, for a total of 196 × 100 = 19,600 numerical experiments. Results are presented in a matrix pictorial form (Fig. 3). Each pixel corresponds to a combination of layers and neurons, the color-bar in Fig. 3a represents the mean squared error (MSE) between outputs [Ym] and targets [T], and the color bar in Fig. 3b represents the correlation coefficients (R) between outputs [Ym] and targets [T]. It was found that for the dataset at hand, the network configuration that minimized the MSE and maximized the correlation coefficient (R) was the one having 2 layers. More precisely: 12 input nodes in the input layer (q = 12 in Eq. 3) and 12 hidden nodes in a single hidden layer (p =12 in Eq. 3), for a total of 24 nodes distributed in 2 layers.

Fig. 3
figure 3

Performances of 196 different ANNs. Each pixel represents a different ANN-setting resulting from the combinations of a varying number of layers-per-network (ranging from 1 to 14) and neurons-per-layer (ranging from 1 to 14). The color bars represent the magnitude of the Mean Square Errors (a) and the Correlation Coefficients (b). In all instances ANNs were trained with 12 dimensional input vectors

Full size image

An additional test was performed in order to establish how stable this configuration was. For this purpose, we measured the magnitude of the standard deviations of the outputs as a function of number of layers; the larger the standard deviation the less stable the network. Experimental results (Table 1) show that output standard deviation increased with the number of layers. Thus, although in the two layer configuration one can find the best forecasting accuracy, the one layer configuration was more stable without a significant decrease in network performance. Therefore, a one-layer network was chosen to be the optimal configuration.

Table 1 Network stability as a function of number of layers per network
Full size table

Finally, within a one layer configuration, we focused on the optimal number of neurons. It was found that 12 neurons consistently returned above average results both in terms of correlation coefficient and mean squared error of outputs versus target. Therefore, this was adopted as the definitive configuration for this study.

To summarize, by means of a step-wise screening where at each step a single parameter was analyzed, we concluded that the network to be used in the remaining part of the study was the one having the following major features: feed-forward back-propagation network with 12 neurons in one hidden layer, fully connected by tan-sigmoid threshold functions to an output layer provided by a linear threshold, trained with a Levenberg-Marquardt algorithm.

3.3 Wavelet-Denoising

Wavelets are orthogonal bases of finite length that can be used to represent a time series into a time-scale domain at different resolutions. In this study, wavelet transforms were used for their denoising capabilities in order to improve ANN forecasting accuracy. Wavelets are described by Compo and Torrence (1998) as a “tool to analyze variation of power within a time series”. Because of the compact support in which wavelets are defined, wavelet filter-banks are also well suited to decompose, manipulate and represent non-stationary time series. A practical guide to wavelet-analysis is provided by Compo and Torrence (1998), fundamental manuals are provided by Blatter (1998), Daubechies (1992), Meyer (1992), Strang and Nguyen (1996), Holschneider (1995), and Mallat (1999).

Wavelet analysis consists of decomposition, and wavelet synthesis consists of reconstruction of a given signal. In the continuous domain, the analysis starts from choosing a mother wavelet (ψ). The continuous wavelet transform (CWT) is then defined by the integration over all time of the signal multiplied by scaled and shifted versions of the mother wavelet (Mallat 1999):

$$ CWT_x^{\psi }\left( {\tau, s} \right) = \frac{1}{{\sqrt {{\left| s \right|}} }}\int\limits_{{ - \infty }}^{{ + \infty }} {x(t){\psi^{*}}\left( {\frac{{t - \tau }}{s}} \right)} $$
(5)

where s is the scale parameter, τ is the translation and ‘*’ stands for the complex conjugate. The CWT produces a continuum of all scales as the output. In the discreet domain, let s = s j 0 and τ = τ 0 . The discrete wavelet given by (Mallat 1999) is then defined as follows:

$$ {\psi_{{\tau, s}}}(t) = \frac{1}{{\sqrt {{\left| {s_0^j} \right|}} }}{\psi^{*}}\left( {\frac{{t - k{\tau_0}s_0^j}}{{s_0^j}}} \right) $$
(6)

where j and k are integers and s0 > 1 is a fix dilation step. The most practical choice for the parameters s 0 is 2 and τ 0 is 1. It results in a power of two logarithmic scaling, also referred to as a dyadic grid arrangement of the mother wavelet. The dyadic wavelet can be written in more compact notation as:

$$ {\psi_{{j,k}}}(t) = {2^{{ - j/2}}}\psi \left( {{2^{{ - j}}}t - k} \right) $$
(7)

such that \( \left\{ {{\psi_{{j,k}}}} \right\}{}_{{\left( {j,k} \right) \in {Z^2}}} \) forms an orthonormal basis for L2(ℜ), the vector space of measurable, square integrable one-dimensional functions. One of the inherent challenges of using the discrete wavelet transform (DWT) for forecasting applications is that it is not shift invariant (i.e. if we shift the beginning of our time series, all of the wavelet coefficients will change). To overcome this problem, a redundant algorithm, known as the “à trous” algorithm was used in this study. Finally, the wavelet can be used as a low-pass filter to prevent any future information from being used during the decomposition. For more information on the issue of shift invariance and causal-filtering, readers are directed to Renaud et al. (2005).

The transform can be presented according to Mallat (1999):

$$ {c_{{i + 1}}}(k) = \sum\limits_{{ - \infty }}^{{ + \infty }} {h(t){x_i}\left( {k + {2^i}t} \right)} $$
(8)

where h are the coefficients of the filters of choice, x i (t) is the original time series and c i+1 are the coefficients of the wavelet analysis. In practice, in the discrete domain, we implemented a two-channel sub-band coding using quadrature mirror filters (QMFs). This consisted in the analysis of the signal by different filter banks (Low-pass and High-pass filters). In the two band decomposition scheme, starting from x(t), the first step produces two sets of coefficients: approximation coefficients (cA1), and detail coefficients (cD1). These vectors are obtained by convolving x(t) with the low-pass filter Lo_D, and with the high-pass filter Hi_D, followed by dyadic decimation. A dyadic decimation must be applied at each step (i.e. downsampling). In practice the decomposition can continue iteratively on the low-pass transform cA1. Several levels of wavelet decomposition were tested; the first level was chosen as the most adequate for our denoising purposes. The inverse transform (IDWT) started from cA1, thus the signal was reconstructed backwards and up-sampled. The algorithm guaranties perfect reconstruction unless the coefficients are somehow manipulated. In our case we suppressed the coefficients of the high-pass transform (i.e. the details at level 1). In this study we used a number of compactly supported discrete wavelet-functions of the type: Haar, db2, db3, db4, and db5 named respectively after Alfred Haar and Ingrid Daubechies (Daubechies 1992). The Haar wavelet family is the simplest; it redefines the original signal in terms of averages and differences:

$$ \matrix{ {\psi (x) = 1} \hfill &{if} \hfill &{x \in \left[ {0,0.5} \right)} \hfill \\ }<!end array> $$
(9)
$$ \matrix{ {\psi (x) = - 1} \hfill &{if} \hfill &{x \in \left[ {0.5,1} \right)} \hfill \\ }<!end array> $$
(10)
$$ \matrix{ {\psi (x) = 0} \hfill &{if} \hfill &{x \notin \left[ {0,1} \right)} \hfill \\ }<!end array> $$
(11)
$$ \matrix{ {\phi (x) = 1} \hfill &{if} \hfill &{x \in \left[ {0,1} \right)} \hfill \\ }<!end array> $$
(12)
$$ \matrix{ {\phi (x) = 0} \hfill &{if} \hfill &{x \notin \left[ {0,1} \right]} \hfill \\ }<!end array> $$
(13)

Daubechies wavelets (dbN) have no explicit expression except for db1, which actually is the above mentioned Haar wavelet. They are ranked in terms of their vanishing moments which are equal to 2N-1; we used N ranging from 2 to 5, thus wavelet types db2, db3, db4, db5 (Fig. 4). When non-normalized, dbN are Finite Impulse Response (FIR), low pass-filters, of length 2N, of sum 1, of norm 1/√2.

Fig. 4
figure 4

Wavelet coefficients for low-pass reconstruction

Full size image

From Haar and dbN we defined four FIR filters, of length 2N and of norm 1. Once five filter-banks were constructed the decomposition started from the original signal (84 data points of monthly water supply). Usually, the DWT is defined for sequences with length of some power of 2. In order to get a perfect reconstruction we used a symmetrization method for extending our signal on the boundaries to the next power of 2 of the time-series length. Symmetrization assumes that signals can be recovered outside their original support by symmetric boundary value replication. Details on the rationale of these schemes are given in Strang and Nguyen (1996).

3.4 One Step and Multi-Step Ahead Forecasting

Three groups of models were constructed: WANNdbN, ANNRaw, and MLR. The WANNdbN implies the alternative use of five different filter-banks: Haar, db2, db3, db4, db5. The ANNRaw is the non-denoised Artificial Neural Network that is used as a comparison model, as is the Multiple Linear Regression (MLR) model. Having considered that ANNs are embedded with a slight randomness in the initial attribution of weights that ultimately affect predictions, each model was reiterated 200 times with the aim of approaching statistically significant results.

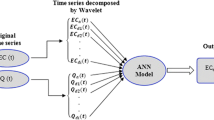
Model simulations begin from the original time series which is used both for building input matrices, as well as target vectors for model benchmarking (Fig. 5). In the WANN models, input matrices were filtered by Low-pass and High-pass filter-banks. High-pass decompositions were suppressed; Low-pass reconstructions were fed into the WANN models. The outputs of 200 reiterations per model were averaged, thereafter benchmarked against targets (i.e. “Compare” in Fig. 5) and ultimately saved as model results. It must be noted that given that only off-set output were used to infer model performances, and considering that off-set outputs can cover only 20 % of the forecasting domain at each model reiteration, the combined result of 200 reiterations per model provided about 30 different off-set forecasting per month for all the months of the forecasting domain.

Fig. 5
figure 5

Flow chart including data source, data pre-processing, forecasting, model comparison against targets and final results

Full size image

4 Model Comparison

We used several indices to obtain our estimates of model performances. Indices were selected to meet two objectives: (i) measuring the overall performance of the model over several reiterations; and (ii) comparing results among different models. The following indices were used: Fractional Standard Error (FSE), the coefficient of determination (R2), the correlation coefficient (R), the Nash-Sutcliffe model efficiency (E), and indication of the overall model performance was assessed using bias and the bias indicator (B). In particular:

  1. (i)

    Fractional Standard Error (FSE) is the RMSE divided by the corresponding mean of the targets (observed values). It is a scalable measure of model precision, expressed as:

    $$ FSE = \sqrt {{\frac{{\frac{1}{n}\sum\limits_{{i = 1}}^n {{{\left( {{T_i} - {Y_i}} \right)}^2}} }}{{\overline T }}}} $$
    (14)

    where T i , Y i , and \( \overline T \) are the observed, forecasted, and mean of the observed monthly water consumption, respectively. The model becomes more precise as the FSE reaches zero.

  2. (ii)

    The correlation coefficient (R), expressed as:

    $$ R = \frac{{{\sum\limits_{i = 1}^n {{\left( {T_{i} - \overline{T} } \right)}} }{\left( {Y_{i} - \overline{Y} } \right)}}} {{{\sqrt {{\sum\limits_{i = 1}^n {{\left( {T_{i} - \overline{T} } \right)}^{2} } }} }{\sqrt {{\sum\limits_{i = 1}^n {{\left( {Y_{i} - \overline{Y} } \right)}^{2} } }} }}} $$
    (15)

    The coeffcient R shows how much variability in the data set is accounted for by the model and provides a measure of how likely future outcomes will be forecasted. Values for R range from −1 to 1, with 1 referring to maximal correlation.

  3. (iii)

    The Nash-Sutcliffe model efficiency (E), expressed as:

    $$ E = 1 - \frac{{\sum\limits_{{i = 1}}^n {{{\left( {{T_i} - {Y_i}} \right)}^2}} }}{{\sum\limits_{{i = 1}}^n {{{\left( {{T_i} - \overline T } \right)}^2}} }} $$
    (16)

    E is used widely in hydrology because it measures the ability of the model to forecast values different from the mean. Values of E range from −∞ to 1, with 1 showing perfect model performance.

  4. (iv)

    Bias (B), expressed as:

    $$ B = \frac{{\sum\limits_{{i = 1}}^n {{Y_i}} }}{{\sum\limits_{{i = 1}}^n {{T_i}} }} $$
    (17)

    The index B provides a good measure of whether the model is overestimating (B >1) or underestimating (B < 1) compared to observed values. B = 1 indicates non-biased model performance.

5 Results

5.1 Denoising

The original time-series of monthly water demand was denoised by means of six wavelet filter-banks, namely, Haar, db2, db3, db4, and db5. The denoised versions are reconstructions of the original signal after the high-pass transforms were suppressed at the first level of decomposition (Fig. 6). Several levels of decomposition were tested but the first level was sufficient for suppressing the highest frequencies of the parent time-series. Higher levels of decomposition would be suitable for multi scale analysis. In this case wavelets were used as a denoising tool only; representing the parent series into different scales was not one of the objectives of the study.

Fig. 6
figure 6

Signal denoising. In (a) the original signal is presented, in the remaining plots the denoised time-series according to different filter-banks are presented

Full size image

Different filter-banks had different impacts on the original parent signal (Table 2). It was noted that: i) the parent mean is preserved by all filter-banks; ii) the variance of the reconstructions decreased when the number of vanishing moments in the filter-banks increased; iii) in all instances the data range of the reconstructed signals was smaller than the data range of the parent signal; iv) the norm of the difference between the parent and denoised versions increased with the number of vanishing moments in the filter-bank; and; v) the correlation coefficients (R) decreased when the number of vanishing moments in the filter-banks increased.

Table 2 Statistics of parent and denoised time-series
Full size table

5.2 Forecasting

We first present results for 1 month-ahead forecasting, thereafter multi-months ahead forecasting. The non-coupled ANNRaw and MLR models had correlation coefficients R = 0.84 and 0.77 respectively, and fractional standard error FSE = 2.6 % and 3.3 %, respectively. On the other hand the best coupled model, WANNHaar, had correlation coefficient R = 0.91 and FSE = 2 %. Models WANNdb2 and WANNdb3, although slightly less accurate than the WANNHaar, outperformed ANNRaw. ANNs coupled with db4 and db5 filter-banks did not outperform the non-coupled ANN (Table 3).

Table 3 Model-performances for 1 month-ahead forecasting
Full size table

WANNHaar also provided more accurate results than ANNRaw for each and every month separately (Fig. 7). February and September were the most problematic months to be predicted; nevertheless Haar filtering increased forecasting accuracy for those months too. It was noted that relatively large errors are also coupled with large variance in model outputs.

Fig. 7
figure 7

Comparison of WANNHaar versus ANNRaw on a month by month basis over the entire forecasting domain

Full size image

Focusing on the best model only (i.e. WANNHaar), the forecasting error is normally distributed around a zero mean and in 68.2 % of cases it is expected to be within ±0.038 (106 m3/month) from the mean. Visual observation suggested, and statistical analysis confirmed, that not all years can be predicted with the same accuracy (Fig. 8). For instance, the WANNHaar achieved best results in the forecasting of the year 2003, with a correlation coefficient between predicted and measured values equal to 0.98; on the other hand, in 2007, the same model achieved a correlation R = 0.88.

Fig. 8
figure 8

WANNHaar forecasts. Multi colored dots represent outputs of different experimental repetitions (Yr). Plain dots in violet represent model forecasts (Ym = mean of Yr). Black circles represent model targets (T)

Full size image

For the multi-step ahead forecasting WANNHaar, as well as WANNdb2 and WANNdb3, provided better results than non-coupled models at lag-time: 2, 3, 4 and 6 months (Fig. 9). A particular case is the 5th month ahead forecasting; at this time-lag: i) all models provided the largest errors and the lowest correlations; ii) in contrast to what had been previously observed, MLR, WANNdb4 and WANNdb5 returned the best performances. A table of results is presented in Annex A.

Fig. 9
figure 9

Error and correlation of model-output vs. targets at different time-lags

Full size image

When considering the variance of output generated by different iterations of the same model, it was observed that reducing variance in the input data-set (by means of denoising) resulted in increased variance in model outputs (Fig. 10). A particular case is Haar denoising; on the one hand it did not affect ANN stability, while on the other hand, it drastically reduced input variance (Fig. 10), preserving and actually increasing ANN performances (Table 3). A different case is provided by db5 denoising that induced an oversimplification of input patterns which resulted in both reduced ANN performances and increased ANN instability.

Fig. 10
figure 10

Input–output variance of WANN models

Full size image

Results can be summarized as follows: Haar, db2, and db3 filter-banks provided similar (and above average) performances for all lead times (with the exception of 5 months lead time); any extension in the future of the forecasting horizon corresponded to a decrease in forecasting accuracy; and lower variance in the input matrix resulted in higher instability of the outputs of the ANNs (with the exception of Haar filtering that provided high accuracy without affecting stability).

6 Discussion

ANNs do not require any a priori assumptions on the underlying process generating the data at hand. Nevertheless, in our case, the WANNdbN models are based on a fundamental assumption regarding the frequency domain of our dataset. In this respect, it is assumed that the original time series is likely to be affected by some type of noise either induced by intrinsic randomness in the studied phenomena, and/or imprecision of the water-meters. Noise is usually concealed in the shortest frequencies of the time-series, while meaningful information is likely to be carried in the longest frequencies. Wavelets, orthogonal waves of finite duration, can be used for localized denoising of non-stationary signals. In our case, wavelet-denoising was applied by suppressing high-pass coefficients at the first scale of decomposition as this was found to provide the best results. It was observed that filter-banks of type Haar, db2 and db3 improved neural performances.

The correlation coefficients between measured and forecasted values (for a lead time of one month) of the non-denoised network was R = 0.84 while, the same network trained with Haar-denoised input had a correlation of R = 0.91. The error over the entire testing domain followed suit, with RMSE = 0.045 for the ANNRaw, and 0.36 for the ANNHaar. With respect to multi-step ahead forecasting (for 2, 3, 4 and 6 months ahead), Haar, db2 and db3 improved the performance of the model. Forecasting of the 5th month returned contradictory results. In all instances wavelet filter-banks of type db4 and db5 did not improve the forecasting task assigned to the ANN.

We suggest that removing part of the variance from the original time series simplified the generalization process in ANNs. When considering ANNs as a pattern recognition device, denoising reduces the heterogeneity of the patterns presented to the network, thus facilitating classification (i.e. Haar, db2, db3). On the other hand, an oversimplification of the training-set can create ambiguities resulting in lower forecasting performances as well as greater network instability (e.g. db4, db5). However, variance alone cannot entirely explain the impact of denoising on ANN performance.

The original impact of signal denoising has to be found in the shape and the length of the filter-banks. In this respect, according to our preliminary results it cannot be excluded that wavelet transforms provided the best denoising (reflected by improved accuracy of ANN forecasting) when the filters had their highest coefficients as close as possible to zero. Thus, in our case, causal filters seem to have provided the best results when they could emphasize the most correlated components of the parent time series.

7 Conclusions

In this study we addressed the forecasting of future water consumption of the municipality of Syracuse, Italy. The objective was to build an adaptive tool that when trained may be readily used for operational applications such as water budgeting. We also attempted to tackle a problematic gap in the theoretical foundations regarding the choice of wavelets to be used in conjunction with ANNs for water resources forecasting applications.

Experimental results showed that first level decomposition by means of wavelet-filters can improve generalization in ANNs. In particular, filter-banks of type Haar, db2 and db3 alternatively coupled with the same ANN, provided more accurate forecasting than the non-coupled ANN, the Multiple Linear Regression and the coupled models with wavelets of type db4 and db5 on the forecasting horizons from 1 to 4 and 6 months-ahead. Preliminary results suggest that in our case, attenuation of variance in the input vectors may be a significant driver of improvements in ANN forecasting. It is also observed that variance alone cannot entirely explain the impact of denoising on ANNs. Thus, it cannot be excluded that using filters that can emphasize the components of the parent time series with the highest autocorrelation may be a key issue in the coupled wavelet-neural network models. Additional work will be required for a complete understanding of these findings, and the use of larger and more diversified datasets may help to confirm the empirical results obtained in this study. It is suggested that future investigations should be oriented to the featuring of tailor-made orthogonal wavelets, for time series denoising in an attempt to generate sparse neural-weight matrices in back propagation networks.