1 Introduction

Water is essential for all living things including human beings, and hence is one of our most important resources. Global warming and climate change significantly altering various environmental variables in many countries around the world. This situation could have important effects that seriously threaten the population as well as agriculture, environment, economy and industry. Changes in precipitation patterns directly affect water resources management, agriculture, hydrology, and ecosystems (Bostan and Akyürek 2007). All the necessary water for life on earth originates from rain. For this reason, it is important to understand the spatial and temporal patterns of rainfall and their variability in order to gain knowledge about the balance of water dynamics for water resources management, and to plan strategies for solving many problems such as predicting natural hazards caused by heavy rain (Shoji and Kitaura 2006; Cannarozzo et al. 2006; Diodato et al. 2010). Exploring the spatial distribution and variation of precipitation can contribute to ideas about water resources in the future, and helps to make plans for stabilizing environmental conditions. It is also recognized that trends in precipitation are one of the key climatic variables that affect the future, in terms of population growth, economic expansion and, in the longer term, climate change, which affects both the spatial and temporal patterns of water availability (Shoji and Kitaura 2006; Basistha et al. 2008; Yılmaz and Harmancığlu 2010).

In recent years, geographical information system (GIS) technology has been increasingly used in a wide variety of disciplines such as resource management, asset management, archeology, cartography, surveying, environmental assessment, scientific investigations, urban planning, criminology, meteorology, and climatology With the advent of GIS technology, large amounts of spatial data were able to handled, and sophisticated ready-to-use spatial statistical techniques were included in GIS software (Erdoğan 2010). The main aims of spatial analyses are the description and visualization of geographical events, the exploratory spatial analysis of the pattern of events, and spatial interpolation and modeling (Haining 2003). As stated by many researchers, useful methods of rainfall analysis are based on techniques of spatial analysis and interpolation using information collected from rain gauges in relevant areas (Goovaerts 2000; Şen and Habib 2001; Naoum, and Tsanis 2004; Li et al. 2010). Spatial interpolation of rainfall from point measurements depends on existing spatial relationships, which derived from the relationships shown at the measured point values.

Among all the meteorological and hydrological parameters, rainfall is the most difficult to predict due to its inherent variability in time and space. In meteorological researches, interpolation methods have been applied to assess changes in magnitude in spatial dimensions. A number of methods have been proposed for the interpolation of rainfall measurements, obtainable from irregularly distributed sites up to gridded networks (Şen and Habib 2000; Bargaoui and Chebbi 2009). These methods offer a good approach to the spatial distribution of the magnitude of changes, but provide no information on their significance (Mardikis et al. 2005; Basistha et al. 2008). Furthermore, spatial analysis of trends is rarely carried out (Suppiah and Hennessy 1998; De Luis et al. 2000). While geostatistical interpolation methods such as Kriging were shown as superior to these methods in some researches (Tabios and Salas 1985), several studies showed deterministic methods to be superior (Dirks et al. 1998; Apaydın et al. 2004). Şen and Habib (1998) alternatively presented the point cumulative semivariogram method of spatial precipitation assessments in mountainous areas.

In Turkey, many previous studies regarding trends in surface climatic variables focused on temperature and precipitation patterns (Türkeş et al. 1996; Kadıoğlu 1997). A number of trend analysis studies are available for rainfall analysis (Türkeş 1996; Partal and Küçük 2006; Tayanç et al. 2009; Türkeş et al. 2009). Türkeş (1996) used various non-parametric tests to identify the long-term spatial and temporal characteristics of Turkish annual mean rainfall over a period of 54 to 64 years. In addition, Partal and Kahya (2006) used the Mann-Kendall test and Sen’s T test to verify regional hydro-climatic conditions using 96 rainfall measurement stations across Turkey for monthly totals and for calculating their annual mean values. Recently, Türkeş et al. (2009) analyzed long-term changes and trends in a series of monthly, seasonal and annual precipitation totals using 97 stations for the period between 1930 and 2002.

Obviously, meteorological variables cannot be measured in all places at all times. Only samples, mainly in the form of specific point observations, are available at irregular intervals. Therefore, to estimate precipitation accurately, it is necessary to have rain gauges distributed in optimal locations, and to apply appropriate interpolation techniques for estimating important parameters. Trend-related studies about Turkey have predominantly concentrated on the temporal dimension of rainfall data. Spatial analysis of trends and signs of trends has not been carried out. Moreover, there is no study describing rainfall trends, which include different interpolation algorithms covering the whole country. In this context, and considering all these factors, this study is aimed at the analysis of trends from rainfall records, and to point out the presence of spatial patterns in these trends by using different spatial interpolation techniques in GIS environment.

2 Data and Methods

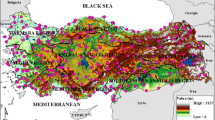
Turkey lies within the north subtropical climatic zone of the earth, situated between 36°–42°N and 26°–45°E. All coastal areas of Turkey are influenced by mild maritime weather, which occurs in a Mediterranean type of climate (Şen and Habib 2001). The information used in this study was collected from data obtained from 120 rainfall-measuring stations between 1975 and 2009. The density of the distribution of these stations is shown in Fig. 1. All stations had continuous measurements over a period of 33 years. Monthly and annual precipitation totals (mm) were obtained from the Turkish State Meteorological Service.

Fig. 1
figure 1

Location and density of the distribution of the meteorological stations

Full size image

Analyses of the trends in rainfall data were identified using the Mann-Kendall non-parametric test. This test is known as the Kendall’s tau statistic, which is a non-parametric test, meaning that it does not assume any priority in the distribution of the data and allows the presence of a tendency over long period of rainfall data to be observed. It was found to be an excellent tool for trend detection in different applications (Lettenmaier et al. 1994; Burn and Hag-Elnur 2002; Libiseller and Grimvall 2002; Machiwal and Jha 2008).

The World Meteorological Organization (WMO) has also suggested using the Mann-Kendall method for assessing trends in meteorological data (WMO 1988). The Mann-Kendall rank correlation statistic τ is derived from the following equation;

$$ \tau = {\frac{{4\sum\limits_{{i = 1}}^{{N - 1}} {{n_i}} }}{{N\left( {N - 1} \right)}} - 1} $$
(1)

The Mann-Kendall test has two parameters that are of particular importance for trend detection. These parameters are the slope magnitude estimate, which indicates the direction as well as the magnitude of the trend, and the significance level, which indicates the value of the test. A positive value in the test results indicates an upward trend while a negative value indicates a downward trend.

It is known that meteorological time series may show serial correlation and the existence of serial correlation will affect the ability of the Mann-Kendall test (von Storch 1995). The majority of the previous studies have assumed that sample data are serially independent (Yue and Wang 2002; Yue and Wang 2004). In order to decrease the influence of serial correlation on the Mann-Kendall test, pre-whitening was proposed by von Storch 1995. Some studies documented that von Storch’s prewhitening is only suitable for eliminating the influence of serial correlation on the MK test when there is no trend exists. Therefore, prewhitening has the disadvantage of accepting the hypothesis of no trend with a high probability when a trend exists (Yue and Wang 2004). Bayazit and Önöz (2007) suggested that prewhitening should be applied except when the sample size and the magnitude of slope are large, or when the coefficient of variation is very small.

3 Interpolation Procedure

Interpolation methods are techniques that estimate the value at a given location by using values from sample points. For each computation, the values of rainfall trends from measured points are weighted according to the existing spatial relationships of their locations. Therefore, it is important to find procedures devised to understand the relationships among the recorded values at various points in a given region. In the interpolation process three different algorithms Inverse Distance Weighting (IDW), Kriging and Radial Basis Function (RBF) algorithms were used and compared in order to find both monthly and annual rainfall trends. The IDW and Completely Regularized Spline algorithms were applied to describe the changes in the magnitude of the trends as determining methods. Of these, IDW method is a simple but effective interpolation method, which is based on the assumption that the values of the variables at the points to be predicted are similar to the values of nearby observation points. IDW implies that each station has a local influence, which decreases with distance by means of the use of a power parameter (Isaaks and Srivastava 1989).

The general formula of IDW is

$$ \widehat{Z}\left( {{s_0}} \right) = \sum\limits_{{i = 1}}^N {{\lambda_i}} Z\left( {{s_i}} \right) $$
(2)

where;

\( \widehat{Z}\left( {{s_0}} \right) \) :

is the value of prediction for location S0

N:

is the number of measured sample points surrounding the prediction location

λ i :

are the weights assigned to each measured point

Z(S i ):

is the observed value at the location si

The weighting is a function of inverse distance. The formula determining the weighting is

$$ {\lambda_i} = \frac{{d_{{i0}}^{{ - p}}}}{{\sum\limits_{{i = 1}}^N {d_{{i0}}^{{ - p}}} }} $$
(3)

The IDW method requires the choice of a power parameter and a search radius. The power parameter p, controls the significance of measured values on the interpolated value based upon their distance from the output point (Erdoğan 2009). The choice of a relatively high power parameter ensures a high degree of local influence and gives the output surface increased detail. The power parameter in this study was optimized by using cross validation method. The search radius has been specified by choosing at least four neighboring stations.

RBF algorithms are conceptually similar to fitting a rubber membrane through the measured sample values while minimizing the total curvature of the surface. The selected RBF algorithm determines how the rubber membrane will fit among the values (Burrough and McDonnell 1998). There are several types of spline functions. These methods are a linear combination of the different basis functions. The general formula of RBF is;

$$ \widehat{z}\left( {{s_0}} \right) = \sum\limits_{{i = 1}}^n {{w_i}\phi \left( {\left| {{s_i} - {s_0}} \right|} \right) + {w_{{n + 1}}}} $$
(4)

where;

ϕ (r):

is a radial basis function

\( r = \left| {{s_i} - {s_0}} \right| \) :

is the Euclidean distance between the prediction location s0

wi: I = 1,2,..n:

are the weightings to be estimated. In a completely regularized spline (CRS) this function is

$$ \phi (r) = - \sum\limits_{{n = 1}}^{\infty } {\frac{{{{\left( { - 1} \right)}^n}{{\left( {\sigma .r} \right)}^{{2n}}}}}{{n!n}} = \ln {{\left( {\sigma \sigma /2} \right)}^2} + {E_l}{{\left( {\sigma \sigma /2} \right)}^2} + {C_E}} $$
(5)

Here, σ is the optimal smoothing parameter which is calculated by minimizing the root mean square errors using cross validation, and El is the exponential integral (Mitasova and Mitas 1993).

Lastly, Ordinary Kriging (OK), which provides statistically unbiased estimates of surface values from a set of observations at recorded locations, was performed using the estimated spatial and temporal covariance model of the observed data as discussed in Cressie (1993). Kriging provides a means of interpolating values for points using knowledge about the underlying spatial relationships in a data set to do so. Variogram provides this knowledge. Kriging is based on regionalized variable theory, which provides an optimal interpolation estimate. Instead of the Euclidian distance, Kriging uses the semivariogram as a measure of dissimilarity between observations. The semivariogram is a function of both distance and direction, and so it can account for direction-dependent variability. The variogram suggests how optimally the rain gauges are set.

The semivariogram is the key function of geostatistics and represents the variability of spatial and temporal patterns of physical phenomena. Usually, a mathematical variogram model is fitted to empirical semivariogram values calculated for given angular and distance classes. Lag distances used in the empirical semivariogram were determined by calculating the average distance from each station to its nearest neighboring station. The parameters of the variogram model (sill, range and nugget) were then used to assign optimal weights for spatial prediction using cross-validation. The general Kriging model is based on a constant mean μ for the data and random errors ε (S) with spatial dependence.

$$ {\text{Z}}\left( {\text{s}} \right) = \mu \left( {\text{s}} \right) + \varepsilon \left( {\text{S}} \right) $$
(6)

where;

Z(s):

is the variable of interest

μ(s):

is the deterministic trend

ε (S):

are the random, auto correlated errors.

Variations on this formula form the basis for all the different types of Kriging. OK assumes a constant, unknown mean, and estimates a mean value in the researched neighborhood.

4 Performance of the Interpolation Methods

The performance of the interpolation methods can be evaluated in different ways. The most straightforward is to predict some single, global accuracy measurements that characterize the interpolation accuracy via a different validation method. In this way, the accuracy of the interpolation process can be assessed and compared using cross-validation. The most common form of cross-validation is the “leave one” method, which consists of temporarily removing one rainfall record at a time from the data set and performing the interpolation and re-estimating the value from the remaining data from the station. The comparison criteria are the root mean square error (RMSE), mean error (ME), and maximum error. The cross-validation results are shown in Table 1.

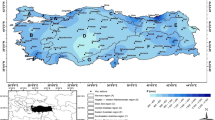
Table 1 Cross-validation results for the interpolation algorithms
Full size table

It should be noted that the accuracy of the interpolation using the cross-validation method assumes uniform error values for the entire country. This assumption of uniformity is invalid and interpolation errors could be spatially variable. In this context, the spatial distribution of absolute errors introduced by the interpolation methods was examined by plotting the location and magnitude of the absolute errors and by obtaining a graphical representation of accuracy by generating error maps. Error maps of the three interpolation methods for the whole year are shown in Fig. 2.

Fig. 2
figure 2

Error maps of algorithms

Full size image

Furthermore, global (Morans I, Getis-Ord general G) and local spatial autocorrelation (Local Moran I, Getis Ord Gi*) methods were also used to check the extent of error clustering in the interpolation process. Moran’s I was used to identify and measure the strength of spatial patterns, while the general G statistic was used to measure concentrations of high or low error values of over the entire country. Positive Moran’s I values indicated spatial clustering of similar values while negative ones indicated the clustering of dissimilar values. High values for the G statistic indicated that high error values were clustered within the study area while low ones indicated that low error values tend to cluster (Erdoğan 2009).

As shown in Table 2 both the IDW and CRS algorithms showed a significant clustering of errors in 3 months’ trend analyses using Moran’s I. The OK algorithm did not show a significant clustering of errors in any month’s trend detection. These indices yield only one statistic to summarize the whole country. In other words, these analyses demonstrate homogeneity. However, if there is no global autocorrelation or clustering, clusters can be still found at a local level in the country. Therefore, the local version of Moran’s I and the Getis and Ord’s Gi* statistics were used to detect local pockets of dependence. The clustering of errors at local levels in the country for annual precipitation trends are shown in Fig. 3.

Table 2 Results of the cluster analysis of errors
Full size table
Fig. 3
figure 3

Cluster maps of algorithms for annual precipitation trends

Full size image

5 Results and Conclusion

The aim of this study was to compare different interpolation algorithms on rainfall trends in Turkey. The study was performed by using monthly and annual rainfall data, recorded from 120 rain gauge stations during the period 1975–2008. These stations are not very homogeneously distributed over the Turkey as can be seen in Fig. 1. The M–K test was applied to monthly and annual precipitation records. According to the resulting test statistics obtained from the Mann-Kendall rank correlation test, both upward and downward trends in the precipitation records were found to be statistically significant at the 5% and 10% level in many stations. The interpolated trend results of the precipitation records are shown in Fig. 4 at the 5% and 10% level of significance using a completely regularized spline method.

Fig. 4
figure 4

Interpolated maps of monthly M-K trends according to the CRS algorithm

Full size image

In the monthly results, there is an apparent downward trend in precipitation totals for January, February, March, April, and May. However, a substantial upward trend for August, October, and December is apparent. While the east of the Black Sea region has an upward trend in precipitation totals for all months, the Salt Lake region has a downward trend for all months except October. At the same time, the results showed that significant positive trends are very infrequent and were found only in a few stations in March, April and October. Instead, significant negative trends were much more common, mainly in annual and January, February and May. A great number of stations with a statistically significant negative trend were located in the middle regions of Turkey.

Trend analysis results were subjected to spatial analysis and interpolation. Visualization using proportional symbols to show trends in the rain gauge stations was the first step towards a spatial data analysis. As seen in graphical representations of meteorological records, stations on the north, south and west coasts and in southeastern Anatolia were seen to have higher precipitation values but only the northeast coast showed significantly upward trends. Next, interpolation processes were performed using the OK, IDW and CRS algorithms.

The three assessment criteria provide us different information about the method’s reliability. By comparing the ranking of the studied interpolation methods, based on the assessment criteria, it was clearly indicated that the criterion RMSE led to somehow different results than the other two criteria. These assessment criteria provide us with different information about the method’s reliability, thus they should all be taken into account together in order to have a more complete and detailed description of the method’s performance. More particularly, ME is an indicator of bias but it should be used cautiously as an indicator of accuracy, since it usually tends to be lower than the actual error because negative and positive values counteract each other. RMSE is an indicator of the sensitivity to outliers (Nalder and Wein 1998). RMSE indicates the magnitude of extreme errors and it is low when there is a central tendency and extreme errors are small. (Ashraf et al. 1997; Mardikis et al. 2005).

According to the results, the OK algorithm performed slightly better than the others did. The CRS algorithm showed the worst values in terms of RMS. Although the OK algorithm produced the smallest RMS values, the difference in the average of the RMS values was not seen as significant according to an ANOVA test. Furthermore, as shown in Figs. 2 and 3 the error maps of the IDW and CRS algorithms showed a clear clustering of error regions around the country. In addition, the OK error map showed poor clustering around the study area.

Upon examination of the cross-validation and spatial error clustering results, the OK method was concluded to be the best algorithm in the interpolation process. However, the performance of these methods when applied to one set of data is likely to be different from that used on a larger data set. As a result of this study, OK method must be preferred for the spatial analysis of trend values. Meanwhile, to increase the best interpolation results it is highly advisable to obtain data from close neighboring regions.