Sources of students’ frustration in pre-university level, prerequisite mathematics courses

Abstract

This paper looks at sources of frustration in students of “prerequisite” mathematics courses (PMC), that is, courses required for admission into undergraduate programs in a large, urban, North American university. The research was based on responses to a questionnaire addressed to students and interviews with students and instructors. In the design of the questionnaire and the analysis of responses, an “institutional” theoretical perspective was taken, where frustration was conceived not only as a psychological process but also as a situation experienced by participants in a concrete educational institution. Several sources of frustration were identified as important in the group of respondents: the fast pace of the courses, inefficient learning strategies, the need to change previously acquired ways of thinking, difficult rapport with truth and reasoning in mathematics, being forced to take PMC, insufficient academic and moral support on the part of teachers, and poor achievement. These sources of frustration are discussed from the point of view of their impact on the quality of the mathematical knowledge that students develop in the PMC. Consideration is also given to the possibilities of improving the quality of this knowledge, given the institutional constraints implicated in the sources of students’ frustration.

Introduction

This paper looks at sources of frustration among students of “prerequisite” or “bridging” mathematics courses (PMC) required for admission into undergraduate programs in a large, urban, North American university (“The University”), where students are admitted based on their previous education records (not on entrance examinations) and pay a tuition fee for their studies. These are courses in elementary algebra, linear algebra, functions and one variable calculus. They are offered by the mathematics department of The University for candidates who, for some reason, had not taken them in secondary school or college, and now need them as prerequisites to academic programs of their choice.

These courses are difficult to teach. Some students behave as if they were unjustly forced to take them, protesting about the irrelevance of the course material for their future studies or professions. Some others accept the need to take the courses but complain about the teachers, or the material being too hard. The word that comes to mind in describing the emotions that sometimes flare in classes, the word “frustration” comes to mind. Our research was an attempt to better understand the sources of this frustration.

The study belongs to the area of research on affect¹ in mathematics education (for surveys of this area, see Reyes 1984; McLeod and Adams 1989; McLeod 1992; Malmivuori 2001; Zan et al. 2006; Smith III and Star 2007), particularly in relation to adults learning (FitzSimons 1994a, b; FitzSimons et al. 1996; FitzSimons and Godden 2000; Evans 2000). In this area, attitudes toward mathematics and beliefs about mathematics have received more attention than emotions. Emotions are the least stable components of affect and are therefore very difficult to study. Interviews or questionnaires can only produce rationalizations of past emotions; they do not allow observing actual emotional processes. However, knowledge about rationalizations of emotion can be useful in mathematics education; it may help in planning to deal with emotions in teaching and learning situations.

This study used a questionnaire and interviews and therefore only rationalizations of frustration could be obtained. But this approach was consistent with our goal in the study, which was understanding the reasons, or sources, of students’ frustration, based on students’ rationalizations of their frustrations and researchers’ interpretations of students’ rationalizations. We were particularly interested in sources related to the fact that students’ learning was taking place in a concrete institution, namely the “PMC.” Learning mathematics in any educational institution may be an emotional process, but there may be specific emotions involved if this institution is PMC, where people are told at the outset that they have some “deficiency” in their academic preparation. Therefore, in this research, it is important both that the learning and teaching takes place within an institution, and that this institution is the institution of PMC.

The data were obtained through interviews with four teachers and six students, and 96 students’ responses to a questionnaire² with 76 items. Sixty-three of the 96 students were “mature”, i.e., according to the definition of The University, 21+ years old and having spent some time away from formal education. At the time of answering the questionnaire, the student-respondents were enrolled in four courses, devoted, respectively, to basic algebra, precalculus focused on trigonometric functions, precalculus focused on exponential and logarithmic functions and one-variable calculus.³

Analyses of the data were structured by:

• 1. A conceptualization of frustration as deception or disappointment;

• 2. A framework for analyzing institutions;

• 3. A distinction between mature students and non-mature students and

• 4. Discrimination between four different positions from which respondents could speak about their experience with PMC: as Persons—members of the society at large; as Learners—cognitive subjects; as Students—subjects of a school institution who have to abide by its rules and norms, and as Clients of this institution who pay for services and have the right to evaluate their quality.

It would be impossible to give justice to all aspects and details of the study in a single journal article. Therefore we decided to publish the raw data and most of the technical details on the web.⁴ We also wrote a separate paper (Sierpinska et al. 2007) about participants’ expression⁵ of emotions and its relations with the positions and achievement. Preliminary results of the study were presented in a conference paper (Sierpinska 2006).

Although the analysis of the data includes quantitative results, such as a higher frequency of one source of frustration over another—we do not attach much weight to them. The sample is small compared to the whole (and changing) population of PMC, and it is a single and opportunistic sample. The merits of this study are more in that it draws attention to certain legitimate sources of students’ frustration and poses questions about the purpose of PMC if they continue to be designed and taught the way they are at The University.

The present paper has seven sections including this Introduction. The second section describes the theoretical framework used in the study; the third—some aspects of the methodology. The fourth section gives an overview of the results about sources of students’ frustration; the fifth contains a discussion of the results; the sixth—a reflection on possible solutions to the problem of students’ frustration. The last section offers a few remarks on avenues of future research.

Theoretical framework

In this paper, “theoretical framework” refers to a set of variables that we used to name and explain the sources of PMC students’ frustration. The choice of these variables was guided by our deliberate decision to consider frustration not only as a psychological process but as a “situation” experienced by participants in a concrete institution.

In this situation, participants were learning mathematics. Following Illeris (2004), we assumed that all learning involves not only cognitive, but also emotional and social processes.

A conceptualization of frustration as an emotion accompanying deception or disappointment proposed by Handa (2003) was consistent with our perspective—one that focuses on rationalization of sources of people’s frustration—and we adopted it in our research. The choice of this conceptualization is justified in more detail in (Sierpinska et al. 2007).

All learning has a social dimension: it involves interactions between the learner and his or her social environment. This environment can be made of spontaneous encounters with other people. But it can also be structured by an educational institution. These are very different learning situations (see, e.g., Lave 1988; Brenner and Moschkovich 2002). In our study, this educational institution was a sector of a university: a set of PMC. We decided to focus on sources of PMC students’ frustrations related to aspects of this particular institutional environment (and not, for example, to individual personality traits or life histories).

To structure our study around this institutional perspective ⁶ on learning, we identified certain crucial elements of PMC as an institution and of participating in this institution as a student. We drew inspiration from two main sources: general theories of institutions in sociology and political science (Crozier and Friedberg 1980; Peters 1999; Ostrom 2005; Ostrom and Hess 2007) and the framework of praxeology developed within mathematics education research by Chevallard (e.g., 1999, 2002).⁷

In the next section, we present the concept of institution adopted for the purposes of our research. This presentation introduces and explains the meanings of variables used in our theoretical framework. In the subsequent section we show how we used these variables to formulate our hypotheses about sources of frustration and discipline our analysis of the data.

A concept of institution

Reflection on institutions has a long history, including Plato’s The Republic and Aristotle’s Politics. Twentieth century has seen a proliferation and diversification of theoretical approaches to institutions (Peters 1999). Looking for commonalities among this variety, Peters identified four features that are widely accepted as characterizing an institution, and distinguish it from other kinds of social activity:

• 1. An institution is a structural feature of a society, where the structure may be formal (as in a legal framework) or informal (as in networks of organizations or in sets of shared norms).

• 2. An institution has some stability over time.

• 3. An institution constrains the individual behavior of its members (also called “participants”), through more or less explicit and formal rules and norms.

• 4. Members of an institution share certain values and goals and give common meaning to the basic actions of the institution (summarized from Peters 1999: 18).

Theories of institutions vary in aspects on which they focus. Crozier and Friedberg (1980) and Ostrom (2005) highlight the fact that institutions are active bodies. An institution is a “collective action” (Crozier and Friedberg 1980), structured within a network of other such actions; the action is purposeful, enforced and regularized (Ostrom 2005). Chevallard (2002) also focuses on institutional activity, since the main object of his theory is the practice of teaching and learning of mathematics as regularized by curricula, typical school tasks, legitimate techniques of solving them and discourses used to justify these.

We now discuss in more detail the “purposeful, enforced and regularized collective action” characteristics of institutions in a way which blends Ostrom’s, Crozier and Friedberg’s and Chevallard’s theories, and also explains the necessity of certain elements of an institution. In particular the “technology” and “theory” elements of Chevallard’s praxeology find their justification here.

An institution is purposeful collective action

Society organizes itself to achieve certain objectives, obtain certain outcomes (Ostrom 2005) or fulfill certain tasks (Chevallard 2002).⁸ Objectives can be described as desirable outcomes. But, of course, a collective action will have actual outcomes, expected and unexpected; desirable and less desirable (those less desirable and unexpected are called “perverse effects” in Crozier and Friedberg 1980: 99).

An institution is enforced action

There are sanctions for not participating in the action or for not participating in the way prescribed by rules, norms and strategies that are considered legitimate (Ostrom and Hess 2007: 50; Ostrom 2005: 139–140). Institutions are social artifacts, not natural phenomena (Crozier and Friedberg 1980: 97). They are the result of conscious social and legislative effort; they are not just spontaneous behavior that has acquired the status of “normal” or “routine” proceeding in given circumstances. Not every practice is an institution. For example, education through participation in family or community activities is not an institution as long as the society does not define this activity as a task producing valuable outcomes and has no sanctions against parents failing to engage in it.

Institutions are regularized collective actions

Regularization is mediated by division of labor, coordination of actions and, of course, a specific discourse (the “logos” part of Chevallard’s “praxeology”: technology and theory). The discourse allows regularization to be made explicit and justified; it makes it possible to define when a task has been accomplished or an objective—reached, and to teach all this to others. Without the discourse, it would be hard to enlist participants and their collaboration would be difficult to obtain. The justification is necessary, because—as stressed by Crozier and Friedberg (1980: 3)—an institution’s reason for being and its ways of functioning are forever put into question. Teaching would not be possible if the institution had not developed some communicable tools for accomplishing types of tasks (routines, procedures, techniques, strategies...).

Participants’ actions are regulated and coordinated by rules, norms and strategies of accomplishing the tasks and achieving the objectives. Ostrom’s framework for institutional analysis and development carefully distinguishes between these three forms of regularization by analyzing their representations as “institutional statements”, i.e., parts of the institution’s discourse (Ostrom 2005: 139–140).

A rule is an institutional statement that specifies which subgroup of participants is obliged or forbidden to do so and so in such and such circumstances, or else faces such and such sanctions. An example of a rule could be, Candidates to the Commerce program must have passed Course X or else they will not be admitted. A norm has the form, “in such and such circumstances, such and such subgroup of participants will normally do so and so.” Thus a norm has all the components of a rule except for the sanctions. For example, Teachers will normally devote the last class of the course to a review of the whole material is a norm, because no sanctions can be applied to teachers who decide not to do that. Strategies are what a certain subgroup of participants tends to do in certain circumstances. For example, Teachers who did not have the time to review the material in the last class of the course sometimes organize an extra class session for their students.

Where there is enforced action, rules and regulations, there is inevitably a struggle for power, be it power to make the rules and regulations, or agency in deciding about matters that the institution leaves to the discretion of participants. The first kind of power imposes constraints, the second aims at preserving autonomy in spite of the constraints. In Crozier and Friedberg (1980) this duality of constraints and autonomy is used in their definition of the “organizational phenomenon” (of which institutions are a kind):

[T]he organizational phenomenon is a political and cultural construct. It is the instrument which the social actors forge in order to “govern” their interactions in such a way as to obtain the minimum cooperation necessary to the pursuit of collective objectives, while preserving their autonomy as relatively free agents. (Crozier and Friedberg 1980: 97)

From the point of view of an individual’s rapport with an institution (as a client or a member), the above duality can be interpreted also as follows: constraints are welcome if they force other people to help me obtain what I want, and frustrating insofar as they constrain my autonomy. It makes sense therefore to look for sources of frustration of PMC students in aspects which constrain their autonomy.

In the above we have used the words “power”, “autonomy” and “agency.” These words are also frequently used in mathematics education research, in various contexts and meanings. We clarify below how we use them in our research.

We use the word “power” in Ostrom’s sense: “the ‘power’ of an individual in a situation is the value of the opportunity (the range in the outcomes afforded by the situation) times the extent of control” (Ostrom 2005: 50). Control, roughly speaking, is the probability that the individual’s intervention will change the outcomes of a collective action. It may be small or it may be big, but it is only a potential. Even if this potential is close to 1, no opportunity to actually intervene means no power. For example, one variable that the PMC students control is study time. However, they may not have the opportunity to exercise this control, because of family obligations or a part-time job. Another variable they control is attention in class, but in this case opportunity to actually exercise this control is not lacking. Even if only a few students refuse to listen, (Sesonske 1966)⁹ putting down their pens, turning around and talking to their neighbors, the lecture is interrupted. Refusal to listen thus gives students some power over the content of the lectures.

A participant “has agency” in an institutional situation if he or she “makes things happen”, according to Wagner’s (2007) interpretation of Pickering’s (1995) notion of agency. If one makes things happen, then one has power, i.e., both control and opportunity. Association of “agency” with “power” is consistent with the way these words are used, for example, by Gutstein (2006) or Diez-Palomar et al. (2007). “Autonomy” as it is used by Crozier and Friedberg (1980), implies having agency or power, but highlights the independence associated with power. While agency and power draw attention to acting or doing things, independence suggests the possibility of refusing to act. Independence means both that one will not be forced to do certain things, and that one will be able, without external help, to do the things that are essential for survival in the situation.

We will distinguish between “agency” and “sense of agency.” A participant may enjoy a sense of agency without having agency. Sense of agency means that the participant believes he or she makes things happen in a situation. Agency means that the participant actually makes things happen. It may not be obvious which is the case in more complex institutional situations. For example, in a discussion on a mathematical question in a classroom, two games are simultaneously going on: the social game of winning an argument and the mathematical game of deciding what is true and what is false through reasoning. An eloquent and popular student may have a sense of agency, seeing that he or she is influencing the choice of the course of argumentation and/or solution. But the student may have actual agency only in the social game and not in the mathematical game, if the arguments he or she uses do not settle the mathematical question. Solving the mathematical problem requires playing by the rules of the mathematical game, focusing on consistency (and not, for example, on simplicity or easiness of a method) and using reasoning (rather than, for example, rhetoric, vivid metaphors or reference to the authority of a learned procedure). The risk of confusion between social and mathematical agency in discussion-based classrooms is one of the hardest problems to solve in mathematics education (see, e.g., Balacheff 1991; Arsac et al. 1992).

A framework for an institutional analysis of sources of PMC students’ frustrations

Prerequisite mathematics courses form an institution: they satisfy the minimal conditions put forward by Peters (1999). Firstly, they form a structural element of a larger institution, The University, which appoints the department of mathematics to organize the courses, appoint course coordinators and hire instructors. Secondly, PMC are a stable and regular element of the teaching operation of the mathematics department, established several decades ago. Thirdly, PMC constrain the behavior of some candidates for The University; most students enrolled in these courses do not have the option of not taking them. Participation in each course is, moreover, regulated by administrative rules (e.g., deadlines for registration, deadlines for dropping out, supplemental examination rules, deferred examination rules, penalties for not having paid the fees, rules for reimbursement of fees in case of dropping the course) as well as academic rules (e.g., writing the final examination). There are, moreover, mathematical rules, implied by the mathematical theory taught in the course, which must be respected or else the student loses marks and the teacher is considered incompetent. There are also norms that are not as explicit as rules, yet sometimes equally binding: for example, norms of classroom behavior, or norms of writing and presenting solutions that may be suggested by the teacher in one way or another. Finally, PMC satisfy the condition of shared values: The need of a certain level of mathematical skills and knowledge in the study of psychology, computer science, engineering or commerce has long been taken for granted at The University, as it has in the society at large. Students, therefore, do not massively protest against the rule of PMC. Faculty may debate about the details of the content of the courses, teaching approaches, or yet about the position of the courses in the structure of the university (e.g., whether the management of calculus courses for candidates to engineering should be delegated to the engineering department or left with the mathematics department), but the reason of being of PMC is never put into question.

The University and PMC have their tasks to accomplish and they are governed by their own rules, norms and strategies, communicated and justified using a range of discourses. One of the tasks of PMC is to select candidates to academic programs. Ranking students using grades greatly facilitates this task. Another is to prepare candidates for the programs as fast as possible, so as to save both the candidates’ time and The University’s resources. This yields intensive, fast paced courses.

Trying to imagine the situation of the individual student in PMC and hypothesize possible sources of frustration, we assumed the following:

• The participant tries to preserve as much autonomy as possible within the existing constraints (rules, norms, strategies), and feels frustrated when losing this autonomy;

• The participant may share some of the goals and values of the institution but may resist others; he or she may consider some of the constraints as superfluous (e.g., question the “PMC rule”, i.e., the requirement of taking PMC for admission into certain academic programs);

• Rules, norms and strategies of the institution may be ambiguous; participants may feel deceived by their assumptions concerning these (e.g., thinking that since the content of PMC is pre-university mathematics, the style of teaching will be similar to that in secondary school, and then being surprised by the fast pace of the courses);

• Participants have their individual desired outcomes (e.g., getting admitted to Commerce) and tasks (e.g., learning mathematics; passing the course) within the institution; but they may be...

  • disappointed with the actual outcomes of their actions (e.g., poor achievement or failure)

  • disappointed in achieving their goals by finding the tasks excessively difficult (e.g., finding mathematics hard or the examination difficult)

  • deceived by the strategies they used for accomplishing the tasks (e.g., memorizing solutions to past finals and finding the actual final examination very different from the past ones).

We also assumed that participants may experience PMC in different ways, depending on their position at the moment, whether as Persons, Learners, Students or Clients. For example, for the Person, mathematics is part of the world; for the Learner, it is a mental activity; for the Student, mathematics is a course. Students not only engage in certain mental activities but are called on to demonstrate the outcomes of this mental activity within the more or less formal constraints imposed by this institution. From the position of the Client, mathematics is a price to pay for gaining admission into a desired field of study.

Our hypotheses were reflected in the design of a questionnaire which we briefly describe in the next section.

Methodology

We describe only the research instrument—the questionnaire—here, and we focus on its structure corresponding to our theoretical framework. Other methodological details such as: justification of the choice of courses from which we recruited participants, detailed description of the hypotheses about sources of frustration underlying the questionnaire items, and an outline of the procedures used in analyzing responses are described in Sierpinska et al. (2007).

The questionnaire items were inspired by existing research instruments for research on affect (e.g., Haladyna et al. 1983; Schoenfeld 1989), interviews with PMC instructors, and the first two authors’ experience as PMC instructors. The closed items were mostly statements with which respondents could agree, disagree or remain neutral. The statements were speaking about various elements of the PMC institution, from the positions of Person, Learner, Student and Client (see the overall structure of the Questionnaire in Table 1). We were trying to cover as many aspects of the students’ experience as appeared relevant from the point of view of the hypothesized sources of frustration.

Table 1 The structure of the questionnaire

Consistent with our adopted notion of institution and especially the importance of autonomy in an individual’s rapport with an institution, we were particularly interested in students’ sense of agency in relation to their task of learning mathematics (18 items were devoted to the task). A sense of lack of agency with respect to the value of one’s mathematical productions could be an important source of frustration for especially the mature PMC students because it stands in stark contrast with the likely sense of agency in their out-of-school lives (Bandura 1989). By coming back to school these people have demonstrated to themselves that they are capable of deciding about their lives. As parents, at home, they are the ones who tell others what is right and what is wrong. They may be doing this as bosses at work as well. And here they are, as students in a mathematics course, being told what’s right and what’s wrong by a teacher sometimes younger than themselves.

In the questionnaire, one item directly addressed the participants’ perception of control over the correctness of their solutions in mathematics (item 56. I need the teacher to tell me if I am right or wrong). More indirectly, this issue was addressed in items where participants’ judgment about what counts as correct answer or solution in mathematics was probed. For example, in item 72, participants were asked if writing a final answer to a problem as “2/4” rather than as “1/2” should be considered as a minor, major or no mistake. Two items (74 and 75) asked respondents for their preferences between two kinds of solutions to inequalities with absolute value. One of these solutions was incorrect. We describe these items in more detail below.

Item 74. Given a problem: Solve |2x−1| < 5. Which solution do you like better?

• Solution a.

• |2x−1| < 5

• 2x−1 = 5    neg.    2x−1 = −5

• x = 3                    x = −2

• Answer: −2 < x < 3

• Solution b.

• We use the theorem: |a| < b ⇔ −b < a < b

• |2x−1| < 5 ⇔ −5 < 2x−1 < 5 ⇔ 2x−1 > −5 and 2x−1 < 5 ⇔ x > −2 and x < 3

• Answer: −2 < x < 3

Item 75. Given a problem: Solve |2x −1| > 5. Which solution do you like better?

• Solution a.

• |2x−1| > 5

• 2x−1 = 5    neg.    2x−1 = −5

• x = 3                    x = −2

• Answer: 3 > x > −2

• Solution b.

• We use the theorem: |a| > b ⇔ a < −b or a > b

• |2x−1| > 5 ⇔ 2x−1 < −5 or 2x−1 > 5 ⇔ x < −2 or x > 3

• Answer: x < −2 or x > 3

Solutions of type “a” are commonly taught in high school. The technique consists in reducing the solution of an inequality to solving two equations and then following certain rules to write the final solution to the inequality. Solutions “b” in items 74 and 75 refer explicitly to theorems about properties of absolute value and use logical deduction; the difference between the logical connectives “and” and “or” is stressed. The rules underlying the technique of type “a” are not well remembered by students, who also often have poor understanding of the notion of solution to an inequality. Therefore, there are usually many mistakes in students’ solutions. Solution “a” in item 75 is incorrect; it resembles mistakes that students make in this kind of problems.

We now present our results.

Results related to sources of students’ frustration

The following conventions will be used in the presentation of the results. Frequencies of types of responses in the questionnaire will be given in the form of a triplet of pairs of numbers: A% (A1), B% (B1), C% (C1), where A is the percentage of all 96 respondents to the questionnaire who gave the answer of a given type; A1 is the number of these respondents; B is the percentage of the 63 mature students who gave this type of answer and B1 is the number of these respondents; C is the percentage of the 33 non-mature students who gave this type of answer and C1 is the number of these respondents. A1 is the sum of B1 and C1.

This section contains a general overview of the sources of students’ frustration identified as important in the research. In the overview we will refer to Table 2, which represents a ranking of sources of frustration according to the number of respondents that could be affected by them. The place of a source of frustration in the ranking is represented by a Roman numeral.

Table 2 Sources of frustration with at least 40% frequency in at least one group of participants

The order of ranking in Table 2 is from the highest to the lowest frequency among all respondents. For each source, the table mentions also the positions from which it could be experienced as frustrating (column 4) and the institutional elements involved (column 5). The positions and institutional elements for a given source of frustration are those corresponding to questionnaire items used in calculating the frequency of the source. These items are mentioned in column 4 of Table 2. The correspondence between questionnaire items and positions and institutional elements was taken as assumed in Table 1. Only some details on how the frequencies were obtained will be given in this paper. Justification of all frequencies listed in Table 2 is available on the web.¹⁰

Ranking of the sources of frustration

Eleven sources of frustration were identified as affecting more than 40% of all 96 respondents. The highest ranking was the fast pace of the courses: students could be deceived by their expectation that pre-university level courses should be taught at a slower pace, more common in secondary school or college. But PMC are intensive courses, with relatively little class time; students are expected to study a lot on their own. Second and third ranking were frustrations of learning strategies or ways of thinking, which did not seem successful or adequate in PMC. Disappointment with having to take mathematics courses as a condition of admission into academic programs ranked only sixth; deception by insufficient feedback on the part of the teachers ranked seventh, deception by lack of moral support on the part of the teachers—ninth, and disappointment with achievement—tenth.

Ranking fourth, fifth, eighth and eleventh were sources of frustration related to the “nature of the task”—in this case, learning mathematics—and involved students’ difficult rapport with mathematical truth and reasoning. Many students showed lack of interest in verifying the validity of a solution to a mathematical problem and had a preference for procedural rather than reasoned solutions. Yet, concern with truth and deciding about truth by reasoning are characteristics that distinguish mathematics among other domains of knowledge. Some students were annoyed by these characteristics of mathematics and felt more comfortable in other subjects where reasoning and concern with truth are not so important. Missing one aspect in discussing a social problem does not matter so much as long as interesting thoughts are offered about other aspects; in mathematics, missing one case, for example, in solving an inequality with absolute value, leads to incorrect solution and a strict teacher might give 0 marks for it. Some other students appeared to not even notice these characteristics of mathematics, and tried to do mathematics as if truth and reasoning did not matter, which led to deception when achievement was not as good as hoped for. We rationalized the source of these latter students’ frustration as a consequence of their rapport with mathematical truth and reasoning (in this case—ignoring these aspects of mathematics).

These sources of frustration did not rank the highest among our respondents. But they are important from the point of view of the goals of the PMC institution and the quality of students’ participation in it. As we will further argue in the Discussion section, dislike or disregard for truth and reasoning in mathematics is a threat to students’ autonomy as mathematics learners. It constrains the scope of their participation in the PMC institution and raises doubts about the relevance of the knowledge they learn for their future studies and professions. Moreover, students’ rapport with truth and reasoning in mathematics is related with the highest ranking sources of frustration. The fast pace of the courses may, in fact, encourage learning by rote. There is no time to acquaint students with the conceptual relations necessary for reasoning and deciding about the consistency of a solution.

Explaining how the frequencies in Table 2 were calculated for each source of frustration would take too much space in an article. We had to make a choice and, for reasons outlined above, we decided to speak about the sources of frustration related to students’ rapport with mathematical truth and reasoning, even if they did not rank the highest in the group of our respondents.

Some details about sources of frustration related to students’ rapport with mathematical truth and reasoning

Our evaluation of the magnitude of respondents’ dislike or disregard of the concern with truth in mathematics was based mainly on responses to item 75, presented earlier in this paper, where students were asked to express their preference between two solutions to an absolute value inequality, one of which was incorrect (see Table 3 for frequencies).

Table 3 Distribution of students’ responses in items about absolute value inequalities

We also sought signs of students’ rapport with mathematical truth in their essay responses to open items. More specifically, we looked at

students’ reasons for liking or not liking mathematics (Item 66. Do you like math? Yes, No, Neutral, Explain why),

their attribution of achievement in items 67 (If you did well in a course, complete the sentence, “I did well in a course because...”) and 68 (If you didn’t do as well as you had hoped in a course, complete the sentence, “I didn’t do well in a course, because...”),

their descriptions of mathematics in item 76 (Complete the sentence, “ Math is...”).

We also took into account data from interviews with students.

Altogether, based on the absolute value items, essay responses and interviews, 68% (65), 59% (37), 85% (28) students were counted as having a dislike of or disregard for the concern with truth in mathematics. The difference between mature and non-mature students is striking here. It appears that maturity could be associated with a higher concern with truth.

The intersection of the set of these respondents with the set of those who agreed with Item 9. I was enthusiastic about coming back to school represented 54% (52), 56% (35), 52% (17) of the respondents. It is on this basis that being enthusiastic about coming back to school but frustrated with the concern with truth in mathematics, ranked fourth. This source of frustration does not distinguish between mature and non-mature students.

Taking PMC for credits and grades but finding an obstacle in mathematics’ concern with truth ranked eighth as a source of frustration. This ranking was based on the intersection of the set of students who disliked or had no regard for truth in mathematics with the set of those who were taking the prerequisite courses for credits and grades (Item 65. I took the math course because... (c) the academic advisor told me to, or (f) Other: the course was a prerequisite), which counted 45% (43), 37% (23), 61% (20) respondents and ranked eighth (note the difference between mature and non-mature students).

When evaluating the magnitude of sources of frustration related to students’ rapport with mathematical truth and reasoning, we first thought that students’ agreement with the statement, “I need the teacher to tell me if I am right or wrong” (item 56) should count as representing the students’ disregard for truth in mathematics. However, at least one of the students who agreed with this statement also discovered that solution “b” in item 75 was incorrect. Therefore, we did not use responses to item 56 in evaluating students’ relation with mathematical truth. We interpreted these responses as reflecting students’ poor sense of agency or dependence on teachers with respect to the value of their mathematical productions. This value may not be the same as truth value. The “right or wrong” distinction may be different from the “true or false” distinction. Still, dependence on teachers for the evaluation of their solution may be associated, in some students, with a belief that mathematical truth and reasoning are teacher’s business, not theirs. Our instrument of research did not allow us to identify students holding this belief.

The only way to tell a true statement from a false one in mathematics is by reasoning. But respondents’ rapport with reasoning was also a difficult one. This is the object of sources of frustration ranked fifth and eleventh.

Respondents’ dislike or difficulty with reasoning in mathematics was mostly inferred from students’ responses in the questionnaire and from what they told us in the interviews rather than from their saying anything explicit to this effect. Only five students made explicit statements about their dislike of or problems with reasoning in mathematics. However, students’ preference for procedural solutions over reasoned ones in items 74 and 75 (Table 4) suggests a widespread reluctance to making explicit the theoretical basis and reasons for calculations, this reluctance being much more frequent among non-mature than among mature students. Altogether, dislike or difficulty with reasoning in mathematics was found in 63% (60), 56% (35), 76% (25) of respondents. Let us call this set R.

Table 4 Sources of frustration related with an institutional element and experienced from a position

The intersection of R with the set of those who agreed with Item 9. I was enthusiastic about coming back to school counted 50% (48), 51% (32), 48% (16) respondents (source V). The intersection of R with the set of those who were taking PMC for credits and grades (i.e., chose option c or said “the course was a prerequisite” in option “other” in Item 65. I took this course because...,) counted 45% (43), 37% (23), 61% (20) respondents (source XI). Note the difference between mature and non-mature students.

Very few respondents made reference to reasoning in their explanations for choosing one or the other of the solutions to absolute value inequalities in items 74 and 75. The common explanations were that solutions “a” were “simpler”, “easier” and “clearer.” The choices of solutions “b” were justified by reference to reasoning in at most two responses.

Interviews with students suggested that respondents rarely read and tried to understand the reasoning in items 74 and 75, even when they chose the “b” solutions. One of them said she chose solutions “b” because she was more used to this type of solutions.

Interviewed students spoke about the specificity of mathematical knowledge and thinking as a source of their frustration also outside of the context of items 74 and 75. Here is an example.

The student (female, non-mature) planned to study accounting. She had to take prerequisite pre-calculus and calculus courses. She passed them only in second attempt.

Interviewer: So you are saying that you are “not intelligent in math.”

Student: Oh no, not at all, and I’ll admit it.

I: Why do you think you are not intelligent in math?

S: Because I failed twice... Because I always felt you could wiggle your way out in anything else, like, unless it’s science or mathematics, or statistics, something that’s solid, that’s been proved, that this is what it is. (In social science) you can always have a theory; you can always have your own theory. This is your opinion because so and so and so. In math I could never do that.

Awareness of the specific character of mathematics statements, as “something that’s been proved”, in itself, is not, of course, a sufficient reason for frustration. But in this particular student, this was associated with her difficulties in “understanding the logic behind it”, as she was saying. She could not “prove it to herself.” She gave us the example of her problems with the derivative of the function y = x: “I don’t understand what’s the derivative of x and why it’s 1.” She told us that she went to ask her teacher but all she heard was an angry lecture on how she should have already known it, by doing her homework and reading the book. She failed the course with this teacher. She said she had a nicer teacher the second time she took the course, but still had trouble getting control over her work:

My teacher in the summer, he was a great teacher, he explained well and everything, but it’s just that I could never grasp, like I couldn’t be comfortable enough to sit down in front of an example and do it on my own, instead of looking back at my notes. Okay, what rule was it and why did I do this? I just never understood the logic behind it, even though... he was a great teacher, he gave us all possible examples and he used very simple words..., start from the very easy and try to add things on to make it more difficult. But... how I studied for the final? I was looking at the past finals... All by memorizing, that’s how I passed (this course) the second time.

One of the variables in our research was maturity of students. We expected that students’ age and time away from institutionalized education would make a difference in the sources of their frustration. We present our results about this aspect in the next section.

Differences between responses of mature and non-mature students

Differences between responses of mature and non-mature students were not very big. The reason could be that, in a less technical sense than the formal university rule which classifies as mature anybody over 21 years old and having spent some time away from formal education, all our respondents were “mature students.” They were all past the usual age for studying the level of mathematics taught in PMC, which is high school or college mathematics. The differences were a bit larger in sources of frustration related to academic and moral support (sources VII and IX) where the frustration affected non-mature students respectively 1.8 and 1.3 times more often than the mature students. As one of the instructors said in an interview, younger students more often expect to be “babied” at the university. Also in sources VIII and XI, related to students’ rapport with mathematical truth, the difference was noticeable: non-mature students were about 1.6 times more likely to be frustrated than mature students.

Relative importance of institutional elements and positions in students’ frustration

We attempted to rank the importance of the various institutional elements for their role in respondents’ frustrations, and we tried to do the same with the positions of Person, Learner, Students and Client.

We used the following scheme. We first summarized, from Table 2, the positions and institutional elements involved in the 11 sources of frustration. For example, the institutional element “The University” was associated with four sources, namely sources with ranks IV, V, VI and IX (see column 5 in Table 2). All these sources were associated with the position of Person; sources IV and V were, moreover, associated with the position of Learner; source VI was associated with the position of Client, and source IX—with the position of Student. We listed these associations in Table 4, where rows correspond to institutional elements and columns—to positions (as in Table 1, the structure of the questionnaire).

In Table 4 we also indicated the highest rank of a source (in terms of frequency of responses) associated with each institutional element (column 6), and with each position (second row from below). We also noted the number of different sources of frustration associated with each institutional element (last column) and each position (last row).

Thus, each institutional element and each position became associated with a pair (Roman numeral from I to XI, Hindu-Arabic numeral from 1 to 8). We then introduced the following ordering in the two sets of numerals: XI < X < ... < II < I and 1 < 2 < ... < 8 (rank XI is lower than rank X; one source or frustration is less than two sources of frustration associated with an institutional element or position), and used these orderings to define a lexicographical ordering among the pairs:

$$ {\text{(R1, a1) < (R2, a2)}} \Leftrightarrow {\text{R1 < R2 and (if R1 = R2 then a1 < a2)}} $$

Thus, the order of the pairs which appear in columns 6 and 7 is:

$$ {\text{(IX, 1) < (VIII, 1) < (VI, 4) < (IV, 4) < (IV, 5) < (II, 2) < (I, 2) < (I, 3) = (I, 3)}} $$

Looking at the above sequence from right to left, we interpreted this ordering as a ranking of institutional elements from the most to the least associated with students’ frustration:

Participants’ outcomes (achievement) and tools (i.e., knowledge, ways of thinking, techniques of solving problems, strategies for learning, studying, problem solving);

Rules, norms and strategies governing PMC as a whole;

Didactic contracts in particular PMC classes;

Participants’ task of learning mathematics;

The University;

The PMC rule;

Participants’ task of taking mathematics courses;

Teacher–student rapport.

The order of the pairs which appear in the last two rows of Table 4 is:

$$ {\text{(IV, 4) < (I, 7) = (I, 7) < (I, 8)}} $$

Again, looking at the sequence from right to left, we interpreted it as a ranking of the positions from the most to the least associated with students’ frustration: Learner, Student or Client, Person.

Taking both rankings into account, we concluded that frustration was the most likely to arise for our respondents as Learners as they struggled with the inadequacy of their knowledge, and their strategies for learning and studying. Next ranking is the frustration of the student disappointed with his or her achievement. The position of Person had the weakest association with frustration with any institutional element. This last result is consistent with results about students’ emotional experience of PMC, presented in Sierpinska et al. (2007).

We did not quite expect the frustration with the PMC rule and with teachers to come so far in the ranking. We thought students would blame mostly others or the circumstances, from the positions of Student or Client. But, in fact, most of the sources of frustration appeared to be related with participants’ task as Learners of mathematics. Even the highest ranking source—the fast pace of the courses—is indirectly related with learning: the task of learning mathematics is made harder if a lot of material must be learned in a short period of time. As one student wrote in her explanation of reasons for not having done as well as she had hoped in a course, “I had hard time learning the material, we would learn a new chapter almost every week which didn’t give me time to let it sink in.” Sources ranked second and third were also linked to learning: being disappointed with the strategy of learning by following teacher’s example, and deceived by having to change one’s ways of thinking.

In the next section, we proceed to look at our results from the perspective of hypotheses used in the construction of our research instrument.

Discussion of the results

The general aim of our study was to better understand the reasons—or sources—of students’ frustration in PMC. We were not interested in frustration as a psychological and physiological process, or in describing it as it occurs in various situations. Our focus was rather on rationalizing sources of students’ frustration, under the essential assumption that teaching and learning take place within the institution of PMC. Another important assumption was that students may be frustrated by factors related to the institutional aspects that constrain their autonomy. Such were the main hypotheses underlying our research; they guided our method and provided us with a set of variables that allowed us to label and to explain the sources of PMC students’ frustration.

In the discussion of the results of our study, we organize our thinking along the aforementioned institutional elements. But we will not exactly follow the order in which these elements were mentioned in our hypotheses about sources of frustration or in the table representing the structure of our questionnaire (Table 1), and we will not discuss each of them separately. This could lead to repetition. For example, in our hypotheses, mathematics appears twice: as the knowledge content of the PMC courses and as the object of learning in the participant’s tasks and tools. It will be convenient and logical to discuss all these aspects at once. We do so in the subsections titled, “Content constraints: PMC are courses in mathematics” and “Content constraints: Syllabi of particular courses.”

Admission rules

University is the highest level of educational institution. Accordingly, entering a university is associated with high hopes. However, universities have strict rules of admission, which may temper the candidates’ enthusiasm. One of the rules is that candidates to certain programs will take prerequisite courses in mathematics (the “PMC rule”). Based on our impressions as teachers in PMC and on the literature on adults’ affect in PMC (FitzSimons and Godden 2000¹¹), we presumed that the PMC rule would cause frustration in many candidates. However, this hypothesis was not quite confirmed in the group of our respondents, who were as likely as not to be frustrated with the PMC rule (with little difference between mature and non-mature students).

Time constraints

The University has rigid rules for the length of courses. The content of undergraduate courses is also quite rigid; any change requires a lengthy procedure. The same applies to the pre-university level mathematics courses offered as prerequisite courses. But in the case of PMC, the time constraints appear harsher because each course is supposed to cover in a term what, in high school or college, is done in a whole year.

It is the fast pace of the courses that appeared to frustrate most students. To give an idea of how fast the pace can be we offer the following information, related to teaching inequalities with absolute value in one of the precalculus courses. The syllabus for week 4 of the course lists the topics, “Other types of equations; Inequalities; Absolute value equations and inequalities.” The class time allotted for a week is 2.5 h. Therefore, in the whole course, the teacher has about 50 min for absolute value equations and inequalities. Knowing the extent of students’ conceptual difficulties with the notion of absolute value (Chiarugi et al. 1990; Gagatsis and Thomaidis 1994; Major 2006), it is unlikely the teacher can address even the most basic of these difficulties in the given time. But without understanding the concept, students have no means to judge if what the teacher states or writes on the board, or what they write as a solution is true or false. They thus become dependent on the teacher’s judgment for the validity of their solutions.

Content constraints: PMC are courses in mathematics

Prerequisite mathematics courses students have no control over the object of study as such: it is mathematics and they cannot substitute courses in another subject to satisfy the prerequisites. There are two aspects of mathematics that we assumed to possibly underlie students’ frustration with the subject. One aspect was epistemological in nature, the other—psychological, related to the belief that mathematics is hard. We discuss the epistemological aspect first.

Mathematics has certain epistemological characteristics which cannot be changed by the will of students or teachers, and which do constrain their freedom of expression. In mathematics, it is not the individual’s opinion that counts, but mathematical truth, which is decided by reasoning and not by a speaker’s or writer’s power of persuasion.

This does not mean, however, that there is no room, in mathematics, for individual creativity and human agency (see, e.g., Pickering 1995, for the discussion of human agency in mathematics and science). Within the constraints of logical consistency, there is freedom in choosing the most convenient approach to a modeling problem, constructing an ingenious proof or inventing particularly insightful and operational analytical and graphical means of representation. Research mathematicians have also the freedom to choose the most elegant, in their eyes, organization of a theory, the most economical definition or the most important problem to solve. They bend the conventions and modify the concepts through generalization, specification or analogy and thus create new mathematical worlds or gain new insights into the already constructed ones. For the creative mathematicians, the constraints of consistency are but rules of “the mathematical game”, where the moves are decided by reasoning (Drouhard et al. 1999; Sackur et al. 2005; see also Paquelier 1988; Margolinas 1992). These epistemological constraints make their work all the more challenging and exciting.

This freedom is not accessible to students who don’t even enter the mathematical game, showing no interest in verifying if a solution is correct of not, preferring solving problems by following prescribed procedures rather than using reasoning, and leaving the responsibility for the validity of their solutions to teachers. Many students in our study appeared to satisfy this description.

Students’ lack of interest in mathematical truth is well supported by research. For example, Evans (2000: 179) found the “capacity for critical evaluation of one’s thinking” extremely rare among his subjects—adults—as they engaged with school mathematics and everyday situations involving calculation (e.g., reading pay slips). Similar observation was made by Kantowski (1977, cited in McLeod and Adams 1989: 27): “students seldom look back, or review the problem solution.... Instead, once a solution has been proposed, students tend to lose all interest in the problem and go on to other tasks.” Lester et al. (1989: 83) observed that “some individuals have a propensity for sticking to a task without regard for getting a correct answer”; one of the students in their research said, “Confidence depends on the feeling that I understand how to do it, not in getting the right answer.”

We now turn to discussing the psychological aspect of mathematics assumed as a possible source of frustration.

Mathematics is commonly regarded as “cognitively challenging” (Boaler and Greeno 2000: 171). When designing the questionnaire, we assumed that this belief, combined with a negative attitude to mathematics or lack of success could be a source of frustration for students. It was, but not for many respondents. The belief that mathematics is hard was expressed by slightly over half of the respondents.¹² But this does not mean that the perception of mathematics as hard was considered by all these students as a source of frustration. Some of these students enjoyed the challenge of mathematics. When we counted only responses indicating that this perception was a reason for a negative attitude to mathematics or for lack of success in a course, then the frequency was rather small, about 20%.¹³ Thus the perception of mathematics as “hard” did not appear as a major source of frustration in the group of respondents.

This result is consistent with Boaler and Greeno’s (2000) observations of high school Advanced Placement Calculus classes with two different teaching approaches: Didactic-teaching and Discussion-based. The mathematical content in all these classes was harder than what these students had experienced before, but this was not the reason why some of them were rejecting mathematics as an area they would want to study more of in college or university; of the 17 students in the research who had this negative attitude to mathematics, 16 were students in the Didactic-teaching classes.

Content constraints: the syllabi of particular courses

In principle, students might have some influence on the choice of the particular mathematical topics of study in a given prerequisite course. They might negotiate the specific content of a given course from the position of Clients of the university institution. If a sufficient number of students filed a petition to change the content of a course to fit better with their future study and profession, the curriculum committees of relevant departments and faculties would have to consider introducing some changes in the course outline. But, if the sample in our research is at all representative of the PMC students’ population, the petition might not receive a sufficient number of signatures. Although 59% of our respondents said that they would “rather not take the (mathematics courses) if they had a choice” (item 13), only 34% also considered the material in the courses useless for them in the future (item 64).¹⁴ Lack of agency relative to the choice of the content of the prerequisite courses cannot be considered, therefore, as a major source of frustration.

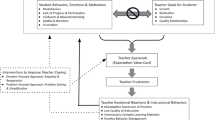
Didactic contract

Second ranking in our study was the frustration of students’ strategy of learning by following teacher’s examples, which, if applied uncritically, may lead to limited, inflexible knowledge and poor achievement. Unfortunately, the didactic contract in PMC may encourage this learning strategy. The courses are lecture-based and focused on procedures and formulas. They satisfy Boaler and Greeno’s (2000) description of “didactic-teaching”: “students come to class, watch teachers demonstrate procedures, and then practice the procedures—alone” (p. 177). According to these authors, this pedagogy is consistent with students’ loss of agency in mathematics and preference for procedural solutions:

Traditional pedagogies and procedural views of mathematics combine to produce environments in which most students surrender agency and thought in order to follow predetermined routines. (Boaler and Greeno 2000: 171).

Instructors’ choice to focus on procedures and techniques useful in solving final examination questions could be explained by the institutional necessity to ensure the “minimum collaboration”¹⁵ on the part of the students and avoid massive failure in the courses. Given the little time available for each topic in the fast paced courses, theory would have to be presented at the expense of solving typical problems. This, instructors fear, could cause an increased failure rate, not to mention the students’ protest. Thus theorems and formulas are presented without proofs, and their meaning is conveyed through examples, graphical representations and application in exercises. However, the graduate students and research professors who teach these courses do not usually provide students with procedural shortcuts or memorization aids (such as the “FOIL Method”¹⁶ for multiplying binomials). Some don’t even know these didactic aids, popular among high school teachers; others refuse to compromise their mathematical integrity by using them.¹⁷ Therefore, students who expect such recipes from teachers are disappointed. Some treat the worked out examples as a substitute for such recipes and memorize their superficial aspects as clues to follow. But then they may be unable to see conceptual connections between problems formulated in a slightly different way. Moreover, teachers can never cover all possible examples, and thus, without understanding why rules and formulas hold and why techniques lead to true statements, students cannot be sure which elements of the worked examples can be generalized to other examples. Therefore, the strategy of “following teacher’s examples” does not always work.

The strategy of “following teacher’s examples” makes students dependent on teachers. Stodolsky et al. (1991) suggest that such dependence on teachers may be specific to mathematics, and students are more autonomous in other subjects. But Boaler and Greeno (2000) claim that dependence on teachers is relative to teaching approaches and that in “discussion-based teaching” students are able to develop autonomous behaviors and a sense of agency toward mathematics.

The “didactic contract”, in the sense of Brousseau (1997), is not an explicitly spelled out set of rules and norms. Most of the time, students only know there is a rule when someone breaks it. The contract is conveyed indirectly, through examples of “good solutions” and “bad solutions”, through feedback on students’ productions, and meanings conveyed by the teacher’s language. This language may be not quite neutral relative to agency (see, e.g., Wagner 2007). It can suggest a didactic contract in which the teacher has the ultimate authority in deciding on the correctness of students’ solutions. It can shift students’ attention from mathematical issues to issues of agency in a social situation.

Such could be, indeed, a consequence of the common use of the words “right” and “wrong” in relation to students’ mathematical productions. These words shift the students’ attention from the truth value of a mathematical statement to the personal worth of the person uttering this statement. Telling a student, “you are wrong” or “your solution is wrong” carries an important emotional charge. Being wrong means not being knowledgeable or not smart enough. Having done something wrong—producing a wrong solution—is associated with punishment: one deserves a bad grade.

In Schoenfeld’s (1989) research on students’ beliefs about mathematics, one statement, with which his subjects could agree or not, was “In mathematics something is either right or wrong.” Many (over 60%) respondents disagreed, because, for them, the statement was not about the epistemological specificity of mathematical statements, but about grades and marking. They were speaking about the values that the school institution attributes to students’ mathematical productions: right, wrong, partly right, incomplete, careless computational mistakes but reasoning approximately correct, etc. Using words “true” and “false” would not convey such meanings but many teachers find them artificial and reserve them for courses in logic or introductory courses in mathematical proof techniques.

By using the words “right” and “wrong” instead of “true” and “false” teachers inadvertently put students in the position of Students rather than Learners relative to mathematics. As Learners of mathematics, students and teachers have equal rights relative to making judgments about the mathematical truth of a statement. But in the positions of Student and Teacher, the former is in a subordinate position to the latter. In an educational institution, the Teacher is called on to make judgments about the value of the Student’s productions, and this value is not necessarily equivalent to the mathematical truth value. The teacher may take away points for mistakes in English or for not reducing a fraction to lowest terms—in fact, many respondents considered writing 2/4 instead of 1/2 a “minor mistake” in Item 72 of our questionnaire.

Teacher–student rapport

Prerequisite mathematics courses students have little control over the choice of teachers. In free comments in the questionnaire and in the interviews, some students used very harsh words to blame particular teachers’ lack of teaching skills or unpleasant behavior for their frustrations. But these were few. More students were affected by systemic features of teacher–students’ rapport, characteristic of university courses: not enough feedback on their solutions and not enough moral support (e.g., understanding of their difficulties to manage life and school duties). Both could be described as caused by a “decreased access to and relations with teachers” at the university as compared with high school, a change that was highlighted in Smith III and Star (2007) as an important aspect of problems of transition between school levels.

Achievement

Candidates must not only pass but obtain good grades to be admitted into certain more popular programs (e.g., commerce). For those who take the mathematics courses mainly for credits and grades (and not, e.g., for developing their analytic skills) and thus equate learning mathematics with taking mathematics courses, poor achievement is frustrating. In our study, almost 70% of the respondents were taking the courses for credits and grades, and about two-thirds were not happy with their results. But this source of frustration affected only about two-fifths of the respondents. To some extent this result corroborates Smith III and Star’s (2007) finding that “disposition¹⁸ can be quite independent from achievement.”

Thinking habits

The content of PMC courses being high school or college mathematics, some students may find it familiar. They are obliged to take the courses because their grades in analogous courses in high school or college were not high enough for admission into their programs of choice. They thus do not expect having to change their previously developed ways of thinking. But, in PMC, the approach may be more formal than in high school. For others, the material is new and may require a different way of thinking. For example, familiar mathematical symbols used in arithmetic or algebra (like the sign of equality) acquire a very different meaning in the context of limits in calculus, and the arithmetic or algebraic notions of equality function as obstacles in the new domain (see, e.g., Artigue 1999). Assuming that changing one’s habits of thinking is a cognitively demanding and emotional experience, especially in adults (e.g., Knox 1978: 445; Sierpinska 1994: 151), and especially when the change is from thinking in concrete contexts to abstract and formal thinking in mathematics (FitzSimons et al. 1996: 774) we concluded that respondents who found that they could not think the way they were used to or liked¹⁹ could feel frustrated. This source of frustration affected about two-thirds of respondents with no difference between mature and non-mature students,²⁰ ranking third in our list.

Ways of thinking are experienced as sources of frustration from the position of Learner. As argued in the Sect. “Results”, among our respondents, frustration was most likely to be experienced from this very position. From the point of view of instructors (rather than university administrators) this is an optimistic result. Instructors are powerless in the face of students’ frustrations as Clients, but they have many opportunities to interact with students as Learners and, if they are able to have some control over students’ learning, they can make a difference in their ways of thinking in mathematics. Control, however, requires knowledge and understanding of students’ problems as Learners. We hope that our research can contribute to the development of this knowledge and understanding.

Reflection on some possible “solutions” to the problem of PMC students’ frustration

We reflect, in this section, on the possibility of reducing the effects of some of the sources of students’ frustration discussed in this paper.

Are on-line courses a solution to the negative effects of the fast pace of prerequisite courses on the quality of students’ ways of learning mathematics?

“Too-much, too-fast” came up as a major source of frustration for the participants in our study. But the reduction of the material taught in the courses is not an easy thing to do. The PMC courses are instituted formally as content-equivalent to certain secondary school or college courses and the content of the former can be changed only if the content of the latter is changed. Changes in secondary school or college curricula are not under the jurisdiction of The University. A solution could be to spread the content over a longer period of time and have a two-semester course where there is now a one-semester, intensive course; one could extend the class time, add tutorial sessions in smaller groups, etc. But this would substantially increase the costs of the PMC operation for The University. Not all students would be happy, either, with extended course time and class time. Two-semester courses would further delay their admission into the university programs. More class time would make it more difficult for students to keep their part-time jobs. If not able to work while they study, many students would have to give up the idea of getting a university education.

Presently, some teachers and administrators at The University have started seeing a solution to the “too-much, too-fast” problem in on-line (or “web-based”) courses (Engelbrecht and Harding 2005a, b). One PMC course already has an experimental on-line version. On-line courses would, indeed, allow students to study each unit at their own pace and at a convenient hour, without having to spend 2–3 h in traffic to come to class. However, the results are not guaranteed as far as other sources of students’ frustration are concerned. Unless the situation has improved dramatically since a survey conducted in 2000, an overwhelming majority of websites designed for mathematics learning are based on “hierarchical, highly structured and directed instruction mode” (Mioduser et al. 2000; cited in Gadanidis et al. 2002), which might deepen students’ tendency to learn by following the worked out examples and worsen their already fragile rapport with mathematical truth and reasoning. The fact that the majority of websites have these characteristics means that they are easier to design. On the other hand, development of on-line courses that would support conceptual learning and autonomous behavior in mathematics requires a non-trivial operational understanding of the complexity of learning in computerized environments (Trouche 2004) and careful design of new tasks and activities that must be substantially different from those typically found in the existing textbooks for college or undergraduate mathematics courses (Stroup 2005).

Much is certainly to be learned from researchers observing and experimenting with computerized learning environments, but the solutions proposed by mathematics educators do not always apply to the institutional and economical conditions in which courses such as PMC are taking place. For example, Borba and Villareal (2006) strongly advocate inquiry-based learning, putting projects, problem solving and modeling at the core of the study, and even giving students the option of choosing the subject of investigation themselves. This approach is likely to enhance students’ sense of agency and help reducing the sources of frustration related with students’ rapport with mathematical truth and reasoning. But, as rightly pointed out by FitzSimons (2007), in order to become a stable element of any course, projects would have to be awarded an important weight in assessment. Projects are, however, long-term and team endeavors, which also require more costly assessment procedures than the usual 3-h paper-and-pencil, individually written final examinations now used in PMC.

Are discussion-based classes a way to improve students’ rapport with mathematical truth and reasoning and therefore help them develop agency as Learners of mathematics?

From the position of Student, it is not mathematical truth that matters but “a sufficient number of sufficiently good answers” on a test, obtained not by reasoning but by knowing which procedure to apply in a given problem. This is not a desirable outcome of mathematics education, and if this is what students learn in PMC then these courses do not prepare them for applying mathematics intelligently and creatively in their future studies and professions. But how can a student not perceive his or her relation to mathematics from the position of Student, if this is the position assigned to him or her in any school institution?

According to educational reformers and researchers, it is possible to engage students with mathematics more as Learners than as Students even in institutionalized education. Boaler and Greeno (2000) make strong claims about the encouraging effects of discussion-based classrooms on the development of sense of agency and positive attitude to mathematics, and the adverse effects of “didactic-teaching” classrooms.

There are doubts, however, if these results can be generalized. Students in Boaler and Greeno’s (2000) research were all high attaining and high socio-economic status students. Neither is true about students in PMC. According to Lubienski’s research (2000) with high school students, the socio-economic status is an important variable whose value may change the effects of pedagogical approaches. Discussion-based classrooms may even have a negative impact on lower socio-economic status students’ understanding, achievement and self-confidence.

Another variable that could change the outcomes of the discussion-based pedagogy is the mastery of the language of instruction. In PMC classes, many students are not fluent in the language of instruction. They could feel intimidated by students with a good mastery of the language, even if they found the discourse of the latter not mathematically interesting or correct.

Moreover, according to the recent survey of research on the impact of reformed mathematics programs by Smith III and Star (2007), little is known about the “specific kinds of mathematical proficiencies that students develop in different programs.” Students in the discussion-based classrooms in Boaler and Greeno’s (2000) research had better attitudes toward mathematics, a good sense of agency and reported actually thinking and reasoning in mathematics classes, but we don’t know what mathematical competence they developed that students in the didactic-teaching classrooms did not. In our research we did not look at the PMC students’ mathematical competence, either. We have deplored their disregard for mathematical truth and reasoning. But our research instrument did not allow us to draw conclusions about PMC students’ rapport with mathematical truth and reasoning when they are actually engaged in solving problems. Perhaps in these situations this rapport is more complex and deeper than what we could glean from our research. We are presently engaged in studying this hypothesis, observing and interviewing PMC students as they solve problems.

Are some tasks better than other for the development of more autonomous, and therefore less frustrated, learners?

Students’ control over the validity of their solutions may depend on the tasks they are given. For example, if the task is to “factor completely a polynomial” in an elementary course where the irreducibility of polynomials is not theoretically grounded but based only on usage and teacher’s approval (Sierpinska 2005), knowing whether the answer is correct or not requires not so much “content knowledge in the cognitive area of mathematics” but “social knowledge, that is, knowledge of the institutional culture of... education” (reference to Surman’s model of adult learning, Surman 1993, reviewed in FitzSimons and Godden 2000: 29). In other words, it is a matter of the didactic contract and not of epistemological validity.

The differences between tasks can be very subtle. For example, Stroup (2005) discusses the advantages of “generative” classroom activities over “overscripted” activities relative to their potential to develop, among others, students’ sense of agency. An example of a generative activity, given by these authors, is a small-group activity, using graphing calculators and involving discussions between the groups, around the problem, “submit functions that are the same or equivalent to the function f(x) = 4x.” If the activity was based on the problem, “create pairs of single-digit, positive integer terms involving x that sum to 4x”, where there is little field for students’ creativity, freedom of choice and points of contention to discuss, the result would be an overscripted activity.

Regular textbook exercises are most often of the overscripted kind. There is some generative potential in “investigative problems” or “exploration” sections that can now be found in undergraduate textbooks. But explorations do not usually appear on the final examinations. Thus, formally, they can be regarded as “extra-curricular activities.” They also take more time than regular exercises, and, in the fast paced courses, they would have to be done at the expense of working on typical examination questions. If the teacher tried to engage students in such activities in class, students who approach their participation in PMC mostly as Students and Clients could refuse to cooperate. Such activities would have to remain optional and done outside of regular classes, for interested students.

Are there any realistic strategies to help students develop agency in mathematics?

Theoretical and empirical studies of institutions warn against the belief in the existence of simple solutions of reforming them. They suggest that such systems develop characteristics that tend to perpetuate themselves (Crozier and Friedberg 1980: 98). We have seen illustrations of this phenomenon above.

Any attempt to reform an institution or to explain why an attempt has failed must be based on understanding its functioning as a system: an answer may lie in the ways the participants govern their spaces of freedom (Crozier and Friedberg 1980: 119). For reasons explained in this paper, PMC participants do not have much freedom as far as time and content of the courses are concerned. Therefore, it may be impossible to remove the frustration caused by the fast pace of the prerequisite courses. But perhaps something can be done about students’ ways of learning and their rapport with mathematical truth and reasoning, because these sources of frustration depend to some extent on the teacher–student interactions and the didactic contract in class which are more under the control of the teacher.

Let us propose the following modest strategy. Suppose the teacher tries to avoid playing the right-or-wrong game with the students and plays the true-or-false game instead. This would entail more than a minor shift in terminology: we believe it would be an important component of a strategy aimed at making students partners in the game, in the mathematical game, that is. This strategy is not only about instructor’s language, but also about his or her whole attitude toward mathematics in the classroom and about choosing tasks for students that would be less dependent on didactic contract and more on knowledge of mathematical meaning and reasoning techniques. Moreover, the teacher could create occasions to discuss the validity of a solution outside of the context of negotiating a grade with a student. For example, the discussion could be engaged by a mistake intentionally made by the instructor. In our experience as instructors of these courses, we saw that this situation can make students more involved in the mathematical activity and, hence, give them some power over the knowledge that is being learned. For instance, we could insert a mistake in a calculation (such as missing a sign) when solving an equation on the board and, when a solution is obtained, make a comment such as, “I’m not sure this is correct. Did you get the same thing? Could you help me check?” We believe this can have a better effect then the authoritative rule, “After you solve the equation you have to check the solution by plugging the solution back into the equation.” In fact, we don’t even have to pretend—we do make mistakes in our mathematical practice, and we often feel unsure and frustrated, so perhaps letting students see us as mathematicians “in practice” and not “in charge” could provide a change of attitude in them, too. The strategy we propose is an example of “behavior modeling”, a practice theorized in social learning theory (Bandura 1963), and studied in mathematics education (see, e.g., Schoenfeld 1992).

Another solution we envision concerns the mathematical tasks used in these courses, i.e., examples used during lectures, problems in the midterm tests or in the final examinations. As we have discussed in the previous section, certain tasks have the potential of cultivating conceptual understanding, but time and easiness of assessment are important constraints in the institutional context we have described. Equations and inequalities are the simplest examples of tasks where the student has control over the validity of solution, if only he or she understands the notion of solution. So, for example, instructors may teach equations and inequalities around the important concept of solution (as opposed to merely providing the students with a set of steps or procedures for solving them). But there exist many more imaginative examples in the literature. Design of tasks that support and probe students’ conceptual understanding is a constant concern of mathematics educators; research suggests that even short but frequent quizzes (see Bobos 2004) or well constructed multiple choice items can fulfill this role (e.g., Taylor 1998; Engelbrecht and Harding 2003; Roddick 2003). Thus solutions may exist even within the time limitations inherent to the prerequisite courses.

Final remarks

Much effort has already been invested in mathematics education to put the focus in teaching on mathematical meaning and reasoning techniques, but mainly at the level of elementary mathematics teaching. There is still a lot of work to be done at the secondary and higher levels and certainly in the too often forgotten area of adult mathematics education. Given the peculiarities of this specific population, it is in this area, we believe, that making a conscious effort to treat students as partners in the mathematical game would greatly pay off in terms of both the emotions that accompany their learning of mathematics and the quality of this learning.

Systematic research into affective and cognitive aspects of institutionalized mathematics education requires rich and fruitful theoretical frameworks. Concepts underlying the frameworks require more precision, stabilization and operationalization for research purposes. Recent developments are quite promising. In our research we invested some effort in synthesizing an institutional framework to study students’ affect within a particular educational institution. But our notion of frustration was conceptualized separately from this institutional framework. There is a need, we believe, of constructing a unified framework. We see a seed of such framework in incorporating, within an institutional framework, the notion of “mathematical experience”, recently proposed by Smith III and Star (2007). This notion has been adapted to study students’ transitions from one educational institution to another and therefore appears particularly relevant for analyzing students’ experience in PMC: students in these courses are students in the process of transition between educational institutions. We envisage exploring this idea in our future research.