Analysis of Coupled Poroviscoelasticity and Hydrodynamic Lubrication

Abstract

As the state of the art pushes triboelements toward greater capabilities and longevity, the need for evolving triboelement technology exists. The following work explores a novel coupling of phenomena inspired by biomimetics. A poroviscoelastic substrate coupled to a fluid film load is modeled and compared to its rigid counterpart. It is hypothesized that poroviscoelasticity can improve triboelement properties such as damping and wear resistance and have utility in certain applications where flexibility is desired (e.g., biomechanical joint replacements, flexible rotordynamic bearings, and mechanical seals). This study provides the framework for the analysis of flexible, porous viscoelastic materials and hydrodynamic lubrication.

1 Introduction

Biomimetics is emerging as an avenue for new tribological technology. A material of particular interest is articular cartilage. This load bearing material is a phenomenal facilitator of motion and has low friction and high wear resistance [19, 20]. Cartilage is a flexible, porous collagen (solid) matrix permeated with synovial fluid. It is desired to mimic this mechanism for application in mechanical systems.

Porous bearings are already commonplace in engineering applications. These sintered, or self-lubricating, bearings consist of a metal matrix impregnated with a lubricant. The interface of the journal and the bearing surface is virtually rigid, and the bearings operate in the mixed lubrication regime. However, if the bearing surface is made compliant, then deformation occurs in the bearing substrate, potentially leading to operation in the full film regime. The mechanism by which deformation occurs can be modeled in a number of ways (e.g., elastic, viscoelastic, elastic-plastic). Poroviscoelasticity (PVE) is one such constitutive model for a flexible, porous material. Certain engineered materials, like polyurethane foams and hydrogel scaffolds, display poroviscoelastic character. It is desired to explore PVE materials in applications such as bearings and dampers.

The objective of the current study is to couple a fully saturated poroviscoelastic bearing material with a hydrodynamic (HDL) fluid load. The fluid mechanics of thin films are well defined for conventional, rigid, triboelements by the Reynolds equation. However, the traditional Reynolds equation assumes no-slip conditions occurring between rigid plates. With a porous and flexible interface, the boundary conditions of the Reynolds equation are modified to allow vertical flow in and out of the substrate material, as well as effective slip in the horizontal direction. The implications of the coupled HDL/PVE problem are studied as they relate to triboelement performance.

Poroviscoelastic materials have two time-dependent mechanisms, giving rich frequency domain characteristics (i.e., stiffness and damping). The properties of stiffness and damping are assessed relative to an equilibrium state. The purpose of the current work is to simulate a coupled HDL/PVE problem to equilibrium and compare to the equilibrium states of similar bearing designs. This work is fundamental to understanding the transient behavior of a coupled HDL/PVE triboelement.

2 Background

The main subcomponents of the coupled system are the poroviscoelastic substrate (bearing surface), and the hydrodynamic lubrication that interacts with the porous bearing pad. Relevant literature is surveyed, and constitutive relationships are developed herein for each phenomena.

2.1 Poroviscoelasticity

Poroviscoelastic theory traces its roots to soil mechanics and later biomechanics [24]. It is the combination of poroelasticity and viscoelasticity. Therefore, poroviscoelastic theory yields two dissipative mechanisms, one through a reversible fluid exodus and one hysteretic effect. Each mechanism acts on a different timescale, giving a wide spectrum of dissipation. The poroelastic equations are provided to illustrate the concept of effective stress, followed by a description of viscoelasticity.

To develop the poroviscoelastic model of the bearing material, poroelasticity is first described. Biot [4, 5, 23] defines the three-dimensional constitutive equations for poroelasticity in terms of stress ($\sigma _{ij}$), strain ($\epsilon _{ij}$), pore pressure (p), and incremental fluid content ($\zeta$):

$$\begin{aligned} \sigma _{ij}=\, & {} 2G\epsilon _{ij} +\left( K-\frac{2G}{3}\right) \epsilon _{kk}\delta _{ij} -\alpha _{b}\delta _{ij}p, \end{aligned}$$

(1)

$$\begin{aligned} \zeta=\, & {} \alpha _{b}\epsilon _{kk}+p\left( \frac{1}{M}\right) . \end{aligned}$$

(2)

K, G, M, and $\alpha _\mathrm{B}$ are physical properties of the poroelastic structure [8, 10, 11, 18, 23]. The linear relationship between strains ($\epsilon ,\zeta$) and stresses ($\sigma , p$) is apparent in Eqs. 1 and 2. If the solid and fluid components are incompressible, and a volume of fluid added to the element is equivalent to the change in the bulk volume ($\alpha _B = 1$, $M \rightarrow \infty$), then the principle of effective stress is utilized. Effective stress is an important concept in poromechanics and is employed by finite element solvers such as ABAQUS [1]. The effective stress ($\sigma _{ij}^*$) in the porous material is defined as [1, 23]:

$$\begin{aligned} \sigma _{ij}^* = \sigma _{ij} + p\delta _{ij}, \end{aligned}$$

(3)

Equation 3 indicates that the effective stress is simply a superposition of the total stress and pore pressure. The effective stress is borne by the solid grains of the porous matrix [22]. When the viscoelastic effects are applied to the solid particles only, poroviscoelasticity is defined within the effective stress:

$$\begin{aligned} \sigma _{ij}^* = (\sigma _{ve})_{ij}, \end{aligned}$$

(4)

The PVE theory is reduced to an effective stress formulation, where the solid grains contain the viscoelastic action, and the solid/fluid interactions give the porous fluid dissipation. Any number of viscoelastic formulations can be used to model the solid particles, as long as they are thermodynamically permissible [6, 7, 9, 14, 21]. A fractional calculus model will be supplied in the current work [19, 21]. The following brief description of linear viscoelasticity provides the framework for the fractional calculus model.

Linear viscoelasticity relates stress and strain with respect to time. If each increment of strain makes an independent contribution to the total stress response, viscoelasticity is described by the following convolution integral [14]:

$$\begin{aligned} \sigma _{ve}\left( t\right) = \int _0^t \! \dot{\epsilon }\left( \tau \right) E\left( t-\tau \right) \, {\mathrm {d}}\tau . \end{aligned}$$

(5)

where $\sigma _{ve}\left( t\right)$ is the stress, $\epsilon \left( t\right)$ is the strain, and the relaxation modulus is denoted by $E\left( t\right)$. Equation 5 describes the relationship of stress and strain in one dimension. The relaxation modulus is formulated herein by a fractional calculus definition, and the one-dimensional formulation is extended to three dimensions for simulation. Fractional calculus is advantageous in modeling viscoelasticity because fewer material terms are often needed relative to integer-order models (e.g., Maxwell–Voigt, Prony series) [19–21]. One such model, the complementary error function fractional calculus model (CERF), has an unambiguous relaxation modulus in the time domain:

$$\begin{aligned} E(t) = E_0 + \sum \limits _{n=1}^{\infty }E_n \mathrm{e}^{\left( {\lambda _n}^2 t\right) } \mathrm{erfc}~(\lambda _n \sqrt{t}), \end{aligned}$$

(6)

where $E_n$ and $\lambda _n$ are material properties related to the elastic and dissipative mechanisms, respectively. The CERF model intersects the convenience of integer-order mathematics with the flexibility of fractional calculus by fixing the fractional derivative at 1/2. Biesel [3] shows that the CERF is a useful model for modeling viscoelastic behavior in many real materials.

The CERF model is implemented in three dimensions as the $(\sigma _\mathrm{ve})_{ij}$ term in Eq. 4. With the specification of permeability and the initial condition void ratio, the poroviscoelastic model is defined. The hydrodynamic load acts as a boundary condition at the interface of the substrate and the fluid film. It remains to define and couple the HDL problem to the substrate mechanics.

2.2 Hydrodynamic Lubrication with Porous Interface

Fig. 1

Thrust bearings in the rigid and porous cases. a Thrust bearing with rigid interfaces. b Thrust bearing with porous interface on bottom boundary

The poroviscoelastic substrate gives two unique dissipation mechanisms: one from hysteresis in the solid particles and one from fluid dissipation. The fluid transmission also provides a strong coupling mechanism with the fluid film. At a porous boundary, fluid flow is allowed to permeate into (or out of) the porous medium. In addition, pressure generated in the fluid causes deformation of the porous substrate. These interfacial mechanisms are considered when developing the constitutive model of the fluid. It is desired to describe the fluid mechanics in this configuration in a similar manner to the rigid case, which generates the well-known Reynolds equation [15]:

$$\begin{aligned}&{\frac{\partial }{\partial x}}\left( {\frac{\partial P}{\partial x}}h^3\right) + {\frac{\partial }{\partial z}}\left( {\frac{\partial P}{\partial z}}h^3\right) = \nonumber \\&\quad 12\mu \left[ {\frac{\partial }{\partial x}}\left( \frac{-U_1 h}{2}\right) + U_1{\frac{\partial h}{\partial x}}+{\frac{\partial h}{\partial t}}\right] . \end{aligned}$$

(7)

Fig. 2

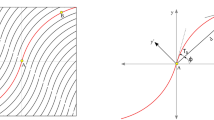
Velocity profile in fluid channel and porous filter (modified from [2])

The introduction of a porous and flexible boundary, as shown in Fig. 1b, modifies the boundary conditions of the Reynolds equation. A popular porous boundary condition is attributed to Beavers and Joseph [2]. Beavers and Joseph provide a slip-flow condition for the porous interface, which is based on experimental findings. Figure 2 shows a snapshot of the fluid velocity profiles in the fluid channel and the porous filter. $U_1$ is the fluid velocity at the no-slip interface ($y=h$), $u_B$ is the fluid velocity at the porous interface ($y=0$), and $U_{x}$ is the porous filter velocity (from Darcy’s law). The Beavers and Joseph boundary condition relates the interface velocity to the filter velocity. In effect, the slip-flow boundary condition approximates the boundary layer shown in Fig. 2. Mathematically, the slip-flow condition is given as [2]:

$$\begin{aligned} {\frac{\partial u}{\partial y}}\bigg |_{y=0}= -{\frac{\alpha }{\sqrt{k}}}\left[ u_B-U_{x}\right] \end{aligned}$$

(8)

where $\alpha$ is a slip coefficient, and k is the permeability of the porous structure. Beavers and Joseph show that this ad hoc boundary condition reasonably captures experimental results for a range of materials. In reality, it is unlikely that slip is actually occurring at the interface; however, the slip coefficient helps to rectify the results from experiments and the theory. Therefore, the slip coefficient is a useful parameter for the designer to retain. The porous interface is incorporated in the Reynolds equation by modifying one of the rigid boundary conditions, leading to a modified velocity profile in the horizontal direction:

$$\begin{aligned} u(y) = -{\frac{1}{2\mu }}\,{\frac{\partial P}{\partial x}}\left( y-h\right) \left( y+{\frac{1}{3}}h\xi _1\right) +{\frac{U_1}{h}} \left[ y\left( 1-\xi _0\right) + h\xi _0\right] , \end{aligned}$$

(9)

where $\xi _0$ and $\xi _1$ are film thickness modifiers [17]:

$$\begin{aligned} \xi _0= & {} \frac{{\sqrt{k}}/{\alpha }}{h+{\sqrt{k}}/{\alpha }} \end{aligned}$$

(10)

$$\begin{aligned} \xi _1= & {} \frac{3\left[ h\left( {\sqrt{k}}/{\alpha }\right) +2k\right] }{h\left( h+{\sqrt{k}}/{\alpha }\right) }. \end{aligned}$$

(11)

Applying continuity to the fluid film (retaining the sign convention of Fig. 2):

$$\begin{aligned} {\frac{\partial (\rho v)}{\partial y}} -{\frac{\partial (\rho u)}{\partial x}} +{\frac{\partial (\rho w)}{\partial z}} + {\frac{\partial \rho }{\partial t}} = 0, \end{aligned}$$

(12)

and integrating across the film thickness, the porous Reynolds equation is obtained:

$$\begin{aligned}&{\frac{\partial }{\partial x}}\left\{ {\frac{\partial P}{\partial x}}\left[ h^3\left( 1+\xi _1\right) \right] \right\} + {\frac{\partial }{\partial z}}\left\{ {\frac{\partial P}{\partial z}}\left[ h^3\left( 1+\xi _1\right) \right] \right\} = \nonumber \\&\quad 12\mu \left\{ {\frac{\partial }{\partial x}}\left[ \frac{-U_1 h\left( \xi _0+1\right) }{2}\right] + U_1{\frac{\partial h}{\partial x}}+\left( V+V_0+V'\right) \right\} , \end{aligned}$$

(13)

where V is the traditional squeeze term (${\frac{\partial h}{\partial t}}$). Equation 13 describes the pressure in a thin film with a porous, flexible interface. In addition to the film thickness modifiers, two additional “squeeze” terms are present: $V_0$ and $V'$. These terms represent the vertical flow of fluid and the rate of change of the porous interface, respectively. The vertical fluid flow is governed by Darcy’s law:

$$\begin{aligned} V_0 = k {\frac{\partial p}{\partial y}} \bigg |_{y=0} \end{aligned}$$

(14)

As permeability approaches zero $(k\rightarrow 0)$, Eq. 13 becomes the conventional Reynolds equation (Eq. 7). As a result of the porous interface, three types of coupling effects are apparent: film thickness modifiers ($\xi _0$ and $\xi _1$), deformation of the substrate ($V'$), and vertical fluid flow ($V_0$). The material properties of the substrate have a strong influence on the coupling terms. These parameters will be explored in the following section.

3 Results

The Beavers–Joseph boundary condition is considered for its effect on the velocity profile in the fluid channel (Eq. 9). Figure 3 shows the apparent slip at the porous boundary ($y=0$) for a virtually parallel channel (as shown in Fig. 2). The parameters used for Fig. 3 are given in Table 1. At the top interface ($y=h$), no slip occurs, and the fluid moves with the journal’s velocity $U_1$, while the lower, porous interface experiences nonzero velocity, $u_b$. This is in contrast to the rigid, no-slip case, where $u/U_1 = 0$ at $y=0$ (also shown in Fig. 3). Beavers and Joseph indicate that real materials have slip coefficients between $\alpha = 0.001$ and $\alpha =10$. The implications of a porous boundary are to change the relative fluid velocity between the two plates. In cases where $\alpha$ is large (e.g., lattice foametals), there is a large effect on the velocity profile. This can even cause a negative velocity at the interface if the Poiseuille flow is large enough and acts counter to the Couette flow. In the case of the Poiseuille flow acting counter to the Couette flow, there is a unique combination of $\alpha$ and k that replicates the no-slip condition.

Fig. 3

Velocity profiles in the fluid channel for various slip values ($\alpha$)

Table 1 Parameters for Beavers–Joseph slip analysis

Fig. 4

Solid and fluid boundary conditions on porous pad. a Fluid pressure boundary conditions on the PVE pad. b Solid boundary conditions on the PVE pad

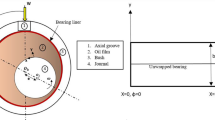
Considering the porous bearing surface, the domain of the porous substrate is defined. Figure 4 shows the boundary conditions imposed on the porous pad. Assuming a submerged bearing, the leading and trailing edges of the pad are exposed to atmospheric pressure (gauge), which allows fluid flow across the boundary. The same condition is imposed on the lateral direction (into and out of the page). The bottom boundary is fixed and rigid, and the top boundary is flexible and the pressure, p, is equal to the fluid film pressure, P. The pressure gradient in the porous pad facilitates fluid flow throughout the pad. The pressure boundary and initial conditions are defined mathematically:

$$\begin{aligned}&p(0,y,z,t) = p(L,y,z,t) = 0 \end{aligned}$$

(15)

$$\begin{aligned}&p(x,y,0,t) = p(x,y,D,t) = 0 \end{aligned}$$

(16)

$$\begin{aligned}&{\frac{\partial p}{\partial y}} (x,-H,z,t) = 0 \end{aligned}$$

(17)

$$\begin{aligned}&p(x,0,z,t) = P(x,0,z,t) \end{aligned}$$

(18)

$$\begin{aligned}&p(x,y,z,0) = 0 \end{aligned}$$

(19)

$$\begin{aligned}&\epsilon (0,y,z,t) = \epsilon (L,y,z,t) = 0 \end{aligned}$$

(20)

$$\begin{aligned}&\epsilon (x,y,0,t) = \epsilon (x,y,D,t) = 0 \end{aligned}$$

(21)

$$\begin{aligned}&\epsilon (x,-H,z,t) = 0 \end{aligned}$$

(22)

$$\begin{aligned}&\sigma (x,0,z,t) = -P(x,0,z,t) \end{aligned}$$

(23)

$$\begin{aligned}&\sigma (x,y,z,0) = 0 \end{aligned}$$

(24)

Equations 15–18 enforce the fluid pressure boundary conditions, while Eqs. 20–23 are placed on the solid matrix. Equation 17 enforces no flow across the rigid boundary at $y=-H$.

Before simulating the fully coupled HDL/PVE problem, the corresponding rigid/porous case is studied under a hydrodynamic load. The rigid/porous case gives insight into the pressure distribution in the porous pad, which indicates where deformation will occur in the flexible/porous case. The pressure in the porous substrate is known analytically by Laplace’s equation. If the 2D case is considered, the coupled HDL/porous problem also has an analytical solution [13, 17]. Figure 5 shows the pressure in an example rectangular porous pad ($L/H = 4$), exposed to a hydrodynamic fluid load (from Eq. 13). Within the porous pad, the pressure is highest at the film interface and decays throughout the body to the zero pressure boundaries. The lower, rigid interface also experiences a pressure load, dependent on the geometric dimensions H and L. The solution of the rigid/porous case is calculated from Laplace’s equation as a reference for the HDL/PVE problem. In addition, the rigid/porous solution is used to initialize the HDL/PVE problem for efficient numerical calculations.

Fig. 5

Pressure in the porous pad from HDL load. a Isometric view of pressure in the porous pad. b Top view of pressure in the porous pad

The coupled PVE/HDL problem is solved with a combination of finite elements and finite difference/finite volume methods. The commercial finite element program ABAQUS is used to simulate the PVE problem, by using pore pressure elements (CPE8RP) and a fractional calculus viscoelastic constitutive model for the solid grains. The CPE8RP element is a plane-strain, 8-node biquadric displacement element with pore pressure degrees of freedom [1]. An ABAQUS user-subroutine solves the Reynolds equation with a combination of finite difference and finite volume methods [16]. The subroutine is written in FORTRAN to comply with the requirements of ABAQUS. At each increment in time, nodal information is stripped from the results file. This information is used to determine V, $V'$, $V_0$, and h. The Reynolds equation is solved explicitly at each time increment and applied to the solid-fluid boundary of the PVE pad. ABAQUS incorporates the new boundary condition and proceeds forward in time ($t+\Delta t$). Effectively, the HDL solution acts as a continuously updating load and boundary condition on the substrate. Figure 6 shows the control schematic for the coupled simulation. The simulation runs until a steady state is achieved. This means that the viscoelastic, porous, and squeeze mechanisms have all achieved steady-state behavior. At that point, the analysis is queried for the metrics of interest, including load support/film thickness, vertical flow. The parameters used in the current study are listed in Table 2. These parameters are chosen to establish a methodology for solving problems of this nature and are not specific to an application; however, the material properties of the solid ($E_0$, $E_1$, $\lambda _n$, v) are loosely based on biological materials [19].

Fig. 6

Flow of information schematic

Fig. 7

Film thickness and pressure profile evolution with time. a Film thickness over time. b Pressure profile over time

Table 2 Parameters for PVE/HDL analysis

A long bearing ($L>> D$) is analyzed to reduce computation time and provide insight into the coupling process of the fluid film and poromechanics. The film thickness ratio, $a=2.2$, is known to maximize load carrying capacity in the rigid case. The solution to the coupled problem is performed in two steps to alleviate convergence issues. The first step places a hydrodynamic load on the surface of the poroviscoelastic pad and reaches a fluid pressure equilibrium without deformation in the body (corresponding to the rigid/porous case). The second step “releases” the pad to deform according to the pressure load obtained from the porous Reynolds equation (Eq. 13). The coupling terms are updated at every increment in time. The simulation is run to steady state, where the temporal processes have completed. From this equilibrium, the desired system properties are obtained. An example simulation is characterized in Table 3.

Table 3 Simulation metrics

During the simulation to steady state, the film profile and corresponding pressure profile in the bearing are tracked in time. Figure 7a shows the evolution of the film thickness over time, and Fig. 7b shows the evolution of the pressure profile. Initially, the porous pad is undeformed. As the porous and viscoelastic mechanisms respond to a HDL load, deformation occurs. In a viscoelastic sense, this relates to the transition from the glassy ($t=0_+$) to rubbery modulus ($t=\infty$). The pressure profile (Fig. 7b) also evolves in time, as the maximum pressure increases and changes lateral location in the bearing. The time-dependent action of the bearing gives stiffness and damping character in the frequency domain as well [19, 21].

Figure 8 shows results of the rigid, rigid/porous, and flexible porous cases simulated at steady state ($t\rightarrow \infty$). Figure 8a shows the fluid film thickness generated by each case for equivalent geometries and loads ($k=10^{-14}$ $[m^2]$). Here, the rigid/porous and flexible/porous bearings have a smaller film thickness to support an applied load, as flow from the fluid film is forced into the porous medium. Figure 8b shows the corresponding pressure profiles produced to sustain a fixed load (W). The pressure profiles are different for the flexible/porous case and shifted to compensate for the deformation in the porous pad. Finally, Fig. 8c shows the flow of fluid into the porous pad for the rigid/porous and flexible/porous cases. There is no vertical flow in the corresponding rigid case ($U_y = 0$). The flow spikes near the location of $P_{max}$ in the flexible/porous case. For low permeabilities, the fluid mechanics are dominated by the film profile (wedge term) rather than the vertical flow of fluid into the porous pad. The film thicknesses, maximum pressures, and vertical flow values are provided in Table 4.

Table 4 Results from the simulations in Fig. 8

The results shown in Fig. 8 indicate that the PVE/HDL solution changes the character of the film profile. There does not appear to be a significant penalty to the porous/flexible configuration, except for smaller outlet film thicknesses. The hypothesized benefits of the porous/flexible case (damping and lubricant availability) are weighed relative to these costs. The implications of this are discussed in the following section, after varying permeability is considered.

When the inlet film thickness is fixed ($h_i = 40\, \upmu \mathrm{m}$), the effect of permeability on the load support capacity is shown in Fig. 9. The PVE case is compared to the rigid case with respect to permeability. The load support has a strong dependency on the permeability in the substrate, which highlights the importance of substrate material selection. In particular, permeability changes between $k = 10^{-16}$ $[\mathrm{m}^2]$ and $k = 10^{-9}$ $[\mathrm{m}^2]$ have a strong influence on the load support, as shown in Fig. 9b.

Substrate geometry proves to be less influential for the example parameters chosen. This is shown in Fig. 10 for various pad length to width ratios (at the said fixed inlet film thickness). The influence of the porous pad’s depth on load support capacity is marginal except for extremely shallow or deep pads. For permeabilities low enough to support fluid film loads, the pressure gradient at the interface does not appear to be significantly influenced by the pad’s dimensions. The pad depth is larger than the film thickness by at least one order of magnitude in this simulation. Larger pressures may alter the sensitivity to pad geometry; however, general bearing pad configurations will not see a large variation in load support (or film thickness for fixed loads) due to the pad dimensions.

Fig. 8

Comparison of rigid, rigid/porous, and flexible pad designs at $t \rightarrow \infty$. a Comparison of film thickness required to sustain load. b Pressure profile obtained from above film profile. c Normalized flow in the rigid/porous and flexible porous cases

Fig. 9

Load support versus permeability. a Load support versus permeability for the full HLD/PVE solution. b Load support in permeability range of potential engineering materials

Fig. 10

Load support versus permeability for different pad length to height ratios

4 Discussion

The coupled HDL/PVE problem is simulated for a simple configuration to study flexible/porous pads in tribological applications. The temporal nature of poroviscoelasticity demands that the film thickness evolves in time, giving stiffness and damping properties. However, once a steady state is reached, the resulting film profile can be significantly different from the rigid/porous and rigid cases. This has implications for bearing performance. The discussion of a PVE/HDL problem begins at the porous/film interface.

The Beavers–Joseph boundary condition is ad hoc; however, it has been verified experimentally [2]. The advantage of using the slip coefficient is that the boundary condition is applicable across a wide range of materials and material properties. Also, the formulation decouples the lateral directions of flow from the PVE solution, helping to manage model size and convergence issues. Therefore, the film profile (h) and vertical flow ($U_y$) into, or out of, the porous pad are the only coupling terms between the fluid film and porous pad.

The current study highlights a number of considerations for flexible/porous bearings and dampers. When compared to the rigid case, the inlet and outlet film thicknesses are reduced (Fig. 8a) for the rigid/porous and flexible/porous simulations. However, the flexible/porous case sustains a larger film thickness on the trailing end of the pad, due to deformation in the PVE pad. Considering the porous Reynolds equation (Eq. 13), the $V_0$ term acts in opposition to the “wedge” term; therefore, the film thickness must be reduced to sustain an equivalent load. The reduced film thickness could have implications on friction and wear. The cost of a reduced film thickness should be compared to the benefits of increased damping in the system. As shown by Etsion [12, 13], porous mechanical face seals provide stiffness in mechanical face seals, with marginal costs from increased leakage. The permeability of the porous pad strongly influences this effect and must be carefully designed with the desired application.

When film thickness is fixed, as shown in Fig. 9, the sensitivity to permeability is apparent. The permeabilities shown in Fig. 9 span many orders of magnitude, but also encompass many promising materials, from articular cartilage ($k \approx 10^{-16}$ $[\mathrm{m}^2]$) to polyurethane foams ($k \approx 10^{-9}$ $[\mathrm{m}^2]$). To sustain appreciable loads, a relatively low permeability is required. However, coupled with an elastic or viscoelastic action, the PVE pad can significantly influence triboelement performance. Like a sintered bearing, lubricant availability from the porous substrate is an operational advantage. It is hypothesized that these bearing types could have use in harsh operating environments, where shock loads or lubricant loss are possible. Considering the rigid/porous and flexible/porous cases, the flexible boundary allows more vertical flow across the porous interface. The fluid flow contributes to the solution of the Reynolds equation and may be important for the dynamic properties of the bearing. This is the subject of continued study.

For materials with permeabilities that could be used in triboelements, the influence of the porous pad dimensions are minimal with respect to the load support. Therefore, special consideration of the porous pad dimensions is not required for load support concerns. However, unique geometries or configurations (e.g., porous region followed by an impermeable region) could be employed to create effective converging gaps. Etsion and Michael [13] propose a similar concept for the rigid/porous case, with special consideration for sealing applications. The tools developed herein allow for studies of this type and are the foundation of study into the dynamic performance of coupled HDL/PVE problems.

5 Conclusion

The genesis of coupled PVE/HDL comes from biomimetics, where biological solutions exist for many tribological problems. With biological materials, the engineer cannot control the material properties; however, the physics can be described. The proposed PVE/HDL describes the physics of a flexible/porous material interacting with a fluid film load. Potentially, the model has use in the study of biological mechanisms, as well as biomimetic tribological applications. Articular cartilage is of particular interest in biomimetics because of its adaptability and longevity. Coupling mechanisms like a fluid film and porous pad help to translate from biomechanical to tribological applications.

New demands in triboelement performance require innovative technology. A coupled HDL/PVE bearing is a feasible configuration for certain applications. These include biomechanics, flexible bearing technology, and sealing elements. In addition, PVE materials have strong dissipation characteristics, making them suitable for shock absorption and damping elements. The results of the coupled HDL/PVE simulation indicate that flexible, porous substrates can promote tunable triboelement performance. This can potentially improve tribological considerations, especially wear and damping. Additional study is required to quantify this performance.

The current work addresses the mathematics of coupling unique mechanisms, and merging solid and fluid mechanics of triboelements. The concepts established in this work provide the foundation for future simulations. Possible research avenues include: determining dynamic stiffness and damping, transient analysis of coupled PVE/HDL problems, nonuniform permeability patterns in the PVE pad, geometric tailoring of the PVE pad, and new confining boundary conditions on the PVE pad, among others.