The influence of operating and design parameters on the magnetic tape/guide friction coefficient

The classical belt drive equation is modified to obtain a more accurate model, which allows the investigation of the effect of various parameters such as sliding speed, tape tension, surface roughness, material properties and guide and tape geometry on the magnetic tape/guide friction coefficient. The friction coefficient between a guide and a tape sample is also determined from experimental measurements as a function of these various parameters. Theoretical predictions and experimental results are compared.

Introduction

The classical belt drive equation [1] relates the “tight-side” tension T ₁ (upstream of pulley) to the “slack-side” tension T ₂ (downstream of pulley) as an exponential function of the product of the friction coefficient μ and the belt/pulley wrap angle θ, i.e.,

$$ \frac{T_{1}}{T_{2}}=\exp \left( {\mu \theta } \right) $$

(1)

This classical equation, which assumes a constant friction coefficient independent of operating conditions, is often used to measure the “belt/pulley” friction coefficient in applications such as paper, polymer and textile processing. In light of some recent findings that show deviation of the friction coefficient from the classical friction laws [2], a more detailed understanding of the dependence of the friction coefficient on operating parameters such as sliding speed, pulley diameter or surface finish is desirable. One of the most intricate applications of the “belt/pulley” concept can be found in magnetic tape recording, where accurate knowledge of the friction coefficient is needed. Magnetic tape is transported from the supply reel to the take-up reel, thereby passing over guides, rollers and a magnetic read/write head.

Lateral tape motion (LTM), defined as the time-dependent displacement of magnetic tape perpendicular to the tape transport direction, can cause track misregistration. This, in turn, limits the recording density. A key issue in LTM is the friction between tape and cylindrical guides and rollers. By investigating the effect of operating conditions such as tape speed and tape tension in conjunction with design parameters such as guide diameter, surface quality, and material properties, one can optimize the frictional behavior between tape and guide to reduce LTM and tape wear.

Broese van Groenou [3] suggested that the friction between tape and guides is determined by the mechanical interaction of the microscopic asperities on the two surfaces in contact. He defined the friction coefficient as the ratio of the shear strength at which the asperities yield irreversibly and the normal stress on the asperities. Osaki [4] pointed out tribological obstacles, which need to be overcome in order to achieve higher recording area densities in tape drives. The use of metal evaporated (ME) tape, which has superior magnetic characteristics compared to magnetic particulate (MP) tape, allows increasing the recording density. However, the smoother surface of ME tapes causes a higher friction coefficient at low speed due to stiction effects. This results in unstable tape drive operation. Osaki and Endo [5] investigated the tribology of helical scan tape drive systems and found that a higher static friction coefficient increases the generation of wear debris. They concluded that a solid lubricant reduces the friction coefficient but might damage the tape. Panda and Engelmann [6] studied the dependence of the friction coefficient on tape speed and investigated the importance of estimating the correct friction coefficient in the control of reel-to-reel tape drives without a tension transducer. No experimental or analytical validation of their hypothesis was provided. Taylor and Talke [7] investigated LTM and reported on roller interactions with a flexible tape medium. They showed that lateral tape motion is a function of the tape/roller friction coefficient. Bhushan [8] investigated the friction coefficient between a magnetic tape and a guide and concluded that the friction coefficient depends on the guide radius and the nominal tape tension, but is independent of the wrap angle and the speed. In [8], operational parameters were used that are not within the range of parameters used in state of the art high performance tape drives. Thus, a more detailed study is desirable.

The friction coefficient at the tape/guide interface is a strong function of speed. This speed dependence is caused by the formation of a partial air bearing at the tape/guide interface, which leads to a reduction in the contact load between tape and guide. The air bearing causes “load sharing”, i.e., the tape is partially supported by contacting asperities and partially supported by the pressure in the air bearing. This reduces the friction coefficient significantly. At high tape speeds, a self-acting air bearing is created between the tape and the guide and hence, very low friction coefficients are observed for this regime. At low tape speeds, boundary lubrication exists and the interactions between the magnetic tape and the guide are dominated by asperity contact. A transition region exists between high and low tape speeds where air-bearing effects coexist with partial asperity contact. Lacey and Talke [9] studied the hydrodynamic flying and the transition region effects for the case of a magnetic head in a tape drive.

Current tape friction models [8] rely mostly on equation (1) and hence, neglect the effects of tape speed, partial hydrodynamic lubrication, surface characteristics, material properties and guide dimensions. No published papers appear to be available that consider the effect of these parameters on the coefficient of friction between a tape and a guide. It is the purpose of this paper to bridge this gap and present a model that includes the effects of operation and design parameters on the friction coefficient between a tape and a guide.

Theoretical model

There are two issues involved in developing a friction model for the tape/guide interface. These are: (a) partial air bearing formation and “load sharing”, and (b) modeling of the friction contributed by the contacting asperities.

Load sharing

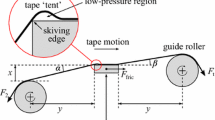
Figure 1(a) shows a tape element of width w in contact with a cylindrical guide of radius R. The relative linear velocity between tape and guide is, ωR as shown in the figure. The local tape tension is denoted by T while dT is the increment in tape tension due to the local friction force F _f that resists the sliding of the tape. As shown in figure 1(b), the angular coordinate is denoted by α and the wrap angle by θ. The tape tension results in a normal load, which is partially supported by the air bearing pressure and partially by asperity contact. It is justifiable to assume that contacts between tape and guide are absent if the spacing h≥3σ _s , where σ _s is the standard deviation of asperity summit heights distribution [10].

Figure 1.

Free body diagram of a tape element.

In the case of hydrodynamic lubrication between a perfectly smooth tape and guide, the spacing can be obtained from the steady-state, one-dimensional, compressible Reynolds equation with first order rarefaction effects [9].

$$ \frac{d}{dx}\left({ph^{3}\frac{dp}{dx}+6\lambda^{\ast} p^{\ast} h^{2}\frac{dp}{dx}} \right)=6U\mu_{a} \frac{d}{dx}\left({ph} \right) $$

(2)

 μ _a represents the air viscosity, λ^* is the mean free path of air under atmospheric conditions, p ^* is the atmospheric pressure, x denotes the coordinate along the tape/guide interface (air flow direction), p(x) is the air bearing pressure and h(x) is the spacing between the magnetic tape and the guide. In the case of rough surfaces, the mean through the surface is generally used to denote the effective spacing. Alternatively, Patir and Cheng [10] introduced averaging procedures ending in pressure flow and shear flow terms.

Lacey and Talke [9] presented an empirical expression relating the load carried by contacting asperities to the spacing at the head/tape interface. This expression depends on two parameters a and b. The parameter a represents the spacing at which head/tape contact begins. Hence, according to [10], a is equivalent to 3σ _s in our model. The parameter b represents the pressure required to force zero spacing between the head and the tape.

Based on the analysis in [9], one can express the load portion N _asp carried by the contacting asperities in the form:

$$ N_{\rm asp} =N(1-h /3\sigma_{s} )^{2},\quad \hbox{for }h\le 3\sigma_{s} $$

(3)

in which N is the maximum tape/guide contact load in the absence of any air bearing support (equivalent to parameter b in [9]).

In the absence of an air bearing between tape and guide, and assuming that dα is small [1], (i.e., ${\sin \alpha \cong \alpha }$ and ${\cos \alpha \cong 1}$), static equilibrium of forces in the z- and y- direction gives:

$$ dN=Td\alpha $$

(4)

$$ \mu dN=dT $$

(5)

Assuming that the friction coefficient is constant, one obtains equation (1). This classical equation represents a simplified situation of the tape/guide interface, since it neglects the effects of surface characteristics, material properties and guide dimensions on the friction coefficient. In the following, a more realistic model will be developed in which these neglected effects will be included.

Friction model

Several friction models of rough surfaces have been proposed in the past [11–15]. Recently, Brizmer et al. [16] proposed a new model for the static friction coefficient for a single deformable asperity in contact with a rigid flat based on the assumption that the contact interface is under stick condition (frictional contact). They obtained numerical results for the friction coefficient μ, which they presented in the form

$$ \mu =0.27\coth \left({0.27\left( {P^{\ast} } \right)^{0.35}} \right) $$

(6)

where the non-dimensional load P ^* on one asperity has the form P ^* = P/L _C . Here P is the normal load on one asperity and L _C is its critical normal load at yield inception under frictional contact, given by [17]

$$ L_{C} =\overline{L_{C}} P_{C} $$

(7)

where

$$ \overline{L_{C}} =8.88\nu -10.13\left( {\nu^{2}+0.089} \right) $$

(8)

and

$$ P_{C} =\frac{\pi^{3}}{6}C_\nu^{3} Y\left({r\left( {1-\nu^{2}} \right)\frac{Y}{E}} \right)^{2} $$

(9)

In equation (9), P _C (see Ref. [17]) is the critical normal load in slip (frictionless), r is the radius of the asperity tip. The material properties Y, E and ν are the yield strength, Young’s modulus, and Poisson’s ratio, respectively, of the deformable asperity and C _ν = 1.234 + 1.256ν.

To apply equation (6) to the case of the tape/guide interface, the following simplifying assumptions are made:

• 1. The effects of the various relevant parameters such as tape tension, guide radius, surface roughness and material properties on the dynamic friction between tape and guide are similar as on the static friction. Hence, equation (6) can be used for a qualitative evaluation of these effects. This assumption is justifiable based on experimental observations reported in the literature [18].

• 2. The tape is assumed “rigid” so that local elastic deformations of the tape are neglected. In addition the tape is assumed to conform to the guide.

• 3. The contact of two rough surfaces as in the tape/guide case can be modeled by an equivalent rough surface in contact with a perfectly smooth one [19].

• 4. The actual load on each individual asperity can be approximated by an average local asperity load.

Assuming a Gaussdian distribution of asperity heights [20], one can show that the number of contacting asperities, n, over a tape section of angular extent dα is given by [21]:

$$ n=\frac{\eta wRd\alpha }{\sqrt {2\pi } }\int_{h^{\ast} }^\infty {\exp [-0.5(z^{\ast} )^{2}]dz^{\ast} } =\frac{\eta wRd\alpha }{2}[1-erf(\sqrt {0.5} h^{\ast} )] $$

(10)

where η represents the asperity density and h ^* = h/σ _s is a dimensionless spacing. Using equations (2), (3) and (9), we can express the average local load per asperity P = dN _asp/n as

$$ P=\frac{T(\alpha )}{\eta wR}\frac{2(1-h^{\ast} /3)^{2}}{[1-erf(\sqrt {0.5} h^{\ast})]} $$

(11)

In non-dimensional quantities, equation (11) can be written as:

$$ \Gamma =\frac{T(\alpha )}{\eta wRL_c }\frac{2(1-h^{\ast} /3)^{2}}{[1-erf(\sqrt {0.5} h^{\ast} )]} $$

(12)

where ${{\Gamma ={P}/{L_C }}}$ is a local dimensionless tape tension, which is identical to the parameter P ^* in equation (6). Hence, equation (6) can thus be re-written as:

$$ \mu =0.27\coth (0.27\Gamma^{0.35}) $$

(13)

Finally, from equations (4), (5), (12) and (13) one obtains:

$$ 0.27d\alpha =\frac{d\Gamma \left( \alpha \right)}{\Gamma \left( \alpha \right)\coth \left( {0.27\left( \Gamma \right)^{0.35}} \right)} $$

(14)

Equation (14) is a non-linear ordinary differential equation, which yields a solution of the form:

$$ \Gamma /\Gamma_{2} =f\left( {\alpha ,\Gamma_{2} } \right), $$

(15)

where

$$ \Gamma_{2} =\frac{T_{2} }{\eta wRL_c }\frac{2(1-h^{\ast} /3)^{2}}{[1-erf(\sqrt {0.5} h^{\ast} )]} $$

(16)

is the initial condition. Since in equation (15) the normalization factor is the same in the nominator as in the denominator, it can also be expressed as

$$ T/T_{2} =f\left( {\alpha ,\Gamma_{2} } \right), $$

(17)

For a given wrap angle α = θ, equation (17) provides the ratio T ₁/T ₂, which can be used in equation (1) to determine an average friction coefficient that now depends on Γ₂. Hence, this friction coefficient incorporates the tape speed (through the tape/guide spacing), the surface characteristics, the material properties and the guide geometry (see equation (16)).

In order to relate the initial condition Γ₂ to a rough surface with many asperities rather than to a single asperity, we assume that each asperity in a tape section of angular extent dα carries the same average local load (see assumption 4). The critical interference ω _C at yield inception of a single asperity was defined in [17] as

$$ \omega_C =\left[ {C_\nu \frac{\pi \left( {1-\nu^{2}} \right)}{2}\frac{Y}{E}} \right]^{2}r $$

Hence from this ω _C and equations (6) and (8) one can obtain the relation

$$ L_C =\frac{2\pi }{3}\overline{L_C } C_\nu Yr\omega_C $$

(18)

The plasticity index ψ of contacting rough surfaces can be written as [19]

$$ \psi =\left( {\frac{\sigma_{s} }{\omega_C }} \right)^{1/2} $$

(19)

Substituting L _C from equation (18) in equation (16) and using equation (19) we finally obtain

$$ \Gamma_{2} =\frac{3}{\pi }\frac{T_{2} }{wR\bar {L}_c C_\nu Y}\frac{(1-h^{\ast} /3)^{2}}{[1-erf(\sqrt {0.5} h^{\ast} )]}\frac{\psi^{2}}{\eta r\sigma_{s} } $$

(20)

Equation (20) reveals that the plasticity index ψ, which is proportional to (E/Y)(σ _s /r )^1/2, has a significant effect on the solution of equation (14) and hence on the average friction coefficient. In addition, the material properties ν and Y as well as the guide radius R and tape speed, which from the analysis of [22] determines h ^*, have also an effect on the friction coefficient. While the trend of the effects of material properties and guide radius on Γ₂ can easily be seen in equation (20), the effect of tape speed is more complex. To determine this relationship we define an “asperity load factor” of the form:

$$ \beta =\frac{(1-h^{\ast} /3)^{2}}{[1-erf(\sqrt {0.5} h^{\ast} )]} $$

(21)

The variation of β as a function of h ^* is illustrated in figure 2, showing a maximum for β around ${h^{\ast} \approx 2.2}$. Since hydrodynamic flying occurs at h ^*≥3, our model predicts that the asperity load factor reaches a maximum somewhat before flying inception. The model also predicts (as will be shown in the discussion of figure 5) that the friction coefficient becomes very small and independent of Γ₂ if β and thus Γ₂ approaches zero.

Figure 2.

Asperity load factor β versus dimensionless tape spacing h*.

Experimental set-up

Apparatus

While in a real application the tape is sliding over a stationary guide, it is more convenient for the purpose of tension measurements to use a stationary tape sample in combination with a rotating guide.

The experimental set-up, shown in figure 3, consists of a guide mounted on an adjustable speed DC-motor. A tape sample is positioned over the guide surface and is connected to a load cell that measures the tension T ₁ at one end, while at the other end it is subjected to a known tension T ₂ by a dead weight (see figure 3(a)). The load cell is mounted on a sled that can slide in a circular groove to allow a variable wrap angle. Figure 3(b) indicates the forces T ₁ and T ₂ and the wrap angle θ.

Figure 3.

Experimental set-up.

The wrap angle can be adjusted from 80° to 100° and the rotational speed of the guide in a clockwise direction is adjustable from 0 to 125 Hz, corresponding to a maximum circumferential speed of 11.8 m/s for a guide with a radius of 15 mm. The measured force T ₁ combined with the known “slack side tension” T ₂ and the wrap angle θ enable calculation of the average friction coefficient μ from the ratio T ₁/T ₂ using equation (1).

Test specimens

Commercially available metal particulate (MP) tape and metal evaporated (ME) magnetic tape were used for the tests. MP tape consists of a polymer substrate, coated with a mixture of metal particles and binder material. The magnetic coating of MP tape also contains abrasive particles for recording head cleaning. ME tape is manufactured by evaporating cobalt on a polymeric substrate in a vacuum chamber.

Two types of aluminum guides with radii of 7.5 mm, 10 mm and 15 mm were used. In one case, a ceramic coating was applied and in the other case an anodizing heat treatment was used. AFM scans of the guides revealed that the surface roughness is isotropic.

Table 1 shows the average asperity tip radius r, the asperity density η, the standard deviation of asperity summit heights σ _s , the ratio σ _s /r and the product ηrσ _s for the individual tape samples and guides. The equivalent roughness parameters for two contacting rough surfaces are also shown for three tape/guide combinations. These combinations are: MP tape and a ceramic guide (C1), ME tape and a ceramic guide (C2) and MP tape in combination with an anodized guide (C3).

Table 1. Surface characteristics of the test specimens.

The values in table 1 were obtained using the three spectral moments m ₀, m ₂ and m ₄ of the surface roughness as described by McCool [23] (see Appendix). The average radius of the asperity tips r, the asperity density η and the standard deviation of the asperity summit heights σ _s were calculated and averaged over 15 cross sections of an AFM scan for each tape and guide sample. From table 1 we observe that the ratio σ _s /r of the anodized guide surface is an order of magnitude smaller than that of the ceramic guide surface, i.e., the surface of the anodized guide is much smoother than the surface of the ceramic guide. We also observe that the ME tape is much smoother than the MP tape. We note that while the ratio σ _s /r for the three combinations C1, C2 and C3 changes over an order of magnitude, the product ηrσ _s for these combinations changes much less. Hence, Γ₂ (see equation 20) is less sensitive to the dimensionless parameter ηrσ _s in the tested combinations.

Test procedure

Tape specimens of 0.1 m length were cut out of commercially available tape reels. For each test a new tape specimen was connected to the load cell through a tape clamp on one end and a 0.5 N dead weight on its other end (figure 3(a)). The tape specimen was run-in for five minutes at a rotational speed ω = 16 Hz. Following this run-in procedure, the “tight-side tension” T ₁ was measured for stepwise increments of guide rotational speeds up to 125 Hz and was stored on a PC for further processing. The “slack-side” tension T ₂ was then adjusted by adding weight, while keeping the DC-motor running. The measurements of T ₁ were taken for the same range of speeds. This procedure was repeated up to a maximum slack-side tension T ₂ = 1.2 N. The test series for each of the three combinations C1, C2 and C3 were repeated three times with a new tape specimen for each test. The calculated friction coefficient for each test was averaged over the three repetitions.

Results and discussion

Theoretical results

The minimum spacing between tape and guide was calculated using the numerical procedure outlined in [22]. The following parameters were used: (a) polyethylene terephtalate tape (PET) with a density of 1370 kg/m³, (b) a Young’s modulus of 7 GPa and (c) a Poisson ratio of 0.3. Figure 4 shows the minimum spacing versus tape speed at a nominal tape tension of 1 N for guide radii of 15 mm, 10 mm and 7.5 mm, respectively.

Figure 4.

Calculated minimum spacing versus tape speed for different guide radii at a nominal tension of 1 N.

From figure 4 we observe that the minimum spacing increases for increasing tape speed as well as for increasing guide radius. Based on the analysis in [10], full fluid film lubrication occurs when the minimum spacing between the tape and the guide is equal to or larger than 3σ _s . Thus, for each of the three tape/guide combinations shown in table 1, we can define a critical speed at which the transition from boundary lubrication to fluid film regime occurs. For example, for the combinations C1 and C2 (ceramic guide) in table 1, we obtain 3σ _s  = 1.164μm, while for the combination C3 (anodized guide) we have 3σ _s = 0.227 μm. Correlating these values with figure 4, we conclude that with a guide radius of 15 mm at 1 N tape tension, the critical speed for combinations C1 and C2 is 8.5 m/s, while for combination C3 this critical speed is only 2 m/s, as indicated in figure 4 by the dashed lines. As we will show later (see discussion of figure 10), these values agree well with the experimental results.

For the case where the tape spacing is less than 3σ _s , the asperity load factor ${\beta =(1-h^{\ast}/3)^{2}/[1-erf(\sqrt {0.5}h^{\ast})]}$ can be calculated from the data in figure 4 and table 1. This asperity load factor is required to calculate Γ₂ according to equation (20). Table 2 presents the values of β for some typical cases in our tests.

Table 2. Typical values for the asperity load factor β for tape/guide combinations C1 (MP/ceramic) and C3 (MP/anodized) at different tap tension T ₂ and guide radius R.

Equation (14) was integrated numerically using the fourth order Runge Kutta method to obtain the ratio Γ/Γ₂ or, equivalently, T/T ₂, according to equation (15) or (17). Figure 5 shows the results as T/T ₂ versus the angular coordinate α for different initial conditions Γ₂ (see equation (17)). We point out that the tape speed, surface characteristics, mechanical properties and guide geometry are all included (see equation 20) in the model.

Figure 5.

T/T ₂ versus α for different values of Γ₂.

The solid lines in figure 5 present the solution of equation (14) for θ = π /2 from which the ratio T ₁/T ₂ at α = θ = π/2 can be determined. At a given T ₂, according to equation (20), a higher plasticity index ψ, which indicates a rougher surface, yields a higher Γ₂ value. Similarly, a smaller guide radius R and a smaller yield strength Y will also give higher Γ₂. As shown in figure 5, a higher Γ₂ is associated with a higher T ₁ /T ₂ ratio and hence, according to equation (1), a higher average friction coefficient. Thus, the average friction coefficient depends on tape speed, surface characteristics, material properties, and guide geometry, and is not a constant as assumed in the classical belt drive model. The average friction coefficient, can be used in equations (4) and (5) to determine the local ratio T/T ₂ versus α in the form T/T ₂ = exp(μ α ). These results are also plotted in figure 5 as dashed lines. The results for T/T ₂ that are based on the average friction coefficient clearly deviate from the results based on the more complete solution of equation (14). The average friction coefficient, which is governed by an exponential function of α, overestimates the local tension compared to the solution of equation (14) that is best described by a third order polynomial function of α.

Figure 6 shows the theoretical friction coefficient μ versus Γ₂ for wrap angles of 50°, 80°, 90° and 100°.

Figure 6.

Friction coefficient versus Γ₂ for different wrap angles.

As can be seen, the friction coefficient increases slightly for a higher wrap angle in the range 80–100° but is substantially lower for θ = 50°.

Experimental results

Figure 7 presents experimental results for the MP tape/ceramic guide combination (C1 in table 1), showing the effects of sliding speed, guide radius and tape tension T ₂ on the average friction coefficient calculated from equation (1). The range of the tape tension varies from 0.5 N to 1.2 N and the guide radii are 15, 10 and 7.5 mm shown in figure 7(a), (b) and (c), respectively.

Figure 7.

Average friction coefficient versus speed for C1 (MP/Ceramic) combination at different nominal tape tensions and for a guide radius of (a) 15 mm, (b) 10 mm, (c) 7.5 mm.

Note that at the maximum rotational speed of 125 Hz, the maximum linear speeds for the radii 15, 10 and 7.5 mm are about 12, 8 and 6 m/s, respectively. From figure 4 it is clear that a smaller guide radius requires a higher speed to maintain a given spacing. As a consequence, the friction coefficient at a given tension and speed is higher for a smaller guide radius, in agreement with our model that shows higher Γ₂ for smaller R values. Indeed, as can be seen in figure 7, full fluid lubrication (h ^*≥3) seems to exist in our tests only for the largest guide radius of 15 mm.

From figure 7(a) we observe that at the lowest speed (about 1.5 m/s) the friction coefficient is almost independent of the tension T ₂. This differs from the prediction of our model probably because at very low speed no air bearing effects are present and elastic deformations of the tape may occur. This would violate the simplifying assumption of a “rigid” tape made in our model. It is also seen from figure 7(a) that as the speed increases, the friction coefficient decreases monotonically and becomes a strong function of tape tension, i.e., higher tape tension T ₂ results in a higher Γ₂ and hence higher friction coefficient in agreement with our model (see equation (20)). At the highest speed the friction coefficient is again independent of the tape tension due to the formation of an air bearing, which completely removes the load from the asperities. This situation is also predicted by our model for a non-dimensional spacing of h ^*≥3. A similar behavior is observed in figure 7(b) and (c). However, in these cases, because of the lower sliding speed, we only see partial formation of an air bearing. Identical tests were also carried out for different wrap angles between 80° and 100° showing that the effect of the wrap angle on the friction coefficient is small, similar to the theoretical prediction for this range of θ in figure 6.

Figure 8 shows the average friction coefficient versus guide radius for the C1 (MP/ceramic) combination at a sliding speed of 6 m/s. As can be seen, the average friction coefficient decreases with increasing guide radii as was also predicted by our model (see equation (20)).

Figure 8.

Average friction coefficient versus guide radius for C1 (MP/Ceramic) combination at different nominal tape tensions and a tape speed of 6 m/s.

In order to increase the recording density, tape manufacturers use metal evaporated (ME) tape, consisting of a high coercivity cobalt film, evaporated on the tape substrate in a vacuum chamber. Hempstock and Sullivan [24] studied the durability and signal performance of ME and MP tapes and concluded that MP tape exhibits far greater durability than ME tape. In another study Hempstock and Sullivan [25] identified the mechanical failure mechanism of ME tape as a form of delamination wear. Bijker et al. [26] discussed the use of wear protective coatings such as diamond like carbon (DLC) and a so-called super protective layer (SPL) to potentially improve the wear characteristics of ME tape. They concluded that protective coatings need further development to withstand abrasive wear.

The rotating guide of our test set-up stalled due to high stiction when attempting to test the ME tape over the full operating range (speed and tension) that was previously used with MP tape. Hence, in order to overcome the higher stiction tendency inherent to ME tape [4], and allow comparison with MP tape, a test was performed for both media using a low tape tension of 0.1 N in combination with an 80 degree wrap angle and a guide radius of 15 mm. Figure 9 presents the comparison between the ME and MP tapes showing very similar values of friction coefficient over the entire speed range. From table 1 we observe that although the ME tape has a σ _s /r value that is three times lower than that of the MP tape, the equivalent σ _s /r values for the combinations C1 (MP tape and ceramic guide) and C2 (ME tape and ceramic guide), and their corresponding plasticity index values, are almost identical. Hence, as can be seen from equation (20), a similar trend of the average friction coefficient versus speed for the MP and ME tapes is predicted by the model in agreement with the experimental results.

Figure 9.

Average friction coefficient versus speed for ME and MP tapes and a ceramic guide with a radius of 15 mm at a tape tension of 0.1 N.

Model validation

The model derived in this paper predicts qualitatively the effects of various design and operating parameters on the friction coefficient. In order to quantitatively correlate the theoretical and experimental results, it is desirable to use accurate material properties (E, Y and ν) of the tape/guide combinations. Because the MP magnetic coating consists of nano particles with a complex composition (cobalt–iron alloy core with a passivation shell composed of oxidized compounds of the core material (Personal communication)), it is difficult to measure its material properties accurately and hence, the following average values were used: (a) E/Y = 100, (b) a yield strength ${Y\cong 180}$  MPa and (c) Poisson ratio of 0.3.

Figure 10(a) shows the experimentally measured (solid lines) and theoretically predicted (dashed lines) friction coefficient versus the tape speed for the rougher ceramic (C1) and the smoother anodized (C3) guide/tape (MP tape) combinations both with a radius R = 15 mm, a tape tension T ₂ = 1 N and a wrap angle θ = 90°. Figure 10(b) shows a similar comparison for a 7.5 mm ceramic guide/MP tape (C1) combination at two different tape tensions of 1 N and 0.5 N.

Figure 10.

Experimental and theoretical results for the average friction coefficient versus tape speed (a) for MP tape and anodized (C3) and ceramic (C1) guides with radius of 15 mm at a tape tension of 1 N and (b) for MP tape and a ceramic guide with radius of 7.5 mm at tape tensions of 1 N and 0.5 N.

We observe that the model predictions are of the same order of magnitude as the experimental results. The friction coefficient of the smoother anodized guide (see table 1) is clearly much lower than that for the rougher ceramic guide at the same tape speed.

From figure 7 we note that the friction coefficient decreases monotonically with increasing speed. Full fluid lubrication begins when the friction coefficient versus speed curve shows a diminishing rate of decrease. According to figure 10(a) the flying speed for C1 (ceramic guide) appears to be 9 m/s, while for C3 (anodized guide) it is 3 m/s. These values are in good agreement with the corresponding theoretical prediction of 8.5 and 2 m/s, respectively (See discussion of figure 4). From figure 10(b) very similar differences in the friction coefficient are seen for the two different tensions.

The monotonic reduction in the experimental friction coefficient with increasing speed in figure 10(a) and (b) is not well captured by our model, which shows a behavior similar to that of the asperity load factor β versus h ^* (see figure 2). This is probably due to the assumption of conformal tape having a uniform minimum spacing along the entire wrap angle. In reality, the tape/guide spacing will be larger than the minimum at the leading and trailing edges of the tape/guide interface. From figure 2 we can see that at low speeds (to the left of the maximum at ${h^{\ast} \approx 2.2}$) an increased h ^* will yield a higher asperity load factor β and hence will result in a higher Γ₂ and a higher predicted friction coefficient. At higher speeds (to the right of the maximum at ${h^{\ast} \approx 2.2}$), an increased h ^* will yield a lower asperity load factor β and hence will result in a lower predicted friction coefficient. Additionally, the assumption of a rigid tape may differ from reality and therefore may cause the theoretical results to deviate from the experimental results. Local deformations of the tape due to air bearing pressure and/or (partial) asperity contact might affect the friction coefficient. Also, we assumed that each asperity carries the same average load, despite the Gaussian distribution of asperity heights. Taking care of these effects could make the predicted results of friction coefficient versus speed closer to the experimental ones.

Figure 11 compares theoretical predictions (dashed line) and experimental results (solid line) of the effect of the guide radius on the friction coefficient for a tape tension of 1 N and a ceramic guide/MP tape (C1) combination. As can be seen the agreement between the model and experiments is fairly good.

Figure 11.

Experimental and theoretical results for the average friction coefficient versus guide radius for a ceramic guide and MP tape at 1 N tape tension

Conclusion

A model was developed that predicts the local tape tension along the circumference of the tape/guide interface, based on a local friction coefficient model for a single contacting asperity. The model provides an average friction coefficient for different tape/guide combinations taking into account the effects of tape sliding speed, tape and guide surface characteristics, material properties and guide dimensions. An experimental set-up was implemented to measure the average friction. Good agreement was found between theoretical predictions and the experimental results for moderate tape speeds where an air bearing coexists with partial asperity contact. The main conclusions of the present study are:

• 1. The classical belt drive equation that relies on a constant friction coefficient can be significantly improved to include such effects as sliding speed, surface roughness, material properties and guide and tape geometry.

• 2. The plasticity index ψ, which is proportional to (E/Y )(σ _s /r )^1/2, has a significant effect on the average friction coefficient. A higher ψ value yields higher friction coefficients. The material properties ν and Y as well as the guide radius R also affect the friction coefficient.

• 3. The speed at the transition from boundary lubrication to full fluid film regime can be predicted from surface characteristics and from tape/guide flying height simulations. This speed is higher for rougher surfaces and smaller guide radii.

• 4. The average friction coefficient shows only a small dependence on the wrap angle, over the 80°–100° range. However, it increases substantially for increasing dimensionless tape tension Γ₂, especially at high values of this parameter.

• 5. The average friction coefficient decreases for increasing speed and decreasing tape tension T ₂.

• 6. The model can be further improved by relaxing some of its simplifying assumptions such as: rigid tape bulk and constant spacing between guide and tape.

Appendix

According to McCool’s analysis [23], the spectral moments of a rough isotropic surface are given by

$$ \begin{aligned} &m_{0} =\hbox{AVG}\left[ {y^{2}} \right]\\ &m_{2} =\hbox{AVG}\left[ {\left( {\frac{dy}{dx}} \right)^{2}} \right]\\ &m_{4} =\hbox{AVG}\left[ {\left( {\frac{d^{2}y}{dx^{2}}} \right)^{2}} \right] \end{aligned} $$

where y(x) is the height distribution of the surface profile.

The radius of curvature of asperity summits, the area density of the asperities and the standard deviation of asperity summit heights can be calculated as

$$ \begin{aligned} &r=0.375\left( {\frac{\pi }{m_{4} }} \right)^{1/2}\\ &\eta =\frac{m_{4} }{6\pi \sqrt 3 m_{2} }\\ &\sigma_{s} =\left( {m_{0} -\frac{3.717\times 10^{-4}}{\eta^{2}r^{2}}} \right)^{1/2} \end{aligned} $$

For the case of two contacting isotropic rough surfaces 1 and 2, an equivalent rough surface in contact with a smooth flat can be defined. The spectral moments of this equivalent rough surface are given by summing the spectral moments of the individual surfaces. Hence,

$$ m_i =\left( {m_i } \right)_{1} +\left( {m_i } \right)_{2} $$

where i = 0, 2, 4