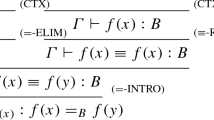The Justification of Identity Elimination in Martin-Löf’s Type Theory

Abstract

On the basis of Martin-Löf’s meaning explanations for his type theory a detailed justification is offered of the rule of identity elimination. Brief discussions are thereafter offered of how the univalence axiom fares with respect to these meaning explanations and of some recent work on identity in type theory by Ladyman and Presnell.

1 Introduction

Let us say that a formal language $L$ serves as a foundation for a mathematical theory T if (i) the concepts of T are definable in $L$—that is, for each concept of T there is a concept in $L$ that ‘translates’ it; and (ii) any theorem of T (after its translation) is demonstrable in $L$. For $L$ to serve as such a foundation it is clear that it must contain certain concepts on the basis of which the concepts of T may be defined and support certain modes of reasoning on the basis of which the theorems of T may be demonstrated. Moreover, if we are to recognize $L$ as a foundation for T, it is clear that we must understand these concepts and appreciate that these modes of reasoning are valid. This latter requirement will be met, it seems, if the language $L$ has been given an intended interpretation: if it has been laid down what statements made in $L$ mean and how the symbols of $L$ contribute to this meaning. On the basis of the meaning explanations provided we should, namely, come to an understanding of the concepts of $L$ and come to see that the forms of reasoning supported by $L$ are valid.

On pain of circularity the meaning explanations for $L$ cannot rely on concepts from T. Hence, if T is ‘all of mathematics’, then the meaning explanations for $L$ cannot themselves rely on a mathematical theory, in particular not on model theory. Thus, axiomatic set theory, which is often taken to be a candidate for a foundation of all of classical mathematics, has been explained in terms of the so-called iterative conception of set (Zermelo 1930; Boolos 1971; Shoenfield 1977). I shall be concerned with Martin-Löf’s constructive type theory, which aims to be a foundation for constructive mathematics. In particular, I wish to consider in detail how, on the basis of the meaning explanations offered by Martin-Löf for this language, a certain mode of reasoning supported by it known as the identity elimination rule can be justified.

I shall approach the justification of elimination rules in a manner that differs somewhat from that of Martin-Löf (1984) and Nordström et al. (1990). In order to justify an elimination rule it is necessary to make it evident, on the assumption that the premisses of the rule are known, that a certain object a evaluates to a canonical element of some $\mathbf {set}$A (the notation and terminology here will be explained presently). In the cited works an informal description of this evaluation is taken to justify both the elimination rule and the corresponding equality rule. I shall instead take the equality rule to be definitional in nature and to provide the main ingredient of the justification of the elimination rule. More generally, I shall distinguish rules that are definitional, or meaning-giving, in nature from rules, such as the elimination rules, that are postulational in nature and that require justification.

There are at least two reasons why the rule of identity elimination deserves attention. In the paper (Martin-Löf 1982), where Martin-Löf first gave meaning explanations for his type theory, the justification of the rules of the system is left to the reader. In the booklet (Martin-Löf 1984), where both meaning explanations and justifications of the rules are given, another rule of identity elimination is employed, much stronger than the one found in (Martin-Löf 1975) and that interests us. The textbook (Nordström et al. 1990) gives meaning explanations and treats of the relevant rule of identity elimination, but provides only a very cursory justification of it (ibid. p. 58). In many cases it will be obvious to anyone who has seen the justification of, for instance, $\Sigma$-elimination how the justification of an elimination rule should go. Owing to certain peculiarities of identity-$\mathbf {set}$s, a justification of identity elimination cannot, however, be obtained by a straightforward adaptation of the justification of, say, $\Sigma$-elimination. That a thorough justification of identity elimination is thus not found in any of the well-known introductory works on type theory (not in any publication, as far as I am aware) and involves features not found in the justification of other elimination rules is one reason to devote attention to it.

Another reason is that, in a recent paper, Ladyman and Presnell (2015) have claimed that identity elimination has so far not been satisfactorily justified from ‘pre-mathematical’ principles. More precisely, Ladyman and Presnell claim that the rule called path induction in homotopy type theory (The Univalent Foundations Program 2013, ch. 1.12.1) has so far not been thus justified. Path induction is formally identical to identity elimination—if the two rules differ, it is in the meaning explanations assumed by the homotopy interpretation of type theory on the one hand and the intended interpretation on the other. Ladyman and Presnell emphasize, however, that the kind of justification they seek will not be found in the homotopy interpretation (p. 401); and the justification they themselves offer is free of concepts from homotopy theory (pp. 401–405). What Ladyman and Presnell think about the mode of justification of the rules of type theory employed by Martin-Löf (1984) and Nordström et al. (1990) is not easy to say, since they do not discuss it. But in order to forestall the impression readers of Ladyman and Presnell’s paper may get that this mode of justification cannot satisfactorily be applied to identity elimination, it seems worthwhile showing in detail that the contrary is the case. Some discussion of Ladyman and Presnell’s own suggested justification will be given at the end of this paper (Sect. 6). After having presented what I shall call the intended, or standard, interpretation of type theory (Sects. 2, 3) and shown how identity elimination (Sect. 4) may be justified on the basis of it, I shall also briefly discuss the univalence axiom of homotopy type theory in the light of this interpretation (Sect. 5).

2 Preliminaries

2.1 Syntax and Notation

Statements made in Martin-Löf’s type theory are called ‘judgements’. In particular, the premisses and conclusion of an inference made in the system are judgements. A judgement may be categorical or hypothetical. There are two forms of categorical judgement:

$$\begin{aligned} \begin{array}{r} a:\mathscr {C}\\ a=b : \mathscr {C}\end{array} \end{aligned}$$

The first may be read ‘a is an object of category $\mathscr {C}$’ and the second ‘a and b are equal objects of category $\mathscr {C}$’. (The term ‘category’ is here being used in the traditional, philosophical sense and not in the sense of category theory.) A judgement of the latter form presupposes the judgements $a:\mathscr {C}$ and $b:\mathscr {C}$ for its meaningfulness. In the basic formulation of the theory the categories are

• (1) $\mathbf {set}$;

• (2) A for any $\mathbf {set}$A.

Extensions of the basic formulation may be obtained by admitting as categories higher types or, for instance, a category of contexts, as in the so-called substitution calculus. We shall here restrict ourselves to the basic formulation, thereby following Martin-Löf (1975, 1982, 1984) and Nordström et al. (1990). In this formulation the forms of categorical judgement are thus

$$\begin{aligned} \begin{array}{r} A :\mathbf {set}\\ A=B : \mathbf {set}\end{array} \end{aligned}$$

and for any $\mathbf {set}$A,

$$\begin{aligned} \begin{array}{r} a:A \\ a=b :A \end{array} \end{aligned}$$

The form of a hypothetical judgement is

$$\begin{aligned} x_1:A_1,\ldots , x_n:A_n\vdash J \end{aligned}$$

where J has the form of a categorical judgement.

We write boldface $\mathbf {set}$ so as to make it clear that a set in the sense of constructive type theory is meant. A $\mathbf {set}$ in this sense is not at all a set in the sense of axiomatic set theory. The notion in axiomatic set theory that corresponds most closely to a $\mathbf {set}$ in type theory is not the notion of a set, but rather that of a universe of sets. Namely, a $\mathbf {set}$ is a domain, or type, or sort, of individuals, just as a universe of, say, ZFC-sets is (cf.  Zermelo 1930). A $\mathbf {set}$ should thus be thought of as a type of individuals. It is not uncommon in the literature to call the category $\mathbf {set}$ ‘type’. Indeed, this is the terminology employed in Martin-Löf (1975, 1982). With higher types present, it is, however, necessary to distinguish terminologically between types of individuals and types in general.¹ We follow Martin-Löf (1984) in calling the former ‘sets’.²

2.2 General Remarks on the Intended Interpretation

The intended, or standard, semantics of Martin-Löf’s type theory may be said to be determined by three components:

• The explanation of the forms of categorical judgement.

• The explanation of the forms of hypothetical judgement.

• The rules of the system.

The explanation of a form of judgement provides the assertion-conditions for judgements of the form in question. It lays down what one must know in order to have the right to make such a judgement. These explanations in effect also determine what is understood by the four basic notions of being a $\mathbf {set}$; being equal $\mathbf {set}$s; being an element of a $\mathbf {set}$A; and being equal elements of a $\mathbf {set}$ A.

The rules of the system are of two kinds. Firstly, there are general rules governing judgements of the forms $A=B:\mathbf {set}$ and $a=b:A$, as well as rules of substitution and assumption. These rules can be seen to be justified by the explanations of the forms of judgement.

Secondly, there are rules associated with the primitive constants of the theory. These are of four kinds: formation rule, introduction rule, elimination rule, and equality rule. Formation-, introduction-, and elimination rules come in pairs: one rule has $a:\mathscr {C}$ as conclusion and the other has $a=b:\mathscr {C}$ as conclusion, where in formation rules $\mathscr {C}$ is $\mathbf {set}$, and in introduction- and elimination rules, $\mathscr {C}$ is A for some $\mathbf {set}$A. I will call the rule whose conclusion is $a:\mathscr {C}$ the primary rule, and the rule whose conclusion is $a=b:\mathscr {C}$ the secondary rule, of the pair in question. Secondary rules are often left implicit in presentations of type theory. But in a lower-order presentation their presence must be assumed, since without them one cannot justify in general that if $a=b:\mathscr {C}$, then a and b are intersubstitutable ‘salva identitate’.

Introduction- and equality rules, as well as the secondary elimination rules, are definitional, or meaning-giving, in nature. Introduction rules determine what are the so-called canonical elements, and what are equal canonical elements, of a canonical $\mathbf {set}$ introduced by a formation rule (the notion of canonicity will be explained in more detail below). Equality rules in effect determine how an element of a $\mathbf {set}$ introduced by means of an elimination rule is to be evaluated to canonical form. A secondary elimination rule determines that the identity of the element a : A in the conclusion of the corresponding primary elimination rule does not depend on the ‘mode of presentation’ of the b’s occurring in the premisses $b:\mathscr {C}$ of this rule. Being definitional, these rules require no justification—which is not to say that any rule one might think of can serve as, for instance, an introduction rule. An example of a purported introduction rule that fails its task as a definition will be given below.

In regarding equality rules as definitional our approach to the standard semantics differs somewhat from that found in Martin-Löf (1984) and Nordström et al. (1990). There, a primary elimination rule and its corresponding equality rule are taken to be justified on the basis of an informal explanation of how an element introduced by the application of an elimination rule is to be evaluated to canonical form. Such an informal explanation can, however, be extracted from the equality rule together with the explanation of the forms of categorical judgement. Since we already need to assume that certain rules are meaning-giving in nature, we might as well also make that assumption regarding the equality rules. Doing so reduces the reliance on informal explanations and, it seems to me, also leads to a cleaner division of labour among the rules.

Formation rules and primary elimination rules are postulational in nature and do require justification. Formation rules postulate that such and such is a canonical $\mathbf {set}$ and that such and such are equal canonical $\mathbf {set}$s; but to have the right to assert that A is a canonical $\mathbf {set}$ I must know what are the canonical elements of A as well as what are equal canonical elements of A; and to have the right to assert that A and B are equal canonical $\mathbf {set}$s I must know that any canonical element of A is a canonical element of B, and vice versa, and that equal canonical elements of A are equal canonical elements of B, and vice versa. A primary elimination rule postulates that such and such, a, is an element of a $\mathbf {set}$, and to have the right to assert this I must know that a evaluates to a canonical element.

What all of this means in practice should become clearer in the course of this paper. But one may see already now that, in the context of the explanations of the basic notions of the theory, the justification of a formation rule is provided by the associated introduction rules, and the justification of a primary elimination rule by the associated equality rule(s).

2.3 The Notion of Evaluation

In the explanation of the forms of categorical judgement the notion of evaluation plays an important role. In particular, the relation

$$\begin{aligned} a \,\, \mathrm{evaluates \, to} \,\, b \end{aligned}$$

is assumed as a primitive notion, not itself explained, but used in the explanation of the forms of judgement. The following examples suggest what one should understand by evaluation.

$$\begin{aligned} \begin{array}{r} (3+2)! \times 4 \,\, \mathrm{evaluates\, to} \,\, 480 \\ \mu x.( Prime (x)\wedge x>(3+2)! \times 4) \,\, \mathrm{evaluates \, to} \,\, 487 \end{array} \end{aligned}$$

Thus, ordinary arithmetical computation as well as computation in an extended language of arithmetic are instances of evaluation. Another instance of evaluation is the passage from the definiendum to the definiens of an explicit definition. Hence, if we have defined $\lnot A$ as $A\supset \bot$, then

$$\begin{aligned} \lnot \, A \,\,\mathrm{evaluates \, to} \,\, A\supset \bot \end{aligned}$$

Also reduction steps in the sense of Prawitz (1965) should be thought of as instances of evaluation.

It follows from the explanations of the forms of categorical judgement to be given below that if $a \,\, \mathrm{evaluates\, to} \,\, b$, then $a=b:\mathscr {C}$. That evaluation thus preserves equality is reasonable in light of the above examples. The number $(3+2)! \times 4$ evaluates to, and is equal to, the number 480. If the proposition $\lnot A$ is explicitly defined as $A\supset \bot$, then it is clear that $\lnot A$ is the same proposition as $A\supset \bot$. In general, if an a of some category $\mathscr {C}$ is explicitly defined as $a'$, then it is clear that a is the same $\mathscr {C}$ as $a'$. That a natural deduction derivation is equal to one to which it reduces is a well-known conjecture regarding the identity of proofs due to Martin-Löf (cf. e.g. Prawitz 1971, p. 257–261).³

There is a clear sense in which $5!\times 4$ is not the answer wanted when a schoolboy is asked to compute $(3+2)! \times 4.$ The answer wanted is 480, which we may therefore think of as the ‘end point’ of the evaluation of $(3+2)! \times 4$. We introduce the term ‘canonical object’ for an object that within type theory serves as an end point of evaluation.⁴ A canonical object is therefore an object that evaluates to itself. What are regarded as the end points of evaluation is, to some extent at least, a matter of convention. In type theory it is stipulated that a $\mathbf {set}$A is canonical if and only if $A:\mathbf {set}$ is the conclusion of a primary formation rule. Whenever a primary formation rule is laid down it must be specified, for any $\mathbf {set}$A such that $A:\mathbf {set}$ is the conclusion of an application of this rule, what a canonical element of A is. In most cases this specification follows directly from the associated primary introduction rule(s), so that a will be a canonical element of a $\mathbf {set}$A if and only if a : A is the conclusion of an application of an associated introduction rule. Instead of ‘canonical element’ we sometimes say ‘element of canonical form’.

Evaluation as implemented in constructive type theory operates from without and not from within (cf.Martin-Löf 1982, p. 160).⁵ That is to say, whether an object is canonical depends only on the form of its outermost operator. It is therefore necessary also to specify what equal canonical objects of a category are, since we must allow for canonical objects’ being equal although they are syntactically different. It is stipulated that A and B are equal canonical $\mathbf {set}$s if $A=B:\mathbf {set}$ is the conclusion of a secondary formation rule. Whenever a primary formation rule is laid down it must be specified, for any $\mathbf {set}$A such that $A:\mathbf {set}$ is the conclusion of an application of this rule, what equal canonical elements of A are. In most cases this specification follows directly from the associated secondary introduction rule(s), so that a and b will be the same canonical element of a $\mathbf {set}$A if and only if $a=b:A$ is the conclusion of an application of an associated secondary introduction rule.

In the explanation of the forms of judgement we thus take ourselves to be dealing with objects of which it makes sense to say that they evaluate to canonical objects. More precisely, we are assuming that if $a:\mathscr {C}$ is a valid judgement of the theory, then it makes sense to speak of the evaluation of a to canonical form. That any such a is indeed an object follows from the fact that through the explanation of the forms of judgement $a:\mathscr {C}$ and $a=b:\mathscr {C}$, the category $\mathscr {C}$ is provided with criteria of application and identity. A category is therefore what philosophers have called a sortal concept, and most would agree that whatever falls under a sortal concept deserves to be called an object.

2.4 Explanation of the Forms of Categorical Judgement

In explaining the four forms of categorical judgement we shall follow (Martin-Löf 1982). The perhaps more well-known explanations of (Martin-Löf 1984) may be regarded as a special case of these. Namely, we may regard the latter explanations as obtained from the former if we assume that all $\mathbf {set}$s are canonical. The latter explanations therefore do not suffice when one or more so-called universes are assumed or when something as basic as explicit definitions of $\mathbf {set}$s is allowed.

The judgement

$$\begin{aligned} A:\mathbf {set}\end{aligned}$$

means that A evaluates to a canonical $\mathbf {set}$. We are free to postulate that C is a canonical $\mathbf {set}$—that is, to lay down a formation rule whose conclusion is $C:\mathbf {set}$—provided we specify what a canonical element of C is and what equal canonical elements of C are. The latter specification must be done so that the relation of equality between canonical objects in C is rendered reflexive, symmetric, and transitive.

The judgement

$$\begin{aligned} A=B:\mathbf {set}\end{aligned}$$

means that A and B evaluate to equal canonical $\mathbf {set}$s. We are free to postulate that the canonical $\mathbf {set}$s C and D are equal—that is, to lay down a formation rule whose conclusion is $C=D:\mathbf {set}$—provided we can justify that any canonical element of C is also a canonical element of D, and vice versa; and that equal canonical elements of C are equal canonical elements of D, and vice versa.

Assume $A:\mathbf {set}$. Then A evaluates to some canonical set C. The judgement

$$\begin{aligned} a:A \end{aligned}$$

means that a evaluates to a canonical element of C. The judgement

$$\begin{aligned} a=b:A \end{aligned}$$

means that a and b evaluate to equal canonical elements of C.

2.5 Example

We postulate the following rules of $\text{N}$-formation.

$$\begin{aligned} \text{(N-form)}\qquad \qquad \quad \qquad \text{N}:\mathbf {set}\qquad \quad \qquad \text{N}=\text{N}:\mathbf {set}\end{aligned}$$

Thus, we postulate that $\text{N}$ is a canonical $\mathbf {set}$ and that $\text{N}$ is the same canonical $\mathbf {set}$ as $\text{N}$. In the case of a constant, such as $\text{N}$, the secondary formation rule is, in general, trivial. To be justified in postulating $\text{N}:\mathbf {set}$, we must specify what the canonical elements of $\text{N}$ are and what equal canonical elements of $\text{N}$ are. That is done by stipulating the following $\text{N}$-introduction rules.

By virtue of these rules 0 is a canonical element of $\text{N}$, as is $\text{s}(n)$ provided n is a $\text{N}$ (n itself does not have to be canonical). Moreover, 0 is the same canonical element of $\text{N}$ as 0, and $\text{s}(n)$ is the same canonical element of $\text{N}$ as $\text{s}(m)$ provided $n=m:\text{N}$ (n and m do not have to be canonical elements of $\text{N}$). Since 0 is a constant, the secondary introduction rule $0=0:\text{N}$ is trivial.

Having specified what the canonical elements of $\text{N}$ are we must justify the secondary $\text{N}$-formation rule. But in this case, that is entirely trivial; namely, it is entirely trivial that any canonical element of $\text{N}$ is a canonical element of $\text{N}$ and that equal canonical elements of $\text{N}$ are equal canonical elements of $\text{N}$.

Since $\text{N}$ is a canonical $\mathbf {set}$, the judgement

$$\begin{aligned} n:\text{N}\end{aligned}$$

means that n evaluates to a canonical element of $\text{N}$. For instance, by means of the rule of $\text{N}$-elimination, which will not be stated here, one can define the addition function, $+.$ Making the definitions $1=\text{s}(0):\text{N}$ and $2=\text{s}(1):\text{N}$, one can then see that $2+2$ is an element of $\text{N}$, since it evaluates to $\text{s}(2+1)$, which is of canonical form, since we can show $2+1:\text{N}$. The judgement

$$\begin{aligned} m=n:\text{N}\end{aligned}$$

means that m and n evaluate to equal canonical elements of $\text{N}$. Thus, making the definition $3=\text{s}(2):\text{N}$, we have $2+2=3+1:\text{N}$, since the left hand side evaluates to $\text{s}(2+1)$ and the right hand side to $\text{s}(3+0)$, and we can show $2+1=3+0:\text{N}$.

2.6 Principles Justified by the Explanations

It may be instructive to see that the explanations given justify the following important rule.

The premisses presuppose $A:\mathbf {set}$ and $B:\mathbf {set}$. Hence, A evaluates to a canonical $\mathbf {set}$C and B to a canonical $\mathbf {set}$D. By the first premiss, viz. a : A, a therefore evaluates to some canonical element c : C. By the second premiss, C and D are equal canonical $\mathbf {set}$s. By the explanation of what it is for canonical $\mathbf {set}$s to be equal, we may infer that c is a canonical element of D. Hence a evaluates to a canonical element of D, which is a canonical $\mathbf {set}$ to which B evaluates; whence a : B. The rule

can be justified in a similar manner.

The explanations likewise justify rules to the effect that the relations of equality between $\mathbf {set}$s and equality between the elements of a $\mathbf {set}$A are reflexive, symmetric, and transitive. In what follows I shall rely on all of these rules without explicit mention.

It is stipulated that a canonical object evaluates to itself. Hence, if the $\mathbf {set}$A evaluates to the canonical $\mathbf {set}$C, then $A=C:\mathbf {set}$ according to the explanation of this form of judgement. Likewise, if a : A evaluates to c : C, then $a=c:C$, and therefore also $a=c:A$. Thus, in general, if $a \,\, \mathrm{evaluates \, to} \,\, b$ in some category $\mathscr {C}$, then $a=b:\mathscr {C}$. This fact is important for the justification of elimination rules.

2.7 Propositions

In constructive type theory the category $\mathbf {prop}$ of propositions is identified with the category $\mathbf {set}$. If A is a $\mathbf {set}$, we may therefore also regard it as a $\mathbf {prop}$, and vice versa. When regarding A as a $\mathbf {prop}$, the judgement a : A may be read as saying that a is a proof of A. The explanation of the forms of categorical judgement given above carries over to explanations of the forms of judgement $A:\mathbf {prop},$$A=B:\mathbf {prop},$a : A, and $a=b:A$, where $A:\mathbf {prop}$. In particular, when stipulating that A is a canonical $\mathbf {prop}$ we must specify what the canonical proofs, and what equal canonical proofs, of A are. The proposition A is true if a proof of A exists.

2.8 Explanation of the Forms of Hypothetical Judgement

Assume $A:\mathbf {set}$. The hypothetical judgement

$$\begin{aligned} x:A\vdash B:\mathbf {set}\end{aligned}$$

means that $B[a/x]:\mathbf {set}$ whenever a : A and that $B[a/x]=B[a'/x]:\mathbf {set}$ whenever $a=a':A$. We here use square brackets to indicate substitution. Thus, B[a/x] is the result of substituting a for x in B. The judgement $x:A\vdash B:\mathbf {set}$ may therefore be thought of as saying that B is a family of $\mathbf {set}$s over A, or a $\mathbf {set}$-valued function over A. Owing to the condition that $B[a/x]=B[a'/x]:\mathbf {set}$ whenever $a=a':A$, the family is extensional in the sense that it does not depend on the ‘mode of presentation’ of the index a. The judgement $x:A\vdash B:\mathbf {prop}$ may be thought of as saying that B is a unary propositional function over A.

The hypothetical judgement

$$\begin{aligned} x:A\vdash B=B':\mathbf {set}\end{aligned}$$

means that $B[a/x]=B'[a/x]:\mathbf {set}$ whenever a : A.

Assume $x:A\vdash B:\mathbf {set}$. The hypothetical judgement

$$\begin{aligned} x:A\vdash b:B \end{aligned}$$

means that b[a/x] : B[a/x] whenever a : A and that $b[a/x]=b[a'/x]:B[a/x]$ whenever $a=a':A$. The judgement $x:A\vdash b:B$ may therefore be thought of as saying that b is a function whose domain is A and such that b[a/x] is of category B[a/x]; thus the category of b[a/x] may depend on the argument a.

The hypothetical judgement

$$\begin{aligned} x:A\vdash b=b':B \end{aligned}$$

means that $b[a/x]=b'[a/x]:B[a/x]$ whenever a : A.

Note that we here in effect reduce the explanation of a hypothetical judgement $x:A\vdash J[x]$ to the corresponding categorical judgement J[a]. In particular, the judgement $x:A\vdash B:\mathbf {set}$ is taken to mean that B[a/x] evaluates to a canonical $\mathbf {set}$ whenever a : A and that B[a/x] and $B[a'/x]$ evaluate to equal canonical $\mathbf {set}$s whenever $a=a':A$. The judgement $x:A\vdash b:B$ is taken to mean that b[a/x] evaluates to a canonical element of the canonical $\mathbf {set}$ to which B[a/x] evaluates and that b[a/x] and $b[a'/x]$ evaluate to equal canonical elements of the canonical $\mathbf {set}$ to which B[a/x] evaluates.

The above explanations are generalized by induction to hypothetical judgements with an arbitrary number of assumptions. We give one example. Assume

$$\begin{aligned} x_1:A_1,\ldots ,x_{n-1}:A_{n-1}\vdash A_n:\mathbf {set}\end{aligned}$$

Let $\bar{a}$ be a sequence $a_1,\ldots ,a_n$ such that

$$\begin{aligned} a_1:A_1,\ldots , a_n:A_n[a_1/x_1,\ldots ,a_{n-1}/x_{n-1}] \end{aligned}$$

We call $x_1:A_1,\ldots , x_n:A_n$ a context and $\bar{a}$ an environment for this context. Environments $\bar{a}$ and $\bar{a}'$ are said to be equal if

$$\begin{aligned} a_1=a_1':A_1,\ldots , a_n=a_n':A_n[a_1/x_1,\ldots ,a_{n-1}/x_{n-1}] \end{aligned}$$

Note that $\bar{a}$ is a sequence of closed terms. Let $\bar{a}/\bar{x}$ stand for

$$\begin{aligned} a_1/x_1,\ldots ,a_n/x_n \end{aligned}$$

Then

$$\begin{aligned} x_1:A_1,\ldots ,x_n:A_n\vdash B:\mathbf {set}\end{aligned}$$

means that

$$\begin{aligned} B[\bar{a}/\bar{x}]:\mathbf {set}\end{aligned}$$

whenever $\bar{a}$ is an environment for $x_1:A_1,\ldots , x_n:A_n$, and that

$$\begin{aligned} B[\bar{a}/\bar{x}]=B[\bar{a}'/\bar{x}]:\mathbf {set}\end{aligned}$$

whenever $\bar{a}$ and $\bar{a}'$ are equal environments for $x_1:A_1,\ldots , x_n:A_n.$

Note that a $\mathbf {set}$$A_k$ occurring within a context $x_1:A_1,\ldots ,x_{n}:A_{n}$ may be a family of $\mathbf {set}$s over $A_1,\ldots ,A_{k-1}$.

From these explanations the rules of substitution and assumption may be justified. By rules of substitution we mean the rules

and their generalizations to hypothetical judgements with longer contexts. The rule of assumption is

Thus, the assumption that x is an element of a $\mathbf {set}$A is treated as a tautological hypothetical judgement. We are allowed to make the assumption $x:A\vdash x:A$ only if we have established $A:\mathbf {set}$. If higher types are present, one can also make assumptions of the form $A:\mathbf {set}$.

3 The Justification of Elimination Rules

3.1 General Remarks

Introduction-, equality-, and secondary elimination rules are, as noted, definitional, or meaning-giving, in nature. Doubts about their correctness can therefore only concern their felicity as meaning-giving rules. In particular, doubts concerning an introduction rule can only concern its felicity in determining what are the canonical elements of a purported $\mathbf {set}$A. Martin-Löf (1982, p. 166) notes that

there are certain limits to what verbal explanations can do when it comes to justifying axioms and rules of inference. In the end, everybody must understand for himself.

It may, for instance, not be obvious how one could bring about an understanding of the rules of $\text{N}$-introduction in someone who insists that he fails to grasp by their means what is a canonical element of $\text{N}$. By contrast, it is possible to argue that certain purported introduction rules fail to be meaning-giving. Suppose we postulate a formation rule,

and provide the following introduction rule.⁶

Here x.a indicates that x has become bound in a. Thus $\text{L}$ is a variable-binding operation. This introduction rule fails to be meaning-giving because the postulated canonical $\mathbf {set}$$\Lambda (A)$ occurs negatively in its premiss.⁷ According to the explanation of the forms of hypothetical judgement, the premiss $x:\Lambda (A)\vdash a:A$ means that

$$\begin{aligned} a[b/x]:A \,\, \mathrm{whenever} \,\, b:\Lambda (A) \end{aligned}$$

Hence, in order to understand this premiss I must know what is an arbitrary element of $\Lambda (A)$. But in order to know what is an arbitrary element of $\Lambda (A)$, I must know what is a canonical element of $\Lambda (A)$, and this I do not know before having grasped the $\Lambda$-introduction rule. Understanding the premiss of this rule thus presupposes knowledge that the rule is meant to provide. The rule therefore fails to specify what is a canonical element of $\Lambda (A)$, that is, it fails to be meaning-giving.

Formation- and primary elimination rules are not meaning-giving, but postulational. They must therefore be justified in the manner in which rules of inference in general are to be justified: the conclusion of the rule must be made evident on the assumption that we know the premisses.

It has been stipulated that a $\mathbf {set}$A is canonical if and only if $A:\mathbf {set}$ is the conclusion of an application of a primary formation rule and that A and B are equal canonical $\mathbf {set}$s if and only if $A=B:\mathbf {set}$ is the conclusion of an application of a secondary formation rule. To have the right to postulate that A is a canonical $\mathbf {set}$ I must specify what the canonical elements of A are and what equal canonical elements of A are. In most cases, this specification is given directly through the associated introduction rules. Assuming that the introduction rules for A are felicitous as meaning-giving rules, they therefore directly justify the formation rule whose conclusion is $A:\mathbf {set}$. To have the right to postulate that A and B are equal canonical $\mathbf {set}$s I must make it evident that any canonical element of A is a canonical element of B, and vice versa, and that equal canonical elements of A are equal canonical elements of B, and vice versa. This justification rests on the specification of what a canonical element is, and what equal canonical elements are, of A and B, together with the explanation of the forms of judgement $A=B:\mathbf {set}$ and $a=b:A$.

The rules of the system are applicable under assumptions. For instance, from the assumption $x:\text{N}\vdash x:\text{N}$, I can apply $\text{N}$-introduction to infer $x:\text{N}\vdash \text{s}(x):\text{N}$. The notion of canonicity may be extended to such cases. Thus, $\text{s}(x)$ may be regarded a canonical element of $\text{N}$ in the context $x:\text{N}$.⁸ Likewise, the application of a formation rule in a context $\Gamma$ may be regarded as yielding a canonical $\mathbf {set}$ in $\Gamma$.

Consider a primary elimination rule whose major premiss has the form a : A and whose conclusion has the form b : B. To justify the rule we must make the conclusion b : B evident on the assumption that we know the premisses of the rule. We distinguish the cases where the major premiss, a : A, is categorical and where it is hypothetical. If the major premiss is categorical, then—as we shall see in detail below—we can use the equality rule associated with A to argue that b evaluates to a canonical element of C, where C is the canonical $\mathbf {set}$ to which B evaluates.

Assume next that the major premiss is a hypothetical judgement

$$\begin{aligned} x_1:A_1,\ldots , x_n:A_n\vdash a :A \end{aligned}$$

The conclusion then has the form

$$\begin{aligned} x_1:A_1,\ldots , x_n:A_n, \Gamma \vdash b:B \end{aligned}$$

where $\Gamma$ is a, possibly empty, context stemming from the minor premiss(es). To make this conclusion evident it must be argued that for any environment $\bar{a}$ for $x_1:A_1,\ldots , x_n:A_n,$ we have

$$\begin{aligned} \Gamma [\bar{a}/\bar{x}]\vdash b[\bar{a}/\bar{x}]: B[\bar{a}/\bar{x}] \end{aligned}$$

and that for any equal environments $\bar{a}$ and $\bar{a}'$ we have

$$\begin{aligned} \Gamma [\bar{a}/\bar{x}]\vdash b[\bar{a}/\bar{x}]=b[\bar{a}'/\bar{x}]: B[\bar{a}/\bar{x}] \end{aligned}$$

But, for any such environment $\bar{a}$, the major premiss becomes the categorical judgement $a[\bar{a}/\bar{x}]:A[\bar{a}/\bar{x}]$, and the justification for this case has already been given.

The second part will be seen to follow from the secondary elimination rule.

3.2 Illustration: $\wedge$-elimination

We postulate the following rules of $\wedge$-formation.

To justify this postulation we must, firstly, specify what the canonical elements of $A\wedge B$ are and what equal canonical elements of $A\wedge B$ are. Secondly, we must argue, on the assumption that $A=A':\mathbf {prop}$ and $B=B':\mathbf {prop}$, that any canonical element of $A\wedge B$ is a canonical element of $A'\wedge B',$ and vice versa; and that equal canonical elements of $A\wedge B$ are equal canonical elements of $A'\wedge B'$, and vice versa.

What the canonical elements, and what equal canonical elements, of $A\wedge B$ are is specified by the rules of $\wedge$-introduction.

Thus $\langle a,b\rangle$ is a canonical element of $A\wedge B$ provided a : A and b : B; and $\langle a,b\rangle$ and $\langle a',b'\rangle$ are equal canonical elements of $A\wedge B$ provided $a=a':A$ and $b=b':B$. This justifies the primary formation rule.

Towards justifying the secondary formation rule, assume the premisses $A=A':\mathbf {prop}$ and $B=B':\mathbf {prop}$. Any canonical element of $A\wedge B$ has the form $\langle a,b\rangle$ with a : A and b : B. Then $a:A'$ and $b:B'$ by the premisses; therefore $\langle a,b\rangle :A'\wedge B'$ by the primary $\wedge$-introduction rule. Any equal canonical elements of $A\wedge B$ have the form $\langle a,b\rangle$ and $\langle a',b'\rangle$, with $a=a':A$ and $b=b':B.$ Then $a=a':A'$ and $b=b':B'$ by the premisses; therefore $\langle a,b\rangle =\langle a',b'\rangle :A'\wedge B'$ by the secondary $\wedge$-introduction rule.

We postulate the following rules of $\wedge$-elimination.

The secondary rules, on the second line here, are definitional; but the primary rules require justification. Namely, it must be made evident, on the assumption that we know the premiss $c:A\wedge B$, that $\text{l}(c)$ and $\text{r}(c)$ evaluate to canonical form. The most important ingredient of this justification is provided by the $\wedge$-equality rules, which tell us how to evaluate $\text{l}(\langle a,b\rangle )$ and $\text{r}(\langle a,b\rangle )$.

We may now justify primary $\wedge$-elimination as follows. We first assume that the premiss $c:A\wedge B$ holds categorically, hence that c is a closed term. By this premiss, c evaluates to some $\langle a,b\rangle :A\wedge B$, where a : A and b : B. Hence we get an equality $c=\langle a,b\rangle :A\wedge B$. By the secondary $\wedge$-elimination rules and $\wedge$-equality we thence get $\text{l}(c)=\text{l}(\langle a,b\rangle )=a:A$ and $\text{r}(c)=\text{r}(\langle a,b\rangle )=b:B$. Let D be the canonical $\mathbf {set}$ to which A evaluates and let E be the canonical $\mathbf {set}$ to which B evaluates. Since a : A, a evaluates to a canonical element d of D; since $\text{l}(c)=a:A$, $\text{l}(c)$ evaluates to a canonical element $d'$, equal to d, of D. Likewise, since b : B, b evaluates to a canonical element e of E; since $\text{r}(c)=b:B$, $\mathrm{r}(c)$ evaluates to a canonical element $e'$, equal to e, of E.

When the premiss is hypothetical, the first $\wedge$-elimination rule has the form

To make the conclusion of this rule evident we must, firstly, argue that for any environment $\bar{a}$ for $x_1:A_1,\ldots ,x_n:A_n$,

$$\begin{aligned} \text{l}(c[\bar{a}/\bar{x}]): A[\bar{a}/\bar{x}] \end{aligned}$$

Here $c[\bar{a}/\bar{x}]$ is a closed term, so the justification just given shows that $\text{l}(c[\bar{a}/\bar{x}])$ evaluates to canonical form. Secondly, we must argue that for any equal environments $\bar{a}$ and $\bar{a}'$,

$$\begin{aligned} \text{l}(c[\bar{a}/\bar{x}])=\text{l}(c[\bar{a}'/\bar{x}]): A[\bar{a}/\bar{x}] \end{aligned}$$

But for any such equal environments the premiss $x_1:A_1,\ldots ,x_n:A_n\vdash c:A\wedge B$ yields

$$\begin{aligned} c[\bar{a}/\bar{x}]=c[\bar{a}'/\bar{x}]:(A\wedge B)[\bar{a}/\bar{x}] \end{aligned}$$

The secondary $\wedge$-elimination rule for l therefore yields the required equality.

4 The Justification of $\text{Id}$-elimination

The elimination rules for a $\mathbf {set}$A give us means to define functions from A into a $\mathbf {set}$ or a family of $\mathbf {set}$s. They do not give us means to define functions from A into $\mathbf {set}$ itself; that is, they do not give us means to define families of $\mathbf {set}$s, or propositional functions, over A. Thus, although we may define addition by means of $\text{N}$-elimination, we cannot thus define the relation $\le$ on $\text{N}$. To provide for the possibility of defining $\mathbf {set}$-valued functions over a $\mathbf {set}$ we postulate a formation rule whose premisses include judgements of the form a : A. More specifically, we postulate the following rules of $\text{Id}$-formation.

Provided we have justified the first of these rules, viz. the primary $\text{Id}$-formation rule, then whenever $A:\mathbf {set}$, we may form a binary propositional function over A,

$$\begin{aligned} x:A, y:A\vdash \text{Id}(A,x,y):\mathbf {prop}\end{aligned}$$

From this, further relations may be defined by means of the same or other operators available in the language.

Since the relation of identity—unlike, say, the relation of less than—is defined over any individual domain, and since $\text{Id}(A,a,b)$ is to be defined whenever $A:\mathbf {set}$, a : A, and b : A, we intend $\text{Id}(A,a,b)$ to be a proposition to the effect that a and b are identical. Martin-Löf (1971), in a paper concerned with natural deduction, and not type theory, provides a general scheme for natural deduction introduction- and elimination rules, as well as reduction procedures, for inductively defined predicates. As examples of such predicates captured by this scheme of rules Martin-Löf gives the 0-ary predicate of absurdity, the unary predicate of being a natural number, and the binary relation of identity. Identity, which Martin-Löf designates by E, is the predicate that has the introduction rule

$$\begin{aligned} (E\text{-intro})\qquad \qquad \qquad \quad \quad \quad Exx \end{aligned}$$

with no premisses and where x is a variable. Martin-Löf’s scheme determines that E should have the following elimination rule.

Here C is any formula of the language, and C[z, z] is the result of substituting the variable z for, say, x and y in C. The terms t and u may be any terms of the language. The rule can be read as saying that whenever C is a reflexive relation, and Etu holds, then C[t, u] holds as well; thus, E is the least reflexive relation. The reduction rule for E becomes

Here $\mathcal {D}[t]$ is the result of substituting t for z everywhere in $\mathcal {D}$, where variables in t may have to be renamed to avoid unintended binding.

The introduction-, elimination-, and equality rules for $\text{Id}$ follow the pattern of the corresponding rules for E. The rules of $\text{Id}$-introduction are as follows.

Thus, provided a : A, we stipulate that $\text{refl}(A,a)$ is a proof of $\text{Id}(A,a,a)$.

We cannot use these introduction rules directly in specifying what a canonical element of $\text{Id}(A,a,b)$ is and what equal canonical elements of $\text{Id}(A,a,b)$ are. We cannot do so, since the $\mathscr {C}$ of the conclusion of the introduction rules has the form $\text{Id}(A,a,a)$ and not the form $\text{Id}(A,a,b)$. If $a=b:A$, then the judgements $\text{refl}(A,a):\text{Id}(A,a,b)$ and $\text{refl}(A,b):\text{Id}(A,a,b)$ follow from $\text{Id}$-introduction and the rules of substitution. But since evaluation in type theory operates from without, we cannot expect that the evaluation of an arbitrary $p:\text{Id}(A,a,b)$ yields either $\text{refl}(A,a)$ or $\text{refl}(A,b)$. We stipulate that

a canonical element of $\text{Id}(A,a,b)$ is any $\text{refl}(A',a')$ such that

$$\begin{aligned} \begin{array}{l} A'=A:\mathbf {set}\\ a'=a:A \\ a'=b:A \end{array} \end{aligned}$$

This stipulation makes sense, since $A'=A:\mathbf {set}$, $a':A'$ and a, b : A entail that $a',a,b$ are all elements of A. The stipulation, moreover, agrees with the primary $\text{Id}$-introduction rule in the sense that it deems $\text{refl}(A,a)$ to be a canonical element of $\text{Id}(A,a,a)$.

We stipulate that

$\text{refl}(A',a')$ and $\text{refl}(A'', a'')$ are equal canonical elements of $\text{Id}(A,a,b)$ provided

$$\begin{aligned}\begin{array}{l} A=A'=A'':\mathbf {set}\\ a=a'=a'':A \\ b=a'=a'':A \end{array} \end{aligned}$$

This stipulation agrees with the secondary $\text{Id}$-introduction rule in the sense that it deems $\text{refl}(A,a)$ and $\text{refl}(A',a')$ to be equal canonical elements of $\text{Id}(A,a,a)$ provided $A=A':\mathbf {set}$ and $a=a':A$. By means of these two stipulations the primary $\text{Id}$-formation rule has been justified.

Towards justifying the secondary $\text{Id}$-formation rule, assume the premisses $A=A':\mathbf {set}$, $a=a':A$ and $b=b':A$. Assume that $\text{refl}(A'',a'')$ is a canonical element of $\text{Id}(A,a,b).$ Then $A''=A:\mathbf {set}$, $a''=a:A$, and $a''=b:A$, whence by the premisses, $A''=A':\mathbf {set}$, $a''=a':A$, and $a''=b'$, so $\text{refl}(A'',a'')$ is also a canonical element of $\text{Id}(A',a',b').$ Assume next that $\text{refl}(A'',a'')$ and $\text{refl}(A''',a''')$ are equal canonical elements of $\text{Id}(A,a,b)$. Then $A=A''=A''':\mathbf {set},$$a=a''=a''':A$ and $b=a''=a''':A$, whence by the premisses, $A'=A''=A''':\mathbf {set}$, $a'=a''=a''':A$ and $b'=a''=a''':A$, so $\text{refl}(A'',a'')$ and $\text{refl}(A''',a''')$ are also equal canonical elements of $\text{Id}(A',a',b')$.

A direct adaptation of the above natural deduction E-elimination rule to the syntax of type theory with $\text{Id}$ instead of E yields the following rule.

The premisses presuppose $A:\mathbf {set}$, a : A, b : A, and $x:A, y:A\vdash C:\mathbf {prop}$. From now on we shall use the simplified substitution notation exemplified by C[a, b] in place of C[a/x, b/y]. The minor premiss, $z:A\vdash c:C[z,z]$, says that c[a] is a proof of C[a, a] whenever a : A. The conclusion says that $\text{J}^*(p,z.c)$ is a proof of C[a, b]. The notation z.c indicates that z has become bound in c. The reduction rule for E yields the following equality rule.

Thus the proof of C[a, a] got by applying $\text{Id}$-elimination* to $\text{refl}(A,a)$ and c such that $z:A\vdash c:C$ is stipulated to be the same proof as c[a].

In the language of type theory elimination rules may, however, be generalized by allowing the $\mathbf {prop}$C appearing in the conclusion of such a rule to depend on the $\mathbf {prop}$A of its major premiss. In particular, we may let the C occurring in the conclusion of $\text{Id}$-elimination be a ternary propositional function.

$$\begin{aligned} x:A, y:A, w:\text{Id}(A,x,y)\vdash C:\mathbf {prop}\end{aligned}$$

The resulting rules are as follows.

If $x:A,y:A\vdash C:\mathbf {set}$, then also $x:A, y:A, p:\text{Id}(A,x,y)\vdash C:\mathbf {set}$, by weakening, hence $\text{Id}$-elimination is indeed a generalization of $\text{Id}$-elimination*. In many applications of $\text{Id}$-elimination the third argument in C is not needed, but it may be needed if one wishes to prove things about elements of $\text{Id}$-$\mathbf {set}$s.

The secondary $\text{Id}$-elimination rule is definitional, but the primary rule requires justification. Namely, assuming that we know the premisses of the rule, it must be made evident that $\text{J}(p,z.c)$ evaluates to a canonical element of C[a, b, p]. An important ingredient of this justification is provided by the $\text{Id}$-equality rule, which tells us how to evaluate $\text{J}(\text{refl}(A,a),z.c)$.

 We may now justify $\text{Id}$-elimination. Assume that we know its premisses, viz. $p:\text{Id}(A,a,b)$ and $z:A\vdash c:C[z,z,\text{refl}(A,z)].$ Let us first assume that the premiss $p:\text{Id}(A,a,b)$ holds categorically, in particular that p is a closed term. Then p evaluates to a canonical element of $\text{Id}(A,a,b)$, that is, p evaluates to some $\text{refl}(A',a')$, where $A'=A:\mathbf {set}$, $a'=a:A$, and $a'=b:A.$ Therefore $p=\text{refl}(A',a'):\text{Id}(A,a,b)$. Furthermore, from the equalities holding for $A'$ and $a'$ we may infer

$$\begin{aligned} \begin{array}{c} A=A=A':\mathbf {set}\\ a=a=a':A \\ b=a=a':A \end{array} \end{aligned}$$

showing that $\text{refl}(A',a')$ and $\text{refl}(A,a)$ are equal canonical elements of $\text{Id}(A,a,b)$. Thus

$$\begin{aligned} p=\text{refl}(A',a')=\text{refl}(A,a):\text{Id}(A,a,b) \end{aligned}$$

Secondary $\text{Id}$-elimination and $\text{Id}$-equality then yields

$$\begin{aligned} \text{J}(p,z.c)=\text{J}(\text{refl}(A',a'), z.c)=\text{J}(\text{refl}(A,a),z.c)=c[a]:C[a,a,\text{refl}(A,a)] \end{aligned}$$

Note that in order to apply $\text{Id}$-equality here, the first argument of $\text{refl}$ must be A, since the minor premiss we have assumed is $z:A\vdash c:C[z,z,\text{refl}(A,z)]$ and not $z:A'\vdash c:C[z,z,\text{refl}(A',z)]$.

Let D be the canonical $\mathbf {set}$ to which $C[a,a,\text{refl}(A,a)]$ evaluates. By the equalities already established, and the rules of substitution, we have

$$\begin{aligned} C[a,a,\text{refl}(A,a)]=C[a,b,p]:\mathbf {set}\end{aligned}$$

Whence, C[a, b, p] evaluates to some canonical $\mathbf {set}$$D'$ equal to D. By the premiss $z:A\vdash c:C[z,z,\text{refl}(A,z)]$ we know that c[a] evaluates to a canonical element e of D. From $\text{J}(p,z.c)=c[a]:C[a,a,\text{refl}(A,a)]$, we may infer that $\text{J}(p,z.d)$ evaluates to some canonical element $e'$, equal to e, in D. Since $D=D':\mathbf {set}$, $e'$ is also a canonical element of $D'$. This justifies $\text{J}(p,z.c):C[a,b,p]$.

It should be clear that this justification remains valid if we assume that C has more than three arguments, that is, if we assume

$$\begin{aligned} x:A, y: A, p:\text{Id}(A,x,y),\Gamma \vdash C:\mathbf {set}\end{aligned}$$

The additional context $\Gamma$ may be carried along without causing any additional complications.

Assume next that the major premiss of $\text{Id}$-elimination is hypothetical.

$$\begin{aligned} x_1:A_1,\ldots ,x_n:A_n\vdash p:\text{Id}(A,a,b) \end{aligned}$$

Then we must also assume

$$\begin{aligned} \begin{array}{l} x_1:A_1,\ldots ,x_n:A_n\vdash A:\mathbf {set}\\ x_1:A_1,\ldots ,x_n:A_n\vdash a:A\\ x_1:A_1,\ldots ,x_n:A_n\vdash b:A \end{array} \end{aligned}$$

The minor premiss then becomes

$$\begin{aligned} x_1:A_1,\ldots ,x_n:A_n, z:A\vdash c:C[z,z,\text{refl}(z)] \end{aligned}$$

where

$$\begin{aligned} x_1:A_1,\ldots ,x_n:A_n, x:A, y:A, w:\text{Id}(A,x,y)\vdash C:\mathbf {set}\end{aligned}$$

For any environment $\bar{a}$ for $x_1:A_1,\ldots ,x_n:A_n$, we have

$$\begin{aligned} \begin{array}{rcl} \text{J}(p,z.c)[\bar{a}/\bar{x}]&{}\equiv &{}\text{J}(p[\bar{a}/\bar{x}], z.c[\bar{a}/\bar{x}])\\ C[a,b,p][\bar{a}/\bar{x}]&{}\equiv &{}C[\bar{a}/\bar{x}][a[\bar{a}/\bar{x}], b[\bar{a}/\bar{x}], p[\bar{a}/\bar{x}]] \\ \text{Id}(A,a,b)[\bar{a}/\bar{x}]&{}\equiv &{}\text{Id}(A[\bar{a}/\bar{x}], a[\bar{a}/\bar{x}], b[\bar{a}/\bar{x}]) \end{array} \end{aligned}$$

where $\equiv$ stands for syntactic identity.

It must be argued, firstly, that for any such environment $\bar{a}$,

$$\begin{aligned} \text{J}(p,z.c)[\bar{a}/\bar{x}]: C[a,b,p][\bar{a}/\bar{x}] \end{aligned}$$

But the major premiss is then the categorical judgement

$$\begin{aligned} p[\bar{a}/\bar{x}]:\text{Id}(A[\bar{a}/\bar{x}], a[\bar{a}/\bar{x}], b[\bar{a}/\bar{x}]), \end{aligned}$$

and the justification in this case has already been given.

Secondly, it must be argued that for any equal environments $\bar{a}$ and $\bar{a}'$, we have

$$\begin{aligned} \text{J}(p,z.c)[\bar{a}/\bar{x}]=\text{J}(p, c.d)[\bar{a}'/\bar{x}] : C[a,b,p][\bar{a}/\bar{x}] \end{aligned}$$

For any such environments the major premiss yields

$$\begin{aligned} p[\bar{a}/\bar{x}]=p[\bar{a}'/\bar{x}]:\text{Id}(A,a,b)[\bar{a}/\bar{x}] \end{aligned}$$

The minor premiss yields

$$\begin{aligned} z:A[\bar{a}/\bar{x}]\vdash c[\bar{a}/\bar{x}]=c[\bar{a}'/\bar{x}]:C[z,z,\text{refl}(A, z)][\bar{a}/\bar{x}] \end{aligned}$$

The secondary $\text{Id}$-elimination rule therefore yields the required equality.

It should be clear this justification remains valid if we assume that C has more than $n+3$ arguments, that is, if we assume

$$\begin{aligned} x_1:A_1,\ldots ,x_n:A_n, x:A, y:A, w:\text{Id}(A,x,y), \Gamma \vdash C:\mathbf {set}\end{aligned}$$

 The main aim of this paper has now been reached. The two next sections may be regarded as appendices. They presuppose a bit more familiarity with type theory than what has been presupposed in the foregoing.

5 Remarks on the Univalence Axiom

Homotopy type theory adds to Martin-Löf’s type theory the so-called univalence axiom as well as so-called higher inductive types. A thorough discussion of these additions, and of how they may be justified, lies outside the compass of this paper; but a few remarks on how the univalence axiom fares with respect to the standard interpretation of type theory presented above may not be out of place.

It seems that it will be difficult, if not impossible, to justify the univalence axiom on the grounds of this interpretation. There are at least two problems.

The univalence axiom is the postulation, for any $A,B:\mathbf {set},$ of a judgement

$$\begin{aligned} \text{ua}(A,B) : \text{Univ}(A,B) \end{aligned}$$

where $\text{Univ}(A,B)$ is a certain $\mathbf {set}$ whose definition is not important for current purposes. Since $\text{Univ}(A,B):\mathbf {set},$ it evaluates to some canonical $C:\mathbf {set}$. The judgement $\text{ua}(A,B) : \text{Univ}(A,B)$ is therefore justified according to the standard interpretation if it can be made evident that $\text{ua}(A,B)$ evaluates to a canonical element of C. A first problem for the univalence axiom from the point of view of the standard interpretation is then that the postulation is made without directions as to how $\text{ua}(A,B)$ is to be evaluated to such a canonical element. In particular, the postulation is not accompanied by anything like equality rules or informal descriptions of the evaluation. Hence we have not been given the information needed to see that the postulation is justified according to the standard interpretation. This is in effect a problem that attends all outright postulations in type theory, for instance also that of the law of the excluded middle in the form

Without directions as to how $\text{lem}(A)$ is to be evaluated to a canonical element of $A\vee \lnot A$ this postulation remains unjustified on the standard interpretation.

The second problem is more specific to the univalence axiom. A judgement of the form $p:\text{Id}(A,a,b)$ means, according to our explanations above, that p evaluates to some $\text{refl}(A',a')$ where $A'=A:\mathbf {set}$, $a'=a:A$, and $a'=b:A$. It follows, however, from the univalence axiom that for some $A:\mathbf {set}$ and a, b : A there is a $p:\text{Id}(A,a,b)$ that cannot be taken to evaluate to such a canonical element. Let us consider one example.

Let $\mathbf {2}$ be the $\mathbf {set}$ of booleans, whose canonical elements are $\mathsf {t}$ and $\mathsf {f}$. A universe $\mathcal {U}$ is, intuitively, a $\mathbf {set}$ whose elements are themselves $\mathbf {set}$s, so that we may for instance have $\mathbf {2}:\mathcal {U}.$ A canonical element of $\mathcal {U}$ is a canonical $\mathbf {set}$. With one universe present one can form the proposition

$$\begin{aligned} \text{Id}(\mathcal {U}, \mathbf {2}, \mathbf {2}) \end{aligned}$$

that is, a proposition to the effect that $\mathbf {2}$ is identical to $\mathbf {2}$. Let us make the definition

$$\begin{aligned} \mathbf {I}_\mathbf {2}=\text{Id}(\mathcal {U}, \mathbf {2}, \mathbf {2}):\mathbf {prop}\end{aligned}$$

According to our explanations, a canonical element of this $\mathbf {set}$ is any $\text{refl}(\mathcal {A}, B)$ such that

$$\begin{aligned} \begin{array}{l} \mathcal {A}=\mathcal {U}:\mathbf {set}\\ B=\mathbf {2}:\mathcal {U}\end{array} \end{aligned}$$

From the univalence axiom and certain basic facts concerning $\mathbf {2}$ it follows that there is a function

$$\begin{aligned} F:\mathbf {2}\rightarrow \mathbf {I}_\mathbf {2}\end{aligned}$$

that is injective and surjective in a suitable sense. We write $\text{ap}(F,a)$ for the application of F to the argument a. For $A:\mathbf {set}$ we introduce a new form of judgement, $A\,\,\text{true}$, governed by the rule

The injectivity of F is the following property: for any $x, y:\mathbf {2},$ if

$$\begin{aligned} \text{Id}(\mathbf {I}_\mathbf {2}, \text{ap}(F,x), \text{ap}(F, y))\,\,\text{true}\end{aligned}$$

then

$$\begin{aligned} \text{Id}(\mathbf {2}, x, y)\,\,\text{true}\end{aligned}$$

The surjectivity of F is the following property: for any $p:\mathbf {I}_\mathbf {2}$ there is $x:\mathbf {2}$ such that

$$\begin{aligned} \text{Id}(\mathbf {I}_\mathbf {2}, \text{ap}(F,x),p)\,\,\text{true}\end{aligned}$$

Without loss of generality, we may assume that $\mathsf {t}:\mathbf {2}$ is such that

$$\begin{aligned} \text{Id}(\mathbf {I}_\mathbf {2}, \text{ap}(F,\mathsf {t}), \text{refl}(\mathcal {U}, \mathbf {2}))\,\,\text{true}\end{aligned}$$

Then $\text{ap}(F,\mathsf {f}):\mathbf {I}_\mathbf {2}$ cannot be evaluated to canonical form. For, if it did, we should have

$$\begin{aligned} \text{ap}(F,\mathsf {f})=\text{refl}(\mathcal {U}, \mathbf {2}):\mathbf {I}_\mathbf {2}\end{aligned}$$

and therefore also

$$\begin{aligned} \text{Id}(\mathbf {I}_\mathbf {2}, \text{ap}(F,\mathsf {t}), \text{ap}(F, \mathsf {f}))\,\,\text{true}\end{aligned}$$

The injectivity of F would then allow us to infer

$$\begin{aligned} \text{Id}(\mathbf {2}, \mathsf {t}, \mathsf {f})\,\,\text{true}\end{aligned}$$

but it is a theorem of type theory with one universe that

$$\begin{aligned} \lnot \text{Id}(\mathbf {2}, \mathsf {t}, \mathsf {f})\,\,\text{true}\end{aligned}$$

 Thus, not only is it not clear how to justify the univalence axiom on the grounds of the standard interpretation—the univalence axiom appears to be in direct conflict with this interpretation. Precisely how one should think of homotopy type theory as a foundation for mathematics, be it classical or constructive, is thus not straightforward. The standard interpretation provides Martin-Löf type theory, and therefore also the mathematics based on it, with solid foundations; but it seems that those foundations are not strong enough to carry the extension of that theory that is homotopy type theory.

6 Other Suggested Justifications

Assume that $\Pi$ and $\Sigma$ have been introduced into type theory in the usual way and that moreover $\text{Id}$-formation and $\text{Id}$-introduction have been laid down. Then, for any $A:\mathbf {set}$ and C such that $z:A\vdash C:\mathbf {prop}$, we may define

$$\begin{aligned} \text{Ind}(A,C)=(\Pi x,y:A)(\text{Id}(A,x,y)\supset (C[x]\supset C[y])):\mathbf {prop}\end{aligned}$$

The proposition $\text{Ind}(A,C)$ says that if $\text{Id}(A,x,y)$ and C[x] are true, then so is C[y]; in other words, that C does not discern elements of A that stand in the $\text{Id}(A)$-relation. For any $A:\mathbf {set}$ and a : A we may also define

$$\begin{aligned} E(A,a)=(\Sigma x:A)\text{Id}(A,a,x):\mathbf {prop}\end{aligned}$$

and

$$\begin{aligned} G(A,a)=(\Pi z : E(A,a))\,\text{Id}(E(A,a),\langle a,\text{refl}(A,a)\rangle ,z):\mathbf {prop}\end{aligned}$$

A canonical element of E(A, a) is a pair $\langle b,p\rangle$ where b : A and $p:\text{Id}(A,a,b)$. An element of G(A, a) is a function f such that for any b : A and $p:\text{Id}(A,a,b)$,

$$\begin{aligned} \text{ap}(f,\langle b,p\rangle ):\text{Id}(E(A,a),\langle a,\text{refl}(A,a)\rangle ,\langle b,p\rangle ) \end{aligned}$$

It is known that if we postulate

$$\begin{aligned} \text{(Ind)} \qquad \quad \quad \quad \text{subst}(A,C):\text{Ind}(A,C) \end{aligned}$$

and

$$\begin{aligned} \text{(Uniq)}\quad \quad \quad \quad \text{uniq}(A,a):G(A,a) \end{aligned}$$

then the rule of $\text{Id}$-elimination may be derived.

The justification of $\text{Id}$-elimination suggested by Ladyman and Presnell (2015, p.401ff.) consists in treating (Ind) and (Uniq) as primitive principles of type theory and showing how $\text{Id}$-elimination may be derived on that basis.

It is not clear to me what is gained by this approach. Although the postulation of (Ind) and (Uniq) allows one to derive $\text{Id}$-elimination, these postulations themselves of course have to be justified. According to the standard interpretation it must thus be made evident that $\text{subst}(A,C)$ and $\text{uniq}(A,a)$ evaluate to elements of canonical form. Ladyman and Presnell, however, provide no indication—in the form of equality rules or informal description, say—of how such an evaluation should proceed. Instead they provide only certain heuristic considerations. Thus, they say of (Ind) that it expresses ‘a fundamental part of our pre-mathematical understanding of identity’ that ‘any formalisation of identity must respect’ (p. 404). One can agree with this without regarding it as a justification of (Ind). That a proposition ought to be true is no justification that it is true.

The heuristic considerations offered in support of (Uniq) seems to be that some propositional uniqueness principle ought to hold for $\text{Id}$-$\mathbf {set}$s, since such principles hold for the other $\mathbf {set}$-forming operators of Martin-Löf type theory.⁹ It can, for instance, be shown that for every element z of $A\wedge B$ there are a : A and b : B such that $\text{Id}(A\wedge B, z, \langle a,b\rangle )$ is true; in other words, that every element of $A\wedge B$ stands in the $\text{Id}(A\wedge B)$-relation to a canonical element. It is, however, difficult to see why this heuristic in the case of $\text{Id}$ should lead to the postulation of (Uniq) rather than to the postulation of

$$\begin{aligned} \text{uip}(A,a): (\forall p : \text{Id}(A,a,a))\,\text{Id}(\text{Id}(A,a,a), p , \text{refl}(A,a)) \end{aligned}$$

where $A:\mathbf {set}$ and a : A. Let us call the displayed judgement (UIP). Canonical elements of $\text{Id}$-$\mathbf {set}$s have the form $\text{refl}(A,a),$ and, in particular, when a : A, then $\text{refl}(A,a)$ is a canonical element of $\text{Id}(A,a,a)$. According to (UIP), every element of $\text{Id}(A,a,a)$ stands in the $\text{Id}(\text{Id}(A,a,a))$-relation to $\text{refl}(A,a).$ This judgement therefore expresses a uniqueness principle. The postulation of (UIP) is, however, inconsistent with the univalence axiom, as the example of $\text{Id}(\mathcal {U},\mathbf {2}, \mathbf {2})$ above shows.¹⁰

In another paper, Ladyman and Presnell (2016) present what they call a semantics for type theory (§§ 5.2, 7.2). They take type theory furnished with this semantics to be a theory that may provide what they call an autonomous foundation for mathematics (§§ 2.2, 9). The so-called semantics amounts, however, to saying that a judgement of the form a : A means that a is a specific concept that falls under the general concept A. In addition, some very general remarks on concepts are made, such as: the existence of a concept is independent of whether anything real falls under it; concepts ‘may or may not depend for their existence on mental activity’ (§ 5.2 point (3)); concepts are intensional in nature; and they have structure and may be composed from other concepts. All of this might be reasonable, but does not suffice as a semantics in any serious sense. It is, for instance, quite impossible to use this semantics to determine whether the various postulations considered above are justified or not. Being told merely that $\text{uniq}(A,a):G(A,a)$ means that the concept $\text{uniq}(A,a)$ falls under the concept G(A, a), I am not in a position to say whether this judgement is justified or not. In order to determine that I would at least need to know more precisely what is understood by specific and general concepts; by something’s falling under a concept; and which concepts $\text{uniq}(A,a)$ and G(A, a) are.

The approach suggested by Ladyman and Presnell moreover breaks the general pattern in type theory of furnishing $\mathbf {set}$-forming operators with introduction- and elimination rules, since the $\text{Id}$-elimination rule is now replaced by two postulates that cannot be regarded as elimination rules. It seems to me a great insight, first developed in Martin-Löf (1971), that propositional identity can be treated by means of such rules. As a constant of the language, the propositional identity symbol is thereby shown to admit of a treatment similar to that of the standard logical constants. Ladyman and Presnell have given no justification for why we should let go of this insight.

Walsh (2017), in a paper presented as a response to Ladyman and Presnell (2015), suggests a very different approach to the topic. He describes how the proof-theoretical notion of harmony can be characterized in category-theoretic terms and how various logical operators, including identity, is captured by this characterization. This is then meant to constitute a justification of the elimination rules of these operators. In Walsh’s own words, $\text{Id}$-elimination is in harmony with $\text{Id}$-introduction because ‘path induction [i.e. $\text{Id}$-elimination] is determined by the adjoint which defines identity’ (p. 319). This result will certainly be of interest to those fluent in the language of category theory, but the sense in which it could be taken to constitute a justification for $\text{Id}$-elimination is not that which has been assumed here. There, the justification proceeds by translation into another mathematical theory, viz., category theory. Here, we have provided informal yet precise explanations of the basic notions and of the forms of statement of type theory that do not rely on any other mathematical theory. The explanations have been rigorous enough both to render meaningful the question of whether a certain postulation is justified and to answer that question positively in the case of $\text{Id}$-elimination.