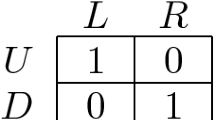Do Conventions Need to Be Common Knowledge?

Abstract

Do conventions need to be common knowledge in order to work? David Lewis builds this requirement into his definition of a convention. This paper explores the extent to which his approach finds support in the game theory literature. The knowledge formalism developed by Robert Aumann and others militates against Lewis’s approach, because it shows that it is almost impossible for something to become common knowledge in a large society. On the other hand, Ariel Rubinstein’s Email Game suggests that coordinated action is no less hard for rational players without a common knowledge requirement. But an unnecessary simplifying assumption in the Email Game turns out to be doing all the work, and the current paper concludes that common knowledge is better excluded from a definition of the conventions that we use to regulate our daily lives.

1 Conventions

Two men who pull the oars of a boat, do it by an agreement or convention, although they have never given promises to each other. Nor is the rule concerning the stability of possessions the less derived from human conventions, that it arises gradually, and acquires force by a slow progression, and by our repeated experience of the inconveniences of transgressing it. On the contrary, this experience assures us still more, that the sense of interest has become common to all our fellows, and gives us confidence of the future regularity of their conduct; and it is only on the expectation of this that our moderation and abstinence are founded. In like manner are languages gradually established by human conventions without any promise. In like manner do gold and silver become the common measures of exchange, and are esteemed sufficient payment for what is of a hundred times their value.

David Hume’s (1978) wisdom in this famous passage was not appreciated by his contemporaries. It was only with the advent of game theory some 200 years later that less able folk were provided with a crutch that allowed them to walk where he had run. Nowadays, we are able to follow Thomas Schelling (1960) in regarding a convention as a social device whose function is to coordinate our actions on one particular equilibrium when the game that life calls on us to play has multiple equilibria.

When two men row a boat, it isn’t in equilibrium for one man to row more strongly than the other, because the boat will then go round in a circle. If this happens, each man will prefer to change his rowing rhythm to match that of his partner. If they succeed in doing so, they will have reached an equilibrium. But the rowing game admits many possible equilibria. The equilibrium they actually adopt is a convention for their game. It may be unique to the minisociety consisting of just the two rowers, or it may be a convention shared by a whole community of rowers. Either way, it is a cultural artifact that might have been different without contravening any principle of individual rationality.

1.1 Metaphysics?

Most people have no difficulty in accepting the conventional nature of language or money, but draw the line when philosophers like Hume suggest that the same is true in more sensitive subjects like ethics or religion. In his Convention, David Lewis (1969) boldly extends the argument even to epistemology, essentially arguing that the boundaries of what we call conventional wisdom need to be set far wider than convention currently allows.

My own view is that caution is necessary when arguing that culture is free to make anything whatever into a convention. For example, Chomsky has shown that all human languages have a common deep structure which is presumably written into our genes. I argue elsewhere that the same may be true of human fairness norms (Binmore 2005). However, I am completely sold on the idea that conventions run much deeper than is generally accepted, and that we shall never understand how human societies work as long as we continue to confuse pieces of conventional wisdom that are products of our biological and cultural history with metaphysical principles carved into the fabric of the universe.

1.2 Evolutive and Eductive Game Theory

Game theory splits into two branches that reflect the same philosophical divide. I call the two branches evolutive and eductive game theory (Binmore 1987). The players in evolutive game theory need not be thinking creatures at all. In some of the more successful applications, they are fish or insects. Insofar as game theory is able to predict their behavior, it is because some process of trial-and-error adjustment kept moving the ecology of which they are a part until it settled down into an equilibrium of their underlying game of life. Similarly, we do not imagine that the men who row Hume’s boat will think at all deeply about how they should row. We take for granted that they will unconsciously adjust their rhythm until the boat is moving smoothly through the water in the direction they wish to go.

The tradition in game theory inherited from Von Neumann and Morgenstern (1944) that I call eductive could equally well be called rationalistic. Axioms are proposed that supposedly govern the behavior of ideally rational players. The behavior of different agents is linked by hypothesizing that they know relevant things about each other and the game they are playing. Their behavior in the game is then deduced from these assumptions.

The first jewel in the crown of eductive game theory was Von Neumann’s minimax theorem for two-person, zero-sum games, which says that it is optimal for both players to choose a strategy on the apparently paranoid assumption that their opponent will guess their choice and act to minimize their payoff. Many strategies commonly satisfy this requirement, but this is not a problem for Von Neumann, because it doesn’t matter how one solves the equilibrium selection problem for two-person, zero-sum games.¹ It is perhaps because there was no equilibrium selection problem in the original domain of game theory that it took a relative outsider like Schelling (1960) to make it clear that conventions are inescapable in the general case.

In this paper, I plan to argue—contra David Lewis (Lewis 1969)—that the study of conventions is more fruitfully pursued from the foundations on which evolutive game theory is based rather than the much more demanding foundations of eductive game theory. This is not to argue that eductive game theory may not also have a role to play. Indeed, Don Ross’s article in this volume explores some of the possibilities for an eductive theory of conventions. However, unless we are to regard Lewis as having invented a metaphysical notion of convention that doesn’t relate to the conventions of ordinary life that David Hume was talking about, then we must turn to evolutionary game theory if we want to understand how conventions are established and sustained.

It is true that David Hume tells us (immediately before the passage quoted at the head of this section) that a human convention should be understood as “a general sense of common interest” from which “a suitable resolution and behaviour’’ follows when “it is mutually expressed and is known to us both”. However, I shall argue that accepting Lewis’s attempt to formalize Hume’s remarks in terms of what should or should not be construed as common knowledge would make it almost impossible for new conventions to get established in a large society. Rather than invent a new term for the coordination devices that do succeed in colonizing a society, I therefore argue for a more relaxed attitude to what should count as a convention. In particular, I think we should recognize that Lewis led us down a blind alley when he insisted a convention cannot be operational unless it is common knowledge in the society in which it operates.

It follows that I think it unproductive to seek to separate the idea of a convention from Schelling’s (1960) notion of a focal point. Schelling gives examples of equilibria in coordination games that laboratory subjects mostly agree are focal or salient without the prior existence of any understanding to this effect. Some authors take this to imply that Schelling only intended that conventions which have to be formulated on the spot should be regarded as focal points. But Schelling was clearly writing on a much broader canvas, since he includes fairness as a focalizing consideration.

2 Game Theory

Figure 1 shows four payoff tables for some canonical toy games. I call the two players Alice and Bob. In each game, Alice has two strategies represented by the rows of the payoff table. Bob also has two strategies represented by its columns. The four cells of the payoff table correspond to the possible outcomes of the game. Each cell contains two numbers, one for Alice and one for Bob. The number in the southwest corner is Alice’s payoff for the corresponding outcome of the game. The number in the northeast corner is Bob’s payoff.

Fig. 1

Some toy games

In Matching Pennies, each player shows a coin. Alice wins if they differ, and Bob if they are both the same. The payoffs in each cell of Matching Pennies add up to zero. One can always fix things to make this true in such a game of pure conflict. For this reason, games of pure conflict are said to be zero sum.

We play the Driving Game every time we get in our cars to drive to work in the morning. The payoffs in each cell of the Driving Game are equal. One can always fix things to make this true in such a game of pure coordination.

The Prisoners’ Dilemma and the Stag Hunt Game lie between the two extremes of pure conflict and pure coordination, with the dove strategy representing cooperation and the hawk strategy representing defection. In spite of Brian Skyrms’ (2003) book, the Stag Hunt Game seems to be less widely known than the Prisoners’ Dilemma. Lewis (1969) derived it from a story of Jean-Jacques Rousseau (1913) in which Alice and Bob agree to cooperate in hunting a stag. When they separate to put their plan into action, each may be tempted to abandon the joint enterprise by the prospect of bagging a hare for themselves.

2.1 Nash Equilibrium

Each player is assumed to seek to maximize his or her expected payoff in a game. This would be easy if a player knew what strategy the other were going to choose. For example, if Alice knew that Bob were going to choose left in the Driving Game, she would maximize her payoff by choosing left as well. That is to say, left is Alice’s best reply to Bob’s choice of left, a fact indicated in Fig. 1 by circling Alice’s payoff in the cell that results if both players choose left.

A cell in which both payoffs are circled corresponds to a Nash equilibrium, because each player is then simultaneously making a best reply to the strategy choice of the other (Nash 1951). Sometimes players have more than one best reply, but if both players make best replies to each other that are strictly better than all their alternatives, a Nash equilibrium is said to be strict.

Why should anyone care about Nash equilibria? There are at least two reasons. The first is that if a game has a rational solution that is common knowledge among the players, then it must be a Nash equilibrium. If it weren’t, then some of the players would have to believe that it is rational for them not to make their best reply to what they know the other players are going to do. But it can’t be rational not to play optimally.

The second reason why Nash equilibria matter is equally important. If the payoffs in a game correspond to how fit the players are, then evolutionary processes—either cultural or biological—that favor strategies that currently generate a higher payoff at the expense of those that generate a lower payoff will stop working when we get to an equilibrium, because all the surviving strategies will then be as fit as it is possible to be in the circumstances. Only Nash equilibria can therefore be evolutionarily stable.²

Much of the power of game theory as a conceptual tool derives from the possibility of moving back and forward between these eductive and evolutive interpretations of an equilibrium.

2.2 The Security Dilemma

Both payoffs are circled in two cells of the payoff table of the Driving Game, and so both these cells correspond to Nash equilibria. It is an equilibrium if everyone drives on the left. It is also an equilibrium if everyone drives on the right. The players get the same payoff at each of these equilibria and so they don’t care whether they both drive on the left or they both drive on the right. Their only concern is that they both coordinate on the same equilibrium. However, the same isn’t true of the Stag Hunt Game.

Like the Driving Game, the Stag Hunt Game has two cells in which both payoffs are circled. Both of these cells correspond to Nash equilibria, but now both players prefer the cooperation equilibrium in which both play dove to the defection equilibrium in which both play hawk. If they live in a society in which it is conventional to play the cooperation equilibrium then all is well, but what if defection is the established convention?

What can rational players do to persuade each other before playing the game that their minisociety should shift to the cooperation convention? Experts in international relations study the Stag Hunt Game under the name of the Security Dilemma because it is the simplest case where the answer to this question is problematic. It is important to realize that the problem isn’t just a question of one player pointing out the advantages of shifting to a new convention. Alice may tell Bob that she plans to play dove on the assumption that he will be convinced by her arguments in favor of the new convention, but will Bob believe her?

Whatever Alice is planning to play, it is in her interests to persuade Bob to play dove. If she succeeds, she will get 5 rather than 0 when playing dove, and 4 rather than 2 when playing hawk. Rationality alone therefore doesn’t allow Bob to deduce anything about her plan of action from what she says, because she is going to say the same thing no matter what her real plan may be! Alice may actually think that Bob is unlikely to be persuaded to switch from hawk and hence be planning to play hawk herself, yet still try to persuade him to play dove.

The point of this Machiavellian story is that attributing rationality to the players isn’t enough to resolve the equilibrium selection problem—even in a case that seems as transparently straightforward as the Stag Hunt Game. If we see Alice and Bob playing hawk in the Stag Hunt Game, we may regret their failure to coordinate on playing dove, but we can’t accuse either player of being irrational, because neither player can do any better given the behavior of their opponent.

A common criticism of such arguments is that game theory fails to appreciate that it is rational for people to trust each other because their payoffs will be higher if they have faith in each other’s honesty. This argument fails for the same reason that it fails in the Prisoners’ Dilemma, but people may well come to trust each other for other good and sufficient reasons. Game theorists don’t say it is never rational to trust other people—only that trust can’t be taken on trust. Or, to quote David Hume (1978) again, “Surely I am not bound to keep my word because I have given my word to keep it.”

Of course, there is usually a lot more going on in the real world than in the highly idealized microcosm of a formal game. For example, Sweden switched from driving on the left to driving on the right in the early hours of September 1st, 1967. But who thinks that the notoriously misanthropic Ik would have responded similarly to a call from the Ugandan government to shift to a more cooperative equilibrium of their tribal game of life? (Turnbull 1972).

2.3 Categorical Imperative?

The Prisoners’ Dilemma is mentioned by way of counterpoint to the Stag Hunt Game. It has the same payoffs, except that mutual cooperation has been made less attractive by reducing the payoffs the players receive at the cooperation outcome from 5 to 3. The result is that hawk now strictly dominates dove, which means that hawk is a strict best reply whatever strategy the other player may choose. In particular, the Prisoners’ Dilemma has only one Nash equilbrium, in which both players choose hawk.

Immanuel Kant’s categorical imperative would seem to contradict the claim that only the play of hawk is rational in the Prisoners’ Dilemma. In fact, Kant is only one of many scholars who have argued that play can be rational without being in equilibrium (Binmore 1994, Chap. 3). It may therefore be worthwhile to clarify the Humean sense in which game theorists understand rational play.

So as not to beg any questions, we begin by asking where the payoff table that represents the players’ preferences in the Prisoners’ Dilemma comes from. The game theory answer is that we discover the players’ preferences by observing the choices they make (or would make) when solving one-person decision problems.

Writing a larger payoff for Alice in the bottom-left cell of the payoff table of the Prisoners’ Dilemma than in the top-left cell therefore means that Alice would choose hawk in the one-person decision problem that she would face if she knew in advance that Bob had chosen dove. Similarly, writing a larger payoff in the bottom-right cell means that Alice would choose hawk when faced with the one-person decision problem in which she knew in advance that Bob had chosen hawk. The very definition of the game therefore says that hawk is Alice’s best reply when she knows that Bob’s choice is dove, and also when she knows his choice is hawk. So Alice doesn’t need to know anything about Bob’s actual choice to know her best reply to it. It is rational for her to play hawk whatever strategy he is planning to choose.

2.4 Mixed Strategies

The payoff table of Matching Pennies has no cell with both payoffs circled. It follows that the game has no Nash equilibrium in pure strategies. But the players aren’t restricted to playing heads or tails. They can also mix between these strategies by randomizing their choice.

Nash (1951) proved that all finite games have at least one Nash equilibrium when such mixed strategies are allowed. Matching Pennies has a unique mixed equilibrium that requires each player to choose heads or tails with equal probability. Since Matching Pennies is a zero-sum game, this strategy is the same as Von Neumann’s paranoid strategy. If Alice plays heads or tails with equal probability, she is sure to win half the time on average, whatever Bob may do.³ Since the same is true of Bob, both players will be making a best reply to the (mixed) strategy choice of their opponent if they both play heads or tails with equal probability.

Both the Driving Game and the Stag Hunt Game also have a mixed-strategy equilibrium as well as their two pure-strategy equilibria. Such a multiplicity of equilibria is typical of more realistic games. Matching Pennies and the Prisoners’ Dilemma are unusual in not posing an equilibrium selection problem.

2.5 Lewis on Game Theory

David Lewis’s (1969) game theory isn’t very orthodox, and so some clarification may be helpful.

Lewis (1969, p.8) doesn’t mention John Nash, but what he calls an equilibrium is a Nash equilibrium in pure strategies. He doesn’t consider mixed Nash equilibria. What he calls a proper equilibrium is not a proper equilibrium in the sense of Myerson (1991), but what is normally called a strict Nash equilibrium. Lewis (1969,p. 17) offers only one formal proof: that a game of pure coordination with a unique Nash equilibrium must have a dominated strategy. Figure 2a shows this to be false with the standard definition of a dominated strategy, but Lewis uses a nonstandard definition.⁴

Fig. 2

A game of pure coordination and a game of pure conflict

Lewis’s (1969, p. 14) definition of a coordination equilibrium is also eccentric. He notes that an equilibrium is a combination of strategies in which no one would have been better off if he alone had acted otherwise. He then says that “a coordination equilibrium is a combination of strategies in which no one would have been better off if any one agent alone acted otherwise, either himself or someone else.” Rather than use this definition, I shall not speak of coordination equilibria at all.

Lewis’s definition makes the unique equilibrium of Matching Pennies into a coordination equilibrium, and it seems perverse to speak of coordination in a game in which each player’s aim is to prevent the opponent’s attempt to coordinate their strategies. If it is objected that the equilibrium is mixed in Matching Pennies, one can make the same point with the game of Fig. 2b, in which a pure strategy has been introduced that has the same effect as playing heads or tails with equal probabilities. Lewis (1969, p. 15) uses the same example without its first row and column.

3 Nash Demand Game

Schelling (1960) conducted some instructive experiments in the 1950s on how people manage to solve various games of pure and impure coordination. In his best known experiment, the subjects were asked what two people should do if they had agreed to meet up in New York tomorrow without specifying a place and time in advance. The standard answer was that they should go to Grand Central Station at noon. When people commonly agree on such a resolution of a coordination problem, Schelling says that the consensus they report constitutes a focal point. If it were necessary to distinguish between a focal point and a convention, perhaps the criterion would be that a focal point is a convention that the players aren’t aware that they are likely to share in advance of playing a coordination game.

A politically incorrect version of Schelling’s meeting problem is traditionally called the Battle of the Sexes. Adam and Eve are a pair of honeymooners who get separated in a big city after failing to agree at breakfast on whether to meet up at the ballet or a boxing match. Alice prefers the former and Bob the latter. The Nash Demand Game (Nash 1950) can be regarded as a more elaborate version of this game in which partial coordination is also possible.

However, the Nash Demand Game is more commonly interpreted as a primitive bargaining model in which the feasible payoff pairs lie in a set X like that shown in Fig. 3. Alice and Bob each simultaneously demand a payoff. If the pair of payoffs demanded is in the feasible set, both players receive their demands. If not, both players receive the disagreement payoff of zero.

Fig. 3

What is fair in the Nash demand game?

The game poses the equilibrium selection problem in an acute form, because every efficient outcome that assigns both players no less than their disagreement payoffs is a Nash equilibrium of the game. For this reason, the game has become a standard test bed for trying out equilibrium selection ideas (Skyrms 1996). In Sect. 6, we explore the fairness conventions that people may come to regard as appropriate in this game.

Nash himself proposed dealing with the equilibrium selection problem strategically by studying a smoothed version of the Nash Demand Game in which the players aren’t certain where the boundary of the feasible set starts and stops. As one moves out along a curve from the disagreement point, the probability that the current payoff pair is feasible declines smoothly from one to zero in the vicinity of the boundary. All the Nash equilibria of the unsmoothed game are still approximate equilibria of the new game, but the exact Nash equilibria of the smoothed game all lie near a payoff pair N called the Nash bargaining solution that Nash (1950) famously characterized axiomatically.

4 Common Knowledge

In a discussion of how particular equilibria in games of pure coordination become focal, Schelling (1960, p. 109) proposes a mind experiment in which the players are envisaged as being connected to machines that register the focus of their attention: “Each can see the meter on his own machine, each can see the meter on the other’s machine, and each is aware that both are aware that both can see both meters.”

Lewis (1969, p. 58) took this line of thought further by insisting that a convention can only operate in an informational environment with such a character. After reminding us that his conception of the nature of a convention requires a regularity in behavior, a system of mutual expectations, and a system of preferences, he then requires that these properties must be common knowledge in the population in which the convention is established. His formal expression of the latter requirement is reproduced below:

A regularity R in the behavior of members of a population P when they are agents in a recurring situation S is a convention if and only if it is true that, and it is common knowledge in P that, in any instance of S among members of P,

• (1) everyone conforms to R;

• (2) everyone expects everyone else to conform to R;

• (3) everyone prefers to conform to R on condition that the others do, since S is a coordination problem and uniform conformity to R is a coordination equilibrium in S.

Lewis continues by observing that these requirements set up an infinite chain of expectations in accordance with the current understanding in game theory that something is common knowledge if everybody knows it, everybody knows that everybody knows it, everybody knows that everybody knows that everybody knows it; and so on. Bob Aumann’s (1976) later definition of common knowledge in terms of the players’ knowledge partitions allowed this insight to be put onto a formal basis, but space doesn’t permit a discussion of the ingenious manner in which Aumann avoids following Lewis into a tangle of infinite regressions. Instead, I shall say only enough to make it clear that the propositions of the theory have the status of theorems (Binmore 2007, Chap. 12).

4.1 Modeling Knowledge

We can specify what Alice knows with the help of a knowledge operator K. The proposition that an event has occurred can be modeled as a subset of a finite set X of states of the world. For each event E, KE is the event that Alice knows E has occurred.

In the small world created when a game is specified, the knowledge operator K is assumed to satisfy the requirements of the modal logic S-5 listed below.⁵

• (K0) KX = X

• (K1) K(E and F) = KE and KF

• (K2) KE implies E

• (K3) KE implies K ² E

• (K4) (not K)² E implies KE

Game theorists who are surprised that they believe all these propositions may be comforted at the news that they are equivalent to using Von Neumann’s information sets to handle what the players know in a game.

I say that something that cannot be true without Alice knowing it is a truism for her. So T is a truism if and only if T implies KT. By (K2), we then have T = KT. If we regard a truism as capturing the essence of what happens when making a direct observation, it can be argued that all knowledge derives from truisms. This observation is reflected in the following trivial theorem:⁶

Alice knows that E has occurred if and only

if a truism T that implies E has occurred.

4.2 Public Events

The crudest way to define the common knowledge operator CK is to define (CK)E to be the event that (everybody knows)^N E is true for all values of N. The common knowledge operator inherits all the properties (K0)–(K4) of an individual knowledge operator. In particular, an event is common knowledge if and only if it is implied by a common truism—an event that can’t occur without its becoming common knowledge. It turns out that a common truism is the same thing as a public event, which has a simpler characterization. An event E is a public event if and only if it cannot occur without everybody knowing it has occurred, so that E =  (everybody knows) E.

This observation returns us to Schelling’s mind experiment in which each player is aware that both are aware that both can see both meters. With remarkable prescience, he sets up the conditions of his mind experiment so that the focalizing behavior of the players is a public event. As Lewis then observes, the outcome is that the resulting focal point or convention will be common knowledge between the players.

I don’t want to downplay the importance of public events to the maintenance of human social systems. The significance we attach to making eye contact is enough in itself to show that it matters that some events are public. When Alice refuses to make eye contact with Bob, she is refusing to make it common knowledge between them that they recognize each other as persons. Presumably, this is why we are careful not to make eye contact with beggars when we plan to disregard their need.

However, it seems to me that the main consequence of modern advances in our understanding of knowledge operators for the theory of conventions is to bring forcibly to our attention how difficult it is for something to become common knowledge. How often do we have the opportunity to observe each other observing something? For large numbers of people, I guess the answer is never. So how can a language have become a convention if a convention needs to be common knowledge in a society? How can it have become conventional for gold to be valuable? How can it even have become conventional to drive on the right? And if we don’t know the answer to such questions as these, how are we ever to find our way to an equilibrium of the game of life we play on this planet in which we get global warming and the like under control?

This is not to deny that we sometimes behave as if conventions are common knowledge when we use them. Perhaps this is what authors like Cubitt and Sugden (2005) have in mind when they speak of conventions being culturally transmitted. I have been guilty of similar loose thinking myself (Binmore 1994). If one accepts that conventions must be common knowledge to be operational and that societies nevertheless operate conventions, then one is forced to the conclusion that some matters can become common knowledge without the intervention of a public event. But one then denies a theorem. The alternative is to abandon Lewis’s insistence that conventions must be common knowledge in order to be operational.

Lewis (1969, p. 78) relaxes his definition of a convention to the requirement that it only need be common knowledge that a convention is honored by some fraction of a population, but I do not see that this helps with the problem identified above. It is true that Bob need only believe that his opponent will play dove more than two thirds of the time in our version of the Stag Hunt Game for it to be optimal for him to play dove himself, but Lewis still requires this belief to be common knowledge. A further modification in which the requirement of common knowledge is replaced by Monderer and Samet’s (1989) notion of common p-belief⁷ would be a more useful response to the problem I am raising, but one would still be left with essentially the same difficulty.

5 Byzantine Generals

In computer science, the difficulties that arise when two people seek to upgrade a piece of knowledge held by one into a piece of knowledge held in common are illustrated by the ``coordinated attack problem’’ (Halpern 1987).

Two Byzantine generals occupy adjacent hills with the enemy in the valley between. If both generals attack together, victory is certain, but if only one general attacks, he will suffer badly. The first general therefore sends a messenger to the second general proposing an attack. Since there is a small probability that a messenger will be lost while passing through the enemy lines, the second general sends a messenger back to the first general confirming the plan to attack. But when this messenger arrives, the second general doesn’t know that the first general knows that the second general received the first general’s message proposing an attack. The first general therefore sends another messenger confirming the arrival of the second general’s messenger. But when this messenger arrives, the first general doesn’t know that the second general knows that the first general knows that the second general received the first general’s message. The fact that an attack has been proposed is therefore not common knowledge because, for an event E to be common knowledge, all statements of the form (everybody knows)^N E must be true. Further messengers may be shuttled back and forward until one of is picked off by the enemy, but no matter how many confirmations each general may receive before this happens, it never becomes common knowledge that an attack has been proposed.

This looks like a major problem for the coherence of the distributed systems studied in computer science, because two different smart agents will necessarily have different information as a consequence of their differing experience. How can they act together in a joint enterprise if they cannot succeed in sharing their knowledge adequately?

A clue to the fact that a wrong question is possibly being asked here is to be found in the coordinating behavior of ordinary people. When Alice texts a suggestion to Bob that they meet at noon in the coffee shop and Bob texts the reply OK, this is usually enough to ensure that Alice and Bob will meet up successfully. But their agreement isn’t common knowledge between them because Bob didn’t get his confirmation confirmed. This commonplace observation suggests that it may be worth reconsidering the arguments which suggest that coordinated action must be based on common knowledge.

It is not true—as sometimes claimed—that there must be common knowledge of the game and of the players’ rationality in order to justify the play of a Nash equilibrium. For two optimizing players to operate a Nash equilibrium, it is obviously sufficient if each knows the strategy that the other plans to play. In the Prisoners’ Dilemma, even this much knowledge is superfluous. However, Rubinstein’s Email Game would seem to show that such a removal of the focus of the discussion from what the players know to the actions they need to take to implement a Nash equilibrium does not eliminate the problem.

5.1 The Email Game

Independently of the computer science literature, Rubinstein (1989) formulated a version of the coordinated action problem in terms of his Electronic Mail Game. Instead of two Byzantine generals, we have Alice and Bob communicating by email. They have an opportunity from which they can both profit only if they coordinate on exploiting it. Only Bob knows of the opportunity, and hence must communicate with Alice if the opportunity is to be seized. Bob can send a message to Alice, but there is some probability that her message won’t arrive. If the message arrives, Alice sends an acknowledgement which again may fail to arrive. Bob acknowledges the acknowledgement, and so on. The question is whether Alice and Bob will be able to exploit their opportunity.

The Email Game is a formal version of this problem in which Alice and Bob must independently choose between DOVE and HAWK (where the use of capitals is significant). Their payoffs are then determined by whether Chance makes DOVE correspond to dove, and HAWK to hawk in the Stag Hunt Game, or whether she reverses these correspondences. It is common knowledge that Chance chooses the first possibility two thirds of the time.

Only Bob learns what decision Chance has made. On the understanding that the default action is DOVE, a message goes to Alice that says “Play HAWK” whenever Bob learns that dove corresponds to HAWK. Alice’s machine confirms receipt of the message by bouncing it back to Bob’s machine. Bob’s machine confirms that the confirmation has been received, by bouncing the message back again. And so on.

The (everybody knows)^N operator applies with ever higher values of N as confirmation after confirmation is received. So if the players could wait until infinity before acting, Chance’s choice would become common knowledge. However, the Email Game is realistic to the extent that the probability of any given message failing to arrive is very small but positive. The probability of Chance’s choice becoming common knowledge is therefore zero. But we can still ask whether coordinated action is possible for Alice and Bob. Is there a Nash equilibrium in which they do better than always playing their default action of DOVE?

The possible states of the world are the number of messages that get sent. Neither player knows the actual state of the world. For example, if the state of the world is 2 (so that the third message went astray), then Bob thinks it also possible that the second message (sent by Alice’s machine) wasn’t sent because the first message (sent by Bob’s machine) didn’t arrive. Bob’s possibility set is therefore {1,2}. Similarly, Alice’s possibility set is {2,3} when the state of the world is 2.

In the Email Game, a pure strategy specifies an action (either DOVE or HAWK) for each of a player’s possible informational states. Rubinstein showed that the only Nash equilibrium consistent with Bob’s choosing DOVE when no message is sent requires both players to choose DOVE in all informational states.⁸ No convention that allows Alice and Bob always to coordinate on the cooperation equilibrium in the Stag Hunt Game is therefore available.

5.2 Byzantium Rescued!

Rubinstein’s (1989) widely quoted result on the Email Game seems to support Lewis’ intuition that common knowledge is necessary for a convention to be operational. No matter how many times we succeed in iterating the (everybody knows) operator, we get no nearer to implementing a fully cooperative convention.⁹

However, one should never put too much weight on a single formal model. It turns out that Rubinstein’s conclusion depends on the fact that Alice and Bob’s machines automatically bounce back a confirmation when they receive a message. This seems an innocent simplification, but if we allow Alice and Bob the freedom to choose whether or not to send back a confirmation, then the results of the model are turned upside down (Binmore and Samuelson 2001). Instead of full cooperation being unavailable as a Nash equilibrium no matter how many messages are sent, we find that there is a plethora of Nash equilibria that support full cooperation. Whatever positive number of messages is specified in advance, there is a Nash equilibrium in which both players use HAWK after that number of messages have been sent and received.¹⁰ It therefore turns out that common knowledge is irrelevant to the operation of the convention.

5.3 The Long Goodbye

In the most pleasant Nash equilibrium of the modified Email game, both players play HAWK whenever Bob proposes doing so and Alice says OK—as when friends agree to meet in a coffee shop. But there are other Nash equilibria in which the players settle on HAWK only after a long sequence of confirmations of confirmations. Hosts of polite dinner parties suffer from such equilibria when their guests start moving with glacial slowness towards the door at the end of the evening, stopping every inch or so in order that the host and the guest can exchange assurances that departing at this time is socially acceptable to both sides. One might hope that social evolution would eventually eliminate such long goodbyes, but the prognosis isn’t good. Only the unique equilibrium of the original Email Game—in which HAWK is never played—fails to pass an appropriate evolutionary stability test (Binmore and Samuelson 2001).

6 The Evolution of Conventions

My own view is that to focus on the knowledge requirements for an operational convention is to lose track of what is most important. This isn’t to say that what the players in a game may or may not know doesn’t matter, but that knowledge issues are secondary. Conventions can sometimes be sustained without anyone knowing anything at all in the formal sense required by current theories of knowledge.

For example, the songs that certain species of birds sing is a cultural phenomenon. Young birds learn to sing complicated arrangements of notes by listening to the songs of experienced birds. It matters a lot to them what song they sing, because the songs are used as a coordinating device in deciding who mates with whom. But the birds do not “know”’ any of this. Nor I think do humans when they operate most of the conventions woven into our social contracts. As Hume (1978) observes, most conventions arise gradually and acquire force by a slow progression. Or, as we would say nowadays, they are the product of a largely unconscious process of cultural evolution.

6.1 What is Fair?

An experiment on the smoothed Nash Demand Game that I ran with some colleagues at the University of Michigan may perhaps serve to illustrate the evolutive attitude to conventions that I advocate (Binmore et al. 1993; Binmore 2007).

The feasible set in the experiment is shown in Fig. 3, with serious money substituting for utility. The exact Nash equilibria correspond to points on the thickened line.¹¹ The letters E and U refer to the egalitarian and utilitarian outcomes. The egalitarian outcome is what one gets by applying Rawls’ (1972) difference principle in this context. The utilitarian outcome is the point in X where the sum of the players’ payoffs is largest (Harsanyi 1977). The letter N corresponds to the Nash bargaining solution (Nash 1950). The letter K refers to an alternative bargaining solution proposed by Kalai and Smorodinsky (1975).

The experiment began with ten trials in which different groups of subjects knowingly played against robots programmed to converge on one of the possible focal points E, K, N, and U. This conditioning phase proved adequate to coordinate the play of a group on whichever of the four focal points we chose. The conditioning phase was followed by thirty trials in which the subjects played against randomly chosen human opponents from the same group. The results were unambiguous. Subjects started out playing as they had been conditioned, but each group ended up at an exact Nash equilibrium.

It is striking that the different conventions that evolved in the experiment selected only exact Nash equilibria, even though some groups were initially conditioned on the egalitarian and utilitarian solutions, which were both approximate equilibria from which players would have no incentive to deviate if they neglected amounts of less than a dime.

In the computerized debriefing that followed their session in the laboratory, subjects showed a strong tendency to assert that the convention that evolved in their own group was the “fair” outcome of the game. But different groups found their way to different exact equilibria. Indeed, for each exact equilibrium of our smoothed demand game, there was some group willing to say that this was near the fair outcome of the game.

I think the results exemplify David Hume’s view of how conventions work. The subjects in each experimental group behaved like the citizens of a minisociety in which a fairness norm evolved over time as an equilibrium selection device. However, the circumstances in which the experiment was run allowed no opportunities for anything to become common knowledge.

7 Conclusion

This paper argues that David Lewis’s attempt to restrict the notion of a convention to equilibrium selection devices whose usage is common knowledge among the players is so restrictive that it excludes almost all conventions on which actual societies rely. It is a theorem that an event can become common knowledge if and only if it is implied by a public event—one that cannot occur without its becoming common knowledge. However, the paradox of the Byzantine generals (or its formal incarnation as Rubinstein’s Email Game) shows that it is very hard for a public event to occur without the players each observing each other observing it. The manner in which we learn to drive on the right or to regard gold as valuable certainly do not satisfy this criterion. The idea that cultural transmission as normally understood is adequate to make a convention commonly known is therefore mistaken.

The fact that conventions like driving on the right or speaking French operate very successfully in spite of not being common knowledge in the societies that have adopted them shows that David Lewis was mistaken in supposing that common knowledge of conventions is necessary for them to work. This paper presses this point home by offering an analysis of Rubinstein’s Email Game to show how a convention may become established in an evolutionary environment. It also reviews an experiment on the Nash Demand Game which shows cultural evolution can establish essentially arbitrary fairness conventions in a society. In neither case is it possible that any feature of the situation can become common knowledge according to Lewis’s (and Aumann’s) formal definition.

In summary, there is no reason to follow Lewis in abandoning the view held of conventions by David Hume and Thomas Schelling. His attempt to improve on their efforts would make the idea of a convention relevant only in very small-scale societies.