Effective Forchheimer Coefficient for Layered Porous Media

Abstract

Inertial flow in porous media, governed by the Forchheimer equation, is affected by domain heterogeneity at the field scale. We propose a method to derive formulae of the effective Forchheimer coefficient with application to a perfectly stratified medium. Consider uniform flow under a constant pressure gradient $\Delta P/L$ in a layered permeability field with a given probability distribution. The local Forchheimer coefficient $\beta$ is related to the local permeability k via the relation $\beta =a/k^c$, where $a>0$ being a constant and $c\in [0,2]$. Under ergodicity, an effective value of $\beta$ is derived for flow (i) perpendicular and (ii) parallel to layers. Expressions for effective Forchheimer coefficient, $\beta _e$, generalize previous formulations for discrete permeability variations. Closed-form $\beta _e$ expressions are derived for flow perpendicular to layers and under two limit cases, $F\ll 1$ and $F\gg 1$, for flow parallel to layering, with F a Forchheimer number depending on the pressure gradient. For F of order unity, $\beta _e$ is obtained numerically: when realistic values of $\Delta P/L$ and a are adopted, $\beta _e$ approaches the results valid for the high Forchheimer approximation. Further, $\beta _{e}$ increases with heterogeneity, with values always larger than those it would take if the $\beta - k$ relationship was applied to the mean permeability; it increases (decreases) with increasing (decreasing) exponent c for flow perpendicular (parallel) to layers. $\beta _{e}$ is also moderately sensitive to the permeability distribution, and is larger for the gamma than for the lognormal distribution.

1 Introduction

An understanding of the interplay between nonlinear effects in porous media flow and domain heterogeneity is of great importance in several engineering and geological disciplines. Darcy’s law, usually adopted to model fluid flow in porous media, implies a linear relationship between flow rate and pressure (or head) gradient. However, for high flow rates, the pressure gradient is higher than that predicted by Darcy’s law, the deviation increasing with the flow rate. This phenomenon, known as non-Darcy or Forchheimer flow, occurs in several civil, environmental, and industrial engineering applications, such as flow in rockfill dams; flow in coarse-grained, fractured or karstic porous media; flow in the vicinity of pumping or injection wells; gas flow in natural or artificial porous media; industrial filtration processes; reservoir exploitation. The importance of the aforementioned applications generated a large body of scientific and technical literature in the past decades aimed at understanding the mechanisms governing non-Darcy flow in porous media. The nonlinear relationship between flow rate and pressure drop is usually attributed to the insurgence of inertial effects within the laminar flow regime; these inertial effects are commonly represented by adding to Darcy’s equation an additional term proportional to the fluid density and to the second power of the flow rate; the coefficient of proportionality is known as Forchheimer, or inertial, or non-Darcy coefficient. For a review of the different existing formulations of Forchheimer’s law see, among others, Trussell and Chang (1999), Sidiropoulou et al. (2007), and Huang and Ayoub (2008). An alternative to Forchheimer’s law is the Izbash equation, which states that the hydraulic gradient is a power function of the specific discharge (Bordier and Zimmer 2000; Moutsopoulos et al. 2009); more complex polynomial equations also exist (Balhoff et al. 2010; Lofrano et al. 2020), based on the fact that inertial flow in porous media may be classified into different subregimes depending on the form of the inertial correction (Agnaou et al. 2017).

In field-scale modeling of porous media flow at scales ranging from local to regional, heterogeneity in model parameters plays a crucial role; as a consequence, a relevant effort was devoted in the scientific literature at characterizing heterogeneity in hydraulic and transport properties, and at deriving representative properties as functions of statistical parameters describing heterogeneity. While most of the effort was directed at hydraulic conductivity (Sanchez-Vila et al. 2006), heterogeneity in the Forchheimer coefficient was also recognized in the field (Jones 1987; Narayanaswamy et al.. 1999), prompting researchers to investigate the concept of a representative Forchheimer coefficient at a given upscaled scale, as a function of its local value (Fourar et al. 2005; Auriault et al. 2007; Garibotti and Peszynska 2009; Aulisa et al. 2014). The nonlinearity of the flow complicates the upscaling problem; related work in the context of geologic media includes the determination of the effective conductivity for non-Newtonian fluid flow (Di Federico et al. 2010; Airiau and Bottaro 2020).

The value of the Forchheimer coefficient has long been recognized as being empirically correlated to other properties of the porous medium, namely porosity, tortuosity, and permeability; a recent summary of proposed correlations was provided by Arabjamaloei and Ruth (2017). In particular, the correlation of the Forchheimer coefficient $\beta$ with permeability k was found to be a power-law inverse one since the work of Ergun (1952) and Geertsma (1974). The present paper incorporates the $\beta - k$ correlation into deriving an upscaled Forchheimer coefficient for flow under a uniform pressure gradient in a stratified porous medium.

The Forchheimer seepage law, related experimental findings, and the nature of the $\beta - k$ correlation are illustrated in Sect. 2, while effective parameters for Forchheimer flow in one-dimensional stratified porous media are derived in Sect. 3 for flow perpendicular and parallel to layers; in the latter case, two analytical approximations are presented for low- and high-Forchheimer number case, together with a general option for numerical evaluation. These results are discussed as a function of problem parameters in Sect. 4. A set of conclusions closes the paper (Sect. 5), while details on the permeability distribution functions adopted and special values of the quantities of interest are presented in Appendices A through D.

2 Seepage Law and Experimental Findings

2.1 Forchheimer Flow Law

For high seepage velocities, Darcy’s law is inadequate to represent fluid flow in porous media due to inertial effects, which are no longer negligible when the pore-scale Reynolds number exceeds a threshold value between 1 and 10 (Bear 1979), while turbulence usually occurs at much higher values of the pore Reynolds number (Huang and Ayoub 2008). In turn, inertial effects derive from the nonlinear terms in the general momentum balance equation.

The inertial effects are commonly represented by adding to Darcy’s law an additional term proportional to the fluid density and the second power of the flow rate; the resulting equation is termed Forchheimer’s flow law; its isotropic form reads (Auriault et al. 2007)

$$\begin{aligned} -\nabla P=\big (\frac{\mu }{k_F}+\rho \beta |\mathbf {q} |\big )\mathbf {q}, \end{aligned}$$

(1)

where $P=p+\rho g z$ is the generalized pressure including gravity effects, p the pressure, $\rho$ and $\mu$ the fluid density and dynamic viscosity, $\mathbf {q}$ the specific discharge vector $[LT^{-1}]$, $k_F$ the Forchheimer permeability coefficient $[L^2]$, larger than, but close to, the Darcy permeability coefficient $k_D$ appearing in Darcy’s law (El-Zehairy et al. 2019). Finally, $\beta$ is the Forchheimer coefficient $[L^{-1}]$, also termed velocity coefficient, inertial coefficient, or non-Darcian coefficient; when $\beta =0$, Eq. (1) reduces to Darcy’s law with $k_D$ in place of $k_F$. In the following, we will assume $k_D=k_F=k$.

Values of the Forchheimer coefficient $\beta$ reported in the literature vary over several orders of magnitude. In their review, Venkataraman and Rao (1998) summarized a large number of data from earlier laboratory experiments; when interpreted with Forchheimer’s law, these yielded values of $\beta$ in the range $270-24,550$ $m^{-1}$. Bordier and Zimmer (2000) obtained $\beta =302-344$ $m^{-1}$ for coarse granular materials and $\beta =43-308$ $m^{-1}$ for man-made drainage products. The review paper by Sidiropoulou et al. (2007) cites experimental values of $\beta$ ranging from 42 to 7, 962 $m^{-1}$. The experimental work of Moutsopoulos et al. (2009) in a vertical metal column yielded $\beta =448-6,389$ $m^{-1}$ for eight different types of coarse porous media. Values of $\beta$ for flow through woodchips (Ghane et al. 2016) range from $2.16\times 10^4$ to $1.58\times 10^5$ $m^{-1}$. Yang et al. (2017) performed seepage experiments in sand columns with nine different particle sizes, obtaining $\beta =2.06\times 10^5-1.50\times 10^9$ $m^{-1}$, though the larger value is associated with actual turbulence. For fine-grained sands typical of geotechnical applications, centrifuge and bench tests yielded $\beta =5.27\times 10^3-5.94\times 10^6$ $m^{-1}$ (Ovalle-Villamil and Sasanakul 2019). The 3-D direct pore-scale simulations of Muljadi et al. (2016) yielded estimates of $\beta$ of $2.57\times 10^5$ $m^{-1}$, $2.07\times 10^6$ $m^{-1}$ and $6.15\times 10^8$ $m^{-1}$, for water flowing in beadpack, Bentheimer sandstone and Estaillades carbonate, in good agreement with available experimental data.

All experimental values cited above pertain to water flow, while values of $\beta$ found experimentally for gas flow tend to be higher by a couple of orders of magnitude: values of the Forchheimer coefficient measured by Jones (1987) on a total of 364 core plugs were in the range $10^5$ to $10^{13}$ $m^{-1}$; Zeng and Grigg (2006) performed laboratory experiments with nitrogen gas, finding $\beta =2.88\times 10^8-1.57\times 10^{10}$ $m^{-1}$; Wells et al. (2008) obtained for airflow values of $\beta$ in the range $1.41\times 10^6-5\times 10^8$ $m^{-1}$ with a field permeameter. For fracture proppant packs in hydrofracturing, $\beta$ lies in the range $7.2\times 10^4-3.8\times 10^7$ $m^{-1}$ (Friedel and Voigt 2006).

2.2 Empirical $\beta - k$ Correlations

Several researchers found a correlation to exist between local values of the Forchheimer coefficient $\beta$ and other properties of the porous medium; the different formulations of this relationship, either theoretically or empirically based, are summarized by Li and Engler (2001); according to them, a good representation of most of the previous work, either of theoretical or experimental nature, is provided by the formulation

$$\begin{aligned} \beta =\frac{c_1 \tau }{k^{c_2} \phi ^{c_3}}, \end{aligned}$$

(2)

in which $\phi$ is porosity, $\tau$ is tortuosity, and $c_1$, $c_2$, and $c_3$ are three experimental constants for an assigned porous medium. Similar formulations are reported in Skjetne et al. (2001) and Saboorian-Jooybari and Pourafshary (2015), albeit with $\tau =1$. The former authors note that as $[k]=[L^2]$ and $[\beta ]=[L^{-1}]$, media that are scaled copies of each other have $c_2=0.5$. According to the analysis of Geertsma (1974), conducted both via dimensional and field data analysis, $c_2=0.5$; according to Narayanaswamy et al. (1999), who also cites previous experimental work, $c_2=1.25$. Jones (1987) analyzed a large number of field samples with differing lithologies, obtaining $c_2=1.55$; the reticular model of Thauvin and Mohanty (1998) and the experimental data of Cooper et al. (1998) suggest $c_2=1$. The values of $c_2$ in Eq. (2), according to the review by Li and Engler (2001), are generally in the range of 0.5 to 1.88. The same range is reported in the more recent review of Saboorian-Jooybari and Pourafshary (2015). In the sequel of this note, aimed at investigating the impact of heterogeneity in the permeability distribution on the effective Forchheimer coefficient, porosity $\phi$, and tortuosity $\tau$ will be considered as constants, under the hypothesis that permeability varies across several order of magnitudes while porosity and tortuosity do not (Bear 1979); this allows writing Eq. (2) as

$$\begin{aligned} \beta (k)=\frac{a}{k^{c}}, \quad a=\frac{c_1 \tau }{\phi ^{c_3}}, \end{aligned}$$

(3a-b)

where $c=c_2$ $[-]$ is a non-negative empirical exponent, which will be assumed to lie in the range $0-2$, and the empirical parameter $a=a(c)$ has dimensions $[L^{(2c-1)}]$; the case $c=0$ is equivalent to assuming a value of the local-scale Forchheimer coefficient $\beta$ independent from permeability.

The value of the parameter a is highly sensitive to the exponent c and the medium properties, porosity $\phi$ and tortuosity $\tau$. For $c=0.5$, Ergun (1952) measured $a=361480\,[-]$ for sand packs and Macdonald et al. (1979) calculated $a=339408\,[-]$ for unconsolidated and consolidated sandstone. For $c=1$, the experimental data of Liu et al. (1995) result in $a=71274432\,m$ considering as mean values of porosity and tortuosity $\phi =0.25$ and $\tau =2$. For $c=1.55$, Jones (1987) obtained $a=187724450\,m^{2.1}$ for limestone, and fine-grained sandstone considering $\phi =1$. In what follows, we assume the latter value of a to be valid also for the case $c=1.5$ as $a=187724450\,m^2$. Additional, different experimental values of a can be found in Saboorian-Jooybari and Pourafshary (2015) for different correlations of $\beta$ and k.

3 Effective Parameters for Forchheimer Flow in Stratified Porous Media

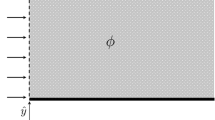
Consider an heterogeneous, perfectly stratified porous domain of length L, subject to an external, generalized pressure difference $\Delta P=P(0)-P(L)=P_1-P_2$ in the x-direction; the domain permeability k is taken to vary as a weakly stationary random field characterized by its probability density function (PDF) f(k). The ergodic assumption is assumed to hold; hence spatial averages and ensemble averages are interchangeable, and a single realization can be examined. To derive an expression for the effective permeability $k_{e}$ and effective Forchheimer coefficient $\beta _{e}$ in perfectly layered media, two limiting cases are examined, coincident with those providing the lower and upper bound for the effective permeability (Matheron 1967): (i) flow perpendicular to the layering (serial-type layers), when the pressure gradient is parallel to the permeability variation; (ii) flow parallel to the layering (parallel-type layers) when the pressure gradient is transverse to the permeability variation, as shown schematically in Fig. 1a and b, respectively. Such perfect layering is an idealization of real-world conditions frequently employed in the stochastic hydrology literature (Dagan 2017).

Fig. 1

Schematic of the heterogeneous layers arranged (a) perpendicular to flow and (b) parallel to flow

3.1 Flow Perpendicular to Layers

For flow perpendicular to layers, the domain is made of N homogeneous layers of equal thickness $\Delta x$, each having an area A perpendicular to the flow direction; the i-th layer has a permeability of $k_i$ and a Forchheimer coefficient $\beta _i=\beta _i(k_i)$ given by Eq. (3a-b). By virtue of mass conservation, volumetric flux $Q=qA$ through each layer is the same; assuming that the one-dimensional version of the flow law given by Eq. (1) holds locally, the pressure difference in each layer is provided by

$$\begin{aligned} \Delta P_i = \frac{\mu q}{k_i} \Delta x+\rho \beta _i q^2 \Delta x. \end{aligned}$$

(4)

Since $\Delta x=L/N$ and $\Delta P=\sum _{i}^{n}\Delta P_i$, summing over the layers and then taking the limit as $N\rightarrow \infty$, the length of each layer tends to zero and the discrete permeability variation to a continuous one; then under ergodicity

$$\begin{aligned} \frac{\Delta P}{L} = \int _{0}^{\infty } \bigg (\frac{\mu q}{k}+\rho \beta q^2\bigg ) f(k) dk=\mu q \langle k^{-1} \rangle +\rho a q^2 \langle k^{-c}\rangle , \end{aligned}$$

(5)

where $\langle \cdot \rangle$ is the expected value, and the relationship $\beta =\beta (k)$ given by Eq. (3a-b) was employed. Eq. (5) extends to a continuous permeability distribution the discrete equation of Narayanaswamy et al. (1999). The result on the r.h.s. is valid unless f(k) is a constant, e.g. for a uniform distribution: see Appendix 1 for this case.

The effective parameters $k_{es}$ and $\beta _{es}$ for flow perpendicular to layers are defined by

$$\begin{aligned} \frac{\Delta P}{L} = \frac{\mu q}{k_{es}}+\rho \beta _{es} q^2. \end{aligned}$$

(6)

Comparison between Eqs. (6) and (5) gives for the effective parameters

$$\begin{aligned} k_{es}= \langle k^{-1} \rangle ^{-1}=k_H, \quad \beta _{es}= a\langle k^{-c} \rangle , \end{aligned}$$

(7a-b)

where $k_H$ is the harmonic mean.

3.2 Flow Parallel to Layers

In this case the porous domain is still constituted by N homogeneous layers, with the i-th layer having an area $\Delta A=A/N$ perpendicular to the direction of the external pressure gradient, a permeability $k_i$ and a Forchheimer coefficient $\beta _i=\beta _i (k_i)$ according to Eq. (3a-b). The volumetric flux $\Delta Q_i$ in the i-th layer is, solving the quadratic Eq. (1) in terms of flow rate

$$\begin{aligned} \Delta Q_i=\mu \Delta A \frac{\sqrt{1+\big (\frac{4\rho \beta _i k_i^2}{\mu ^2}\big )\big (\frac{\Delta P}{L}\big )}-1}{2\rho \beta _i k_i}. \end{aligned}$$

(8)

Summing over the layers and switching to a continuous parameter variation gives

$$\begin{aligned} Q=\mu A \int _{0}^{\infty } \Bigg (\frac{\sqrt{1+\big (\frac{4\rho \beta k^2}{\mu ^2}\big )\big (\frac{\Delta P}{L}\big )}-1}{2\rho \beta k}\Bigg )f(k) dk, \end{aligned}$$

(9)

where the quantity

$$\begin{aligned} F=\Big (\frac{4\rho \beta k^2}{\mu ^2}\Big )\Big (\frac{\Delta P}{L}\Big ) \sim \frac{\rho \beta q k}{\mu }, \quad q=Q/A, \end{aligned}$$

(10a-b)

is the dimensionless external pressure gradient, essentially a Forchheimer number, the ratio of liquid-solid interaction to viscous resistance (Ruth and Ma 1992). Substituting the expression of $\beta (k)$ given by Eq. (3a-b) gives $F=(4 \rho a k^{2-c}/ \mu ^2)(\Delta P/L)$, and Eq. (9) is not amenable to closed-form integration for the most commonly adopted formulations of the probability density function f(k), except for the uniform distribution, see Appendix C.

For $c=2$, Eq. (9) with Eq. (3a-b) gives

$$\begin{aligned} Q=\frac{\mu \langle k \rangle A}{2 \rho a} \Bigg (\sqrt{1+\bigg (\frac{4\rho a}{\mu ^2}\bigg )\bigg (\frac{\Delta P}{L}\bigg )}-1\Bigg ), \end{aligned}$$

(11)

while the flowrate in terms of the effective parameters is

$$\begin{aligned} Q=\frac{\mu A}{2 \rho \beta _e k_e} \Bigg (\sqrt{1+\bigg (\frac{4\rho \beta _e k_e^2}{\mu ^2}\bigg )\bigg (\frac{\Delta P}{L}\bigg )}-1\Bigg ). \end{aligned}$$

(12)

Comparing Eqs. (11) and (12) leads to

$$\begin{aligned} k_{ep}= \langle k \rangle =k_A, \quad \beta _{ep}= \frac{a}{\langle k\rangle ^2}, \end{aligned}$$

(13a-b)

where $k_A$ is the arithmetic mean.

For $c\ne 2$, we note that for F both small and large with respect to unity, an approximate closed-form solution for the flow rate and the effective Forchheimer coefficient can be found explicitly. In particular, for $F\ll 1$ (case 1), where the quantity F is small, but not so small that inertial effects on the flow could be disregarded, the quantity $\sqrt{1+F}$ in Eq. (9) can be approximated by its second-order Taylor’s expansion $\sqrt{1+F}\approx 1+F/2-F^2/8$. When, on the other hand, $F\gg 1$ (case 2), we assume in Eq. (9) at leading order $\sqrt{1+F}-1\approx \sqrt{F}$ and hence $Q\propto \sqrt{\Delta P/L}$ (Fourar et al. 2005), i.e. the Forchheimer term in Eq. (9) is dominant with respect to the Darcy one.

Both approximations examined may be appropriate for laboratory or field applications, depending on the fluid involved, the values of the porous medium properties, and the pressure gradient. Typically, laboratory and field measurements involve water or gas flow. In the first case, taking for the fluid properties those of water at $10^{\circ }C$ ($\rho =999.7$ $kg/m^3$, $\mu =1.337\times 10^{-3}$ $kg/m/s$), and further assuming $k=10^{-8}$ $m^2$, $\beta =50$ $m^{-1}$, $\Delta P/L=10^4$ $Pa \cdot m$ (corresponding approximately to a unit hydraulic gradient), yields $F=0.117$, while larger values of permeability, Forchheimer coefficient, and/or pressure gradient bring about larger values of F. The data reported in Moutsopoulos et al. (2009) lead to $F=1.82-2025$ (depending on the actual temperature during the experiments), those of Bordier and Zimmer (2000) to $F=0.80-44.23$, those by Wahyudi et al. (2002) to $F=0.16-5.32$. In applications involving gas flow, typically the values of the ratio $\rho /\mu ^2$, the Forchheimer coefficient $\beta$, and pressure gradient $\Delta P/L$ are decidedly higher when compared to water flow, while the permeability values are lower. Taking $\rho =1.25$ $kg/m^3$, $\mu =1.79\times 10^{-5}$ $\,kg/m/s$ for air at $10^{\circ }C$, a porous medium with $k=10^{-12}-10^{-10}\,m^2$ and $\beta =2 \cdot 10^8 - 8 \cdot 10^8 \,m^{-1}$, yields for a pressure gradient in the range $\Delta P/L=10^6-10^7 Pa / m$ a wide interval $F=75-1.87\times 10^{6}$. Values of $F=280-4.2\times 10^6$, consistently much higher than unity, are associated with the gas condensate field results of Narayanaswamy et al. (1999). The field air permeameter data of Wells et al. (2008) lead to values in the interval $F=0.03-27.97$, with five out of sixteen samples providing values of F less than one. For the laboratory measurements of Zeng and Grigg (2006), $F=4.5\times 10^{-5}-2.6\times 10^{-3}$, while for those of Cooper et al. (1998), $F=1.68\times 10^{-3}-1.28\times 10^{-1}$.

3.2.1 Low Forchheimer case ($F\ll 1$)

Substituting $\sqrt{1+F} \approx 1+F/2-F^2/8$ in Eq. (9) yields

$$\begin{aligned} Q=\frac{A}{\mu } \frac{\Delta P}{L} \int _{0}^{\infty } k \Bigg (1-\frac{\rho \beta k^2}{\mu ^2}\frac{\Delta P}{L}\Bigg )f(k) dk. \end{aligned}$$

(14)

Inserting Eq. (3a-b) in Eq. (14) gives

$$\begin{aligned} Q=\frac{A}{\mu } \frac{\Delta P}{L} \langle k \rangle - \frac{\rho A a}{\mu ^3} \bigg (\frac{\Delta P}{L}\bigg )^2 \langle k^{3-c} \rangle . \end{aligned}$$

(15)

Now taking an upscaled equation like (6) written in terms of the effective parameters for parallel-type layers in this case, namely $k_{ep1}$ and $\beta _{ep1}$, solving it for $Q=qA$ and adopting the same second-order Taylor’s approximation employed in Eq. (14), gives

$$\begin{aligned} Q=\frac{A}{\mu } \frac{\Delta P}{L} k_{ep1} - \frac{\rho A \beta _{ep1} k_{ep1}^3}{\mu ^3} \bigg (\frac{\Delta P}{L}\bigg )^2. \end{aligned}$$

(16)

Comparison between Eqs. (15) and (16) yields

$$\begin{aligned} k_{ep1}=\langle k \rangle =k_A, \quad \beta _{ep1}=a\frac{\langle k^{3-c} \rangle }{\langle k\rangle ^3}, \end{aligned}$$

(17a-b)

where $k_A$ is the arithmetic mean (Matheron 1967).

3.2.2 High Forchheimer Case ($F\gg 1$)

Performing the same steps as in the previous case and adopting in Eq. (9) the zero order approximation $\sqrt{1+F}-1\approx \sqrt{F}$ yields as counterparts of Eqs. (14)-(16) the following expressions for the approximate flow rate, the approximate flow rate incorporating the $\beta -k$ relationship, and the flow rate as a function of the effective parameters:

$$\begin{aligned} Q=A \int _{0}^{\infty } \Bigg (\frac{1}{\rho ^{1/2} \beta ^{1/2}} \bigg (\frac{\Delta P}{L}\bigg )^{1/2}\Bigg )f(k) dk, \end{aligned}$$

(18)

$$\begin{aligned} Q=A \int _{0}^{\infty } \Bigg (\frac{1}{\rho ^{1/2} a^{1/2}} \langle k^{c/2} \rangle \bigg (\frac{\Delta P}{L}\bigg )^{1/2}\Bigg )f(k) dk, \end{aligned}$$

(19)

$$\begin{aligned} Q=A \int _{0}^{\infty } \Bigg (\frac{1}{\rho ^{1/2} \beta _{ep2}^{1/2}}\bigg (\frac{\Delta P}{L}\bigg )^{1/2}\Bigg )f(k) dk. \end{aligned}$$

(20)

Comparison between Eqs. (19) and (20) yields the effective Forchheimer coefficient for $F\gg 1$ as

$$\begin{aligned} \beta _{ep2}= \frac{a}{\langle k^{c/2}\rangle ^2}. \end{aligned}$$

(21)

For $c=2$, the approximate result given by Eq. (21) is equal to the exact one provided by Eq. (13a-b).

3.3 Effective Parameters $\beta _{es}$, $\beta _{ep1}$, $\beta _{ep2}$ for given Permeability Distribution

The effective parameters are evaluated for two given PDFs of permeability, the lognormal and the gamma distributions, both suitable to represent non-negative permeability distributions. Their expressions are illustrated in Appendices A and B, respectively.

Utilizing Eqs. (7a-b), (17a-b), and (21) with the distributions of Eqs. (A1) and (B2) provides the following expressions of effective parameters for the lognormal (Eqs. (22a-b)-(24)) and gamma distributions (Eqs. (25a-b)-(27)) and flow perpendicular or parallel to layers; in the latter case, results for low Forchheimer ($F\ll 1$) and high Forchheimer ($F\gg 1$) are reported.

Lognormal PDF:

$$\begin{aligned} k_{es}&= k_G \exp {\bigg (-\frac{\sigma _y^2}{2}\bigg )}, \quad \beta _{es} =\frac{a}{k_G^c}\exp {\bigg (c^2\frac{\sigma _y^2}{2}\bigg )}, \end{aligned}$$

(22a-b)

$$\begin{aligned} k_{ep1}= k_G \exp {\bigg (\frac{\sigma _y^2}{2}\bigg )}, \quad \beta _{ep1} =\frac{a}{k_G^c}\exp {\bigg ((c^2-6c+6)\frac{\sigma _y^2}{2}\bigg )}, \end{aligned}$$

(23a-b)

$$\begin{aligned} \beta _{ep2}=\frac{a}{k_G^c}\exp {\bigg (-c^2\frac{\sigma _y^2}{4}\bigg )}. \end{aligned}$$

(24)

Gamma PDF:

$$\begin{aligned} k_{es}= \theta (\alpha -1), \quad \beta _{es}= \frac{\alpha }{\theta ^c} \frac{\Gamma (\alpha -c)}{\Gamma (\alpha )}, \end{aligned}$$

(25a-b)

$$\begin{aligned} k_{ep1}= \alpha \theta , \quad \beta _{ep1}=\frac{\alpha }{\theta ^c} \frac{\Gamma (\alpha +3-c)}{\alpha ^3\Gamma (\alpha )}, \end{aligned}$$

(26a-b)

$$\begin{aligned} \beta _{ep2}=\frac{\alpha }{\theta ^c} \frac{\big (\Gamma (\alpha )\big )^2}{\big (\Gamma (\alpha +\frac{c}{2})\big )^2}. \end{aligned}$$

(27)

3.4 Numerical Evaluation of Effective Forchheimer Coefficient $\beta _{epN}$ for Flow Parallel to Layers and any F

Considering the specific flow rate $q=Q/A$ directly, Eq. (9) can be rearranged as

$$\begin{aligned} q=\frac{\mu }{2 \rho a} \int _{0}^{\infty } k^{c-1} \Bigg (\sqrt{1+\bigg (\frac{4\rho a}{\mu ^2} k^{2-c} \frac{\Delta P}{L}\bigg )}-1\Bigg )f(k)dk. \end{aligned}$$

(28)

For $c=1$, Eq. (28) is amenable to a simpler solution for the lognormal distribution and a closed-form solution for the gamma distribution; these are reported in Appendix D. In general, once q is evaluated numerically from Eq. (28) for a given permeability distribution, the numerical effective Forchheimer coefficient $\beta _{epN}$ for the parallel-type layers will be

$$\begin{aligned} \beta _{epN}=\frac{1}{\rho q^2} \frac{\Delta P}{L}-\frac{\mu }{\langle k \rangle \rho q}. \end{aligned}$$

(29)

Note from Eq. (29) that, in variance with Eq. (7a-b) for flow perpendicular to layers, the effective Forchheimer coefficient for flow parallel to layers depends on the boundary conditions.

4 Discussion of Results

The effective properties, permeability and Forchheimer coefficient, are functions of the parameters describing heterogeneity. While the results for effective permeability recover well-known results (Matheron 1967; Sanchez-Vila et al. 2006), those for the effective Forchheimer coefficient are novel. Some general tendencies of its behavior are evident from Eqs. (22a-b)-(27): (i) for flow perpendicular to layers, the effective Forchheimer coefficient increases with increasing heterogeneity; (ii) the same is true for flow parallel to layers and low Forchheimer number; (iii) the reverse is true for flow parallel to layers and high Forchheimer number; (iv) the shape of the distribution does not influence the aforementioned tendencies; (v) the parameter c influences the effective Forchheimer coefficient for serial and parallel arrangements in a non-trivial way.

4.1 Analytical Results for Flow Perpendicular or Parallel to Layers

We express Eqs. (22a-b)-(27) in the dimensionless form

$$\begin{aligned} \hat{k}_{e}= \frac{k_e}{\langle k \rangle }, \quad \hat{\beta }_{e}&=\frac{\beta _e}{a\langle k \rangle ^{-c}}, \end{aligned}$$

(30a-b)

adopting as a scale for $\beta _e$ the value of the effective Forchheimer coefficient would take if the correlation given by Eq. (3a-b) was applied to a representative permeability equal to the mean value $\langle k \rangle$ of the random permeability field. One then obtains for the lognormal distribution and gamma distribution the following expressions:

Lognormal PDF:

$$\begin{aligned} \hat{k}_{es}= \exp {\big (-\sigma _y^2\big )}, \quad \hat{\beta }_{es} =\exp {\bigg (c(c+1)\frac{\sigma _y^2}{2}\bigg )}, \end{aligned}$$

(31a-b)

$$\begin{aligned} \hat{k}_{ep1}= 1, \quad \hat{\beta }_{ep1} =\exp {\bigg ((3-c)(2-c)\frac{\sigma _y^2}{2}\bigg )}, \end{aligned}$$

(32a-b)

$$\begin{aligned} \hat{\beta }_{ep2}=\exp {\bigg (c(2-c)\frac{\sigma _y^2}{4}\bigg )}, \end{aligned}$$

(33)

Gamma PDF:

$$\begin{aligned} \hat{k}_{es}= \frac{\alpha -1}{\alpha }, \quad \hat{\beta }_{es}= \alpha ^c \frac{\Gamma (\alpha -c)}{\Gamma (\alpha )}, \end{aligned}$$

(34a-b)

$$\begin{aligned} \hat{k}_{ep1}= 1, \quad \hat{\beta }_{ep1}= \frac{\Gamma (\alpha +3-c)}{\alpha ^{3-c}\Gamma (\alpha )}, \end{aligned}$$

(35a-b)

$$\begin{aligned} \hat{\beta }_{ep2}=\alpha ^c \frac{\big (\Gamma (\alpha )\big )^2}{\big (\Gamma (\alpha +\frac{c}{2})\big )^2}. \end{aligned}$$

(36)

Specific expressions of the effective Forchheimer coefficient for special values of c are listed in Table 1.

Table 1 The effective Forchheimer coefficient for $c=0.0$, 0.5, 1.0, 1.5, and 2.0

In the following, the dimensionless effective Forchheimer coefficient $\hat{\beta }_e$ for flow perpendicular and parallel to layers is illustrated as a function of the permeability coefficient of variation $C_{vk}=\sigma _k/\langle k \rangle$ for the lognormal and gamma distributions (see Appendix A and Appendix B). Note that for a lognormal distribution the classical upper limit of validity of the first-order approximation in stochastic hydrology, $\sigma _y^2=\sigma _Y^2=1$, corresponds to $C_{vk}=1.31$, and conversely $C_{vk}=1$ is equivalent to $\sigma _y^2=0.693$. The deviation of $\hat{\beta }_e$ from unity represents the relative error made upon adopting the correlation Eq. (3a-b) and the mean permeability to evaluate $\beta _e$.

Figures 2, 3 and 4 show $\hat{\beta }_e$ as a function of $C_{vk}$ for different values of exponent c and for the lognormal and gamma distributions, respectively for flow perpendicular to layers, parallel to layers with low Forchheimer number (case 1), and parallel to layers with high Forchheimer number (case 2).

Fig. 2

Dimensionless effective Forchheimer coefficient $\hat{\beta }_{es}$ for flow perpendicular to layers as a function of the permeability coefficient of variation $C_{vk}$, for different values of exponent c for (a) lognormal and (b) gamma distribution

Figure 2a and b depict the effective Forchheimer coefficient for lognormal and gamma distributions for flow perpendicular to layers. The effective Forchheimer coefficient $\hat{\beta }_{es}$ increases as a function of increasing heterogeneity (higher $C_{vk}$); an increase in the value of c has a similar effect. For $c=0$ (no correlation between $\beta$ and k), the effective Forchheimer coefficient coincides with the value calculated inserting the mean permeability in the empirical relationship Eq. (3a-b).

Even for flow parallel to layering (Figs. 3 and 4), as the heterogeneity grows, the value of $\hat{\beta }_{ep1}$ and $\hat{\beta }_{ep2}$ increases. However, unlike in serial geometry, the increase in the coefficient c corresponds to a smaller rise of $\hat{\beta }_{ep1}$ and $\hat{\beta }_{ep2}$ as $C_{vk}$ grows; in this case, a value $c=0$ corresponds to the maximum difference between the value of the actual Forchheimer coefficient and its local value. The values of $\hat{\beta }_{ep2}$ are smaller than that of $\hat{\beta }_{ep1}$, showing that the high Forchheimer case implies smaller upscaled $\beta _e$. We remark that the estimation of high Forchheimer values for $c=0.5$ and $c=1.5$, shown by a solid line and black dots in Fig. 4a, are identical, as is evident from Eq. (33).

Fig. 3

Effective dimensionless Forchheimer coefficient $\hat{\beta }_{ep1}$ for flow parallel to layers ($F\ll 1$ or case 1), as a function of the permeability coefficient of variation $C_{vk}$, for different values of exponent c for (a) lognormal and (b) gamma distribution

Finally, upon comparing the results relating to the two adopted distributions in the two limit cases of low and high Forchheimer numbers, it is noted that with the same $C_{vk}$ and the value of the exponent c, for flow perpendicular to layering the values of $\beta _{e}$ for the lognormal distribution are lower than those for the gamma distribution; the reverse is true for flow parallel to layering. The differences between distributions are modest for low-Forchheimer numbers and more significant for high-Forchheimer numbers. We note that in the low Forchheimer number regime (see Fig. 3), the calculated value of $\beta _{e}$ for $c=1$ is identical for the lognormal and gamma distributions.

Fig. 4

Effective dimensionless Forchheimer coefficient $\hat{\beta }_{ep2}$ for flow parallel to layers (high Forchheimer number or case 2), as a function of the permeability coefficient of variation $C_{vk}$, for different values of exponent c for a lognormal and b gamma distribution

4.2 Numerical Estimation of Parallel Flow

We assume water as the reference fluid ($\rho =1000\,kg/m^3$, $\mu =10^{-3}\,Pa \cdot s$), and a mean permeability $\langle k \rangle =10^{-10}\,m^2$ to perform the numerical integration of Eq. (28). The realistic values of $a=361480\,[-],71274432\,m,187724450\,m^2$ are considered for $c=[0.5,1.0,1.5]$, respectively, as discussed in Sec. 2.2. In addition, the pressure gradient is taken to be $\Delta P/L=400\,Pa/m$. We then introduce a further set of dimensionless parameters for the numerical estimation of the Forchheimer coefficient of the parallel-layer case as

$$\begin{aligned} \hat{q}= \frac{\rho q \langle k \rangle ^{1/2}}{\mu }, \quad \hat{a} = \frac{a}{\langle k \rangle ^{c-1/2}}, \quad \widehat{\frac{\Delta P}{L}}= \frac{\rho \langle k \rangle ^{3/2}}{\mu ^2}\frac{\Delta P}{L}, \end{aligned}$$

(37 a-c)

where $\hat{q}$, $\widehat{\frac{\Delta P}{L}}$, and $\hat{a}$ are normalized flow rate, pressure gradient, and proportionality constant a, respectively. Then, Eq. (28) can be written in terms of the dimensionless parameters of Eqs. (30a-b) and (37a-c) as

$$\begin{aligned} \hat{q}=\frac{1}{2\hat{a}} \int _{0}^{\infty } (\hat{k}_{epN})^{c-1} \Bigg (\sqrt{1+\bigg (4\hat{a}\widehat{\frac{\Delta P}{L}}(\hat{k}_{epN})^{2-c}\bigg )}-1\Bigg )f(\hat{k}_{epN})d\hat{k}_{epN}. \end{aligned}$$

(38)

Eq. (38) can be specialized for the lognormal distribution as

$$\begin{aligned} \begin{aligned} \hat{q}=&\frac{1}{2\hat{a}} \int _{0}^{\infty } (\hat{k}_{epN})^{c-1} \Bigg (\sqrt{1+\bigg (4\hat{a}\widehat{\frac{\Delta P}{L}} (\hat{k}_{epN})^{2-c}\bigg )}-1\Bigg )\\&\frac{1}{\hat{k}_{epN} \sigma _y \sqrt{2 \pi }} \exp \Bigg [-\frac{\big (\ln \big (\hat{k}_{epN} \exp {\big (\frac{\sigma _y^2}{2}\big )}\big )\big )^2}{2 \sigma _y^2}\Bigg ]d\hat{k}_{epN}, \end{aligned} \end{aligned}$$

(39)

and for Gamma distribution by substituting Eq. (B3) and $C_{vk}=\sigma _k/\langle k \rangle$

$$\begin{aligned} \begin{aligned} \hat{q}=&\frac{1}{2\hat{a}} \int _{0}^{\infty } (\hat{k}_{epN})^{c-1} \Bigg (\sqrt{1+\bigg (4\hat{a}\widehat{\frac{\Delta P}{L}} (\hat{k}_{epN})^{2-c}\bigg )}-1\Bigg )\\&\frac{(\hat{k}_{epN})^{\frac{1}{C_{vk}^2}-1} e^{-\frac{\hat{k}_{epN}}{C_{vk}^2}}}{(C_{vk}^2)^\frac{1}{C_{vk}^2} \Gamma \left( \frac{1}{C_{vk}^2}\right) }d\hat{k}_{epN}. \end{aligned} \end{aligned}$$

(40)

The dimensionless effective Forchheimer coefficient for the parallel-type layers obtained from the direct numerical analysis is derived by substituting the dimensionless parameters of Eq. (30a-b) and Eqs. (37a-c) into Eq. (29), as:

$$\begin{aligned} \hat{\beta }_{epN}=\frac{1}{\hat{a}}\bigg (\frac{1}{\hat{q}^2} \widehat{\frac{\Delta P}{L}}-\frac{1}{\hat{q}}\bigg ). \end{aligned}$$

(41)

The outcomes of the direct numerical integration are shown in Fig. 5 for $\widehat{\frac{\Delta P}{L}}=0.0004$, $c=0.5,1.0,1.5$, and their corresponding a values, where the left and right panels depict the lognormal and gamma PDFs, respectively. For $c=0.5$ and for both distribution functions, the effective Forchheimer coefficient obtained from the direct numerical integration $\hat{\beta }_{epN}$ approaches to the high Forchheimer number estimation $\hat{\beta }_{ep2}$. For the cases $c=1.0$ and $c=1.5$, the numerical results are almost identical to the high Forchheimer approximation.

Fig. 5

Effective dimensionless Forchheimer coefficient $\hat{\beta }_{ep}$ for flow in heterogeneous layers arranged in parallel as a function of the permeability coefficient of variation $C_{vk}$, for $c=0.5,1.0,1.5$, for lognormal (left panels) and gamma distribution (right panels). The numerical results obtained from the integration of Eq. (41) are shown compared with their corresponding low and high Forchheimer number approximation

We then perform a parametric study on the pressure gradient and proportionality parameter a to analyze their impact on the numerical evaluation of the effective Forchheimer coefficient for flow parallel to layers considering $c=0.5$, the most common value in the literature (Ergun 1952). Figure 6a and b show the effective Forchheimer coefficient for $\widehat{\frac{\Delta P}{L}}=0.0001,0.0004,0.0020$ (or equivalently $\frac{\Delta P}{L}=100,400,2000\,Pa/m$) upon assuming a constant value of $\hat{a}=361480$.

For the larger pressure gradients, the numerical estimation approaches the high Forchheimer approximation ($F\gg 1$). Figure 6c and d highlight the variation of $\hat{a}=36148,361480,3614800$ where $\widehat{\frac{\Delta P}{L}}=0.0004$ (or equivalently $\Delta P/L=400\,Pa/m$) is assumed to be constant. In this case, larger $\hat{a}$ values produce $\hat{\beta }_{epN}$ values very close to the high Forchheimer approximation. The trends are similar for both distribution functions, while the actual values of $\hat{\beta }_{epN}$ are higher for the lognormal distribution.

Fig. 6

Dimensionless effective Forchheimer coefficient $\hat{\beta }_{epN}$ for flow in heterogeneous layers arranged in parallel as a function of the permeability coefficient of variation $C_{vk}$ and $c=0.5$, considering the variation of pressure gradient and assuming $\hat{a}=361480$ as a constant in panels (a) and (b); and for constant pressure gradient case $\widehat{\frac{\Delta P}{L}}=0.0004$ considering the variation of $\hat{a}$ in (c) and (d). Left panels represent the outcomes of the lognormal distribution, and right panels represent gamma distribution results. Low ($\hat{\beta }_{ep1}$) and high Forchheimer approximation ($\hat{\beta }_{ep2}$) results are over-imposed to the figures

5 Conclusions

Nonlinear seepage in heterogeneous, perfectly layered porous media is investigated in this work with the aim of deriving expressions for the effective permeability and effective Forchheimer coefficient. The local Forchheimer coefficient is expressed as a function of the local permeability value with an inverse power relationship of exponent c and constant of proportionality a.

The effective permeability for flow perpendicular or parallel to layers coincides respectively with the harmonic and arithmetic mean, and therefore decreases or increases as the heterogeneity of the domain increases. The increase in heterogeneity determines an increase in the effective Forchheimer coefficient for all setups and dimensionless parameters. Its value is always larger than that it would take if the $\beta - k$ correlation was applied to the mean permeability. The effective $\beta$ increases (decreases) with increasing (decreasing) exponent c for flow perpendicular (parallel) to layers. The influence of the permeability distribution adopted is most evident for flow perpendicular to layers and the high Forchheimer limit for flow parallel to layers: in both cases, the gamma distribution yields larger values of the effective Forchheimer coefficient than the lognormal. When realistic values of the pressure gradient and of the a parameter are adopted, the effective Forchheimer coefficient for flow parallel to layers is very close or identical to the result of the high Forchheimer approximation ($F\gg 1$). For flow parallel to layers, the effective Forchheimer coefficient depends on boundary conditions, in variance with the effective permeability. The outcomes of this work, despite model simplifications, provide additional insight into nonlinear effects on flow in heterogeneous porous media, emphasizing the sensitivity of the effective Forchheimer coefficient to heterogeneity.

A desirable extension is the determination of the effective Forchheimer coefficient for two- and three-dimensional geometry, to be obtained either: (i) via a conjecture, assuming that the effective Forchheimer coefficient for a 2-D isotropic domain is the weighted average (geometric mean) of the results obtained for the two limit geometries (flow perpendicular and parallel to layers) examined here; the conjecture extends to the Forchheimer coefficient the procedure classically adopted for the effective permeability, equal to the geometric mean in 2-D; (ii) by composing the 1-D expressions to model flow geometries at the field scale that are intermediate between the two limit situations of motion parallel and perpendicular to the medium stratification; or (iii) by means of appropriate formal developments in line with the theory of composites. In all cases, results can then be validated via Monte Carlo simulations. A further avenue for validation is the comparison of $\beta$ values obtained at the laboratory scale with larger values obtained in the field.

Appendices

Appendix A The Lognormal Distribution

The lognormal distribution has the form

$$\begin{aligned} f(k)=\frac{1}{k \sigma _y \sqrt{2 \pi }} \exp \Bigg [-\frac{\big (\ln (\frac{k}{k_G})\big )^2}{2 \sigma _y^2}\Bigg ], \end{aligned}$$

(A1)

where $k_G=\langle k \rangle \exp (-\sigma _y^2/2)$ is the geometric mean, $\langle k \rangle$ the expected value and $\sigma _y^2$ the variance of $y=\ln {k}$. The permeability variance is $\sigma _k^2=\langle k \rangle ^2 (e^{\sigma _y^2}-1)=k_G^2e^{\sigma _y^2} (e^{\sigma _y^2}-1)$, and the coefficient of variation is $C_{vk}=\sqrt{e^{\sigma _y^2}-1}$.

Appendix B The Gamma Distribution

The gamma distribution with a zero lower bound of permeability takes the form (Loáiciga et al. 2006)

$$\begin{aligned} f(k)=\frac{k^{\alpha -1} e^{-k/\theta }}{\theta ^\alpha \Gamma (\alpha )}, \end{aligned}$$

(B2)

where $\alpha$ and $\theta$ ($\alpha ,\theta >0$) are the shape and scale parameters, respectively, and $\Gamma (\cdot )$ is the gamma function; its mean and variance are given respectively by $\langle k \rangle =\alpha \theta$ and $\sigma _k^2=\alpha \theta ^2$; the coefficient of variation is $C_{vk}=\sqrt{1/\alpha }$. For $\alpha =1$, Eq. (B2) reduces to the exponential distribution.

An alternative expression of the gamma distribution (B2) as a function of its mean $\langle k \rangle$ and variance $\sigma _k^2$ is

$$\begin{aligned} f(k)=\frac{k^{\frac{\langle k \rangle ^2}{\sigma _k^2}-1} e^{-\frac{k\langle k \rangle }{\sigma _k^2}}}{\left( \frac{\sigma _k^2}{\langle k \rangle }\right) ^{\frac{\langle k \rangle ^2}{\sigma _k^2}} \Gamma \left( \frac{\langle k \rangle ^2}{\sigma _k^2}\right) }. \end{aligned}$$

(B3)

Appendix C Results for the Uniform Distribution

The continuous uniform distribution on support $[k_1,k_2]$ takes the form

$$\begin{aligned} f(k)=\frac{1}{k_2-k_1}\quad \text {for}\quad k_1\le k\le k_2,\quad 0\quad \text {for}\quad k<k_1\quad \text {or}\quad k>k_2; \end{aligned}$$

(C4)

the mean and variance are given respectively by $\langle k \rangle =(k_1+k_2)/2$ and $\sigma _k^2=1/[12(k_2-k_1)^2]$; the coefficient of variation is $C_{vk}=(k_2-k_1)/[\sqrt{3}(k_1+k_2)]$.

For flow perpendicular to layers and $c\ne 1$, Eq. (5) becomes

$$\begin{aligned} \frac{\Delta P}{L} = \frac{1}{k_2-k_1}\left[ \mu q\ln {\left( \frac{k_2}{k_1}\right) }+\frac{\rho a q^2 (k_2^{1-c}-k_1^{1-c})}{(1-c)(k_2-k_1)}\right] , \end{aligned}$$

(C5)

and the effective parameters are by comparison with Eq. (6):

$$\begin{aligned} k_{es}= \frac{k_2-k_1}{\ln {\left( k_2/k_1\right) }}, \quad \beta _{es}= \frac{a (k_2^{1-c}-k_1^{1-c})}{(1-c)(k_2-k_1)}, \end{aligned}$$

(C6a-b)

while for $c=1$, Eq. (C5) gives

$$\begin{aligned} \frac{\Delta P}{L} = \frac{1}{k_2-k_1}\left[ \mu q\ln {\left( \frac{k_2}{k_1}\right) }+\frac{\rho a q^2 \ln {\left( k_2/k_1\right) }}{(k_2-k_1)}\right] , \quad \beta _{es}= \frac{a \ln {\left( k_2/k_1\right) }}{k_2-k_1}. \end{aligned}$$

(C7a-b)

For flow parallel to layers, Eq. (9) with Eq. (3a-b) gives (Wolfram 2022),

$$\begin{aligned} q=\dfrac{\mu }{2\rho a c (k_2-k_1)}\left[ k^c\left( _2F_1\left( -\frac{1}{2},\frac{c}{2-c};\frac{2}{2-c};-F\right) -1\right) \right] ^{k_2}_{k_1},\,F=\frac{4\rho a k^{2-c}}{\mu ^2} \frac{\Delta P}{L} \end{aligned}$$

(C8a-b)

where F is the Forchheimer number, k is a dummy variable, $_2F_1(\cdot ,\cdot ;\cdot ;\cdot )$ is the hypergeometric function of parameters $-1/2$, $c/(2-c)$, $2/(2-c)$ and argument F and the transformation formulae (9.130) in Gradshteyn and Rhyzik (1994) can be used for analytic continuation if $F>1$, as $_2F_1$ in Eq. (C8a-ba) converges in the entire unit circle. Comparing Eqs. (C8a-ba) and (12) leads to numerically determined values of $k_{ep}$ and $\beta _{ep}$ for any c.

For a lower limit of the distribution $k_1=0$, a possible and likely case being k the permeability, Eq. (C8a-ba) simplifies to

$$\begin{aligned} q=\dfrac{\mu }{2\rho a c k_2^{1-c}}\left[ _2F_1\left( -\frac{1}{2},\frac{c}{2-c};\frac{2}{2-c};-F\right) -1\right] . \end{aligned}$$

(C9)

In turn, Eq. (C9) further reduces to (Wolfram 2022)

$$\begin{aligned} q=\dfrac{\mu }{2\rho a}\left[ \dfrac{2}{3 Z_1}\left( (1+Z_1)^{3/2}-1\right) -1\right] ,\,Z_1=\frac{4\rho a k_2}{\mu ^2} \frac{\Delta P}{L}=2\langle F_1 \rangle , \end{aligned}$$

(C10a-b)

$$\begin{aligned} q=\dfrac{\mu k_2^{1/2}}{3\rho a}\left[ \dfrac{2}{35 Z_{3/2}^2}\left( (1+Z_{3/2})^{3/2}\left( 8-12Z_{3/2}+15Z_{3/2}^2\right) -8\right) -1\right] ,\,Z_{3/2}=\frac{4\rho a k_2^{1/2}}{\mu ^2} \frac{\Delta P}{L} \end{aligned}$$

(C11a-b)

respectively for $c=1$ and $c=3/2$, and to Eq. (11) (see (15.1.8) in Abramowitz and Stegun 1972) for $c=2$; see Eq. (D14a) for the definition of <F₁>. In Eqs. (C10a-b) and (C11a-b), $Z_1$ and $Z_{3/2}$ are modified forms of the Forchheimer number for the uniform distribution, see also Eqs. (D14a-b-c) in Appendix 1.

Appendix D Flow Rate Parallel to Layers, $c=1$, Lognormal and Gamma Distributions

For $c=1$, the specific flowrate q in Eq. (28) takes the following simpler form for the lognormal distribution (A1) after a change of variable

$$\begin{aligned} q=\frac{\mu }{2 \rho a} \left[ \frac{1}{\sigma _y \sqrt{2\pi }}\int _{-\infty }^{\infty } \left( 1+Z_l\, e^u\right) ^{1/2} e^{-u^2/(2\sigma _y^2)}du-1\right] , \end{aligned}$$

(D12)

and the following closed-form expression for the gamma distribution (B2) (see eq. (3.383.5) in Gradshteyn and Rhyzik 1994)

$$\begin{aligned} q=\frac{\mu }{2 \rho a} \left[ Z_g^{-\alpha } \Psi \left( \alpha ,\alpha +3/2;Z_g^{-1}\right) -1\right] , \end{aligned}$$

(D13)

where

$$\begin{aligned} \langle F_1 \rangle =\frac{4\rho a \langle k \rangle }{\mu ^2} \frac{\Delta P}{L},\quad Z_l=\frac{\langle F_1 \rangle }{1+C_{vk}^2},\quad Z_g=\langle F_1 \rangle C_{vk}^2 \end{aligned}$$

(D14a-b-c)

are the expected value of the Forchheimer number for $c=1$ and its modified values for the lognormal and gamma distributions, respectively; $\Psi (\cdot ,\cdot ;\cdot )$ is the degenerate hypergeometric function, and $\alpha =1/C_{vk}^2$. Using identities (8.331), (8.338.2), (8.338.3) and (9.210.2) in Gradshteyn and Rhyzik (1994) allows rewriting Eq. (D13) as

$$\begin{aligned} \begin{aligned} q_{1g}(\langle F_1 \rangle ,C_{vk})=&\frac{\mu }{2 \rho a} \left[ \frac{\Gamma (\alpha +1/2)}{\Gamma (\alpha )}Z_g^{1/2} \Phi \left( -1/2,1/2-\alpha ;Z_g^{-1}\right) +\right. \\ {}&\left. +\frac{\Gamma (1/2-\alpha )}{\sqrt{\pi }(2\alpha +1)}Z_g^{-\alpha }\Phi \left( \alpha ,\alpha +3/2;Z_g^{-1}\right) -1\right] , \end{aligned} \end{aligned}$$

(D15)

where $\Phi (\cdot ,\cdot ;\cdot )$ is the confluent hypergeometric function. The same expression may be obtained also via the following steps: (i) integrating Eq. (28) with the gamma distribution (B2) obtaining the result reported in (3.383.5) of Gradshteyn and Rhyzik (2007), including generalized binomial coefficients and generalized Laguerre polynomials, both containing real, non-integer values; (ii) transforming the binomial coefficients into gamma functions via (3.1.2) and (6.1.5) in Abramowitz and Stegun (1972) and the Laguerre polynomials into confluent hypergeometric functions via (8.972.1) in Gradshteyn and Rhyzik (2007); (iii) simplify the resulting expressions via (8.331), (8.334.3), (8.338.2), and (8.338.3) in Gradshteyn and Rhyzik (2007).