1 Introduction

Pore pressure reduction during production from a reservoir can result in effective stress increase (Xiao et al. 2016). The compression effect due to increase in effective stress can have a dramatic influence on the rock properties including permeability, and hence, permeability becomes a pressure-dependent property (Lv et al. 2013; Feng et al. 2016). The pressure-dependent permeability is probably the most pronounced parameter in tight sandstone (Warpinski and Teufel 1989; Bhandari et al. 2015; Pengpeng et al. 2014; Zhang et al. 2015). Tight gas productivity is directly related to interactions between pore pressure variation, reservoir permeability and porosity. In most cases, the porosity loss due to compression may be ignored (Huo and Benson 2016; Schutjens et al. 2004). Pressure-dependent permeability can play a significant role in well production performance (Jones and Owens 1980; Lorenz 1999; Zhang et al. 2014).

The experiments show that permeability of tight sandstone samples can experience great loss due to increase in effective stress (Lorenz 1999; Dou et al. 2015). A wide range of rock properties contributes to the tight sandstone permeability, including shale content, pore structure, rock skeleton structure, rock mineral composition, initial permeability, microfractures and clay cement (Gangi 1978; Boosari et al. 2016; Schmitt et al. 2015; Ostad et al. 2016). As tight gas production had an unprecedented growth over the past few years, the pressure-dependent permeability and its impacts on gas productivity, well testing, reservoir simulation and total recovery have received more attention (Chen et al. 2015; Ostensen 1986; Aguilera 1999).

The sensitivity of permeability to stress is variable in different types of rocks. The laboratory investigation of permeability change with stress indicates that permeability may reduce up to 90% (Sun et al. 2004; McKee et al. 1988; Ma et al. 2012). In these experiments, most researches focused on permeability reduction in micro- or natural fractures, but not matrix permeability. Caulk et al. (2016) found that the influence of stress on permeability of a core sample with microfractures is more significant than matrix permeability. Meanwhile, a similar method is reported by Walsh (1981) to predict the permeability reduction due to fracture closure mechanism. It was found that matrix permeability in tight sandstone reservoirs is also sensitive to effective stress (Duan et al. 2014; Zhang et al. 2015).

The pressure-dependent permeability is generally expressed by relations between permeability and effective stress of the rock (Bernabe 1986; David et al. 1994; Karacan 2010; Dong et al. 2010). The pressure-dependent permeability models can be summarized as exponential type, power type, logarithmic type, binomial type and hybrid type (combination of these four types). Different models can depict different permeability performances of rocks. While there is few microfracture and the pore system is well connected, the pressure-dependent permeability of tight sandstone can be well described by the exponential and binomial models (Jones and Owens 1980; Zhang et al. 2015). When the mixed-layered mineral is the main clay cement and there are microfractures in the rock, the power model and logarithmic model may describe the relationship between of permeability and effective stress (Chen and Bai 1998). For example, the Walsh model is a combined model of power type and logarithmic type, which can predict permeability change in naturally fractured rocks (Walsh 1981; Xiao et al. 2016). The experimental procedures for determination of pressure-dependent permeability of tight sandstone core samples have been well developed (Zhao et al. 2011; Sander et al. 2016). Mostly, the current models for prediction of pressure-dependent permeability are empirically obtained (Xiao et al. 2016). These empirical models, which are based on experiments, cannot reflect the stress influence on pore deformation and the deformation effects on pressure-dependent permeability. Hence, a theoretical model is still needed to explain relation between permeability and pore pressure change.

The pressure-dependent permeability contributes to the well productivity loss (Vairogs et al. 1971; Jones and Owens 1980; Lorenz 1999; Dou et al. 2015; Zhang et al. 2015). Cho et al. (2012) performed reservoir simulation and production history matching for tight sandstone reservoirs and concluded that pressure-dependent permeability has a slight influence on well productivity. In addition, most experiments change the confining pressure to conduct pressure-dependent permeability tests. However, confining pressure change in the laboratory does not replicate the reservoir condition and it will overestimate sensitivity of permeability to stress (Li et al. 2014). Thus, the confining pressure change should be transformed to pore pressure change based on the effective stress theory. According to the Biot theory and the nonlinear effective stress theory (Bernabe 1986; Li et al. 2009), the effective stress coefficient of each core is not the same and it is difficult to measure (Li et al. 2009, 2014).

With reference to pressure-dependent permeability of tight sandstone, there are two fronts remaining to be resolved. First, how to identify the stress state of core which can represent stress state in reservoir. Since the transformation of stress condition by effective stress theory is not a direct method, the evaluation test is necessary to be performed with pore pressure changing instead of confining pressure. Second, how to model the permeability reflecting the stress effects. Since the relation between permeability and pore pressure is described by various empirical formulas, there is a need for an analytical model to develop.

In this study, a range of pressure-dependent permeability tests are performed on tight sandstone core samples of the Ordos Basin, China, using a modified procedure. Then, a semi-analytical model is developed to predict pressure-dependent permeability of cores in the laboratory. This model is verified by 8 cores of our experiment result and available results of 16 cores from the literature. Then, regression results of these 24 cores were compared by exponential model, power model, logarithmic model, binomial model, the combination model and the new model. The objectives of this research are (1) to improve the permeability sensitivity experiment and evaluation method (2) and to explore the theoretical relation between permeability and fluid pressure.

2 Experiment and Permeability Model

2.1 The Cores and Gas Reservoir Background

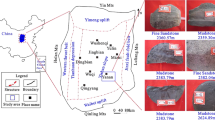
Tight sandstone core samples were taken from upper Paleozoic Shanxi Formation and Xiashihezi Formation, in the South Ordos Basin. The overburden pressure and initial pore pressure of the tight gas reservoir are 67.85 and 35.42 MPa, respectively. The cores were obtained mostly parallel to the bedding plane to represent the flow condition in reservoir. All cores were cut cylindrically into 1 inch of diameter sections, and the length of the cores varied from 1.9 to 2.2 inches. The average length was approximately 2 inches. The samples are jacked in the heat shrinkable polyolefin tube. Eight samples are labeled as Erdos-4-7, Erdos-4-8, Erdos-4-9, Erdos-5-1, Erdos-5-3, Erdos-5-4, Erdos-36 and Erdos-44 and are utilized in our experiment to observe the permeability response to change in effective stress.

The Young modulus of elasticity of Erdos-4-7, Erdos-4-9, Erdos-36 and Erdos-44 was obtained after the pressure-dependent permeability experiment by core rock mechanics test, having an average value of 43.57 GPa. The initial porosity was tested by the CMS-300 Automated Permeameter without confining pressure at room temperature. Table 1 lists rock type, density, collected depth and basic parameter of 8 cores.

Table 1 Description of tight sandstone samples for basic parameter
Full size table

The purpose of this experimental study is not only to generate rigorous data to show the pressure-dependent permeability under reservoir stress condition, but also to verify the theoretical model developed to identify the relationship between permeability and pore pressure changes.

2.2 Experiment Procedures

Figure 1 indicates the experiment apparatus to measure pressure-dependent permeability of core samples. This permeability measurement system included nitrogen gas tank, gas pump, inlet and outlet pressure gages, core holder, confining pressure system, flow meter and the calculation system. The confining pressure system consisted of a confining pressure gage, a pump and a valve. The minimum scale of pressure gauge is 0.05 MPa, and the confining pressure pump can provide 100 MPa pressure. The flow influx of nitrogen was measured by a digital gas flowmeter ranging between 1.0 and 500.0 ml/min. The accuracy of the flowmeter is 0.2 ml/min. The back pressure valve can provide 0.101–25 MPa outlet pressure in the core holder, which can simulate the pore pressure in the gas reservoir.

A data acquisition system and computer program were used to collect experimental data and measure permeability variation with pore pressure changes in core samples. The digital flow meter, inlet and outlet pressure gauges were directly connected to the computer, and the software can automatically calculate the permeability under different stress conditions.

Fig. 1
figure 1

The schematic diagram of the experiment apparatus

Full size image

The steady-state flow method was employed to measure the pressure-dependent permeability of the core samples. The 40 MPa uniform confining stress was created around the core, which created the biaxial condition during the experiment to simulate the reservoir overburden pressure. The pore pressure decreased gradually from 20 to 1.5 MPa simulating the pressure decline in reservoir during due to depletion. The average pore pressure was controlled by both the gas pump and the backpressure valve. The pore pressure setting was realized by 2 steps. First, the gas pump was used to set the inlet pressure to approximately 0.2 MPa higher than the target pressure. Second, the backpressure valve was used to set the outlet pressure to ensure that the pressure difference between inlet and outlet pressure is approximately 0.5 MPa. The inlet pressure is influenced by the outlet pressure setting, and hence, this process was repeated until the average pressure of inlet and outlet pressure becomes equal to the target value. The permeability was measured under a constant hydraulic gradient at constant flow rate.

Because average pressure in core was larger than 2 MPa and the pressure difference between inlet and outlet pressure maintained approximately equal to 0.5 MPa, the Klinkenberg effect and high-speed non-Darcy phenomenon may be ignored (Shi and Durucan 2004; Guo et al. 2014). The experiment was conducted at room temperature. Nitrogen gas was used as the fluid in the test, and the viscosity of nitrogen at different pressures and temperatures was obtained from the tables of the Beijing Chemical Industrial Company Inc (1979). Following the recommendations of Bernabe (1987, 1988) and Li et al. (2009), core aging treatment was applied to all core samples, with the maximum confining pressure of 40 MPa for the test. This treatment was conducted because history effects (i.e., dependence of permeability, in identical confining pressure and fluid pressure conditions, on the previous loading history) make it impossible that permeability is dominated by pore pressure. These factors become negligible once the second stress path been performed, which will be discussed in Sect. 3.1. The core samples are tested using the procedure introduced by Sun et al. (2004) and Sun (2007), to determine stress-dependent permeability.

2.3 The Theoretical Model for Permeability and Fluid Pressure

The relation between permeability and fluid pressure plays an important role in predicting the dynamic reservoir parameter performance. This relation is commonly expressed by empirical models. A theoretical model to explain the relation between permeability and pressure is put forward in this section.

Heid et al. (1950) developed a simplified flow model based on Poiseuille’s and Darcy’s laws, assuming that the core is composed of a bundle of parallel capillary tubes. This model was widely applied to study the flow in sandstone (Aguilera 2002). In tight sandstone and siltstone, the capillary bundle model can also represent the flow situation (Ziarani and Aguilera 2012; Tian et al. 2015; Xiao et al. 2016). Therefore, the capillary bundle model is utilized in this paper to represent the flow channel in tight sandstone. The flow in tight sand can be transformed into capillary bundle flow by Kozeny–Carman model (Fig. 2), and assumptions of model can be made as following:

  1. (1)

    The tight stone is consisted of multiple capillaries, and these capillaries are parallel with each other. There is no connection between each capillary.

  2. (2)

    The flow process is under steady state. The flow in tight stone follows the Darcy law, and the flow in capillary follows Hagen–Poiseuille law.

  3. (3)

    The flow in core is one dimensional flow, and there is only one fluid in the core. The temperature of flow remains constant.

Fig. 2
figure 2

Capillary bundle flow and flow in porous media

Full size image

The porous media porosity and permeability can also be transformed from Darcy law to capillary bundle flow. In the capillary bundle model, the porosity and permeability can be expressed by Kozeny–Carman equation (Tiab and Donaldson 2015), as below

$$\begin{aligned} \phi= & {} \frac{nA\pi \overline{r} ^{2}\tau \Delta l}{A\Delta l}=n\pi \overline{r} ^{2}\tau \end{aligned}$$
(1a)
$$\begin{aligned} K= & {} \frac{\phi \overline{r} ^{2}}{8\tau ^{2}} \end{aligned}$$
(1b)

where \(\varphi \) is porosity of capillary bundle. A is the core section area, \(\hbox {m}^{2}\), and \(\overline{r}\) is the average pore radius of core, \(\upmu \hbox {m}\). \(\tau \) is the tortuosity of the core. \(\Delta l\) is the length of core, m. K is permeability, mD. n is density of capillaries on cross section, 1/ \(\hbox {m}^{2}\).

Substitute Eqs. 1a into 1b and obtain the permeability expression in capillary bundle flow as below

$$\begin{aligned} K=\frac{n\pi \overline{r} ^{4}}{8\tau } \end{aligned}$$
(2)

Equation 2 implies the physical meaning of the capillary bundle permeability, and it also provides a direct relation between permeability and the average pore radius.

The typical flow channel of capillary bundle flow is a single capillary. The relation between radius and pressure situation can be described in one capillary flow (Fig. 2). In this typical capillary, inner and external radius of the typical capillary is \(r_{1}\) and \(r_{2}\). And \(r_{1}\) represents the average radius \(\overline{r} \). The porosity of this typical capillary equals to the porosity of the capillary bundle, which can be expressed by \(r_{1}\) and \(r_{2}\), as

$$\begin{aligned} \phi =\frac{r_1^2 }{r_2^2 } \end{aligned}$$
(3)

where \(r_{1}\) is internal radius of pipe, m. \(r_{2}\) is external stress of pipe, m.

And the stress condition can be analyzed on this capillary. Inner and external pressure are \(p_{2}\) and \(p_{1}\), which represent the average fluid pressure and overburden stress, respectively. According to material mechanics (Jaeger et al. 2009), the displacement at arbitrary radius r can be expressed as

$$\begin{aligned} {d}r=\frac{1-\nu }{E}\cdot \frac{r_1^2 dp_{1} -r_2^2 dp_2 }{r_2^2 -r_1^2 }r+\frac{1+\nu }{E}\cdot \frac{r_1^2 r_2^2 (dp_1 -dp_2 )}{r_2^2 -r_1^2 }\cdot \frac{1}{r} \end{aligned}$$
(4)

where dr is the displacement at radius r, m. E is the Young modulus, MPa. v is Poisson’s ratio, dimensionless. \(p_{1}\) is internal pressure (fluid pressure), MPa. \(p_{2}\) is external pressure of rock (overburden stress), MPa.

During the reservoir production and experiment, the overburden stress and confining pressure remain constant. As the external pressure is constant, the displacement at the \(r_{1}\) is shown as

$$\begin{aligned} {d}r_1 =\frac{1-\nu }{E}\cdot \frac{r_1^3 dp_1 }{r_2^2 -r_1^2 }+\frac{1+\nu }{E}\cdot \frac{r_1 r_2^2 dp_1 }{r_2^2 -r_1^2 } \end{aligned}$$
(5)

Separate variables to each side of the equation, Eq. 5, can be transformed as

$$\begin{aligned} \frac{1}{r_1 }{d}r_1 =\left[ {\frac{1-\nu }{E}\cdot \frac{\phi }{1-\phi }+\frac{1+\nu }{E}\cdot \frac{1}{1-\phi }} \right] {d}p_1 \end{aligned}$$
(6)

The relation between capillary porosity and fluid pressure is expressed as Eqs. 7, and 8 is the Maclaurin expansion of Eq. 7, which indicates a simpler expression and is used commonly.

$$\begin{aligned} \phi= & {} \phi _0 \hbox {e}^{-c_{\mathrm{p}} \left( {p_0 -p} \right) } \end{aligned}$$
(7)
$$\begin{aligned} \phi= & {} \phi _0 \left[ {1-c_{\mathrm{p}} \left( {p_0 -p} \right) } \right] \end{aligned}$$
(8)

where \(c_\mathrm{p}\) is the pore compressibility, 1/MPa. p is the fluid pressure, MPa. \(p_{0}\) is the initial fluid pressure, MPa.

Substitute Eqs. 8 into 6 and calculate the integration of new equation; the relation between inner radius \(r_{1}\) and fluid pressure can be obtained as.

$$\begin{aligned} \ln r_1 =-\left( {\frac{1-\nu }{E}} \right) p+\frac{2}{E\phi _0 c_{\mathrm{p}} }\ln \left[ {\frac{1}{\left( {1-\phi _0 } \right) -\phi _0 c_{\mathrm{p}} \left( {p_0 -p} \right) }} \right] \end{aligned}$$
(9)

The Young modulus and Poisson’s ratio of reservoir rock are usually among \(2{-}5\times 10^{4}\hbox {MPa}\) and 0.1–0.3, respectively. Therefore, \(p(1-v)/E\) is usually smaller than \(10^{-4}\), which has a slight influence on the relation and can be ignored. Then, the relation between inner radius \(r_{1}\) and fluid pressure can be written as

$$\begin{aligned} r_1 =\left[ {1/{\left( {1-\phi _0 } \right) -\phi _0 c_{\mathrm{p}} \left( {p_0 -p} \right) }} \right] ^{\frac{2}{E\phi _0 c_{\mathrm{p}} }} \end{aligned}$$
(10)

Substituting Eqs. 10 into 2, the theoretical relation between permeability and fluid pressure is shown as

$$\begin{aligned} K=\frac{n\pi }{8\tau }\times \left[ {1/{\left( {1-\phi _0 } \right) -\phi _0 c_{\mathrm{p}} \left( {p_0 -p} \right) }} \right] ^{\frac{8}{E\phi _0 c_{\mathrm{p}} }} \end{aligned}$$
(11)

Linearizing Eq. 11, it can be obtained as Eq. 12a. Considering the effective stress, the linearized relation also exists in Eq. 12b.

$$\begin{aligned} \left( {\frac{1}{K}} \right) ^{c}= & {} b-a\Delta p \end{aligned}$$
(12a)
$$\begin{aligned} \left( {\frac{1}{K}} \right) ^{c}= & {} b+a\Delta \sigma _{{\mathrm{net}}} \end{aligned}$$
(12b)

where \(\Delta \sigma _{\mathrm{net}}\) is the net confining pressure, MPa.

The expression of parameters in Eq. 12 is \(a=\frac{\phi _0 c_{\mathrm{p}} }{\root \frac{8}{E\phi _0 c_{\mathrm{p}} } \of {\frac{n\pi }{8\tau }}}\), \(b=\frac{1}{\left( {1-\phi _0 } \right) \root \frac{8}{E\phi _0 c_{\mathrm{p}} } \of {\frac{n\pi }{8\tau }}}\) and \(c=\frac{E\phi _0 c_{\mathrm{p}} }{8}\), respectively.

Parameter c is a constant and can be calculated in one core. Parameter a and b change with different cores because of the tortuosity. Therefore, there exists a linear relation between the power function of permeability reciprocal and pressure drop. In the following section, this theoretical model will be tested by our experiment data and the data from the literature.

3 Results and Discussion

3.1 The Effect of Core Aging Treatment and Experimental Results

Core aging treatment is an approach to eliminate the plastic deformation in the core holder by loading confining pressure to a certain value and unload the confining pressure. During this process, the core permeability is measured by steady method at each confining pressure, then repeat the process until the permeability difference between two stress paths is less than 5%. Because tight sandstone is well cemented and 40 MPa confining pressure cannot lead to plastic deformation (Jaeger et al. 2009), the core aging treatment has little effect on the core. The core aging treatment is necessary because of the microinterstice consisted by core skin and the sleeve. The effect of these microinterstices is documented as core skin effect in mercury injection experiment (Rashid et al. 2015). The difference between experiment and theory capillary pressure curves illustrates the effect of these microinterstices (Fig. 3).

Fig. 3
figure 3

The effect and deformation of microinterstices

Full size image

During mercury injection test, it is usually difficult to measure the displacement pressure directly because the displacement pressure of capillary pressure curve drops almost to 0 due to the experiment (Fig. 3). This is because the mercury flows into microinterstices instead of the core pore system at first. A well-developed method (Nojabaei et al. 2016) is to reduce the skin effect to solve the displacement pressure, which is named as skin modification of the capillary pressure test.

These microinterstices are consisted of the core surface and the sleeve. The effect of microinterstice results from its plastic and elastic deformation as the confining pressure changes (Fig. 3). Once confining pressure increases in the experiment test, the sleeve in the core holder will be out of shape. Then, the effective stress comes back to the initial value, and the sleeve cannot recover to the initial state due to its plasticity. However, the deformation of sleeve does not exist in the reservoir. Thus, it should be eliminated. And the core aging treatment is a mature method (Mbia et al. 2013, 2014) to reduce this plastic deformation.

Figure 4 provides the case of core aging treatment on the core Erdos-4-7, and it can be observed that the permeability difference between the second stress loading and unloading process is quite small, which can be concluded that the effect of the micro interstice deformation is very weak and the plastic deformation effect is reduced to a small degree after the second core aging treatment. After the core aging treatment, the permeability change of core is dominated by stress effect.

Fig. 4
figure 4

The permeability measurements during the core aging treatment

Full size image

Experimental results for eight cores are presented in Fig. 5. The net confining pressure is the difference between confining pressure and fluid pressure. Obviously, the permeability decreases as the fluid pressure declines and effective stress increases.

Fig. 5
figure 5

Pressure-dependent permeability performance after core aging treatment

Full size image

3.2 New Model Verification

In the linearized relation of our model (Eq. 12), parameter a and b can be obtained by data matching. And the parameter c needs to be computed before the regression. Because parameter a and b in Eq. 12 cannot be calculated precisely. This linearized relation is a semi-analytical formula to predict the relation between the fluid pressure and permeability. The Young modulus is obtained with the average value 43.57 GPa. The initial porosity is tested and listed in Table 1. The pore compressibility of core is calculated by Hall’s plot (Hall 1953; Jaeger et al. 2009).

Then, the permeability performance of cores from the Ordos Basin can be plotted to test the linear relation between the power function of permeability reciprocal and net confining pressure (Fig. 6). \(R^{2}\) is the correlation coefficient of the regression, ranging from 0 to 1. A higher \(R^{2 }\)means the better matching result. The new model can be transformed into the linear relation between the power function of permeability reciprocal and net confining pressure change, which will not change on the correlation coefficient value.

Fig. 6
figure 6

The new model verified by Erdos Basin cores. a Erdos-4-7, Erdos-5-3, Erdos-4-9 and Erdos-5-1; b Erdos-4-8, Erdos-5-4, Erdos-36 and Erdos-44

Full size image

Figure 6 indicates that the new model can well match the experiment data of cores from the Ordos Basin. Then, the pressure-dependent permeability and porosity data of 8 tight cores in Xiao’s research (Xiao et al. 2016) are collected to verify the semi-analytical model The Young modulus of elasticity is estimated as 30.0 GPa for calculation. The pore compressibility of core is calculated by Hall’s plot (Jaeger et al. 2009). Figure 7 shows the regression results of 8 tight sandstone core samples obtained from the literature.

Fig. 7
figure 7

The new model verified by tight core in the literature a D15-2, DT1-8, HH103-3 and D24-4; b D23-8, S-8, D141-7 and MJ5515

Full size image

In Fig. 7, it can be considered that there exists the linearized relation in the experiment observations of tight sandstone in the literature. The experimental results obtained by Sigal (2002), Sun et al. (2004) and Abass et al. (2007) are also used to test the applicability of the new model presented in this research. The Young modulus of carbonate core, mid-perm core and low-perm core is estimated as 70.0, 25.0 and 30.0 GPa for calculation, respectively. And the porosity of carbonate core, mid-perm core and low-perm core is estimated as 0.025, 0.10, 0.06 for calculation, respectively. The pore compressibility of core is calculated by Hall’s plot. The regression results are shown in Fig. 8.

Fig. 8
figure 8

The new model verified by experiment observation in the literature. a Carbonate cores in SPE110973; b mid-perm cores in SPWLA2002; c mid-perm cores in SUN’s research; d low-perm cores in SUN’s research

Full size image

This indicates that regardless of the magnitude of core permeability, there is a linear relationship between the power function of permeability reciprocal and net confining pressure drop. Obviously, the correlation coefficients in Figs. 7 and 8 are smaller than that in Fig. 6. This is because the Young modulus of elasticity of tight sandstone cores in the Ordos Basin is measured by tests and the Young modulus elasticity of cores in the literature (Xiao et al. 2016; Sigal 2002; Sun et al. 2004; Abass et al. 2007) is estimated.

3.3 Compare with Other Permeability Models

The commonly used pressure-dependent permeability models (Jones and Owens 1980; Walsh 1981; Chen and Bai 1998; Zhang et al. 2015; Xiao et al. 2016) are listed in Table 2.

Table 2 Commonly used models for permeability and effective stress
Full size table

The data of 24 cores (8 from our experiment and 16 from the literature) are also matched by five empirical relations including the exponential model, power function relation, Walsh model, GP model and binomial model. Tables 3 and 4 list the match results of the experiment data in our research and the data in the literature, respectively.

Table 3 Match results of data in our experiment
Full size table
Table 4 Match results of data in the literature
Full size table
Fig. 9
figure 9

The average coefficient of correlation of each pressure-dependent model

Full size image
Fig. 10
figure 10

Different pressure drops in laboratory and reservoir

Full size image

Compared with empirical models, the semi-analytical model can satisfy the data on the same level. With reference to the average correlation coefficient of each model based on the data of 24 cores (Fig. 9), it can be observed that the semi-analytical model in our paper has the best regression result, with \(R^{2}=0.979\) (Fig. 9). The Walsh model and power model are ranked in the second and third place, with \(R^{2}=0.976\) and \(R^{2}=0.975\), respectively. This means our model can match the pressure-dependent permeability of different rock types in the theoretical relationship.

3.4 Permeability Change Under Reservoir Condition and Evaluation

The pressure drop range in laboratory should be in correspondence with that in reservoirs. Commonly, it is adopted the whole fluid pressure drop or confining pressure change to evaluate permeability sensitivity to stress (Sun et al. 2004, Sun, et al., 2007). This pressure drop range in laboratory is much larger than that in a gas reservoir (Fig. 10). This is because the aquifer and fluid injection maintain the reservoir pressure in most cases. Besides, different gas reservoirs have different pressure drop ranges. So it is not appropriate to evaluate the stress sensitivity by whole pressure drop in laboratory and this will exaggerate the permeability sensitivity to stress.

Meanwhile, during the different pressure range, the core deformation behaviors are also different. Ignoring this phenomenon will also exaggerate the permeability stress sensitivity. The permeability performance can be obviously divided into two stages (Jiao et al. 2011). In first stage, there is an abrupt reduction in permeability. And during the second stage, permeability changes slowly as the net confining pressure increases (Fig. 10). This double-stage phenomenon comes from the microfractures in the core. If the microfracture plays an important role in the flow, this double-stage phenomenon will occur in the experiment. In the first stage, the microfractures are the main flow channels.

Because these microfractures own a large aperture, of which permeability is very sensitive to the stress. During the second stage, the microfractures are all closed as the effective stress increases. The main flow channel is the pore system in the tight rock, which results in the slow reduction in permeability.

Under most reservoir conditions, the core stress path belongs to the second stage. The fact that all the microfractures being closed decides that the permeability is less sensitive to the stress. Therefore, it is not appropriate to evaluate the stress sensitivity level within the first stage because the permeability change in this stage does not happen in reservoirs. Considering the reservoir net confining pressure, the permeability performance stage I should not be adopted to evaluate permeability sensitivity to stress. If the permeability change has no obvious two-stage phenomenon, the reservoir initial stress state should be chosen as the beginning point. In the reservoir where these cores come from, the initial net confining stress is 32.43 MPa. According to the production experience, the pressure drop is recommended to be 10 MPa in the second stage in this paper.

4 Conclusions

In this paper, the core aging treatment was adopted to eliminate the microinterstice deformation and stabilize the core prior to the experiments. A semi-analytical model was developed to describe the permeability change with pore pressure variation. This model was verified using results from various sources in the literature. The model also well predicted the pressure-dependent behavior of permeability in 8 tight sandstone core samples tested in this study. The following conclusions can be drawn:

  1. (1)

    The new semi-analytical model is based on capillary bundle model indicates that there is a linear relationship between inverse of permeability to a constant power and pore pressure changes. This relationship can well satisfy the experimental data, and it may also be used for other type of rocks.

  2. (2)

    Compared with commonly used empirical models, the semi-analytical model can also satisfy the experiment observations on the same level. The model verification also indicates that the semi-analytical model can match the pressure-dependent permeability of different rock types.

  3. (3)

    The permeability variation under reservoir condition is different from that under laboratory condition. And its performance is divided into two stages. The permeability reduction in stage I is slower than that in stage II. In most reservoirs, the permeability performance under reservoir condition is located in stage II. The evaluation with whole pressure drop range in laboratory will exaggerate permeability sensitivity to stress in reservoir.