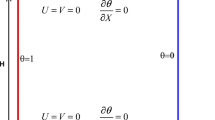Thermal Non-equilibrium Natural Convection in a Square Enclosure with Heat-Generating Porous Layer on Inner Walls

Abstract

Differentially heated enclosure with heat-generating porous layer on inner walls is studied computationally for non-Darcy flow and thermal non-equilibrium models. In this study, this problem is investigated for different internal and external Rayleigh numbers, Darcy numbers, porosity-scaled thermal conductivity ratio, solid-/fluid-scaled heat transfer coefficient and dimensionless thickness of the porous layer. The results indicate that the dimensionless thickness of the porous layer has an important effect on the heat transfer in the enclosure. It was found that the thermal non-equilibrium model is needed for small values of the porosity-scaled thermal conductivity ratio and the solid-/fluid-scaled heat transfer coefficient. It is shown that the convection of heat due to internal heat generation is increased in the enclosure when the ratio of internal Rayleigh number to external Rayleigh number is larger.

1 Introduction

Free convection in heat-generating and saturated porous structures has widespread applications in different fields such as cooling of electronic devices, heat recovery or loss in geothermal sources, diffusion of pollutants in underground, storage of agricultural and food products, the radioactive waste storage, insulation of buildings, packed sphere beds and solar power collectors. The convective heat transfer in a porous medium is essentially a two-phase problem. The solid phase is the porous matrix, and the fluid phase is the fluid in the void of the porous matrix. If the temperature of the both phases is approximately equal, then the fluid and the solid phases are in local thermal equilibrium (LTE) state. In the literature, the natural convection in porous media using local thermal equilibrium model has been investigated in several studies such as Nithiarasu et al. (1997), Marcondes and Mede (2001), Jue (2003) and Datta et al. (2016). When the temperature difference between solid and fluid phases is very large, the porous medium is considered as in local thermal non-equilibrium (LTNE) state. Free convection in a fluid-saturated square porous enclosure was studied using Darcy model and thermal non-equilibrium approach by Baytaş and Pop (2002). Authors found that the thermal non-equilibrium model affects considerably the flow characteristics and heat transfer between solid and fluid phases in porous matrix. The natural convection in a porous enclosure was examined using non-Darcian and the two-equation model (LNTE) in Khashan et al. (2006). Authors studied the flow field by taking into account non-Darcian effects, Brinkman effect and Forchheimer quadratic inertial effect. The effects of viscous dissipation on free convection in a porous cavity under thermal non-equilibrium case were examined by Alhashash et al. (2014). Their results showed that the average Nusselt number of the fluid decreases and the average Nusselt number of the solid increases by increasing the modified conductivity ratio. This result is valid for all of the viscous dissipation parameters. Bera et al. (2014) investigated the effect of local thermal non-equilibrium (LTNE) state on the phenomenon of thermosolutal convection in a square porous enclosure with the non-Darcy model. They showed that the effect of LTNE model was meaningful for temperature distribution and the heat transfer rate; however, it was negligible on the mass transfer rate. Chen et al. (2016) studied the free convection problem in a fluid-saturated porous cavity by using Darcys model, and LTE and LTNE models by using spectral collocation method. Baytaş (2003) examined natural convection in a heat-generating porous enclosure by using the Brinkman–Darcy–Forchheimer and thermal non-equilibrium models. Author showed that the non-equilibrium assumption was convenient for small values of dimensionless volumetric heat transfer coefficient between solid and fluid, and of modified conductivity ratio. Baytaş (2007) has also investigated entropy generation in the square heat-generating porous enclosure with isothermally cooled walls by using non-Darcy and thermal non-equilibrium models. Author showed that the entropy generation due to viscous drag should be considered for the LNTE model. The convection characteristics of the heat-generating porous enclosure with linear thermal boundary conditions using the non-Darcy and LNTE models were reported by Wu et al. (2015). In another study of Wu et al. (2016), they investigated free convection in a rectangular heat-generating porous cavity for thermal non-equilibrium model. As a boundary condition, the left wall temperature was changed sinusoidally. They showed that the sinusoidal boundary condition caused to the periodical variations of the temperature fields near the left wall and the local Nusselt number. Beckermann et al. (1987) studied the fluid flow in a rectangular enclosure containing fluid and porous layers. The non-Darcy equation and thermal equilibrium model were used in the porous layer. In another study, the free convection in the enclosure partially filled with the vertical and horizontal porous layers was investigated by Beckermann et al. (1988). They found that the degree of fluid penetration into the porous layer increased with increasing Darcy and Rayleigh numbers. They also showed that the penetration of the fluid was large in the case of vertical porous layer. Du and Bilgen (1990) examined the natural convection in rectangular enclosures partially filled with various porous layer orientations and aspect ratios. Song and Viskanta (1994) studied both experimentally and theoretically on the free convection in a cavity partially filled with anisotropic porous layer. Chen et al. (2009) studied the free convection in a partly filled porous cavity and the porous layers which are placed at the top and bottom parts of the cavity. They showed that the Darcy number, the Rayleigh number and the thickness of the porous layer in this case had some influences on the heat transfer.

The main goal of the present study is to investigate the effects of the internal and the external Rayleigh numbers, Darcy number, the solid-/fluid-scaled heat transfer coefficient and the porous-scaled conductivity ratio on the fluid flow and the natural convection in an enclosure. It was assumed that the heat-generating porous layers are placed on the inner walls of the enclosure. The effects of different thicknesses of the porous layers were also analyzed. It is considered that the fluid flow is non-Darcian, and the porous medium is considered to be in local thermal non-equilibrium with the fluid. The numerical results, in this study, are presented in the forms of isotherms, streamlines and the tables.

2 Mathematical Model and Formulation

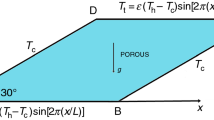
A fluid-saturated porous medium with heat-generating solid phase on all of the walls of a square enclosure is considered. As shown in Fig. 1, there is a clear fluid region in the middle of the enclosure. The height and the width of the enclosure are denoted by D, and the thickness of the porous layer is by d. The left and right walls of the enclosure are maintained at temperatures $T_H$ and $T_C$, respectively, where $T_H>T_C$. The horizontal walls are isolated. The fluid flow is unsteady, incompressible and Boussinesq fluid. Non-Darcian fluid flow model is used for porous medium. The porous medium is also considered to be in local thermal non-equilibrium with the fluid.

Fig. 1

Schematic of the physical problem

The governing equations for the clear fluid and the porous layer can be formed into a single set of equations by the following binary parameter:

$$\begin{aligned} \lambda =\left\{ \begin{array}{ll} 0, &{} \quad \text {in the fluid region} \\ 1, &{} \quad \text {in the porous region} \end{array}\right. \end{aligned}$$

(1)

By above considerations and definition of the proposed problem, the dimensionless form of the governing equations can be written as follows: the mass balance equation:

$$\begin{aligned} \frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0 \end{aligned}$$

(2)

The momentum balance equation in X-direction:

$$\begin{aligned} \frac{\partial U}{\partial \tau }+U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-\frac{\partial P}{\partial X}+\frac{\partial ^2 U}{\partial X^2}+\frac{\partial ^2 U}{\partial Y^2}-[\lambda ]S_U \end{aligned}$$

(3)

where pressure loss due to porous matrix is computed using Ergün equation, Ergün (1952) which is modified by MacDonald et al. (1979) as follows.

$$\begin{aligned} S_U=\varepsilon \frac{Pr}{Da}U+1,76\sqrt{\frac{\varepsilon }{150 Da}}\sqrt{U^2+V^2}U \end{aligned}$$

The momentum balance equation in Y-direction:

$$\begin{aligned} \frac{\partial V}{\partial \tau }+U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\partial P}{\partial Y}+\frac{\partial ^2 V}{\partial X^2}+\frac{\partial ^2 V}{\partial Y^2}-[\lambda ]S_V+Ra_EPr\theta _f \end{aligned}$$

(4)

where

$$\begin{aligned} S_v=\varepsilon \frac{Pr}{Da}V+1,76\sqrt{\frac{\varepsilon }{150 Da}}\sqrt{U^2+V^2}V \end{aligned}$$

The energy balance equation for fluid phase:

$$\begin{aligned} \frac{\partial \theta _f}{\partial \tau }+U\frac{\partial \theta _f}{\partial X}+V\frac{\partial \theta _f}{\partial Y}=\frac{\partial ^2 \theta _f}{\partial X^2}+\frac{\partial ^2 \theta _f}{\partial Y^2}+[\lambda ]H\left( \theta _s-\theta _f \right) \end{aligned}$$

(5)

The energy balance equation for solid phase:

$$\begin{aligned} \xi \frac{\partial \theta _s}{\partial \tau }=\frac{\partial ^2 \theta _s}{\partial X^2}+\frac{\partial ^2 \theta _s}{\partial Y^2}+ \gamma H(\theta _f-\theta _s)+\frac{Ra_I}{Ra_E} \end{aligned}$$

(6)

The non-dimensional governing equations are obtained by using the following non-dimensional variables.

$$\begin{aligned} X= & {} \frac{x}{D}\quad Y=\frac{y}{D}\quad U=\frac{uD}{\alpha _f\varepsilon }\quad V=\frac{vD}{\alpha _f \varepsilon }\quad P=\frac{pD^2}{\rho _f \alpha ^2_f}\quad \tau =\frac{t \alpha _f}{D^2}\quad Da=\frac{K}{D^2} \nonumber \\ T_o= & {} \frac{T_H+T_C}{2}\quad \Delta T =T_H-T_C \quad Ra_E=\frac{g\beta \Delta {T} D^3}{\nu \alpha _f}\quad Ra_I=\frac{g\beta D^5 q^{\prime \prime \prime }}{\nu \alpha _f k_s} \nonumber \\ \theta _f= & {} \frac{T_f-T_o}{\Delta {T}}\quad \theta _s=\frac{T_s-T_o}{\Delta {T}}\quad H=\frac{h_vD^2}{\varepsilon k_f}\quad \gamma =\frac{\varepsilon k_f}{(1-\varepsilon )k_s} \quad \xi =\frac{\alpha _f}{\alpha _s} \quad \eta =\frac{d}{D} \nonumber \\ \end{aligned}$$

(7)

where $\varepsilon$ is the porosity, K is the permeability of the porous medium, $h_v$ is the volumetric heat transfer coefficient, $q^{\prime \prime \prime }$ is the volumetric heat source strength in the solid phase; T is the temperature and the subscripts f and s indicate the fluid and solid phases, respectively.

The non-dimensional initial and boundary conditions for Eqs. –6 are as follows:

$$\begin{aligned} \tau \leqslant 0 \quad \text {for} \qquad U= & {} V=\theta _f=\theta _s=0 \quad \text {everywhere} \nonumber \\ \tau >0 \quad \text {for} \qquad X= & {} 0 \quad 0\leqslant {Y}\leqslant {1} \quad U=V=0 \quad \theta _f=\theta _s=0.5 \nonumber \\ \qquad X= & {} 1 \quad 0\leqslant {Y}\leqslant {1} \quad U=V=0 \quad \theta _f=\theta _s=-0.5 \nonumber \\ \qquad Y= & {} 0,1 \quad 0\leqslant {X}\leqslant {1} \quad U=V=0 \quad \frac{\partial {\theta _f}}{\partial {Y}}=\frac{\partial {\theta _s}}{\partial {Y}}=0 \end{aligned}$$

(8)

The average Nusselt numbers for the fluid and solid phases are defined, respectively, as:

$$\begin{aligned} Nu_{f}= & {} \int _0^1{-\frac{\partial {\theta _f}}{\partial X}\text {d}Y} \nonumber \\ Nu_{s}= & {} \int _0^1{-\frac{\partial {\theta _s}}{\partial X} \text {d}Y} \end{aligned}$$

(9)

3 Numerical Solution Procedure and Its Validation

The governing differential Eqs. –6 in unsteady state with Darcy modified Navier–Stokes equations, energy equations and boundary conditions Eq. 8 are solved numerically using well-known SIMPLE algorithm, Patankar (1980). Non-uniform collocated grids are used to operate on the pressure, velocity and temperature at the same grid point. Then, all governing equations are discretized by using finite volume method, and the power-law scheme is used for the convection diffusion terms as given by Patankar (1980). The system of algebraic equations is solved by the alternating direction implicit (ADI) technique. The ADI uses the tridiagonal matrix algorithm (TDMA) to obtain solutions for the discretized equations. The control volume discretization provides the continuity of the convective and diffusive fluxes. The harmonic mean of the diffusion coefficient among control volumes at the interface is introduced in order to minimize the effect of the sudden changes without using fine mesh at the interface between porous/fluid layer, Betchen et al. (2006). The continuity conditions at the interface between clear fluid and porous layer can be defined, see also Beckermann et al. (1988) and Baytaş et al. (2009):

$$\begin{aligned}&\displaystyle U|_\mathrm{{porous}}=U|_f \quad V|_\mathrm{{porous}}=V|_f \quad P|_\mathrm{{porous}}=P|_f \nonumber \\&\displaystyle \frac{1}{\varepsilon }\frac{\partial U}{\partial n}|_\mathrm{{porous}}=\frac{\partial U}{\partial n}|_f \\&\displaystyle \theta |_\mathrm{{porous}}=\theta |_f \quad \frac{\partial {\theta }}{\partial n}|_\mathrm{{porous}}=\frac{\partial {\theta }}{\partial n}|_f\nonumber \end{aligned}$$

(10)

The numerical solution is iterated from the initial state to the steady state by satisfying the following criterion:

$$\begin{aligned} \sum {\left| \phi _{i,j}^\mathrm{{new}}-\phi _{i,j}^\mathrm{{old}}\right| }{/}\sum {\phi _{i,j}^\mathrm{{new}}}\le 10^{-6} \end{aligned}$$

(11)

where $\phi$ stands for $\theta _s$, $\theta _f$, P, U and V. The results in this study are compared with the results of Nithiarasu et al. (1997) and Chen et al. (2009) for $\varepsilon = 0.4$, 0.6 with different Rayleigh numbers and Darcy numbers in a differentially heated porous enclosure, under consideration of the local thermal equilibrium and non-Darcian fluid flow model. As listed in Table 1, our results match very well with their published results. Another comparison made with the results of Chen et al. (2009) about horizontal velocity and temperature profiles at mid-width of the cavity is presented in Fig. 2. A partially filled porous cavity, which has the porous layers in the upper and bottom parts, is studied as in Chen et al. (2009) for $Ra_E =10^5$, $Da=10^{-5}$, $\varepsilon =0.4$ under consideration of the local thermal equilibrium. As shown in Fig. 2, the results of the current study are in good agreement with the results of Chen et al. (2009). The differentially heated non-Darcy porous enclosure problem is solved for thermal non-equilibrium state in this study, and the results are presented in Table 2. The values of average Nusselt number for fluid and solid increase as external Rayleigh number increases for all values of H and $\gamma$ parameters. However, this increment is small when the Darcy number decreases. The effect of H and $\gamma$ parameters on Nusselt numbers decreases as Darcy number decreases. For example, the effect of H and $\gamma$ on Nusselt numbers is very small at $Ra_E =10^6$ and $10^7$ for $Da=10^{-6}$. The average Nusselt numbers for fluid and solid are almost the same for $Da=10^{-6}$ and $Ra_E =10^6$. As a result, the thermal non-equilibrium model can be used for high values of the Rayleigh number when the Darcy number is very low. Additionally, the Nusselt numbers for fluid and solid phases increase as $\gamma$ values increase at every H values. On the other hand, the average Nu numbers for fluid and solid phases have different behaviors when H parameter increases at the constant value of $\gamma$. The average Nusselt number for fluid phase decreases, but Nu number for solid increases as H increases. Grid dependency tests were carried out at steady state as listed in Table 3. A non-uniform grid $(102\times 102)$ was chosen for all calculations.

Fig. 2

Comparison of: a U-velocity and; b temperature profiles at mid-width of the cavity for $Ra=10^{5}$, $Da=10^{-5}$, $\varepsilon =0.4$.

Table 1 Comparison of average Nusselt number values for a differentially heated porous enclosure with thermal equilibrium model ($Pr=1.0$)

Table 2 Average Nusselt number values for a differentially heated non-Darcy porous enclosure with thermal non-equilibrium for $Pr=1.0$ and $\varepsilon =0.4$

Table 3 Accuracy test with $Ra_I=10^5$, $Ra_E=10^7$, $H=100$, $\gamma =10$, $Pr=1.0$, $\varepsilon =0.4$ at steady state

4 Results and Discussion

In this investigation, the Prandtl number and porosity are fixed at 1.0 and 0.4, respectively. The effects of the external and internal Rayleigh numbers, Darcy numbers, the dimensionless thickness of porous layer, $\eta$, solid-/fluid-scaled heat transfer coefficient, H, the porous-scaled conductivity ratio, $\gamma$, on the fluid flow and heat transfer are presented in this study. The results for dimensionless thickness of porous layer, $\eta$ of 0.15, 0.25 and 0.35, Rayleigh numbers $Ra_E$ from $10^5$ to $10^8$ and $Ra_I$ from $10^7$ to $10^8$, Darcy number, Da, from $10^{-6}$ to $10^{-4}$ are presented.

The effects of variation of $Ra_E$ and $Ra_I$ numbers on natural convection in thermal non-equilibrium porous model are shown in Figs. 3 and 4 where H and $\gamma$ parameters are kept constant as 100. $Ra_E$ ranges between $10^5$ and $10^8$ in Figs. 3 and 4. $Ra_I$ value is $10^7$ in Fig. 3 and $10^8$ in Fig. 4. When $Ra_I$ is $10^7$, the isotherms for the fluid and the solid phases spread smoothly all over the regions as shown in Fig. 3a, b. The distribution of the temperature gradients at the vertical walls is uniform in both the fluid and the porous layer regions. When $Ra_E$ increases, the natural convection in enclosure turns into the differentially heated enclosure type problem. The temperature gradients at the left bottom and the right top sides of the vertical walls are stronger than the other sides as shown in Fig. 3c, d. The fluid flow in the porous layer becomes stronger and dominant as $Ra_E$ increases as shown in Fig. 3. When the ratio of $Ra_I$ to $Ra_E$ is large, the fluid flow in the clear fluid region of the enclosure is more powerful than the fluid flow in the porous layer of the enclosure in Fig. 3a, b. Three cells appear in the clear fluid region for $Ra_E=10^7$ in Fig. 3c.

Fig. 3

Isotherms for fluid (left column) and solid (middle column) and streamlines (right column) for $H=100$, $\gamma =100$, $Pr=1.0$, $Da=10^{-5}$, $Ra_I=10^7$, $\eta =0.25$, a $Ra_E=10^5$; b $Ra_E=10^6$; c $Ra_E=10^7$; d $Ra_E= 10^8$

Internal heat generation in solid phase has very large values when $Ra_E$ is smaller than $Ra_I$, therefore the convection of heat due to internal heat generation becomes dominant in the enclosure. When $Ra_I$ is $10^8$ and $Ra_E$ is $10^5$, the maximum temperatures in fluid and solid phases are larger than wall temperature. Moreover, the temperature gradients at vertical walls have large values and their distributions on the right wall are smooth as shown in Fig. 4a, b. In Fig. 4a, the fluid flow is very strong in the clear fluid region and the fluid flow spreads into the porous layer since the heat generation in the porous layer is large. There are two cells at the upper left and the bottom left corners of the porous layer as shown in Fig. 4a. As $Ra_E$ is increased, the fluid flow becomes dominant in the porous layer and the clear fluid regions. In Fig. 4c, the fluid flow in the clear fluid region has three cells when $Ra_E$ is $10^7$, and at the same time the fluid flow is very strong in the porous layer. The cells in the clear fluid region disappear when $Ra_E$ is $10^8$, but the fluid flow remains very strong all over the enclosure as shown in Fig. 4d.

Fig. 4

Isotherms for fluid (left column) and solid (middle column) and streamlines (right column) for $H=100$, $\gamma =100$, $Pr=1.0$, $Da=10^{-5}$, $Ra_I=10^8$, $\eta =0.25$, a $Ra_E=10^5$; b $Ra_E=10^6$; c $Ra_E=10^7$; d $Ra_E= 10^8$

Fig. 5

Isotherms for fluid (left column) and solid (middle column) and streamlines (right column) for $Ra_E=10^6$, $Ra_I=10^8$, $Da=10^{-5}$, $H=10$, $Pr=1.0$, $\eta =0.25$, a $\gamma =0.01$; b $\gamma =1$; c $\gamma =50$; d $\gamma =100$

Fig. 6

Isotherms for fluid (left column) and solid (middle column) and streamlines (right column) for $Ra_E=10^6$, $Ra_I=10^8$, $Da=10^{-5}$, $Pr=1.0$, $\gamma =10$, $\eta =0.25$, a $H=1$; b $H= 50$; c $H=100$; d $H=1000$

The effects of variation of H and $\gamma$ parameters on natural convection in non-equilibrium porous model are presented in Figs. 5 and 6. $Ra_I$ and $Ra_E$ are selected as $10^8$ and $10^6$, respectively. H is 10 and $\gamma$ values are 0.01, 1, 50, 100 in Fig. 5. $\gamma$ is selected as 10 and H values are 1, 50, 100, 1000 in Fig. 6. The temperature differences between the fluid and the solid phases in the enclosure are high for $\gamma =0.01$ and 1.0 in Fig. 5a, b. The solid-phase temperature is greater than the fluid-phase temperature near the top and bottom left corners. For this reason, two cells occur at the top and the bottom left corners as shown in Fig. 5a, b. The direction of the cells is counterclockwise, but the direction of the main fluid flow in the enclosure is clockwise. In this situation, the heat energy cannot be well convected from left to right in the enclosure because of these cells.

When H increases, the temperature differences between the fluid and the solid phases decrease as seen in first and second columns of Fig. 6. The thermal equilibrium case is valid for large H values. The fluid flow is strong all over the enclosure. However, a cell occurs at the top left corner of the enclosure when H increases as shown in Fig. 6b–d. When dimensionless thickness of porous layer is increased, the temperature values of the fluid and the solid phases increase as shown in Fig. 7. Because more heat is convected to the fluid from the heat-generating solid phase as the dimensionless thickness of the porous layer is increased. There is one main cell in the enclosure when $\eta$ is 0.15. When $\eta$ is increased to 0.25, there is a main cell in enclosure and two cells also occur at the left top and the bottom of the enclosure in the opposite direction of the main cell. When $\eta$ is 0.35, two main cells in the opposite directions appear in the enclosure. The fluid flow in the clear fluid region is always stronger than that in the porous layer region.

Fig. 7

Effect of the dimensionless thickness of porous layers on isotherms for fluid and solid phases and streamlines for $Ra_I=10^8$, $Ra_E=10^6$, $Da=10^{-5}$, $H=10$ and $\gamma =0.01$, a $\eta =0.15$; b $\eta =0.25$; c $\eta =0.35$

A comparison of average Nusselt number values for left wall for different dimensionless thicknesses of porous layer is given in Table 4. The results are given for $H{=}1.0$ and different values of $\gamma$. When the dimensionless thickness of porous layer increases, the Nusselt number for the solid phase increases but the Nusselt number for fluid phase decreases. Another comparison is given for $\gamma =0.01$ and different values of H in Table 5.

Table 4 Comparison of average Nusselt number values for three dimensionless thickness of porous layer for $Ra_I=10^8$, $Ra_E=10^6$, $Da=10^{-5}$, $H= 1.0$, $Pr=1.0$, $\varepsilon =0.4$

The Nusselt numbers for solid phase have greater values as the dimensionless thickness of porous layer increases as listed in Tables 4 and 5. However, the Nusselt number for fluid phase decreases when $\eta$ increases for H $\le 1.0$, but it increases with $\eta$ for $H>1$ as listed in Table 5. When $H>1$, the heat transfer between solid and fluid phases increases. Therefore, the Nusselt numbers for fluid phase have greater values as $\eta$ increases.

Table 5 Comparison of average Nusselt number values for three dimensionless thickness of porous layer for $Ra_I=10^8$, $Ra_E=10^6$, $Da=10^{-5}$, $\gamma =0.01$, $Pr=1.0$, $\varepsilon =0.4$

5 Conclusion

In this study, the natural convection of differentially heated enclosure containing heat-generating porous layer at the enclosure walls is investigated. It is observed that low values of Darcy number have influence on heat transfer in the enclosure for thermal non-equilibrium model. When the ratio of $Ra_I$ to $Ra_E$ is large, the convection heat transfer due to internal heat generation is more effective in the enclosure. It is also shown that if $Ra_E$ is increased, the natural convection behaves like a differentially heated enclosure problem. The fluid flow in the clear fluid region is generally strong. However, the fluid flow in the porous layer becomes strong as $Ra_E$ increases. The results show that the temperature differences between the solid and the fluid phases are high when the porosity-scaled conductivity ratio, $\gamma$, and solid-/fluid-scaled heat transfer coefficient, H have small values. When H and $\gamma$ are small, the thermal non-equilibrium model is indispensable. The increment of dimensionless thickness of porous layer causes an increment in the difference between temperatures of the fluid and the solid phases. Therefore, the cells in the opposite direction of the main cell appear in the fluid flow. It is found that the average Nusselt number for solid phase increases when the dimensionless thickness of porous layer and the heat generation in the solid phase increase.