Computational Permeability Determination from Pore-Scale Imaging: Sample Size, Mesh and Method Sensitivities

Abstract

In this work, a complete work flow from pore-scale imaging to absolute permeability determination is described and discussed. Two specific points are tackled, concerning (1) the mesh refinement for a fixed image resolution and (2) the impact of the determination method used. A key point for this kind of approach is to work on enough large samples to check the representativity of the obtained evaluations, which requires efficient parallel capabilities. Image acquisition and processing are realized using a commercial micro-tomograph. The pore-scale flows are then evaluated using the finite volume method implemented in the open-source platform OpenFOAM^®. For this numerical method, the influence of the different aspects mentioned above are studied. Moreover, the parallel efficiency is also tested and discussed. We observe that the level of mesh refinement has a non-negligible impact on permeability tensor. Moreover, increasing the refinement level tends to reduce the gap between the methods of computational measurements. The increase in computation time with the mesh is balanced with the good parallel efficiency of the platform.

1 Introduction

Understanding the interactions between the microstructural geometry and the macroscopic effective properties of porous media is an issue in a wide range of industrial fields as hydrology, petrology, catalysis, filtration and so on. A huge effort has been spent to theoretically estimate or to numerically establish a relation between geometric microstructure and macroscopic physical properties (Adler 1994). For porous materials, permeability is the macroscopic parameter of basic practical interest, and its measurement is important to predict macro-scale behavior of flows.

Recently, considerable progresses in pore-space imaging and high-performance computing have accelerated the development and the use of digital rock physics (DRP) tools in complement to physical laboratory measurements (Renard et al. 2001) by providing fast and effective access to rock properties from three-dimensional images (Andrä et al. 2013; Andrew et al. 2013; Blunt et al. 2013).

However, a lot of different studies have been realized for several decades. In the pioneering calculations of porous media transport properties by direct resolution of the local equations in a micro-tomographic image (Spanne et al. 1994), the influences of the sampling volume and of boundary conditions have been investigated. Their works are based on the innovative solver of Stokes equations in three-dimensional pore spaces described in Lemaitre and Adler (1990). Moreover, detailed computed micro-tomography-based analyses of rock geometrical and transport characteristics, and in particular of their scaling with the sampling volume, have been already realized for Fontainebleau (Thovert et al. 2001), Vosges (Jones et al. 2003) and Bentheim (Thovert and Adler 2011) sandstones. The transport properties of a metallic foam and their dependence on the sampling volume have also been investigated, as the influences of the mesh resolution and of the numerical boundary conditions (Gerbaux et al. 2010).

The numerical determination of permeability, and more generally of effective properties, follows a classic upscaling strategy (Adler 1994). This strategy is based on two major elements: (1) the knowledge of the local geometry and (2) the evaluation of the flow inside this local complex structure. The first key point is to check that the considered sample is representative of the porous medium, i.e., the effective properties are unchanged for larger volume than the reference used. This minimal required volume is commonly called the representative elementary volume (REV). The upscaling principle is illustrated in Fig. 1.

Fig. 1

Sketch of the different scales involved in the upscaling procedure

At the pore scale, as classically admitted (Bear 1972), the single phase flow in porous media is governed by the Stokes equation. At the macro-scale, the fluid flow is commonly described by Darcy’s law (Whitaker 1986) and characterized by the macroscopic permeability, which can be evaluated by integrating the local fields. This upscaling work flow has several crucial aspects that may affect the resulting computed permeability.

Experimentally, the major source of uncertainty in permeability determination is the statistical error caused by the insufficient resolution. This can lead to a loss of essential local information of the materials (micro- and meso-porosities, pore geometry, pore network connectivity or surface roughness of the minerals) (Arns et al. 2005). The image processing, that also includes signal treatments and binarization processes, is known to affect the pore morphology reconstruction and therefore the transport properties (Andrä et al. 2013).

Numerically, several aspects can influence the computed macroscopic permeability such as the numerical method, for example. Finite volume (FV) (Gerbaux et al. 2010; Jones et al. 2003; Lemaitre and Adler 1990; Thovert et al. 2001; Thovert and Adler 2011) and lattice Boltzmann (Hyväluoma et al. 2012; Khan et al. 2012; Pazdniakou and Adler 2013) are the two most commonly used methods for pore-scale flow evaluation. It has been shown that the used numerical approach has non-negligible influence on the permeability determination (Manwart et al. 2002; Andrä et al. 2013). Moreover, considering a continuous approach such as the FV method, the mesh refinement affects also the local flow simulation and consequently macroscopic properties calculations.

Mainly due to the large computation time required in DRP, numerical simulations are usually performed on a cartesian grid mesh directly extracted from the initial tomographic image. However, the relative difference in terms of intrinsic permeability for different meshes obtained from the same tomographic image has not been explored. Finally, calculated macroscopic properties may depend on the boundary conditions used. The two main conditions are pressure imposed, which mimics an experimental permeameter configuration (Mostaghimi et al. 2013), and the resolution of a closure problem with periodic conditions (Anguy et al. 1994).

The main objective of this work is to evaluate the influence of the several parameters mentioned above (volume of the sample, mesh refinement level and applied boundary conditions) on the permeability computation for a single given sample. Direct numerical simulations are performed using the FV method implemented in the open-source platform OpenFOAM^® (2013). This software has efficient parallel capacities required for the following study, particulary for the mesh sensitivity study, which leads to large computation time.

We present first in Sect. 2 the technical aspects of the work flow (experimental and numerical). Then, numerical results are presented and discussed in Sect. 3: sample representativity, mesh sensitivity, configuration comparison and parallel efficiency.

2 Materials and Methods

In this technical section, we firstly describe the experimental imaging and associated post-processing of the considered sandstone sample. Next, we present the different aspects (boundary conditions, meshing, models and methods) used for the numerical evaluation of absolute permeability.

2.1 Experimental Imaging and Processing

The core plug used in this work is an outcrop Dausse sandstone (Permian) whose composition is close to the widely referenced Berea sandstone. The porosity, computed from binarized images of the core plug, is 12.7 %, and the detailed mineral composition of the sample is given in Table 1.

Table 1 Rock sample composition

2.1.1 Pore-Space Imaging Protocol

The used X-ray microscope computed tomograph (XRMCT) is the Versa 500 XRM manufactured by Xradia^®. The spatial resolution is purely determined by the selected objective and the geometrical magnification relative to source/object/detector distances. However, most of in-lab micro-tomographs exploit the geometrical magnification limited by the focus spot size. For the used XRMCT, the setup is based on an optical magnification of visible light by a microscope installed behind the scintillator to magnify the converted visible light. The limiting resolution is here due to Rayleigh’s diffraction criterion limiting the reachable detail $d$ to

$$\begin{aligned} d=\frac{1.22\lambda }{\hbox {N. A.}}, \end{aligned}$$

(2.1)

where $\lambda$ is the re-emitted wavelength by the scintillator once X-rays converted by the scintillator and N. A. is the numerical aperture of the microscope.

This XRMCT technology collects 1,000 radiographies at 1 s of exposure time and is performed at 60 kVp. The reconstructor, also developed by Xradia^®, provides a resolution of $9.6\,\upmu \hbox {m}$ per voxel. In a purely absorption mode, the gray values associated with each voxel are theoretically proportional to its X-ray attenuation. The refraction index $n$, in X-ray wavelengths, is defined as

$$\begin{aligned} n=1-\delta +i\beta , \end{aligned}$$

(2.2)

with $\delta$ related to the phase shift and $\beta$ to the attenuation of X-ray wave in a medium. The imaginary term is the absorption term, which is purely dependent on the electronic density of the material and the length of the wave vector. The naturally polychromatic X-ray light emitted from electron collisions on a tungsten anode is also the origin of numerous artifacts linked to the refraction terms, such as the phase propagation artifact or blurring caused by X-ray deviations. The occurring summation of the whole energies may also contribute to low contrast level between dissimilar materials. The low flux and low contrast specificities of the visible photons re-emitted by the X-ray scintillators are quite limited with the Versa 500 XRM thanks to the presence of a specific scintillator optimized in thickness and quantum efficiency. The coupled detector is a CCD manufactured by Andor^® technology. It is characterized by a very high detectability and low noise matched to low light fluxes conditions. Nevertheless, a few noisy pixels are produced by the detector. The filtered back projection algorithm contributes to produce additional noise mainly caused by the conical beam geometry.

However, in a transmitted mode of tomography, the refracted X-rays impact the detector, causing a blurring. This defect may alter the reconstructed image causing a phase propagation artifact at the origin of a ghost at the interface levels. It may be possible to reduce this structured artifact adjusting the relative positions between source, object and detector, but the most common process consists to apply an image treatment to eradicate the defect.

The complete 3D pore-space imaging is performed to $9.6\,\upmu \hbox {m}^{3}$ per voxel size with a total size of $4.272 \times 4.272 \times 3.437\,\hbox {mm}^{3} (\sim$62.7 mm$^{3})$. To reduce computational effort in the following sensitivity studies, the image is cropped to a sample size of $1.344 \times 1.344 \times 2.006\,\hbox {mm}^{3}~(\sim$3.62 mm$^{3})$.

2.1.2 Image Processing

Image processing is performed with the commercial software Avizo^® to regularize images. This step permits to avoid potential misclassification of materials during the segmentation phase. By eradicating noise and structured defects such as phase propagation, the voxels intensity values become representative of the refraction index and therefore of the material in the polychromatic X-rays conditions of the experiment. The used numerical filter is the bilateral filter. The dataset was segmented by choosing an intensity threshold, with values below the threshold assigned to one phase/material, and those above the threshold assigned to the other phase. Histogram thresholding is currently compared to obtained image to enhance the segmentation accuracy. The original plug and binarized sub-sample used are represented in Fig. 2.

Fig. 2

Visualization of a original core plug imaged and b considered sub-sample

2.1.3 Experimental Characterization

From the obtained binarized image, a REV analysis is performed to check that the concerned sample is representative of the studied porous medium. The applied REV determination method is the direct application of the Bear definition (Bear 1972), i.e., based on the sample computed porosity. Porosity is calculated from successive sub-volumes, obtained by progressive centered cropping of the full initial 3D volume, i.e., from $\sim$62.7 to $\sim$0.001 mm$^{3}$. This procedure is repeated until microscopic effects dominate the porosity measurement. Figure 3 reports the computed porosity as a function of the sample volume and exhibits a REV of about $1\hbox { mm}^{3}$. The volume of the core plug used for numerical computation $(3.62\hbox { mm}^{3})$ is larger than obtained REV and can therefore be considered, at least in terms of porosity, as representative of the studied porous medium. This result is in good agreement with the observations of Biswal et al. (1998) where REV characteristic size of 230–$700\,\upmu \hbox {m}$ in Berea sandstone has been determined using the same analysis in image processing.

Fig. 3

Sample porosity as a function of considered sub-volume. REV characteristic length size ($\sim$1 mm$^{3}$) is determined from this pore-space characterization [same procedure as Bear (1972)]

Note that the REV definition depends on the physical problem studied and, for that reason, the representativity of the sample is also explored numerically in terms of permeability in Sect. 3.1. The reference value of permeability for the following numerical study is the experimental value, measured on a sandstone sample using a pressure-decay profile permeameter. The size of the cylindrical core plug tested is 2 cm long and 8 mm diameter, and the measured liquid permeability is 320 mD.

2.2 Numerical Work Flow

In this subsection, we describe the different steps of the procedure used to evaluate the effective permeability from the digitalized rock surface, evaluating microscale flows.

The considered sample is a rectangular parallelepiped (the sub-sample presented in Fig. 2b) whose greatest length is the $z$-direction. The initial image is composed of $140 \times 140 \times 209$ voxels. The surface describing the fluid space is based on the original image voxels. The choice of keeping an hexahedral description of the surface is done to limit the influence of an additional processing.

2.2.1 Configurations

Two different numerical configurations, illustrated in Fig. 4, are used to determine the sample permeability. These configurations mainly differ in the boundary conditions used for the evaluation of the flow at the pore scale.

The first one mimics to the experimental setup of a permeameter (Fig. 4a). It consists in solving Stokes equations with a pressure difference imposed on either side of the sample and a no-slip boundary condition on the other faces of the sample.

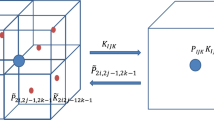
The second method consists in solving a closure problem, which has the structure a Stokes problem (see Sect. 2.2.3) and implies that the REV considered is periodic (Whitaker 1986; Quintard and Whitaker 1989). This is obviously not the case of the real sample used in our study, and it requires to artificially generate the periodicity by periodizing the sample as illustrated in Fig. 4b. The fields numerically solved are thus periodic in each spatial direction.

Fig. 4

Description of the two configurations used for the determination of permeability: a configuration 1 reproduces the experimental setup of a permeameter and b configuration 2 is based on the periodization (by symmetry) of the initial sample which enables the use of a volume averaging approach

In both configurations, a no-slip boundary condition is imposed at the solid surface and three calculations (one in each principal direction) are required to evaluate the permeability tensor. In the following, these two configurations are, respectively, referred as configuration 1 for fixed pressures boundary conditions and configuration 2 for periodic boundary conditions.

2.2.2 Meshes

Using the rock surface identified by image processing (see Sect. 2.1.2), we generate the mesh representing the pore space of the sample necessary to simulate fluid flow inside the porous medium. For that purpose, we used one of the native meshers of the open-source CFD toolbox OpenFOAM^®, snappyHexMesh. A hexahedral mesh perfectly matching the original surface mesh is thus reconstructed as depicted in Fig. 5.

Fig. 5

Visualization of the meshed pore space constructed from binary images. The sample is a parallelepiped $(\sim$1.3$\times 1.3\times 2\hbox { mm}^{3})$ and the $z$-direction is the larger one. This mesh respects the image resolution (one cell per voxel). The zoom permits to observe the local refinement of one pore space

The zoom on a part of the mesh (Fig. 5) allows to illustrate the initial refinement level, corresponding to the native image resolution (refinement level 1 is defined as one computational cell per voxel). In the following, refined meshes are generated from this initial level to check spatial convergence of computations. To increase refinement level, each cell is equally divided into eight new cells. The sample porosity and rock surface are unchanged.

Table 2 Spatial discretization and number of mesh elements for the different studied configurations

The different tested levels of refinement in this study are reported in Table 2. Three levels are used in the configuration 1, while only two levels are used in the configuration 2. For an equivalent refinement level, the configuration 2 needs eight times more cells because of the periodization (see Fig. 4b). Therefore, the third level of refinement in configuration 2 will require too much computational resources (more than 250 million of cells).

2.2.3 Mathematical Models

In the following, we consider two scales: the microscale, where the pore-space geometry of the sample is explicitly represented (see Fig. 1), and the macro-scale, where the sample is considered as a unique computation cell (containing both solid and pore space) with effective properties. In this study, we consider incompressible non-inertial single phase flow characterized by low Reynolds numbers, involving the resolution of Stokes’ equations. Neglecting gravity, the conservation and momentum equations at the pore scale read:

$$\begin{aligned} \nabla \cdot \mathbf{u}=0,\end{aligned}$$

(2.3)

$$\begin{aligned} \mu \Delta \mathbf{u}=\nabla p, \end{aligned}$$

(2.4)

where $\mathbf{u}(\mathbf{x})$ is the microscale velocity field, $p(\mathbf{x})$ the pressure and $\mu$ the dynamic viscosity of the fluid. At the macro-scale, the Stokes’ momentum Eq. 2.4 is reformulated as the so called Darcy’s law

$$\begin{aligned} \mathbf{v}=-\frac{\mathbf{K}}{\mu }\cdot \nabla P, \end{aligned}$$

(2.5)

where $\mathbf{v}$ is the average fluid velocity, $\mathbf {K}$ the permeability tensor and $\nabla P$ the macroscale pressure gradient. Using the Darcy’s law, the permeability tensor can be determined from pore-scale simulations, by averaging the microscale velocity field $\mathbf{u}(\mathbf{x})$ over the sample. Three simulations are performed, one for each spatial direction, and each simulation gives one column of the permeability tensor $\mathbf {K}$. For example, imposing $\Delta P_{x}$ along the $x$-axis across the sample, the first column of the permeability tensor is given by

$$\begin{aligned} K_{ix}=-\frac{v_{i}\mu }{\Delta P_{x}}\text { for }i=x,y,z, \end{aligned}$$

(2.6)

where $v_{i}$ is the $i$-th component of the Darcy velocity $\mathbf{v}$ inside the sample

$$\begin{aligned} \mathbf{v}=\frac{1}{V}\int _{V}\mathbf{u}(\mathbf{x})\, \hbox {d}V. \end{aligned}$$

(2.7)

with $V$ is the sample volume.

For the following sensitivity studies (mesh and methods), we mainly focus our attention on the diagonal part of the permeability tensor. To complete the set of Eqs. (2.3, 2.4), we need boundary conditions that depend on the different configurations described in Sect. 2.2.1.

For the configuration 1 (Fig. 4a), Dirichlet boundaries conditions are used for the pressure (inlet and outlet boundaries) and the velocity (lateral boundaries). When imposing a no-slip condition on lateral boundaries, this configuration mimics the classical experimental setup (Renard et al. 2001) to measure permeability and can be directly compared with experimental data (see comparison in Sect. 3.3).

For the configuration 2 (Fig. 4b), to impose periodic boundary conditions, the pressure gradient in Eq. (2.4) is decomposed as

$$\begin{aligned} \nabla p=\overline{\nabla p}+\nabla \tilde{p} \end{aligned}$$

(2.8)

with $\overline{\nabla p}$ an average pressure gradient and $\nabla \tilde{p}$ the deviation of the pressure gradient. The average pressure gradient is imposed as a volumic source term, and the computed deviation needs a pressure reference value (fixed at the outlet, for example). This configuration is, a priori, more representative of the real permeability because it mimics the encapsulation of the considered sample within a larger porous medium. However, as the periodicity is enforced by mirroring the sample, it could increase significantly computation time.

2.2.4 Numerical Methods

In previous DRP works, different numerical methods have been used to compute the fluid flow at the microscale. For example, finite difference (FD) method (Mostaghimi et al. 2012) and FV method (Petrasch et al. 2008) are classically used. Several works use also particle-based methods such as lattice Boltzmann methods (see, for example, Keehm et al. 2004; Boek and Maddalena 2010; Ahrenholz et al. 2006; Hyväluoma et al. 2012). Recently, a study comparing different numerical methods has been proposed (Andrä et al. 2013).

Simulations within the context of DRP involve a significant number of discretization cells and therefore require suitable software with parallel computation abilities. The open-source toolbox OpenFOAM^®, based on FV method, seems to be an appropriate platform thanks to its parallel capacities (Bijeljic et al. 2013). Our two different solvers are based on the classic Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm, and all the discretization schemes are second order. The required precision on the pressure field is of the order of $10^{-12}$.

3 Results and Discussion

In this section, we present and discuss numerical results obtained on the sample. First, the representativity of the sample, initially defined in terms of porosity, is also explored in terms of permeability. Then, the mesh sensitivity for permeability determination is discussed. Next, we compare the measures obtained using the different configurations (see Sect.  2.2.1). Finally, after a discussion about the non-diagonal terms of the permeability tensor, the parallel efficiency of the solvers used in this study is evaluated.

Figure 6 shows an illustration of the computed pressure and velocity fields in the configuration 1 for the mesh corresponding to original image resolution. It permits to bring out the preferential paths of the fluid flow through the rock in a permeameter configuration.

Fig. 6

Illustration of a pressure and b velocity vector field obtained on the considered sample in the configuration 1 with initial image refinement

3.1 Representativity of the Sample

To test the representativity of the considered sample, we evaluate using configuration 1 and refinement level 1 the equivalent permeability varying the volume of the considered region. Results are reported in Fig. 7.

Fig. 7

Relative error of $K_{zz}$ function of the normalized volume considered (configuration 1, refinement 1)

The different considered sub-volumes are constructed from the initial sample mesh, removing computational cells along sample boundaries. To respect the initial sample aspect ratio, note that the number of removed cells depends on the considered direction. For example, the initial sample has a size of $140\times 140\times 209$ voxels and the two first sub-volumes considered have $136\times 136\times 203$ (92 % of initial volume) and $132\times 132\times 197$ voxels (84 %).

We observe that the relative deviation for computed permeabilities in $z$-direction is lower than 7 % for sufficient large volumes (50 % of the initial volume). This does not allow to conclude on the representativity in terms of permeability of the considered volume but suggests that the permeability REV is approximatively reached. Note that the order of the characteristic length for the computed permeability REV (around 2 mm) is larger than that the porosity one (around 1 mm, see Fig. 3) computed from binarized images.

3.2 Mesh Sensitivity

The mesh sensitivity is discussed on the configuration 1 for which we dispose of three refinement levels. The diagonal terms of the obtained permeability tensor are reported in Table 3.

Table 3 Diagonal permeability tensor terms for the configuration 1 (in darcies) varying the mesh refinement

Table 4 shows the relative error evaluated following

$$\begin{aligned} \epsilon _{ii}=\frac{|K_{ii}^{3}-K_{ii}^{j}|}{|K_{ii}^{3}|}\,\,\hbox {with}\,\, i=x,y,z\quad \hbox {and}\,\, j=1,2 \end{aligned}$$

(3.1)

where the superscript $j$ is related to the refinement level (the maximal refinement, i.e., the level 3, is considered as the reference solution).

Table 4 Relative errors of the diagonal permeability tensor terms for the configuration 1

We observe that the sample permeability decreases when increasing the refinement level. The first refinement level exhibits a relative error close to 50 % while for the second, the relative error is reduced to 15 %. Moreover, these observations are consistent with those previously made on small size random media (Lemaitre and Adler 1990). This suggests that the numerical error of permeability determination is probably related to the number of cells discretizing the smallest pore spaces of a sample. This point also highlights the fact that the computed absolute permeability values must be taken with the greatest caution. Moreover, we cannot ensure that the third level is sufficient (see Sect.  3.3 for comparison with experimental data).

Anisotropic permeability is generally of great importance in reservoir engineering and can be evaluated using the anisotropy ratio $R$ (Clavaud et al. 2008) defined as

$$\begin{aligned} R=\frac{K_\mathrm{min}}{\sqrt{K_\mathrm{int}K_\mathrm{max}}}, \end{aligned}$$

(3.2)

where $K_\mathrm{min}, K_\mathrm{max}$ and $K_\mathrm{int}$ stand, respectively, for the minimal, maximal and intermediate value of diagonal permeability tensor. The permeability measurements performed by Clavaud et al. (2008) over a large set of various sandstone highlight a large range of possible values for anisotropy factor $R$. It varies from $0.84$ for the less anisotropic porous medium to $0.19$ for the higher anisotropic sample. Recently (Mostaghimi et al. 2013), numerical determination of permeability values was done using some samples, including sand packs and carbonates, and gave a ratio $R$ close to $0.78$ for sandstone and Berea sandstone. For our sample, the computed anisotropy ratio varies from $0.715$ for the refinement level 1 to $0.693$ for the level 3, i.e., of the same order as the study of Mostaghimi et al. (2013). We can note that even if the absolute permeability strongly depends on the considered refinement level, the anisotropy is conserved and is therefore well predicted by the coarsest mesh.

3.3 Comparison Between Experimental and Numerical Permeability Evaluations

The numerical permeameter configuration (configuration 1) can be compared to experimental values along the $z$-axis on the complete core plug. The relative differences with numerical evaluation of $K_{zz}$ are about 80 and 18 %, respectively, for the lower and higher refinement level. This highlights the fact that successive refinements on the same image are necessary and tend to improve the numerical permeability determination. However, the relative difference is not negligible even for the finest mesh and cannot be entirely attributed to numerical errors since numerical and experimental conditions are different. In the experiment, the permeability is measured on a much larger sample (the volume is close to 1,000 mm$^3$ in that case and $3.62\hbox { mm}^3$ for the numerical computation). Other possible physical sources of uncertainties might be caused, for example, by the presence of clay contents in the rock, which can react with the flow during experiment and modify locally fluid properties or pore-space geometry.

3.4 Comparison of Numerical Methods

The configuration 1 has a variant consisting in imposing a no-flux condition on the lateral borders instead of the no-slip condition. In practice, this configuration is obtained imposing a symmetry conditions on the lateral faces. We have compared results obtained with the two boundary conditions for the refinement level 1. We observe a difference around 1 % for the three spatial directions that permits to conclude about a weak impact of the lateral boundary conditions on the evaluation of the permeability tensor. We assume that the volume of the studied sample is sufficiently large to significantly reduce the boundary conditions effects. Variations of greater amplitude between the two methods can probably be observed when reducing the domain (sample) size.

Permeability determination is then performed with the configuration 2 and the diagonal terms obtained, for different refinement levels, are reported in Table 5.

Table 5 Diagonal permeability tensor terms for configuration 2 (in darcies)

For the same refinement level, we observe significantly superior values to those obtained with the configuration 1. Selecting configuration 2 as reference, the relative difference for refinement level 1 is superior to 27 % and is close to 7 % for refinement level 2. Numerical results highlight that the flow in a constrained environment, i.e., in the permeameter configuration, has a non-negligible influence on the computed permeability and potentially underestimates its value. However, this effect seems to decrease when increasing the refinement level.

The method comparison can also be performed in terms of complete permeability tensor. Off-diagonal terms are obtained by the transverse components of the averaged velocity field for a given main direction (see Eq. 2.6). We should note that in the configuration 2, the velocity averaging is performed on the initial sample and not on the whole computational domain. The domain mirroring imposes zero transverse components to the averaged velocity field. Note that this has no effects on the main component on the velocity as longitudinal components are the same in both cases. The numerical evaluations of permeability from pore-scale flow resolution do not guarantee the symmetry of the tensor, which depends on the used method. The symmetry of the tensor can be imposed by the used numerical method (periodic boundary conditions on the velocity) or by the reconstruction method used to compute the permeability (Piller et al. 2009). In the case of the direct computation from averaged velocity components (as in this study), the permeability tensor is by default non-symmetrical as reported by several studies (Manwart et al. 2002; Galindo-Torres et al. 2012; Khan et al. 2012).

From our computation at the first refinement, we obtain the following complete tensors (in darcies):

$$\begin{aligned} \mathbf{K}_{1}=\left( \begin{array}{ccc}0.762676 &{} 0.134729 &{} -0.138165\\ 0.077101 &{} 0.850044 &{} -0.036075\\ -0.043193 &{} -0.025040 &{} 0.576021 \end{array}\right) \end{aligned}$$

(3.3)

for the configuration 1 and

$$\begin{aligned} \mathbf{K}_{2}=\left( \begin{array}{ccc}1.027449 &{} 0.139428 &{} -0.146501\\ 0.084241 &{} 1.111863 &{} -0.040395\\ -0.047042 &{} -0.025816 &{} 0.847282 \end{array}\right) \end{aligned}$$

(3.4)

for the configuration 2. Note that configuration 2 gives also non-symmetry, even with periodic conditions, because averaging is performed on one-eighth of the field, i.e., the initial sample. The off-diagonal terms are, as for the main directions, superior for the configuration 2. However, the maximal absolute difference between the two methods is much lower ($\sim$0.008 darcies) than for the diagonal terms ($\sim$0.264 darcies). The relative difference between the two methods is inferior for the off-diagonal terms ($<$10 %) than for the diagonal terms ($>$20 %).

3.5 Parallel Efficiency

This study is based on the open-source platform OpenFOAM^®, and the domain decomposition method, available in the toolbox, used for parallel computing is scotch (Chevalier and Pellegrini 2008). The following tests have been performed on the Hyperion cluster¹ consisting in $368$ computation nodes of two quad-core Nehalem EX processors at $2.8$ GHz with $8$ MB of cache per processor. The reference computations are launched on $16$ cores, which represent an elementary block of the cluster. Computation time for $16$ to $256$ processors and for two refinement levels are reported in Fig. 8. This figure gives an order of magnitude of the required computational time ($\sim$2,200 s for the level 1 and $\sim$184,000 s for the level 2). This physical time strongly depends on several parameters, such as the fixed tolerance and the linear solvers.

Fig. 8

Evolution of the computational time function of cores number used for the configuration 1 and two refinement levels

The speedup $S$ for a computation with $n$ processors is computed as follows:

$$\begin{aligned} S_{n}=\frac{T_{16}}{T_{n}} \end{aligned}$$

(3.5)

where $T_{n}$ is the computation time for $n$ processors and the parallel efficiency $E_{n}$ is defined:

$$\begin{aligned} E_{n}=\frac{16}{n}S_{n} \end{aligned}$$

(3.6)

We reported the speedup of the solvers for the configurations 1 and 2, respectively, Fig. 9a, b for the same size of linear systems, i.e., for the same number of cells. It corresponds to the refinement level 2 for the configuration 1 and the level 1 for the configuration 2 (see Table 2). The scaling, shown in the $z$-direction, is similar for the other spatial directions.

Fig. 9

Strong scaling: a for the configuration 1 (refinement level 2, $z$-direction), this graph shows a superlinear scalability and b for the configuration 2 (refinement level 1, $z$-direction)

For the configuration 1, the observed speedup is better than the linear speedup: For $256$ processors, the parallel efficiency is even superior to 2 ($E_{256}\sim 2.12$). This superlinear speedup could be partially explained by a cache memory effect : The high access memory is needed because of the wide amount of meshes, which are subdivided when increasing the processors used. This behavior has already been observed on this platform with other solvers (Horgue et al. 2015). For each linear problem, it exists a number of processors from which the speedup should decrease and this limit has not been reached here.

For the configuration 2, the speedup is superlinear until $64$ processors ($E_{64}=1.24$) but decreases rapidly above $128$ processors ($E_{128}=0.81$). The main difference between the two cases is related to the boundary conditions: using periodic boundary conditions implies more information exchanges between processors than no-slip conditions. This may explain that the speedup break appears for fewer processors than in configuration 1.

4 Conclusion

In the study, we describe a complete work flow from pore-scale imaging to rock effective permeability determination. Due to the large computation time involved in such work, very few studies have explored the work flow sensitivity, whether in terms of mesh or configuration. Objective of this work was to evaluate these sensitivities using a open-source tool, OpenFOAM^®, in constant evolution and presenting interesting parallel abilities.

Preliminarily to this study, the representativity of the considered sandstone sample imaged with a resolution of $9.6\,\upmu \hbox {m}^{3}/\hbox {voxel}$ has been explored. The representativity of the sample, experimentally assumed in terms of porosity, has been confirmed numerically in terms of permeability. Then, the mesh sensitivity has been tested, and the study shows a maximal relative difference, which can reach 50 % between the original tomographic refinement and the finest tested mesh. The comparison with experimental results shows that the mesh refinement on a given tomographic image is necessary to improve permeability evaluation. In terms of configurations, the periodic one exhibits a permeability greater than about 20 % and also increases substantially the computation time required. However, we note that refining the mesh decreases the difference between the methods. We also noticed that relative difference was inferior for the off-diagonal terms, whose magnitude is lower. Finally, although this study was limited in terms of computing capacities ($256$ cores), the parallel efficiency study performed shows that the limit was not reached and, therefore, that is possible to perform simulations on finer grids using more computational cores.

Insufficiency in discretization process has the consequence to lead not only to an insufficiency in the description of micro- and meso-porosities, but also in the description of the grain curvatures especially in the narrow pores. The discretization problem is linked to the impossible representation of the continuum mechanics with a low level of gridding. Following the work flow presented herein, it is necessary to have a better representation of the surface between fluid and solid phases. This is clearly governed by technical constraint and reached resolution. A part of the forthcoming work will be to use volumic mesh conformal to the real non-voxelized surface.