1 Introduction

Fluid flow in composite channel has continued to attract interest because of its practical applications in geophysical environments and industries. These include engineering applications such as thermal-energy storage system, crude oil extraction, and cores of nuclear reactors.

Beavers and Joseph (1967) first studied the flow mechanism at porous/fluid interface utilizing the Darcy law to model flow in porous region. Neale and Nader (1974) showed that for the flow in a channel having fluid and porous region, the Darcy model with the Beavers-Joseph condition gives the same result as that obtained by using the Brinkman model when continuity of the velocity and shear stress at the interface is considered. Vafai and Kim (1990) revisited the work of Beavers and Joseph (1967) and obtained an exact solution describing the interfacial mechanics. Kuznetsov (1996) also carried out investigation of steady fluid flow in the interface region between a porous medium and clear fluid in channels partially filled with a porous medium by considering three different channels. Latter, Kuznetsov (1997) worked on the influence of the stress jump condition at the porous medium/clear fluid interface in a composite channel in steady-state operating condition.

Paul and Singh (1998) studied steady fully developed natural convection between coaxial vertical cylinders partially filled with a porous material. Paul et al. (1999) then worked on transient natural convection in a vertical channel partially filled with a porous medium using numerical method. Al-Nimr and Alkam (1998) used Green’s function method to obtain analytical solutions for problems of transient fluid flow in parallel-plate channels partially filled with porous material. The work of Hajipour and Dehkordi (2012) focused on the effect of inertial term and viscous dissipation on transient fluid flow and heat transfer in vertical channel partially filled with porous medium using numerical method. In another paper, Hajipour and Dehkordi (2011) considered mixed convective heat transfer of nanofluids in a parallel-plate channel partially filled with a porous material analytically and numerically for constant temperature boundary condition. The transient and non-Darcian effects on natural convection fluid flow in a vertical channel partially filled with porous medium are studied by Singh (2011). Singh and Gorla (2008) in their work on heat transfer between two vertical parallel walls partially filled with porous material, observed that for large values of Darcy number, the effect of Brinkman term is on the entire porous domain, while for small values of Darcy number, its effect is confined in the vicinity of the interface only. Jaballah et al. (2008) treated the numerical simulation of the heat transfer and the mixed convection of an incompressible fluid filling a horizontal channel, where some porous blocks were intermittently inserted transverse to the channel axis. Singh (2011) considered transient and non-Darcian effects on natural convection flow in a vertical channel partially filled with porous medium using the Forchheimer-Brinkman-extended Darcy model.

According to Muzychka and Youanovich (2006), Couette flow can be used as a fundamental method for the measurement of viscosity and as a means of estimating the drag force in many wall-driven applications. The case of heat transfer in Couette flow through a porous medium using a Brinkman-Darcy porous medium is investigated by Bhargava and Sacheti (1989). In a similar work, Daskalakis (1990) considered heat transfer in Couette flow through a porous medium of high Prandtl number fluid with temperature-dependent viscosity. Ochoa-Tapia and Whitaker (1995a, b) studied momentum transfer at the boundary between a porous medium and a homogeneous fluid. Kuznetsov (1998) utilized the boundary conditions at the interface suggested in Ochoa-Tapia and Whitaker to investigate Couette flow in a composite channel partially filled with a porous medium and partially with a clear fluid. Jain et al. (2006) studied Couette flow through a highly porous medium between two horizontal parallel porous flat plates with transverse sinusoidal injection of the fluid at the stationary plate and its corresponding removal by constant suction through the moving plate in a uniform motion. The effect of transpiration on free convective Couette flow in a composite channel was investigated by Jha et al. (2011). The paper concentrated on the analytical investigation of steady-state convective Couette flow of fluid between two vertical parallel plates partially filled with porous medium and partially with clear fluid in the presence of suction / injection.

The objective of this work is to analyze unsteady Couette flow in a composite channel partially filled with porous material using a semi-analytical approach which to the best knowledge of the authors has not been done yet. This study is limited to the fluid-flow analysis only. In it, the solutions of the governing equations are obtained by using a Laplace transform technique, while the Riemann-sum approximation method is used to invert the Laplace domain to the time domain.

2 Mathematical Analysis

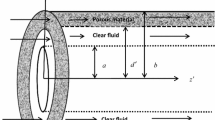
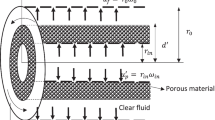
We considered unsteady Couette flow in a composite channel bounded by two infinite horizontal parallel plates as shown in Fig. 1

Fig. 1
figure 1

Geometrical illustration of the problem

Full size image

The gap between the plates is \(H\). The lower part of the channel is occupied by clear fluid \((0\le {y}'\le {d}')\), while the upper part \(({d}'\le {y}'\le H)\) is occupied by a fully saturated porous medium with uniform permeability.

The direction of the flow is taken along the horizontal \({x}'\)-axis, while the \({y}'\)-axis is taken perpendicular to it. At time \({t}'\le 0\), the fluid and the plate are assumed to be at rest. At time \({t}'>0\), the lower plate begins to move in its own plane with a constant velocity \(U_0 \). The governing equations in dimensional form are given as

$$\begin{aligned}&\displaystyle \frac{\partial {u}'}{\partial {t}'}=\nu \frac{\partial {u}'_\mathrm{f}}{\partial {y}'^{2}}\end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle \frac{\partial {u}'_\mathrm{p} }{\partial {t}'}=\nu _\mathrm{eff} \frac{\partial ^{2}{u}'_\mathrm{p} }{\partial {y}'^{2}}-\nu \frac{{u}'_\mathrm{p} }{k} \end{aligned}$$
(2)

The initial and boundary conditions in dimensional form are

$$\begin{aligned} \begin{aligned} {t}'&\le 0:{u}'_\mathrm{f} ={u}'_\mathrm{p} =0 \quad \mathrm{for} \quad 0\le {y}'\le H\\ {t}'&>0:\left[ {\begin{array}{ll} {u}'_\mathrm{f} =U_0 ,&{}\quad \mathrm{at}\;{y}'=0; \\ {u}'_\mathrm{p} =0,&{}\quad \mathrm{at}\;{y}'=H. \\ \end{array}} \right] \\ {t}'&>0:{y}'={d}'\left[ {\begin{array}{l} {u}'_\mathrm{f} ={u}'_\mathrm{p} ={U}'_i ; \\ \nu _\mathrm{eff} \frac{\partial {u}'_\mathrm{p} }{\partial {y}'}-\nu \frac{\partial {u}'_\mathrm{f} }{\partial {y}'}=\frac{\beta \nu {u}'_\mathrm{p} }{\sqrt{k}}. \\ \end{array}} \right] \\ \end{aligned} \end{aligned}$$
(3)

Introducing the following dimensionless quantities in Eq. (1)–(3),

$$\begin{aligned} y&= \frac{{y}'}{H};\quad \gamma =\frac{\nu _\mathrm{eff} }{\nu };\quad d=\frac{{d}'}{H};\quad Da=\frac{k}{H^{2}};\quad u_\mathrm{p} =\frac{{u}'_\mathrm{p} }{U_0 };\\ u_\mathrm{f}&= \frac{{u}'_\mathrm{f} }{U_0 };\quad U_i =\frac{{U}'_i }{U_0 };\quad t=\frac{{t}'\nu }{H^{2}} \end{aligned}$$

Equations (1) and (2) can then be written in dimensionless form as

$$\begin{aligned}&\displaystyle \frac{\partial u_\mathrm{f} }{\partial t}=\frac{\partial ^{2}u_\mathrm{f} }{\partial y^{2}}\end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \frac{\partial u_\mathrm{p} }{\partial t}=\gamma \frac{\partial ^{2}u_\mathrm{p} }{\partial y^{2}}-\frac{u_\mathrm{p} }{Da} \end{aligned}$$
(5)

subject to the following dimensionless initial and boundary conditions:

$$\begin{aligned} \begin{aligned}&{t}' \le 0:u_\mathrm{f} =u_\mathrm{p} =0,\quad \mathrm{for}\;0\le y\le 1 \\&t >0:\left[ {\begin{array}{l} u_\mathrm{f} =1,\quad \mathrm{at}\;y=0 \\ u_\mathrm{p} =0,\quad \mathrm{at}\;y=1 \\ \end{array}} \right] \\&t >0:y=d:\left[ {\begin{array}{l} u_\mathrm{f} =u_\mathrm{p} =U_i \\ \gamma \frac{\mathrm{d}u_\mathrm{p}}{\mathrm{d}y}-\frac{\mathrm{d}u_\mathrm{f} }{\mathrm{d}y}=\frac{\beta }{\sqrt{Da}}u_\mathrm{p}\\ \end{array}} \right] \end{aligned} \end{aligned}$$
(6)

The solutions of Eqs. (4) and (5) can be obtained using the Laplace transforms technique. Define the following transform variables:

$$\begin{aligned} \overline{{u}}\left( {y,s} \right) =\int _0^\infty {u\left( {y,t} \right) } e^{-st}\mathrm{d}t, \end{aligned}$$

where \(s\) is the Laplace parameter and \(s>0\). Taking the Laplace transform of Eq. (4) and (5),

$$\begin{aligned}&\displaystyle \frac{\mathrm{d}^{2}\overline{{u}}_\mathrm{f} }{\mathrm{d}y^{2}}-s\overline{{u}}_\mathrm{f} =0\end{aligned}$$
(7)
$$\begin{aligned}&\displaystyle \frac{\mathrm{d}^{2}\overline{{u}}_\mathrm{p} }{\mathrm{d}y^{2}}-\left( {\frac{s+\frac{1}{Da}}{\gamma }} \right) \overline{{u}}_\mathrm{p} =0 \end{aligned}$$
(8)

The solutions of Eqs. (7) and (8) are, respectively,

$$\begin{aligned}&\displaystyle \overline{{u}}_\mathrm{f} (y,s)=\frac{1}{s}\frac{\sinh \left( {\left( {d-y} \right) \sqrt{s}} \right) }{\sinh \left( {d\sqrt{s}} \right) }+\frac{U_i \sinh \left( {y\sqrt{s}} \right) }{s\sinh \left( {d\sqrt{s}} \right) }\end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle \overline{{u}}_\mathrm{p} (y,s)=\frac{U_i \sinh \left( {F\left( {y-1} \right) } \right) }{s\sinh (F\left( {d-1} \right) }, \end{aligned}$$
(10)

where

$$\begin{aligned} F&= \sqrt{\frac{s+\frac{1}{Da}}{\gamma }};\quad U_i =\frac{\frac{1}{\sqrt{s}}\sinh \left( {d\sqrt{s}} \right) -x_5 \sqrt{s}\cosh \left( {d\sqrt{s}} \right) }{x_2 x_3 -x_1 x_4 -\sqrt{s}\cosh \left( {d\sqrt{s}} \right) x_6 }; \\ x_1&= \gamma F\sinh \left( {dF} \right) -\frac{\beta }{\sqrt{Da}}\cosh \left( {dF} \right) ;\quad x_2 =\gamma F\cosh \left( {dF} \right) -\frac{\beta }{\sqrt{Da}}\sinh \left( {dF} \right) ; \\ x_3&= \frac{\cosh \left( F \right) }{\sinh \left( {F\left( {d-1} \right) } \right) };\quad x_4 =\frac{\sinh \left( F \right) }{\sinh \left( {F\left( {d-1} \right) } \right) };\quad x_5 =\frac{1}{s}\frac{\cosh \left( {d\sqrt{s}} \right) }{\sinh \left( {d\sqrt{s}} \right) };\\ x_6&= \frac{1}{\sinh \left( {d\sqrt{s}} \right) }. \end{aligned}$$

Equations (9) and (10) are then inverted in order to determine the velocities in the time domain. The numerical procedure used in Jha et al. (2011) and Khadrawi and Al-Nimr (2007) which is based on the Riemann-sum approximation is applied to find the inverse of Eqs. (9) and (10). In this method, functions in the Laplace domain can be transformed to the time domain as follows:

$$\begin{aligned} u(y,t)=\frac{e^{\varepsilon t}}{t}\left[ {\frac{1}{2}\overline{{u}}(y,\varepsilon )+Re\sum _{k=1}^N {\overline{{u}}\left( {y,\varepsilon +\frac{ik\pi }{t}} \right) \left( {-1} \right) ^{k}} } \right] \end{aligned}$$
(11)

where \(Re\) is “real part of,” \(i=\sqrt{-1}\), the imaginary number, \(N\) is the number of terms used in the Riemann-sum approximation, and is the real part of the Bromwich contour that is used in inverting Laplace transforms. The Riemann-sum approximation for the Laplace inversion involves a single summation for the numerical process. Its accuracy depends on the value of \(\varepsilon \) and the truncation error dictated by \(N\). In the work of Tzou (1997) the value of \(\varepsilon t\) that best satisfied the result is 4.7.

2.1 Skin Friction and Volumetric Flow Rate

The skin friction at \(y=0, \tau _0 (y,s)\), and \(y=1, \tau _1 (y,s)\) in terms of the Laplace parameter \(s\) is computed by differentiating Eq. (9) and (10), respectively. Similarly, the volumetric flux in terms of the Laplace parameter \(s, Q(y,s)\), is obtained by adding the integrals of Eqs. (9) and (10). The solutions are as follows:

$$\begin{aligned} \tau _0 (y,s)&= \frac{\mathrm{d}\overline{{u}}_\mathrm{f} (y,s)}{\mathrm{d}y}\bigg |_{{y}=0} \;=\frac{U_i }{\sqrt{s}\sinh \left( {d\sqrt{s}} \right) }-\frac{\cosh \left( {d\sqrt{s}} \right) }{\sqrt{s}\sinh \left( {d\sqrt{s}} \right) }\end{aligned}$$
(12)
$$\begin{aligned} \tau _1 (y,s)&= \frac{\mathrm{d}\overline{{u}}_\mathrm{p} (y,s)}{\mathrm{d}y}\bigg |_{{y}=\hbox {1}} =\frac{U_i F}{s\sinh (F(d-1))}\end{aligned}$$
(13)
$$\begin{aligned} Q(y,s)&= \int _0^d {\overline{{u}}_\mathrm{f} } (y,s)+\int _d^1 {\overline{{u}}_\mathrm{p} (y,s)} =\frac{\left( {U_i +1} \right) \left( {\cosh (d\sqrt{s})-1} \right) }{s\sqrt{s}\sinh (d\sqrt{s})}\nonumber \\&+\frac{U_i }{s\sinh (F(d-1))}\left( {\frac{1-\cosh (F(d-1))}{F}} \right) \end{aligned}$$
(14)

The solutions are converted to time domain by applying the Riemann-sum approximation stated in Eq. (11).

2.2 Validation of the Method

In order to validate the accuracy of the Riemann-sum approximation method, we set out to find the solution of the steady-state velocity analytically, which should coincide with the transient solution at large time. The expression for steady-state velocity distribution is obtained by setting \(\frac{\partial ()}{\partial t}\) in Eqs. (4) and (5) to zero. We now obtain the following ordinary differential equations:

$$\begin{aligned}&\displaystyle \frac{\mathrm{d}^{2}u_\mathrm{f} }{\mathrm{d}y^{2}}=0\end{aligned}$$
(15)
$$\begin{aligned}&\displaystyle \gamma \frac{\mathrm{d}^{2}u_\mathrm{p} }{\mathrm{d}y^{2}}-\frac{u_\mathrm{p} }{Da}=0 \end{aligned}$$
(16)

The solution of (15) and (16) using the boundary conditions stated in (6) is

$$\begin{aligned}&\displaystyle u_\mathrm{f} =\frac{U_i y}{d}-\frac{y}{d}+1\end{aligned}$$
(17)
$$\begin{aligned}&\displaystyle u_\mathrm{p} =\frac{U_i \sinh (\alpha (y-1))}{\sinh (\alpha (d-1)}, \end{aligned}$$
(18)

where

$$\begin{aligned} \alpha =\sqrt{\frac{1}{\gamma Da}};\quad x_7 =U_i \left( {\frac{\gamma \alpha \cosh (\alpha (d-1))}{\sinh (\alpha (d-1))}-\frac{1}{d}-\frac{\beta }{\sqrt{Da}}} \right) ;\quad U_i =-\frac{1}{dx_7 } \end{aligned}$$

The numerical results obtained for velocity using the Riemann-sum approximation method are found to be in excellent agreement with exact solutions obtained from solving Eq. (9) and (10) analytically when time is large as shown in Table 1. Furthermore, solving Eqs. (4) and (5) numerically using implicit finite difference method results in numerical values that agree with those obtained using Riemann-sum approximation method as shown in Table 1.

Table 1 Numerical values of the steady-state velocity obtained using the Riemann-sum approximation method, exact solution and implicit finite difference method when \(Da=0.1, \beta =0.7, \gamma =1.0, d=0.5\)
Full size table
Fig. 2
figure 2

Velocity profile showing the effect of \(t\left( {Da=1.0,\;d=0.5,\;\beta =-0.7,\;\gamma =0.5} \right) \)

Full size image
Fig. 3
figure 3

Velocity profile showing the effect of \(t\left( {Da=1.0,\;d=0.5,\;\beta =-0.7,\;\gamma =0.5} \right) \)

Full size image
Fig. 4
figure 4

Velocity profile showing the effect of \(t\left( {Da=0.01,\;d=0.5,\;\beta =-0.7,\;\gamma =0.5} \right) \)

Full size image
Fig. 5
figure 5

Profile of volumetric flux showing the effect of different values of \(t\) and \(\beta \,( d=0.5,\;Da=0.1,\;\gamma =0.5 )\)

Full size image
Fig. 6
figure 6

Profile of volumetric flux showing the effect of different values of \(t\) and \(\beta \, ( d=0.5,\;Da=0.01,\gamma =0.5)\)

Full size image
Fig. 7
figure 7

Profile of volumetric flux showing the effect of \(t\) and \(d\,( \beta =0.4,\;Da=0.1,\;\gamma =0.5 )\)

Full size image
Fig. 8
figure 8

Profile of volumetric flux showing the effect of \(t\) and \(d \left( {\beta =0.4,\;Da=0.01,\;\gamma =0.5} \right) \)

Full size image
Fig. 9
figure 9

Profile of skin friction at \(y=0, \tau _0\) showing the effect of \(t\) and \(\beta \;(Da=0.1, d=0.5, \gamma =0.5)\)

Full size image
Fig. 10
figure 10

Profile of skin friction at \(y=0, \tau _0\) showing the effect of \(t\) and \(d\; (Da=0.1, \beta =0.4, \gamma =0.5)\)

Full size image
Fig. 11
figure 11

Profile of skin friction at \(y=1, \tau _1\) showing the effect of \(t\) and \(\beta \; (Da=0.1, d=0.5, \gamma =0.5)\)

Full size image
Fig. 12
figure 12

Profile of skin friction at \(y=1\, \tau _1\) showing the effect of \(t\) and \(d\; (Da=0.1, \beta =0.4, \gamma =0.5)\)

Full size image
Fig. 13
figure 13

Profile of interfacial velocity, \(U_i\) showing the effect of \(t\) and \(\beta \; (Da=0.1, d=0.5, \gamma =0.5)\)

Full size image
Fig. 14
figure 14

Profile of interfacial velocity, \(U_i\) showing the effect of \(t\) and \(\beta \;( Da=0.01, d=0.5, \gamma =0.5)\)

Full size image
Fig. 15
figure 15

Profile of interfacial velocity, \(U_i\) showing the effect of \(t\) and \(d\; (Da=0.1, \beta =0.4, \gamma =0.5)\)

Full size image
Fig. 16
figure 16

Profile of interfacial velocity, \(U_i\) showing the effect of \(t\) and \(d\; (Da=0.01, \beta =0.4, \gamma =0.5)\)

Full size image
Fig. 17
figure 17

Profile of interfacial velocity, \(U_i\) showing the effect of \(t\) and \(Da\; (d=0.5, \beta =0.4, \gamma =0.5)\)

Full size image

3 Results and Conclusions

MATLAB program is written to compute and generate line graphs for velocity, skin friction at both plates, and volumetric flux for different values of the dimensionless parameters so as to comment on their relative significance in the flow formation.

The variation of velocity with time, \(t\) is illustrated in Figs. 2, 3, and 4 when Darcy number, \(Da\) is 1.0, 0.1, and 0.01, respectively. It is observed that for different values of \(Da\), velocity increases with \(t\). However, the rate of increase becomes smaller as \(t\) increases and finally steady state is reached. As \(Da\) increases, porous region becomes more permeable and this increase in permeability allows greater fluid motion in the porous region. A decrease in Darcy number therefore results in a decrease in velocity and steady state is reached faster for smaller value of \(Da\). This agrees with the finding of Kuznetsov (1997) who presented an exact solution for steady flow formation in composite channel.

Figures 5 and 6 depict volumetric flux, \(Q\) for different \(t\) and the adjustable coefficient in the stress jump boundary condition, \(\beta \) when \(Da=0.1\) and 0.01, respectively. It is observed that \(Q\) increases as increases but decreases as \(\beta \) increases. Steady state \(Q\) is reached faster with reduction in the value of \(Da\).

As \(d\) increases, thickness of clear fluid region increases and thickness of porous region decreases. From Figs. 7 and 8, it is clear that as \(d\) increases, \(Q\) increases. The increase is more obvious as time increases. This is physically true because as \(d\) increases, the thickness of the porous layer decreases and hence flow experiences less resistance. The rate of increase in \(Q\) is more significant in Fig. 7 than in Fig. 8 at high value of \(t\) because of the reduction in the value of \(Da.\)

Figure 9 shows variation in skin friction, \(\tau _0\), at \(y=0\), with respect to \(t\) and \(\beta \). It is observed that \(\tau _0\) decreases as \(t\) increases. It is also noticed that \(\beta \) suppresses \(\tau _0\) at the moving plate since \(\tau _0\) decreases as \(\beta \) increases. Variation of \(\tau _0\) with \(d\) is shown in Fig. 10, where \(\tau _0\) increases as \(d\) increases. Thus a thin porous layer induces high-fluid velocity resulting in larger skin friction at the plate \(y=0\). In both Figs. 9 and 10, \(\tau _0\) decreases as \(t\) increases and finally, steady state is reached.

Figure 11 shows the effect of \(t\) and \(\beta \) on skin friction \(\tau _1\), at \(y=1\). It is observed that \(\tau _1\) increases as \(\beta \) increases. The increase is more prominent as \(t\) increases. In Fig. 12, decrease in \(\tau _1\) is noticed as \(d\) increases. Increase in time results in a decrease in \(\tau _1\). Comparing Fig. 9 with Fig. 11, steady state is reached faster at the plate \(y=1\) than the plate \(y=0\).

The combined effect of \(t\) and \(\beta \) on interfacial velocity, \(U_i\) is depicted in Figs. 13 and 14 for \(Da=0.1\) and 0.01, respectively. It can be seen that \(U_i\) increases as \(t\) increases but decreases as \(\beta \) increases. This effect of \(\beta \) follows a similar trend as observed by Kuznetsov (1996) who considered steady-state interfacial fluid flow. \(U_i\) also decreases as \(d\) decreases. This is shown in Figs. 15 and 16. Steady state is reached faster for smaller value of \(Da\).

The effect of \(Da\) on \(U_i\) is shown in Fig. 17. For each value of \(Da, U_i\) increases as time increases until the steady state is reached. Also an increases in \(Da\) increases the interface velocity, \(U_i\).

4 Conclusion

An unsteady Couette flow formation in a composite channel partially filled with porous material is considered. Laplace Transform technique is used to solve the governing equations, while the Riemann-sum approximation method is used to invert the Laplace domain solution to the time-domain solution. The results obtained at large time using the Riemann-sum approximations method agree considerably with steady-state results derived exactly and that obtained numerically using implicit finite difference method, demonstrating the reliability of the Riemann-sum approximation method.

The roles of \(t, d, Da, \beta \), on velocity, skin friction, and volumetric flux are investigated. We conclude that the effect of time is significant in determining fluid velocity. Velocity increases with time for each value of the parameters considered. However, because the porous region creates resistance to the fluid flow, the fluid velocity decreases with distance away from the moving plate. Skin friction decreases, while volumetric flux increases as time increases. The value of \(\beta \) and \(d\) is significant in determining skin friction, volumetric flux, and interfacial velocity.