1 Introduction

Fine particles migration is one of the main reasons behind the formation damage in unconsolidated sandstone reservoirs (Boek et al. 2012; Civan 2010; Wong and Mettananda 2010). It has been explained by the release of indigenous particles from the surface of deep bed filters (porous media), their motion with the flow, and finally their deposition on the rock surface or capture at some pore throats (Ju et al. 2007). Pore throat blockage can drastically reduce the reservoir permeability resulting in severe decline in oil production rate. In addition, colloidal particles migration in the medium gives rise to many concerns such as sand production from wells, impairment of the downhole logging tools, wearing out of the downhole facilities like downhole pumps, screens, etc. Therefore, mitigation of fines migration is of great interest and various investigators suggested some remedies to control fines migration and remove the accumulated formation fines in the near wellbore region. These techniques include using organic/inorganic clay stabilizer agents, some acid systems to wash out the fines that plugged the pores in the near wellbore region, gravel packs, sand control screens, and some completion methods such as using sand exclusion component to reduce fines migration from the sandface (Belcher et al. 2010; Hibbeler et al. 2003; Huang et al. 2008a, b; Zhou et al. 1995). It seems that the aforementioned remedies are impractical and/or ineffectual or if they can be applicable, then they have some detrimental side effects.

Whether the particles adhere to the pore walls or dislodge and migrate through the medium is a function of some parameters such as fluid salinity, pH, particles-surface interaction, fluid rate, fluid viscosity, and temperature (Bedrikovetsky et al. 2011; Civan 2010; Gravelle et al. 2011; Khilar and Fogler 1998; Schembre and Kovscek 2004). Aforementioned parameters affect the surface forces existing between a fine particle and the rock surface which in turn, govern the particles’ fate in the medium. It is believed that the particle detachment occurs when the critical colloidal and hydrodynamic conditions are met (Civan 2007; Khilar and Fogler 1998). Entrapment of the already released fines at the pore constrictions can be occurred due to different capture mechanisms such as size exclusion, bridging or convective jamming, and surface deposition (Khilar and Fogler 1998). The size of the migrating fines with respect to the pore constrictions determines which of the aforementioned mechanisms take place.

Nanotechnology-assisted remedy seems to be very efficient to mitigate fines migration. Due to their size, which ranges from 1 to 100 nm, nanomaterials show very enhanced properties which are of great interest in many aspects of engineering. These properties of nanoparticles (NPs) include their very high specific surface area, distinguished heat conductivity and thermal properties, chemical potential to modify and alter the wettability of the reservoir rocks, surface charges, ability to alter the surface charge of the reservoir rock, and effects on the rheological properties of suspension and drilling muds (Ayatollahi and Zerafat 2012; Baird and Walz 2007; Maghrebi et al. 2012; Maghzi et al. 2011; Pourafshary et al. 2009; Rahbar et al. 2010; Rodriquez et al. 2009; Timofeeva et al. 2011; Vadasz 2011; Zamani et al. 2010). There are some indications in the literature addressing the remedial effects of NPs to fix in-situ tiny particles. NPs deposited on the medium surface can disturb the force balance existing between a particle and the rock surface. Therefore, strengthening the attractive forces due to the effect of NPs with respect to the repulsive ones can be a promising remedy to prevent the fine particles detachment (Ahmadi et al. 2013; Arab et al. 2013; Belcher et al. 2010; Habibi et al. 2013; Huang et al. 2008a, b, 2010).

Models of formation damage due to fines migration can be subdivided into two categories: microscopic models and phenomenological /macroscopic models. Micro-scale models represent the porous medium either as a collection of pores interconnected by throats which is the case in network models or as a series of elements consisting of a number of collectors that attract the fines which is the case in unit bed element (UBE) models (Boek et al. 2012; Rege and Fogler 1988; Schramm 1996; Sharma and Yortsos 1987). Phenomenological models consist of the mass conservation equations with some phenomenological coefficients which should be determined by matching the experimental results. We will follow this approach to model the fines migration in the medium treated by nanoparticles. In the current work, the classical filtration theory has been applied to quantify/describe the response of the NP-treated medium, as a system, to the flow of suspension through it. The filtration coefficients representing the total kinetics of the particles interactions with the bed surface have been calculated for various scenarios, and their variations with respect to time have been studied as well. Based on the optimized filtration coefficients, the model was utilized to history match the particles concentration breakthrough profiles obtained in the flooding tests. In addition, the effect of the bed surface potential, which is modified by the NPs deposited on the bed surface, on the filtration coefficients has been investigated. In the experimental section, five types of metal oxide NPs, \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\), CuO, MgO, \(\hbox {SiO}_{2}\) and ZnO, were chosen to investigate their effects on colloidal particles migration in the medium. In twelve flooding tests, a stable suspension was injected into the already NP-treated bed and fines concentration of effluents was measured using a turbidimeter apparatus. In addition, in order to investigate the effect of the type of NP dispersing fluid on the NPs’ performance, two sets of experiments were conducted. In the first set of experiments, NPs were uniformly dispersed in distilled water (DW) whereas in the second set of tests, NPs were dispersed in synthetic brine (SB).

2 Deep Bed Filtration Model

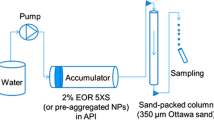
In order to predict the response of the NP-treated bed to the suspension transport through it, a phenomenological model has been developed. The model consists of solving mass conservation equation in order to describe the overall behavior of the filtration process. The conservation equation of migrating particles presents the change in the effluent’s particle concentration with time. In such a way, the bed capability to collect the suspended particles may be predicted from the calculated particles concentration breakthrough profiles. For that purpose, a system depicted in Fig. 1 was considered.

Fig. 1
figure 1

Schematic visualization of the colloidal particles filtration by the NP-treated medium

Full size image

Due to the very small value of the grain to bed diameter ratio, the flow within the bed is considered one-dimensional. In addition, the following assumptions are applied:

  • A stable non-flocculating suspension flows at a constant superficial velocity, \(u_\mathrm{s}\), through the bed which was treated by different kinds of nanofluids.

  • Due to the very small volume of the NPs deposited on the medium surface, the porosity change is neglected. In addition, it is assumed that the fine particles adsorbed on the NP-treated medium do not alter the bed porosity.

  • The permeable bed is isotropic and homogeneous.

  • Initially, there are no in-situ deposited fine particles in the packed bed.

  • The diffusive mass transfer in the axial direction is negligible compared with the convective transport.

As depicted in Fig. 1, \(C\) is the volumetric concentration of the particles dispersed in the flowing suspension, and \(\sigma \) is the volumetric concentration of the particles deposited on the surface of the bed which is a local function varying with time. For the system shown in Fig. 1, the mass conservation equation for particles migrating through the filter bed is given in Eq. 1.

$$\begin{aligned} u_\mathrm{s}\frac{{\partial C}}{{\partial z}} + \phi \frac{{\partial C}}{{\partial t}} + \frac{{\partial \sigma }}{{\partial t}} = 0. \end{aligned}$$
(1)

Here, \(\phi \) is the bed porosity and \(u_\mathrm{s}\) is the fluid superficial velocity. The rate of particles release or retention is reflected in the term \(\frac{{\partial \sigma }}{{\partial t}}\) which is called deposition rate. The deposition rate depends on the amount of particles available for retention which is quantified in \(C\), and also on the state of the filter medium which can be characterized by the amount of the particles deposited on the surface area per unit bed volume, \(\sigma \). It should be mentioned that since the homogeneous engineered porous medium was utilized in this work, the specific surface area of pores existing between the uniform grains of glass beads is assumed to be uniform across the bed. Thus, the deposition rate can be written as follows:

$$\begin{aligned} \frac{{\partial \sigma }}{{\partial t}} = u_\mathrm{s} \lambda (\sigma )C. \end{aligned}$$
(2)

Here, \(\lambda \) is called the filtration coefficient which is a criterion indicating the bed capability to filter the suspended particles. Equations 1 and 2 plus to an equation representing the filtration coefficient are called the classical filtration theory (Bedrikovetsky et al. 2011; Tien and Ramarao 2007; Wong and Mettananda 2010). This approach is the most commonly utilized method to evaluate colloidal particles migration deep into the bed and is also called the convective–diffusive attachment–detachment model (Bradford et al. 2003; Bedrikovetsky et al. 2011; Tien and Ramarao 2007; Tufenkji 2007).

It is customary to introduce a more convenient time variable (corrected time) which allows Eq. 1 to be written in its original form (Elimelech et al. 1998; Schramm 1996; Zamani and Maini 2009). The corrected time is given in Eq. 3.

$$\begin{aligned} \theta = t - \frac{{\phi z}}{{u_\mathrm{s} }}. \end{aligned}$$
(3)

The corrected time is a time variable which is placed at the front of the fluid. In other words, the corrected time has positive values after passing the real time which is required for the front of fluid to reach a specific axial distance. Furthermore, the negative values of the corrected time mean that the front of fluid does not already reach the axial point of interest, which is corresponding to the initial conditions of the filtration process.

After some mathematical manipulation, one can obtain Eq. 4 for the classical filtration equation. Thorough description of the mathematical manipulation is presented by Schramm (1996).

$$\begin{aligned} u_\mathrm{s} \frac{{\partial C}}{{\partial z}} + \frac{{\partial \sigma }}{{\partial \theta }} = 0. \end{aligned}$$
(4)

In practice, there is a very slight difference between the real and corrected time (Schramm 1996; Zamani and Maini 2009). Thus, Eq. 2 can be expressed as Eq. 5.

$$\begin{aligned} \frac{{\partial \sigma }}{{\partial \theta }} = u_\mathrm{s} \lambda (\sigma )C. \end{aligned}$$
(5)

By knowing the functionality of the filtration coefficient, \(\lambda \), from the deposited particles concentration, \(\sigma \), the system of Eqs. 4 and 5 subject to the appropriate initial and boundary conditions can be solved to predict the dynamic behavior of the bed filtration process. Initial and boundary conditions consistent with the system depicted in Fig. 1 are presented in Eqs. 6 and 7, respectively.

$$\begin{aligned}&\displaystyle C = 0, \sigma = 0\quad \hbox {for} \quad z \ge 0,\ \theta \le 0\end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle C = C_\mathrm{in}\quad \hbox {at} \quad z = 0,\theta > 0 \end{aligned}$$
(7)

The filtration coefficient, \(\lambda \), is a single parameter accounting different plausible mechanisms for particles deposition in the course of suspension transport in the bed. Therefore, different functions were suggested to account for the functionality of the filtration coefficient from particles size, pore geometry, suspension concentration, flow velocity, particle-grain, and particle–particle interaction (Bedrikovetsky et al. 2011, 2012; Wong and Mettananda 2010). The filtration coefficient is constant only during the initial stage of filtration and due to the particles retention within the bed and in turn alteration of the surface qualities of the bed, \(\lambda \) varies with time. In order to consider the variation of \(\lambda \) with time, Tien and Ramarao suggested the following relation (Tien and Ramarao 2007; Zamani and Maini 2009).

$$\begin{aligned} \lambda = \lambda _{0} F(\sigma ), \end{aligned}$$
(8)

where \(\lambda _{0}\) is the initial filtration coefficient and \(F(\sigma )\) is the correcting factor to account for the variation of \(\lambda \) with time; thus, at the initial stage of filtration in which no particles deposited on the bed: \(\lambda =\lambda _{0}\) and \(F (0) =1\). The filtration coefficient should be determined from the experiments with the specific filter bed and the suspension to be filtered. As mentioned, \(\lambda \) is a criterion indicating particles capture during suspension transport in the bed; therefore, in order to quantify the effect of NPs on the fines migration through the medium, we developed a macro-scale model to obtain \(\lambda \) for different scenarios.

In order to determine the initial filtration coefficient, \(\lambda _{0}\), we utilized the method suggested by Tien and Ramarao (Tien and Ramarao 2007). They utilized the particle concentration breakthrough history (\(C_{\mathrm{eff}}\) vs. \(\theta \)) to obtain the \(\lambda _{0}\). For the bed which is initially devoid of any indigenous deposited particles, the particle concentration profile throughout the bed can be described by the logarithmic law which is as follows (Iwasaki 1937; Tien and Ramarao 2007).

$$\begin{aligned} \frac{{\partial C}}{{\partial z}} = - \lambda C. \end{aligned}$$
(9)

Therefore, if a homogeneous suspension of constant particle concentration equal to \(C_{\mathrm{in}}\) is injected into the medium with the depth of L; one can obtain the normalized fine particle concentration breakthrough profile (\(C_{\mathrm{eff}}/C_{\mathrm{in}}\)) using Eq. 9.

In order to obtain the \(\lambda _{0}\), one has to measure the value of the effluent’s particle concentration (\(C_{\mathrm{eff}})\) at \(\theta =0\) from the flooding experiments. However, measuring such a value is very difficult if not impossible. Instead, one can measure the particle concentration breakthrough history over an interval of time (\(C_{\mathrm{eff}}\) vs. \(\theta \)) and then, \(\lambda _{0}\) can be determined from Eq. 10.

$$\begin{aligned} \lambda _{0} = \frac{1}{L}\mathop {\lim }\limits _{{\theta \rightarrow 0}} \left[ {\hbox {ln}\left( {\frac{{C_{\mathrm{in}} }}{{C_{\mathrm{eff}} }}} \right) }.\right] \end{aligned}$$
(10)

In other words, \(\lambda _{0}\) can be obtained by knowing the limiting value of \(\hbox {ln}{\frac{{C_{\mathrm{in}} }}{{C_{\mathrm{eff}} }}}\) at \(\theta \rightarrow 0\) which can be determined from a given particle concentration breakthrough profile. It should be mentioned that the obtained \(\lambda _{0}\) from the aforementioned procedure was utilized as the initial guess. The optimized values of the filtration coefficient including the initial filtration coefficient are obtained in the course of the data processing.

As mentioned, deposition of the colloidal particles on the surface of deep bed filters during suspension transport in the medium is, by nature, an unsteady state phenomenon. Particles retention may alter the bed structure and surface circumstances which in turn, results in alteration of the filter’s ability to collect the suspended particles and also, the required pressure drop across the filter to maintain a constant flow rate. The bed quality can be enhanced due to the deposition of the particles on the medium surface (Jung and Tien 1992; Tien and Ramarao 2007). In such a case, deposited particles act as additional collectors which in turn, enhance the ability of the medium to filter the suspended colloidal particles. In this case, \(F\) is an increasing function of \(\sigma \), and the particle concentration breakthrough profile (\(C_{\mathrm{eff}}\) vs. time) can be expected to decrease as time passes. On the contrary, if the nature of the particle-particle surface interactions is less favorable than that of the particle-bed surface, the filter performance deteriorates with time which makes the particle concentration profile ascendant (Johnson and Elimelech 1995; Liu et al. 1995). In such a scenario, \(F\) is a decreasing function of \(\sigma \) which indicates the deterioration of the bed ability to filter the suspended particles with respect to time, and one expects an increase in particle concentration profile in the course of filtration. The combination of the two aforementioned behaviors is also reported, in which the filter performance initially improves in the course of filtration and then deteriorates with further particles deposition (Ahfir et al. 2009; Vigneswaran and Chang 1989). The initial increase of \(F\) followed by its decline with further deposition (increasing the \(\sigma \)) depicts this combined behavior. Therefore, based on the particle concentration history observed in the experiments, one should select the congruous equation for the filtration coefficient which appropriately addresses the filtration behavior. Based on the three possible aforementioned behaviors, different kinds of empirical expressions of \(F (\sigma )\) have been suggested by various investigators (Tien and Ramarao 2007).

Bai and Tien presented a general method to obtain the filtration coefficient from effluent’s particle concentration history. They suggested a general function for \(F\) which is an approximation of all the possible functions of \(F\) (Bai and Tien 2000; Zamani and Maini 2009). This function, which expresses all of the aforementioned filtration behaviors, is given in Eq. 11.

$$\begin{aligned} F(\sigma ) = 1 + \sum \limits _{{i = 1}}^{n} {K_{i} \sigma ^{i} }, \end{aligned}$$
(11)

where \(K_{i}\) are the coefficients which should be determined in the course of the experimental data processing. In their work, \(F\) is assumed to be a polynomial of order 3; however, the limitation can be easily eliminated if necessary. Thus, the filtration coefficient is as follows:

$$\begin{aligned} \lambda = \lambda _{0} \left( {1 + K_{1} \sigma + K_{2} \sigma ^{2} + K_{3} \sigma ^{3} } \right) . \end{aligned}$$
(12)

Combining Eqs. 9 and 12 and integrating from \(z=0\) to \(z=L\), one has:

$$\begin{aligned} C_{\mathrm{eff}} = C_{\mathrm{in}} e^{{ - \lambda _{0} L}} e^{{- \lambda _{0} \left[ {K_{1} \int \limits _{0}^{{_{L} }} {\sigma \mathrm{d}z + K_{2} \int \limits _{0}^{L} {\sigma ^{2} \mathrm{d}z_{{}} } } + K_{3} \int \limits _{0}^{L} {\sigma ^{3} \mathrm{d}z} } \right] }}. \end{aligned}$$
(13)

Using Eq. 13 with the initial guess for the coefficients of the \(F\) function (i.e., \(K_{i}\)), the effluent’s particle concentration profile can be calculated. Afterwards, by solving a nonlinear least square (NLLSQ) problem to minimize the objective function presented in Eq. 14, one can obtain the optimum values for the coefficients, \(K_{i}\), to be searched.

$$\begin{aligned} \psi = \sum \limits _{{j = 1}}^{M} {\left[ {(C_{\mathrm{eff}} )_{\mathrm{exp }} - C_{\mathrm{in}} e^{{ - \lambda _{0} L}} e^{{ - \lambda _{0} \left[ {K_{1} \int \limits _{0}^{L} {\sigma \,\mathrm{d}z} + K_{2} \int \limits _{0}^{L} {\sigma ^{2} \,\mathrm{d}z} + K_{3} \int \limits _{0}^{L} {\sigma ^{3} \,\mathrm{d}z} } \right] }} } \right] ^{2} _{j}}. \end{aligned}$$
(14)

As inferred from Eq. 14, the proposed method is based on the comparison of the effluent’s particle concentration history predicted by the model with the history obtained from the experiments. Bai and Tien assessed the results of the proposed search algorithm with the data of transient state deep bed filtration which was previously published by Vigneswaran and Chang (1989) and Liu et al. (1995). They reported that the algorithm yields correct results which are independent of the initial guesses for the \(K_{i}\) coefficients (Bai and Tien 2000).

In the current work, a FORTRAN program was written to simultaneously solve the system of Eqs. 4, 5, 6, and 7 in order to predict the response of the NP-treated bed to fines migration through it. The general expression for the filtration coefficient (Eq. 12), which is proposed by Bai and Tien, was applied and the search algorithm was utilized to optimize the coefficients (\(\lambda _{0},\,K_{1,}K_{2,}\) and \(K_{3})\). Optimum values of filtration coefficients have been obtained by minimizing the objective function presented in Eq. 14. As reported by Bai and Tien, it was found that the algorithm presents the unique results with different initial guesses which revalidates the independency of the algorithm from the initial guess. Finally, based on the optimized filtration coefficients, the model was applied to calculate the particle concentration breakthrough profiles for different scenarios which are well matched with the lab data.

3 Experiments

In order to investigate the effect of NPs on fines migration in porous media, two series of core flooding experiments were conducted and particle concentration breakthrough profiles were obtained. In order to mimic sandstone reservoirs in which fines migration is a challenging problem, spherical glass beads with an average diameter of 420–595 microns (30–40 U.S. mesh) were utilized. The glass beads were packed into a sleeve of 11.5–cm length and 3.8–cm diameter. A prepared core was fitted into the core holder and 700 psia overburden pressure was applied to its surroundings. In order to saturate the porous medium, the packed bed was vacuumed for 2 h. Then the porous medium was saturated with different types of nanofluids. After that, the medium was soaked with the nanofluids for 24 h. Subsequent to the soaking time, a stable suspension including naturally occurring fine particles, cationic surfactant, and distilled water was injected into the already NP-treated bed and particle concentration breakthrough profile was analyzed using a turbidimeter apparatus (Hach 2100 Q). It should be mentioned that the injection rate of suspension was held constant at \(4\,\hbox {mL min}^{-1}\) in all the experiments. The schematic view of the experimental set-up is shown in Fig. 2.

Fig. 2
figure 2

Schematic view of experimental set-up

Full size image

As shown in Fig. 2, there is a valve prior to the inlet of the core which was used to take four influent samples. After taking these influent samples, the flooding tests were started. The influent concentration was determined from the average of these samples’ concentrations. This procedure was repeated in all the tests in order to obtain the precise concentration of the influent suspension.

In order to investigate the effect of the type of NP-dispersing fluid on the treatment efficiency, two sets of flooding experiments were designed. In the first set of experiments, NPs were uniformly dispersed in DW using an ultrasonic probe. The selected concentration of NPs was constant and equal to 0.03 wt% for different scenarios. In the second set of experiments, NPs were dispersed in SB containing NaCl (0.03 M) and then utilized to saturate the bed. In addition, the fine particles suspension utilized in this set of tests was prepared by SB. The salinity of the suspension was chosen exactly the same as that of the NP- dispersing fluid (i.e., 0.03 M of NaCl); therefore, in this way one can conclude that the potentially remedial effects on the migration of colloidal particles in the medium solely resulted from the NPs deposited on the surface of the beads. It is believed that there exists a critical salt concentration (CSC) in the water sensitive sandstones, below which particles tend to dislodge and migrate through the medium. The CSC depends on the valency of the cations and the type of porous media in which fine particles migrate (Khilar and Fogler 1998; Kia et al. 1987). The CSC for the solution containing \(\hbox {Na}^{+}\) cations permeating into a packed bed of glass beads, which is the case of this study, is equal to 0.2 M (Khilar and Fogler 1998). So, the selected salt concentration of the suspension (0.03 M of NaCl) is much lower than the critical salt concentration for \(\hbox {Na}^{+}\) cations. In this way, we tried to ensure that the adsorption of suspended colloidal particles on the medium surface did not occur due to the effect of salt concentration.

The utilized fine particles were characterized using X-ray fluorescence (XRF) method, and the results are presented in Table 1. It should be mentioned that the mean grain size of dry fine particles is between 1 and 10 microns, and the precise particle size existing in the suspension is equal to 1.34 microns which was obtained by the dynamic light scattering (DLS) method.

Table 1 Mineralogy of fine particles based on XRF
Full size table

Nanosized gamma alumina (\(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\)), copper oxide (CuO), silica (\(\hbox {SiO}_{2}\)), magnesium oxide (MgO), and zinc oxide (ZnO) nanoparticles were purchased from U.S. Research Nanomaterials Company, and their characteristics are shown in Table 2. The main criterion for the selection of the NPs was their role in adsorption phenomena reported in the literature as well as their specific surface area. Furthermore, in order to compare the capability of the NPs to alter the surface charges of the glass beads, zeta potential analysis was done using a Zetasizer Nano series (Malvern Instrument Inc., London, UK, ZEN 3600).

Table 2 Characteristics of nanoparticles
Full size table

4 Results and Discussion

4.1 Core Flood Experiments Results

As mentioned, prior to the flooding tests the medium was saturated with different types of nanofluids, whereas in the reference tests, the medium was saturated with DW and SB (0.03 M NaCl) in the first and seventh experiments, respectively. The specifications of the experiments are presented in Table 3. In each test, the influent suspension concentration was measured based on the turbidity analysis, and the results are presented in nephelometric turbidity units (NTU) (Table 3).

Table 3 Specification of the core-flooding tests
Full size table

The fine-particle concentration of effluents obtained at different values of pore volume injected (PVI) are presented in Fig. 3. In order to compare the capability of different NPs to adsorb the migrating fines, the particle concentration breakthrough profiles got dimensionless with respect to the pertinent influent suspension concentrations presented in Table 3.

Fig. 3
figure 3

Dimensionless form of particle concentration breakthrough profiles: a for the tests which were done with distilled water; b for the tests which were done with synthetic brine

Full size image

It was found that soaking the porous medium with a nanofluid slug can be a very promising remedy to mitigate fines migration. As inferred from Fig. 3, the fine particle concentration breakthrough profiles for the NP-treated scenarios have dramatically lower values with respect to that of the reference tests. Furthermore, the ionic strength of the NP-dispersing fluid was recognized as an important parameter that critically affects the NP’s capability to adsorb the suspended colloidal particles. Among the tests with distilled water, ZnO NP is the best adsorbent of migrating fines (Fig. 3a). Gamma alumina NP dispersed in SB acts as a distinguishably good adsorbent of migrating particles. As Fig. 3b shows, more than 70 % of the particles existing in the influent were adsorbed by the bed treated by SB-based \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\) nanofluid. In order to specify the effect of NPs on migrating fines, zeta potential of the beads in different scenarios was measured, and the results are presented in Table 4.

Table 4 Zeta potential of the beads in different scenarios
Full size table

As Table 1 indicates, more than 80 weight percentages of the utilized fines are silica which is the main mineral-constituting sandstone rocks. The negative charges on the surface of these fines cause them to become dislodged from the surface of the similarly charged medium and as a result, migrate through the bed. This occurrence resulted from the electrical double layer repulsive forces forming between a fine and the rock surface. Based on the results presented in Table 4, the presence of NPs on the surface of the bead alters the surface charge of the beads, which is the main parameter affecting the fate of the migrating fines. In addition, the salinity of the NP-dispersing fluid has a critical effect on the NPs’ ability to alter the surface charge of the beads.

In our previous work, we presented a comprehensive description of surface forces and applied Derjaguin–Landau–Verwey–Overbeek (DLVO) theory as a quantified tool to reflect the effect of NPs on improving the zeta potential of the beads (Arab et al. 2013). The dimensionless form of the DLVO potentials existing between a fine and the bed surface is presented in Fig. 4. It should be mentioned that the positive and negative signs indicate the repulsive and attractive surface forces, respectively. Furthermore, the DLVO potentials include electric double layer repulsion, London–van der Waals attraction, Born repulsion, and hydrodynamic potentials. One can find the detailed description of all the aforementioned potentials and their formulas in our previous work (Arab et al. 2013).

Fig. 4
figure 4

Dimensionless form of DLVO potentials as a function of the particle–surface separation distance: a for the tests in which NPs were dispersed in DW; b for the tests in which NPs were dispersed in SB (Arab et al. 2013)

Full size image

As inferred from Fig. 4, for the reference tests, the energy barrier formed by the electric double layer repulsion potential makes the DLVO potentials repulsive which in turn, causes the particles to become dislodged from the surface. Due to the NP-assisted surface charge modification of the beads, there is a critical reduction of electric double layer repulsion potential. Accordingly, no repulsive energy barrier exists for the scenarios treated by NPs, and the resultant force is much more attractive which facilitates the adsorption of suspended particles on the medium surface. This is especially observed in the case treated by SB-based \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\) nanofluid. The differences among the NP-treated cases resulted from different capabilities of NPs to alter the zeta potential of the beads. So commensurate with the capability of NPs to make the surface charge of the beads more positive, the resultant surface forces are more attractive and as a result, there will be the greater tendency for the beads to adsorb the negatively charged suspended fines. Based on the aforementioned point, the remedial effect of NPs on adsorbing the suspended fines (Fig. 3) can be justified.

Table 4 indicates that \(\hbox {SiO}_{2}\) NP shows a slight capability to alter the surface charge of the bed, but on the contrary, the bed treated by silica NP shows a relatively good tendency to filter the suspended particles (Fig. 3). This remedial effect of \(\hbox {SiO}_{2}\) NP on migrating fines resulted from its critically high specific surface area compared with the other nanoparticles. Specific surface area is a controlling parameter in adsorption phenomena. As Table 2 indicates, the specific surface area of SiO\(_{2}\) nanoparticle is more than \(600\,\hbox { m}^{2}\hbox { g}^{-1}\); therefore, the presence of \(\hbox {SiO}_{2 }\) nanoparticle on the surface of the glass beads provides more collector sites on which the suspended particles have the chance to attach.

4.2 Mathematical Modeling Results

As mentioned, a phenomenological model was developed for modeling the suspension transport through the NP-treated medium. The model was used to history match the particle concentration breakthrough profiles obtained in the flooding tests. Figures 5 and 6 present the fine-particle concentration breakthrough profiles calculated by matching the results of the core-flooding experiments.

Fig. 5
figure 5

Matching experimental results of particle concentration breakthrough profiles by the deep bed filtration model: a 1st; b 2nd; c 3rd; d 4th; e 5th, and f 6th run

Full size image
Fig. 6
figure 6

Matching experimental results of particle concentration breakthrough profiles by the deep bed filtration model: a 7th; b 8th; c 9th; d 10th; e 11th, and f 12th run

Full size image

As can be inferred from Figs. 5 and 6, the model results match the results of the flooding tests remarkably well. However, since the model does not consider the mass transfer due to diffusion, the breakthrough time predicted by the model is at \(\theta =0\), or:

$$\begin{aligned} t = \frac{{\phi L}}{{u_\mathrm{s} }}. \end{aligned}$$
(15)

It should be mentioned that prior to the breakthrough time the effluents contain the pertinent fluid which was utilized to saturate the core. Accordingly, it is reasonable that the model predicts the experimental behavior for the effluents obtained subsequent to 1 PVI (Figs. 5 and 6).

Table 5 presents the optimized values of \(\lambda _{0 }\)and matching parameters, \(K_{1},\, K_{2}\), and \(K_{3}\), for each test.

Table 5 Optimized \(\lambda _{0}\) and matched coefficients of \(F\) function: \(K_{1},\, K_{2}\), and \(K_{3}\)
Full size table

In order to quantify the effect of NPs on improving the bed performance to filter the suspended particles, filtration coefficients were obtained for different scenarios. The filtration coefficients were calculated using Eq. 12 and based on the optimized values of the matching parameters presented in Table 5. As Eq. 12 indicates, \(\lambda \) is a function of \(\sigma \) which is a time-dependent local function. Accordingly, \(\lambda \) is also a function of spatial coordinate and time. The values of \(\lambda \) at different values of PVI for the two sets of lab data are presented in Fig. 7. It should be mentioned that the filtration coefficients were calculated at the axial distance near the outlet of the core. In this way, the filtration coefficients can be utilized to explain the fine-particle concentration of effluents obtained in the flooding tests.

Fig. 7
figure 7

Filtration coefficients versus PVI: a for the tests which were done with distilled water; b for the tests which were done with synthetic brine

Full size image

Prior to 1 PVI, because the suspension front has not reached the end of the core the filtration coefficients are constant and equal to the initial filtration coefficients, \(\lambda _{0}\) (Fig. 7). After this time, some suspended particles separate from the fluid and attach on the bed surface which in turn, alters the bed quality to filter the forthcoming particles. In all the scenarios, the filtration coefficients decline during the course of filtration process which indicates the deterioration of the bed capability to filter the suspended particles with respect to time. Due to this deterioration of the bed capability to adsorb the fines, all the particle concentration breakthrough profiles increase as time passes (Figs. 5 and 6). This increase in the particle concentration breakthrough profiles with time indicates that the particle-bed surface interactions are more favorable for particle capture than that of the particle–particle. In addition, although the filtration coefficients decline with time, they have values greater than zero which indicates the adsorption of some particles on the pore wall even after six PVI. Due to the adsorption of fines on the bed surface at the late times, the normalized particle concentration breakthrough profiles do not meet the fine-particle concentration of the influents (i.e., \(C_{\mathrm{eff}}/C_{\mathrm{in}}\,<\,1\)) (Fig. 3).

As mentioned, NP deposited on the bed surface significantly alters the zeta potential of the medium which in turn, reduces the repulsive electrostatic forces existing between a fine particle and the bed surface (Fig. 4). Therefore, due to this NP-assisted surface charge modification, the bed shows a strong tendency to filter the suspended fine particles. This effect of NP on migrating fines can be quantified by the matched filtration coefficients. As inferred from Fig. 7, the filtration coefficients for the NP-treated scenarios are of greater values than that of the reference tests, which evinces the greater tendency of the treated bed to adsorb the migrating fines compared with the non-treated case. The results presented in Fig. 7 are in broad agreement with the fine-particle concentration breakthrough profiles presented in Fig. 3. Based on the results presented in Fig. 7, it can be concluded that the filtration coefficient is a criterion reflecting the zeta potential of the bead. The increase in the zeta potential of the bead, resulted from the effect of NPs, results in an increase in the matched filtration coefficient. The greater filtration coefficient indicates the stronger tendency of the treated beads to collect the fines. Therefore, the matched filtration coefficients obtained from the macro-scale model appropriately address the remedial effect of NPs on migrating fines. Furthermore, by comparing Figs. 4 and 7, one can conclude that the matched filtration coefficients are in good agreement with the calculated surface forces which are representative of the micro-scale viewpoint, so that the filtration coefficients are of greater values for the scenarios in which the surface forces are more attractive.

As Fig. 7a indicates, there is a slight difference between the matched filtration coefficients for the cases treated by \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\), MgO, and ZnO NPs. This resulted from the approximately similar capabilities of these NPs, dispersed in DW, to improve the zeta potential of the bed (Table 4). As mentioned, although the presence of \(\hbox {SiO}_{2}\) NP on the bead’s surface does not noticeably modify the SC of the bead, the treated bead shows a noticeable tendency to adsorb the migrating fines which resulted from the high specific surface area of silica nanoparticle. Accordingly, the filtration coefficient for the case treated by silica nanoparticle is of pretty high value. Figure 7b shows the matched filtration coefficients at different values of PVI for the scenarios in which NPs were dispersed in SB. Among these tests, \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\) NP showed very distinguished remedial effect on adsorbing the migrating fines, which resulted from the critically good capability of \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\) NP to enhance the zeta potential of the beads. As Fig. 4b indicates, for the case treated by SB-based \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\) nanofluid, the DLVO potential is remarkably attractive, and as a result, the filtration coefficient is of critically high value (Fig. 7b) which justifies the critical adsorption of fines (Fig. 3b).

5 Conclusion

Deep bed filtration model was developed to quantify the effect of nanoparticles on migrating fines. The filtration coefficients representing the total kinetics of the particles’ interactions with the bed surface were calculated based on the optimization work. Based on the optimized filtration coefficients, the model was utilized to history match the particle concentration breakthrough profiles obtained in the flooding tests. In the core flood experiments, five types of metal oxide NPs, \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\), CuO, MgO, \(\hbox {SiO}_{2}\), and ZnO, were utilized to treat the core. Two series of tests were done to investigate the effect of the type of NP-dispersing fluid on the efficiency of the treatment. The zeta potential of the bed was recognized as an import parameter that critically affects the filtration process. It was found that the presence of NPs on the bed surface alters the zeta potential of the bed which in turn, facilitates the adsorption of fines on the bed surface. Among the tests with distilled water, ZnO NP was found as the best adsorbent of fines. The results showed that the salinity of the nanofluid is an important parameter which governs the capability of NPs to enhance the zeta potential of the bed. The filtration coefficient was recognized as a criterion representing the effect of nanoparticles to modify the surface charge of the bed. The NP-assisted increase in the zeta potential of the bead results in an increase in the matched filtration coefficient which justifies the stronger tendency of the treated bead to collect the fines. By comparing the results with our previous work, it is concluded that the matched filtration coefficients obtained from the macro-scale model and the DLVO potentials, which are representative of the micro-scale viewpoint, are two different quantified tools which are in agreement to represent the remedial effect of NPs on migrating fines. It was found that the filtration coefficients are of greater values for the scenarios in which the DLVO potentials are more attractive. The DLVO potentials for the case treated by SB-based \(\upgamma \hbox {-Al}_{2}\hbox {O}_{3}\) nanofluid is dramatically attractive, and as a result, the filtration coefficient is of remarkably high value which justifies the critically adsorption of fines in this scenario. The predicted particle concentration breakthrough profiles remarkably well matched with the experimental data.