1 Introduction

Modeling of fluid flow in naturally fractured reservoir (NFR) is a topic of great interest. A NFR is a highly heterogeneous porous medium, most of these reservoirs are studied by means of Euclidean models. Euclidean models implicitly assume a uniform distribution of interconnected fractures. Camacho-Velázquez et al. (2008) relate evidence indicating that euclidean modeling is not enough to describe the dynamic \({ anomalous}\) behavior observed in some NFR. An alternative is to regard the media as fractal, that is a set of non-integral Haussdorff dimension. Supporting evidence is presented in Miranda-Martínez et al. (2006), from X-ray computerized tomography of actual core images a non-integral Haussdorff dimension is estimated. See also Arizabalo et al. (2004). Application of fractal geometry in the study of porous media is a very active area of research. Noteworthy is the work of Acuna and Yortsos (1995), where an in-depth analysis is carried out on fractal network of fractures. Recently, Li and Zhao (2012) present a fractal characterization of rocks for modeling production rate by spontaneous imbibition.

For some authors heterogeneity manifests itself as transport of fluid in a system with non-local and memory effects leading to fractional operators, a recent discussion in Raghavan (2012). Therein a generalized Darcy law capturing these effects is introduced in the continuity equation. In a sense the main problem is modeling the non-Darcian feature of the flow. This is pursued in Wen and Wang (2012) for numerical modeling of flow to a well. It is pointed out that the flow could be non-Darcian near the pumping wells because of the high velocities when the pumping rate is relatively large.

We argue that this is the case in NFR, or more generally in highly heterogeneous media, the anomalous behavior of the flow is significant in a neighborhood of a well. Consequently, the aim in this work is to provide a model for flow in such a case. As customary in reservoir modeling, we assume cylindrical symmetry and propose a generalized diffusion equation which accounts for heterogeneity and the anomalous flow. Our model falls within the scope of diffusion on fractals or anomalous diffusion models.

The problem is far from settled and contributions are vast on the subject. In O’Shaughnessy and Procaccia (1985) a theory of the probability distribution for a random walker on a fractal lattice is presented obtaining a model for diffusion on fractals. Barker (1988) generalizes flow dimension to non-integral values, while retaining the assumptions of radial flow and homogeneity. The resulting model is referred to as the generalized radial flow (GRF) model. Chang and Yortsos (1990) consider flow in a fractal fracture network characterized by a set of fractal exponents. The exponents are proposed by a scaling argument obtaining a modified diffusion equation, the model is derived under rather general considerations. Finally, Metzler et al. (1994) part from the behavior for a random walk’s asymptotic probability density. It is demonstrated that the anomalous diffusion with the asymptotic behavior is provided by an appropriate fractional partial differential equation.

Most if not all of these models are derived in part under ad hoc arguments. Our purpose is to provide a derivation consistent with continuum mechanics. We consider a porous medium as fractal if its Haussdorff dimension is non-integral. Following Tarasov (2005), we assume that the fractal medium can be replaced by some continuous medium that is described by fractional integrals. Next we introduce a fractional divergence Gauss theorem, consequently we can do continuum mechanics and obtain the continuity equation. The equation is complemented with a generalized Darcy law as in Raghavan (2012). The classical models above will be derived as particular cases.

Our motivation comes from the oil industry, as a first step we develop the basics fort well test analysis.

The outline is as follows.

In Sect. 2 we derive a partial differential equation to model slightly incompressible flow in well configuration in fractal media. First we introduce fractional continuum mechanics in this geometry. Then we present a generalized Darcy law which is defined in terms of a fractional time derivative. With these ingredients the equation of flow is derived in the framework of Continuum Mechanics.

In Sect. 3 we carry out well test analysis as is done in practice. We solve the equation in Laplace domain and show that a well-known expression for cumulative fluid influx at the radius of the well is valid in the general case.

In Sect. 4 we review some classical models of anomalous diffusion, our exposition is only descriptive of the fractal parameters in the different equations. We point out that the model presented here belong to this class, arguably with a clearer meaning of the parameters in the equation. Next we show some numerical results for modeling anomalous diffusion. We consider non-integral Haussdorff dimension and illustrate the qualitative behavior observed in field cases.

For the reader convenience, in Sect. 5 we sketch the derivation of a generalized Darcy law in the framework of continuous time random walks (CTRW). This law is commonly used to model non-local non-stationary phenomena as the case under study.

We end with conclusions and some directions for future research.

2 Fractional Continuum Mechanics for Radial flow in Fractal Media

2.1 Continuity Equation for Vertically Homogeneous Fractal Media

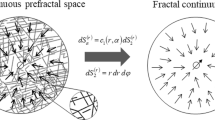
Let \(W\) be a subset of \(\mathbb R ^{3}\) with Hausdorff dimension \(D, \dim _{\fancyscript{H}}(W)=D.\) If D is not an integer the set is called fractal. It will be referred to as fractal medium.

We call W vertically homogeneous if W is of the form

$$\begin{aligned} W=V_{\fancyscript{H}}\times [0,h], \end{aligned}$$

for some \(h>0,\) and \(V_{\fancyscript{H}}\subset \mathbb R ^{2}\) with \(1<\dim _{ \fancyscript{H}}(V)=d\le 2.\) From Mattila (1995) we have that \(\dim _{\fancyscript{H}}(W)=1+d.\)

Following Tarasov (2005), we assume that the fractal medium \(V_{\fancyscript{H}}\) can be replaced by some continuous medium, denoted by \(V,\) that is described by fractional integrals. Namely, the d—mass of \(V_{\fancyscript{H}}\) is defined by the fractional integral

$$\begin{aligned} M_{d}(V_{\fancyscript{H}},\mathbf x _{0})=\int \limits _{V}\rho (\mathbf x )dS_{d},\quad \mathbf x _{0}\in V, \end{aligned}$$

where \(dS_{d}\) is the d—surface element,

$$\begin{aligned} dS_{d}=c_{2}\left( d,\mathbf x \right) dS_{2},\qquad c_{2}\left( d,\mathbf x \right) =c_{d}\left| \mathbf x-x _{0}\right| ^{d-2},\qquad c_{d}= \frac{2^{2-d}}{\Gamma \left( d/2\right) }. \end{aligned}$$

Here \(\rho \) is density, and \(\mathbf x _{0}\in V\) is the initial point of the fractional integral. Note that if \(d=2,\) the expression \(M_{d}(V_{ \fancyscript{H}},\mathbf x _{0})\) coincides with the Euclidean case.

A drawback of Tarasov’s approach is that there is some ambiguity on the initial point for the fractional integral. Our interest is to model flow in a cylindrical well, the natural initial point is the center which we locate at the origin. Consequently, the \((1+d)\)—mass of \(W\) is given by the fractional integral

$$\begin{aligned} M_{\left( 1+d\right) }(W,\mathbf 0 )\equiv M_{\left( 1+d\right) }(W)=h\int _{V}\rho (\mathbf x )dS_{d}. \end{aligned}$$

As in Tarasov (2005) we may derive the \(d-\beta \) Gauss theorem

$$\begin{aligned} \int _{\partial V}\mathbf F \cdot \mathbf n \,dL_{\beta }=\int _{V}c_{2}\left( d,\mathbf x \right) ^{-1}\nabla \cdot \left( c_{1}\left( \beta ,\mathbf x \right) \mathbf F \right) \,dS_{d}, \end{aligned}$$

where the \(\beta \)—line element is

$$\begin{aligned} dL_{\beta }=c_{1}\left( \beta ,\mathbf x \right) dL_{1},\qquad c_{1}\left( \beta ,\mathbf x \right) =c_{\beta }\left| \mathbf x \right| ^{\beta -1},\qquad c_{\beta }=\frac{2^{1-\beta }\Gamma \left( 1/2\right) }{\Gamma \left( \beta /2\right) }. \end{aligned}$$

We are led to the continuity equation

$$\begin{aligned} \frac{\partial \rho }{\partial t}+\frac{1}{c_{d}}\left| \mathbf x \right| ^{2-d}\nabla \cdot \left( c_{\beta }\left| \mathbf x \right| ^{\beta -1}\rho \mathbf u \right) =0. \end{aligned}$$

To model radial flow we assume that \(V\) is a disk. Thus \(\left| \mathbf x \right| =r,\) which yields

$$\begin{aligned} \frac{\partial \rho }{\partial t}+\frac{1}{c_{d}}r^{2-d}\nabla \cdot \left( c_{\beta }r^{\beta -1}\rho \mathbf u \right) =0. \end{aligned}$$
(1)

2.2 A Generalized Darcy Law

We shall introduce a generalized Darcy law that involves fractional derivatives. Hereafter, we shall use freely some basic results form Fractional Calculus. See Kilbas et al. (2006).

The fractional integral of Riemann–Liouville of order \(\alpha >0\) of a function \(f:\mathbb R ^{+}\rightarrow \mathbb R \) is given by

$$\begin{aligned} I^{\alpha }f(t)=\frac{1}{\Gamma (\alpha )}\int \limits _{0}^{t}\left( t-s\right) ^{\alpha -1}f(s)\,ds. \end{aligned}$$

The fractional derivative (of Riemann–Liouville) of order \(0<\alpha <1\) of a function \(f: \mathbb R ^{+}\rightarrow \mathbb R \) is given by

$$\begin{aligned} D^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )}\frac{d}{{\text{ d }}t}\int \limits _{0}^{t}\left( t-s\right) ^{-\alpha }f(s)\,{\text{ d }}s. \end{aligned}$$

In terms of the Riemann–Liouville integral

$$\begin{aligned} D^{\alpha }f=D\,I^{1-\alpha }f \end{aligned}$$

Let us consider the flux \(\mathbf u(x, t\mathbf ) \) given by the gradient law

$$\begin{aligned} \mathbf u (\mathbf x ,t)=-\frac{k_{\alpha }}{\mu }\frac{\partial }{\partial t }\int \limits _{0}^{t}\left( t-s\right) ^{\alpha -1}\nabla P(\mathbf x ,s)\,{\text{ d }}s, \end{aligned}$$
(2)

where \(0<\alpha <1.\)

In Sect. 5 we present a derivation of this generalized law in the framework of CTRW. It is intended to capture the non-local behavior of flux in a fractal reservoir. See Raghavan (2012) and references therein. The derivation starts with the non-local master CTRW equations. Consequently anomalous diffusion phenomena in the CTRW approach are thus considered non-local processes, and with that they are far from equilibrium processes. More on this later.

In terms of the time fractional Riemann–Liouville derivative, (2) is written in the form

$$\begin{aligned} \mathbf u (\mathbf x ,t)=-\frac{k_{\alpha }}{\mu }\Gamma (\alpha )\partial _{t}^{1-\alpha }\nabla P(\mathbf x ,t). \end{aligned}$$

Note that \(k_{\alpha }\) may be considered to be a function of location, that is, a function of \(\mathbf x. \) In this work we consider only \(k_{\alpha }\) constant.

As expected, for \(\alpha =1,\) we obtain the classical Darcy law

$$\begin{aligned} \mathbf u=- \frac{k}{\mu }\nabla P. \end{aligned}$$

2.3 Slightly Compressible Radial Flow

If flow is slightly compressible we have, Chen (2007),

$$\begin{aligned} \frac{\partial \rho }{\partial t}=\phi c_{t}\rho \frac{\partial P}{\partial t}. \end{aligned}$$

As customary, we ignore density change, Eq. (1) reduces to

$$\begin{aligned} \phi c_{t}\frac{\partial P}{\partial t}=\frac{c_{\beta }}{c_{d}}\frac{ k_{\alpha }}{\mu }\Gamma (\alpha )\frac{\partial ^{1-\alpha }}{\partial t^{1-\alpha }}\left( r^{2-d}\nabla \cdot \left( r^{\beta -1}\nabla P(\mathbf x ,t)\right) \right) . \end{aligned}$$
(3)

Let \(P_{\text{ i }}\) be the initial pressure, that is \(P(r,0)=P_{\text{ i }}.\) Pressure drop is defined as \(\Delta P(r,t)=P_{\text{ i }}-P(r,t).\) Let us denote pressure drop by \(P\) again.

Next we show, formally, that Eq. (3) is equivalent to a time fractional derivative equation. Note that \(P(r,0)=0\), applying \(I^{1}\) we have

$$\begin{aligned} \phi c_{t}P=\frac{c_{\beta }}{c_{d}}\frac{k_{\alpha }}{\mu }\Gamma (\alpha )I^{\alpha }\left( r^{2-d}\nabla \cdot \left( r^{\beta -1}\nabla P(\mathbf x ,t)\right) \right) . \end{aligned}$$

It is well known that the fractional derivative \(D^{\alpha }\) is a left inverse of the fractional integral \(I^{\alpha }\). We are led to a model for radial flow in fractal media

$$\begin{aligned} \frac{1}{\chi ^{\alpha }}\frac{\partial ^{\alpha }P}{\partial t^{\alpha }}= \frac{1}{r^{d-1}}\frac{\partial }{\partial r}\left( r^{\beta }\frac{\partial P}{\partial r}\right) , \end{aligned}$$
(4)

where

$$\begin{aligned} \chi ^{\alpha }=\frac{\Gamma (\alpha )}{\phi c_{t}}\frac{c_{\beta }}{c_{d}}\frac{k_{\alpha }}{\mu }. \end{aligned}$$

Notice that for \(\alpha =1,\) \(d=2,\) \(\beta =1,\) we obtain the Euclidean case as expected.

Let

$$\begin{aligned} r_{\text{ D }}=\frac{r}{r_{\text{ w }}}, \end{aligned}$$
$$\begin{aligned} P_{\text{ D }}=\frac{P}{P_{\text{ i }}-P_{\text{ wf }}} \end{aligned}$$
$$\begin{aligned} t_{\text{ D }}=\lambda t \end{aligned}$$

where

$$\begin{aligned} \lambda =\left( r_{\text{ w }}\right) ^{\left( \beta -d-1\right) /\alpha }\chi . \end{aligned}$$

Writing \(P\) instead of \(P_{D}\) we obtain the normalized equation.

$$\begin{aligned} \frac{\partial ^{\alpha }P}{\partial t^{\alpha }}=\frac{1}{r^{d-1}}\frac{ \partial }{\partial r}\left( r^{\beta }\frac{\partial P}{\partial r}\right) . \end{aligned}$$
(5)

We shall refer to Eq. (4), or its dimensionless version (5), as the fractional fractal media, (FFM) equation.

2.4 On the Stationary Case

As pointed out above CTRW is suited for non-stationary phenomena. A reduction to the stationary case requires an in-depth analysis to be addressed elsewhere. The first step is as follows. Let \(P(\mathbf x ,t)\) be stationary, that is \(P\) is independent of time \(P(\mathbf x ,t) = P(\mathbf x ).\) The generalized law (2) becomes \(\mathbf u (\mathbf x )=-\frac{k_\alpha }{\mu }\nabla P(\mathbf x ) t^{\alpha -1}\) which is non-stationary. But \(\frac{\partial P}{\partial t} = 0\) and we obtain a stationary model

$$\begin{aligned} \nabla \cdot \left( \frac{k_{\alpha }}{\mu }r^{\beta -1}\nabla P(\mathbf x ,t)\right) = 0. \end{aligned}$$
(6)

We stress that the fractional derivative in the derivation of (2) is that of Riemann–Liouville. An alternative definition is the fractional derivative of Caputo, namely

$$\begin{aligned} D_{c}^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}\left( t-s\right) ^{-\alpha }\frac{{\text{ d }}f}{{\text{ d }}s}(s)\,{\text{ d }}s. \end{aligned}$$

It is a popular choice due to the fact that it yields zero for constant functions. In particular for stationary \(P\) we get the unrealistic law \(\mathbf u (\mathbf x ) = 0\).

3 Application to Well Test Analysis

3.1 General Solution in Laplace Variable

In order to relate (5) to some classical model in the literature we introduce

$$\begin{aligned} \theta =d-\beta -1, \end{aligned}$$

and write the Eq. (5) in the form

$$\begin{aligned} \frac{\partial ^{\alpha }P}{\partial t^{\alpha }}=\frac{1}{r^{\beta +\theta } }\frac{\partial }{\partial r}\left( r^{\beta }\frac{\partial P}{\partial r} \right) . \end{aligned}$$

Applying Laplace transform

$$\begin{aligned} s^{\alpha }\bar{P}=\frac{1}{r^{\theta }}\frac{\partial ^{2}\bar{P}}{\partial r^{2}}+\frac{\beta }{r^{\theta +1}}\frac{\partial ^{2}\bar{P}}{\partial r^{2}} \end{aligned}$$
(7)

Defining

$$\begin{aligned} x=\frac{2}{\theta +2}s^{\alpha /2}r^{\frac{\theta +2}{2}},\quad \bar{P} =x^{\nu }\,y(x),\quad \nu =\frac{1-\beta }{\theta +2}, \end{aligned}$$

Eq. (7) becomes the modified Bessel equation of order \(\nu \):

$$\begin{aligned} x^{2}\,y^{\prime \prime }(x)+x\,y^{\prime 2}+\nu ^{2})\,y(x)=0. \end{aligned}$$
(8)

The solution of (8) is of the form

$$\begin{aligned} y=aK_{\nu }(x)+bI_{\nu }(x). \end{aligned}$$

Let us make the change of variable \(\varTheta =(\theta +2)/2\), we may write the solution of (7) as follows

$$\begin{aligned} \bar{P}=x^{\nu }y=as^{\nu \alpha /2}r^{\nu \varTheta }K_{\nu }(s^{\alpha /2}r^{\varTheta }/\varTheta )\;+\;bs^{\nu \alpha /2}r^{\nu \varTheta }I_{\nu }(s^{\alpha /2}r^{\varTheta }/\varTheta ). \end{aligned}$$

The constants \(a,b\) are determined by imposing appropriate boundary conditions.

3.2 Well Test Analysis

In well test analysis two cases are to be considered, constant terminal pressure (CTP) and constant terminal rate (CTR). These configurations are classical, van Everdingen and Hurst (1949), and lead us to initial condition and boundary condition at the well:

  • CTP:

    $$\begin{aligned} P(r,0)&= 1; \\ \\ P(1,t)&= 0,\quad t>0. \end{aligned}$$

  • CTR:

    $$\begin{aligned} P(r,0)&= 0; \\ \\ \dfrac{\partial P}{\partial r}(1,t)&= -1,\quad t>0. \end{aligned}$$

Let \(r_{\text{ e }}\) be the outer radius of the reservoir, possibly infinity. The boundary conditions to consider are

  • Unbounded reservoir:

    $$\begin{aligned} \lim _{r\rightarrow \infty }P(r,t)&= 0 \end{aligned}$$

  • Closed bounded reservoir:

    $$\begin{aligned} \dfrac{\partial P}{\partial r}(r_{\text{ e }},t)&= 0. \end{aligned}$$

Next we determine constants \(a,\) \(b\) to obtain pressure drop in (7).

  • Unbounded reservoir under CTP

$$\begin{aligned} \bar{P}(r,s)=\frac{r^{\nu \varTheta }K_{\nu }(s^{\alpha /2}r^{\varTheta }/\varTheta ) }{sK_{\nu }(s^{\alpha /2}/\varTheta )}. \end{aligned}$$

  • Unbounded reservoir under CTR

$$\begin{aligned} \bar{P}(r,s)=\frac{r^{\nu \varTheta }K_{\nu }\left( \frac{s^{\alpha /2}r^{\varTheta }}{ \varTheta }\right) }{s^{1+\alpha /2}K_{\nu -1}\left( \frac{s^{\alpha /2}}{\varTheta }\right) } \end{aligned}$$

  • Closed bounded reservoir under CTP

$$\begin{aligned} \bar{P}(r,s)=\frac{r^{\nu \varTheta }}{s}\cdot \frac{I_{\nu -1}\left( \frac{s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) K_{\nu }(s^{\alpha /2}r^{\varTheta }/\varTheta )+K_{\nu -1}\left( \frac{s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) I_{\nu }(s^{\alpha /2}r^{\varTheta }/\varTheta )}{K_{\nu }(s^{\alpha /2}/\varTheta )I_{\nu -1}\left( \frac{s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) +I_{\nu }(s^{\alpha /2}/\varTheta )K_{\nu -1}\left( \frac{ s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) }. \end{aligned}$$

  • Closed bounded reservoir under CTR

$$\begin{aligned} \bar{P}(r,s)=\frac{r^{\nu \varTheta }}{s^{\alpha /2+1}}\frac{I_{\nu -1}\left( \frac{s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) K_{\nu }(s^{\alpha /2}r^{\varTheta }/\varTheta )\;+\;K_{\nu -1}\left( \frac{s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) I_{\nu }(s^{\alpha /2}r^{\varTheta }/\varTheta )}{K_{\nu -1}(s^{\alpha /2}/\varTheta )I_{\nu -1}\left( \frac{s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) -I_{\nu -1}(s^{\alpha /2}/\varTheta )K_{\nu -1}\left( \frac{s^{\alpha /2}r^{\varTheta }}{\varTheta }\right) } \end{aligned}$$

To obtain \(P\) in terms of \((r,t)\) we invert (7) numerically. Our algorithm follows those of Davies and Martin (1979) and de Hoog et al. (1982).

Let \(P(r,t)\) be a solution of the FFM equation in the CTP case. Of interest in well test analysis is the cumulative fluid influx at the field radius \(r=1,\) namely

$$\begin{aligned} Q(t)=\int _{0}^{t}\left( \frac{\partial P}{\partial r}\right) _{r=1}\,dt, \end{aligned}$$

with Laplace transform,

$$\begin{aligned} \bar{Q}(s)=\frac{1}{s}\left( \frac{\partial \bar{P}}{\partial r}\right) _{r=1}. \end{aligned}$$

Consider now \(P(r,t),\) a solution of the FFM equation in the CTR case, let \( P_{\text{ w }}(t)=P(1,t).\) In the Euclidean case, in van Everdingen and Hurst (1949) the very useful relation in well test analysis was noted

$$\begin{aligned} \bar{P}_{\text{ w }}\bar{Q}=\frac{1}{s^{3}}. \end{aligned}$$

Noteworthy, this relation also holds for the FFM equation. In fact, for unbounded reservoir under CTP the Laplace transform of the cumulative fluid influx is

$$\begin{aligned} \bar{Q}(s)=\frac{K_{\nu -1}\left( \frac{s^{\alpha /2}}{\varTheta }\right) }{s^{2-\alpha /2}K_{\nu }\left( \frac{s^{\alpha /2}}{\varTheta }\right) }. \end{aligned}$$

Multiplying by \(\bar{P}_{\text{ w }}\)

$$\begin{aligned} \bar{P}_{\text{ w }}\bar{Q}=\frac{K_{\nu }\left( \frac{s^{\alpha /2}}{\varTheta }\right) }{ s^{1+\alpha /2}K_{\nu -1}\left( \frac{s^{\alpha /2}}{\varTheta }\right) }\cdot \frac{K_{\nu -1}\left( \frac{s^{\alpha /2}}{\varTheta }\right) }{s^{2-\alpha /2}K_{\nu }\left( \frac{s^{\alpha /2}}{\varTheta }\right) }=\frac{1}{s^{3}}. \end{aligned}$$

Similarly, in a closed bounded reservoir under CTP the Laplace transform of the cumulative fluid influx is

$$\begin{aligned} \bar{Q}(s)=\frac{I_{\nu -1}(x_{e})K_{\nu -1}(s^{\alpha /2}/\varTheta )-K_{\nu -1}(x_{e})I_{\nu -1}(s^{\alpha /2}/\varTheta )}{s^{2-\alpha /2}D_{1}} \end{aligned}$$

where \(x_{e}=\left( \frac{s^{\alpha /2}R_{e}^{\varTheta }}{\varTheta }\right) \), and \( D_{1}=K_{\nu }(s^{\alpha /2}/\varTheta )I_{\nu -1}(x_{e})+I_{\nu }(s^{\alpha /2}/\varTheta )K_{\nu -1}(x_{e})\).

Hence, for \(\bar{P}_{\text{ w }}\bar{Q}\) we obtain

$$\begin{aligned} \bar{P}_{\text{ w }}\bar{Q}&= \frac{1}{s^{\alpha /2+1}}\frac{D_{1}}{K_{\nu -1}(s^{\alpha /2}/\Theta )I_{\nu -1}(x_{e})-I_{\nu -1}(s^{\alpha /2}/\Theta )K_{\nu -1}(x_{e})}\cdot \\&\\&\cdot \frac{1}{s^{2-\alpha /2}}\frac{I_{\nu -1}(x_{e})K_{\nu -1}(s^{\alpha /2}/\Theta )-K_{\nu -1}(x_{e})I_{\nu -1}(s^{\alpha /2}/\Theta ) }{D_{1}} \\&\\&= \frac{1}{s^{3}} \end{aligned}$$

Consequently, if the Laplace transform for one of \(\bar{P}_{\text{ w }},\) \(\bar{Q}\) is known, the transform of the other is established.

4 Anomalous Diffusion

In this section we shall review several models for anomalous diffusion and/or fractal reservoirs that have been proposed in the literature. Equation FFM belongs to this class. We shall note that the concept of fractality is not unified, and sometimes correspondence on related parameters from different models is unclear. Hence we follow the notation and description of the original works.

4.1 Classical Models

In O’Shaughnessy and Procaccia (1985) a theory of the probability distribution \(P(r,t)\) for a random walker on a fractal lattice is presented. In particular a generalization of the Fickian diffusion law for Euclidean lattices fo fractal lattices is introduced. The equation is derived on the basis of scaling arguments. Given a fractal of dimension D embedded in Euclidean space of dimension d, the mean-square displacement after time t of a random walker on the fractal obeys

$$\begin{aligned} \left\langle r^{2}(t)\right\rangle \sim t^{2/\left( 2+\theta \right) } \end{aligned}$$

where \(r\) is measured in the Euclidean space. The index \(\theta \) is nonzero (in contrast to Euclidean lattices where \(\theta =0\)). Together with \(D\) it determines the scaling exponent for the conductivity.

$$\begin{aligned} \frac{\partial P}{\partial t}=\frac{1}{r^{D-1}}\frac{\partial }{\partial r} \left( Kr^{D-1-\theta }\frac{\partial P}{\partial r}\right) . \end{aligned}$$

In Barker (1988) a typical hydraulic test in fractured rock is considered, where water is injected between packers in to an interval of a borehole known to contain at least one fracture. After considering a variety of possible variations on the models it was concluded that the most natural variation was to generalize the flow dimension to non-integral values, while retaining the assumptions of radial flow and homogeneity. The resulting model is referred to as the GRF model.

$$\begin{aligned} S_{\text{ sf }}\frac{\partial P}{\partial t}=\frac{K_{\text{ f }}}{r^{n-1}}\frac{\partial }{ \partial r}\left( r^{n-1}\frac{\partial P}{\partial r}\right) , \end{aligned}$$

therein Hydraulic conductivity \(K_{\text{ f }},\) specific storage \(S_{\text{ sf }}.\) The exponent n is possibly non integer.

Chang and Yortsos (1990) consider flow in a fractal fracture network characterized by a set of fractal exponents. The exponents are proposed by a scaling argument obtaining a modified diffusion equation

$$\begin{aligned} c_{f}\frac{\partial P}{\partial t}=\frac{m}{\mu }\frac{1}{r^{D-1}}\frac{ \partial }{\partial r}\left( r^{\beta }\frac{\partial P}{\partial r}\right) . \end{aligned}$$
$$\begin{aligned} \beta =D-\theta -1 \end{aligned}$$

Here \(D\le 2\) is the mass fractal dimension, \(D=2\) for cylindrical symmetry reservoirs. \(\theta \) is related to the so-called spectral exponent of the fractal network.

While the motivation of Chang and Yortsos (1990) was to describe fractured reservoirs, their analysis was for arbitrary fractal porous media. We have built on the rather general formalism of Tarasov, but the approach in Sect. 2.1 is in essence that of Chang and Yortsos (1990). For \(\alpha = 1\) Eq. (5) is derived in Chang and Yortsos (1990) by similar arguments.

In Metzler et al. (1994) they let \(d_{\text{ w }}=2+\theta \) the anomalous diffusion exponent, and part from the behavior for the random walk’s asymptotic probability density. Namely

$$\begin{aligned} P(r,t)\sim At^{d_{\text{ f }}/d_{\text{ w }}}e^{c\left( r/R\right) ^{u}} \end{aligned}$$
(9)

valid in the asymptotic range \(r/R>>1\) and \(t\rightarrow \infty .\) \(R\) and \(u \) are defined by

$$\begin{aligned} R=\sqrt{\left\langle r^{2}(t)\right\rangle }, \\ u=\frac{d_{\text{ w }}}{d_{\text{ w }}-1}. \end{aligned}$$

In the paper it is demonstrated that the anomalous diffusion with the asymptotic behavior (9) is provided by the fractional partial differential equation, the MGN model,

$$\begin{aligned} \frac{\partial ^{2/d_{\text{ w }}}P}{\partial t^{2/d_{\text{ w }}}}=\frac{1}{r^{d_{\text{ s }}-1}}\frac{ \partial }{\partial r}\left( r^{d_{\text{ s }}-1}\frac{\partial P}{\partial r}\right) . \end{aligned}$$
(10)

where \(d_{\text{ s }}\) is the spectral dimension of the fractal (fracton dimension).

$$\begin{aligned} d_{\text{ s }}=\frac{2d_{\text{ f }}}{d_{\text{ w }}}, \end{aligned}$$

\(d_{\text{ f }}\) the fractal dimension of the underlying object. Then the model is generalized to

$$\begin{aligned} \frac{\partial ^{\gamma }P}{\partial t^{\gamma }}=\frac{1}{r^{D-1}}\frac{ \partial }{\partial r}\left( r^{D-\Theta -1}\frac{\partial P}{\partial r} \right) . \end{aligned}$$
(11)

The parameter \(\varTheta \) is introduced rather artificially.

Noteworthy, for \(\gamma =1\) this equation is identical to that of Chang and Yortsos (1990).

To conclude this section we remark that the model introduced in this work is derived from the precise definition of fractal media, the generalized Darcy law, and fractional continuum mechanics. The so-called fractal exponents in the partial differential equation come out naturally.

4.2 Numerical Results

The FFM equation is derived under rather general conditions. It is intended to explain anomalous behavior in terms of the fractal media parameters, \(\alpha ,\) \(\beta ,\) \(d.\) These are to be estimated from field data. Here we just explore qualitative behavior in the case that follows.

It is pointed out in Camacho-Velázquez et al. (2008) that in fractal systems the flow rate from fractal systems is smaller than that from the Euclidean system because the diffusion is slower in fractal reservoirs than in traditional ones. In such a case one may argue that the Haussdorf dimension of the porous medium is smaller than 2. Thus we consider

$$\begin{aligned} \frac{\partial P}{\partial t}=\frac{1}{r^{d-1}}\frac{\partial }{\partial r}\left( r\frac{\partial P}{\partial r}\right) . \end{aligned}$$

Let \(r_{\text{ e }}=500\) and time scale as in Camacho-Velázquez et al. (2008). We plot in Figs. 1 and 2 flow rate and cumulative production varying only \(d.\) The fractal dimension \(d=1.85\) is reported in Miranda-Martínez et al. (2006). It is apparent that this parameter suffices to explain the anomalous behavior.

Fig. 1
figure 1

Influence of dimension on flow rate

Full size image
Fig. 2
figure 2

Influence of dimension on cumulative flow

Full size image

5 The Fractional Diffusion Equation and CTRW

Consider a random walk on a lattice for which the times \(t_{\text{ j }}\) between successive steps are independent, identically distributed (iid) random variables. The common probability density function \(\psi (t),\) is called the waiting time density. Also associated is a sequence of iid random jumps \(x_{\text{ i }}\) with common probability density \(\lambda (x).\)

Let \(p(x,t)\) be the conditional probability density that a walker starting from the origin at time zero is at position x at time t. By natural probabilistic arguments, Hughes (1995), it is possible to arrive to the fundamental master equation for CTRW.

$$\begin{aligned} p(x,t)=\Psi (t)p(x,0)+\int \limits _{0}^{t}\psi (t-t^{\prime })\int \limits _{-\infty }^{+\infty }\lambda (x-x^{\prime })p(x^{\prime },t^{\prime }){\text{ d }}x^{\prime }{\text{ d }}t^{\prime }. \end{aligned}$$
(12)

Where the survival probability

$$\begin{aligned} \Psi (t)=\int \limits _{t}^{+\infty }\psi (t^{\prime }){\text{ d }}t^{\prime } \end{aligned}$$

denotes the probability that at instant t the particle is still sitting in its starting position \(x=0.\)

The generalized Darcy law (2) arises in the derivation of the fractional diffusion equation from (12). The standard argument is to assume asymptotic properties of the densities \(\psi (t),\) and \(\lambda (x),\) approximate to leading order, substitute on the Fourier and Laplace transforms of the master equation and invert. Let us sketch this process in one dimension.

Aassume that the Fourier transform of the jump density has the asymptotic expansion

$$\begin{aligned} \hat{\lambda }(q)\sim 1-\frac{q^{2}\sigma ^{2}}{2}+O\left( q^{4}\right) , \end{aligned}$$

where

$$\begin{aligned} \sigma ^{2}=\int x^{2}\lambda (x){\text{ d }}x, \end{aligned}$$

is finite. This is a general expansion for an even function \(\lambda (x)=\lambda (-x)\) with a finite variance \(\sigma ^{2}.\) An example of such a density is the Gaussian density

$$\begin{aligned} \lambda (x)=\frac{1}{\sqrt{2\pi \sigma ^{2}}}\exp \left( -\frac{x^{2}}{ 2\sigma ^{2}}\right) . \end{aligned}$$

If the mean time \(\tau \) between successive steps is finite, we have

$$\begin{aligned} \tau =\int \limits _{0}^{\infty }t\psi (t){\text{ d }}t=\left. -\frac{d}{{\text{ d }}s}\tilde{\psi } (s)\right| _{s=0}, \end{aligned}$$

where \(\tilde{\psi }(s)\) is the Laplace transform of \(\psi (t).\) This ensures that

$$\begin{aligned} 1-\tilde{\psi }(s)\sim \tau s,\quad \text{ as } \quad s\rightarrow 0. \end{aligned}$$

The canonical case is the exponential time density

$$\begin{aligned} \psi (t)=\frac{1}{\tau }\exp \left( -\frac{t}{\tau }\right) . \end{aligned}$$

Consider the following situation, sometimes referred to as fractal time random walk, where the mean time diverges, but the jump length variance \(\sigma ^{2}\) is still kept finite.

The classic example is provided by a waiting time density \(\psi (t)\) with

$$\begin{aligned} \psi (t)\sim {\text{ cons }}\tan {\text{ t }}\times t^{-1-\alpha }, \end{aligned}$$

with \(0<\alpha <1.\) The Laplace transform of \(\psi (t)\) in this case has the asymptotic behavior

$$\begin{aligned} 1-\tilde{\psi }(s)\sim B\tau ^{\alpha }s^{\alpha },\quad \text{ as }\quad s\rightarrow 0. \end{aligned}$$

With \(B\) a positive constant.

Applying Laplace and Fourier transform to the master equation and using the asymptotic expansion to leading order we obtain

$$\begin{aligned} sP(q,s)-P(q,0)=-\frac{q^{2}\sigma ^{2}}{2\tau ^{\alpha }}s^{1-\alpha }P(q,s). \end{aligned}$$

The inverse Fourier and Laplace transform and basic results from fractional calculus yield the fractional subdiffusion equation

$$\begin{aligned} \frac{\partial p}{\partial t}=D\partial _{t}^{1-\alpha }\frac{\partial ^{2}p }{\partial x^{2}}. \end{aligned}$$
(13)

For \(\alpha =1,\) the standard diffusion equation follows.

$$\begin{aligned} \frac{\partial p}{\partial t}=D\frac{\partial ^{2}p}{\partial x^{2}}, \end{aligned}$$

where

$$\begin{aligned} D=\frac{\sigma ^{2}}{2\tau }. \end{aligned}$$

From (13) an ad hoc generalized Darcy law is obtained

$$\begin{aligned} q(x,t)=-D\partial _{t}^{1-\alpha }\frac{\partial p}{\partial x}. \end{aligned}$$

6 Conclusions

We have introduced a model for slightly compressible flow in fractal media in well configuration. There are neither scaling nor heuristic arguments on fractality for the derivation. It is apparent that well test analysis can be carried for this general model as is done in the Euclidean case. Also we have developed a robust numerical solver of the direct problem. For application, the great interest is to estimate the fractal parameters in the partial differential equation. This inverse problem is part of our current investigation.