Exploring the fruitfulness of diagrams in mathematics

Abstract

The paper asks whether diagrams in mathematics are particularly fruitful compared to other types of representations. In order to respond to this question a number of examples of propositions and their proofs are considered. In addition I use part of Peirce’s semiotics to characterise different types of signs used in mathematical reasoning, distinguishing between symbolic expressions and 2-dimensional diagrams. As a starting point I examine a proposal by Macbeth (Realising reason. A narrative of truth & knowing, Oxford University Press, Oxford, 2014). Macbeth explains how it can be that objects “pop up”, e.g., as a consequence of the constructions made in the diagrams of Euclid, that is, why they are fruitful. It turns out, however, that diagrams are not exclusively fruitful in this sense. By analysing the proofs given in the paper I introduce the notion of a ‘faithful representation’. A faithful representation represents as either an image (resembling what it stands for) or as a metaphor (sharing some underlying structure). Secondly it represents certain relevant relations (that is, as an iconic diagram in Peirce’s terminology). Thirdly manipulations on the representations respect manipulations on the objects they represent, so that new relations may be found. The examples given in the paper illustrate how such representations can be fruitful. These examples include proofs based on both symbolic expressions as well as diagrams and so it seems diagrams are not special when it comes to fruitfulness. Having said this, I do present two features of diagrams that seem to be unique. One consists of the possibility of exhibiting the type of relation in a diagram—or simply showing that a relation exists—as a contrast to stating in words that it exists. The second is the spatial configurations possible when using diagrams, e.g., allowing to show multiple relations in a single diagram.

1 Introduction

This paper explores the role of diagrams in mathematics in particular regarding their capacity to point to new results. The main question to be addressed is whether diagrams are unique in some way in this respect, and—if this is the case—to search for an explanation for why it is so. In order to investigate this question I consider diagrams as a certain type of representation and compare them with other types of representations to be explained. The notions of ‘pointing to new results’ or ‘fruitful’ will not be taken in any dramatic sense. It has been proposed that visualisation is sometimes remarkably fruitful, for example referring to the work of Riemann, see Tappenden (2005). Here I consider only results where, e.g. new objects are constructed or relations between concepts are found. My hope is that an understanding of how the signs work in these simpler cases may be of use when explaining what goes on also in the other more exceptional ones. The objects of study will consist of a number of different examples of proofs (and their corresponding propositions) in order to examine which role the different types of representations play. The conclusion of these investigations is that in many respects diagrams do not differ from other types of representations. I will make a case that other types of representations also fulfil certain properties put forward to explain the fruitfulness of diagrams. Having said this I do point to a couple of features of diagrams that seem advantageous for our understanding.

Even though diagrams—or figures—have been used in mathematics throughout times, for the last hundred years or so the reference to them in mathematical reasoning has been discredited. In order to explain this development scholars have often referred to statements by Hilbert or Pasch, such as the following:

For the appeal to a figure is, in general, not at all necessary. It does facilitate essentially the grasp of the relations stated in the theorem and the constructions applied in the proof. Moreover, it is a fruitful tool to discover such relationships and constructions. However, if one is not afraid of the sacrifice of time and effort involved, then one can omit the figure in the proof of any theorem; indeed, the theorem is only truly demonstrated if the proof is completely independent of the figure. (Pasch, 1882/1926, 43). (Quote and translation from Mancosu 2005.)

When discussing the rigour of proofs the focus is most often on the first sentence in combination with the last three lines. I wish to emphasise the three points made in the middle. Firstly that a diagram is a fruitful tool to discover new results. Secondly that it ‘facilitates the grasp of the statement of the proposition and constructions made’, in other words it contributes to understanding; and finally that a diagram may represent relations.

I am mainly interested in stating something about diagrams used in contemporary mathematics, but my starting point will concern diagrams used in Euclid’s Elements or Greek mathematics in general. The main reason for this is to take advantage of some of the detailed studies that have been made on, in particular, Euclid’s diagrams. The first task, therefore, is to establish that some—but not all—of the roles diagrams in Greek mathematics have been noted to play can be transferred to contemporary examples. The first section, then, considers some of the roles diagrams have been stated to play in Greek mathematics. In this part Reviel Netz’s claim that diagrams are metonyms for propositions and Philip Catton’s and Clemency Montelle’s statement that they are “metonyms for an epiphany” will be compared with a contemporary example. It will be noted that this example plays similar cognitive roles but differ in other respects to be explained.

Having found that there are uses of diagrams that cut across history, I move in the second part to investigate whether diagrams—compared to other types of representations—are unique in some respects. The second part considers a proposal made by Danielle Macbeth pertaining to the fruitfulness of Euclidean diagrams and notes that proofs not based on figures exemplify the same features. Macbeth commences her paper on Euclidean diagrams by expressing the hope that a detailed understanding of the Euclidean practice may contribute to further understanding also in later practices. This accords well with the just mentioned conclusion: “My aim is to clarify the nature of this practice in hopes that it might ultimately teach us something about the nature of mathematical practice generally. Perhaps if we better understand the first (and for almost the whole of the long history of the science of mathematics the only) systematic and fruitful mathematical practice, we will be better placed to understand later developments.” (Macbeth 2010, p. 236).

Macbeth bases the fruitfulness of diagrams on the observation that objects “pop up” as a consequence of the constructions made. She gives two explanations for the fact that this is possible: The first is due to alternative readings of the involved representations of geometric objects, such as line segments. The second item states it is possible to identify 3 ‘levels of articulation’ in the diagrams enabling the multiple readings. Macbeth (2014) furthermore illustrates that objects pop up and that alternative readings are also used in mathematical reasoning in general. Her (historical) examples include reasoning as described by Kant and a derivation of Euler’s formula. Macbeth’s last and most elaborated example of objects popping up in a non-diagrammatic proof is taken from Frege’s concept-script.

In the final section, based on the examples presented throughout the paper, I introduce one type of representation, denoted a ‘faithful representation’ that seems to hold a key for explaining fruitfulness. An important property of a faithful representation is that it can be manipulated in a way, so that new relations may be discovered. In addition I point to two features of 2-dimensional diagrams that seem to be advantageous for our understanding—and so indirectly for fruitfulness in case one takes understanding as a prerequisite for the further development of mathematics. The first has to do with the spatial configurations possible when using diagrams. In diagrams, exploiting the two-dimensionality of a page, the same sign can be part of different (representations of) objects, but need only be drawn once. We shall see that this is the case in Euclid I.1 where a single line segment is both the radii of two different circles and the base line of a triangle. In contrast we may use a single letter to stand for an object in a textual argument but the letter will be placed at different places on the page for each time the object is referred to. My proposal is that placing a sign or object only in one place in the diagram and showing which relations it has to the other objects displayed provides a cognitive advantage.

The second suggestion is based on what was emphasised above, namely that a diagram displays relations. One may draw a diagram composed of e.g. letters (standing for some objects) and lines between these letters suggesting that objects connected are related in some way. This allows us to show that the objects are related, but not necessarily expressing how they are related. In the examples to be presented we shall see that sometimes the intended relations can be read off directly from the diagram whereas in other cases a connecting line simply illustrates that some relation holds between the objects. In particular in the last case symbols and other types of signs makes it possible to state which relation(s) is at stake. My proposal is that the advantage of some diagrams consists in a capacity to show the relation as compared to text or symbolic expressions simply stating that a relation holds.

1.1 Peirce on icons, indices and symbols

Because of the references to be made to Peirce’s theory of signs I need to make some notes about terminology. According to Peirce ‘diagram’ refers to the (iconic) sign that represents relations. In order to avoid confusion I will use the term ‘diagram$_P$’ when this meaning is intended. I will continue to use ‘diagram’ in its ordinary sense referring to certain (2-dimensional) visual representations composed of lines and sometimes letters standing for mathematical objects. Sometimes, as did Pasch, I will use ‘figure’ or ‘geometric figure’ as well.

In general Peirce takes a representation or sign to be one of three components of an irreducible triadic relation. In addition to the sign itself it consists of the object the sign stands for and the interpretant of the sign. I will make use of his icons, indices and symbols. When referring to these one asks how a sign accomplishes to refer to, or stand for, an object.¹ An icon is a sign that represents because it resembles, or holds some kind of likeness, to the object represented. According to Peirce there are three ways in which ‘likeness’ can be understood, see Table 1. The simplest is when the sign resembles what it represents, as in an image. Example of iconic images are drawn pictures and geometric figures. Second the sign may show certain relations. Such a sign Peirce denotes a diagram, or an iconic diagram. Note that on this understanding ‘a diagram’ may also refer to, for example, an algebraic formula as long as it is read as expressing a relation. As an example take the identity $a^2+b^2=c^2$ that expresses that a particular relation holds between the sides of a right-angled triangle. Peirce writes the following: “In fact, every algebraical equation is an icon, in so far as it exhibits, by means of the algebraic signs (which are not themselves icons), the relations of the quantities concerned”(CP 2.282, italics in original).² As noted above I will refer to icons representing relations as ‘diagram$_P$’.

Table 1 Different types of icons

Finally an icon may represent by “parallelism in something else” (CP 2.277) in which case it is called a metaphor.³ Peirce writes: “Particularly deserving of notice are icons in which the likeness is aided by conventional rules. Thus, an algebraic formula is an icon, rendered such by the rules of commutation, association, and distribution of the symbols. $\ldots$ For a great distinguishing property of the icon is that by the direct observation of it other truths concerning its object can be discovered”(CP 2.279). A simple example is that for real numbers, a, b, the expression $(a+b)^2$ is seen to be an icon of $a^2+b^2+2ab$ (or vice versa) because of the laws holding for operations on real numbers. That the two expressions are equal indicate they share some kind of likeness. This likeness does not hold because they look alike, that is they are not images. Neither do they represent the same relation. The only way to see that the expressions are alike is to use the properties of real numbers (distributive and commutative law) and the convention that $a^2=a\cdot a$. So the likeness is what Peirce refers to as metaphorical. I will give further examples of all three kinds of icons throughout the paper.

Since mathematics deals extensively with relations, the use of diagrams$_P$, in the sense of representations of relations, abounds. Note that referring to the diagrams used in Euclid’s Elements as ‘diagrams$_P$’, makes sense also on this interpretation. Instead of taking them to be images or pictures of the geometric figures (squares, triangles, circles etc.), when reasoning it is the relations between various points (denoted by letters) and other geometric objects that are relevant. Take the example of a circle. What we should note when seeing a circle is not (only) its form. When reasoning it is particularly relevant to note the special relation that holds between any point on the circumference and the centre of the circle, namely that the distance between them is constant—a property used in, for example, Proposition I.1.

An index, as it is used in mathematics, is a sign that for some purpose is associated with a certain object without saying anything about the object.⁴ We use an index when we wish to reason about, say, a function calling it ‘f’. Peirce gives as an example the geometricians’ use of letters placed next to various points in figures to stand for these points, allowing them to reason about the points.

The last type of sign is the symbol. A symbol represents because of some law fixing the reference of the sign. Symbols used in mathematics are for example, ‘$\cdot$’, ‘$\pi$’ and ‘$+$’. In this paper I will use the term ‘symbolic expression’ to denote an expression, or relation, composed of symbols. An example is the identity $a\cdot b= b\cdot a$ stating that multiplication is commutative by using the symbols ‘$\cdot$’ and ‘$=$’. A last—but important—thing to note is that signs often are composed of other signs and that a sign may represent in different ways, that is, it could represent both as, e.g., a symbol and as an icon. An example of a compound sign is the iconic diagram$_P$, $a\cdot b= 1$ (e.g., for $a,b\in \mathbb {Q}$) which has both indexical and symbolic parts. As a whole it states that a and b are multiplicative inverses of each other. a and b act as indices, referring to numbers, and the relation is expressed using the symbols ‘$\cdot$’ and ‘$=$’.

2 Diagrams in Greek mathematics

In the Shaping of Deduction Netz argues that the diagrams used in Greek mathematics are metonyms for propositions. One component of this characterisation consists of the documented interdependence between the text and diagram. Note that this point—as well as many others—is also stressed by Manders (2008/1995). In order to argue for the dependence of the diagram Netz conducts a detailed study on how specification of letters is accomplished in Greek mathematical texts, that is, how one comes to learn what the letters used stand for. One important finding is the use of letters, whose reference is not given by the text. Such letters are only fixed by the accompanying diagram. Netz introduces various types of categories of letters, one being being ‘completely unspecified’ which means it is not possible to recover from the text alone which point the letter stands for. Netz bases the claim that the demonstration is dependent on the accompanying diagram by counting the number of occurrences of letters in these categories finding (for Euclid book XIII) that 19% of the occurrences are completely unspecified (p. 23). The conclusion is that the diagram is required in order to fix reference in these cases. In addition Netz finds that information used in demonstrations is extracted from diagrams. Below is an example (Elements proposition II.11) where information used in a demonstration is read off of a diagram. Reversely Netz argues that the text is not recoverable from the diagram, concluding that the diagram and text are interdependent.

Besides the above conclusion, that the diagram is a necessary component of certain demonstrations in Greek mathematics, Netz bases the claim that a diagram is a metonym for the proposition on an analysis of the use of the word ‘diagram’ in Greek texts. He finds, for example, that Aristotle uses the word ‘diagram’ to refer to the proposition. The Greeks never seem to use ‘diagramma’ (or similar) to refer to the accompanying geometric figure. Instead a number of different words are being used non systematically. Referring to the figure, they could use, for example katagraphe—the ‘drawing’. Secondly Netz observes that the diagram is unique to the proposition: “The overwhelming rule in Greek mathematics is that propositions are individuated by their diagrams”(p. 38). This leads to the conclusion that the ‘diagram is a metonym for the proposition’ (p. 37).

Catton and Montelle in their To diagram, to demonstrate: To do, to see, and to judge in Greek geometry also start out with an analysis of the meaning of ‘diagram’ in the context of Greek geometry. They note it can act both as a verb and a noun. As a verb it designates “concerted manual steps that in the end allow something to be seen. These steps also allow concepts to be formed or clarified that may then ultimately allow clear things to be said” (Catton and Montelle 2012, p. 25). As a noun it might mean a number of things, but most often “the figure provided with the text”(p. 26). Other meanings could be (here freely reproduced from their text) (i) the set of marks necessary in order to follow the demonstration (ii) the set of marks required in order to understand the proposition or (iii) the set of marks produced in order to perform the construction that the proposition states is possible (p. 25).⁵ One of their points is that a diagram satisfying any one of these descriptions would look quite different from one constructed to satisfy another—and that the diagram chosen has to balance each of these objectives. They further show that the figure provided with the text does not show the actual constructions performed; rather it “brings to mind better what the proposition embodies...the diagram helps us call to mind the demonstration, and still more importantly, helps us better intuit what it is, practically, that is proposed to be done”(p. 37). Furthermore they note Plato’s fascination with the duality of timelessness and temporality and so, taking the various meanings into account, they claim the diagram combines the temporality of moving about in the diagram following the demonstration with the timelessness of the insight thereby obtained—and so claim the diagram is a metonym for an epiphany.

To sum up I have pointed to the following roles diagrams play in Euclid’s Elements (or Greek mathematics):

• 1. They are metonyms for propositions. This could mean a number of different things, including that a diagram individuates the given proposition (as indicated by Netz), it helps recollecting the formulation of the proposition and it indicates the constructions to be made to prove the proposition (as proposed by Catton and Montelle).

• 2. Furthermore the proof depends on the diagram, features of diagrams are used in the proofs as pointed out by Netz (1999) and Manders (2008).

• 3. The diagram is a metonym for an epiphany. Moving about in the diagram, following the instructions made in the text, one comes to see that the proposition holds.

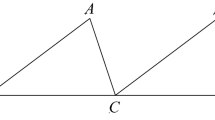
I illustrate these points by an example from Euclid. I find that Euclid’s Elements proposition II.11—also used as example by Catton and Montelle—illustrates these points well.

The accompanying figure is the following:

Fig. 1

The diagram of Euclid’s Elements proposition II.11

Focussing first on the line AB in this diagram⁶, divided in the point H, and second the geometric figures thereby obtained, allows recollecting the formulation of the proposition:

To cut a given straight line so that the rectangle contained by the whole and one of the segments is equal to the square on the remaining segment.

Using the letters given in the diagram the proposition can be stated as follows. The line AB is cut in H so that the square on AH is equal to the rectangle formed by HB and BD.⁷

The diagram furthermore helps recollecting the constructions made in order to follow the demonstration. The line AC is cut in half giving a point E, a straight line connects this point with B, producing EB. AC is extended to F so that EF is equal to EB. The final step is to produce the square on AF and extend the line GH to K. The proposition then states that the square on AH is equal to the rectangle formed by HB and BD.

I omit details of the first part of the proof. It consists in using proposition II.6—observing that the figure contains a straight line that is divided in half and then extended.⁸ Next an instance of I.47 “Pythagoras’ theorem” is applied, noticing that ABE is a right angled triangle. Combining these two results one obtains that the rectangle formed by FC and AH is equal to the square formed on AB. Looking at the figure one sees that they have the rectangle formed by AH and AC in common. [In the English translation Heath simply writes “Let AK be subtracted from each” (Euclid 1956, p. 403).] If this is removed, the result follows.

As claimed above, the diagram plays a number of roles in this proposition. It helps recalling the formulation of the proposition, it points to constructions as well as steps to be made to go through the demonstration. One even reads off properties of the diagram, used in the demonstration. Finally, as argued by Catton and Montelle, performing the constructions indicated by the diagram and following the steps of the demonstration should move one into a timeless insight.

My next aim is to investigate which of these roles diagrams in contemporary mathematics play. The example to be presented is chosen because it plays some of the above articulated roles. It is taken from Haagerup and Thorbjørnsen (1999) and Carter (2010). It concerns permutations that can be pictured by drawing lines between points placed on a circle as in Fig. 2. Recall that a permutation, $\pi \in S_p$ is a bijection on the set $\{1, 2, \ldots ,p\}$. In this case we further require that $\pi (i)\ne i$ and that $\pi ^2(j)=j$. The figure above—Fig. 2—shows the permutation that in two-cycles can be written as (12)(36)(45).⁹

Fig. 2

A representation of a permutation on $\{1, 2, 3, 4, 5, 6\}$

We need two further definitions. A permutation, $\pi$ on $\{1, 2, \ldots ,p\}$ is said to have crossings or be a crossing permutation if it is the case for some numbers, $a<b<c<d$ in the set $\{1, 2, \ldots ,p\}$ that $\pi (a)=c$ and $\pi (b)=d$. If such a permutation is represented as before, the line joining a and c and the line joining b and d will cross. If the permutation does not fulfil this property, it is said to be non-crossing. The permutation in Fig. 2 is non-crossing. Figure 3 represents a crossing permutation.

If a number i in $\{1, 2, \ldots ,p\}$ fulfils that $\pi (i)=i+1$ (or $\pi (i+1)=i$) calculating mod p then $(i, i+1)$ is said to be a neighbouring pair. In Fig. 2 (1, 2) and (4, 5) are neighbouring pairs. The permutation pictured in Fig. 3 has no neighbouring pairs.

Fig. 3

A representation of a crossing permutation on $\{1, 2, \ldots 7, 8\}$. The numbers $\{1,2,3,6\}$ form a crossing. Another crossing is $\{2, 4, 6, 7\}$

The theorem I will prove—by drawing on a diagram—is that

If a permutation $\pi \in S_p$ has no neighbouring pairs, it will have a crossing. ¹⁰

Fig. 4

A proof based on a diagram: Choose i so that $\pi (i)-i=m$ is as small as possible. Considering what $i+1$ is mapped to one sees that a crossing necessarily occurs

The argument is as follows. For $\pi$, a permutation in $S_p$ that has no neighbouring pairs, choose i in $\{1, 2, \ldots ,p\}$ so that m in $\pi (i)=i+m$ is as small as possible, see Fig. 4. We now consider what happens to $i+1$ under $\pi$, corresponding to the dotted lines in the figure. Either $\pi (i+1)$ is less than i and we see that a crossing occurs. (i is already joined by $i+m$ and the map is one-to-one, so $i+1$ cannot map to i.) If $\pi (i+1)$ is greater than i its value must be greater than $i+m$, since m was chosen to be the minimum ”distance” between any number and $\pi$ of that number. So again a crossing must occur.

I claim the diagram used in this argument plays similar roles as described above. First it helps recalling the formulation of the proposition. Seeing the lines that cross allows me to retrace the steps made in order to formulate the statement that a permutation with no neighbouring pairs has a crossing. In addition the main idea of the proof, the choice of i, is indicated by the drawing. Finally, following the argument and moving about in the diagram, one sees that the conclusion follows, namely that the lines must cross. (I am very sympathetic to Catton’s and Montelle’s insistence on the practical aspect of following a demonstration or proof. Indeed in the proof just given, one must, in one’s mind or on paper, follow the “constructions” made in order to see that the proposition is correct. In general one may take a given proof as instructions to follow in order to see that a proposition holds.¹¹) Moving to consider differences between the two examples, it is debatable whether it makes sense to claim that the diagram considered individuates the proposition. One objection would be that most propositions in contemporary mathematics are not accompanied with diagrams. This entails that one of the items used in Netz’s argument for the claim that a diagram is a metonym for a proposition does not hold in general.

A further issue relevant when comparing the ancient Greek with contemporary practice concerns reading off information from diagrams. It was noted that this was done in proposition II.11 as well as in the example just shown. In this respect it is important to stress that it is possible to prove the last proposition without reference to a figure (following the advice of Pasch in the introductory quote).¹² Indeed the argument just given is not the one presented in the journal. Part of it goes like this: (As before) choose i so that m in $\pi (i)=i+m$ is as small as possible. Next consider what $i+1$ is mapped to. If that value is less than i then $\pi (i+1)< i< i+1 < \pi (i)$ is a crossing for $\pi$. If the value of $i+1$ is greater than i, it must be greater than $i+m$ because of the way i was chosen. Then $i<i+1<i+m<\pi (i+1)$ is a crossing for $\pi$. I wish to emphasise here the difference between the two arguments. In the first diagram-based argument one sees the crossing, that is, the lines actually cross in the diagram. In the text-based proof one states, using appropriate signs (i.e., indices and symbols), that the relation holds. I shall return to this point in the last section.

The conclusion is that reasoning based on diagrams as practiced in Euclid’s Elements is not exclusive to Greek geometry although there are some differences. I observed that the diagram in both cases contributed to a recollection of the proposition, that it indicated either the constructions to be performed or the main idea of the proof and that it yields understanding. These roles were also emphasised in the quote of Pasch in the introduction. In contrast diagrams in contemporary mathematics do not in general individuate propositions and I noted that contemporary proofs need not depend on a diagram to the extent that Netz claims Greek demonstrations do.¹³ I thus move to the second question to be dealt with here, namely whether diagrams are special in terms of their capacity to point to new results. That is, the question posed is whether it is possible to point to certain features of diagrams that allows us to explain why they are fruitful. In order to do this I start by considering the proposal made by Danielle Macbeth explaining the fruitfulness of the diagram-based reasoning found in the Elements.

3 Macbeth’s diagrammatic reasoning

In Macbeth’s Realizing Reason, chapter 2, (Macbeth 2014) the perceived fruitfulness of the diagrams used in Euclid is investigated. According to Macbeth Euclid’s results, obtained by diagrammatic reasoning, constitute “real extension of our knowledge” (p. 88).¹⁴ That diagrammatic reasoning extends knowledge is explained by the fact that objects pop up¹⁵ as a result of constructions made in the diagrams. Macbeth points to two ways of our handling diagrams that make this possible. The first concerns the reading of (parts of) diagrams as iconic diagrams$_P$. She argues that figures in Euclid should be regarded not as images, signs that represent because of similarity, but as signs showing relations. Furthermore she finds that this implies that multiple readings are possible. Taking Euclid’s proposition I.1 as an example (see Fig. 5) one may take the given line segment AB as part of a triangle, that is, in relation to the shown triangle. On a different reading one considers the line segment as part of, that is, radius, of a circle. Macbeth explains how such alternative readings are realised as follows: “An icon of a radius essentially involves reference to a circle; radii are and must be radii of circles. An icon of a side of a triangle makes no reference to a circle. So nothing could at once be an icon of both. But one and the same thing could serve now (at time t) as an icon of a radius, and now(at time $t'\ne t$ ) as an icon of a side. The familiar duck-rabbit drawing is just such a drawing; it is a drawing that is an icon of a duck (though of course no duck in particular) when viewed in one way and an icon of a rabbit (no one in particular) when viewed in another” (Macbeth 2014, p. 89, italics in original).

Fig. 5

The diagram accompanying Euclid’s Elements I.1

In proposition I.1 an equilateral triangle is constructed on a given line. In the course of the demonstration one exploits the stated fact, i.e., that the given line AB plays different roles. It represents the radius of two different circles as well as the side of the constructed triangle. The second component of Macbeth’s explanation is to ensure that parts of a given diagram, such as a line or a point, may indeed be taken to belong to different figures relevant to the argument. Macbeth argues this is possible since diagrams may be construed as having three levels of articulation:

At the lowest level, then, are the primitive parts, namely, points, lines, angles, and areas, and their corresponding icons. At the second level are the (concepts of) geometrical objects we are interested in, those that form the subject matter of geometry, all of which are wholes of those primitive parts (and similarly for their icons). At this level we find points as endpoints of lines, as points of intersection of lines, and as centers of circles; we find angles of various sorts that are limited by lines that are also parts of those angles; and we find figures of various sorts. A drawn figure such as (say) a square has as parts: four straight line lengths, four points connecting them, four angles all of which are right, and the area that is bounded by those four lines. ... At the third level, finally, is the whole diagram, which is not itself a geometrical figure but within which can be discerned various second-level objects depending on how one configures various collections of drawn lines within the diagram (Macbeth 2014, p. 91).

The matter being investigated here is whether it is possible to point to specific features of diagrams that explain their fruitfulness. In that light note that Macbeth shows that shifts of focus and thus change of the meaning intended also occurs in arguments that do not depend on diagrams. In addition something similar to different levels of articulation can be formulated for proofs not based on diagrams. Among Macbeth’s examples of objects popping up is Euler’s formula, $e^{ix}=\cos (x) + i\cdot \sin (x)$, found by considering the power series expansions of the three functions, $e^x, \sin (x)$ and $\cos (x)$. I will present a version of this proof in the next section. As a simple example of objects popping up, one could mention performing calculations corresponding to the constructions of Euclid I.1 in analytic geometry. One places the given line segment in a coordinate system, see Fig. 6.

Fig. 6

Placing the circles of Euclid I.1 in a coordinate system

Let us suppose it has the endpoints (0, 0) and (1, 0). The equations of the two circles can then be written as $x^2+y^2=1$ and $(x-1)^2+y^2=1$ and their intersection point(s) be calculated. It is obvious the x- coordinate is $x=\frac{1}{2}$, but this can also be calculated by noting the two different representations of 1 in the two expressions, that is, $x^2+y^2=1=(x-1)^2+y^2$. The corresponding y-coordinates are $\pm \frac{\sqrt{3}}{2}$.¹⁶ In addition to multiple representation in this example notice that the three levels of articulation apply. At the first level are the individual signs used, e.g., x, y and $\cdot$. At the second level are the different formed expressions, such as $x^2+y^2=1$. The last level consists of the proof.

3.1 A different role of signs

In this section I will present a proposition where a new object is constructed, a group of permutations. I will note that it is possible to point to signs that represent in alternative ways similar to Macbeth’s analysis. But more importantly I will argue that signs play different roles in this example. The example is Cayley’s theorem in group theory: Any group, G, is isomorphic to a group of permutations onG.

Proof

¹⁷ Let G be a group.¹⁸ We have to construct a group of permutations and show that this group is isomorphic to G.

I give some details of the first part, the construction of the group of permutations. We construct such a group by the following. For any $a\in G$ we define the function $\phi _a: G\rightarrow G$ by $\phi _a(x)=a\cdot x$. Since $a\cdot x\in G$ for $a,x \in G$ it is clear that $\phi _a$ is a map from G to itself. We prove $\phi _a$ so defined is a bijection. It is one-to-one: If $\phi _a(x_1)=\phi _a(x_2)$ we would obtain that $a\cdot x_1=a\cdot x_2$ which implies that $x_1=x_2$. It is onto, since given any element, $g\in G$, we would have that $a^{-1}g$ is mapped to g: $\phi _a(a^{-1}g)=aa^{-1}g=1g=g$. $\phi _a$ is therefore a permutation. Now let $\Phi =\{\phi _a|a\in G\}$.

One may prove that the collection of $\phi _a$’s, that is $\Phi$, is a group under composition, so that it is a group of permutations.

Next we define a map between G and $\Phi$, the collection of all $\phi _a$ for $a\in G$. Define $f: G\rightarrow \Phi$ by $f(a)=\phi _a$. One then proves that this map is a homomorphism between groups and that it is injective and onto. It follows that G is isomorphic to a group of permutations. $\square$

Analysis of the proof illustrating the multiple use of representation and in order to see how the object is constructed. The main object that is constructed in this theorem is the group of permutations, $\Phi$. It consists of the elements denoted $\phi _a$ for each element a in G. First I make a few notes about different types of representations used in the proof. First note the use of ‘G’ and later ‘a’ to fix reference, enabling us to refer to the given group and an (arbitrary) element of this group. In this capacity they act as indices. When constructing the group of permutations, the letter a denoting an element of the group is used in combination with a new letter $\phi$ together with a law stating what this sign is supposed to stand for, namely $\phi _a(x)=a\cdot x$. Since the meaning of $\phi _a$ is given by a law the use of the sign has symbolic elements. But later in the proof, e.g. when defining the homomorphism between the group G and the group of permutations, $\phi _a$ is used as an index, simply representing an element of the group of permutations. That is, $\phi _a$ represents in some cases as an index, and in other as a symbol.

An important ingredient in order to understand the theorem is to be able to see the correspondence between the element $a\in G$ and the permutation $\phi _a$ in $\Phi$. The particular choice of using the letter (sign) a to represent a particular element of the given group and using this in combination with the sign used to represent the permutation is a good trick to make readers notice this correspondence. Returning to the alternative readings of signs in the example above, that is Elements I.1, I claim something similar occurs here. It was noted that an object (or sign representing the object) may be read as standing in different relations to different objects. E.g., in Euclid I.1 the given line AB is taken both as a side of a triangle and as radii of two different circles. In Cayley’s theorem the sign a represents both an element of the group G and—in combination with $\phi$—an element of the constructed group of permutation, $\Phi$. That is, a stand in a relation both to the group, G, (as a member of) and to a particular element of the group of permutations, $\Phi$. (In order to define the members of $\Phi$, $\phi _a$ one needs to refer to a.) Moreover, because of the group operation, elements of the group stand in certain relations to other elements of the group. These relations are drawn upon in the above proof. An element a in a group is, on the one hand, related to its inverse, $a^{-1}$, in the sense that $a\cdot a^{-1} =1$. On the other hand, any element is related to 1, the identity element, so that $a\cdot 1=a$.

Having said this I also find that different uses of signs occur in this example. First note that in this example the object constructed is not pictured. In the examples given from the Elements the constructed triangle as well as the figures mentioned in proposition II.11 are pictured, so that these figures also work as images. In Cayley’s theorem objects are primarily named. Letters (functioning as indices) are being used, for example, to name members of the group, and later the Greek letter, $\phi$ is used to refer to the permutations. Second, since the objects are not pictured a different type of representation is required to let us know how they are defined. In this case we are shown how objects are defined in terms of symbolic expressions, for example, by the expression $\phi _{a}(x)=a\cdot x$. Third, relations holding between objects considered are also given in terms of symbolic expressions. In Euclid I.1 relations are exhibited in the figure and reported in the text, but not in terms of symbolic expressions. I will return to these points in the next section. I mention a final difference namely that in the above proof only relations actually used are expressed in the proof whereas multiple irrelevant relations can generally be read off the diagrams of Euclid.

As was established above proofs exploit signs in multiple ways even when no figures are referred to and this practice is fruitful in the sense described by Macbeth, that is, new objects appear as a consequence of the constructions made. The conclusion is that it is not simply the possibility of multiple readings of signs that makes diagrams stand out compared to text-based arguments in combination with symbolic expressions. Considering Emily Grosholz’s book Representation and Productive Ambiguity (2007) one finds what appears to be a similar conclusion. It should be stressed, however, that Grosholz’s notion of multiple readings (or, as she refers to it, ambiguity) is of a different kind. She refers mostly to signs representing both as icons and as symbols. Grosholz’s first example illustrating this ambiguity concerns Galileo’s multiple reading of line segments. On one reading they are taken (iconically) as finite segments and so allowing to use the results of geometry. On a symbolic reading they represent infinitesimals and so lead to the notions of motion, speed and acceleration. She argues (or shows) that such ambiguity is exploited in mathematics in general, that is, ambiguous reading of signs that allows mathematicians to draw on different fields. Her examples are taken from a wide range of mathematical fields, starting with geometric diagrams moving on to, e.g., algebra, topology and logic.

Besides different functions of signs (e.g. naming vs picturing and showing vs expressing), one feature appears to be different in the examples just considered, that is, proposition I.1 of the Elements and Cayley’s theorem. In Cayley’s theorem I noted the index a representing an element of the group and that it is used in combination with a new sign, $\phi$ to name the permutation corresponding to a, namely $\phi _a$. Comparing this double use of a with the ambiguous use of the line segment AB, one may notice that the line is located at the same place, whereas the letter a is located at different places on the page. My proposal is that the fact that the line is located spatially in just one place is an advantage for our understanding.

A few remarks are in place explaining in which sense ‘understanding’ is taken here. This brief description is based on Carter (2012b)—which is inspired by (in part unpublished) writings of Ken Manders, see e.g. Manders (1999). ‘Understanding’ is characterised as a relation between a given subject matter and human agents. The subject matter in this case consists of presentations of proofs. What is of interest to us is a comparison between the use of diagrams and other means (based on text and symbolic expressions) of presenting proofs. When referring to understanding I am considering whether certain (objectively statable) properties of diagrams are advantageous in some ways as compared to what is expressible using other means of representations. When saying what is advantageous we have to keep in mind that we are dealing with human beings who have limited cognitive abilities. An important component of Ken Manders’ characterisation of understanding is ‘control of types of responses’ (and a converse notion of ‘indifference’). A practice may be considered advantageous based on the types of responses rendered superfluous as compared to another practice.¹⁹ By stating that the figure of Euclid I.1 has cognitive advantages I suggest that fewer cognitive resources must be drawn upon in order to see that the line segment is part of, e.g. both the triangle and one of the circles. It is simply the same line. In the proof of Cayley’s theorem one must actively construct the relation that holds between a and $\phi _a$, a relation that can be pictured as $a \mapsto \phi _a$. The correspondence between the two is not explicitly shown by any sign during the proof I presented above.

4 Fruitfulness of diagrams?

I have found that diagrams in contemporary mathematics play some of the roles as the diagrams are said to play in Euclid’s Elements. Furthermore I have considered Macbeth’s explanation of why they are fruitful—and noted that diagrams are not exclusively so. It remains to say something about the peculiarity of diagrams. The first difference is already stated above, namely exploiting the 2-dimensionality of diagrams to allow the representation of, e.g., a geometric object to be part of different geometric figures. This is the case of the line segment AB in Fig. 5. Another example is displayed below in Fig. 7. The figure presented there may be used in order to determine the value of $\cos (\tan ^{-1} (x))$. The angle $\theta$ corresponds to $\tan ^{-1}(x)$, so the sought for value, $\cos (\theta )$, corresponds to the length of the line marked by a (that is OC) in the figure.

Fig. 7

A diagram used to determine the value of $\cos (\tan ^{-1} (x))$, for example showing $\theta =\tan ^{-1}(x)$

Having represented the relevant parts of the expression in the 2-dimensional diagram, the next step consists of formulating relations holding between a, b and x. Such relations can be “read off” from the diagram noticing first, that a and b are the sides of a right angled triangle, OCA. Second one sees that the same sides are also part of a triangle that is similar to the triangle ODE. The equations thus obtained are

$$\begin{aligned} a^2+b^2=1 \text { and } \frac{b}{x}=\frac{a}{1} \end{aligned}$$

Notice here that the line segment named a (corresponding to $\cos (\tan ^{-1}(x))$) is located only once in the diagram even though it is part of two different configurations. This allows us to express two different relations. In order to formulate these relations a shift of attention enables one first to focus on the right-angled triangle, triggering certain “category specifications” for such triangles recognising it as a right-angled triangle. Second one’s attention has to shift so that one instead recognises the two similar triangles.²⁰ That is, the first identity is obtained by drawing on one’s knowledge of right-angled triangles, and the second by considering the two similar figures. Since the relevant line segment is part of both configurations this shift of attention does not compromise the final result. In contrast, when writing the equations and performing the calculations in order to determine the value of a, a (as well as the other indices used) has to be repeated for each occurrence.²¹

A second observation—the third mentioned point from Pasch’s quote—is that figures enable one to show that certain objects are related. In general one may indicate that a relation exists between two objects by connecting letters denoting them by a line. Showing that a connection exists need not imply that the type of relation is given by the diagram. The examples shown here illustrate different degrees of explicitness of the given relation. In Fig. 5, showing the diagram of Euclid I.1, one directly reads off the relations of the line AB to the other figures. In Figs. 2 and 3, showing representations of permutations, the lines joining points indicate that these points stand in some relation. The accompanying text tells us that they are to be interpreted as showing the values of permutations. One could illustrate Cayley’s theorem with a diagram like $a\rightarrow \phi _a$ for $a\in G$, indicating by the arrow that there is a relation between a and $\phi _a$. The arrow, however, does not state what the relation is. The accompanying text lets us know that there is an isomorphism $f: G\rightarrow \Phi$ given by $f(a)=\phi _a$. In all these cases—whether the relation is explicit or not—is an advantage for our understanding: The role of the diagram is to show that there is some connection, not necessarily precisely what the connection is. It was noted, though, that in some cases the diagram is able to display the intended relation(s). This fact gives rise to the notion of a ‘faithful representation’ that I will try to characterise. This type of representation may point to one explanation of why certain representations are fruitful. In general, in the course of a proof, certain signs are produced in order to handle the objects under study. (‘Objects under study’ may be properties, relations, concepts or simply objects.) In brief, a sign may represent both as an image and as a diagram${}_P$ (that is, displaying relations). If, in addition, the sign may be produced so that it respects manipulations made on the object under study, I denote the sign ‘a faithful representation’. I find that these properties of signs, representation both as image and diagram$_P$ and respecting manipulations, hold for a number of the cases presented here—but not the main signs produced in the proof of Cayley’s theorem.

In the Elements I.1 the lines produced in the diagram (see Fig. 5) represent simultaneously parts of the geometric figures and relations holding between points on these figures. That is, the diagram represents both as an image (e.g., a triangle) and as a diagram$_P$. Furthermore constructions—or manipulations—are made on the shown objects, allowing us to discover new relations among the parts. The main relation we are supposed to realise in the end is that the constructed line segments AC and BC are equal to AB.

Similarly in Figs. 2, 3 and the proof of Fig. 4, representing permutations on $\{1, 2, \ldots , n\}$ by joining points by a line, are parts that represent both as images and as diagrams$_P$: The properties of being a neighbouring pair and a crossing permutation are both directly observed in the figures: Neighbouring points are joined by a line (Fig. 2) and lines actually cross (Fig. 3). So they represent partly as images. At the same time the diagrams intend to represent these properties as relations holding between elements in the set $\{1, 2, \ldots , n\}$ and so expressing properties of a permutation. As such the diagrams also represent metaphorically. Finally we see in the proof that “constructions” made on the diagram respect these properties, so that it is possible to make a picture proof of the statement that a permutation with no neighbours has a crossing.

Taking into account that signs used in mathematics often represent metaphorically, the notion of a ‘faithful representation’ is extended to include representations that represent as a metaphor. To sum up, I denote a representation a ‘faithful representation’ in case the following holds:

• (i) It represents either as an image or as a metaphor.

• (ii) It represents certain relevant relations, that is, it represents as a diagram$_P$,

• (iii) Manipulations can be performed on the representation, respecting relevant relations holding between objects, in such a way that new relations may become visible.

For a final example, and one that does not depend on a diagram, I consider a derivation of Euler’s identity, $e^{ix}=\cos (x) + i \cdot \sin (x)$.²² This example is slightly different, but holds similar key features, in particular that manipulations on the representations respect manipulations on the objects under study. First Euler presented the transcendent functions as power series:

$$\begin{aligned} e^x= & {} 1 + x + \frac{1}{2} x^2 + \frac{1}{3!} x^3 + \frac{1}{4!} x^4 + \frac{1}{5!} x^5\ldots \end{aligned}$$

(1)

$$\begin{aligned} \cos (x)= & {} 1 - \frac{1}{2} x^2 + \frac{1}{4!} x^4 -\cdots \quad \text {and} \quad \sin (x)= x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 -\cdots \end{aligned}$$

(2)

Putting ix in place of x in equation (1) and using the relation $i^2=-1$ gives

$$\begin{aligned} e^{ix}&=1 + ix - \frac{1}{2} x^2 - i \frac{1}{3!} x^3 + \frac{1}{4!} x^4 + i\frac{1}{5!} x^5 - \cdots \nonumber \\&= \left( 1 - \frac{1}{2} x^2 + \frac{1}{4!} x^4 -\cdots \right) + i\left( x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 -\cdots \right) \end{aligned}$$

(3)

The last equality is obtained by rearranging terms and extracting the common factor, i. Substituting $\cos (x)$ and $\sin (x)$ in (3), one may see that the identity $e^{ix}=\cos (x) + i \cdot \sin (x)$ follows.

In this proof the transcendental functions, $e^x, \cos (x)$ and $\sin (x)$ are represented by power series. Euler considered the power series to be equal to the functions (in contemporary terms one has to prove that they converge to the functions in order to do the rearrangements), so they can be taken to be metaphors of the functions considered. Second, because of the power series representations, relations between the functions can be read off from the expressions. Third, observe that the signs can be manipulated, the terms of the sum are rearranged, so that the intended relation can be observed in the final equation.²³ In other words manipulations on the “objects”, i.e. the functions, correspond to manipulations made on their representations, the power series. I therefore find that this example also exploits faithful representations.

5 Conclusion

I have explored the role of different representations in proofs with the intent to say something about the difference between diagrams and other types of representations. The question that drives this investigation is whether diagrams are particularly fruitful. The analysis has resulted in the notion of a ‘faithful representation’. A faithful representation is characterised by its capacity to both represent as an image—or metaphor—and as a diagram$_P$, that is, showing relevant relations. A further requirement is that manipulations on components of the representation correspond to operations on the objects represented so that new relations between parts may be obtained. I have shown two examples of such representations (excluding the examples from Euclid’s Elements). The first consists in part of the figures showing crossing permutations and neighbouring pairs and the picture proof that a permutation with no pairs has a crossing. The second example, done by symbolic expressions, is the proof of Euler’s formula. I also gave an example of a proof where the notion of a ‘faithful representation’ does not apply, namely the proof of Cayley’s theorem. In this case the main objects are merely named and not pictured. Furthermore relations are mainly stated in words and so manipulations on objects respecting relations are not shown.

In the first part of the paper I compared roles that the diagrams of Greek mathematics have said to play with a contemporary example. I found that the contemporary example (the one concerning permutations) displays some of these roles. To mention two things, diagrams function as an aid in recalling the statement of the proposition and they indicate main ideas or constructions in the proof. These roles may also be explained by the fact that the diagram represents partly as an image.

Although the notion of a faithful representation characterised in this paper does not exclusively apply to proofs using diagrams, I do point to two roles I find to be unique for diagrams. The first is that it is made a custom to show that a relation holds between objects by joining representations of the objects by a line. As noted sometimes the nature of the relation is also given by the figure. Second it was found that the 2-dimensionality of a diagram may be used to show that an object is related to multiple other objects. This is the case in Euclid’s Elements I.1 and the diagram used to find an expression for the value of $\cos (\tan ^{-1}(x))$.