1 Introduction

Optimization problems are common in real-world applications, especially in physics, chemistry, and biology [1]. Typically, a fast and effective method is required to find the optimal solution to an optimization problem. The most effective of these is based on metaheuristics.

Various metaheuristic algorithms exist. These can be classified into evolution-based algorithms (which imitate the law of the survival of the fittest), swarm-based algorithms (which simulate the cooperation and communication between animals), human-based algorithms (which imitate various human social behaviors), and physics-based algorithms (which imitate physical or chemical laws). An example of each type of algorithm is shown in Table 1.

Table 1 Summary of partial metaheuristic algorithms
Full size table

Each metaheuristic algorithm has unique characteristics, and no algorithm outperforms others on all criteria. Different algorithms can be combined into a hybrid algorithm to leverage their characteristics, overcoming individual shortcomings and improving performance. Hybrid algorithms have been used in many studies. For example, Kumar et al. [22] proposed a multi-objective hybrid heat transfer search and passing vehicle search optimizer (MOHHTS–PVS) in which heat transfer search (HTS) acts as the main engine and passing vehicle search (PVS) is added as an auxiliary stage to enhance performance when applied to large engineering design problems. Yildiz et al. [23] proposed hybrid taguchi salp swarm algorithm-Nelder–Mead (HTSSA-NM) and hybrid artificial hummingbird algorithm and simulated annealing (HAHA-SA). HTSSA-NM used Nelder–Mead (NM) to improve the local search ability of the hybrid taguchi salp swarm algorithm (HTSSA), to optimize the structure and shape of an automobile brake pedal. HAHA-SA used simulated annealing (SA) to improve the performance of the artificial hummingbird algorithm (AHA), to solve constrained mechanical engineering problems. Li et al. [24] proposed particle swarm optimization-simulated annealing (PSO-SA) to complete seismic inversion in anisotropic media. PSO-SA combined simulated annealing (SA) and particle swarm optimization (PSO) and adjusted temperature by SA to control the particle aggregation jump out of local optima to improve the local search ability of PSO. Mafarja et al. [25] proposed whale optimization algorithm and simulated annealing (WOASA) to solve the problem of feature selection. WOASA embedded simulated annealing (SA) in the whale optimization algorithm (WOA) to enhance exploitation by searching the most promising regions located by WOA. Laskar et al. [26] proposed hybrid whale-particle swarm optimization (HWPSO), which combined particle swarm optimization (PSO) and the whale optimization algorithm, to solve electronic design optimization problems. HWPSO introduced “forced WOA” and “capping”; the former improves local optima avoidance in the exploration phase in PSO, and the latter accelerates the convergence to the global optimum. Han et al. [27] proposed the moth search-fireworks algorithm (MSFWA), which combined the moth search algorithm (MS) and fireworks algorithm (FA) to solve engineering design problems. MSFWA introduced the explosion and mutation operators from FA into MS to strengthen the exploitation capability of MS. Shehab et al. [28] proposed the cuckoo search and bat algorithm (CSBA), which combined the cuckoo search algorithm (CSA) and bat algorithm (BA) to solve numerical optimization problems. CSBA exploited the advantages of BA to improve the convergence ability of CSA.

SSA and WOA are swarm-based metaheuristic algorithms that imitate the predatory behavior of sparrows and whales, respectively. SSA [29] includes a step to help the algorithm escape local optima, which many other algorithms do not have; however, the effect is not obvious, and its global search ability is weak. WOA [30] has a strong local search ability owing to its spiral update mechanism but can easily fall into the local optimum because of its weak global search ability. The purpose of this research was to create a hybrid algorithm that could harness the strengths of each component to overcome these limitations. Accordingly, we improved WOA's spiral update mechanism to enhance its global search capability and used the Levy flight mechanism to improve SSA's ability to escape from the local optimum. Then, we combined the two improved algorithms into a hybrid algorithm that has strong global and local search capabilities and the ability to escape from the local optimum.

To evaluate the performance of ISSWOA, the hybrid algorithm was tested on the standard unimodal benchmark functions, standard multimodal benchmark functions, and standard fixed-dimensional multimodal benchmark functions. In addition, ISSWOA was applied to seven engineering design problems and an electrical engineering problem. The results showed that ISSWOA had strong optimization ability and was a competitive algorithm for solving practical problems.

The remainder of this paper is organized as follows. Sections 2 and 3 describe SSA and WOA, respectively. Section 4 details the proposed ISSWOA. The application of the proposed algorithm to 23 benchmark functions and engineering problems is reported in Sects. 5 and 6, respectively. Finally, Sect. 7 summarizes the paper and outlines future research directions.

2 SSA

SSA [31] is a metaheuristic optimization algorithm based on the sparrows’ foraging and antipredation behaviors and describes a discoverer–follower model with an awareness mechanism. In SSA, sparrows with high fitness in the population are regarded as producers, while others are considered as scroungers, and a proportion of individuals in the population are selected as guards for detection of threats.

2.1 Producers

After initializing the sparrow population, all sparrows are ranked by their fitness, and some of the individuals with better fitness are selected as producers. The producers’ iterative equation is given by

$$\overrightarrow {{X_{i} }} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {\overrightarrow {{X_{i} }} \left( t \right)*\exp \left( {\frac{ - i}{{\alpha \cdot Maxiter}}} \right),} & {\quad R < ST} \\ {\overrightarrow {{X_{i} }} \left( t \right) + Q \cdot L,} & {\quad R > ST} \\ \end{array} } \right.,$$
(1)

where t is the current iteration, \(\overrightarrow {{X_{i} }} \left( t \right)\) is the current location of the ith sparrow, Maxiter is the maximum number of iterations, α is a random number in (0,1], R is a random number in [0,1], ST in [0.5,1] is a safety threshold, Q is a random number drawn from a normal distribution, and L is a 1 × D matrix of ones.

2.2 Scrounger

After the producers update their positions, the other individuals are selected as scroungers, and their position update equation is given by

$$\overrightarrow {{X_{i} }} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} { Q \cdot \exp \left( {\frac{{\overrightarrow {{X_{{{\text{worst}}}} }}\,\,\, \left( t \right) - \overrightarrow {{X_{i} }} \left( t \right)}}{{i^{2} }}} \right),} & {\quad i > \frac{n}{2}} \\ {\overrightarrow {{X_{{\text{P}}} }} \left( t \right) + \left| {\overrightarrow {{X_{i} }} \left( t \right) - \overrightarrow {{X_{P} }} \left( t \right)} \right| \cdot A^{ + } \cdot L,} & {\quad i \le \frac{n}{2}} \\ \end{array} } \right.,$$
(2)

where \(\overrightarrow {{X_{{{\text{worst}}}} }} \left( t \right)\) is the worst position globally, n is the number of sparrows, \(\overrightarrow {{X_{{\text{P}}} }} \left( t \right)\) is the best position of producers, and A is a 1 × D matrix with each element randomly assigned the value of 1 or − 1.

2.3 Guard

After the positions of producers and scroungers are updated, a proportion of sparrows are selected from the population as guards, and their update equation is given by

$$\overrightarrow {{X_{i} }} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {\overrightarrow {{X_{{{\text{best}}}} }} \left( t \right) + \beta *\left| {\overrightarrow {{X_{i} }} \left( t \right) - \overrightarrow {{X_{{{\text{best}}}} }} \left( t \right)} \right|,} & {\quad f_{i} \ne f_{g} } \\ {\overrightarrow {{X_{i} }} \left( t \right) + K \cdot \left( {\frac{{\left| {\overrightarrow {{X_{i} }} \left( t \right) - \overrightarrow {{X_{{{\text{worst}}}}}}\,\,\, \left( t \right)} \right|}}{{\left( {f_{i} - f_{{\text{w}}} } \right) + \varepsilon }}} \right),} & {\quad f_{i} = f_{g} } \\ \end{array} } \right.,$$
(3)

where \(\overrightarrow {{X_{{{\text{best}}}} }} \left( t \right)\) is the current optimal position, β is a random number that controls the step size and obeys a Gaussian distribution, fi is the fitness of the ith sparrow, fg is the optimal fitness, K is a random number in (− 1,1), and fw is the worst fitness.

The pseudocode and flowchart of SSA are shown in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Pseudocode of SSA

Full size image
Fig. 2
figure 2

Flowchart of SSA

Full size image

3 WOA

WOA [32] is a metaheuristic optimization algorithm that mimics the hunting behavior of humpback whales. Humpback whales hunt using a bubble-net strategy. In WOA, this strategy is mathematically modeled as detailed below.

3.1 Encircling prey

For encircling prey, the whale herd moves iteratively toward the current optimal position according to the following iterative equation:

$$\vec{D} = \left| {\overrightarrow {C } \cdot \overrightarrow {{X^{*} }} \left( t \right) - \overrightarrow {X } \left( t \right)} \right|,$$
(4)
$$\overrightarrow {X } \left( {t + 1} \right) = \overrightarrow {{X^{*} }} \left( t \right) - \overrightarrow {A } \cdot \overrightarrow {D } ,$$
(5)

where \(\overrightarrow {{A{ }}}\) and \(\overrightarrow {{C{ }}}\) are vector coefficients, \(\overrightarrow {{X^{*} }} \left( t \right)\) is the current optimal position, \(\overrightarrow {{X{ }}} \left( t \right)\) is the current position of the whale, t is the current iteration, and \(\overrightarrow {{A{ }}}\) and \(\overrightarrow {{C{ }}}\) are expressed as

$$\overrightarrow {A } = 2\overrightarrow {a } \cdot \overrightarrow {r } - \overrightarrow {a } ,$$
(6)
$$\overrightarrow {C } = 2 \cdot \overrightarrow {r } ,$$
(7)

where \(\overrightarrow {{r{ }}}\) is a random vector with values in [0,1] and \(\overrightarrow {{a{ }}}\) decreases from 2 to 0 over the iterations as follows:

$$\overrightarrow {a } = 2 - \frac{2t}{{MaxIter}},$$
(8)

with Maxiter being the maximum number of iterations.

3.2 Bubble-net hunting

The bubble-net strategy of whales can adopt one out of two behaviors: encircling the prey and spiral updating position.

Encircling the prey is achieved by decreasing \(\overrightarrow {a }\) linearly from 2 to 0 over the iterative process to gradually reduce the fluctuation range of \(\overrightarrow {A }\). Vector \(\overrightarrow {r }\) takes a random value in [0,1] for \(\overrightarrow {A }\) to take a random number in \(\left[ { - a,a} \right]\). Hence, whales can appear anywhere at random between their current position and the current best position. For spiral updating position, a spiral equation between the position of the current whale and prey is created to model the following helix-shaped movement of whales:

$$\overrightarrow {X } \left( {t + 1} \right) = \overrightarrow {{D^{\prime } }} \cdot e^{bl} \cdot \cos \left( {2\pi l} \right) + \overrightarrow {{X^{*} }} \left( t \right),$$
(9)
$$\overrightarrow {{D^{\prime } }} = \left| {\overrightarrow {{X^{*} }} \left( t \right) - \overrightarrow {X } \left( t \right)} \right|,$$
(10)

where b is a constant with value 1 to define the helix shape and l is a random number in [− 1,1].

Whales randomly choose one hunting behavior with equal probability as follows:

$$\overrightarrow {X } \left( {t + 1} \right) = \left\{ {\begin{array}{ll} \overrightarrow {{X^{*} }} \left( t \right) - \overrightarrow {A } \cdot \overrightarrow {D } &\quad p < 0.5 \\ \overrightarrow {{D^{\prime } }} \cdot e^{bl} \cdot \cos \left( {2\pi l} \right) + \overrightarrow {{X^{*} }} \left( t \right)&\quad p > 0.5 \\ \end{array} } \right.,$$
(11)

where p is a random number in [0,1].

3.3 Search for prey

To localize a prey, whales move to the random positions rather than to the optimal position. The condition for whales to perform this behavior is \(\left| {\overrightarrow {{A{ }}} } \right| > 1\), and the behavior is described by

$$\overrightarrow {{D^{\prime } }} = \left| {\overrightarrow {C } \cdot \overrightarrow {{X_{{{\text{rand}}}} }} \left( t \right) - \overrightarrow {X } \left( t \right)} \right|,$$
(12)
$$\overrightarrow {X } \left( {t + 1} \right) = \overrightarrow {{X_{{{\text{rand}}}} }} \left( t \right) - \overrightarrow {A } \cdot \overrightarrow {{D^{\prime } }} ,$$
(13)

where \(\overrightarrow {{X_{{{\text{rand}}}} }} \left( t \right)\) is the random position of a whale.

The pseudocode and flowchart of WOA are shown in Figs. 3 and 4, respectively.

Fig. 3
figure 3

Pseudocode of WOA

Full size image
Fig. 4
figure 4

Flowchart of WOA

Full size image

4 Proposed ISSWOA

4.1 Improved SSA

Levy flight [33] uses Levy random number to control the individual step size for the individuals to move randomly. As shown in Fig. 5, using K which control the pace of the guard in the original SSA and Levy generate 100 random numbers, different from the random numbers generated by K, the random numbers generated by Levy are not all in [− 1,1], a small part exceed this range, using Levy random number to control individuals step size and they can move in small steps with a large probability and large steps with a small probability; in this way, we can strengthen the ability of SSA to escape from the local optimum while ensuring the local search ability of the algorithm. Thus, Eq. (3) is rewritten as

$$\overrightarrow {{X_{i} }} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {\overrightarrow {{X_{{{\text{best}}}} }} \left( t \right) + {\text{Levy}} \cdot \left| {\overrightarrow {{X_{i} }} \left( t \right) - \overrightarrow {{X_{{{\text{best}}}} }} \left( t \right)} \right| ,\quad f_{i} \ne f_{g} } \\ {\overrightarrow {{X_{i} }} \left( t \right) + {\text{Levy}} \cdot \left( {\frac{{\left| {\overrightarrow {{X_{i} }} \left( t \right) - \overrightarrow {{X_{{{\text{worst}}}} }}\,\,\, \left( t \right)} \right|}}{{\left( {f_{i} - f_{w} } \right) + \varepsilon }}} \right) ,\quad f_{i} = f_{g} } \\ \end{array} } \right.,$$
(14)
$${\text{Levy}} = 0.1 \cdot \frac{u}{{\left| v \right|^{{\frac{1}{\beta }}} }},$$
(14a)
$$u\sim N\left( {0,\sigma_{u}^{2} } \right),\quad \sigma_{u}^{2} = \left( {\frac{{\Gamma \left( {1 + \beta } \right)\sin \left( {\frac{\beta \pi }{2}} \right)}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right)2^{{\left( {\beta - 1} \right)/2}} \beta }}} \right)^{{\frac{1}{\beta }}} ,$$
(14b)
$$v\sim N\left( {0,\sigma_{v}^{2} } \right),\quad \sigma_{v}^{2} = 1,$$
(14c)

where β is 1.5, and u and v are random numbers drawn from normal distributions with zero mean and variances \(\sigma_{u}^{2}\) and \(\sigma_{v}^{2}\), respectively.

Fig. 5
figure 5

Distribution of 100 random numbers generated by K and Levy

Full size image

4.2 Improved WOA

Spiral updating in WOA is a search method centered at the current optimal position. When the whales are concentrated at a later optimization stage, spiral updating improves the local search ability of WOA. However, global search capability of WOA is weak. To prevent this problem, we define the following spiral updating equation:

$$\overrightarrow {{X_{i} }} \left( {t + 1} \right) = \overrightarrow {{X_{i} }} \left( t \right) + \alpha \left( i \right) \cdot \left( {\overrightarrow {{X_{i} }} \left( t \right) - \overrightarrow {{X_{{{\text{mean}}}} }} \left( t \right)} \right) + \beta \left( i \right) \cdot \left( {\overrightarrow {{X_{i} }} \left( t \right) - \overrightarrow {{X_{i + 1} }} \left( t \right)} \right),$$
(15)
$$\alpha \left( i \right) = \frac{\rho \left( i \right)}{{\max \left( {\left| {xr} \right|} \right)}},\quad \beta \left( i \right) = \frac{\tau \left( i \right)}{{\max \left( {\left| {yr} \right|} \right)}},$$
(15a)
$$\rho \left( i \right) = \varphi \left( i \right) \cdot \sin \left( {\omega \left( i \right)} \right),\quad \tau \left( i \right) = \varphi \left( i \right) \cdot \cos \left( {\omega \left( i \right)} \right),$$
(15b)
$$\varphi \left( i \right) = \omega \left( i \right) + R \cdot {\text{rand}},\quad \omega \left( i \right) = c \cdot \pi \cdot {\text{rand}},$$
(15c)

where \(\overrightarrow {{X_{{{\text{mean}}}} }} \left( t \right)\) is the average position of the current population, \(\overrightarrow {{X_{i + 1} }} \left( t \right)\) is the position of the next whale to be updated, R is a random number in [0.5,2], rand is a random number in [0,1], and c is a random number in [5, 10].

The new spiral updating [34] is centered at the current whale and carries out a spiral search outward to determine the existence of a better surrounding position. This update is adopted before the algorithm completes two-thirds of all the iterations. Then, Eq. (9) is adopted. Hence, the convergence accuracy is ensured by updating the position following Eq. (9) at a later stage, and the global search ability is improved by updating the position according to Eq. (15).

4.3 ISSWOA

The proposed ISSWOA combines our improved versions of WOA and SSA. Combining the two algorithms allows to fully use their advantages while overcoming the shortcomings of the original algorithms, thereby ensuring that the optimal solution can be found faster and more effectively.

The pseudocode and flowchart of the proposed ISSWOA are shown in Figs. 6 and 7, respectively. ISSWOA first gives each individual a random position within the search space to create an initial population. Then, it orders the initial population by fitness and chooses a proportion of the individuals with better fitness as producers and the remaining individuals as scroungers. After the producer updates its position, the scrounger randomly chooses to update its position according to Eq. (2) or the whale’s encircling behavior. After the producer’s position is updated, the population uses spiral updating to find a better position near itself or the optimal solution. Finally, some individuals are selected as guards, and their positions are updated according to Eq. (14). The iterative process is repeated until the optimization criteria are met.

Fig. 6
figure 6

Pseudocode of the proposed ISSWOA

Full size image
Fig. 7
figure 7

Flowchart of the proposed ISSWOA

Full size image

When the population updates its position by spiral updating, if the number of iterations of the population is two-thirds of the maximum number of iterations, the position is updated by Eq. (14). Otherwise, the position is updated by Eq. (9). If the new position is better than the previous one, the position is updated; otherwise, the previous position is maintained.

Spiral updating in WOA strengthens the global searching ability of the individuals. Combined with the alert mechanism of SSA, ISSWOA prevents easily falling into a local optimum and improves the convergence accuracy.

5 Performance evaluation of ISSWOA on benchmark functions

We evaluated results for 100 independent runs of ISSWOA on different benchmark functions and compared it with similar algorithms to verify its superiority.

5.1 Algorithms for comparison

In this research, we compared ISSWOA with the original WOA, SSA, improved SSA (ISSA), and improved WOA (IWOA) to verify the improvement in the algorithm. Then we compared ISSWOA with snake optimization (SO), the pelican optimization algorithm (POA), the grasshopper optimization algorithm (GOA), improved gray wolf optimization (I-GWO) [35], and the hybrid particle swarm optimization and butterfly optimization algorithm (HPSOBOA) [36] to verify the optimization capability. GOA, DOA, SO, and POA are relatively novel metaheuristic algorithms; I-GWO and HPSOBOA are improved algorithms for basic metaheuristic algorithms.

5.2 Parameter settings

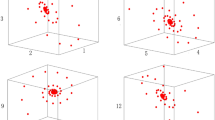
The most obvious parameters that affected the performance of ISSWOA were the number of leaders and number of guards. Initially, 60 positions were randomly generated for the population, and Eq. (1) with R < ST was used to iterate the population 100 times. From the results (Fig. 8), it can be seen that the position of the leader will approach the origin as the number of iterations increases. Consequently, if the number of leaders is set too high, and the optimal solution is far from the origin, the algorithm will have poor performance.

Fig. 8
figure 8

Population iteration graph for discoverer when R < ST

Full size image

The number of guards is not the more the better. After testing, if there are too many guards, the ISSWOA test results of F6, F7, and F8, etc., will become worse. On the contrary, if there are too few guards, the results of ISSWOA for F12 and F13, etc., will also become worse.

From the analysis and early experimental testing, when the population number was set to 100, the number of leaders set at 40, and the number of guards set at 30, the performance of the algorithm was more balanced for most benchmark functions. The population number of other comparison algorithms was also set at 100, and the other parameter settings were the same as those in the original literature.

5.3 Benchmark functions

In this study, ISSWOA was applied to standard unimodal benchmark functions, multimodal benchmark functions, and fixed-dimensional multimodal benchmark functions [37] for testing and comparison with other algorithms. The functional formulas of benchmark functions are shown in Tables 2, 3, and 4, and their 3D views are shown in Figs. 9, 10, and 11.

Table 2 Standard unimodal benchmark functions
Full size table
Table 3 Standard multimodal benchmark functions
Full size table
Table 4 Standard fixed-dimensional multimodal benchmark functions
Full size table
Fig. 9
figure 9

3D view of standard unimodal benchmark functions

Full size image
Fig. 10
figure 10

3D view of standard multimodal benchmark functions

Full size image
Fig. 11
figure 11

3D view of standard fixed-dimensional multimodal benchmark functions

Full size image

5.4 Analysis of ISSWOA for standard unimodal benchmark functions

Table 5 shows the test results of the algorithm on the standard unimodal benchmark functions. It can be seen from the result that IWOA was better than WOA, especially in finding the optimal values of F1, F3, and F5. Because the improvement in the original WOA spiral mechanism significantly enhanced its global search ability, it could quickly find a good approximate position in the early stage and converge more fully by the end. For the ISSA, Levy flight mechanism mainly improved the exploration ability of the algorithm to help it escape local optima; it played only a limited role in the standard unimodal benchmark functions; therefore, the gap between ISSA and SSA was relatively small. Compared with the other algorithms, ISSWOA found the global optimal value for F1, F2, F3, and F4. The optimal values for F5, F6, and F7 found by ISSWOA were superior to those found by other algorithms; in particular, the optimal value for F5 was superior owing to the improved spiral update mechanism of IWOA and discoverer mechanism of ISSA. The above results showed that ISSWOA had good performance on standard unimodal benchmark functions.

Table 5 Comparative result of ISSWOA with other algorithms for standard unimodal benchmark functions
Full size table

Figures 12 and 13 display the iteration curves and box diagrams for ISSWOA and the other algorithms on standard unimodal benchmark functions, respectively. It can be seen from the figure that the iteration speed of ISSWOA was superior to that of other algorithms on seven standard unimodal benchmark functions, and its box diagram shows that its 100 times optimal results were distributed in a centralized manner, indicating that ISSWOA had good robustness.

Fig. 12
figure 12

Iteration curve of ISSWOA and other algorithms for standard unimodal benchmark functions

Full size image
Fig. 13
figure 13

Box plot of ISSWOA and other algorithms for standard unimodal benchmark functions

Full size image

5.5 Analysis of ISSWOA for standard multimodal benchmark functions

Table 6 shows the test results of ISSWOA and other algorithms on multimodal benchmark functions. Compared with SSA, ISSA demonstrated a greater ability to escape local optima under the influence of Levy flight mechanism, as reflected in the mean of F8 and the mean and optimal value of F12. For IWOA, the improved spiral update mechanism conferred a good global search capability; therefore, the optimal values of F12 and F13 found by IWOA were approximately 10−3 times the optimal values found by WOA. ISSWOA inherited the advantages of IWOA and ISSA, had good performance, and was superior to the other algorithms, especially on F12 and F13.

Table 6 Comparative result of ISSWOA with other algorithms for standard multimodal benchmark functions
Full size table

Figures 14 and 15 display the iteration curves and box diagrams of ISSWOA and the other algorithms on standard multimodal benchmark functions. It can be seen from Fig. 14 that ISSWOA still performed better than the other algorithms in terms of convergence speed for the standard multimodal benchmark functions. From Fig. 15, except for F8, the box plot of ISSWOA resembled a straight line, indicating that ISSWOA had good robustness on the standard multimode benchmark function.

Fig. 14
figure 14

Iteration curve of ISSWOA and other algorithms for standard multimodal benchmark functions

Full size image
Fig. 15
figure 15

Box plot of ISSWOA and other algorithms for standard multimodal benchmark functions

Full size image

5.6 Analysis of ISSWOA for standard fixed-dimensional multimodal benchmark functions

Table 7 shows the test results of ISSWOA and other algorithms on standard fixed-dimensional multimodal benchmark functions. Compared with SSA, except for F16 and F17, ISSA escaped the local optimum and found the global optimum under the influence of Levy flight mechanism. For F17, the mean value of ISSA was better, indicating that ISSA had stronger robustness. Under the influence of the improved spiral update mechanism, IWOA found more global optimal solutions than WOA, but because IWOA could not escape from the local optimum, its optimization stability was insufficient. Under the influence of Levy flight mechanism, ISSWOA's optimization performance was more stable compared with other algorithms. ISSWOA performed the best except for F1; however, ISSWOA still found its global optimal solution, and its performance is better than some other algorithms.

Table 7 Comparative result of ISSWOA with other algorithms for standard fixed-dimensional multimodal benchmark functions
Full size table

It can be seen from Fig. 16 that the iteration speed of ISSWOA on standard fixed-dimensional multimodal benchmark functions was optimal except for F17, F18, and F21. It can be seen from Fig. 17 that, although the ISSWOA boxplot was not as good as performance on standard unimodal benchmark functions and standard multimodal benchmark functions, the distribution of ISSWOA 100 times results was the most concentrated and thus the overall performance was better.

Fig. 16
figure 16

Iteration curve of ISSWOA and other algorithms for fixed-dimensional multimodal benchmark functions

Full size image
Fig. 17
figure 17

Box plot of ISSWOA and other algorithms for fixed-dimensional multimodal benchmark functions

Full size image

5.7 Analysis on the optimization efficiency of ISSWOA

The efficiency of finding the optimal solution is also an important indicator of algorithm performance. This information is represented in Tables 8 and 9, which record average time required for 300 iterations and the number of iterations required to find the optimal solution for each benchmark function, respectively. It can be seen from Table 8 that, although ISSWOA was composed of ISSA and IWOA, its running time was short, and on some benchmark functions, its running time was even less than that of its constituent algorithms. Its running time is similar to that of I-GWO and HPSOBOA, which are both improved algorithms. From the number of iterations required for each algorithm to find its optimal solution over 100 trials, shown in Table 9, ISSWOA required fewer iterations to find the global optimal solution on most benchmark functions, compared with some other algorithms. Considering the number of iterations and time required, ISSWOA is a competitive proposal in optimization efficiency.

Table 8 Wall-clock time costs of ISSWOA and other algorithms on 23 benchmarks
Full size table
Table 9 The number of iterations required for ISSWOA and other algorithms to find the optimal solution function
Full size table

5.8 Wilcoxon rank sum test

A Wilcoxon rank sum statistical test with 5% accuracy was used to investigate the differences between ISSWOA and other algorithms. The results are shown in Table 10, There were significant differences between ISSWOA and the other algorithms in the test results of most benchmark functions. Combined with Tables 5, 6, and 7, it can be seen that ISSWOA had significant advantages over other algorithms in most cases. Therefore, ISSWOA displayed strong performance in the optimization of three types of standard benchmark functions.

Table 10 p-values of the Wilcoxon rank sum test with 5% significance for 23 functions
Full size table

6 Application of ISSWOA to engineering problems

Engineering problems are complex, nonlinear optimization problems. Consequently, the performance of optimization algorithms is best evaluated by applying them to practical problems (rather than theoretically). For the simulations, we set the number of iterations as 500 and the population size as 100. The optimization results for 30 independent runs of ISSWOA and similar algorithms were compared, with the number of discoverers set as 40 and the number of guards as 30. The comparison algorithm is shown in Table 11.

Table 11 The algorithm for comparison
Full size table

6.1 Treatment of constraints

For engineering problems with constraints, the punishment function [61] is used to amplify the fitness of solutions according to the number of exceeded constraints. When the solution does not meet the constraint conditions, the equation for fitness is

$$F = f + \mathop \sum \limits_{1}^{i} \left( {{\text{lam}}*g_{i}^{2} *Q_{i} } \right),$$
(16)

where F is the fitness value of introducing the penalty function, f is the fitness value of the unpunished function, lam is a constant greater than 1, gi is the ith constraint value, and Qi is a binary variable, equal to 1 when the current constraints do not meet the conditions (and zero otherwise).

6.2 Tension/compression spring design problem

As illustrated in Fig. 18, the tension/compression spring design problem [62] in mechanical engineering can be used to evaluate optimization algorithms for various parameters. The problem consists of minimizing the mass under certain constraints, including four constraints and three design variables. The design variables are average diameter d of the spring coil (x2), diameter w of the spring wire (x1), and number L of effective spring coils (x3). Tables 12 and 13 compare the optimal solutions and constraints obtained by different algorithms. The statistical optimization results of the algorithms are given in Table 14. The problem is formulated as follows:

$$\min{f} \left( {x_{1} ,x_{2} ,x_{3} } \right) = \left( {x_{3} + 2} \right)x_{1}^{2} x_{2}$$
(17)

subject to

$$\begin{aligned} g_{1} \left( X \right) & = 1 - \frac{{x_{2}^{3} x_{3} }}{{71785x_{1}^{4} }} \le 0, \\ g_{2} \left( X \right) & = \frac{{x_{2} \left( {4x_{2} - x_{1} } \right)}}{{12566x_{1}^{3} \left( {x_{2} - x_{1} } \right)}} + \frac{1}{{5108x_{1}^{2} }} - 1 \le 0, \\ g_{3} \left( X \right) & = 1 - \frac{{140.45x_{1} }}{{x_{2}^{2} x_{3} }} \le 0, \\ g_{4} \left( X \right) & = \frac{{2\left( {x_{1} + x_{2} } \right)}}{3} - 1 \le 0. \\ \end{aligned}$$

The variable ranges are \(0.05 \le x_{1} \le 2,0.25 \le x_{2} \le 1.3\), and \(2.0 \le x_{3} \le 15.0\).

Fig. 18
figure 18

Schematic of tension/compression spring design problem

Full size image
Table 12 Best solutions obtained from ISSWOA and other algorithms for the tension/compression spring design problem
Full size table
Table 13 The constraints of ISSWOA and other algorithms for the tension/compression spring design problem
Full size table
Table 14 Comparison of statistical results using ISSWOA and other algorithm for the tension/compression spring design problem
Full size table

6.3 Pressure vessel design problem

The pressure vessel design problem [63] illustrated in Fig. 19 is a typical hybrid optimization problem for minimizing the total cost while meeting production needs. This problem has four constraints and four design variables. The variables are: shell thickness Th (x1), head thickness Ts (x2), radius R (x3), and container section length L (x4). Tables 15 and 16 show the comparison among the optimal solutions and constraints obtained by different algorithms. The statistical optimization results of the algorithms are given in Table 17. The problem is formulated as follows:

$$\min{f} \left( {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right) = 0.6224x_{1} x_{3} x_{4} + 1.781x_{2} x_{3}^{2} + 3.1661x_{1}^{2} x_{4} + 19.84x_{1}^{2} x_{3} ,$$
(18)

subject to

$$\begin{aligned} g_{1} \left( X \right) & = - x_{1} + 0.0193x_{3} \le 0, \\ g_{2} \left( X \right) & = - x_{2} + 0.00954x_{3} \le 0, \\ g_{3} \left( X \right) & = - \pi x_{3}^{2} x_{4} - \frac{4}{3}\pi x_{3}^{3} + 1296000 \le 0, \\ g_{4} \left( X \right) & = x_{4} - 240 \le 0. \\ \end{aligned}$$

The variable ranges are \(0 \le x_{1} \le 99,0 \le x_{2} \le 99,10 \le x_{3} \le 200\), and \(10 \le x_{4} \le 200\).

Fig. 19
figure 19

Schematic of the pressure vessel design problem

Full size image
Table 15 Best solutions obtained from ISSWOA and other algorithms for the pressure vessel design problem
Full size table
Table 16 The constraints of ISSWOA and other algorithms for the pressure vessel design problem
Full size table
Table 17 Comparison of statistical results using ISSWOA and other algorithm for the pressure vessel design problem
Full size table

6.4 Speed reducer design problem

Figure 20 illustrates the speed reducer design problem [64]. It is an important and complex multi-constraint optimization problem in mechanical systems and consists of 7 variables and 11 constraints. The variables are tooth surface width B (x1), gear modulus M (x2), number Z of teeth in pinions (x3), length l1 of the first shaft between bearings (x4), length l2 of the second shaft between bearings (x5), diameter d1 of the first shaft (x6), and diameter d2 of the second shaft (x7). Tables 18 and 19 compare the optimal solutions and constraints obtained by different algorithms. The statistical optimization results of the algorithms are given in Table 20. The problem is formulated as follows:

$$\begin{aligned} \min{f} \left( {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} } \right) & = 0.7854x_{1} x_{2}^{2} \left( {3.3333x_{3}^{2} + 14.9334x_{3} - 43.0934} \right) - 1.508x_{1} \left( {x_{6}^{2} + x_{7}^{2} } \right) \\ & \quad + 7.4777\left( {x_{6}^{3} + x_{7}^{3} } \right) + 0.7854\left( {x_{4} x_{6}^{2} + x_{5} x_{7}^{2} } \right) \\ \end{aligned}$$
(19)

subject to

$$\begin{aligned} g_{1} \left( X \right) & = \frac{27}{{x_{1} x_{2}^{2} x_{3} }} - 1 \le 0, \\ g_{2} \left( X \right) & = \frac{397.5}{{x_{1} x_{2}^{2} x_{3}^{2} }} - 1 \le 0, \\ g_{3} \left( X \right) & = \frac{{1.93x_{4}^{3} }}{{x_{2} x_{3} x_{6}^{4} }} - 1 \le 0, \\ g_{4} \left( X \right) & = \frac{{1.93x_{5}^{3} }}{{x_{2} x_{3} x_{7}^{4} }} - 1 \le 0, \\ g_{5} \left( X \right) & = \frac{1}{{110x_{6}^{3} }}\sqrt {\left( {\frac{{745x_{4} }}{{x_{2} x_{3} }}} \right)^{2} + 16.9 \times 10^{6} } - 1 \le 0, \\ g_{6} \left( X \right) & = \frac{1}{{85x_{7}^{3} }}\sqrt {\left( {\frac{{745x_{5} }}{{x_{2} x_{3} }}} \right)^{2} + 157.5 \times 10^{6} } - 1 \le 0, \\ g_{7} \left( X \right) & = \frac{{x_{2} x_{3} }}{40} - 1 \le 0, \\ g_{8} \left( X \right) & = \frac{{5x_{2} }}{{x_{1} }} - 1 \le 0, \\ g_{9} \left( X \right) & = \frac{{x_{1} }}{{12x_{2} }} - 1 \le 0, \\ g_{10} \left( X \right) & = \frac{1.5}{{x_{4} }} - 1 \le 0, \\ g_{11} \left( X \right) & = \frac{{1.1x_{7} + 1.9}}{{x_{5} }} - 1 \le 0. \\ \end{aligned}$$

The variable ranges are \(2.6 \le x_{1} \le 3.6,0.7 \le x_{2} \le 0.8,17 \le x_{3} \le 28,7.3 \le x_{4} \le 8.3,7.3 \le x_{5} \le 8.3,2.9 \le x_{6} \le 3.9\), and \(5 \le x_{7} \le 5.5\).

Fig. 20
figure 20

Schematic of the speed reducer design problem

Full size image
Table 18 Comparison of statistical results using ISSWOA and other algorithm for the speed reducer design problem
Full size table
Table 19 The constraints of ISSWOA and other algorithms for the speed reducer design problem
Full size table
Table 20 Comparison of statistical results using ISSWOA and other algorithm for the speed reducer design problem
Full size table

6.5 Rolling element-bearing design problem

As illustrated in Fig. 21, the rolling element-bearing design problem consists of maximizing the dynamic bearing capacity of rolling bearings [65]. There are 10 decision variables in this problem: pitch diameter (Dm), ball diameter (Db), number of balls (Z), inner raceway curvature coefficients (fi), and outer raceway curvature coefficients (fo), KDmin, KDmax, ε, e, and ζ. In addition, this problem has nine constraints, establishing a complex multi-constraint engineering design problem. Tables 21 and 22 compare the optimal solutions and constraints obtained by different algorithms, while the statistical optimization results of the algorithms are given in Table 23. The problem is formulated as follows:

$$\max C_{{\text{d}}} = \left\{ {\begin{array}{*{20}c} {f_{c} Z^{\frac{2}{3}} D_{b}^{1.8} ,} & {\quad {\text{if}}\quad D \le 25.4{\mkern 1mu} {\text{mm}}} \\ {3.647f_{c} Z^{\frac{2}{3}} D_{b}^{1.4} ,} & {\quad {\text{if}}\quad D > 25.4{\mkern 1mu} {\text{mm}}} \\ \end{array} } \right.$$
(20)

subject to

$$\begin{aligned} g_{1} \left( x \right) & = - \frac{{\phi_{0} }}{{2\sin^{ - 1} \left( {D_{b} /D_{m} } \right)}} + Z - 1\leqslant0, \\ g_{2} \left( x \right) & = - 2D_{b} + K_{D\min } \left( {D - d} \right)\leqslant0, \\ g_{3} \left( x \right) & = - K_{D\max } \left( {D - d} \right) + 2D_{b}\leqslant0, \\ g_{4} \left( x \right) & = \zeta B_{w} - D_{b} \le 0, \\ g_{5} \left( x \right) & = - D_{m} + 0.5\left( {D + d} \right)\leqslant0, \\ g_{6} \left( x \right) & = - \left( {0.5 + e} \right)\left( {D + d} \right) + D_{\begin{subarray}{l} m \\ \end{subarray} }\leqslant0, \\ g_{7} \left( x \right) & = - 0.5\left( {D - D_{m} - D_{b} } \right) + \varepsilon D_{b}\leqslant0, \\ g_{8} \left( x \right) & = 0.515 - f_{i}\leqslant0, \\ g_{9} \left( x \right) & = 0.515 - f_{i}\leqslant0. \\ \end{aligned}$$

where

$$\begin{aligned} f_{{\text{c}}} & = 37.91\left[ {1 + \left\{ {1.04\left( {\frac{1 - \gamma }{{1 + \gamma }}} \right)^{1.72} \left( {\frac{{f_{i} \left( {2f_{0} - 1} \right)}}{{f_{0} \left( {2f_{i} - 1} \right)}}} \right)^{0.41} } \right\}^{10/3} } \right]^{ - 0.3} \left[ {\frac{{\gamma^{0.3} \left( {1 - \gamma } \right)^{1.39} }}{{\left( {1 + \gamma } \right)^{\frac{1}{3}} }}} \right]\left[ {\frac{{2f_{i} }}{{2f_{i} - 1}}} \right]^{0.41} , \\ \phi_{0} & = 2\pi - 2\cos^{ - 1} \left( {\frac{{\left[ {\left\{ {\frac{D - d}{2} - 3\left( \frac{T}{4} \right)} \right\}^{2} + \left\{ {\frac{D}{2} - \frac{T}{4} - D_{b} } \right\}^{2} - \left\{ {\frac{d}{2} + \frac{T}{4}} \right\}^{2} } \right]}}{{2\left\{ {\frac{D - d}{2} - 3\left( \frac{T}{4} \right)} \right\}\left\{ {\frac{D}{2} - \frac{T}{4} - D_{b} } \right\}}}} \right), \\ \gamma & = \frac{{D_{{\text{b}}} }}{{D_{{\text{m}}} }},\quad f_{i} = \frac{{r_{i} }}{{D_{{\text{b}}} }},\quad f_{0} = \frac{{r_{0} }}{{D_{{\text{b}}} }},\quad T = D - d - 2D_{{\text{b}}} , \\ D & = 160,\quad d = 90,\quad B_{{\text{w}}} = 30,\quad r_{i} = r_{0} = 11.033. \\ \end{aligned}$$

The variable ranges are

$$\begin{aligned} 0.5\left( {D + d} \right) & \le D_{m} \le 0.6\left( {D + d} \right),\quad 0.15\left( {D - d} \right) \le D_{m} \le 0.45\left( {D - d} \right), \\ 4 & \le Z \le 50,\quad 0.515 \le f_{i} , \quad f_{0} \le 0.6, 0.4 \le K_{D\min } \\ & \le 0.5, 0.6 \le K_{D\max } \le 0.7,\quad 0.3 \le \varepsilon \le 0.4,\quad 0.3 \le e \le 0.4,\quad {\text{and}}\quad 0.6 \le \zeta \le 0.85 \\ \end{aligned}$$
Fig. 21
figure 21

Schematic of the rolling element-bearing design problem

Full size image
Table 21 Best solutions obtained from ISSWOA and other algorithms for the rolling element-bearing design problem
Full size table
Table 22 The constraints of ISSWOA and other algorithms for the rolling element-bearing design problem
Full size table
Table 23 Comparison of statistical results using ISSWOA and other algorithm for the rolling element-bearing design problem
Full size table

6.6 Car side impact design problem

The objective of the car side impact design problem [54] is to find the most appropriate combination of variables to minimize the weight of the car door. The design variables are as follows: thicknesses of B-Pillar inner (x1), thickness of B-Pillar reinforcement (x2), thickness of floor side inner (x3), thickness of cross members (x4), thickness of door beam (x5), thickness of door beltline reinforcement (x6), thickness of roof rail (x7), materials of B-Pillar inner (x8), materials of floor side inner (x9), barrier height (x10), and hitting position (x11). Tables 24 and 25 compare the optimal solutions and constraints obtained by different algorithms, while the statistical optimization results of the algorithms are given in Table 26. The problem is formulated as follows:

$$\min{f} \left( x \right) = 1.98 + 4.90x_{1} + 6.67x_{2} + 6.98x_{3} + 4.01x_{4} + 1.78x_{5} + 2.73x_{7}$$
(21)
Table 24 Best solutions obtained from ISSWOA and other algorithms for the car side impact design problem
Full size table
Table 25 The constraint of ISSWOA and other algorithms in car side impact design problem
Full size table
Table 26 Comparison of statistical results using ISSWOA and other algorithm for the car side impact design problem
Full size table

subject to

$$\begin{aligned} g_{1} & = 1.16 - 0.3717x2x4 - 0.0931x2x10 - 0.484x3x9 + 0.01343x6x10 - 1 \le 0 \\ g_{2} & = 0.261 - 0.0159x_{1} x_{2} - 0.188x_{1} x_{8} - 0.019x_{2} x_{7} + 0.0144x_{3} x_{5} + 0.0008757x_{5} x_{10} \\ & \quad + 0.080405x_{6} x_{9} + 0.00139x_{8} x_{11} + 0.00001575x_{10} x_{11} - 0.32 \le 0 \\ g_{3} & = 0.214 + 0.00817x_{5} - 0.131x_{1} x_{8} - 0.0704x_{1} x_{9} + 0.03099x_{2} x_{6} - 0.018x_{2} x_{7} + 0.0208x_{3} x_{8} \\ & \quad + 0.121x_{3} x_{9} - 0.00364x_{5} x_{6} + 0.0007715x_{5} x_{10} - 0.0005354x_{6} x_{10} + 0.00121x_{8} x_{11} \le 0.32 \\ g_{4} & = 0.074 - 0.061x_{2} - 0.163x_{3} x_{8} + 0.001232x_{3} x_{10} - 0.166x_{7} x_{9} + 0.227x_{2}^{2} \le 0.32 \\ g_{5} & = 28.98 + 3.818x_{3} - 4.2x_{1} x_{2} + 0.0207x_{5} x_{10} + 6.63x_{6} x_{9} - 7.7x_{7} x_{8} + 0.32x_{9} x_{10} - 32\leqslant0 \\ g_{6} & = 33.86 + 2.95x_{3} + 0.1792x_{10} - 5.057x_{1} x_{2} - 11x_{2} x_{8} - 0.0215x_{5} x_{10} - 9.98x_{7} x_{8} + 22x_{8} x_{9} - 32\leqslant0 \\ g_{7} & = 46.36 - 9.9x_{2} - 12.9x_{1} x_{9} + 0.1107x_{3} x_{10} - 32\leqslant0 \\ g_{8} & = 4.72 - 0.5x_{4} - 0.19x_{2} x_{3} - 0.0122x_{4} x_{10} + 0.009325x_{6} x_{10} - 0.0198x_{4} x_{10} + 0.028x_{6} x_{10} - 9.9\leqslant0 \\ g_{9} & = 10.58 - 0.674x_{1} x_{2} - 1.95x_{2} x_{8} + 0.02054x_{3} x_{10} - 0.0198x_{4} x_{10} + 0.028x_{6} x_{10} - 9.9 \le 0 \\ g_{10} & = 16.45 - 0.489x_{3} x_{7} - 0.843x_{5} x_{6} + 0.0432x_{9} x_{10} - 0.0556x_{9} x_{11} - 0.000786x_{11}^{2} - 15.7 \le 0 \\ \end{aligned}$$

The variable ranges are \(0.5\leqslant x_{1} \sim x_{7}\leqslant1.5,x_{8} ,x_{9} \in \left[ {0.192,0.345} \right], - 30\leqslant x_{10} ,x_{11}\leqslant30\).

6.7 Gear train design problem

This gear train design problem [52] is shown in Fig. 22. It is an unconstrained design problem. It is necessary to find the best gear number combination. There are four gears in this problem, with number of teeth MA(x1), MB(x2), MC(x3), and MD(x4). Table 27 compares the optimal solutions obtained by different algorithms, while the statistical optimization results of the algorithms are given in Table 28. The equation for the gear train design problem is shown below

$$\min{f} \left( {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right) = \left( {\frac{1}{6.931} - \frac{{x_{3} x_{2} }}{{x_{1} x_{4} }}} \right)$$
(22)

The variable ranges are \(12\leqslant x_{1} ,x_{2} ,x_{3} ,x_{4}\leqslant 60\).

Fig. 22
figure 22

Schematic of the gear train

Full size image
Table 27 Best solutions obtained from ISSWOA and other algorithms for the gear train
Full size table
Table 28 Comparison of statistical results using ISSWOA and other algorithm for the gear train
Full size table

6.8 Three-bar truss design problem

The structure of the three-bar truss [52] is shown in Fig. 23. To minimize the volume of the three-bar truss and meet the stress constraints on each side of the truss member, the most appropriate cross-section combination of the truss member is found. Tables 29 and 30 show the comparison among the optimal solutions and constraints obtained by different algorithms, and Table 31 gives the statistical optimization results of the algorithms. The equation is as follows:

$$\min{f} \left( x \right) = \left[ {A1,A2} \right] = \left( {2\sqrt 2 x_{1} + x_{2} } \right) \times l$$
(23)

\(\begin{aligned} g_{1} \left( x \right) & = \frac{{\sqrt 2 x_{1} + x_{2} }}{{\sqrt 2 x_{1}^{2} + 2x_{1} x_{2} }}P - \sigma\leqslant0 \\ g_{2} \left( x \right) & = \frac{{x_{2} }}{{\sqrt 2 x_{1}^{2} + 2x_{1} x_{2} }}P - \sigma\leqslant0 \\ g_{3} \left( x \right) & = \frac{1}{{\sqrt 2 x_{2} + x_{1} }}P - \sigma\leqslant0 \\ \end{aligned}\)where \(l = 100\,{\text{cm}},P = 2\frac{{{\text{KN}}}}{{{\text{cm}}^{2} }},\sigma = 2\frac{{{\text{KN}}}}{{{\text{cm}}^{2} }}\).

Fig. 23
figure 23

Schematic of three-bar truss

Full size image
Table 29 Best solutions obtained from ISSWOA and other algorithms for the three-bar truss
Full size table
Table 30 The constraint of ISSWOA and other algorithms in car side impact design problem
Full size table
Table 31 Comparison of statistical results using ISSWOA and other algorithms for the three-bar truss
Full size table

The variable ranges are \(0\leqslant x_{1} ,x_{2}\leqslant1\).

6.9 Economic load dispatch

Economic load dispatch (ELD) [59] is an important engineering problem in power delivery systems. The goal of this problem is to find the best power distribution of available thermal units, to minimize the fuel cost while meeting the load. The calculation formula of the fuel cost is as follows:

$$F\left( {Pg} \right) = \mathop \sum \limits_{i = 1}^{n} \left( {a_{i} Pg_{i}^{2} + b_{i} Pg_{i} + c_{i} } \right) + \left| {d_{i} \sin \left( {e_{i} \left( {Pg_{i}^{\min } - Pg_{i} } \right)} \right)} \right|$$
(24)

where ai, bi, and ci are the fuel-cost coefficients of the ith unit, and di and ei are the fuel-cost coefficients of the ith unit with valve-point effects.

In this research, the number of units was set as 40, and the load was 10,500 MW. Loss of thermal units was considered negligible. The upper and lower limits of each unit of power and the value of the coefficients in Eq. 24 are given in Sinha et al. [66]. The best result obtained by ISSWOA is shown in Table 32. The comparison with other algorithm results is shown in Table 33.

Table 32 The best results obtained by the ISSWOA for ELD
Full size table
Table 33 Comparison of statistical results using ISSWOA and other algorithm for the car side impact design problem
Full size table

It can be seen from the test results of the eight engineering problems that ISSWOA performed best on the element-bearing design problem and ELD problem, clearly outperforming other algorithms in terms of stability and optimal results. For the other six engineering problems, ISSWOA also performed adequately, which showed that ISSWOA is certainly viable for solving practical engineering problems.

7 Conclusion

This study proposed a hybrid ISSWOA that combines the improved SSA with Levy flight strategy and the improved WOA with a novel spiral updating strategy. The performance of ISSWOA was investigated on standard unimodal, multimodal, and fixed-dimensional multimodal benchmark functions. The purpose was to determine its capabilities on three primary criteria: avoidance of trapping in local optima and exploration and exploitation abilities. The results showed that ISSWOA performed significantly better than other metaheuristic algorithms on most benchmark functions.

Since metaheuristic algorithms are suited to complex engineering problems, this paper applied ISSWOA to seven kinds of engineering design problems and a large electrical engineering problem (i.e., the ELD problem). The results showed that ISSWOA achieved good performance, especially in the element-bearing design problem and ELD problem, and was effective compared to other algorithms in other engineering problems.

In this research, the parameter configuration of ISSWOA was balanced to suit different problems However, different parameter configurations will be better suited to certain problems; therefore, the next research objective is to adapt the parameter configuration to different problems. In addition, the binary and multi-objective versions of ISSWOA can be developed further to solve a wider variety of problems.