Introduction. Rock is a naturally inhomogeneous material due to the presence of discontinuities, including bedding planes, faults, fissures, fractures, joints, etc. The orientation of these geological interfaces is a critical factor that governs the stability, deformation and failure of a rock mass [1,2,3]. Orientation is typically observed in the field using the scanline mapping technique [4]. However, this technique can introduce a bias, i.e., the scanline tends to preferentially intersect discontinuities that make large angles with the scanline [4, 5].

Terzaghi [6] suggested the following four-step procedure to correct this bias, which has been widely used by researchers including Fouché and Diebolt [7] and Goodman [8]:

  1. 1.

    Mesh the projection net into grids.

  2. 2.

    Count the poles within each grid.

  3. 3.

    Weight the frequencies according to the Terzaghi equation

    $$ {N}_{90}=\frac{N_{\uptheta}}{ \sin \uptheta}, $$
    (1)

    where θ is the intersection angle between the discontinuity and the scanline (Fig. 1), N θ is the number of discontinuities intersected by the scanline at angle θ, and N 90 is the number of discontinuities that would have been intersected at 90°. Note that N 90 also represents the frequency of discontinuities in a three-dimensional space.

    Fig. 1
    figure 1

    Intersection angle θ between a scanline and a discontinuity. The discontinuity is assumed to be disc-shaped. The line segment AC is the projection of the line segment AB on the discontinuity, while θ is the intersection angle between AB and AC.

    Full size image
  4. 4.

    Because the frequencies defined in this manner must be integers, the weighted frequencies are approximated to the nearest integer. Many authors have adopted this step, e.g., Fouché and Diebold [7], Park and West [9].

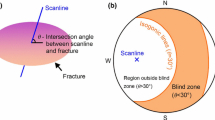
The Terzaghi procedure is invalid when applied to orientations that make a shallow angle (0 to 30°) with respect to a scanline [4, 5]. This angle interval is the so-called blind zone (shown in Fig. 2). Although several recommendations have been proposed to avoid the effect of the blind zone (e.g., Park and West [9] and Priest [10]), little attention has been paid to the accuracy of the Terzaghi procedure outside the blind zone. To the best of the authors’ knowledge, there have been no previous studies on the level of this accuracy or the source of low accuracy, and no methods of its improvement are yet available.

Fig. 2
figure 2

Blind zone, according to Terzaghi [6]. Equal-angle upper-hemisphere projection for a scanline with a trend/plunge of 90/45°. The two isogonic lines represent discontinuities that intersect the scanline at an angle of 30° and define the boundaries of the blind zone. The contours represent the Terzaghi correction factor sin θ in Eq. (1), and the blind zone is the region where θ< 30°.

Full size image

In this paper, a detailed derivation of the Terzaghi equation [Eq. (1)] is used to reveal the source of low accuracy. Next, to improve the accuracy, the optimal values for the grid size and sample density are determined by comparing the accuracies of correction with different grid sizes and sample densities. Finally, the derived values are verified by a case study on the model material – a rock from Wenchuan, China.

1. Derivation of the Terzaghi Equation. Discontinuities that make small angles to a sampling line (0 to 30°) are not always observed, and Terzaghi [6] introduced the concept of a blind zone to explain this effect (Fig. 2). Park and West [9] used the borehole data to confirm the 30° value. Noteworthy is that the blind zone does not depend on the particular data set, but instead is related to the choice of the scanline.

Terzaghi [6] gave a simple derivation of the equation. To help identify the source of a low accuracy, we present here a more detailed derivation using the analytical geometry, probability theory and integrals.

Let set A denote the discontinuities that exist in the rock mass, and set B denote the subset of those discontinuities that intersect the scanline. The conditional probability density p B |A (α, β) denotes the likelihood that set B occurs, given that set A is certain. Here, the case that set A is certain means that both the dip direction and angle of all of the discontinuities in the rock mass are uniform; i.e., all of the discontinuities in the rock mass are parallel (Fig. 3). Hence, p B |A (α, β) represents the probability density of the discontinuities that intersect the scanline given that all of the discontinuities are parallel.

Fig. 3
figure 3

Intersection between the scanline and parallel discontinuities at angle θ. The N discontinuities are parallel to each other. The distance between discontinuity I and discontinuity N is L.

Full size image

For these parallel discontinuities, as shown in Fig. 3, the scanline length, l, is

$$ l=\frac{L}{ \sin \uptheta}, $$
(2)

then

$$ {p}_{B/ A}\left(\upalpha, \upbeta \right)\propto \frac{N}{l}=\frac{N \sin \uptheta}{L}, $$
(3)

which is equivalent to

$$ {p}_{B/ A}\left(\upalpha, \upbeta \right)= k \sin \uptheta \kern1em \left(\upalpha \in \left[{\upalpha}_1,{\upalpha}_N\right],\kern0.5em \upbeta \in \left[{\upbeta}_1,{\upbeta}_N\right]\right), $$
(4)

where k is an undetermined coefficient.

The joint probability density that a particular dip direction and dip angle occur in the rock mass, p A (α, β), is

$$ {p}_A\left(\upalpha, \upbeta \right)=\frac{p_{A B}\left(\upalpha, \upbeta \right)}{p_{B/ A}\left(\upalpha, \upbeta \right)}, $$
(5)

where p AB (α, β) is the joint probability density of the dip direction and dip angle that is observed by the scanline.Any grid D can be subdivided into n sub-grids σ1, σ2, σ3, …, σ n (Fig. 4). Thus, the probability that the given orientation falls within in the interval D can be regarded as the sum of the probabilities for these sub-grids:

$$ {\displaystyle \underset{D}{\iint }{p}_A}\left(\upalpha, \upbeta \right) d\upalpha d\upbeta ={\displaystyle \sum_{i=1}^n{\displaystyle \underset{\upsigma_i}{\iint }{p}_A}\left(\upalpha, \upbeta \right) d\upalpha d\upbeta .} $$
(6)

Substituting Eq. (4) into Eq. (5), and then substituting Eq. (5) into Eq. (6), we obtain

$$ {\displaystyle \underset{D}{\iint }{p}_A\left(\upalpha, \upbeta \right) d\upalpha d\upbeta =\frac{1}{k}{\displaystyle \sum_{i=1}^n{\displaystyle \underset{\upsigma_i}{\iint}\frac{p_{A B}\left(\upalpha, \upbeta \right)}{ \sin \uptheta}} d\upalpha d\upbeta .}} $$
(7)

Note that sin θ in Eq. (7) is a function of the variables α and β. Suppose θ ci is the intersection angle between the scanline and the discontinuity mapped at the center of the sub-grid. The variable sin θ is equal to the constant sin θ ci only if the sub-grids are infinitesimal (i.e., n → ∞). In this case only, Eq. (7) can be rewritten as

$$ {\displaystyle \underset{D}{\iint }{p}_A\left(\upalpha, \upbeta \right) d\upalpha d\upbeta =\frac{1}{k}\underset{n\to \infty }{ \lim }}{\displaystyle \sum_{i=1}^n\frac{{\displaystyle \underset{\upsigma_i}{\iint }{p}_{A B}\left(\upalpha, \upbeta \right) d\upalpha d\upbeta}}{ \sin {\uptheta}_{ci}}}=\frac{1}{k}\underset{n\to \infty }{ \lim }{\displaystyle \sum_{i=1}^n\frac{P_i}{ \sin {\uptheta}_{ci}}}, $$
(8)

where P i is the probability of the observed orientations within the sub-grid σ1.

Fig. 4
figure 4

Subdivision of grid D.

Full size image

However, a true sub-grid cannot be infinitesimal. In this case, the above substitution means that all of the nonparallel discontinuities in sub-grid σ1 are approximated as parallel discontinuities with a uniform orientation mapped at the center of the sub-grid (Fig. 5). This substitution leads to the error under consideration, which can be expressed as

Fig. 5
figure 5

Interpretation of the approximate substitution in the Terzaghi equation.

Full size image
$$ {\displaystyle \underset{D}{\iint }{p}_A\left(\upalpha, \upbeta \right) d\upalpha d\upbeta \approx \frac{1}{k}{\displaystyle \sum_{i=1}^n\frac{P_i}{ \sin \uptheta}},} $$
(9)

Equation (9) is consistent with the Terzaghi equation [6] as shown in Eq. (1).

2. Error Reduction in Taking N 90 as an Integer. Next, we identify the optimal values of grid size and sample density to improve the accuracy of the Terzaghi procedure. Grid size is arbitrarily set within the Terzaghi procedure. Sample density is the sample size per grid size (1°×1°). In this paper, firstly the accuracy is tested under a series of these two parameters. The values of these two parameters that yield the highest accuracy are determined. In the test, the accuracy of correction is characterized in terms of the difference between the true and corrected distributions.

Firstly, the true distribution of orientations is assumed, along with three other parameters that are necessary for modeling (size, intensity and aperture). The parameters used in the model are as follows: length, width, and height of the simulated zone are 20, 20 and 20 m, respectively; number of discontinuity centers per rock volume is 5 m-3; dip direction follows a uniform distribution with a lower limit of 175° and an upper limit of 185°; dip angle follows a uniform distribution with a lower limit of 40° and an upper limit of 50°; radius follows an exponential distribution with a mean of 1 m; in each model, the trend/plunge values for seven scanlines are 0/45, 10/45, 20/45, 30/45, 40/45, 50/45, and 60/45°, respectively; and the sample density is 0.05, 0.1, 0.2, 0.3, 0.4, and 0.5°-2, respectively.

Secondly, the parameters are entered into the discrete fracture network modeling software AutoCAD, and seven different models of a discontinuity network are constructed based on the different scanline directions.

Thirdly, in these models, the orientations observed by scanlines are obtained and then corrected by the Terzaghi procedure. In each model, orientations are observed under six different sample densities: 0.05, 0.1, 0.2, 0.3, 0.4, and 0.5°-2. Thus, for the seven models, forty-two series of observed orientations are obtained, all of which fall outside the blind zone. These orientations are corrected under four different grid sizes: 1×1, 2 ×2, 5 × 5, and 10°×10°. The corrected results are omitted here for brevity sake.

Finally, the difference between the true and corrected distributions is tested by a non-parametric statistical approach (the Kolmogorov–Smirnov two-sample test) with the SPSS software (version 24.0, IBM, Armonk, NY). This non-parametric hypothesis test evaluates the difference between cumulative distribution functions of distributions of two sample data vectors. The test returns an asymptotic significance to quantify the difference. The significance ranges from 0 to 1; a smaller number reflects a greater difference. More information about this test can be found in Senger and Çelik [11] and Ozçomak and co-workers [12].

The relation between this difference and the parameters grid size and sample density is analyzed, and the values of the two parameters that yield the smallest difference are determined to be the optimal ones.

2.1. Effect of Grid Size. The test provided two results corresponding to dip direction and dip angle, respectively. These two results are combined, and their average is shown in Fig. 6. For most sample densities and intersection angles, significance is an increasing function of grid size in the size interval between 1°×1° and 2°×2°, a decreasing function between 2°×2° and 5°×5°, and a constant function between 5°×5° and 10°×10°. This suggests that a decrease in grid size from 10°×10° to 5°×5° cannot improve the accuracy of correction, a decrease from 5°×5° to 2°×2° can improve the accuracy, while a decrease from 2°×2° to 1°×1° will reduce the accuracy. In addition, the greatest significance occurs at a grid size of 2°×2° for the most sample densities and intersection angles. To ensure that this optimal value is independent of the sample density and intersection angle, a partial correlation test was performed using the SPSS. When the control variable is sample density, and the test variables are intersection angle and this optimal grid size, the correlation coefficient is 0.467. Similarly, when the control variable is the intersection angle, and the test variables are sample density and this optimal grid size, the correlation coefficient is - 0.301. The test results indicate that this optimal grid size poorly correlates with the sample density and the intersection angle. Thus, the optimal grid size is assessed as 2°×2°.

Fig. 6
figure 6

Significance versus grid size. The significances of dip direction and angle were tested by the Kolmogorov–Smirnov two-sample test. The average significance was then calculated from these two values. Sample density: (a) 0.05°-2; (b) 0.1°-2; (c) 0.2°-2; (d) 0.3°-2; (e) 0.4°-2; (f) 0.5°-2.

Full size image

2.2. Effect of Sample Density. The relation between accuracy and sample density was evaluated for the grid size of 2°×2°. Figure 7 shows significance versus sample density curves at different intersection angles. For intersection angles of 89, 83, 63, 56, and 49°, the greatest significance occurs at a sample density of 0.05°-2. In contrast, the greatest significance is observed at 0.1°-2 and at 0.5°-2 for 77° and 70°, respectively. To ensure that this optimal value of sample density (0.05°-2) is independent of the intersection angle, a Pearson correlation test was performed using the SPSS. The correlation coefficient of these two test variables was 0.039, which demonstrates that this optimal value poorly correlates with the intersection angle. Thus, the optimal value of sample density is derived to be 0.05°-2.

Fig. 7
figure 7

Significance versus sample density, under a grid size of 2°×2°.

Full size image

3. Case Study: Slope Cut East of Baihua Bridge. The derived optimal values of grid size and sample density were verified by true data from a study area near the epicenter of the 2008 Wenchuan Earthquake. Firstly, the observed orientations were obtained by the scanline mapping technique. Secondly, the observed orientations were corrected by the Terzaghi procedure. Thirdly, with the use of these corrected orientations the three-dimensional network of discontinuity was modeled by means of discrete fracture network modeling. In this model, the orientations that intersected a virtual scanline were observed. The direction of this virtual scanline was set to be the same as that of the actual scanline used in the field. To distinguish these orientations from the discontinuity orientations observed in the field, the discontinuities derived from the model are referred to as model discontinuities. Finally, the difference between the observed and model orientations was evaluated by the Kolmogorov–Smirnov two-sample test under different grid sizes.

The study area is located near the town of Yingxiu, in Wenchuan, Sichuan Province, China, about 1800 m east of the epicenter of the 2008 Wenchuan Earthquake. The area is 11 m long, 5 m wide and 6 m high, and consists of exposures of upper Triassic lithic arkose of the Xujiahe formation along a road cut. The rock has two joint sets, one of which is the bedding. A scanline with a trend/plunge of 108/15° was fixed on the outcrop to observe the bedding planes. Their poles are shown in Fig. 8.

Fig. 8
figure 8

Contour plot of stereographic projections of observed orientations.

Full size image

The sampling bias of the observed orientations was corrected using the Terzaghi procedure. For verification of the proposed grid size, the projection net was subdivided into grids of 1×1, 2 × 2, 5 × 5, and 10°×10°, respectively. For verification of the proposed sample density, the correction used the first 5, 14, 27, and 55 observed orientations, corresponding to sample densities of 0.02, 0.05, 0.1, and 0.2°-2, respectively. Figure 9 depicts the corrected orientations under a grid size of 5°×5° and a sample density of 0.2°-2. The volume intensity, radius and aperture were calculated by using the respective methods. The volume intensity was 4 m-3, the radius followed an exponential distribution with a mean of 0.25 m, while the aperture followed an exponential distribution with a mean of 3.2 mm.

Fig. 9
figure 9

Contour plot of stereographic projections of the corrected orientations under a grid size of 5°×5° and a sample density of 0.2° -2. Because some poles coincide, it appears that there are only 11 poles, while, in fact, there are 74 poles.

Full size image

By multiplying the volume intensity and the volume of the simulated zone (1000 m3), we calculated that the total number of discontinuities for modeling was 4000. For each of these discontinuities, pseudo-random numbers were generated for each of five elements, i.e., the X-coordinate, Y-coordinate, Z-coordinate, diameter and aperture (not shown). After the pseudo-random numbers and the corrected orientation data were entered into the modeling software, models were constructed that included a scanline with the same direction as the field scanline. In the models, the orientations of discontinuities that intersected the scanline were measured. The number of model discontinuities was equal to the number observed in the field. Figure 10 shows the model orientations.

Fig. 10
figure 10

Contour plot of stereographic projections of model orientations under a grid size of 5°×5° and a sample density of 0.2°-2.

Full size image

The difference between the observed and the model orientations was evaluated using the Kolmogorov–Smirnov two-sample test. This test produced the asymptotic significance values corresponding to the dip direction and dip angle, as shown in Figs. 11 and 12. Figure 11 shows the average significance values for different grid sizes. The curve is an increasing function of grid size in the size interval between 1°×1° and 2°×2°, decreases between 2°×2° and 5°×5°, and is approximately constant between 5°×5° and 10°×10°. Moreover, the highest accuracy is achieved at 2°×2°. The two results are consistent with findings regarding the grid size in Section 2.1. Figure 12 presents the findings related to sample density for the grid size of 2°×2°. The highest accuracy is obtained at a sample density of 0.05°-2. This result is consistent with the findings regarding the sample density in Section 2.2.

Fig. 11
figure 11

Significance versus grid size.

Full size image
Fig. 12
figure 12

Significance versus sample density, under a grid size of 2°×2°.

Full size image

4. Discussion. As shown in Figs. 6, 7, 11, and 12, neither the proposed grid size of 2°×2° nor the proposed sample density of 0.05°-2 could completely eliminate the error. This may be due to the fact that some errors originate from estimating, measuring, or approximating. Furthermore, as it was mentioned in Section 1, one cannot exclude the substitution error possibilities. Therefore, application of the proposed values reduces, but cannot fully eliminate the theoretical error introduced by the Terzaghi procedure.

Conclusions. An approximate substitution in the derivation of the Terzaghi equation gives rise to a theoretical error when the Terzaghi procedure is applied outside the blind zone. In this study, we developed a method for reducing this theoretical error. The highest accuracy was achieved with a grid size of 2°×2° and a sample density of 0.05°-2. The application of these optimal parameters to scanline mapping via the Terzaghi procedure has improved the accuracy of the results obtained.