Effect of surface stress concentrators and microstructure on the fatigue limit of the material

A calculation model is developed that makes it possible to predict the fatigue limit σ₋₁ of specimens with technological surface defects based on the data on the material microstructure and stress concentrator geometry. The fatigue test results are presented for specimens with technological defects under symmetric lateral bending that are made of Ti–6Al–4V titanium alloy condensate produced by the electron-beam physical vapor deposition method. The results obtained are used to calculate σ₋₁ based on the developed model and are in very good agreement with the experimental data.

Introduction. Early in the study of this problem [1], it was found that the fatigue resistance characteristics of Ti–6Al–4V alloy produced by the electron-beam vacuum physical vapor deposition (EB PVD) method are essentially dependent on technological defects, in particular, on separate droplets that are emitted from the melt surface and are deposited in the condensate, forming columns which, while growing during the process of deposition, reach the condensate surface. These columns acting as efficient stress concentrators have a strong negative effect on the fatigue resistance characteristics of the condensate of Ti–6Al–4V alloy. In this case, the fatigue limit decreases by a factor of about 1.5–2 as compared to that of a similar defectless material and a standard cast alloy.

Note that in comparison with the traditional techniques, the EB PVD method has a number of advantages, which enables the creation of materials with unique properties. In particular, it is possible to produce layered and gradient (i.e., with a variable chemical composition and/or microstructure) coatings, materials with a controlled porosity, alloys with a chemical composition that cannot be obtained using the conventional techniques, and also materials with a special structure, etc. [2, 3]. This is indicative that the above method is promising in the production of materials for the state-of-the-art technology and in obtaining coatings on finished products in order to improve their characteristics.

The aim of the present paper consists in a detailed analysis of the effect of the geometry of surface technological defects on the fatigue resistance characteristics of the condensates under study and, on its basis, the development of the model for calculating the fatigue limit of the material taking into account the microstructure and stress concentration.

Materials and Procedures for the Experimental Investigation. The concept of the EB PVD method was described in detail earlier [1]. The EB PVD-coatings of an (α + β)-type titanium alloy Ti–6Al–4V were obtained by deposition on plane substrates of the same alloy. In this way, composite material blanks for specimens of the condensate-substrate system were obtained.

The alloy microstructure was studied using the optical microscopy. Fractographic studies were carried out using a CamScan scanning electron microscope.

The fatigue strength characteristics were investigated experimentally according to the procedure described in detail in [1, 4, 5]. Flat cantilever hour-glass shaped specimens with a thickness h = 1 mm and a minimal width b = 5 mm in the working area were tested under symmetric lateral bending using an electrodynamic vibration testing machine. The 1%-drop in the natural frequency of resonant vibrations of the specimen, which corresponded to the occurrence of a surface half-elliptical crack with a depth of about 10% of the cross section thickness was taken as the criterion for fatigue fracture. After recording the number of cycles to reach the limiting state according to the given criterion, the specimens continued to be loaded within the given vibration range until the final separation into two pieces, in order to further study the fracture surfaces. Moreover, the specimens that survived N = 10⁷ cycles of testing without failure, were tested to failure at higher stress amplitudes with the aim to detect the location of fatigue crack initiation.

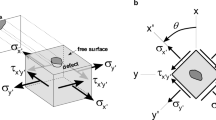
The specimen patterns and the stress diagram experimentally determined using resistance strain gauges under conditions of cantilever bending in relative units (that is, the current value of σ _a with respect to σ _{a max}) are presented in Fig. 1 where the specimen fracture zone is roughly marked with the lines A and B. Prior to testing, specimen surfaces were polished, sharp edges were rounded off to eliminate possible stress concentrators induced by straight edges of a flat specimen.

Fig. 1

Patterns of the specimen, its loading and the diagram of the relative stress amplitudes along the specimen length.

Analysis of the Effect of Geometry of Surface Technological Defects of the Fatigue Strength Characteristics of Condensates under Study. As noted above, droplets in the produced condensates are considered as technological defects. In the process of investigations, the photos of all the fracture surfaces of specimens under testing were made and the geometrical parameters (diameter and depth) were determined for the columns divided into three groups (Table 1) by sizes, namely, by the diameter on the specimen surface.

Table 1 Dimensions of Columns (in μm)

The analysis of the results given in Table 1 has shown that all the specimens tested can be arbitrarily divided into four groups. The first group includes the specimens with columns of a “large” (on the average, approximately 200 μm) diameter (Fig. 2a), the second and third groups include those with the column diameters of about 50 μm (Fig. 2b) and 20 μm (Fig. 2c), respectively, and the fourth group includes specimens of the condensate conventionally considered as defectless, that is, with no revealed defects, such as droplets, on the fracture surface, with fatigue crack initiation occurring from the substrate (Fig. 2d).

Fig. 2

Fracture surfaces of the specimen: (a), (b), (c), and (d) first, second, third, and fourth group, respectively.

Noteworthy here is the fact that for the majority of specimens, the concentrator depth, i.e., the column length, reaches the midline, and even extends over it (see Table 1). Therefore, this geometrical parameter should not be taken into account since the specimen was under lateral bending conditions. Moreover, the analysis of fracture surfaces of the specimens is indicative that the fatigue crack initiation occurred just on the surface of the specimen with a concentrator. Thus, the main geometrical parameter of the concentrator which is responsible for the strength under the cyclic loading is, in this case, its diameter on the specimen surface.

One of the special features of these defects is also noteworthy, namely, that they are not empty but filled with the same deposited material (Ti–6Al–4V) of somewhat another chemical composition and microstructure, i.e., these are foreign impurities. Instead, their typical feature is the porosity near the column (Fig. 3a) resulting, under conditions of loading, in the extension (“the extrusion”) of the column onto the specimen surface (Fig. 3b) and, in some cases, in its complete extraction from the specimen (Fig. 3c). Therefore, when calculating the fatigue limit taking into account the above defects we will consider them as empty.

Fig. 3

The porosity near the column (a), its extrusion (b) and extraction (c).

The fatigue test results are presented in Fig. 4. As seen, the specimens arbitrarily distributed into four groups by mean diameters of the surface columns can be satisfactorily approximated by four fatigue curves. The fatigue limits σ₋₁ for groups 1, 2, 3, and 4 are approximately equal to 275, 375, 525, and 600 MPa, respectively. Thus, condensates with the largest concentrator diameter have the lowest fatigue resistance characteristics (curve 1 in Fig. 4), and accordingly, specimens of the defectless condensate have the highest fatigue limit, that is, the crack therein was initiated from the substrate (curve 4 in Fig. 4). Therefore, we will consider it as the fatigue limit of smooth specimens. Also note that as a result of testing when it is not known a priori in what place within the specimen length and from what defect (in diameter), or in its absence, the specimen will fail, in total, four and five experimental points to construct the fatigue curves were revealed, respectively, for specimens of the third and fourth groups. Therefore, in these cases, the experimental determination of the fatigue limit gave rough values.

Fig. 4

Fatigue curves for specimens under study (specimen numbers are indicated by figures near the points): curves 1–4 correspond to the specimen group numbers. (Open points represent the stress amplitude at the place of fracture, solid points represent the same during re-testing of specimens that withstood at N = 10⁷ cycles of testing without failure.)

Development of the Model for Calculating the Fatigue Limit Taking into Account the Microstructure and Stress Concentration. At present, a considerable amount of experimental data is available, which are indicative that the fatigue limit of polycrystalline materials represents the critical conditions for the propagation of fatigue cracks initiated at this level of stresses. This refers in full measure to both smooth specimens and notched ones, that is, with stress concentrators.

In [6, 7], a concept is proposed of the sensitivity to the stress concentration for blunt concentrators that characterizes the fatigue sensitivity to a notch in terms of the parameter K _td defined as the stress concentration due to a notch at the distance d _i from the notch tip to the ith microstructural barrier in the form

$$ {K_{td}} = \frac{{{\upalpha_\upsigma }}}{{\sqrt {{1 + 4.5\left( {{{{{d_i}}} \left/ {\uprho } \right.}} \right)}} }}, $$

(1)

where ρ is the notch radius and α_σ is the theoretical stress concentration factor.

Defining d _i as the distance from the notch tip to the ith microstructural barrier and $\Delta {\upsigma_{e{d_i}}}$ as the fatigue limit related to the ith barrier, the fatigue limit Δσ _e of the notched specimen for the given factor α_σ is characterized by the highest $\Delta {\upsigma_{e{d_i}}}$:

$$ {\left. {\Delta {\upsigma_e}} \right|_{{\upalpha_\upsigma }}} = {\left. {\max \Delta {\upsigma_{e{d_i}}}} \right|_{{\upalpha_\upsigma }}} = \max \left[ {\frac{{\Delta \upsigma_{e{d_i}}^{\prime}\sqrt {{1 + 4.5\left( {{{{{d_i}}} \left/ {\uprho } \right.}} \right)}} }}{{{\upalpha_\upsigma }}}} \right], $$

(2)

where $\Delta \upsigma_{e{d_i}}^{\prime}$ is the effective characteristic (effective resistance) of the ith barrier, i.e., the fatigue limit of the smooth specimen in the presence of a crack of the length l = d _i .

The above concept is shown schematically in Fig. 5 where three sequential microstructural barriers located at the distances d ₁, d ₂, and d ₃ from the notch tip (d ₁ < d ₂ < d ₃) and the respective effective characteristics $\Delta \upsigma_{e{d_1}}^{\prime}$, $\Delta \upsigma_{e{d_2}}^{\prime}$, and $\Delta \upsigma_{e{d_3}}^{\prime}$ are considered. The fatigue limit of a notched specimen from α_σ = 1 to ${\upalpha_{{\upsigma_1}}}$ is defined as $\Delta {\upsigma_e} = {{{\Delta \upsigma_{e{d_1}}^{\prime}}} \left/ {{{K_{t{d_1}}}}} \right.}$, and that from ${\upalpha_{{\upsigma_1}}}$ to ${\upalpha_{{\upsigma_2}}}$ is defined as $\Delta {\upsigma_e} = {{{\Delta \upsigma_{e{d_2}}^{\prime}}} \left/ {{{K_{t{d_2}}}}} \right.}$, etc.

Fig. 5

Fatigue limit of notched specimens Δσ _e defined as the highest fatigue limit related to the effective characteristic $\Delta \upsigma_{e{d_i}}^{\prime}$ and distance d _i [see (2)].

According to the above model [7], to determine the fatigue limits of specimens with concentrators, it is necessary to know the coefficients $\Delta {\upsigma_{e{d_i}}}$ and d _i which are determined experimentally. Moreover, the theoretical stress concentration factor α_σ should be determined by calculation.

In this paper, using the above model and the dependence of the fatigue limit on the microstructural parameter for smooth specimens [8], an attempt has been made to develop the calculation model which would make it possible to predict the fatigue limit σ_−1k of specimens with stress concentrators from the data on the material microstructure.

It was shown earlier [8, 9] that the dependence of the fatigue limit σ₋₁ on the microstructural parameter d within the range of mean (for titanium alloys) diameters d of α-globules (ranging from 3 to 7 μm) is described very well by the equation below

$$ {\upsigma_{ - 1}} = E\sqrt {{\frac{a}{{\upeta d}}}}, $$

(3)

where E is the elastic modulus, a is the parameter of the crystalline lattice (interatomic distance), d is the linear size of the microstructural element responsible for the fatigue strength, and η is the parameter which means the number of barriers (grains) from the smooth specimen surface to the end of the fatigue crack formed and arrested at the level of the stress amplitude equivalent to the fatigue limit σ₋₁.

As was shown by the microstructural analysis of the obtained condensate of alloy Ti–6Al–4V [1], the average thickness of elements of the α-phase responsible for the fatigue strength of the given material is 3.5 μm, i.e., is within the above indicated range of grain sizes. Moreover, the structure of the condensate is rather uniform, i.e., the deviation of the thickness of elements of the α-phase from the average value is no more than ±0.5 μm. In order to obtain the calculation formula for σ_−1k , we substitute Eq. (3) into relationship (2):

$$ {\upsigma_{ - 1k}} = \frac{E}{{{\upalpha_\upsigma }}}\sqrt {{\frac{a}{{\upeta d}}\left( {1 + 4.5{{{{d_i}}} \left/ {\uprho } \right.}} \right)}} . $$

(4)

It was noted above that the quantity d _i is the distance to the microstructural barrier where the fatigue crack has stopped at the level of the fatigue limit for the specimen having a concentrator with the given α_σ. That is, d _i can be represented as η _t d, where η _t is the coefficient similar to η in formula (3) only for specimens with stress concentrators. Therefore, after elementary transformations, formula (4) can finally be written as

$$ {\upsigma_{ - 1k}} = \frac{E}{{{\upalpha_\upsigma }}}\sqrt {{\frac{a}{\upeta }\left( {\frac{1}{d} + 4.5\frac{{{\upeta_t}}}{\uprho }} \right)}} . $$

(5)

Thus, to calculate the fatigue limit σ_−1k of specimens with a stress concentrator of the radius ρ at the tip, it is necessary to know the elastic modulus E of the given material, the linear grain size d, the crystal lattice parameter a, the parameters η and η _t that define the position of the barrier near which the crack has stopped, or the number of grains from the surface of the smooth specimen and from the concentrator tip, respectively, and to calculate α_σ.

Results of the Calculation According to the Above Model. To calculate α_σ at mean values of the concentrator diameters 2ρ = 20, 50, and 200 μm using the finite-element method, the stress-strain state (SSS) of the model of the specimen under investigation was determined (Fig. 6), which was loaded in pure bending in the plane ZX. The concentrator was simulated by a through hole of the proper diameter. In the calculation of the SSS, the mechanical characteristics of the strip material were assumed to be as follows: the elastic modulus E = 1.25⋅10⁵ MPa and Poisson’s ratio μ = 0.3.

Fig. 6

The regularities of variation in the value of the relationship σ _X /σ _nom at the concentrator tip along the normal OY: (1) column diameter 2ρ = 20 μm; (2) 2ρ = 50 μm; (3) 2ρ = 200 μm (Ymax is the distance from O to the strip edge).

In order to reveal the influence of location of the concentrator on the SSS value, the calculations were performed at its arbitrary location with respect to the longitudinal plane of symmetry of the specimen model. It has been found that due to the smallness of the concentrator size, the influence of its nonsymmetrical location on the calculated results is negligible.

The results of calculating the SSS of the model are presented in Fig. 6 as the regularities of variation in the value of the ratio σ _X /σ _nom in the vicinity of the concentrator. For the average values of concentrator diameters 2ρ = 200, 50, and 20 μm, we have α_σ = 2.701, 2.932, and 2.975, respectively.

As to the parameters η and η _t , it is necessary to focus in more detail on the selection of their values. As was found earlier [8, 9], for the above-indicated range of grain sizes (d = 3–7 μm), the parameter η = 4. That is, the crack that occurs in smooth specimens at the fatigue limit level, extends from the surface to a depth of about four grains and stops. For specimens with concentrators, a quarter elliptical fatigue crack formed at one of the concentrator tips on the specimen surface, has the following dimensions: l _s on the surface and l _d into the depth. According to the data given in [10, 11], the l _d /l _s ratio approaches the unity for “very small” half-elliptical cracks. Moreover, for specimens with concentrators (in our case, the concentrators can be considered as “blunt and shallow” according to the classification given in [12] ) based on the data in Fig. 5, it is reasonable to assume that the fatigue limit will be defined by the location of the same microstructural barrier as in smooth specimens, i.e., it will be also equal to four. Thus, η _t  = η = 4.

For the given alloy, the value of a = 2.95⋅10⁻¹⁰ m was used, which is equal to the interatomic distance in the basal plane of the hexagonal close-packed (hcp) crystal structure of α-titanium [13] (Fig. 7). In selecting this parameter, we were guided by the following considerations. As was found earlier [1, 8, 9], for two-phase (α + β)-titanium alloys, in particular, for alloy Ti–6Al–4V, the hcp α-phase is the microstructural element responsible for the fatigue strength. Under cyclic loading, the slip systems with the Burgers vectors $\vec{a}$ (in the directions $< 112\bar{0} >$ and in planes (002), {10 $\bar{1}$ 0}, {10 $\bar{1}$ 1}) – a total of 12 slip systems in all – and $\left( {\vec{c} + \vec{a}} \right)$ (in the directions $< 11\bar{2}2 >$ and in planes {11$\bar{2}$2}) – a total of 6 slip systems in all – can be activated in the crystal of the hexagonal α-phase (see Fig. 7). Taking into account that the critical shear stress necessary to start the microplastic deformation of the crystal is several times higher during the $\left( {\vec{c} + \vec{a}} \right)$-slip than during the $\vec{a}$-slipe, the percentage of grains deformed due to the $\left( {\vec{c} + \vec{a}} \right)$-slip will be much lower in polycrystals of α-titanium in the absence of the crystallographic texture because the activation of the $\vec{a}$-slip is easier even for the angle of 10° between the stress axis and axis $\vec{c}$ [13]. As was shown by the investigation on the crystallographic texture of the obtained condensate (Fig. 8), the overwhelming majority of crystals is oriented such that the basal plane (0002) is almost perpendicular to the direction of condensation [1], i.e., the angle between the stress axis and the axis $\vec{c}$ is close to 90°. Thus, the slip in the condensate crystals was activated in the planes with the vector $\vec{a}$, the value of which is to be taken into account.

Fig. 7

The unit cell of the hcp crystal of α-titanium [13].

Fig. 8

The pole figure of the condensate under study [1]. (The plane XY of the fatigue testing specimens is parallel to the picture area, with the condensation direction being perpendicular to its plane.)

Thus, we have all the parameters required for calculation. Table 2 presents the calculated results, σ_−1calc , using formula (5) compared to the experimental data, σ_−1exp , and the results of calculating the error Δ using the formula given below

$$ \Delta = \frac{{{\upsigma_{ - 1calc}} - {\upsigma_{ - 1exp}}}}{{{\upsigma_{ - 1exp}}}} \cdot 100\% . $$

(6)

Table 2 Comparison between the Calculated and Experimental Results

It is seen that the calculation is conservative and gives a close agreement with the experimental results.

The developed model (5) can be used both for another titanium alloys or alloys with the same type of the crystal lattice (hcp) and for materials with another type of lattice, namely, the bcc and fcc lattices. A limitation in the use of the proposed model can be the slip in grain for materials with many easy slip systems, which is other than a single planar slip peculiar to titanium alloys, since in this case, the correct determination of the parameter a is problematic.

It should also be noted that for other materials, for which the size d of the structural element responsible for the fatigue strength of the given alloy is not within the above range of grain sizes (3–7 μm), the parameter η is calculated by formula [8]

$$ \upeta = \frac{{{E^2}a}}{d}{\left( {A + B\arctan \frac{{E\sqrt {{{{a} \left/ {{\left( {4d} \right)}} \right.}}} - A}}{B}} \right)^{ - 2}}, $$

(7)

where A = (σ _f  + σ _p )/2, B = (σ _p  − σ _f )/π, σ _f is the internal friction stress (σ _f  ≅ 2⋅10⁻³ G), σ _p is the proportionality limit where the values of σ _p are to be taken from tensile testing results, and G is the shear modulus [G = E/(2(1 + μ)), μ is Poisson’s ratio].

Figure 9 shows the dependence of the quantity η on the grain size d for smooth specimens of alloy Ti–6Al–4V. The data for the calculation using formula (7) were taken from [9]. As seen, with a decrease in the material grain size, the number of barriers the crack has passed through from the surface into the depth before stopping at the level of the stress amplitude, which is equivalent to the fatigue limit σ₋₁, increases. And on the contrary, in materials with a “very large grain” size, a fatigue crack must stop at the first barrier or must not occur at all. The mechanisms governing the fatigue strength depending on the grain size of the material are described in detail in [8].

Fig. 9

Grain size d dependence of the parameter η for alloy Ti–6Al–4V.

The stress concentrator size also imposes restrictions on the use of the proposed model (5). In contrast to the case considered in this paper, for “a deep and sharp” notch (according to the same classification [12]) in compliance with the model described in [7], the parameter η _t will no longer be equal to η, and appropriate experiments have to be carried out to determine it. Moreover, in model (1) and thus in model (5) as well, depending on the concentrator depth and sharpness, another coefficient (4, in particular) can be used rather than 4.5. This was considered in detail in [14] that describes the approaches employed by various authors in due time to solve the problem of predicting the fatigue limit in the presence of stress concentrators.

As to the parameter d, which in formula (5) is the linear size of the structural element responsible for the fatigue strength of the material, then, as was indicated above, the average linear grain size was taken into account because the spread in grain size is not large for the given material. In the case where, for any other material, the spread is large, then, during the calculation, it is necessary to take into account the curve of the grain-size distribution throughout the bulk of the material and substitute into formula (5) the value of d that corresponds to the average value of the relative number of grains on the distribution curve and is greater than the arithmetic mean. This is substantiated in detail in [9].

Conclusions

• 1. Stress concentrators in the form of technological defects (columns) of a large diameter on the specimen surface have the most negative effect on the fatigue resistance characteristics of the studied condensate of alloy Ti–6Al–4V.

• 2. The developed model for calculating the fatigue limit of specimens with surface stress concentrators has shown very good conservative agreement with the experimental results for the studied condensates of alloy Ti–6Al–4V (the error Δ is within the range from −0.8 to −4.3%).

• 3. In order to calculate the fatigue limit of specimens with concentrators, it is necessary to know its geometry, the microstructure parameters: the linear size of the structural element responsible for the fatigue strength, as well as the Burgers vector and the modulus of elasticity.

• 4. The developed model can be applied to alloys with a different type of crystal lattice taking into account certain restrictions.