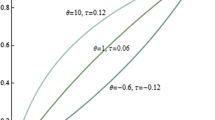A flexible and tractable class of one-factor copulas

Abstract

Copulas are a useful tool to model multivariate distributions. While there exist various families of bivariate copulas, the construction of flexible and yet tractable copulas suitable for high-dimensional applications is much more challenging. This is even more true if one is concerned with the analysis of extreme values. In this paper, we construct a class of one-factor copulas and a family of extreme-value copulas well suited for high-dimensional applications and exhibiting a good balance between tractability and flexibility. The inference for these copulas is performed by using a least-squares estimator based on dependence coefficients. The modeling capabilities of the copulas are illustrated on simulated and real datasets.

1 Introduction

The modeling of random multivariate events (i.e., of dimension greater than 2) is a central problem in various scientific domains and the construction of multivariate distributions able to properly model the variables at play is challenging. The challenge is even more difficult if the data provide evidence of tail dependencies or non Gaussian behaviors. To address this problem, the concept of copulas is a useful tool as it permits to impose a dependence structure on predetermined marginal distributions. Standard books covering this subject include Nelsen (2006), Joe (2001). See also Genest and Favre (2007) for an introduction to this topic. The most common copula models used in high-dimensional applications are discussed below.

The popular Archimedean copulas are tractable and allow us to model a different behavior in the lower and upper tails. For instance, the Gumbel copula is upper, but not lower, tail dependent; the opposite holds for the Clayton copula. Nevertheless, the dependence structure of Archimedean copulas is severely restricted because they are exchangeable, implying that all the pairs of variables have the same distribution. More details about these copulas can be found in the above-mentioned books.

Nested Archimedean copulas are a class of hierarchical copulas generalizing the class of Archimedean copulas. They allow us to introduce asymmetry in the dependence structure but only between groups of variables. This hierarchical structure is not desirable when no prior knowledge on the random phenomenon under consideration is available. Furthermore, constraints on the parameters restrict the tractability of these copulas. These copulas first appeared in Joe (2001) Sect. 4.2.

The class of elliptical copulas arises from the class of elliptical distributions. These copulas are interesting in many ways, but they are tail symmetric, meaning that the lower tail-dependence coefficient is equal to the upper tail-dependence coefficient (these coefficients are defined in Sect. 2.2). This may not be the case in applications. See, e.g., McNeil et al. (2010) Sect. 5 or Frahm et al. (2003) for an introduction to these copulas.

Pair-copula constructions and Vines are flexible copula models based on the decomposition of the density as a product of conditional bivariate copulas. However, these models are difficult to handle. Furthermore, the conditional bivariate copulas are typically assumed not to depend on the conditioning variables. This so-called simplifying assumption can be misleading, as remarked in Acar et al. (2012). Pair-copula constructions first appeared in Joe (2001) Sect. 4.5. See also Bedford and Cooke (2002), Bedford and Cooke (2001), Kurowicka and Cooke (2004) for theoretical developments and Aas et al. (2009) for a practical introduction to modeling with Vines.

As mentioned above, most copula models are either tractable or flexible, but rarely both. In this paper, we propose a tractable and yet flexible class of one-factor copulas well suited for high-dimensional applications. This class is nonparametric, and, therefore, encompasses many distributions with different features. Unlike elliptical copulas, the members of this class allow for tail asymmetry. Furthermore, we derive the associated extreme-value copulas, and, therefore, the analysis of extreme values can be carried out with the presented models. Finally, we show how to perform theoretically well-grounded, and practically fast and accurate, inference of these copulas, thanks to the ability of calculating explicitly the dependence coefficients.

The remaining of this paper is organized as follows. Section 2 presents the proposed class of one-factor copulas, Sect. 3 deals with inference, and, in Sect. 4, the proposed copulas are applied to simulated and real datasets. The proofs are postponed to the Appendix.

2 A tractable and flexible class of one-factor copulas

The class of copulas proposed in this paper, referred to as the FDG class (see Sect. 2.2 for an explanation of this acronym), can be embedded in the framework of one-factor models. We therefore introduce the later in Sect. 2.1. The construction and properties of FDG copulas are given in Sect. 2.2. Parametric examples are proposed in Sect. 2.3. The extreme-value copulas associated to the FDG class are derived in Sect. 2.4.

2.1 One-factor copulas

By definition, the coordinates of a random vector distributed according to a one-factor copula Krupskii and Joe (2013) are independent given a latent factor. More specifically, let $U_0,U_1,\dots ,U_d$ ($d\ge 2$) be standard uniform random variables such that the coordinates of $(U_1,\dots ,U_d)$ are conditionally independent given $U_0$. The variable $U_0$ plays the role of a latent, or unobserved, factor. Let us write $C_{0i}$ the distribution of $(U_0,U_i)$ and $C_{i|0}(\cdot |u_0)$ the conditional distribution of $U_i$ given $U_0=u_0$ for $i=1,\dots ,d$. It is easy to see that the distribution of $(U_1,\dots ,U_d)$, called a one-factor copula, is given by

$$\begin{aligned} C(u_1,\dots ,u_d)=\int _0^1 C_{1|0}(u_1|u_0) \dots C_{d|0}(u_d|u_0) \, du_0. \end{aligned}$$

(1)

The copulas $C_{0i}$ are called the linking copulas because they link the factor $U_0$ to the variables of interest $U_i$. The one-factor model has many advantages to address high-dimensional problems. We recall and briefly discuss them below.

Nonexchangeability The one-factor model is nonexchangeable. Recall that a copula C is said to be exchangeable if $C(u_1,\dots ,u_d)=C(u_{\pi (1)},\dots ,u_{\pi (d)})$ for any permutation $\pi$ of $(1,\dots ,d)$. This means in particular that all the bivariate marginal distributions are equal to each other. For example, Archimedean copulas are exchangeable copulas. Needless to say, this assumption may be too strong in practice.

Parsimony The one-factor model is parsimonious. Indeed, only d linking copulas are involved in the construction of the one-factor model, and since they are typically governed by one or two parameters, the number of parameters in total increases only linearly with the dimension. Parsimony is more and more desirable as the dimension increases.

Random generation The conditional independence property of the one-factor model allows us to easily generate data $(U_1,\dots ,U_d)$ from this copula.

• 1 Generate $U_0,V_1,\dots ,V_d$ independent standard uniform random variables.

• 2 For $i=1,\dots ,d$, put $U_i=C_{i|0}^{-1}(V_i|U_0)$ where $C_{i|0}^{-1}(\; .\; |U_0)$ denotes the inverse of $v\mapsto C_{i|0}(v|U_0)$.

Dependence properties of the one-factor model have been studied in Krupskii and Joe (2013). The authors investigated how positive dependence properties of the linking copulas extend to the bivariate margins

$$\begin{aligned} C_{ij}(u_i,u_j):=C(1,\dots ,1,u_i,1,\dots ,1,u_j,1,\dots ,1). \end{aligned}$$

These properties included positive quadrant dependence, increasing in the concordance ordering, stochastic increasing, and tail dependence. For details about these dependence concepts, see Joe (2001) Sect. 2. The copulas proposed in this paper, presented in Sects. 2.2 and 2.4, admit simple expressions, and therefore the properties mentioned above can be made more specific.

2.2 Construction and properties of FDG copulas

The class of FDG copulas is constructed by choosing appropriate linking copulas for the one-factor copula model (1). The class of linking copulas which served to build the FDG copulas is referred to as the Durante class Durante (2006) of bivariate copulas, which can also be viewed as part of the framework of Amblard and Girard (2009). The Durante class consists of the copulas C of the form:

$$\begin{aligned} C(u,v)=\min (u,v)f(\max (u,v)), \end{aligned}$$

(2)

where $f:[0,1]\rightarrow [0,1]$, called the generator of C, is a differentiable and increasing function such that $f(1)=1$ and $t\mapsto f(t)/t$ is decreasing. The FDG acronym thus stands for “one-Factor copula with Durante Generators”. The advantages of taking Durante linking copulas are twofold: the integral (1) can be calculated, and the resulting multivariate copula is nonparametric.

Theorem 1

Let C be defined by (1) and assume that $C_{0i}$ belongs to the Durante class (2) with given generator $f_i$. Then

$$\begin{aligned}&C(u_1,\dots ,u_d)\nonumber \\&\quad =u_{(1)}\left[ \left( \prod _{j=2}^d u_{(j)} \right) \int _{u_{(d)}}^1 \prod _{j=1}^d f_j'(x)dx\right. \nonumber \\&\qquad + f_{(1)}(u_{(2)})\left( \prod _{j=2}^d f_{(j)}\left( u_{(j)}\right) \right) + \sum _{k=3}^d \left( \prod _{j=2}^{k-1} u_{(j)} \right) \nonumber \\&\qquad \left. \left( \prod _{j=k}^d f_{(j)}\left( u_{(j)}\right) \right) \int _{u_{(k-1)}}^{u_{(k)}} \prod _{j=1}^{k-1} f_{(j)}'(x)dx \right] , \end{aligned}$$

(3)

where $u_{(i)}:=u_{\sigma (i)},\,f_{(i)}:=f_{\sigma (i)}$ and $\sigma$ is the permutation of $(1,\dots ,d)$ such that $u_{\sigma (1)}\le \dots \le u_{\sigma (d)}$.

In expression (3), we use the convention that the $\sum _{k=3}^d$ is zero when $d=2$. The particularity of the copula expression (3) is that it depends on the generators through their reordering underlain by the permutation $\sigma$. For instance, with $d=3$ and $u_1<u_3<u_2$ we have $u_{(1)}=u_1,\,u_{(2)}=u_3,\,u_{(3)}=u_2$, $\sigma =\{1,3,2\}$ and $f_{(1)}=f_{\sigma (1)}=f_1,\,f_{(2)}=f_{\sigma (2)}=f_3,\,f_{(3)}=f_{\sigma (3)}=f_2$. This feature gives its flexibility to the model. Observe also that $C(u_1,\dots ,u_d)$ writes as $u_{(1)}$ multiplied by a functional of $u_{(2)},\dots ,u_{(d)}$, form that is similar to (2). Although the expression of a FDG copula has the merit to be explicit, it is rather cumbersome. Hence, we shall continue its analysis through the prism of its bivariate margins.

Proposition 1

Let $C_{ij}$ be a bivariate margin of the FDG copula (3). Then $C_{ij}$ belongs to the Durante class (2) with generator

$$\begin{aligned} f_{ij}(t) = f_i(t)f_j(t)+t\int _{t}^1f_i'(x)f_j'(x)dx. \end{aligned}$$

In other words,

$$\begin{aligned} C_{ij}(u_i,u_j)=C_{f_{ij}}(u_i,u_j)=\min (u_i,u_j)f_{ij}(\max (u_i,u_j)). \end{aligned}$$

In view of Proposition 1, the FDG copula can be regarded as a multivariate generalization of the Durante class of bivariate copulas. In fact, such a generalization was already proposed in the literature Durante et al. (2007):

$$\begin{aligned} C_f(u_1,\dots ,u_d)=u_{(1)}\prod _{i=2}^d f(u_{(i)}), \end{aligned}$$

where f is a generator in the usual sense of the Durante class of bivariate copulas. Nonetheless, since there is only one generator to determine the whole copula in arbitrary dimension, this generalization lacks flexibility to be used in applications. This issue is overcome by the FDG copula. To illustrate this further, its pairwise dependence coefficients are given next. Note that, since the bivariate margins of the FDG copula belong to the Durante class of bivariate copulas, a more detailed account of their properties can be found in the original paper Durante (2006). Recall that the Spearman’s rho $\rho$, the Kendall’s tau $\tau$, and the lower $\lambda ^{(L)}$ and upper $\lambda ^{(U)}$ tail-dependence coefficients of a general bivariate copula C are, respectively, given by

$$\begin{aligned}&\rho =\displaystyle \ 12\int _{[0,1]^2}C(u,v)dudv-3, \\&\tau =4\int _{[0,1]^2}C(u,v)dC(u,v)-1, \\&\lambda ^{(L)}=\displaystyle \lim _{u \downarrow 0} \frac{C(u,u)}{u}, \text { and }\\&\lambda ^{(U)}=\lim _{u \uparrow 1} \frac{1-2u+C(u,u)}{1-u}. \end{aligned}$$

In the case where C belongs to the Durante class with generator f, these coefficients are, respectively, given by

$$\begin{aligned}&\rho =\displaystyle 12\int _0^1x^2f(x)dx-3,\,&\tau =4\int _0^1xf(x)^2dx-1, \\&\lambda ^{(L)}=f(0),\text { and }&\lambda ^{(U)}=1-f'(1). \end{aligned}$$

Hence, to get the dependence coefficients of the FDG bivariate margins, it is enough to apply the above formulas and Proposition 1. The obtained coefficient expressions are given in Proposition 2 below.

Proposition 2

The Spearman’s rho, the Kendall’s tau, the lower and upper tail-dependence coefficients of the FDG bivariate margins $C_{ij}$ are, respectively, given by

$$\begin{aligned}&\rho _{ij}=12\int _0^1x^2f_i(x)f_j(x)dx+3\int _0^1x^4f_i'(x)f_j'(x)dx-3, \\&\tau _{ij}=4\int _0^1x\left( f_i(x)f_j(x)+x\int _x^1f_i'(t)f_j'(t) dt\right) ^2 dx-1, \\&\lambda _{ij}^{(L)}=\lambda _i^{(L)}\lambda _j^{(L)} \text { and } \\&\lambda _{ij}^{(U)}=\lambda _{i}^{(U)}\lambda _{j}^{(U)}, \end{aligned}$$

where $\lambda _i^{(L)}:=f_i(0),\,\lambda _{i}^{(U)}:=1-f_i'(1),\,i=1,\dots ,d$, are the lower and upper tail-dependence coefficients of the bivariate linking copulas, respectively.

2.3 Examples of parametric families

Four examples of families indexed by a real parameter for the generators $f_1,\dots ,f_d$ are given below.

Example 1

(Cuadras-Augé generators) In (3), let

$$\begin{aligned} f_i(t)=t^{1-\theta _i}, \quad \theta _i\in [0,1]. \end{aligned}$$

(4)

A copula belonging to the Durante class with generator (4) gives rise to the well known Cuadras-Augé copula with parameter $\theta _i$ Cuadras and Augé (1981). By Proposition 1, the generator for the bivariate margin $C_{ij}$ of the FDG copula is given by

$$\begin{aligned}&f_{ij}(t)\\&\quad =\left\{ \!\begin{array}{rl} t^{2-\theta _i-\theta _j}\left( 1-\frac{(1-\theta _i)(1-\theta _j)}{1-\theta _i-\theta _j}\right) +t\frac{(1-\theta _i)(1-\theta _j)}{1-\theta _i-\theta _j} &{} \text {if } \theta _i+\theta _j\ne 1 \\ t(1\!-\!(1\!-\!\theta )\theta \log t) &{} \text {if }\theta \!:=\!\theta _j\!=\!1\!-\!\theta _i. \end{array}\right. \end{aligned}$$

The Spearman’s rho, and the lower and upper tail-dependence coefficients are, respectively, given by

$$\begin{aligned} \rho _{ij}=\frac{3\theta _i\theta _j}{5-\theta _i-\theta _j}, \, \lambda _{ij}^{(L)}=0 \text { and } \lambda _{ij}^{(U)}=\theta _i\theta _j. \end{aligned}$$

The Kendall’s tau is given by

$$\begin{aligned} \tau _{ij}=\left\{ \begin{array}{rl} \displaystyle \frac{ \theta _i\theta _j(\theta _i\theta _j+6-2(\theta _i+\theta _j))}{(\theta _i+\theta _j)^2-8(\theta _i+\theta _j)+15} &{}\displaystyle \text { if } \theta _i+\theta _j \ne 1 \\ \displaystyle \frac{\theta (\theta -1)(\theta ^2-\theta -4)}{8} &{}\displaystyle \text { if } \theta :=\theta _i=1-\theta _j. \end{array}\right. \end{aligned}$$

Example 2

(Fréchet generators) In (3), let

$$\begin{aligned} f_i(t)=(1-\theta _i)t+\theta _i, \quad \theta _i \in [0,1]. \end{aligned}$$

(5)

A copula belonging to the Durante class with generator (5) gives rise to the well-known Fréchet copula with parameter $\theta _i$ Fréchet (1958). By Proposition 1, the generator for the bivariate margin $C_{ij}$ of the FDG copula is given by

$$\begin{aligned} f_{ij}(t)=\left( 1-\theta _i\theta _j\right) t+\theta _i\theta _j. \end{aligned}$$

By noting that $f_{ij}$ is of the form (5) with parameter $\theta _i\theta _j$, one can see that the bivariate margins of the FDG copula based on Fréchet generators are still Fréchet copulas. The Spearman’s rho, and the lower and upper tail-dependence coefficients are, respectively, given by

$$\begin{aligned} \rho _{ij}=\lambda _{ij}^{(L)}=\lambda _{ij}^{(U)}=\theta _i\theta _j, \end{aligned}$$

the Kendall’s tau is given by

$$\begin{aligned} \tau _{ij}=\frac{\theta _i\theta _j(\theta _i\theta _j+2)}{3}. \end{aligned}$$

Example 3

(Durante-sinus generators) In (3), let

$$\begin{aligned} f_i(t)=\frac{\sin (\theta _i t)}{\sin (\theta _i)},\quad \theta _i\in (0,\pi /2]. \end{aligned}$$

(6)

This generator was proposed in Durante (2006). By Proposition 1, the generator for the bivariate margin $C_{ij}$ of the FDG copula is given by

$$\begin{aligned} f_{ij}(t)&= \frac{\sin (\theta _it)\sin (\theta _jt)}{\sin (\theta _i)\sin (\theta _j)}\\&\quad + \frac{t \theta _i\theta _j}{{2(\theta _j^2-\theta _i^2)}\sin (\theta _i)\sin (\theta _j)}\\&\quad \times \Bigg \{ (\theta _i+\theta _j)\left[ \sin \left( (\theta _i-\theta _j)t\right) +\sin \left( \theta _j-\theta _i\right) \right] \\&\quad +(\theta _j-\theta _i)\left[ \sin (\theta _i+\theta _j) -\sin \left( (\theta _i+\theta _j)t\right) \right] \Bigg \} \text { if }\theta _i\ne \theta _j, \\&\quad \text {and }f_{ij}(t) \!=\! \frac{ 4 \sin (t\theta )^2 + t\theta \left( 2(1\!-\!t)\theta +\sin (2\theta )\!-\!\sin (2t\theta ) \right) }{ 4 \sin (\theta )^2 } \\&\quad \text { if } \theta _i=\theta _j=:\theta . \end{aligned}$$

The Spearman’s rho, and the lower and upper tail-dependence coefficients are, respectively, given by

$$\begin{aligned} \rho _{ij}&=12 (\sin \theta _i\sin \theta _j)^{-1} \int _0^1 x^2\sin (\theta _ix)\sin (\theta _jx)\nonumber \\&\quad + \frac{1}{4}\theta _i\theta _jx^4\cos (\theta _ix)\cos (\theta _jx)dx -3, \end{aligned}$$

(7)

$$\begin{aligned} \lambda _{ij}^{(L)}&=0 \text { and } \lambda _{ij}^{(U)}=\left( 1-\frac{\theta _i}{\tan (\theta _i)}\right) \left( 1-\frac{\theta _j}{\tan (\theta _j)}\right) . \end{aligned}$$

(8)

Example 4

(Durante-exponential generators) In (3), let

$$\begin{aligned} f_i(t)=\exp \left( \frac{t^{\theta _i}-1}{\theta _i}\right) , \quad \theta _i >0 \end{aligned}$$

(9)

This generator was proposed in Durante (2006). By Proposition 1, the generator for the bivariate margin $C_{ij}$ of the FDG copula is given by

$$\begin{aligned} f_{ij}(t)&=\exp \left( \frac{t^{\theta _i}-1}{\theta _i}+\frac{t^{\theta _j}-1}{\theta _j} \right) \\&\quad + t\int _t^1 \exp \left( \frac{x^{\theta _i}-1}{\theta _i}+\frac{x^{\theta _j}-1}{\theta _j} \right) x^{\theta _i+\theta _j-2} dx. \end{aligned}$$

The Spearman’s rho, and the lower and upper tail-dependence coefficients are, respectively, given by

$$\begin{aligned}&\rho _{ij}=12\int _0^1\exp \left( \frac{x^{\theta _i}-1}{\theta _i}+ \frac{x^{\theta _j}-1}{\theta _j}\right) \\&\quad \quad \,\,\times \left( x^2+\frac{1}{4}x^{2+\theta _i+\theta _j}\right) dx-3, \\&\lambda _{ij}^{(L)}=\exp \left( -\frac{1}{\theta _i}-\frac{1}{\theta _j}\right) , \text { and } \lambda _{ij}^{(U)}=0. \end{aligned}$$

Remark 1

The calculation of the integral in (7) with $\theta _i=\theta _j=\pi /2$ shows that for the FDG copula with Durante-sinus generators, the Spearman’s rho is such that

$$\begin{aligned} 0 \le \rho _{ij} \le \frac{3\pi ^4-100\pi ^2+840}{40\pi ^2} \simeq 0.37. \end{aligned}$$

The Spearman’s rho values for all the other models in the examples above spread the entire interval [0, 1].

The four above examples allow us to get all possible types of tail dependencies, as shown in Table 1. The Cuadras-Augé and Durante-sinus families allow for upper but no lower tail dependence, the Durante-exponential family allows for lower but no upper tail dependence, and the Fréchet family allows for both. In the Fréchet case, furthermore, the lower and upper tail-dependence coefficients are equal: this is called tail symmetry, a property of elliptical copulas.

Table 1 Lower $\lambda ^{(L)}_{ij}$ and upper $\lambda _{ij}^{(U)}$ tail-dependence coefficients for the four families presented in Sect. 2.3

2.4 Extreme-value attractors associated to FDG copulas

Extreme-value copulas are theoretically well-grounded copulas to perform a statistical analysis of extreme values such as maxima of random samples. Recall that a copula $C_{\#}$ is an extreme-value copula if there exists a copula $\tilde{C}$ such that

$$\begin{aligned} C_{\#}\left( u_1,\dots ,u_d\right)&=\underset{n\uparrow \infty }{\lim }\widetilde{C}^n\left( u_1^{1/n},\dots ,u_d^{1/n}\right) , \nonumber \\&\quad \left( u_1,\dots ,u_d\right) \in [0,1]^d, \end{aligned}$$

(10)

see, e.g., Gudendorf and Segers (2010). The extreme-value copula $C_{\#}$ is called the attractor of $\widetilde{C}$ and $\widetilde{C}$ is said to belong to the domain of attraction of $C_{\#}$. The class of extreme-value copulas corresponds exactly to the class of max-stable copulas, that is, the copulas $C_{\#}$ such that

$$\begin{aligned}&C_{\#}^n\left( u_1^{1/n},\dots ,u_d^{1/n}\right) =C_{\#}(u_1,\dots ,u_d) ,\quad n \ge 1, \\&\quad (u_1,\dots ,u_d)\in [0,1]^d. \end{aligned}$$

The upper tail-dependence coefficient of a (bivariate) extreme-value copula $C_{\#}$ has the particular form

$$\begin{aligned} \lambda ^{(U)}=2+\log C_{\#}(e^{-1},e^{-1}). \end{aligned}$$

(11)

This coefficient is a natural dependence coefficient for extreme-value copulas because of the following representation on the diagonal of the unit square:

$$\begin{aligned} C_{\#}(u,u)=u^{2-\lambda }, \end{aligned}$$

(12)

where $\lambda := \lambda ^{(U)}$. If $\lambda =0$ then $C_{\#}(u,u)=\Pi (u,u)=u^2$, where $\Pi$ stands for the independence copula. If $\lambda =1$ then $C_{\#}(u,u)=M(u,u)=\min (u,u)=u$, where M stands for the Fréchet-Hoeffding upper bound for copulas, that is, the case of perfect dependence. In the case of extreme-value copulas, this interpolation between $\Pi$ and M allows us to interpret $\lambda$ as a coefficient that measures general dependence, not only dependence in the tails. In order to emphasize this interpretation, $\lambda$ will be referred to as the extremal dependence coefficient of an extreme-value copula. See Coles (2001) for more about extreme-value statistics, and, see, e.g., Gudendorf and Segers (2010) for an account about extreme-value copulas.

In the case of FDG copulas, the limit (10) can be calculated. This leads to a new family of extreme-value copulas, referred to as the EV-FDG family. The bivariate margins $C_{\#,ij}$ of this new family are Cuadras-Augé copulas. These results are specified in Theorem 2 and Proposition 3 below.

Theorem 2

Assume that the generators $f_i$ of the FDG copula are twice continuously differentiable on [0, 1]. Then, the attractor $C_{\#}$ of the FDG copula exists and is given by

$$\begin{aligned} C_{\#}(u_1,\dots ,u_d)=\prod _{i=1}^d u_{(i)}^{\chi _i}, \end{aligned}$$

(13)

where

$$\begin{aligned} \chi _i=\left( \prod _{j=1}^{i-1}(1-\lambda _{(j)})\right) \lambda _{(i)}+1-\lambda _{(i)}, \end{aligned}$$

with the convention that $\prod _{j=1}^{0}(1-\lambda _{(j)})=1$ and where $\lambda _i=1-f'_{i}(1)$. As in (3), $u_{(i)}=u_{\sigma (i)}$ and $f_{(i)}'(1)=f_{\sigma (i)}'(1)$ where $\sigma$ is the permutation of $(1,\dots ,d)$ such that $u_{(1)}\le \dots \le u_{(d)}$.

Proposition 3

Let $C_{\#,ij}$ be a bivariate margin of the EV-FDG copula (13). Then $C_{\#,ij}$ is a Cuadras-Augé copula with parameter (and therefore extremal dependence coefficient) $\lambda _{i}\lambda _{j}$. In other words,

$$\begin{aligned} C_{\#,ij}(u_i,u_j)=\min (u_i,u_j)\max (u_i,u_j)^{1-\lambda _i\lambda _j}. \end{aligned}$$

(14)

Remark 2

In view of Table 1, the FDG copulas with Cuadras-Augé and Fréchet generators both lead to the same EV-FDG copula.

Multivariate generalizations of the bivariate Cuadras-Augé copula were already proposed in the literature Mai and Scherer (2009), Durante and Salvadori (2010), but they are less flexible than EV-FDG. Indeed, let us consider the following exchangeable copula proposed in Mai and Scherer (2009):

$$\begin{aligned} A(u_1,\dots ,u_d)=u_{(1)}\prod _{i=2}^d u_{(i)}^{a_i}, \end{aligned}$$

where $(a_1=1,a_2,a_3,\dots ,a_d)$ is a d-monotone sequence of real numbers, that is, a sequence which satisfies $\triangledown ^{j-1}a_k\ge 0, \, k=1,\dots ,d, \, j=1,\dots ,d-k+1$ where $\triangledown ^{j}a_k=\sum _{i=0}^j(-1)^i\left( {\begin{array}{c}j\\ i\end{array}}\right) a_{k+i},\,j,k\ge 1$ and $\triangledown ^0a_k=a_k$. In particular, the bivariate margins are Cuadras-Augé copulas

$$\begin{aligned} A_{ij}(u_i,u_j)=\min (u_i,u_j)\max (u_i,u_j)^{a_2} \end{aligned}$$

with the same parameter $1-a_2$. This means that all of them exhibit the same statistical behavior. For instance, all the upper tail-dependence coefficients are equal and are given by $1-a_2$. This is far too restrictive for most applications. Then let us consider the generalization proposed in Durante and Salvadori (2010):

$$\begin{aligned} B(u_1,\dots ,u_d)=\prod _{i=1}^d u_i^{1-\sum _{j=1,j\ne i}^d\lambda _{ij}} \prod _{i<j}\min (u_i,u_j)^{\lambda _{ij}}, \end{aligned}$$

where $\lambda _{ij}\in [0,1], \lambda _{ij}=\lambda _{ji}$ and

$$\begin{aligned} \sum _{j=1,\dots ,d;\, j\ne i}\lambda _{ij}\le 1, \quad i=1,\dots ,d. \end{aligned}$$

(15)

The bivariate margins $B_{ij}$ are Cuadras-Augé copulas

$$\begin{aligned} B_{ij}(u_i,u_j)=\min (u_i,u_j)\max (u_i,u_j)^{1-\lambda _{ij}} \end{aligned}$$

with parameters $\lambda _{ij}$. Unlike the copula A, the tail-dependence coefficients can take distinct values. Unfortunately, the constraints (15) are quite restrictive, as it was already stressed by the original authors in Durante and Salvadori (2010). The EV-FDG class achieves greater flexibility than these competitors. In particular, one can obtain different bivariate marginal distributions with no conditions on the parameters.

3 Parametric inference

Let $(X_1,\dots ,X_d)$ be a random vector following a distribution F with continuous margins $F_1,\dots ,F_d$. Suppose that its copula, C, is a FDG copula defined by (3). Denote by $(X_1^{(k)},\dots ,X_d^{(k)})$, $k=1,\dots ,n$ independent and identically distributed observations obtained from F. Suppose that all the generators $f_i$ of the FDG copula belong to the same parametric family $\{f_{\theta },\,\theta \in \Theta \subset \mathbb {R}\}$, that is, there exists $\varvec{\theta }_0=(\theta _{01},\dots ,\theta _{0d})\in \Theta ^{d}$ such that $f_{\theta _{0i}}=f_i$. The generators $f_i$ are regarded as functions defined over the product space $[0,1]\times \Theta$ and we write $f_i(t)=f(t,\theta _i)$ for all t in [0, 1]. The nonparametric inference problem has turned into a parametric one where the parameter vector $\varvec{\theta }_0 \in \Theta ^{d}$ has to be estimated.

In order to estimate the parameters of the FDG and EV-FDG copulas, a least-squares estimator based on dependence coefficients is adopted. This estimation strategy was considered in various articles, see  e.g.,  Klüppelberg and Kuhn (2009), Genest and Rivest (1993), Genest and Favre (2007), Genest et al. (2011), Hwan Oh and Patton (2013), Mazo et al. (2014), Durante and Salvadori (2010). Its construction is recalled below. Let us choose a type of dependence coefficient (Spearman’s rho, Kendall’s tau, tail-dependence coefficient, etc.), and let us denote by $r(\theta _i,\theta _j)$ the chosen dependence coefficient between the variables $X_i$ and $X_j$. Suppose that the map r is continuous and symmetric in its arguments. Let $p=d(d-1)/2$ be the number of variable pairs $(X_i,X_j),\, i<j$. Denote by $\mathbf {r}$ be the p-variate map defined on $\Theta ^d$ such that $\mathbf {r}(\theta _1,\dots ,\theta _d)=(r(\theta _1,\theta _2),\dots ,r(\theta _{d-1},\theta _{d}))$. The least-squares estimator based on dependence coefficients is defined as

$$\begin{aligned} \hat{\varvec{\theta }}=\underset{\varvec{\theta }\in \Theta ^d}{\arg \min }&\left\| \hat{\mathbf {r}}-\mathbf {r}(\varvec{\theta })\right\| ^2, \end{aligned}$$

(16)

where the quantity $\hat{\mathbf {r}}=(\hat{r}_{1,2},\dots ,\hat{r}_{d-1,d})$ is an empirical estimator of $\mathbf {r}(\varvec{\theta _0})$. To be more specific, $r(\theta _i,\theta _j)$ may be the Spearman’s rho (4) of $(X_i,X_j)$ and

$$\begin{aligned} \hat{r}_{i,j}=\frac{ \sum _{k=1}^{n}\left( \hat{U}_i^{(k)}-\overline{\hat{U}}_i\right) \left( \hat{U}_j^{(k)}-\overline{\hat{U}}_j\right) }{\left[ \sum _{k=1}^{n}\left( \hat{U}_i^{(k)}-\overline{\hat{U}}_i\right) ^2 \sum _{k=1}^{n}\left( \hat{U}_j^{(k)}-\overline{\hat{U}}_j\right) ^2 \right] ^{1/2}}, \end{aligned}$$

(17)

where $\overline{\hat{U}}_i=\sum _{k=1}^n U_i^{(k)}/n$ and $\hat{U}_i^{(k)}=\sum _{l=1}^n\mathbf {1}(X_i^{(l)} \le X_i^{(k)})/(n+1)$. In the case where $r(\theta _i,\theta _j)$ is the Kendall’s tau (4) of $(X_i,X_j)$, then

$$\begin{aligned} \hat{r}_{i,j}=\left( {\begin{array}{c}n\\ 2\end{array}}\right) ^{-1} \sum _{k<l}\text {sign} \left( \left( X_i^{(k)}-X_i^{(l)}\right) \left( X_j^{(k)}-X_j^{(l)}\right) \right) , \end{aligned}$$

(18)

where $\text {sign}(x)=1$ if $x>0$, $-1$ if $x<0$ and 0 if $x=0$. Eq. (12) suggests that the extremal dependence coefficient can also be used to estimate the parameters of an extreme-value copula. If the margins $F_i$ are known, various empirical estimators of the extremal dependence exist. For instance, assuming that C is an extreme-value copulas, Ferreira (2013) introduced

$$\begin{aligned} \hat{r}_{i,j}=3 - \frac{1}{1-\sum _{k=1}^n\max (U_i^{(k)},U_j^{(k)})/n}, \end{aligned}$$

(19)

where $U_i^{(k)}=F_i(X_i^{(k)})$.

In the context of non-absolutely continuous copulas with respect to the Lebesgue measure—as FDG copulas—, asymptotic properties of (16) were derived in Mazo et al. (2014), see the proposition below.

Proposition 4

Suppose that the following assumptions hold.

• (A1) $\sqrt{n}( \hat{\mathbf {r}}- \mathbf {r}(\varvec{\theta _0}) ) \overset{d}{\rightarrow } N(\mathbf {0}, \varvec{\Sigma })$ as $n\rightarrow \infty$ for some symmetric and positive definite matrix $\varvec{\Sigma }$.

• (A2) The map $\mathbf {r}$ is a twice continuously differentiable homeomorphism from $\Theta ^d$ to its image $\mathbf {r}(\Theta ^d)$.

• (A3) The Jacobian matrix $\mathbf {J}$ of the map $\mathbf {r}$ at $\varvec{\theta _0}$ is of full rank.

Then, as $n\rightarrow \infty$, the estimator $\hat{\varvec{\theta }}$ defined in (16) is unique with probability tending to one, consistent for $\varvec{\theta _0}$, and asymptotically normal

$$\begin{aligned}&\sqrt{n}( \hat{\varvec{\theta }}- \varvec{\theta _0}) \overset{d}{\rightarrow } N(\mathbf {0},\varvec{\Xi }), \\&\quad \text {where } \varvec{\Xi }=\left( \mathbf {J}^T \mathbf {J}\right) ^{-1} \mathbf {J}^T \varvec{\Sigma } \mathbf {J} \left( \mathbf {J}^T \mathbf {J}\right) ^{-1}. \end{aligned}$$

There exist various situations where (A1) holds, as, for instance, in the context of Spearman’s rho (estimator (17)) and Kendall’s tau dependence coefficients (estimator (18)), see Hoeffding (1948) for a proof. In the context of extreme-value copulas with known margins, (A1) also holds for the extremal dependence coefficient (estimator (19)), see Mazo et al. (2014) for a proof.

The remainder of this section is devoted to show that, for certain (EV-)FDG copulas, we are able to show that the assumptions of Proposition 4 hold.

Lemma 1

• (i) Define the univariate function $r_{\theta _j}(\theta _i):=r(\theta _i,\theta _j)$ and assume that it is a twice continuously differentiable homeomorphism. Let $r_{1,2},\dots ,r_{d-1,d}$ be p elements of $\mathbf {r}(\Theta ^d)$. Define $s_{i,j}(\theta ):=r^{-1}_{\theta }(r_{i,j})$ for $\theta \in \Theta$. Then, the function $s_{1,3}\circ s_{1,2}\circ s_{2,3}$ has at least one fix point, that is, the equation

  $$\begin{aligned} s_{1,3}\circ s_{1,2}\circ s_{2,3}(\theta ) = \theta , \quad \theta \in \Theta \end{aligned}$$

  (20)

  has at least one solution.

• (ii) If, moreover, the function $s_{1,3}\circ s_{1,2}\circ s_{2,3}$ has exactly one fix point, that is, Eq. (20) has exactly one solution, then Assumptions (A2) and (A3) of Proposition 4 hold.

Remarking that the extremal dependence coefficients of the EV-FDG bivariate margins write $\lambda _{i,j}(\varvec{\theta })=\lambda (\theta _i)\lambda (\theta _j)$, with $\lambda (\theta )=1-\frac{\partial f(t,\theta )}{\partial t}\Big \vert _{t=1}$, $\theta \in \Theta$, allows us to apply Lemma 1 and therefore to satisfy the assumptions of Proposition 4. The next theorem thus provides some situations where the least-squares estimator is unique with probability tending to one, consistent, and asymptotically Gaussian.

Theorem 3

• (i) Assume that $(X_1,\dots ,X_d)$ has EV-FDG (13) as copula and let $r(\theta _i,\theta _j)$ be the extremal dependence coefficient of $(X_i,X_j)$. Consider one of the following cases:

  • The generators are Cuadras-Augé (4) and $\Theta =(0,1)$.

  • The generators are Fréchet (5) and $\Theta =(0,1)$.

  • The generators are Durante-sinus (6) and $\Theta =(0,\pi /2)$.

  Then, Assumptions (A1), (A2), and (A3) of Proposition 4 hold with $\hat{\mathbf {r}}$ being as in (19).

• (ii) Assume that the copula of $(X_1,\dots ,X_d)$ belongs to the class of FDG copulas given in Example 2 and suppose that $r(\theta _i,\theta _j)$ is Spearman’s rho coefficient of $(X_i,X_j)$ and $\hat{\mathbf {r}}$ is as in (17). Then, assumptions (A1), (A2), and (A3) of Proposition 4 hold.

4 Applications to simulated and real datasets

The modeling of data with (EV-)FDG copulas is illustrated through numerical experiments in Sect. 4.1 and a real dataset application in Sect. 4.2. In the numerical experiments, we first provide empirical evidence that the proposed FDG copulas are well suited for high-dimensional applications. In the real dataset application, critical levels of potentially dangerous hydrological events are estimated. Throughout this section, the four copulas of Example 1–4, are, respectively, referred to as FDG-CA, FDG-F, FDG-sinus, and FDG-exponential.

The minimization of the loss function (16) was carried out with standard gradient descent algorithms whose implementations can be found in the function optim from the R software R Core Team (2013). In principle, several runs with different starting points should be tested to ensure that the global minimizer is reached. Also, formal statistical procedures can be performed to test wether the given minimizer is indeed the global minimizer; see, e.g., (de Carvalho 2011, 2012; Veall 1990). We found that a single run was enough to find what appeared to be the global optimum. Thus, the loss functions one encounters when dealing with FDG copulas seem to be easy to minimize in practice. All the experiments were conducted using the FDG package that we developed and which is freely available on the CRAN archive at http://cran.r-project.org/web/packages/FDG.

4.1 Numerical experiments

Our first goal is to investigate the numerical behavior of the estimation of FDG copulas as the sample size varies from $n=10$ to $n=500$ with fixed $d=9$ (as in the real dataset application). To this aim, 200 datasets are simulated from each of the copulas FDG-CA, FDG-F, FDG-sinus, and FDG-exponential. The coordinates of the parameter vector were chosen to be regularly spaced within [0.3, 0.9], [0.3, 0.9], [1, 1.55] and [3, 20] for FDG-CA, FDG-F, FDG-sinus, and FDG-exponential, respectively. For each replication and each model, the samples are simulated from the copula using the principle described in Sect. 2. The model parameters are estimated by the least squares estimator (16) combined with Spearman’s rho dependence coefficient as in (17). The accuracy of the method is assessed using the mean absolute error and the relative mean absolute error, respectively, defined as

$$\begin{aligned} \text {MAE}_{r}= & {} \frac{1}{p} \sum _{i<j} \vert r_{i,j}-r(\hat{\theta }_i,\hat{\theta }_j) \vert \text { and } \\ \text {RMAE}= & {} \frac{1}{d} \sum _{i=1}^d \frac{\vert \hat{\theta }_i-\theta _{0i} \vert }{\theta _{0i}}, \end{aligned}$$

computed and averaged over the replications. It appears on Fig. 1 that the MAE$_\rho$s are very stable whatever the sample size. FDG-CA, FDG-F, and FDG-sinus models also provide good results in terms of RMAE provided that the sample size is larger than $n=30$. At the opposite, it seems that the estimation of FDG-exponential model requires large sample sizes.

Fig. 1

Fitting errors as a function of the sample size n for a dimension $d=9$. Continuous line (1): MAE$_\rho$, Dashed line (2): RMAE. Four copulas were tested (FDG-CA: upper left, FDG-exponential: upper right, FDG-F: lower left, FDG-Sinus: lower right)

The second experiment examines the scalability of the FDG copulas when the dimension increases from $d=10$ to $d=50$ for a fixed sample size $n=500$. Similarly to the previous experiment, the coordinates of the parameter vector were chosen to be regularly spaced within [0.3, 0.9], [0.3, 0.9], [1, 1.55] and [3, 20] for FDG-CA, FDG-F, FDG-sinus, and FDG-exponential, respectively. It appears on Fig. 2 that the MAE$_\rho$s and RMAEs are very stable whatever the dimension. The inference for these models seems not to be sensitive to the dimension. FDG-exponential has a larger RMAE, but it is still below 17 %, and its MAE$_{\rho }$ is as good as that of the other models.

Fig. 2

Fitting errors as a function of the dimension d for a sample size $n=500$. Continuous line (1): MAE$_\rho$, Dashed line (2): RMAE. Four copulas were tested (FDG-CA: upper left, FDG-exponential: upper right, FDG-F: lower left, FDG-Sinus: lower right)

Figure 3 displays the associated computed times for one sample on a 8 GiB memory and 3.20 GHz processor computer. The simulation time increases linearly with the dimension whereas the estimation time increases exponentially. Simulating all the models even in high dimension is instantaneous because of the conditional independence property seen in (1). Less than two minutes are necessary to fit all the models. In particular, simulating or fitting FDG-F is instantaneous. The computational costs for performing the inference of FDG-exponential and FDG-sinus are larger because their dependence coefficient expressions, given in Example 3 and 4, involve integrals which have to be computed numerically. To summarize, FDG copulas seem to scale up well.

Fig. 3

Computation times (in milliseconds) as a function of the dimension d for a sample of size $n=500$. Left panel: Simulation of the copula, right panel: Estimation of the parameters. Four copulas were tested (C: FDG-CA, F: FDG-F, S: FDG-Sinus, E: FDG-exponential)

4.2 Application to a hydrological dataset

4.2.1 Data and context

The dataset consists of $n=32$ observations $(X_1^{(k)},\dots ,X_d^{(k)}), k=1,\dots ,n$, of annual maxima river flow rates located at $d=9$ sites across south-east France between 1969 and 2007 (some records are missing). Let us denote by F the distribution with continuous margins $F_1,\dots ,F_d$ of the random vector $(X_1,\dots ,X_d)$ whose realizations provide the observed dataset. The location of the sites are shown in Fig. 4. The number of variable pairs is $p=36$. Due to the heterogeneous dispersion of the sites, the span of positive dependence is almost maximum; for instance, Spearman’s rho dependence coefficients range from about 0 to 0.9.

Fig. 4

Location of the nine sites for the flow rate dataset. The sea in dark blue at the bottom (south) is the Mediterranean sea. The rivers are shown in light blue. The river flowing from north to south in the green area is the Rhône. Green indicates low altitude, and orange high altitude. The map of this figure was drawn with Géoportail (www.geoportail.gouv.fr). (Color figure online)

In hydrology, it is of interest to get information about the statistical distribution of a potentially dangerous event, such as $\{F_1(X_1)>q,\dots ,F_d(X_d)>q\}$, or, equivalently, $\{\min (F_1(X_1),\dots ,F_d(X_d))>q\}$, where q is the critical level associated to that event. The return period T is defined as

$$\begin{aligned}&T=\frac{1}{1-M(q)}, \quad \text {where} \nonumber \\&M(q)=P(\min (F_1(X_1),\dots ,F_d(X_d))\le q). \end{aligned}$$

(21)

For instance, a return period of $T=30$ years and a critical level of $q=0.7$ means that each $X_i$ exceeds its quantile of order 70% once every 30 years in average. A common question in the study of extreme events is the following. Given a return period T, how dangerous is the corresponding event? In other words, what is the associated critical level q? The answer is obtained by inverting (21)

$$\begin{aligned} q=M^{-1}\left( 1-\frac{1}{T}\right) . \end{aligned}$$

(22)

Thus, the answer q is the quantile of order $1-1/T$ of the distribution M. This quantile can be estimated empirically from the data and parametrically by fitting a model to the data.

Potentially dangerous events happen with the co-occurrence of extremely high flow rates at several locations. Thus, it is clear that the models to describe this dataset should be upper tail dependent. Hence, good candidates are the copulas of Example 1–3, referred to as FDG-CA, FDG-F, and FDG-sinus, respectively, and all the extreme-value copulas. However, as it was shown in Remark 1, Spearman’s rho of FDG-sinus cannot take values greater than 0.37. Hence, this copula is removed from the candidate models. Hence, the considered models are FDG-CA, FDG-F, and their extreme-value attractor EV-FDG-CAF given in (13) (recall that FDG-CA and FDG-F lead to the same extreme-value copula). Two other popular copula models, the Gumbel and Student copulas, are also fitted to the data. The Gumbel copula is famous among hydrologists Zhang and Singh (2007) and the Student copula is well known in risk management McNeil et al. (2010). They serve as a benchmark for our models. A factor structure is assumed for the Student copula, that is, its (i, j)-th element $(i\ne j)$ of its correlation matrix writes $\theta _i\theta _j$, where $\theta _1,\dots ,\theta _d$ belong to $[-1,1]$. Recall that a Gumbel copula is an extreme-value copula. More details about the Gumbel and the Student copula can be found, respectively, in, e.g., Nelsen (2006), Joe (2001) and Demarta and McNeil (2005).

4.2.2 Method and Results

A practically convenient approach dictated the estimation of the copula parameters. For each copula model, the dependence coefficients with the simplest mathematical forms were chosen to build the loss function (16). In other words, the parameters of FDG-F, FDG-CA, and EV-FDG-CAF were estimated with Spearman’s rho as in (17). The parameters of the Gumbel and Student copulas were estimated with Kendall’s tau as in (18). Finally, the degree of freedom of the Student copula was estimated by maximizing its likelihood but with all the parameters of the correlation matrix held fixed. This approach improves the speed, tractability, and chances of success of the minimization procedure.

The fit of the tested copulas was assessed by comparing the pairwise dependence coefficients and the critical levels.

Pairwise dependence coefficients The mean absolute error (MAE), defined as

$$\begin{aligned} MAE_r=\frac{1}{p}\sum _{i<j}\big \vert \hat{r}_{i,j}-r(\hat{\theta }_i,\hat{\theta }_j)\big \vert \end{aligned}$$

was computed for Spearman’s rho (MAE$_{\rho }$) and Kendall’s tau (MAE$_{\tau }$) dependence coefficients. They are reported in Table 2. The Gumbel copula has the largest errors (more than 0.17) and does not seem to fit the data well. This was expected, because this model has only one parameter to account for a $d=9$ dimensional phenomenon. All the remaining errors are smaller. Thus, according to these criteria, the Gumbel copula is not appropriate.

Table 2 Mean absolute errors for Spearman’s rho ($\hbox {MAE}_{\rho }$) and Kendall’s tau ($\hbox {MAE}_{\tau }$) dependence coefficients of the models

Critical levels The critical levels obtained from the empirical data and the models were calculated by making use of (22). In statistical terms, this amounts to comparison of the quantiles of the distribution M under the empirical data and under the different models. The results are presented in Fig. 5, where the independence copula $C(u_1,\dots ,u_d)=u_1\dots u_d$ was added to emphasize the need for a joint model on such a dataset. The Gumbel model is confirmed to perform poorly. FDG-F, FDG-CA, and EV-FDG-CAF seem to fit the data quite well. In particular, FDG-F and FDG-CA are as close as the Student copula to the empirical curve.

Fig. 5

Critical level q as a function of the return period T. “empirical” stands for the empirical critical levels, and “independence” for the independence copula $C(u_1,\dots ,u_d)=\prod _{i=1}^d u_i$

With such a small sample size $n=32$, one must be extremely careful when looking at empirical data, because one is likely to observe a large deviation from the true underlying statistical distribution. In view of this remark, one should select a statistical model based not only on empirical data, but also on the model properties. The class of FDG copulas is very interesting in this respect. Indeed, the practitioner has with this class three models that fit well the data and with different features: FDG-F is upper, lower, and symmetric tail dependent; FDG-CA is upper tail dependent but no lower tail dependent; and EV-FDG-CAF is an extreme-value copula. The user is then free to choose the model that most suits his expert knowledge about the underlying phenomenon at play. The test of extreme-value dependence Kojadinovic et al. (2011) gave a p-value of 0.21, which means that one does not reject extreme-value copulas at the 5 % level. Of course, as before, one must be extremely careful when looking at the p-value because of the small data sample size. Finally, goodness-of-fit tests for a given parametric family can be found in Kojadinovic and Yan (2011).

5 Discussion

In this article, we have constructed a new class of copulas by combining one-factor copulas, that is, a conditional independent property, together with a class of bivariate copulas called the Durante class of bivariate copulas. This combination led to many advantageous properties. The copulas within the proposed class, referred to as FDG copulas, are tractable, flexible, and cover all types of tail dependencies. The theoretically well-grounded least-squares inference estimator is particularly well suited for FDG copulas because their dependence coefficients are easy to compute, if not in closed form. This allows us to perform fast and reliable inference in the parametric case. We have demonstrated, furthermore, that FDG copulas work well in practice and are able to model both high-dimensional and real datasets. Finally, we have derived the extreme-value copulas (EV-FDG) associated to FDG copulas, yielding a new extreme-value copula, which can be viewed as a generalisation of the well-known Cuadras-Augé copula. This copula benefits from almost all of the many advantageous properties of FDG copulas, and therefore opens the door for statistical analyses of extreme data in high dimension.

One may argue that a model with a singular component, as a FDG copula, is not natural nor realistic to model hydrological data. While this may be true in the bivariate case, this argument becomes weaker when the dimension increases. Indeed, in high-dimensional applications, the focus is less on the distribution itself than on a feature of interest of the data, such as, for instance, the critical levels defined in (22). If the so-called “unrealistic” models are able to better estimate these features than “realistic” models—compare the fit of the Gumbel copula to the fit of FDG copulas in Sect. 4.2—then one should consider using them.

This work raises several research questions. First, how to estimate the generators nonparametrically? The generator of a bivariate Durante copula was estimated nonparametrically in Durante and Okhrin (2014), but the matter is more complicated in our case because this bivariate relationship occurs between the variable of interest and the unobserved latent factor. Second, one may add more factors when building an FDG copula. Nonetheless, the model might not be as tractable as it is, and therefore it may be less appealing in practice. Finally, FDG copulas possess the conditional independence property, but the extreme-value EV-FDG copulas were not shown to do so. If this property held, this would be of great interest for the simulation of datasets from this model.

Appendix

Proof of Theorem 1

Let $C_{j|0}(\cdot |u_0)$ be the conditional distribution of $U_j$ given $U_0=u_0$. The $U_j$’s are conditionally independent given $U_0$; hence,

$$\begin{aligned} C(u)&= \int _0^1 \prod _{j=1}^d C_{j|0}(u_j|u_0) du_0 \nonumber \\&=\int _0^1 \prod _{j=1}^d \frac{\partial C_{0j}(u_0,u_j)}{\partial u_0} du_0 \nonumber \\&=\int _0^1 \prod _{j=1}^d \frac{\partial C_{0(j)}(u_0,u_{(j)})}{\partial u_0} du_0 \nonumber \\&=\int _0^{u_{(1)}}\prod _{j=1}^d \frac{\partial C_{0(j)}(u_0,u_{(j)})}{\partial u_0} du_0 \nonumber \\&\quad + \sum _{k=2}^d \int _{u_{(k-1)}}^{u_{(k)}}\prod _{j=1}^{k-1}\frac{\partial C_{0(j)}(u_0,u_{(j)})}{\partial u_0}\prod _{j=k}^{d}\frac{\partial C_{0(j)}(u_0,u_{(j)})}{\partial u_0} \nonumber \\&\quad + \int _{u_{(d)}}^1 \prod _{j=1}^d \frac{\partial C_{0(j)}(u_0,u_(j))}{\partial u_0} du_0 . \end{aligned}$$

(23)

Since

$$\begin{aligned} \frac{\partial C_{0j}(u_0,u_j)}{\partial u_0}=\left\{ \begin{array}{rl} f_j(u_j) &{}\text { if } u_0<u_j \\ u_j f_j'(u_0) &{}\text { if } u_0>u_j, \end{array} \right. \end{aligned}$$

Eq. (23) yields

$$\begin{aligned} C(u)=&\,u_{(1)}\prod _{j=1}^d f_j(u_j) + \sum _{k=2}^d \prod _{j=k}^d f_{(j)}(u_{(j)}) \\&\quad \int _{u_{(k-1)}}^{u_{(k)}} \prod _{j=1}^{k-1} u_{(j)} f_{(j)}'(u_0)du_0 \\&\quad + \prod _{j=1}^d u_j \int _{u_{(d)}}^1 f_j'(u_0) du_0. \end{aligned}$$

Putting $u_{(1)}$ in factor and noting that $\int _{u_{(1)}}^{u_{(2)}}f_{(1)}'(x)dx=f_{(1)}(u_{(2)})-f_{(1)}(u_{(1)})$ finishes the proof. $\square$

Proof of Proposition 1

It suffices to set all $u_k$ equal to one but $u_i$ and $u_j$ in the formula (3). $\square$

Proof of Proposition 2

It suffices to apply the formulas (4) with $f_{ij}$ given in Proposition 1. To compute the Spearman’s rho, note that

$$\begin{aligned} \int _0^1x^2f_{ij}(x)dx= & {} \int _0^1x^2f_i(x)f_j(x)dx\\&+\int _0^1x^3\int _x^1f_i'(z)f_j'(z)dzdx. \end{aligned}$$

An integration by parts yields $\int _0^1x^3\int _x^1f_i'(z)f_j'(z)dzdx=(1/4)\int _0^1x^4f_i'(x)f_j'(x)dx$, and the result follows. $\square$

Proof of Theorem 2

Fix $(u_1,\dots ,u_d)\in [0,1]^d$ and let $n\ge 1$ be an integer. Let us introduce

$$\begin{aligned}&\alpha _n:=u_{(1)}^{1/n}\prod _{j=1}^d \frac{f_{j}(u_j^{1/n})}{u_j^{1/n}}, \quad \beta _n:=\int _{u_{(d)}^{1/n}}^1 \prod _{j=1}^d f_j'(u_0)du_0, \\&\gamma _n:=\prod _{j=k}^d \frac{f_{(j)}(u_{(j)}^{1/n})}{u_{(j)}^{1/n}}, \quad \delta _{n,k}:=\int _{u_{(k-1)}^{1/n}}^{u_{(k)}^{1/n}} \prod _{j=1}^{k-1} f_{(j)}'(u_0)du_0, \end{aligned}$$

and define

$$\begin{aligned} A_n:=\alpha _n+\beta _n+\sum _{k=2}^d\gamma _{n,k}\delta _{n,k}. \end{aligned}$$

Our goal is to derive asymptotic equivalent sequences for $\alpha _n,\beta _n\gamma _n$ and $\delta _n$. Let $\sim$ denote the equivalent symbol at infinity (i.e., $a_n\sim b_n$ means $a_n/b_n\rightarrow 1$ as $n\rightarrow \infty$). By using the well-known formulas $e^x\sim 1+x$ (when $x\rightarrow 0$), $\log x \sim x-1$ (when $x\rightarrow 1$), and $f_j(x) \sim 1+(x-1)f'_j(1)$ (when $x \rightarrow 1$), we get

$$\begin{aligned}&\alpha _n \sim \left( 1+\frac{1}{n}\log u_{(1)}\right) \left( 1-\frac{1}{n}\log (u_1 \dots u_d) \right) \\&\quad \times \left( 1+\frac{1}{n}\sum _{j=1}^d \log u_{(j)} f'_{(j)}(1)\right) \text { and } \\&\gamma _{n,k} \sim \left( 1-\frac{1}{n}\sum _{j=k}^{d}\log u_{(j)} \right) \left( 1+\frac{1}{n}\sum _{j=k}^d \log u_{(j)} f_{(j)}'(1) \right) . \end{aligned}$$

For $\beta _n$ the equivalence is obtained as follows. Let F(x) be a primitive of $\prod _{j=1}^d f_j'(x)$. It follows that $\beta _n=F(1)-F(u_{(d)}^{1/n})$. A Taylor expansion yields

$$\begin{aligned} F(u_{(d)}^{1/n})=F(1)+(u_{(d)}^{1/n}-1)F'(1)+\frac{(u_{(d)}^{1/n}-1)^2}{2}F''(x_n) \end{aligned}$$

where $x_n$ is between $u_{(d)}^{1/n}$ and 1. Since $F''$ is assumed to be continuous on [0, 1], it is uniformly bounded on this set, and therefore $(u_{(d)}^{1/n}-1)^2F''(x_n)/2=o(1/n)$ where o(1 / n) is a quantity such that $no(1/n)\rightarrow 0$ as $n\rightarrow \infty$. Hence, since $u_{(d)}^{1/n}=\exp (\log (u_{(d)})/n)\sim 1+\log (u_{(d)})/n$, we have as $n\rightarrow \infty$

$$\begin{aligned} F(1)-F(u_{(d)}^{1/n})\sim -\frac{1}{n}\log (u_{(d)})F'(1). \end{aligned}$$

The same arguments apply to enable us get

$$\begin{aligned} \beta _n&\sim - \frac{1}{n} \log u_{(d)} \prod _{j=1}^d f_j'(1) \\ \delta _{n,k}&\sim \frac{1}{n} \log \left( \frac{u_{(k)}}{u_{(k-1)}}\right) \prod _{j=1}^{k-1} f_{(j)}'(1) . \end{aligned}$$

The quantity $A_n$ is a polynomial with respect to $n^{-1}$ of order at most three. In (24), the coefficients of order 0, 2, and 3 vanish at infinity. There only remain the terms of order 1, and hence,

$$\begin{aligned} \lim _{n\uparrow \infty }n(A_n-1)&= \log u_{(1)}-\log (u_1 \dots u_d)\nonumber \\&\quad +\sum _{j=1}^d\log u_{(j)} f_{(j)}'(1)\nonumber \\&\quad -\log u_{(d)} \prod _{j=1}^d f_{(j)}'(1) \nonumber \\&\quad + \sum _{k=2}^d \prod _{j=1}^{k-1} f_{(j)}'(1)\log \left( \frac{u_{(k)}}{u_{(k-1)}}\right) . \end{aligned}$$

(24)

From Abel’s identity for two sequences $(a_i)$ and $(b_i)$ of real numbers, that is,

$$\begin{aligned} \sum _{i=1}^{d-1} a_i(b_{i+1}-b_i) = \sum _{i=1}^{d-1}b_i(a_{i-1}-a_i) + a_{d-1}b_d - a_1b_1 \end{aligned}$$

it follows

$$\begin{aligned}&\lim _{n\uparrow \infty }n(A_n-1)\\&=\sum _{k=1}^d \left( \underset{=:\chi _k}{\underbrace{\left( \prod _{j=1}^{k-1}f_{(j)}'(1)\right) (1{-}f_{(k)}'(1)){+}f_{(k)}'(1)-1}} \right) \log u_{(k)}, \end{aligned}$$

with the convention that $\prod _{j=1}^{0}f_{(j)}'(1)=1$. Then (3) entails that

$$\begin{aligned} C^n(u_1^{1/n},\dots ,u_d^{1/n}) =&\, u_1 \dots u_d \exp \left[ n \log A_n \right] \\ =&\, u_1 \dots u_d \exp \left[ n(A_n-1)(1+o(1)) \right] \\ \rightarrow&\prod _{i=k}^d u_{(k)}^{\chi _k} \end{aligned}$$

as $n \rightarrow \infty$. $\square$

Proof of Lemma 1

(i) Since the p-uple $(r_{1,2},\dots ,r_{d-1,d})$ belongs to the image space $\mathbf {r}(\Theta ^d)$, the system

$$\begin{aligned} \left\{ \begin{array}{ccc} r(\theta _1,\theta _2) &{}=&{} r_{1,2} \\ \vdots &{} &{} \vdots \\ r(\theta _{d-1},\theta _d) &{}=&{} r_{d-1,d} \end{array} \right. \end{aligned}$$

has at least one solution. In particular, there exist $(\theta _1,\theta _2,\theta _3)$ in $\Theta ^3$ such that

$$\begin{aligned} \left\{ \begin{array}{ccc} r(\theta _1,\theta _2) &{}=&{} r_{1,2} \\ r(\theta _{1},\theta _3) &{}=&{} r_{1,3} \\ r(\theta _{2},\theta _3) &{}=&{} r_{2,3}. \end{array} \right. \end{aligned}$$

(25)

The system (25) is rewritten as

$$\begin{aligned} \left\{ \begin{array}{ccc} r_{\theta _2}(\theta _1) &{}=&{} r_{1,2} \\ r_{\theta _3}(\theta _{1}) &{}=&{} r_{1,3} \\ r_{\theta _3}(\theta _{2}) &{}=&{} r_{2,3}, \end{array} \right. \end{aligned}$$

or equivalently,

$$\begin{aligned} \left\{ \begin{array}{ccc} \theta _1 &{}=&{} s_{1,2}(\theta _2) \\ \theta _{1} &{}=&{} s_{1,3}(\theta _3) \\ \theta _{2} &{}=&{} s_{2,3}(\theta _3). \end{array} \right. \end{aligned}$$

This yields

$$\begin{aligned} s_{1,3}(\theta _3) = s_{1,2} \circ s_{2,3}(\theta _3). \end{aligned}$$

(26)

Let us note that $s_{1,3}$ is involutive at $\theta _3$, that is, $s_{1,3}\circ s_{1,3}(\theta _3)=\theta _3$. Indeed, $r(\theta _1,\theta _3)=r_{\theta _3}(\theta _1)=r_{1,3}$ is equivalent to $\theta _1=r_{\theta _3}^{-1}(r_{1,3})=s_{1,3}(\theta _3)$. This implies $r(s_{1,3}(\theta _3),\theta _3)=r_{1,3}$, and, composing by $r_{s_{1,3}(\theta _3)}^{-1}$ in both sides, we get $r_{s_{1,3}(\theta _3)}^{-1}(r_{1,3})=s_{1,3}(s_{1,3}(\theta _3))=\theta _3$. Therefore, one can compose both sides of (26) by $s_{1,3}$ to get

$$\begin{aligned} \theta _3 = s_{1,3}\circ s_{1,2} \circ s_{2,3}(\theta _3). \end{aligned}$$

Hence, (20) has at least one solution.

(ii) If (20) admits exactly one solution $\theta _3$, then $\theta _2$ and $\theta _1$ are also unique. Furthermore, for all $j \ge 3$,

$$\begin{aligned} \theta _{j+1} = s_{j,j+1}(\theta _j) \end{aligned}$$

which concludes the proof that assumption (A2) holds. It is now shown that assumption (A3) holds as well. Define $\partial _1 r$, respectively, $\partial _2 r$, the derivative of r with respect to the first, respectively, second, variables of r. Hence, for all $\theta _i$ and $\theta _j$ in $\Theta$, the quantities $\partial _1 r(\theta _i,\theta _j)$ and $r_{\theta _j}(\theta _i)$ only differ in the notation. The first step in the proof is to consider the case $d=3$. The Jacobian matrix of $\mathbf {r}$ at $\varvec{\theta _0}$ is given by

$$\begin{aligned} \mathbf {J}=\begin{pmatrix} \partial _1r(\theta _{01},\theta _{02}) &{} \partial _2r(\theta _{01},\theta _{02}) &{} 0 \\ \partial _1r(\theta _{01},\theta _{03}) &{} 0 &{} \partial _2r(\theta _{01},\theta _{03}) \\ 0 &{} \partial _1r(\theta _{02},\theta _{03}) &{} \partial _2r(\theta _{02},\theta _{03}) \end{pmatrix}. \end{aligned}$$

To show that $\mathbf {J}$ has full rank, we show that its determinant

$$\begin{aligned}&\partial _1r(\theta _{01},\theta _{02}) \partial _2r(\theta _{01},\theta _{03}) \partial _1r(\theta _{02},\theta _{03})\\&\quad + \partial _2r(\theta _{02},\theta _{03}) \partial _1r(\theta _{01},\theta _{03}) \partial _2r(\theta _{01},\theta _{02}) \end{aligned}$$

is nonzero. Indeed, note that for all $\theta$ in $\Theta$, the map $r_{\theta }:\Theta \rightarrow r_{\theta }(\Theta )$ is a twice continuously differentiable homeomorphism. Furthermore, by assumption, the true parameter vector $\varvec{\theta _0}$ lies in the interior of $\Theta$ that is open. Finally, by symmetry, for all $i<j$,

$$\begin{aligned} \partial {r}_1(\theta _{0i},\theta _{0j}) > 0 \quad (\text {respectively } \partial {r}_1(\theta _{0i},\theta _{0j}) < 0) \end{aligned}$$

is equivalent to

$$\begin{aligned} \partial {r}_2(\theta _{0j},\theta _{0i}) > 0 \quad (\text {respectively } \partial {r}_2(\theta _{0j},\theta _{0i}) < 0). \end{aligned}$$

For the general case, we proceed by mathematical induction. When the dimension is d, we write $\mathbf {J}(\varvec{\theta })=\mathbf {J}^{(d)}(\varvec{\theta })$ to emphasize the dependence on the dimension. Notice that it was already shown above that $\mathbf {J}^{(3)}(\varvec{\theta })$ has full rank. Now suppose that the kernel of $\mathbf {J}^{(d-1)}(\varvec{\theta })$ is null when the dimension is $d-1$. Let $\mathbf {A}=\mathbf {J}^{(d)}(\varvec{\theta })$. Each row of $\mathbf {A}$ is written as

$$\begin{aligned} (0,\dots ,0,\partial _1r(\theta _i,\theta _j),0\dots ,0,\partial _2r(\theta _i,\theta _j),0,\dots ,0) \end{aligned}$$

where $\partial _1r(\theta _i,\theta _j)$ is at the i-th position and $\partial _2r(\theta _i,\theta _j)$ at the j-th position. There are $d-1$ rows of A which depend on $\theta _d$ and $p-d+1$ which do not (recall $p=d(d-1)/2$ is the number of pairs). Since the kernel of a matrix is invariant by permutation, we can without loss of generality put all the rows which do not depend on $\theta _d$ on the top. More precisely, decompose $\mathbf {A}$ as

$$\begin{aligned} \mathbf {A}= \begin{pmatrix} \mathbf {A}_{11} &{} \mathbf {A}_{12} \\ \mathbf {A}_{21} &{} \mathbf {A}_{22} \end{pmatrix} \end{aligned}$$

such that $\mathbf {A}_{11}$ is a $(p-d+1)\times (d-1)$ matrix containing all the rows which do not depend on $\theta _d$ and $\mathbf {A}_{12}$ and $\mathbf {A}_{22}$ are $(p-d+1)\times 1$ and $(d-1)\times 1$ matrices, respectively. Note that $\mathbf {A}_{12}$ is the null vector of size $p-d+1 \times 1$. Let $\mathbf {x}\in \mathbb {R}^d$, $\mathbf {x}=(\mathbf {x}_1^T,x_2)^T$ where $\mathbf {x}_1\in \mathbb {R}^{d-1}$, $x_2\in \mathbb {R}$. It follows that $\mathbf {A}\mathbf {x}=\mathbf {0}$ is equivalent to

$$\begin{aligned} \left\{ \begin{array}{rl} \mathbf {A}_{11}\mathbf {x}_1+\mathbf {A}_{12}x_2=\mathbf {0} \\ \mathbf {A}_{21}\mathbf {x}_1 + \mathbf {A}_{22}x_2 = 0. \end{array} \right. \end{aligned}$$

But $\mathbf {A}_{12}=\mathbf {0}$ and since $\mathbf {A}_{11}=\mathbf {J}^{(d-1)}(\varvec{\theta })$ whose kernel is null, $\mathbf {x}_1=\mathbf {0}$. Then $\mathbf {A}_{22}x_2=0$, and the assumptions imply $x_2=0$, which concludes the proof. $\square$

Proof of Theorem 3

To prove (i), it suffices to apply Lemma 1. Since $r(\theta _i,\theta _j)$ denotes the extremal dependence coefficient of the $\mathcal {E}$ copula bivariate marginal $C_{\#,ij}$ defined in (14), we have

$$\begin{aligned} r(\theta _i,\theta _j)=\lambda (\theta _i)\lambda (\theta _j), \text { where } \lambda (\theta ):=1-\frac{\partial f(t,\theta )}{\partial t}\Big \vert _{t=1}. \end{aligned}$$

(27)

In the Cuadras-Augé and the Fréchet cases, (27) is given by $\lambda (\theta )=\theta$, and in the sinus case, $\lambda (\theta )=1-\theta /\tan (\theta )$. In all these situations, it is easy to see that the map $r_{\theta _j}(\cdot )$ is a twice continuously differentiable homeomorphism. Therefore, Lemma 1 (i) applies. To apply the second part of Lemma 1, note that Eq. (20) translates into

$$\begin{aligned} \lambda (\theta )^2 = \frac{r_{1,3}r_{2,3}}{r_{1,2}}. \end{aligned}$$

Since it has a unique solution, Lemma 1 (ii) applies, and the result is proved.

(ii) The proof is straightforward because under the assumptions of (ii), $r(\theta _i,\theta _j)=\theta _i\theta _j$. However, this is the precise form of $r(\theta _i,\theta _j)$ in (i); hence, one can also apply Lemma 1. $\square$