1 Introduction

The NASA discovery mission Insight is mainly devoted to the exploration of the interior of Mars. For this purpose it carries two main experiments: A seismometer (SEIS) to detect possible seismic events on Mars with the aim to derive its global interior structure, and the Heat Flow and Physical Properties Probe (HP3) which is essentially a probe penetrating itself up to 5 meters into the Martian subsurface. The first instrument (SEIS) has been developed by a French consortium led by IPGP (Yana et al. 2014), while the second one (the instrumented Mole) was developed and built by DLR in Germany (Lichtenheldt et al. 2014) and the Space Research Centre (SRC) in Poland. Due to technical problems the launch of the InSight mission had to be postponed by two years, so that we may expect operation of the experiments on Mars by the year 2018.

Penetrometers of different types have already been developed for and used in different space missions. The first penetrometers used in planetary research date back to the early lunar lander missions in the 1960’s and 1970’s (Ball and Lorenz 1999). These first penetrometers mostly performed quasi-static measurements. A cone was pushed into the ground with a low velocity and the resistance force against this action was measured in order to get some understanding of the soil properties. An alternative possibility is to use a dynamical method. Here a probe is driven into the soil by vibrations or hammer strokes and the penetration progress of the probe is monitored by a depth sensor. For planetary research two types of such instruments have been developed in the past:

(i) The instrument MUPUS-PEN, where a slender cylindrical rod is driven into the soil by a recoilless hammering mechanism mounted the top side of the rod. This probe was recently flown on the Rosetta–Philae mission as part of the experiment MUPUS and was successfully deployed in November 2014 at the surface of the target comet 67P/Churyumov–Gerasimenko (Spohn et al. 2007).

(ii) Penetrometers with a conical tip and a cylindrical body, which contain an internal hammering mechanism used to drive it into the soil. Such instruments are typically supplied with electrical power via a trailing cable, which is also used to transmit data acquired by integrated sensors to a lander residing at the surface. Such devices are called “Moles”, because of their ability to dig themselves into the soil without the help of external driving mechanisms. Prototypes of such “Moles” have been developed and tested by various groups in the recent past, see, e.g. Seweryn et al. (2014a, 2014b). The instrument HP3, which is part of the payload of NASA’s discovery mission Insight, is such a “Mole” type instrument.

The present paper deals with the second instrument aboard the Insight spacecraft, the HP3 Mole. Aside of the planned temperature and heat flow measurements (Spohn et al. 2012; Hansen-Goos et al. 2014) it will also be used to derive soil mechanical parameters of the Martian near surface layers. After the Mole has been placed at its starting position just above the natural ground surface, it will begin to penetrate into the soil by the action of the built-in hammering mechanism. From the information about the depth increment caused by individual strokes, various soil mechanical parameters can be estimated.

One of the methods that will be applied to achieve this goal is a so-called “pile driving model” originally developed for geotechnical applications by Smith (1962). In a recent study (Kömle et al. 2015, hereafter referred to as Paper 1) such an algorithm has been developed for different types of hammering mechanisms. In this paper we extend the algorithm given in the paper mentioned above and apply it specifically to the case of the Insight/HP 3 Mole and its planned operations on Mars. First, the basic model described in Paper 1 provides only the reaction of the system to one particular hammer stroke. However, in reality one full hammering cycle of the InSight Mole consists of two major strokes: a stronger one when the hammer hits the tip and a weaker one when the support mass has inverted its direction of motion and hits the stoppers of the casing. Under certain circumstances even more (minor) hits can occur within one basic stroke cycle.

Furthermore, the physical quantities of tip resistance and shaft resistance are derived and explained in this paper. Note that the applicability of a 1D-modeling approach for describing dynamic penetration has already shown in a recent study by Lichtenheldt and Krömer (2016). Since there is no prescribed analytical equation for the tip resistance for deep penetration, we study here two different approaches to determine the tip resistance. Subsequently 3D-DEM simulations are used to validate the results of our one-dimensional model.

Since we do not know how the soil on Mars is structured or layered, several possible cases that might be encountered will be studied here. As a reference material the soil-mechanical properties of cohesionless quartz sand used for the recent Mole penetration tests at DLR Bremen are taken as input parameters for our numerical model. Based on this we consider various probable scenarios for the ground properties, in particular a layered soft sandy subsurface traversed by layers of more dense and stiff soil.

2 Extensions of Original Pile Driving Model

The presented pile driving model is based on a previous model that is described in detail in Paper 1. The mechanical parameters for the Mole used in the new calculations presented here are listed in Table 1. The values correspond to the latest prototype that is expected to be used as the InSight flight model (of course, further refinements of the currently existing design might be done for the flight model. In this case results reported in this paper may have to be adapted when the real data from the Mole’s action on Mars will be evaluated with the help of our models).

Table 1 Parameters for the InSight HP3 Mole used for the mole penetration calculations presented in this paper
Full size table

As compared to the model presented in Paper 1, the new model contains several important improvements and extensions:

  • It includes the second stroke within one basic stroke cycle, which is caused by the hitting of the support mass onto the stoppers inside the housing of the Mole, accounting for typically 20 %–40 % of the total mechanical energy released during one stroke cycle (Seweryn et al. 2014a, 2014b).

  • One single model run consists now not only of a single stroke cycle, but rather an arbitrary number of strokes can be applied to calculate the progress of the Mole into the subsurface as a quasi-continuous function of time.

  • Soil-mechanical parameters like density, cohesion, etc. can be defined not as constant values, but as functions of depth. This allows to study cases where the soil is not homogeneous, but has a layered structure, e.g. compacted layers sandwiched between softer soil or an increase of density with depth.

2.1 Second Stroke

The motions of the two internal masses (hammer and support mass) inside the Mole’s housing drive the forward motion of the Mole into the soil. They are controlled by the status of the springs connecting them to each other and to the housing. A sketch of the movements of hammer and support mass during a stroke cycle is shown in Fig. 1. A full stroke cycle is composed of two contributing strokes: the first stroke is the hit of the percussion mass (hammer) onto the Mole tip (which is rigidly connected with the housing), and the second stroke (typically weaker than the first one) is due to the hitting of the support mass on the stoppers inside the housing when its motion has reversed. Figure 2 shows the movements of the tip, the hammer mass and the support mass for one stroke cycle. When the hammer mass or the support mass touch the housing at the position of the tip or the stoppers, respectively, a stroke is generated by the corresponding mass.

Fig. 1
figure 1

The process of the hammer mechanism with support mass (yellow), hammer mass (light blue) and casing (dark blue)

Full size image
Fig. 2
figure 2

The relative movements of the tip, the hammer mass and the support mass from the MATLAB model

Full size image

Permanent (not purely elastic) forward motion is induced when one of these masses hits the housing and drives it in forward direction. The main contribution comes from the percussion mass. It is stopped by a mechanical barrier as it hits the tip element of the housing. Due to the oscillatory nature of the motions, it is also possible that within one stroke cycle the hammer hits the tip several times. The reaction of the system to one single stroke by the hammer was already modeled in detail in the first version of our pile driving model described in Paper 1. However, the InSight Mole is designed in such a way that also the support mass makes an active contribution to the penetration of the housing. After the hammer has hit the tip, its motion reverses and it moves in upward direction together with the support mass. After upward motion has been stopped by action of the brake spring, the motion direction of both masses reverses once more and the support mass hits the stoppers positioned in the mid lower part of the housing. This causes another forward motion of the Mole housing in the soil and is referred to as the second stroke. After the second stroke, when all oscillations are damped out, the positions of the interior masses and the strain of the connecting springs are the same as in the initial state. Thus one complete stroke cycle actually consists of the hammer stroke on the tip element, followed by a hit of the support mass onto an internal stopper inside the housing. Typically the first stroke is the stronger one, accounting for the most of the achieved forward movement of the Mole within one stroke cycle, while the second stroke accounts for the rest. From the total energy of the hammering mechanism shown in Fig. 3 it can be seen that 80 % of the energy is lost due to the first stroke and the rest of it dissipates due to the second stroke.

Fig. 3
figure 3

The energies of support mass, hammer mass, support spring and percussion spring over a full stroke cycle

Full size image

3 Methodology

The basic soil-mechanical parameters that determine the properties of the ground are the material density \(\varrho \), the angle of internal friction \(\varphi \), and the material’s cohesion \(c\). Assuming shear failure as the relevant failure mechanism of the regolith, the shear strength of the soil must be overcome by the force exerted by the action of the Mole’s hammering device.

The geometrical dimensions of the Mole are its radius \(r\) and its total length \(L_{\mathit{mole}}\). We define \(s=0\) as the position when the Mole’s rear end coincides with the surface level of the ground, i.e. when the Mole has penetrated by exactly its own length. At this position the tip is at a depth \(L_{\mathit{mole}}\) below the surface. The pressure \(\sigma (s)\) exerted by the soil onto the Mole’s tip in a certain depth \(s\) equals the overburden pressure of the soil in the same depth. Thus \(\sigma (s)\) at the Mole’s tip for a normally consolidated soil is

$$ \sigma_{\mathit{tip}}(s) = \varrho g (s+L_{\mathit{mole}}) $$
(1)

Here \(g\) is the gravitational acceleration, which is on Mars 38 % of the Earth gravity. This has a direct influence on the overburden pressure of the soil when the Mole has reached a particular depth \(s\) below the surface.

3.1 The Model

The model of the penetration process is divided in a model of the Mole along with the hammer mechanism and a model of the soil that defines the resistance force of the soil. These models are based on the pile driving model developed by Smith (1962). The enhancements of the presented model are a well-defined bearing capacity based on standards and a different hammer mechanism which corresponds to the hammer mechanism that will be used for the penetration of the heat flow probe on the NASA InSight mission in 2018. Furthermore, the soil model allows for a multi-layered soil.

The model of the Mole consists of the shaft which is subdivided in many shaft segments, the tip, the support mass and the hammer mass (see Fig. 4). The hammer mass is connected by a spring with the support mass and the support mass is also connected by a spring with the rear end (first element) of the Mole. The support mass is prestressed kept by a rigid connection with one shaft segment that can be freely chosen. The spring between hammer and support mass is fully loaded at the beginning of a stroke cycle. The hammer is then accelerated towards the tip due to the unloading of the spring, while the support mass is accelerated in the opposite direction.

Fig. 4
figure 4

Mole and soil model

Full size image

The rigid connection between hammer and tip as well as between support and casing is modeled by a stiff spring and a damper that act just if the elements overlap. The resulting contact force is limited to be always positive, so that just compressive contact forces are transmitted. The damper force is calculated as:

$$ F_{d} = v \sqrt{\frac{4m^{*} k_{n}}{1+( \frac{\pi }{\ln(c _{e})}) ^{2}}} $$
(2)

where \(m^{*}\) is the mean value of both masses that interact, \(k_{n}\) is the normal contact stiffness, \(c_{e}\) is the coefficient of restitution and \(v\) is the relative velocity. The total contact force consists of the damping force and the spring force and is given by

$$ F = k_{n} \delta_{n} - F_{d}, \quad F>0 $$
(3)

with the overlap \(\delta_{n}\).

The subdivision of the shaft allows for more accuracy in the computation of the resistance force caused by the shaft friction. Due to the segmentation it is possible to apply different friction forces in different parts of the Mole. Thus, it is possible to simulate a stroke cycle where the Mole is partially penetrated into a different soil layer.

The model of the soil consists of a spring and a damper which connects each Mole segment with a fixed clamp. The springs use an ideal elastic plastic model, so that permanent settlements of the Mole are possible. The maximum force at which plasticity begins is defined by the bearing capacity of the corresponding element. The spring characteristics is linear until it reaches the corresponding bearing capacity (see Fig. 4). The spring that connects the tip of the Mole to the soil can just exert a compressive force, while the springs for the shaft-soil connection can be compressed and stretched. The bearing capacity has the main influence on the penetration results and is dependent on the density, the current stress state, which corresponds to different depth, and the peak friction angle.

3.2 Bearing Capacity

The bearing capacity is the largest possible resistance force of the soil before it fails. The Mole must exert the bearing capacity to reach local plasticity and to achieve permanent settlements.

The bearing capacity is calculated based on the analytical formulas of Terzaghi (1943) and corresponds with the formulations of the Austrian Standard for Spread Foundations in Geotechnical Engineering ÖNORM B4435-2:1999-10-01. Usually this equation is restricted to a maximum footing depth of 3 times the width of the foundation. This means that in deeper foundation the complete ground heave will not occur. Instead, the soil will compact locally to accommodate the displaced material. Therefore, as an approach the depth for the calculation of the ground heave can be limited by an effective depth of the pile. This effective depth depends on the relative density of the soil and is assumed to be smaller than 10 times the diameter of the penetrator for a loose sand and smaller than 20 times the diameter for a dense sand. Furthermore, it is assumed that the material is dry soil or at least that no excess pore water pressure occurs in the soil during penetration, as it is appropriate for Mars. Furthermore, the formula for the bearing capacity considers a flat tip of the Mole and for the studied case the following assumptions are made:

  • no inclination of the penetrator,

  • vertical penetration force,

  • no terrain slope,

  • horizontally layered soil,

  • infinite half space.

Under these assumptions the equation for the bearing capacity at the tip of the penetrator is:

$$ R_{\mathit{tip}}= A(\gamma_{u} 2r N_{\gamma } + \gamma_{o} t N_{q} + c N_{c}) $$
(4)

with the radius \(r\) and the cross-section \(A\) of the Mole, the soil specific weight underneath the tip \(\gamma_{u}\), the soil specific weight above the tip \(\gamma_{o}\), the current depth \(t\) and the cohesion \(c\) of the soil. The bearing capacity factors \(N_{\gamma }\), \(N_{q}\) and \(N_{c}\) can be determined considering the preceding assumptions as:

$$\begin{aligned} N_{q_{0}} &= \frac{1+\sin \varphi }{1-\sin \varphi } e^{\pi \tan \varphi } \end{aligned}$$
(5)
$$\begin{aligned} N_{\gamma } &=( N_{q_{0}}-1) s_{\gamma } \tan \phi \end{aligned}$$
(6)
$$\begin{aligned} N_{q} &= N_{q_{0}} s_{q} \end{aligned}$$
(7)
$$\begin{aligned} N_{c} &= \cot \varphi ( N_{q_{0}}-1) s_{c} \end{aligned}$$
(8)

where \(\varphi \) is the peak friction angle of the soil and \(s_{\gamma }\), \(s_{q}\) and \(s_{c}\) are shape factors that are given for a circular foundation and a centric origin of the force by:

$$\begin{aligned} s_{\gamma } &= 0.7 \end{aligned}$$
(9)
$$\begin{aligned} s_{q} &=1+\sin \varphi \end{aligned}$$
(10)
$$\begin{aligned} s_{c} &=\frac{ s_{q} N_{q_{0}}-1}{N_{q_{0}}-1} \end{aligned}$$
(11)

The product of the soil specific weight above the tip and the current depth \(\gamma_{o} t\) in Eq. (4) is equal to the vertical stress at the current depth \(\sigma_{v}\), see Eq. (14).

The additional resistance caused by the shaft friction between soil and Mole can be added to the bearing capacity at the tip to derive the entire bearing capacity acting on the Mole. The resistance force of the shaft friction is determined by the horizontal stress of the soil \(\sigma_{h}\) at the current depth \(t\) integrated over the shaft area \(A_{\mathit{shaft}}\) and multiplied by the friction parameter between soil and Mole \(\mu_{\mathit{inter}}\). The integral over the Mole length can be replaced by a sum over all shaft segments due to the discretization. The resistance force of the shaft friction is

$$ R_{\mathit{shaft}}=\int\limits_{A_{\mathit{shaft}}}\mu_{\mathit{inter}} \sigma_{h}(t) dA= \sum _{i=1}^{n_{\mathit{segments}}} \mu_{\mathit{inter}} A_{\mathit{shaft}\_\mathit{segment}_{i}} \sigma_{h}(t) $$
(12)

with the area of each shaft segment \(A_{\mathit{shaft}\_\mathit{segment}_{i}}\). The horizontal stress can be approximated as

$$ \sigma_{h}=\sigma_{v} (1-\sin \varphi ) $$
(13)

for normally consolidated sand.

The vertical stress \(\sigma_{v}\) in the current depth can be calculated for an undisturbed normally consolidated soil as:

$$ \sigma_{v} = \sum_{i=1}^{n_{\mathit{layers}}} \varrho_{i} t_{i} g $$
(14)

where \(n_{\mathit{layers}}\) is the number of layers above the current depth, \(\varrho_{i}\) is the density of the \(i\)th soil layer and \(t_{i}\) is the corresponding thickness of each layer. Thus, the resistance at the tip \(R_{\mathit{tip}}\) and the resistance at the shaft \(R_{\mathit{shaft}}\) are defined and can be applied to the corresponding elements.

3.3 Multi-layered Soil

The bearing capacity in the multi-layered soil model can be computed by applying the corresponding bearing capacity of the layer at the current depth to each segment and to the tip. The tip has a certain influence depth, where the failure originates. If the rupture line is already inside of a different soil layer, the bearing capacity is changed. The presented model can only consider one different soil layer inside the influence depth of the tip. The bearing capacity near a different soil layer is linearly interpolated between the bearing capacity of the current layer and the layer close beneath the tip. The influence depth \(d_{s}\) of the tip can be calculated from German Standard DIN 4017:

$$ d_{s}=\frac{2r}{\sin ( \frac{\pi }{2}-\varphi_{0}) } \sin \biggl( \frac{\pi }{4}+\frac{\varphi_{0}}{2}\biggr) \cos \varphi_{0}\ e ^{(\frac{\pi }{4}+\frac{\varphi_{0}}{2})\tan \varphi_{0}} $$
(15)

where \(\varphi_{0}\) is the arithmetic mean value of the two different friction angles of each layer. Before the tip rupture line gets in contact with the second layer the influence depth can be approximated by setting \(\varphi_{0}\) to the current friction angle.

3.4 Local Shear Failure at Tip

The introduced bearing capacity by Terzaghi assumes a certain shape of the rupture plane which will not always occur in this way. For a very loose sand the area of shear failure of the soil due to the penetration will be quite small. Considering a local shear failure just in front of the tip of the penetrator leads to another approach for the calculation of the tip resistance. The idea is to add the stress that is induced by the tip to the initial stress of the soil and determine the force that is necessary to generate a shear failure corresponding to the Mohr–Coulomb failure criterion:

$$ r_{\mathit{iter}} \cos (\varphi )\leq \sigma_{M}\tan (\varphi )+C $$
(16)

where \(r_{\mathit{iter}}\) is the radius of the Mohr’s circle for the stress state, \(\sigma_{M}\) is the normal stress at which the Mohr’s circle fulfills the failure criterion and \(C\) is the cohesion which can be neglected for the case of cohesionless material.

For the computation of the local stress state, the induced stress can be defined as:

$$ \left(\textstyle\begin{array}{c@{\quad }c} \sigma_{n}& \sigma_{t} \\ \sigma_{t} & \kappa \sigma_{n} \end{array}\displaystyle \right) $$
(17)

where the tangential induced stress at mobilization is

$$ \sigma_{t}=\sigma_{n} \tan (\varphi_{\mathit{inter}}) $$
(18)

with \(\varphi_{\mathit{inter}}\) as the interface friction angle between soil and penetrator. The coefficient \(\kappa \) is introduced to allow a reaction pressure that is produced by the contact normal stress \(\sigma_{n}\) and the resulting lateral strain which is confined by the surrounding soil. The induced stress is in a tilted position due to the cone angle of the tip (see Fig. 5). Therefore, the initial stress state needs to be rotated by the cone angle \(\alpha \):

$$ \left(\textstyle\begin{array}{c@{\quad }c} \sigma_{v}& 0 \\ 0 & K_{0} \sigma_{v} \end{array}\displaystyle \right) \rightarrow \left(\textstyle\begin{array}{c@{\quad }c} \sigma_{v} \frac{(1+K_{0})}{2} + \sigma_{v} \frac{(1-K_{0})}{2}\cos (2 \alpha ) & \sigma_{v} \frac{(1-K_{0})}{2}\sin (2\alpha ) \\ \sigma_{v} \frac{(1-K_{0})}{2}\sin (2\alpha ) & \sigma_{v} \frac{(1+K _{0})}{2} - \sigma_{v} \frac{(1-K_{0})}{2}\cos (2\alpha ) \end{array}\displaystyle \right) $$

with the lateral earth pressure coefficient \(K_{0}\). The resulting stress tensor is given by the sum of the rotated initial stress and the induced stress tensor:

$$\begin{aligned} &\left(\textstyle\begin{array}{c@{\quad }c} \sigma_{n} +\sigma_{v} \frac{(1+K_{0})}{2} + \sigma_{v} \frac{(1-K _{0})}{2}\cos (2\alpha ) &\sigma_{t} + \sigma_{v} \frac{(1-K_{0})}{2} \sin (2\alpha ) \\ \sigma_{t} + \sigma_{v} \frac{(1-K_{0})}{2}\sin (2\alpha ) & \kappa \sigma_{n} + \sigma_{v} \frac{(1+K_{0})}{2} - \sigma_{v} \frac{(1-K _{0})}{2}\cos (2\alpha ) \end{array}\displaystyle \right) \\ &\quad = \left(\textstyle\begin{array}{c@{\quad }c} \sigma_{1}& \sigma_{t}' \\ \sigma_{t}' & \sigma_{2} \end{array}\displaystyle \right) \end{aligned}$$

The radius of the so created Mohr’s circle is given by

$$ r_{\mathit{iter}} = \sqrt{\biggl( \frac{\sigma_{1}-\sigma_{2}}{2}\biggr) ^{2}+ \sigma_{t}^{\prime\,2}} $$
(19)

and the normal stress at shear failure is

$$ \sigma_{M}=\frac{\sigma_{1}+\sigma_{2}}{2}-r_{\mathit{iter}} \sin (\phi ) $$
(20)

Using Eq. (19) and Eq. (20) in the Mohr–Coulomb failure criteria (Eq. (16)) leads to an equation from that the induced normal and tangential stress which is necessary to fail the soil at the tip can be derived.

Fig. 5
figure 5

Left: induced stress and the stress at rest; right: Mohr’s circle of the total stress at failure

Full size image

3.5 Time Integration

The time domain is integrated by a finite difference scheme that uses the Euler method:

$$\begin{aligned} \ddot{x}_{k} &=f(x_{k},\dot{x}_{k}) \end{aligned}$$
(21)
$$\begin{aligned} \dot{x}_{k+1} &=\dot{x}_{k} + \ddot{x}_{k} \Delta T \end{aligned}$$
(22)
$$\begin{aligned} x_{k+1} &=x_{k} + \dot{x}_{k+1} \Delta T \end{aligned}$$
(23)

where \(x_{k}\) denotes the displacement at the \(k\)th calculation step and \(\Delta T\) is the time increment. The time increment is selected to be 10 % of the critical time increment \(\Delta T_{\mathit{crit}}\), which can be derived from the highest eigenfrequency of the system:

$$ \Delta T_{\mathit{crit}}=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{m}{K}} $$
(24)

3.6 3D Discrete Element Model

As an alternative approach to the one-dimensional model of the Mole’s penetration, we have also considered a three-dimensional model, based on a discrete element method (DEM). It is numerically by far more demanding than the pile driving approach, but has the advantage that more information about the impact of the penetration on the soil conditions can be retrieved from the results.

The DEM model contains a simplified dynamic model of the hammering mechanism as it is present in the pile driving model described before. The soil is simulated as an assembly of about \(4 \times 10^{5}\) particles surrounding the penetrator, which turned out to be enough particles for obtaining reliable results. The material parameters for the DEM simulation were determined by a triaxial shear test and an angle of repose experiment. An overburden pressure is applied by a thin layer of heavy particles atop. The initial insertion phase of the penetrator has a crucial impact on the penetration results and is currently done by applying a constant velocity of 1 m/s to the penetrator until the penetrator is fully embedded by particles. Also slower and faster insertion were examined and their influence on the penetration will be discussed. Results of these 3D simulations are reported below.

4 Modeling Results

The results focus on the penetration rates in different soils where each stroke is simulated with the dynamics of the hammer mechanism and the soil response. This allows to study the dynamics of each stroke in the range of milliseconds. Thus, it is possible to see what happens to the hammer mechanism in different soils and what causes its performance exactly by analysing a single stroke cycle.

In the following we present some calculation results for two scenarios, namely a homogeneous ground and a ground containing compacted layers. The bearing capacity in all simulations, where it is not explicitly declared, is calculated by the equation of Terzaghi described in Sect. 3.2. We consider first the cases where the particles composing the soil are purely granular, i.e. not connected by cohesive or adhesive forces. The simplest case is a homogeneous ground, where density, cohesion and the angle of internal friction can have different values, but do not change with depth. Next, a model which includes one or several layers, where these parameters suddenly change with depth, is considered. This could, for example, be a fine grained sandy soil with coarse grained material embedded in certain depths. The second set of results to be presented below includes a non-negligible cohesion of the soil in order to see its influence on the penetration behavior. We will study the same cases as described above, but including the cohesion factor.

4.1 Homogeneous Ground

The penetration performance of the Mole in a cohesionless soil is mainly controlled by two soil parameters: (i) the soil density and (ii) the angle of internal friction. In order to study the relative importance of these two parameters, we choose the quartz sand used for the mole penetration tests recently performed at DLR Bremen as the reference material and use the material parameters determined at the laboratory of the University in Kaiserslautern as reference values: \(\varrho =1550~\mbox{kg}\,\mbox{m}^{-3}\) and \(\varphi =37^{\circ}\). To evaluate the sensitivity of the Mole penetration performance with respect to these two parameters we compute the penetration curve (depth versus time) for different values of \(\varrho \) and \(\varphi\), as listed in Table 2. The gravity acceleration is for Mars conditions, i.e. compared to Earth just 38 % of the acting gravity. The results are plotted in Fig. 6.

Fig. 6
figure 6

Mole penetration into a homogeneous cohesionless soil for different densities and internal friction angles

Full size image
Table 2 Soil parameters used for the computation of mole penetration under the assumption of a homogeneous density and angle of internal friction
Full size table

Here we have assumed that the material is cohesionless, which is a realistic assumption for the quartz sand used in lab tests on Earth, because this material is granular and dry without any salts. However, in the soil to be penetrated by the Mole on its landing place on Mars might contain such components, which could cause some cohesion of the soil. In order to evaluate their possible influence on mole penetration, we have repeated the calculations described above by assuming a non-zero cohesion value. A maximum value for the cohesion of a dry sand is 5 kPa. An extreme case would be wet clayey sand, the cohesion of which can be up to 20 kPa. In order to evaluate the influence of cohesion we used the reference values of the quartz sand as listed in Table 2 and a cohesion value of 5 kPa to mimic dry loamy sand. The results are shown in Fig. 7.

Fig. 7
figure 7

Mole penetration into a homogeneous soil for different densities and internal friction angles, but including a nonzero cohesion value

Full size image

As can be seen, even this relatively low cohesion can cause a significant reduction of the penetration depth reached after the same number of strokes, as compared with the corresponding case without cohesion. In these calculations we have always used 6000 stroke cycles, which corresponds to about 6 hours operation time with a hitting frequency of 1 stroke cycle in 3.7 s. This was the typical frequency used in the penetration tests to be presented later in this paper.

4.2 Layered Ground

Next we explore the penetration performance of the Mole when it is driven into a ground that is not homogeneous in terms of the basic soil parameters, i.e. density, internal friction angle and cohesion, but contains layers in the interior that are compacted and exhibit a larger friction angle (possibly caused by a different particle size distribution or composition) and a nonzero cohesion. Figure 8 shows two cases: the first case (full red line) contains one layer of 1 m thickness beginning in a depth of 1 m and extending to 2 m, while the rest of the region (above and below) consists of loose cohesionless sand. The second example (blue dashed line) is a cohesionless sand layer of 3 m depth atop of a denser cohesive soil with a thickness much larger than the expected mole penetration depth. The values used for the different layers are listed in Table 3. The penetration profiles clearly show the kinks associated with the positions where the soil parameters change discontinuously. When the penetrator tip enters the compacted soil the penetration speed slows down significantly, until the tip has crossed the compacted layer and continues to move into the softer layer below, as illustrated in Example 1. If the compacted layer extends into larger depth, the penetration speed remains slow, as can be seen from Example 2.

Fig. 8
figure 8

Mole penetration into cohesionless soil containing cohesive layers with a larger angle of internal friction and a higher density

Full size image
Table 3 Soil parameters used for the computation of mole penetration under the assumption of a homogeneous density and angle of internal friction
Full size table

4.3 3D-DEM Simulation

In order to validate the accuracy of the 3D-DEM simulation results reported below we have first done a comparison of the simulation results with a lab experiment. Hereby the angle of repose for the sand used as sample material in all our simulations was determined. The angle of repose experiment provides the most important parameter for the DEM simulations, namely the inter-particle friction and the rolling resistance values. A comparison of the stable slope angle derived from lab test and DEM simulation, respectively, can be seen in Fig. 9.

Fig. 9
figure 9

Angle of repose experiment in lab (top) and from a DEM simulation (bottom)

Full size image

The two graphics in Fig. 10 show the total displacements and the induced total stress changes of the particles after one full stroke cycle. The changes in the total stress after one cycle reveals that the stress in the soil is reduced due to the penetration of the Mole and the particles are compacted in the vicinity of the penetrator, in particular near the tip, as can be seen from the total displacements of the particles. At the rear end of the penetrator the particles fall back into the cavity, which results in large displacements of the particles without any compaction.

Fig. 10
figure 10

Left: total displacements of particles due to one stroke cycle. Right: changes in total stress due to one stroke cycle

Full size image

Another point of interest that can be investigated by applying the 3D-DEM model is the resistance force felt by the mole tip and mantle during a stroke cycle. It is shown in Fig. 11. As can be seen, the 3D simulation reveals that this resisting force is in reality not constant (as it is assumed in the pile driving model), but there is a slight increase of the resisting force with displacement. In the DEM simulations the profile of the resisting force also varies depending on the initial soil conditions. Still it can be seen that the resisting force increases rapidly in the beginning and only slightly during the rest of a stroke cycle of the Mole.

Fig. 11
figure 11

Force-displacement curve over a stroke cycle

Full size image

The displacement of the Mole due to the strokes can be seen in Fig. 12. The permanent settlement of the Mole is in good agreement with the results from our simple 1D-model computed by a (much faster) MATLAB program, as can be seen by comparing Fig. 12 with Fig. 2. The timing of the first and second stroke corresponds also in both simulations. The rebound after each stroke is less pronounced in the MatLab calculation than in the DEM simulation.

Fig. 12
figure 12

The relative movements of the tip, the hammer mass and the support mass from the 3D-DEM model

Full size image

5 Comparison with Laboratory Tests

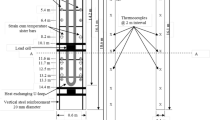
The performance of the InSight Mole was also extensively tested experimentally at DLR Bremen by letting it penetrate vertically into a sand bed of 5.5 m depth bounded by a cylindrical container with 0.8 m diameter, as illustrated in Fig. 13. The soil parameters of the sand used as sample material have been determined with the help of triaxial and shear tests at the soilmechanical laboratory of the University of Kaiserslautern Germany. The loose density of the sand was found to be about \(1550~\mbox{kg}\,\mbox{m}^{-3}\) and the angle of internal friction was determined to be in the range of \(30^{\circ }\) to \(37^{\circ }\).

Fig. 13
figure 13

Experimental setup for the InSight Mole penetration test performed at DLR Bremen

Full size image

The test setup with the relevant dimensions is shown schematically in Fig. 13. The sample material is filled into a container with an internal diameter of 80 cm and a total height of 550 cm. In its starting configuration the mole is typically buried in the sand so that its rear end coincides roughly with the sample surface. This means that the tip is initially buried in a depth of approximately 40 cm, which is enough to start the penetration process and to avoid too large rebounces due to the missing shaft friction.

The initial horizontal position of the mole at the sample surface was in all cases central, i.e. the distance of the mole from the boundary of the container was about 40 cm and the initial orientation was vertical. However, in some cases it was observed that the orientation changed in the course of a penetration test, leading to an inclined trajectory of the Mole w.r.t. the vertical axis of the sample container. Since in our model it is always assumed that the Mole penetration takes place in vertical direction only, this fact could be one of the reasons for deviations between the experimental results and the model calculation. However, in general we still may assume that the distance of the mole from the container walls was always large enough so that the influence of the walls on the penetration behavior can be neglected.

Figure 14 shows the result of a typical penetration test in comparison with several modeling results. The initial situation is that the Mole is already buried one Mole length in the sand, i.e. at the beginning the tip of the Mole resides at a depth of 0.4 m below the soil surface. This condition is important to have some side friction from the beginning in order to avoid rebounds, which would otherwise occur both in the model and in the experiment. It should be noted that after the soil has been penetrated for a few meters the friction of the trailing cable along the hole may start to play a role.

Fig. 14
figure 14

Measured penetration curve of the Insight Mole plotted versus time, as observed by a penetration test in cohesionless sand (dashed blue line), in comparison with modeling results obtained from the extended pile driving model

Full size image

In Fig. 15 penetration processes using different densities and different soil internal friction angles are compared with the laboratory test results. All simulations were performed under earth gravity in an infinite space using the local shear failure assumption for the tip resistance from Sect. 3.4. In the green plot a simulation is performed adding a friction force with quadratic dependence on depth to the rear end of the Mole to consider the trailing cable. The density is \(1360~\mbox{kg}/\mbox{m}^{3}\) with a void ratio of 1 and an internal friction angle of 32 degrees. The light blue penetration curve is done using a loose sand with a density of \(1360~\mbox{kg}/\mbox{m}^{3}\) and an internal friction angle of 30 degrees. The black penetration curve results from an increase of the density to \(1560~\mbox{kg}/\mbox{m}^{3}\), that correspond to a void ratio of 0.7426, and an internal friction angle of 30 degrees. The red penetration curve results from an increase of the internal friction angle to 37 degrees and a density of \(1360~\mbox{kg}/\mbox{m}^{3}\). These soil parameter combinations are just artificial, since the increase of the density would usually cause also in increase of the peak friction angle.

Fig. 15
figure 15

Penetration results of 6000 strokes with different soil parameters and once with additional friction force due to the trailing cable

Full size image

6 Discussion and Conclusions

6.1 Pile Driving Model

Comparing the different modeling results with the observed penetration curve in sand shows that a close match of the model with the experimental data is difficult to achieve if constant values are used for the soil parameters \(\varrho \), \(\varphi \) and \(c\). With constant parameters it is possible to fit the first part of the penetration curve quite well, but then the model curves show first a slower penetration than the observed profile, while in deeper layers the calculated curve again crosses the observed curve indicating a higher penetration velocity than observed. In other words, the model curves with constant soil parameters show a rather “smooth” decay of the penetration velocity with depth, which is caused by the gradual increase of the overburden pressure of the soil, which leads to a corresponding increase of the bearing capacity and the wall friction of the soil.

The observed penetration curve seems to suggest a rather constant penetration speed down to a depth of approximately 3 m, but a rather sharp change to a slower penetration mode beyond 3 m. Such a behavior could be modeled more closely if one allows for depth-dependent values of the soil parameters. In particular the angle of internal friction turns out to be the most sensitive parameter influencing the penetration behavior. In Fig. 14 we have also included the penetration profile into a soil which has the soil properties of loose sand in the uppermost 3 m, but contains a thick compacted layer with different soil parameters below this depth. The kink in the calculated profile when the tip starts to penetrate the compacted layer is very well reproduced. However, in order to reproduce such a profile demands strong changes in the soil parameters. These changes in the soil could be generated by the hammering penetrator, due to compaction of the soil in front of the tip.

Another reason for the rough decay of the penetration rate at 3 m depth from the laboratory experiments could be a change of the failure mechanism. In a loose sand at shallow depth the penetrator can simply compact the soil to the sides, locally near the penetrator, to move forward, while when it gets deeper and the penetrator has compacted already the soil in front of the tip, a ground heave is necessary to move further downwards. Also dilatancy becomes more import as soon as the soil is in a dense state, which would cause a higher peak resistance. Since the changes in the soil during the penetration process can not result out of the one dimensional MatLab simulation, other modeling approaches are necessary to investigate the soil behavior more precisely.

The influence of the trailing cable increases the resistance force in a quadratic way with depth. This results in a distinct decay of the penetration rate as can be seen in Fig. 15. Furthermore, it can be seen that the internal friction angle of the soil has a major influence on the soil resistance. The simulations does not consider the effect of arching in the soil due to the narrow chamber that is used in the laboratory tests. It has to be considered that the arching effects in the soil are not just depth-dependent and also additional arching effects that are generated due to the dynamic penetration need to be considered. For this purpose, more sophisticated numerical simulations of the penetration in a narrow chamber need to be done.

6.2 3D-DEM Simulations

The 3D-DEM simulations reveal that the penetration ability of the Mole depends also on the initial stress distribution in the soil. The insertion of the penetrator influences this stress distribution and can cause a loosening or a bracing of the Mole. Both cases can occur by applying different insertion velocities. Various simulations with different insertion velocities reveal that fast insertion causes a loosening of the horizontal stress in the soil surrounding the Mole and can result in a large rebound of the Mole after the first stroke, due to the force of the support mass acting backwards, which is usually balanced by the shaft friction. A bracing of the Mole due to large horizontal forces may be artificially generated in the DEM model by a too slow insertion of the penetrator and a constant movement in the vertical direction. This can have the fatal consequence that there occurs no significant settlement due to the hammering action during a single stroke cycle. The artificial bracing can be avoided by integrating the Moles sideways movements and rotation.

If multiple stroke cycles are able to cause a loosening or bracing of the Mole, this could be another reason for the abrupt change in the penetration rate observed in the DLR laboratory tests described in Sect. 5. Furthermore, the results from the DEM simulations have already shown that a reduction of stresses due to the cyclic loading can occur. A fast insertion of the penetrator reveals that local loosening of the soil surrounding the penetrator is possible also in large depths, due to arching effects.