The Effect of Sunspot Weighting

Abstract

Although W. Brunner began to weight sunspot counts (from 1926), using a method whereby larger spots were counted more than once, he compensated for the weighting by not counting enough smaller spots in order to maintain the same reduction factor (0.6) as was used by his predecessor A. Wolfer to reduce the count to R. Wolf’s original scale, so that the weighting did not have any effect on the scale of the sunspot number. In 1947, M. Waldmeier formalized the weighting (on a scale from 1 to 5) of the sunspot count made at Zurich and its auxiliary station Locarno. This explicit counting method, when followed, inflates the relative sunspot number over that which corresponds to the scale set by Wolfer (and matched by Brunner). Recounting some 60,000 sunspots on drawings from the reference station Locarno shows that the number of sunspots reported was “over counted” by ${\approx}\,44~\%$ on average, leading to an inflation (measured by an effective weight factor) in excess of 1.2 for high solar activity. In a double-blind parallel counting by the Locarno observer M. Cagnotti, we determined that Svalgaard’s count closely matches that of Cagnotti, allowing us to determine from direct observation the daily weight factor for spots since 2003 (and sporadically before). The effective total inflation turns out to have two sources: a major one (15 – 18 %) caused by weighting of spots, and a minor source (4 – 5 %) caused by the introduction of the Zürich classification of sunspot groups which increases the group count by 7 – 8 % and the relative sunspot number by about half that. We find that a simple empirical equation (depending on the activity level) fits the observed factors well, and use that fit to estimate the weighting inflation factor for each month back to the introduction of effective inflation in 1947 and thus to be able to correct for the over-counts and to reduce sunspot counting to the Wolfer method in use from 1894 onwards.

1 Introduction

In 1945, Max Waldmeier became Director of the Zürich Observatory. In 1961, Waldmeier published the definitive Zürich sunspot numbers up until 1960 (Waldmeier 1961). He noted that “Wolf counted each spot – independent of its size – but single. Moreover, he did not consider very small spots, which are visible only if the seeing is good. In about 1882 Wolf’s successors changed the counting method, which since then has been in use up to the present. This new method counts also the smallest spots, and those with a penumbra are weighted according to their size and the structure of the umbra”. Waldmeier (1948, 1968) described the weighting scheme as follows “Später wurden den Flecken entsprechend ihrer Größe Gewichte erteilt: Ein punktförmiger Fleck wird einfach gezählt, ein größerer, jedoch nicht mit Penumbra versehener Fleck erhält das statistiche Gewicht 2, ein kleiner Hoffleck 3, ein größerer 5”.¹ However, Wolfer (1907) explicitly stated: “Notiert ein Beobachter mit seinem Instrumente an irgend einem Tage $g$ Fleckengruppen mit insgesamt $f$ Einzelflecken, ohne Rücksicht auf deren Grösse, so ist die daraus abgeleitete Relativzahl jenes Tages $r = k(10g+f)$”.² We can verify that Wolfer, contrary to Waldmeier’s assertion that the Zürich observers began to use weighting “around 1882”, did not weight the spots according to Waldmeier’s scheme by comparing Wolfer’s recorded count with sunspot drawings made elsewhere, e.g. Figure 1.

Figure 1

Drawing from Mount Wilson Observatory (MWO) of the single spot with penumbra on 21 November 1920. The insert at the left shows a similar group observed at MWO on 5 November 1922. For both groups, Wolfer should have recorded the observation as “1.3” if he had used the weighting scheme, but they were recorded as “1.1” (one group, dot, one spot), thus counting the large spot only once (i.e. with no weighting).

There are many other such examples (e.g. 16 September 1922 and 3 March 1924) for which MWO drawings are available at ftp://howard.astro.ucla.edu/pub/obs/drawings and even earlier e.g. 20–23 June 1912 for which we have drawings from the Jesuit-run Haynald Observatory (Kalocsa, Hungary: http://fenyi.sci.klte.hu/deb_obs_en.html , see Slide 11 of www.leif.org/research/SSN/Svalgaard3.pdf ). We can thus consider it established that Wolfer did not apply the weighting scheme. This is consistent with the fact that nowhere in Wolf’s and Wolfer’s otherwise meticulous yearly reports in Mittheilungen über die Sonnenflecken series is there any mention of a weighting scheme. We recall the format of Wolf’s published observations (Figure 2).

Figure 2

The number of groups [$g$] and the number of spots (Flecken) [$f$] for each day is recorded as “$g$.$f$”, (Wolf 1856). On days where the seeing was poor or when Wolf used a smaller telescope, the entries are in small type font or have no spot count.

To calculate the relative sunspot number, [$R$], e.g. on 4 April (IV), Wolf used the well-known formula $R = k (10\times12 + 58) = 178$, where the scale factor [$k$] is 1.00 for Wolf himself.

Clette et al. (2014) reviewed the evidence of other solar indices for time when the weighting was introduced and also determined the magnitude of the effect. Svalgaard (2014) provided further details of the weighting issue. In the present article we further explore, quantify, and characterize how much the weighting of the sunspot count affects the Relative Sunspot Number.

2 Weighting at Locarno: The Reference Station

At the reference station “Locarno” situated in the city of Locarno on the northern shore of Lago Maggiore in the Swiss canton of Ticino, weighting of the sunspot count has been employed since the beginning in 1957, closely following Waldmeier’s prescription (Cortesi et al. 2016). To assess the magnitude of the increase due to weighting, Svalgaard undertook to examine all the nearly 4000 drawings with individual counts of groups and spots in each group made at Locarno ( http://www.specola.ch/e/drawings.html ) for the past decade (and some years before that) and to recount the spots without weighting. An example of a drawing with the original weighted counts and the recounted number of actual spots present is shown in Figure 3.

Figure 3

Drawing from Locarno showing the effect of weighting for the five groups present. Magnified views of the groups allow assessing the weighting, e.g. to see that group 141 consists of one spot with a penumbra, which was assigned weight 3 according to Waldmeier’s rule. For this drawing the weight factor of the day becomes 1.36.

At times, the observer did not count and report the very smallest spots even if they were included in the drawing, as seen in Figure 4.

Figure 4

Drawing from Locarno showing tiny spots that were not counted (in green circles) for group number 70. Observers might differ on the “rule” for omitting tiny spots, but the number of omitted spots is in any case small overall. A useful addition to the report would be the number of omitted spots, if it was not zero.

In case of the rare very large groups, it is quite a challenge to determine the actual spot count, as seen in Figure 5, especially if not all the weakest spots were counted. In this rather extreme case, the top drawing shows 74 spots, but the weighted count is only 58, which clearly shows that many spots (at least $74 - 58 = 16$) were not counted. One way to determine the number of uncounted spots would be to weight the large spots (none of which are omitted) according to Waldmeier’s prescription, then subtract the sum of all the weighted values, and finally add the number of spots that were weighted. The figure shows how that would work. The shaky assumptions underscore the importance of recording the number of omitted spots, or what we could call the “equivalent” number of omitted spots, if some tiny spots were “lumped together”.

Figure 5

(Top) Drawing from Locarno showing a large, complicated group with many spots that were not counted. The number of spots according to the drawing was 74, but the weighted count was only 58. There were 13 spots (and umbrae) with weights of 3 and 2. The sum of the weighted spots was 35, so that the number of spots with weight 1 must be $58 - 35 = 23$, to which we must add 13 for a total of (actual?) spots of 36. This example is, admittedly, extreme, but such is the material that we have to work with. (Bottom) Drawing of group 134, which on Svalgaard’s count had 40 actual spots (and umbrae). The reader is invited to count as well.

To verify that the re-count is valid, i.e. that Svalgaard has understood and correctly applied the Waldmeier weighting scheme, the observer Marco Cagnotti in Locarno had agreed to maintain a (double-blind) parallel count of unweighted spots on a continuing basis since 1 January 2012, following a brief trial in August 2011, and the unweighted count is now a part of the routine daily reports. Figure 6 shows that Svalgaard and Cagnotti very closely match each other in applying the weighting scheme, thus sufficiently validating the approach.

Figure 6

Comparison of the number of sunspots per day determined by Cagnotti (blue) and Svalgaard (green) without weighting, i.e. by counting each spot singly as prescribed by Wolfer, with the number reported by Locarno (pink) employing the Waldmeier weighting scheme. The insert shows the nearly identical distribution of unweighted counts in bins of five.

Is the weight factor observer dependent? With a novice one might be inclined to think so, but with training, observers tend to converge to agreement. We can compare the weighted counts and the number of groups reported by the veterans Cortesi and M. Bianda and the new observer Cagnotti from 2008 to the present (Figure 7): there does not seem to be much systematic difference with the possible exception of a very recent decline of Cortesi’s weight factor. Observer Andrea Manna (AM) has a weight factor that is systematically about 0.04 lower than the other observers, in spite of seeing the same number of groups, so weighting does depend weakly on the observer.

Figure 7

(Left) The weight factor for Locarno observers Cortesi (SC, blue, since 1957), Cagnotti (MC, red, since 2008), Manna (AM, open dashed blue, since 1991), and Bianda (MB, green, since 1983). (Right) The number of groups per day for each year reported by the same observers.

3 The Weighting Quantified by the Locarno Observers

Since August 2014, the observers in Locarno have augmented their observations of the number of groups, [$g$], and of weighted spots, [$f$], with a count of actual, non-weighted spots, [$s$] (denoted “LW” at the right on the drawing – LW is the WDC SIDC/SILSO code designation for unweighted Locarno counts), allowing us the calculate the weight factor as $w = (10g + f)/(10g + s)$ (Figure 8).

Figure 8

The recent Locarno determination of both the weighted [$f$] and of the unweighted number of sunspots [LW]. For this day, the weight factor becomes $w = (30+17)/(30+8) = 47/38 = 1.237$.

Figure 9 shows the weight factors determined from the Locarno observations since August 2014. The red curve shows the 27-day running average of the weight factor calculated using the relationship determined by Clette et al. (2014). It is clear that the Clette et al. (2014) expression for the weight factor agrees well with the observations for this level of solar activity. It is also clear that the value (1.116) marked by the blue line, that was suggested by Lockwood, Owens, and Barnard (2014), is not a good fit to the observations and as such must be discarded.

Figure 9

Weight factors (pink dots) computed from the recent Locarno daily data. The red curve shows the 27-day running average of the weight factor calculated using the relationship determined by Clette et al. (2014). The green curve at the bottom of the Figure shows the 27-day running average sunspot number (V2).

Figure 10 shows the Locarno weight factor as determined by Svalgaard (blue symbols) for both solar-maximum and solar-minimum conditions and continued (red symbols) by the Locarno observers until the present [and hopefully beyond]. The green dots show yearly averages.

Figure 10

Locarno weight factor as determined by Svalgaard (blue symbols) for both solar-maximum and solar-minimum conditions and continued (red symbols) by the Locarno observers until the present. The green dots show yearly averages of the weight factor when there were spots to count; note the weak solar cycle modulation.

The problem that we need to solve is not really to calculate the weight factor for the current data. We do not need to: we know what the factor is for every day (with an observation). The problem is to determine the weight factor retroactively for the interval 1947 – 1980. For the Zürich data before 1980 we know the number of groups for each month and the relative sunspot number (encumbered by weighting because all observers were normalized to Zürich) for each day (and hence for each month). Can we correct the sunspot number for weighting based on this? Before we attack this problem, we consider the daily data more closely.

On a daily basis, the dependences of the weight factor on $\mathit{Ri}$ and on the number of groups are decidedly nonlinear, with a rapid drop-off towards low activity, but even a slightly incorrect weight factor applied to a low value will have very little effect on the result. However, it is clear that the daily weight factor is not merely a simple function of the relative number [SSN] or of the group count [$\mathit{GN}$] alone, but is a function of both (and of the observer as well): $w = F ( \mathit{SSN}, \mathit{GN}, \mathit{Obs})$. The situation is further complicated by SSN being also a function of $\mathit{GN}$, Obs, and of the number of spots [$\mathit{SN}$]: $\mathit{SSN} = Q (\mathit{GN}, \mathit{SN}, \mathit{Obs})$, so that we should write $w = F(Q(\mathit{GN}, \mathit{SN}, \mathit{Obs}),\mathit{Obs})$. As the dependence on the Zürich observers is slight, we ignore the observer differences as is also necessitated by the fact that we don’t know who the observers were for each day during 1947 – 1980. To separate the influence of $\mathit{GN}$ and $\mathit{SN}$ we now plot the daily Locarno weight factor as a function of the reported (i.e. weighted) $\mathit{SN}$ for bins of each group number (Figure 11).

Figure 11

For each bin of group number $\mathrm{G} = 1, 2, 3, \dots$ the graphs show the Locarno weight factor for recounted days of 1997 – 2015 as a function of the reported (thus weighted) number of sunspots (note: not the sunspot number). A least-squares fit to a logarithmic function of the sunspot count is derived for each group.

Using the functional fits derived from Figure 11, we calculate the weight factor on a grid of one unit of GN and five units of SN to obtain a visual representation of the weight factor “landscape” function [$w = F(Q(\mathit{GN}, \mathit{SN}))$], as shown in Figure 12 (left panel). The “jagged” appearance could be improved by suitable smoothing, but the gain seems marginal. We can thus quantify the average effect of Weighting given the group and (reported) spot counts for daily values, should such values become available.

Figure 12

(Left) Contour map of the daily Locarno weight factor for 1997 – 2015 as a joint function of the reported (thus weighted) number of sunspots [$S$] and of the number of groups [$G$]. (Right) Contour map of the monthly Locarno weight factor for 2003 – 2015 as a function of both $S$ and $G$.

It is also of interest to repeat the analysis for monthly values, e.g. as given in Waldmeier (1968, 1978), as the scatter is much smaller, cf. Figure 12 (right). The results are shown in Figures 13 and 12 (right panel).

Figure 13

(Left) The Locarno weight factor for each month for 2003 – 2015 dipping down to unity for no activity and rising to 1.2 for the moderate activity at the maximum of the weak Solar Cycle 24. At the bottom we show the temporal variation of the International Sunspot Number Version 1 (red circles), which is very closely the same as the Locarno relative number multiplied by the nominal $k$-factor of 0.60 (blue curve). (Right) The monthly weight factors as a function of the International Sunspot Number. The nonlinear function shown is a decent fit to the weight factor data.

4 Correcting for Weighting

For monthly values, the group count and the spot count are constrained to a rather narrow diagonal band in Figure 12 (right) which suggests that a one-dimensional relationship with the relative sunspot number, such as given in Figure 13 (right), might be sufficient for correction of said number to an unweighted value. We can test this assertion by calculating the weight factor using that formula ($w = 1.0044 + 0.0398 \ln(R_{i})$; $R_{i} \geq 0.2$), dividing the International Sunspot Number since 2003 by the computed weight factor, and comparing the thus corrected number with the unweighted relative number obtained by recounting the spots without weighting on the Locarno drawings, see lower left panel of Figure 13. The agreement is excellent, with a linear coefficient of determination $R^{2} = 0.99$.

Under the assumption that the weight factor function is also valid for the Waldmeier era at Zürich we can now correct the Zürich sunspot number for the inflation introduced by the weighting scheme, Figure 14 and Table 1.

Figure 14

(Top) Comparison of monthly values of the International Sunspot Number as published by the WDC-SILSO in Brussels (Version 1, before 1 July 2015), pink curve, and the values corrected for weighting (black curve) using the weight factors shown by the upper blue symbols. (Bottom) The monthly values smoothed (using the standard method introduced by Wolf). Blue-open symbols show yearly values of unweighted counts from Locarno, i.e. not relying on the weight factor formula. Again, the agreement is excellent.

Table 1 Old $R_{i}$ is the International Sunspot Number (version 1.0), Corr. $R_{i}$ is Old $R_{i}$ divided by the Weight Factor (calculation actually performed month-by-month, then averaged per year). “New” $R_{i}$ is Corr. $R_{i}$ divided by 0.60, but does not quite match SILSO version 2.0 because of further (small) corrections to the latter.

In constructing Figure 14 (and in this paper generally) we used the pre-1 July 2015 values of the International Sunspot Number without the corrections and reassessments introduced as of that date. It is important to take into account that the weight factor varies with the sunspot number itself, so one cannot (except as a first, crude approximation) use a constant weight factor throughout. The average yearly weight factors given in Table 1 are valid regardless of the sunspot numbers determined for each year and of the adopted $k$-factors. The factors were derived from the formula of Figure 13 using the nominal $k$-factor of 0.60, so its $R_{i}$-argument could be written $R_{i} = 0.6 R_{k} /k$, where $k$ is the $k$-factor for the relative sunspot number $R_{k}$. For $R_{k}$ from the ‘new’ SILSO sunspot number series, $k$ is equal to unity.

An interesting question is how this “corrected New $R_{i}$” (which is simply SILSO $\mathrm{V}1 R_{i}$ freed from weighting and brought onto Wolfer’s scale by removing the obsolete $0.6 k$-value scale factor) compare with WDC-SILSO $\mathrm{V}2 R_{i}$ released on 1 July 2015. Figure 15 provides a preliminary answer to this question.

Figure 15

Dark-blue diamonds [V1 Ri – old official Ri], scaled down to the “Corr. Ri”, light-blue triangles], by dividing by the weight factor $[w]$ (upper pink squares). The “Corr. Ri” is then scaled to the Wolfer scale (New Ri, red-open circles) by dividing by the no longer used $k$-value 0.60 and compared with SILSO V2 Ri (red filled circles). The ratio $f = \mathrm{V}2$/New is shown by the brown dots.

The ratio $f = \mathrm{V}2$/New (brown dots) is generally close to unity, although there is a weak solar cycle variation, probably due to an inadequate (constant) $w$-factor used for SILSO V2. The ratio varies irregularly for the years in the rectangle, possibly indicating some further adjustments (unexplained, but probably arising from issues with the data from Locarno). The irregularity is not serious near solar minima, as the sunspot number is small at such times, but the ${\approx}\,10~\%$ difference at the maximum and declining part of Sunspot Cycle 23 is a concern that should be addressed and explained.

5 Comparison with Sunspot Areas

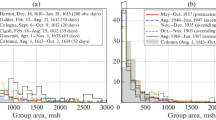
Up to this point we have been concerned with direct measurement of the effect of weighting, which is, of course, the preferred and correct approach. Historically, the “discovery” (Svalgaard, 2007, 2010, 2012, 2014) of the weighting came about by comparing the International Sunspot Number to other solar variables and activity indices and noticing (and quantifying) the Waldmeier “Discontinuity” in 1947. Comparing with sunspot areas (Figure 16), shows the discontinuity clearly enough, as well as showing that there is no discontinuity prior to 1947, e.g. related to change of observers from Wolf to Wolfer (in 1894) and finally to Brunner (in 1926).

Figure 16

The yearly averaged projected (i.e. observed) area of the solar disk covered with sunspots in millionths of the area of the visible disk (Balmaceda et al. 2009; red curve with small dots and left-hand scale) compared to the International Sunspot Number Version 1 (blue curve with small plus-symbols and right-hand scale) scaled to match the areas before 1947. For yearly averages the nonlinearity of the relationship between sunspot numbers and sunspot areas becomes small enough that simple linear scaling largely suffices to compare the two measures. The rectangle near year 1970 has a height of 20 sunspot units. The green vertical line in 1947 shows where we would place the discontinuity.

In particular, Brunner and Wolfer seem to have the same calibration relative to the sunspot areas. Brunner also explicitly stresses (e.g. Brunner 1945) that his reduction factor to Wolf’s old value is the same, 0.6, as Wolfer’s. This is also clearly seen in Figure 17 comparing the number of spots reported by the Zürich (and Locarno) observers with the sunspot areas and the group number (Svalgaard and Schatten 2016).

Figure 17

Comparing the number of sunspots (note: not the relative sunspot number) to the (scaled) sunspot areas (gray curve, upper panel) and the group number (gray curve, lower panel). The average of Wolfer, Broger, Brunner, and Waldmeier before 1947 is shown by a thick-blue curve. The individual observers’ data are shown by light-blue curves. After 1947, the data are color-coded (and labeled) by observer (Waldmeier, red; Locarno before 2000, yellow; recent Locarno, purple).

Incidentally, the good agreement between the several sunspot observers (before 1947) and the sunspot areas shows that the sunspot areas are likely to be correct as no systematic drift or difference is noticeable.

6 Weighting Before Waldmeier

William Brunner (1945) wrote in his last contribution to the Astronomische Mitteilungen: “Die Grundlage der Zürcher Statistik für die Sonnenfleckenhäufigkeit bilden die aus Beobachtungen von $g$ und $f$ ermittelten täglichen Wolfschen Relativzahlen $r = k (10g + f)$, wobei $g$ die Anzahl der beobachteten Fleckengruppen, $f$ die Gesamtzahl der in diesen Gruppen vorhandenen Einzelflecken und $k$ eine von Beobachter und instrument abhängige Konstante bedeuten.”³

Brunner thus stipulated that $f$ is the number of all single spots, with no weighting at all, just simple counting. This is consistent with all previous Mitteilungen. Weighting is never mentioned; on the contrary, it was always emphasized that counting was done “as always before”. On the other hand, weighting was clearly practiced by some Zürich observers, e.g. Max Broger. Our problem is to identify who and when and with what effect, if any. Brunner (1936) let slip a hint (“In large centers of activity one is inclined – and this perhaps rightly – to give some single spots according to their sizes a different weight”) that some weighting was likely performed. Figure 18 shows three drawings from Mount Wilson Observatory. The leftmost is for a day where Wolfer reported observing one group with one spot (1.1). For the middle drawing, Wolfer reported one group with two spots (1.2). The weighted counts for these spots with penumbra would have been 1.3 and 1.6 (or perhaps 1.5), respectively, attesting that Wolfer did not weight at those times. The rightmost drawing is of a sole, large spot reported as 1.4 by Brunner, showing that he counted the single spot with weight 4. Several other examples of such weighting by Brunner can be found, e.g. on 16 August 1930, 5 March 1931, 5 February 1932, 29 March 1932, and 27 May 1935.

Figure 18

Mount Wilson Observatory drawings for the dates indicated where the Sun had only a single sunspot group on the disk. The two leftmost were also observed by Wolfer and given (red text) in the standard Wolf notation (groups.spots), indicating no weighting was performed. The rightmost group was observed by Brunner and reported as 1.4, indicating that this single, large spot was counted with weight 4.

So, we must consider it established that Brunner weighted at least some of the spots, perhaps especially very large spots, which would explain the dearth of 7’s for Brunner on Figure 33 of Clette et al. (2014). The questions are now how large the effect of this would be on the sunspot number and how consistently the weighting was performed. Because Brunner reports that his overall reduction factor is the same as Wolfer’s, the inflation caused by weighting large spots must be precisely compensated by an under-count of small spots, such as to leave no overall effect of the weighting. Figure 19 (right-hand panel) shows directly that on average, Brunner and Wolfer reported the same number of spots (the slope of the linear fit though the origin is unity: $1.003\pm0.011$) during the time (1926 – 1928) of their overlapping observations, but also shows that for low solar activity (number of spots less than, say, 75), Brunner reports more spots than Wolfer, while the opposite is the case for high activity with number of spots larger than 75. A large number of spots means that there are many small spots; in fact, high sunspot numbers are dominated by the number of small spots which can run in the hundreds.

Brunner reminds us that “Wolf hat auch größere Hofflecken als 1 gezählt und nicht auf die structur und Auflösung des Kerns in Teilkerne geachtet und von den kleinsten Flecken nur mitgenommen, was bei genügend gutem Bild auf den ersten Blick su sehen ist”,⁴ as being the principal reason for the 0.6 reduction factor. In addition, Wolf could not even see the smallest spots anyway with his handheld portable small telescope in use after 1861.

If the Locarno observers faithfully followed Waldmeier’s prescription for weighting (presumably assured by Waldmeier’s ongoing quality control) and if Waldmeier just took over the procedure unchanged from Brunner (and as claimed by Waldmeier (1961) even from Wolfer, going all the way back to 1882) we would expect the distribution of the ratios of the weighted number of spots to the unweighted as a function of activity to be the same for Brunner as for Locarno. Figure 19 (left) shows that it is not.

Figure 19

(Left) The slope of the correlation between weighted spots reported by Locarno (blue circles) and unweighted spots at same for 2003 – 2015, between spots reported by Broger (pink squares) and unweighted spots reported by Wolfer for 1897 – 1935, and between spots reported by Brunner (green triangles) and unweighted spots reported by Wolfer 1926 – 1928, as a function of the maximum unweighted sunspot count used for the correlation. (Right) Correlation between daily values of Brunner’s reported (with some weighting) spot count and Wolfer’s reported unweighted count.

It is clear that the effect of (assumed) weighting by Brunner (and Broger) does not follow the same distribution as that for Locarno (and presumably Waldmeier), but that the effect is much smaller for high solar activity (with many spots) explaining why Brunner could maintain the same reduction factor as Wolfer. The effect of weighting for high solar activity is what essentially determines the amplitude or size of the sunspot cycles and thus heavily influences the reduction factor.

7 What is a Group?

Comparing the relative sunspot number with various other indices in order to assess the effect of weighting relies on the assumption that the “other half” of the relative sunspot number – 10 times the number of groups – has had a constant calibration over time. Kopecký, Kuklin, and Růžičková-Topolová (1980) cite the Zürich observer A. Zelenka drawing attention to the possible inflationary effect of the introduction of the Waldmeier Group Classification around 1940. We discussed the problem in Clette et al. (2014) and in Svalgaard and Schatten (2016), and show here just some examples (Figure 20).

Figure 20

(Left) Group designations from Locarno drawings showing over-count compared to what simple proximity would dictate. (Right) Group designations from Schwabe’s drawings (Adapted after Pavai et al. 2015) showing under-count. The two groups in red ovals would most likely be counted as four groups today.

Before the advent of magnetic measurements, a sunspot group was defined solely on the basis of its morphology and location relative to other groups. Sunspot groups were at first considered to be merely spatially separate assemblies of sunspots. Beck (1984) and Friedli (2009) recall that after the Waldmeier (1938) Classification was introduced, the evolution of a group became a determining factor in the very definition of a group, which now, in addition to be a spatially isolated collection, also must evolve as an independent unit, going through (at least partly) the evolution sequence of the Waldmeier classification.

If Wolfer is to be the new standard it would seem that earlier groups are under-counted (e.g. very pronounced for the Staudach data (Svalgaard 2017)), while later groups are over-counted. This has been taken into account in the construction of the group number, but more research is needed to integrate that with the sunspot number. In Clette et al. (2014) we found the over-count to be 7.5 %. For the groups observed at Locarno since then, the over-count is 7.7 %. This inflates the relative sunspot number by 4 – 5 %.

8 The Weighting Effect Seen in the Ionosphere

Above ${\approx}\,250~\mbox{km}$ altitude, the primary constituent of the Earth’s atmosphere is atomic oxygen, which can be ionized by EUV radiation with wavelength below 103 nm. The resulting conductive air is called the F-layer. Because the density is so low, recombination is so slow that the F-layer persists even during the night. During the day, the F-layer splits into two layers, with F2 being at the highest altitude. The F2 layer is a dependable reflector of radio signals as it reflects normal-incident frequencies at or below the (observable) critical frequency controlled by the EUV flux and hence by solar activity. Ostrow and PoKempner (1952) in a careful study of the critical frequency 1934 – 1952 that was observed at Washington D.C. found that the relationship with the sunspot cycle was not stable, but changed during the rise of Cycle 18 and concluded that “the Zürich sunspot number is not an entirely satisfactory index of the solar activity responsible for ionospheric ionization” (Figure 21). We can see today that the relationship is not at fault, but the sunspot number, due to the introduction of effective weighting.

Figure 21

12-month running averages of the monthly median critical frequency [$\mathrm{f}^{\circ}\mathrm{F}2$] (MHz) versus 12-month running averages of monthly Zürich sunspot numbers for local night $00^{\mathrm{h}}$ (left) and local day ($12^{\mathrm{h}}$) at Washington D.C. (adapted after Ostrow and PoKempner 1952). The (red) arrows show that a 20 % correction of the sunspot number during the rise of Cycle 18 restores the strong, uniform relationship between critical frequency and (corrected) sunspot number.

A dynamo current in the E-layer where the density is high enough produces a diurnal magnetic effect (discovered in 1722) observable on the ground and also shows the same clear discontinuity in ${\approx}\, 1947$ (Svalgaard 2016).

9 Conclusions

In 1947, Waldmeier formalized the weighting (on a scale from 1 to 5) of the sunspot count made at Zürich and its auxiliary station Locarno, whereby larger spots were counted more than once. This counting method inflates the relative sunspot number over that which corresponds to the scale set by Wolfer and Brunner. Brunner had also weighted the largest spots, but evidently compensated by not counting enough small spots such that the overall effect on the sunspot number turned out to be nil. Svalgaard re-counted some 60,000 sunspots on drawings from the reference station Locarno and determined that the number of reported sunspots was “over counted” by 44 % on average, leading to an inflation (measured by a weight factor) in excess of 1.2 for high solar activity. In a double-blind parallel counting by the Locarno observer Cagnotti, we determined that Svalgaard’s count closely matches that of Cagnotti, allowing us to determine the daily weight factor since 2003 (and sporadically before). We find that a simple empirical equation fits the observed weight factors well, and we use that fit to estimate the weight factor for each month back to the introduction of effective weighting in 1947 and thus to be able to correct for the over-count and to reduce sunspot counting to the Wolfer method in use from 1894 onward. The Locarno observers have counted spots since August, 2014 both with and without weighting, and the unweighted (real) spot count is now used in determining the official relative sunspot number.