Comparison of New and Old Sunspot Number Time Series

Abstract

Four new sunspot number time series have been published in this Topical Issue: a backbone-based group number in Svalgaard and Schatten (Solar Phys., 2016; referred to here as $\mathit{SS}$, 1610 – present), a group number series in Usoskin et al. (Solar Phys., 2016; UEA, 1749 – present) that employs active day fractions from which it derives an observational threshold in group spot area as a measure of observer merit, a provisional group number series in Cliver and Ling (Solar Phys., 2016; $\mathit{CL}$, 1841 – 1976) that removed flaws in the Hoyt and Schatten (Solar Phys. 179, 189, 1998a; 181, 491, 1998b) normalization scheme for the original relative group sunspot number ($R_{\mathrm{G}}$, 1610 – 1995), and a corrected Wolf (international, $R_{\mathrm{I}}$) number in Clette and Lefèvre (Solar Phys., 2016; $S_{\mathrm{N}}$, 1700 – present). Despite quite different construction methods, the four new series agree well after about 1900. Before 1900, however, the UEA time series is lower than $\mathit{SS}$, $\mathit{CL}$, and $S_{\mathrm{N}}$, particularly so before about 1885. Overall, the UEA series most closely resembles the original $R_{\mathrm{G}}$ series. Comparison of the UEA and SS series with a new solar wind $B$ time series (Owens et al. in J. Geophys. Res., 2016; 1845 – present) indicates that the UEA time series is too low before 1900. We point out incongruities in the Usoskin et al. (Solar Phys., 2016) observer normalization scheme and present evidence that this method under-estimates group counts before 1900. In general, a correction factor time series, obtained by dividing an annual group count series by the corresponding yearly averages of raw group counts for all observers, can be used to assess the reliability of new sunspot number reconstructions.

1 Introduction

For over two decades, following the introduction by Hoyt, Schatten, and Nesmes-Ribes (1994) of the group sunspot number as an alternative to the Wolf or international number (Berghmans et al. 2006; Clette et al. 2007), the solar community has lived with two sunspot numbers that differ significantly before about 1885. This divergence provided the motivation for the Sunspot Number Workshops (Cliver, Clette, and Svalgaard 2013, 2015, Clette et al. 2014) and this Topical Issue. In the present volume, four new sunspot number time series (Svalgaard and Schatten 2016; Usoskin et al. 2016; Cliver and Ling 2016; Clette and Lefèvre 2016) are proposed. The Svalgaard and Schatten (2016) and Usoskin et al. (2016) series are intended as replacements for the original group number (Hoyt and Schatten, 1998a, 1998b), while the Clette and Lefèvre (2016) series is a correction of the Wolf or international number. The Cliver and Ling (2016) group number is a provisional series that examines the effect of flaws in the Hoyt and Schatten construction.

The principal differences between the four new series concern (1) the normalization scheme used to put observers on equal footing, (2) the choice of primary or reference observers, (3) the linkage of primary observers to non-overlapping secondary observers, and (4) the data base used. We consider each of these in turn.

The normalization methods for the two new principal group sunspot numbers that have been proposed, viz., those of Svalgaard and Schatten (2016) and Usoskin et al. (2016), are quite different. For each observer, Svalgaard and Schatten compared annual averages of group counts with those of a standard observer for the interval of overlap, using a linear fit forced through zero. They then used the slope of the regression line to scale the group counts of the secondary observer to those of the primary observer. Following Hoyt and Schatten (1998a, 1998b), we refer to such normalization factors as $k$-factors. To obtain their calibration matrices for each observer, Usoskin et al. (2016) first constructed a cumulative probability function ($P(A)$) of the active day fraction ($A$) for their Royal Greenwich Observer (RGO) reference observer (Willis et al., 2013a, 2013b, 2016a, 2016b; Erwin et al. 2013), which was assumed to record all sunspot groups (i.e., the RGO was taken to be a perfect observer). They repeated this step to obtain $P(A,S_{\mathrm{S}})$ functions for a set of hypothetical imperfect observers that were assumed to only report sunspot groups with total areas greater than or equal to a fixed threshold ($S_{\mathrm{S}}$), with $S_{\mathrm{S}} \geq 1$ millionth of a solar disk, ${\geq}\,5$ millionths of a solar disk (msd), ${\geq}\,10~\mbox{msd}$, ${\geq}\,15~\mbox{msd}$, etc., ranging up to ${\geq}\,50~\mbox{msd}$ and beyond. Then, for each actual observer, they used a Monte Carlo method that took into account the fraction of days of observation ($f$) over their entire observing interval to create an ensemble of calibration curves $P(A,S_{\mathrm{S}},f)$ from which $S_{\mathrm{S}}$, with uncertainties, could be determined. In this normalization method, a low $S_{\mathrm{S}}$ value will correspond to a low $k$-factor. Cliver and Ling (2016) used the observer normalization approach of Hoyt and Schatten (1998a, 1998b), which defined a $k$-factor for a given observer to be the ratio of the summed group counts of a primary observer to those of the (secondary) observer for days on which both reported at least one group. The fourth sunspot time series that we consider, the Wolf (W) or relative international number ($R_{\mathrm{I}}$), is defined to be

$$ W = k \times (10 \times G + S), $$

(1)

where $k$ is the normalization factor for an observer relative to a primary observer, and $G$ and $S$ are the numbers of groups and spots, respectively, observed on a given day. For the Wolf number, which was constructed at the Swiss Federal Institute of Technology in Zürich from 1855 – 1980 and produced thereafter by the World Data Center for the Sunspot Index and Long-term Solar Observations (SILSO) in Brussels, successive primary observers following Wolf (specifically, Wolfer, Brunner, Waldmeier, and Cortesi) maintained by inter-comparison a $k$-factor of 0.6 to extend Wolf’s sunspot number time series after his death in 1893. The $k$-factors for auxiliary or secondary observers in the Zürich/Brussels network of stations were defined to be the ratio of the Wolf number of the primary observer to that of the secondary observer for common observing days. Transitions between primary observers did not always go smoothly, however, as documented in Clette et al. (2014, 2016), necessitating some of the corrections implemented by Clette and Lefèvre (2016) for the Wolf or international sunspot number.

There is no consensus on the choice of the primary observer or observers for the various normalization schemes. Svalgaard and Schatten (2016) used a series of primary “backbone” observers, spanning the indicated intervals: Locarno (1950 – 2015), Koyama (1920 – 1996), Wolfer (1841 – 1944), Schwabe (1794 – 1883), and Staudach (1739 – 1822). Cliver and Ling (2016) followed Hoyt and Schatten (1998a, 1998b)¹ and used the RGO (1874 – 1976) as their primary observer, after correcting for an apparent inhomogeneity in the RGO group counts from 1874 – 1915. As noted above, the Wolf (international) number used a series of individual primary observers. Going forward, however, to better ensure the consistency of the series over time, a core group of high-quality observers selected from the SILSO network will be used to provide a composite reference (Clette et al. 2016). Usoskin et al. (2016) used the RGO as their primary observer for the 1900 – 1976 interval, avoiding the early 1874 – 1899 part of the series because of the inhomogeneity pointed out by Clette et al. (2014) and Cliver and Ling (2016).

A key problem common to all normalization schemes involves how to scale secondary observers to primary observers with whom they do not overlap. The standard approach to this problem, e.g., Hoyt and Schatten (1998a, 1998b) is to compare a non-overlapping secondary observer to an overlapping secondary observer that has been directly scaled to the primary observer. This practice, referred to as “daisy-chaining”, can be used to link successive generations of observers. It must be used with caution because errors introduced for one observer will propagate in time, unless offset by an error in the opposite direction. This inherent danger of daisy-chaining is what prompted Svalgaard and Schatten (2016) to use a series of primary observers forming separate backbones, thus reducing the number of possible links in the chain. In addition, they selected Wolfer as their initial (or base) primary observer. Wolfer’s 1841 – 1944 backbone lies somewhat toward the middle of their 1610 – present time series, thus reducing the span of time in any one direction over which daisy-chaining is used. In their abbreviated 1841 – 1976 series, Cliver and Ling (2016) used only two primary observers, adjusted RGO (1874 – 1976) and Schmidt, scaled to the RGO, for observers that did not overlap with the RGO. In effect, the Wolf or international sunspot number consists of a series of backbones for which the primary observer to primary observer transitions after 1848 were managed by internal comparisons, with some form of daisy chaining used by Wolf for earlier observers. The Usoskin et al. (2016) approach is novel in that it dispenses with the need for daisy chaining by creating a correction matrix for each observer “based on comparison between the statistics of the active day fraction in the observer’s data and that in the reference data set using pre-calculated calibration curves” that can be used to scale observers who did not directly overlap with the RGO from 1900 – 1976. As Usoskin et al. write, “The new method allows, for the first time, totally independent calibration of each observer to a reference data set, without bridging them…. The fact that this technique can be applied to fragments of data that are not continuous with other data demonstrates that the method avoids daisy-chaining and its associated error propagation: in the new method, if one observer is calibrated erroneously, it does not affect in any way the other observers.” Each of the three new group sunspot number time series (Svalgaard and Schatten 2016; Usoskin et al. 2016; Cliver and Ling 2016) employ the Hoyt and Schatten (1998a, 1998b) group count data base ( http://www.ngdc.noaa.gov/stp/space-weather/solar-data/solar-indices/sunspot-numbers/group/ ), although the Svalgaard and Schatten series is based on a modified version (Vaquero et al. 2016) that includes many new observers and removes erroneous entries (primarily zeroes for days when no reports of sunspots were previously taken to mean days when observations were made and no spots were observed). Cliver and Ling (2016) considered all observers in the Hoyt and Schatten data base for the period they considered, while Svalgaard and Schatten (2016), and to a greater degree, Usoskin et al. (2016), considered limited numbers of high-quality observers. No comparable comprehensive data base exists for the international sunspot number, which requires daily counts of individual sunspots as well as groups, but efforts are underway to compile and digitize such a data base going back, insofar as possible, in time.

In this study, we compare the four new sunspot number time series with (1) the original Hoyt and Schatten (1998a, 1998b) group sunspot number series, (2) each other, and (3) a new construction of solar wind $B$ (Owens et al. 2016) over the 1845 – 2013 interval based on the geomagnetic interdiurnal variability (IDV) index (Svalgaard and Cliver 2005, 2010; Svalgaard 2014; Lockwood et al. 2013a, 2013b). We examine the reconstruction of the Usoskin et al. (2016) group sunspot number and point out apparent artifacts and problems with their approach and results.

Our analysis is presented in Section 2 and the results are discussed in Section 3. Digitized data for the time series considered in this article are given in Table 2 in the Appendix.

2 Analysis

2.1 Comparisons of the Four New Sunspot Number Series with the Original Hoyt and Schatten Group Sunspot Number

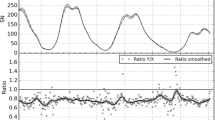
Figure 1 contains plots of annual averages of the new Svalgaard and Schatten (2016) time series, designated $\mathit{SS}$, and the original Hoyt and Schatten (1998a, 1998b) relative group sunspot number ($R_{\mathrm{G}}$) over the 1749 – 1995 time interval. Note that $R_{\mathrm{G}}$ has been rescaled. During the Sunspot Number Workshops, it was determined that the international sunspot number ($R_{\mathrm{I}}$) was too high after 1946 because of a sunspot weighting scheme implemented by Waldmeier (Svalgaard, 2010, 2012, 2016; Clette et al., 2014, 2016; Cortesi et al. 2016). In addition, it was found that the group counts of the Royal Greenwich Observatory used by Hoyt and Schatten as their reference observer are low before ${\sim}\,1915$ in comparison with other long-term observers (Clette et al. 2014; Cliver and Ling 2016). As a result, the factor of 12.08 (based on comparison of $R_{\mathrm{I}}$ and the RGO annual group counts from 1874 – 1976), which Hoyt and Schatten used to scale their annually averaged group counts to $R_{\mathrm{I}}$, is inflated (Clette et al. 2014). Thus the yearly $R_{\mathrm{G}}$ values used in this and subsequent figures are multiplied by 0.91 ($11.00/12.08$), based on the ratio of summed $R_{\mathrm{I}}$ to summed group counts over the 1916 – 1946 interval. The corresponding scale factor for the Svalgaard and Schatten (2016) group number series is 12.07. The figure shows that the two series begin to diverge in about 1900, with $R_{\mathrm{G}}$ systematically lower before.

Figure 1

Comparison of the Svalgaard and Schatten (2016; $\mathit{SS}$) and Hoyt and Schatten (1998a, 1998b; $R_{\mathrm{G}}$) group sunspot numbers over the 1749 – 1995 interval. The top curve shows the difference between the two time series.

Figures 2 and 3 give similar comparisons of $R_{\mathrm{G}}$ with the new Usoskin et al. (2016; UEA) group sunspot number and the abbreviated (1841 – 1976) Cliver and Ling (2016; $\mathit{CL}$) group number, respectively. While the UEA series hews relatively closely to $R_{\mathrm{G}}$ over the entire ${\sim}\,245$ year interval, particularly after Schwabe began his high-cadence observations in 1826, the $\mathit{CL}$ series exhibits a divergence from $R_{\mathrm{G}}$ during the nineteenth century similar to that observed for $\mathit{SS}$ in Figure 1. The scale factors for the UEA and $\mathit{CL}$ group count series are 10.67 and 10.72, respectively.

Figure 2

Comparison of the Usoskin et al. (2016; UEA) and Hoyt and Schatten (1998a, 1998b; $R_{\mathrm{G}}$) group sunspot numbers over the 1749 – 1995 interval. The top curve shows the difference between the two time series.

Figure 3

Comparison of the Cliver and Ling ($\mathit{CL}$, 2016) and Hoyt and Schatten ($R_{\mathrm{G}}$, 1998a, 1998b) group sunspot numbers. The $\mathit{CL}$ series extends from 1841 – 1976. The top curve shows the difference between the two time series.

Figure 4 contains a plot of the revised international sunspot number, designated $S_{\mathrm{N}}$ (Clette and Lefèvre 2016), along with the $R_{\mathrm{I}}$ series it replaced and $R_{\mathrm{G}}$. $S_{\mathrm{N}}$ is multiplied by 0.6 for comparison with $R_{\mathrm{I}}$ and $R_{\mathrm{G}}$. It employs corrections, evident in the upper $S_{\mathrm{N}}\,\mbox{--}\,R_{\mathrm{I}}$ trace, after 1946 for the Waldmeier discontinuity and in the mid-nineteenth century for inhomogeneities during the early years of both Schwabe’s and Wolf’s series of observations (Leussu et al. 2013; Clette and Lefèvre 2016). Note the significant separation of the $R_{\mathrm{G}}$ and $R_{\mathrm{I}}$ series before about 1885 that prompted the current re-examination of the sunspot number.

Figure 4

Comparison of the Clette and Lefèvre (2016) international sunspot number ($S_{\mathrm{N}}$) with the original relative international sunspot number ($R_{\mathrm{I}}$) and the Hoyt and Schatten (1998a, 1998b) group sunspot number ($R_{\mathrm{G}}$), 1749 – 2014.

2.2 Inter-comparisons of the New Group and International Sunspot Numbers

Figure 5(a) contains plots of the three new sunspot number time series ($\mathit{SS}$, $S_{\mathrm{N}}$, and $\mathit{CL}$) that lie above $R_{\mathrm{G}}$ and UEA before about 1900, while Figure 5(b) contains plots of UEA and $R_{\mathrm{G}}$ that track each other reasonably well over their full 1749 – 1995 interval of overlap. Despite the disparate normalization schemes used for each of the four new series ($\mathit{SS}$, $S_{\mathrm{N}}$, $\mathit{CL}$, and UEA), they agree well with each other (as well as with $R_{\mathrm{G}}$) after 1900, as can be seen in Figure 6. The general agreement between the four series is particularly good through about 1976, after which the RGO ceased observations.

Figure 5

(a) Comparison of $\mathit{SS}$, $S_{\mathrm{N}}$, and $\mathit{CL}$, 1749 – 2014; the $\mathit{CL}$ series extends from 1841 – 1976. (b) Comparison of UEA and $R_{\mathrm{G}}$, 1749 – present; the $R_{\mathrm{G}}$ series ends in 1995. The UEA and $R_{\mathrm{G}}$ traces in panel (b) are noticeably lower before 1900 than the $\mathit{SS}$, $S_{\mathrm{N}}$, and $\mathit{CL}$ curves in panel (a).

Figure 6

Comparison of the UEA, $\mathit{CL}$, $S_{\mathrm{N}}$, and $\mathit{SS}$ sunspot number time series, 1749 – 2014. The three group number time series are scaled to $S_{\mathrm{N}}$ over the 1916 – 1946 time interval.

The observer normalization scheme for the Svalgaard and Schatten $\mathit{SS}$ series has been criticized (Lockwood et al., 2016b, 2016c) for its use of linear regressions, forced to fit through zero, based on annual averages of group counts, and for daisy-chaining (Usoskin et al. 2016). Direct proportionality (ratios of summed counts for common observing days) was used in the observer normalization method of Hoyt and Schatten (1998a, 1998b), which was also employed by Cliver and Ling (2016). This raises two questions: (1) Why do such putatively flawed approaches (for $\mathit{SS}$, $\mathit{CL}$, and $R_{\mathrm{G}}$) yield series after 1900 that closely agree with that of Usoskin et al. (2016)? (2) Why do these approaches presumably break down (according to Lockwood, Usoskin, and colleagues) for $\mathit{SS}$ and $\mathit{CL}$ before 1900?

In regard to the first of these questions, it must be noted that Usoskin et al. (2016) only applied their normalization method in a limited fashion after 1900. Quoting from their article: “For the period of the late nineteenth and the twentieth centuries we considered only a few key observers with long stable records since the quality and density of data during the last hundred years were high, and thorough studies of their inter-calibration have been performed (Clette et al. 2014).” The only two observers other than the RGO reference observer listed in their Table 1 for the twentieth century are Quimby and Wolfer, who stopped observing in 1921 and 1928, respectively. Usoskin et al. (2016) note that they did check their final series against Koyama over the interval 1953 – 1976 and found it to be “fully consistent with the RGO data”, implying that a more thorough application of their technique would not yield a series greatly different from the other series in Figure 6 after 1900. Nonetheless, a full application of the Usoskin et al. (2016) technique to the post-1900 data would be helpful to address question (1) above.

Concerning question (2), one possible answer for the change for years before 1900 is that the cadence and quality of observers fell off sharply before 1900. But this conjecture can be dismissed as observers during this period include Schwabe (1826 – 1867), Wolf (1848 – 1893), Weber (1859 – 1883), Spörer (1861 – 1893), Tacchini (1871 – 1900), Wolfer (1876 – 1928), and Quimby (1889 – 1921), all of whom observed for 25 years or more (with ${>}\,6{,}000$ total observations in each case; Hoyt and Schatten 1998a), not to mention other notables such as Schmidt (1841 – 1883), Shea (1847 – 1866), Carrington (1853 – 1860), Leppig (1867 – 1881), Secchi (1871 – 1877), Moncalieri (1874 – 1893), Ricco (1880 – 1892), and Konkaly (1885 – 1905). Also, it is not clear why a change in the quality of observations before 1900 should not affect UEA as well.

Another possible answer for question (2) is that the increase in $\mathit{SS}$, $\mathit{CL}$, and $S_{\mathrm{N}}$ relative to UEA and $R_{\mathrm{G}}$ before 1900 is due to the daisy-chaining employed formally by Svalgaard and Schatten (2016) to link backbones and implicitly in the Clette and Lefèvre (2016) $S_{\mathrm{N}}$ series to forge the link between Wolf and Wolfer in the late nineteenth century. Cliver and Ling (2016) also used this approach to connect their modified RGO primary observer to Schmidt to extend their series to before 1874. We note, however, that the most extensive use of daisy-chaining in any of the sunspot number constructions under consideration was by Hoyt and Schatten (1998a, 1998b) before 1884 (Cliver and Ling 2016) and that their $R_{\mathrm{G}}$ series agrees most closely with that of Usoskin et al. (2016) before 1900 (Figure 5(b)).

2.3 Examination of the Observer Normalization Procedure of Usoskin et al. (2016)

Given the general agreement of the $\mathit{SS}$, $\mathit{CL}$, and $S_{\mathrm{N}}$ during the eighteenth and nineteenth centuries, an examination of the new scaling method of the discordant series of Usoskin et al. (2016) is warranted. Additional motivation for such an examination is provided by the demonstration (Cliver and Ling 2016) that a simple adjustment to the RGO group count series, based on an observed inhomogeneity in the early part of that series, brings $R_{\mathrm{G}}$ into close agreement with $\mathit{SS}$ and $S_{\mathrm{N}}$ before 1900 (series $\mathit{CL}$ in Figures 5(a) and 6).

2.3.1 Comparison of Observer Quality Factors ($S_{\mathrm{S}}$ and $k$)

In the method of Usoskin et al. (2016), $S_{\mathrm{S}}$ serves as a quality factor for the sunspot observers they considered. It corresponds to the smallest sunspot group the observer could detect, with the assumption that, on average, the observer reports all groups with apparent total area ${\geq}\,S_{\mathrm{S}}$, and no groups with $\mathrm{area} < S_{\mathrm{S}}$. Thus we would expect observers with low (high) $S_{\mathrm{S}}$ values in the Usoskin et al. (2016) calibration procedure to have correspondingly low (high) $k$-factors in the approaches used by Hoyt and Schatten (1998a, 1998b), Svalgaard and Schatten (2016), and Cliver and Ling (2016). To check this expectation, we considered the five observers listed in Table 1 who overlapped during the interval from 1882 – 1893 (Spörer, Wolfer, Tacchini, Wolf, Winkler). This interval was selected because (1) it includes Wolf, for whom Usoskin et al. (2016) give their correction factors for the number of groups observed per day; (2) it includes a standard observer, Wolfer (used by Svalgaard and Schatten 2016), with the lowest $k$-factor (from Table 1 of Cliver and Ling 2016) of any of the observers considered by Usoskin et al. (2016) who observed after 1840; (3) it encompasses at least one full solar cycle, bridging the maxima of Cycles 12 (1884) and 13 (1893), with groups reported over the full interval by a sufficient number of observers to permit comparisons; and (4) the five observers have $S_{\mathrm{S}}$ values that span the full range of this parameter for observers considered by Usoskin et al. (2016) that observed after 1840, from 3 msd for Spörer to 53 msd for Winkler.

Table 1 Parameters for selected observers after 1825 from Table 1 of Usoskin et al. (2016).

In Figure 7(a) the plot of $k$-factor vs. $S_{\mathrm{S}}$ for these five observers indicates only a weak relationship, with much scatter, between these two parameters. For example, the $k$-factor of 1.947 for Spörer ($S_{\mathrm{S}} = 3~\mbox{msd}$) is comparable to that (2.082) of Wolf ($S_{\mathrm{S}} = 45~\mbox{msd}$). Figure 7(b) shows a corresponding weak relationship ($R^{2} = 0.335$) between the average raw (unscaled) group counts of the five observers from 1882 – 1893 and their $S_{\mathrm{S}}$ values, while Figure 7(c) shows the expected strong relationship ($R^{2} = 0.947$) between an observer’s $k$-factor measure of merit and the average number of groups they report. Here we see that an increase from a value of 1 to a value of 2 in the $k$-factor corresponds to decrease in average counts by about 50 %. In Figure 8 we show a comparison of $k$-factors vs. $S_{\mathrm{S}}$ for all 11 observers in Table 1. The weak relationship observed in Figure 7(a) ($R^{2} = 0.169$) is substantiated by the larger sample ($R^{2} = 0.076$).

Figure 7

(a) Comparison of the $k$-factors obtained by Cliver and Ling (2016), using the Hoyt and Schatten (1998a, 1998b) observer normalization procedure, and the $S_{\mathrm{S}}$ observer quality measure for the five observers in Table 1 of Usoskin et al. who observed from 1882 – 1893. (b) Plot of the average group counts of these observers for the 1882 – 1893 interval vs. their $S_{\mathrm{S}}$ values. (c) Plot of average group counts (1882 – 1893) for the five observers vs. their $k$-factors.

Figure 8

Comparison of the $k$-factors obtained by Cliver and Ling (2016), using the Hoyt and Schatten (1998a, 1998b) observer normalization procedure, and the $S_{\mathrm{S}}$ observer quality measure for all observers considered by Usoskin et al. (2016) who observed between 1840 – 1900 (same as Figure 7(a) for a larger sample).

2.3.2 Comparison of Observed and Corrected Group Counts (1882 – 1893)

As noted in Section 1, the normalization methods used by Svalgaard and Schatten (2016) and Usoskin et al. (2016) to put observers on a common scale are quite different. Svalgaard and Schatten compared annual averages of group counts for secondary observers with those of a standard (backbone) observer. Their approach, somewhat simplified for illustrative purposes, is shown in Figure 9(a) for the comparison of Rudolf Wolf to the standard observer Albert Wolfer for the 12 years of overlap from 1882 – 1893 considered in Figure 7. Thus the $k$-factors obtained by this method (in this case 1.670) are applied to the average of group counts obtained by Wolf during a year. Svalgaard and Schatten (2016) selected high-quality observers for whom the ratio of counts vs. those of the standard observer remained relatively constant over the full range of solar activity, justifying their use of linear fits. In their approach, Usoskin et al. (2016) obtained a correction factor for each daily group spot count for the observers they considered, based on what a perfect observer would have seen. Their correction factors for Wolf are shown in Figure 9(b).

Figure 9

(a) The correction ($k$) factor for Rudolf Wolf in the Svalgaard and Schatten (2016) normalization scheme (based on the 1882 – 1893 interval) is 1.670, the slope of the Wolfer vs. Wolf regression line forced through zero. This correction factor is applied to Wolf’s raw daily count rate for each year he observed. (b) The optimum correction factors for Wolf in the Usoskin et al. (2016) normalization scheme. A separate correction factor for each group count is applied on a daily basis before obtaining yearly averages. An additive correction factor of 0.38 is used for days that Wolf reported zero groups.

Because the observer normalization methods of Svalgaard and Schatten (2016) and Usoskin et al. (2016) give divergent results before 1900, in Figure 10 we compare the normalized counts they produce for Wolf for the 1882 – 1893 interval considered above. Both panels show the raw group counts for Wolf and Wolfer during this interval. Figure 10(a) includes the scaled Wolf counts using the Usoskin et al. (2016) correction method, while Figure 10(b) includes the Svalgaard and Schatten (2016) normalization of Wolf’s annual counts over this interval. It can be seen that the Usoskin et al. (2016) technique undercorrects, relative to Wolfer, by ${\sim}\,15~\%$ for the cycle peak years of 1884 and 1893, respectively. Using the full range of the conversion matrix instead of just the optimum correction factors as we have done, can increase the normalized value of Wolf’s group counts for 1884 and 1893 by up to ${\sim}\,5~\%$ (based on a preliminary calculation by Ilya Usoskin, personal communication, 2016) and will thus reduce the degree of undercounting. Conversely, based on RGO data from 1916 – 1976, the group counts of a perfect observer ($S_{\mathrm{S}}=0$) will be ${\sim}\,4~\%$ higher than those of Wolfer ($S_{\mathrm{S}} = 6$).

Figure 10

Comparison of the normalizations of Wolf’s group counts by (a) Usoskin et al. (2016) and (b) Svalgaard and Schatten (2016) relative to Wolfer’s raw counts for the 1882 – 1893 interval.

2.3.3 Comparison of Observed and Corrected Group Counts (1826 – 2010): Correction Factor Time Series

To examine the result in Figure 10 for a longer period of time, we consider the averaged un-normalized ($k = 1$) group counts of all observers (Svalgaard and Schatten 2016) from 1826, the onset of Schwabe’s observations, to 2010. In Figure 11(a) this time series, labelled “$k=1$”, is presented along with the un-scaled annual group counts for the new $\mathit{SS}$ and UEA time series. The ratios of the annual $\mathit{SS}$, $S_{\mathrm{N}}$, and UEA group count series to the average raw counts of all observers for corresponding years (Figure 11(b)) may be viewed as “correction factor” time series for $\mathit{SS}$, $S_{\mathrm{N}}$, and UEA (designated SS-cf, $S_{\mathrm{N}}$ -cf, and UEA-cf, respectively) that convert the series of annual averages of un-normalized group counts into the $\mathit{SS}$, $S_{\mathrm{N}}$, and UEA group count time series. Such time series can be constructed in the same manner for individual group count time series such as that of Wolfer and the RGO. Correction factor series may also be viewed as $k$-factor series for which the numerator of the ratio (e.g., annual values of $\mathit{SS}$, RGO) represents the primary observer and yearly values of the $k = 1$ series in the denominator correspond to a composite or average secondary observer (because $k\equiv \mbox{raw counts of a standard observer}/\mbox{raw counts of a secondary observer}$). The $\mathit{cf}$-series scales the secondary observer to the primary.

Figure 11

(a) Un-scaled annual group counts for $\mathit{SS}$, UEA, and $k=1$ (average of all observers with $k$ set equal to 1.0 for each), 1820 – 2014. (b) Top. Three-year running averages of the SS-cf, $S_{\mathrm{N}}$ -cf, and UEA-cf time series, 1827 – 2009. Symbols indicate years of cycle maxima. The ratios of group counts are scaled to each other over the 1916 – 1946 interval as in Figures 1 – 6. Bottom. Scaled $\mathit{SS}$, $S_{\mathrm{N}}$, and UEA group sunspot numbers, 1820 – 2014.

If sunspot groups are counted by a sufficient number of observers, with a quasi-stable distribution in observing circumstances (e.g., telescope aperture, seeing condition, visual acuity, group counting procedure), then we might expect the correction factor curves in Figure 11(b) to be well-behaved, i.e., to be slowly varying without sharp digressions. Sharp features, when observed, are likely to be due to a problem with the observer normalization procedure (for a constructed group series) or to an inhomogeneity in the reference series (for an individual observer), rather than to a common digression by a critical mass of observers. The first two of these possible sources of a sharp change in the correction factor will affect the numerator of the correction factor ratio, while the third will affect the denominator. The two possible causes of changes to the numerator may be one and the same, i.e., an inhomogeneity in the reference series, although such changes may also involve other aspects of the normalization process, e.g., Hoyt and Schatten’s (1998a, 1998b) decision not to obtain $k$-factors for observers who overlapped with the RGO by direct comparison for the years 1874 – 1883 (Cliver and Ling 2016). The main point in either case is that changes in the numerator are more likely than changes in the denominator, which would require the coordinated actions of multiple observers. Therein lies the utility of the correction factor tool – the capability to identify flaws in the reference series and/or observer normalization procedure.

Figure 11(b) shows that SS-cf, $S_{\mathrm{N}}$ -cf, and UEA-cf are in reasonable agreement after 1920 although some separation is apparent after about 1990. The UEA-cf series exhibits erratic behavior going back in time from 1920, first rising to a peak value of ${\sim}\,1.6$ in 1915 and then declining to ${\sim}\,0.9$ by 1900. During the nineteenth century, UEA-cf oscillates about an average value of ${\sim}\,1.1$, with particularly sharp drops at the solar minima near 1880 and 1890. The $\mathit{SS}$ correction factor is reasonably well-behaved from about 1880 – 2010, but before this time shows sharp increases at several solar minima. Like UEA-cf, $S_{\mathrm{N}}$ -cf exhibits dips at a few solar cycle minima; at maxima (indicated by red triangles) it more closely tracks the SS-cf series. Because observers were ample after about 1850,² the erratic or sharp features in the UEA, SS, and $S_{\mathrm{N}}$ correction factor time series are attributed to instability in the primary observer or the normalization method. For example, the peak centered on 1915 in RGO-cf is most likely due to an artifact in the RGO series. The alternative – a coherent decline and improvement in the majority of all other observers’ capability to count groups from the maximum of Cycle 13 (1893) to the maximum of Cycle 16 (1928) – is less plausible.

Figure 12 compares correction factors for the $\mathit{SS}$, $\mathit{CL}$, $S_{\mathrm{N}}$, Wolfer, RGO, UEA, $\mathit{HS}$ (Hoyt and Schatten 1998a; Hoyt and Schatten 1998b), and UEA group count time series. At cycle maxima, the SS-cf, CL-cf, and $S_{\mathrm{N}}$-$\mathit{cf}$ series generally follow the Wolfer-cf series of their primary observer for their 1876 – 1928 period of overlap (black circles), although, as noted in Cliver and Ling (2016), the $\mathit{CL}$ time series overcorrects relative to $\mathit{SS}$ for the maxima of Cycles 12 and 13 while $S_{\mathrm{N}}$ lies ${\sim}\,10~\%$ below $\mathit{SS}$ at these two 11-yr peaks. Similarly, the UEA-cf and HS-cf series closely track RGO-cf at cycle maxima; in fact, the UEA-cf and RGO-cf traces are essentially identical after 1900. These behaviors, i.e., the adherence – by design – of derived series to their reference series underscores the importance of selecting stable long-term observers for reference series.

Figure 12

(Top) Three-year running averages of SS-cf, CL-cf, $S_{\mathrm{N}}$, Wolfer-cf, RGO-cf, HS-cf, and UEA-cf time series, 1827 – 2009. The ratios of group counts are scaled to each other over the 1916 – 1946 interval, with the scale factor for SS-cf used for Wolfer-cf and $S_{\mathrm{N}}$ -cf. The pink oval indicates the decline of UEA-cf and HS-cf in concert with RGO-cf from 1915 – 1900, and the black circles encompass maxima of SS-cf and Wolfer-cf. (Bottom) $\mathit{SS}$ sunspot number time series, 1820 – 2010, with cycle numbers.

Figures 11 and 12 demonstrate the utility of the correction factor series for identifying short-term instabilities in sunspot time series (e.g., the peak at 1915 in RGO-cf and UEA-cf; pronounced dips (rises) at minima in UEA-cf (SS-cf) before 1900). The correction factor series can also be used to assess longer-term variations in sunspot series. The correction factors in Figure 12 for the various sunspot time series differ significantly on long timescales, showing a marked divergence before about 1905, with the UEA-cf series dropping to an average level of ${\sim}\,1.1$ during the nineteenth century (pink oval), while the SS-cf and, after a hesitation, $S_{\mathrm{N}}$ -cf series resume a gradual increase (black circles) that began around 1930. These conflicting trends are echoed in the HS-cf (RGO-cf) and CL-cf (Wolfer-cf) series. The divergent paths exhibited by the two groups of correction factors (UEA-cf and HS-cf vs. SS-cf, CL-cf, and $S_{\mathrm{N}}$ -cf) and those of their underlying primary references (RGO-cf and Wolfer-cf, respectively) cannot both be right. Which of these two behaviors seems more likely? The increase in UEA-cf and RGO-cf from about 1900 – 1915 implies that secondary observers were counting progressively fewer groups during this interval, resulting in an increasing correction factor. Conversely, this rise can be attributed to an increase in RGO counts relative to those of other observers (Clette et al. 2014; Cliver and Ling 2016). Cliver and Ling (2016) demonstrated that adjusting the RGO group count series upward to agree with Wolfer’s over the 1874 – 1915 interval resulted in a time series ($\mathit{CL}$) more similar to $\mathit{SS}$ and $S_{\mathrm{N}}$ (Figure 6). The rise in SS-cf going back in time before about 1905 seems more plausible than the concomitant descent of UEA-cf. The expected average increase in telescope aperture/quality for sunspot observers with time will increase group counts (decreasing the correction factor) as will the tendency, institutionalized at Zürich by Wolfer, to count all groups, including “fine points and gray pores” (Wolf 1857; Wolfer 1895; Kopecký, Kuklin, and Růžičková-Topolova 1980), in contrast to his predecessor Wolf, who with a smaller telescope counted ${\sim}\,40~\%$ fewer groups. Wolfer counted more groups than each of the ten other observers listed in Table 1 used to derive the UEA series after 1825. Their $k$-factors (from Cliver and Ling 2016) relative to the 1.259 $k$-factor of Wolfer (the primary $\mathit{SS}$ observer) are as follows: Spörer, 1.546 ($1.947/1.259$); Tacchini, 1.141; Wolf, 1.654; Winkler, 1.321; Schmidt, 1.313; Schwabe, 1.378; Quimby, 1.257; Weber, 1.366; Shea, 1.788; Leppig, 1.304.³

In the correction factor traces in Figure 11(b), the symbols refer to years of maximum. In Figure 13 we focus on these maxima because it is the cycle peak years that distinguish the various sunspot number constructions. The proposed existence of a grand solar maximum during the twentieth century (Solanki et al. 2004; Usoskin, Solanki, and Kovaltsov 2007), for example, is defined by the amplitudes of 11-year maxima from 1945 – 1995. At cycle minima percentage differences may become large, as the UEA-cf and SS-cf curves show, but the absolute differences are often too small to discern in plots of the sunspot number time series.

Figure 13

Three-year smoothed correction factors for the $\mathit{SS}$, $S_{\mathrm{N}}$, and UEA group count series (scaled from 1916 – 1946) at the maxima of Solar Cycles 7 (1829) through 23 (2001). Note the close correlation of all three series during the twentieth century. The relative constancy of the UEA-cf series during the nineteenth and twentieth centuries is unexpected.

While Wolfer was a very prolific observer, he was not perfect; he did not count every group. The RGO, the reference observer for Usoskin et al. (2016) after 1900, counted more. Thus the ratio of the RGO to Wolfer group counts at the maxima of Cycle 14 (1907) is 1.08. Because Wolfer was one of the strongest observers of the nineteenth century, as indicated by either $k$-factor or $S_{\mathrm{S}}$ parameter in Table 1, any correction factor for UEA during that century can be expected to be significantly higher than 1.08. Yet the average smoothed UEA-cf value for the maxima of Cycles 7 (1829) through 13 (1893) is only 1.17 (light blue squares in Figure 13(a)), nearly equal to the 1.16 value obtained for Cycles 16 (1928) through 23 (2001). Figure 13 shows that the behavior of the $S_{\mathrm{N}}$ -cf (red triangles) and SS-cf (gray circles) time series from the nineteenth to the twentieth centuries is in accord with the expectation that because of advances in instrumentation and procedure (e.g., improved group separation), observers in the twentieth century counted more groups than those before 1900 and as a result had lower $k$-factors on average.

This expectation can be quantified by scaling observers in the nineteenth century to the 1900 – 1976 group count RGO time series that Usoskin et al. (2016) used as their reference observer. To scale the eleven post-1840 observers, including Wolfer, used by Usoskin et al. (2016) to the RGO, we multiplied their $k$-factors (relative to Wolfer) by 1.08, as determined for the maximum of Cycle 14. In Figure 14 we plot the average values of these $k$-factors at the maximum of each cycle from 9 (1848) to 13 (1893) for the observers in Table 1 who made observations during that peak year (skipping Cycle 7 because Table 1 does not include all observers considered by Usoskin et al. (2016) for that maximum, and Cycle 8 because for the observers in Table 1, only Schwabe observed during this 11-year peak, vs. 4 – 6 observers for the remaining maxima). We also plot UEA-cf and SS-cf for these years because of the conceptual similarity of $k$-factors and correction factors. The plotted average $k$-factors for Cycles 9 – 13, which are based on actual group counts in the Hoyt and Schatten (1998a, 1998b) normalization scheme, more closely track the SS-cf series, underscoring the fact that the UEA time series is too low during the nineteenth century – by 28 % on average (range from 15 – 47 %) relative to $\mathit{SS}$ for these maxima.

Figure 14

Comparison of SS-cf and UEA-cf with average $k$-factors for observers considered by Usoskin et al. (2016) for cycle maxima in the second half of the nineteenth century. Cycle numbers are given at the bottom of the figure.

2.4 Comparison of Sunspot Numbers with Solar Wind $B$ (1845 – 2013)

Recently, as the result of an International Space Science Institute team effort that considered the sunspot number, geomagnetic data, cosmogenic nuclide concentrations in ice cores and tree rings as well as in situ space data as input, the time series of solar wind magnetic field strength $B$ has been extended back to 1750 (Owens et al. 2016). Of the various reconstructions obtained, the one based on geomagnetic data, extending from 1845 – 2013, is considered to be the gold standard, in part because of the close agreement obtained by two separate groups (Svalgaard 2014; Lockwood et al., 2013a, 2013b) using complementary approaches. Both of these reconstructions were based on the interdiurnal variability index (Svalgaard and Cliver 2005; 2010). Because IDV is essentially independent of solar wind speed and highly correlated with solar wind $B$, it has a closer connection to the sunspot number than other geomagnetic indices. In Figure 15, the composite IDV-based $B$ series of Owens et al. (2016) is plotted along with the UEA and $\mathit{SS}$ sunspot number time series in panels (a) and (b), respectively. To facilitate comparison with the sunspot number peaks in the twentieth century, the scale of the right-hand axis has been adjusted to remove a putative floor in solar wind $B$ (Svalgaard and Cliver 2007). Here a floor value of 3.8 nT seems to work best; other analyses (Cliver and Ling 2011; Cliver and von Steiger 2015) point to a lower floor of ${\sim}\,2.8~\mbox{nT}$; the difference is not important for the point we wish to make here. After 1900, the level of the peaks of both the UEA and $\mathit{SS}$ agree fairly well with the corresponding peaks in$B$, although there are exceptions, notably Cycle 20. Before 1900, however, the UEA trace clearly falls below that of $B$ (as well as those of $\mathit{SS}$ and $S_{\mathrm{N}}$, Figure 6), indicating that UEA is too low during the nineteenth century. At solar maxima, the solar wind is dominated by cyclic activity involving coronal mass ejections and low-latitude coronal holes (Webb and Howard 1994; Richardson, Cane, and Cliver 2002; Wang and Sheeley 1994), which rides atop the proposed floor attributed to background slow solar wind. The offset between the sunspot number and solar wind $B$ for solar minima periods is primarily due to high-speed wind streams from polar coronal holes (Wang and Sheeley 1994). The polar holes disappear at solar maximum.

Figure 15

Comparison of the UEA (a) and $\mathit{SS}$ (b) sunspot number series with three-year-smoothed solar wind $B$ from Owens et al. (2016; with observed data after 1964), 1845 – 2013. Solar cycle numbers indicated at the bottom of the plots.

3 Summary and Discussion

The principal findings of our comparison of the new sunspot numbers (Svalgaard and Schatten ($\mathit{SS}$, 2016); Usoskin et al. (UEA, 2016); Cliver and Ling ($\mathit{CL}$, 2016); Clette and Lefèvre ($S_{\mathrm{N}}$, 2016)) published in this Topical Issue are listed below.

• (a) Despite disparate observer normalization schemes, all four series ($\mathit{SS}$, UEA, $\mathit{CL}$, $S_{\mathrm{N}}$) agree reasonably well after 1900 (Figures 5, 6, and 13).

• (b) The UEA series, which agrees closely with the original Hoyt and Schatten (1998a, 1998b) group sunspot number ($R_{\mathrm{G}}$) after about 1830, is systematically lower than the $\mathit{SS}$, $\mathit{CL}$, and $S_{\mathrm{N}}$ series before 1900 (Figures 5 and 6).

• (c) The observer quality ($S_{\mathrm{S}}$) factors derived by Usoskin et al. (2016) are only weakly correlated with classical $k$-factors ($R^{2} = 0.076$; Figure 8) and are poorer indicators of the number of spot groups reported by an observer than are $k$-factors (based on $R^{2}$ values of 0.335 ($S_{\mathrm{S}}$) and 0.947 ($k$) for a sample comparison; Figure 7(b, c)).

• (d) The normalization matrix for Wolf from Usoskin et al. (2016) results in an undercorrection of ${\sim}\,15~\%$ relative to the raw group counts of Wolfer at the maxima of Cycles 12 and 13 (Figure 10).

• (e) A correction factor series, defined to be the ratio of the annual group counts for any given series to the corresponding annual averages of group counts for all observers treated equally, i.e., $k = 1$, is a useful tool to test the reliability of sunspot time series and identify artifacts (Figures 11 and 12). This tool can be used with confidence from about 1850, after which multiple high-quality observers recorded sunspots. A similar approach was used by Clette et al. (2016) to check the validity of the post-1980 Locarno time series.

• (f) A comparison of the correction factor series corresponding to the UEA and $\mathit{SS}$ group count time series with average $k$-factors indicates that the UEA group count series is too low before 1900 by an average factor of ${\sim}\,30~\%$ relative to SS for the maxima of Cycles 9 (1848) through 13 (1893), with a range from ${\sim}\,15\,\mbox{--}\,45~\%$ (Figures 13 and 14).

• (g) Solar cycle maxima of solar wind $B$ in a recent reconstruction extending back to 1845 (Owens et al. 2016) agree reasonably well with corresponding maxima of $\mathit{SS}$, UEA, $\mathit{CL}$, and $S_{\mathrm{N}}$ after 1900 and with $\mathit{SS}$, $\mathit{CL}$, and $S_{\mathrm{N}}$ before this year, but lie above 11-year maxima of UEA (and $R_{\mathrm{G}}$) during the nineteenth century (Figures 2, 6, and 15) (cf. Lockwood et al. 2016a).

The Svalgaard and Schatten ($\mathit{SS}$) group series has been criticized for its normalization procedure that is based on linear regressions, forced through the origin, of annual group counts of a primary (or backbone) observer against those of secondary observers. Usoskin et al. (2016) argued that the normalization scheme employed by Svalgaard and Schatten (2016) “grossly over-estimates” solar activity before 1900. Similarly Lockwood et al. (2016c) argued that daisy-chaining of backbones in the Svalgaard and Schatten (2016) reconstruction, combined with faulty regression techniques, yields the “most radically different” of the various sunspot number time series in that it has three approximately equal grand maxima in the eighteenth, nineteenth, and twentieth centuries. This comment necessarily encompasses the new $S_{\mathrm{N}}$ series of Clette and Lefèvre (2016) and the provisional $\mathit{CL}$ series of Cliver and Ling (2016), both of which agree closely with $\mathit{SS}$ during their times of overlap with that series. In Figure 6 we show that the Svalgaard and Schatten (2016) group sunspot number series agrees surprisingly well with that of Usoskin et al. (2016) after 1900. If the normalization method of Svalgaard and Schatten (2016) was flawed in the manner argued by Usoskin et al. (2016) and Lockwood et al. (2016b, 2016c), we would expect it to systematically overestimate the sunspot number relative to the UEA series after the 1916 – 1946 scaling interval as well as for the preceding centuries, but it does not. Rather than the Svalgaard and Schatten (2016) group counts being too high before 1900, it appears that the Usoskin et al. (2016) series underestimates group counts for the nineteenth century ((e) and (f) above). The UEA series yields similar average correction factors for nineteenth and twentieth century sunspot observers, implying similar proficiencies and practices in counting spot groups for these epochs. This is contrary to expectations based on the evolution of instrumentation and group-counting practice over time and is in conflict with a direct comparison of reported group counts between observers spanning the two centuries.

The poor correlation we find between $S_{\mathrm{S}}$ and $k$-values in Figure 8 apparently stems from the use of active day fractions to determine observer quality by Usoskin et al. (2016). Their use of active day fractions represents a significant step away from the use of actual group counts for this purpose. Moreover, it does not seem necessary for a period when observers were relatively plentiful and included many notables such as Schwabe, Wolf, Carrington, Spörer, Wolfer, and Tacchini. In the same vein, we note that the break between the $\mathit{SS}$, $S_{\mathrm{N}}$, and $\mathit{CL}$ series with the new UEA series occurs circa 1900 when Usoskin et al. (2016) stopped using the RGO series for direct comparison with secondary observers and started using synthetic reference observers based on the RGO.

In addition to our comparison with solar wind $B$, reference to other types of non-sunspot data support the validity of the $\mathit{SS}$ and $S_{\mathrm{N}}$ series. Muscheler et al. (2016) recently constructed a solar modulation potential series based on ¹⁴C data that agrees reasonably well with $\mathit{SS}$ ($S_{\mathrm{N}}$) back to 1750 (1700) (cf. Asvestari et al. 2016). Svalgaard and Hathaway (2016), using the Waldmeier (1978) effect that relates solar cycle rise time and amplitude, showed that solar activity has reached similarly high peaks in each of the eighteenth, nineteenth, and twentieth centuries.

Much work remains to be done. The new research precipitated by the adoption of the new $S_{\mathrm{N}}$ series by SILSO in July 2015 (Clette et al. 2015) has raised a number of areas for further investigation, a few of which are listed here:

• (a) The use of a 7 % reduction in group counts by Svalgaard after 1940 bears further scrutiny because it is required to bring the $\mathit{SS}$ series into agreement with the $\mathit{CL}$ series of Cliver and Ling (2016) as well as the $S_{\mathrm{N}}$ series of Clette and Lefèvre (2016), neither of which employed such a reduction in group counts.

• (b) Because the RGO group count time series is used, in varying degrees, as the primary or standard observer in the sunspot number reconstructions of Hoyt and Schatten (1998a, 1998b), Cliver and Ling (2016), and Usoskin et al. (2016), the examination by Willis et al. (2016b) of the stability of the RGO time series over the 1874 – 1882 time interval should be extended to the end of the series in 1976. Detailed investigations of individual observers such as those by Willis et al. (2016a, 2016b) for the RGO, Clette et al. (2016) for Locarno and Friedli (2016a, 2016b) for Wolf would be desirable to check the stability of other key long-term observers.

• (c) The construction of the new UEA time series needs to be more fully developed. At present, $S_{\mathrm{S}}$ values have been obtained for only 16 of the 80 observers who made 1000 or more observations after 1749, and the correction matrix is published for only one observer. A more fleshed-out construction is forthcoming. Usoskin et al. (2016) write, “The series presented here is a basic skeleton, or core, of the reconstruction of the number of sunspot groups, to which other observers with shorter sunspot records can and will be added later by means of direct normalization to this core series.”

• (d) Friedli (2016b) has recently proposed a revision of the Wolf or international sunspot number that more closely resembles the original group number series of Hoyt and Schatten (1998a, 1998b) than the original $R_{\mathrm{I}}$ time series. This series will also need to be examined in detail but, like the UEA and $R_{\mathrm{G}}$ series, it faces objections for the nineteenth century involving its low correction factor and lack of fidelity with solar wind $B$.

• (e) Lockwood et al. (2014a, 2014b; 2016c) developed a new sunspot series that, like the $S_{\mathrm{N}}$ series of Clette and Lefèvre (2016), makes corrections or changes to the original Wolf number ($R_{\mathrm{I}}$). The analysis of Lockwood and colleagues implies a ${\sim}\,11~\%$ downward adjustment after 1946 to remove the Waldmeier jump vs. a ${\sim}\,15~\%$ correction used by Clette and Lefèvre (2016). For the discontinuity circa 1848 noted by Leussu et al. (2013), Lockwood, Owens, and Barnard (2014b) Lockwood et al. (2016c) employed a 20 % downward correction before that year, while Clette et al. applied a 14 % upward correction to $R_{\mathrm{I}}$ from 1849 – 1863. For the early part of the series, Lockwood and colleagues appended $1.3 \times R_{\mathrm{G}}$ before 1749 (Lockwood, Owens, and Barnard 2014b) or 1818 (Lockwood et al. 2016c), while Clette and Lefèvre (2016) made a complex sinusoidal-type correction to $R_{\mathrm{I}}$ for the 1981 – 2015 Locarno drift (Clette et al. 2016). These significant differences between the two revised Wolf series will need to be examined and reconciled.

If the past is a guide, it will take some time to resolve the various questions that have arisen as a result of the comprehensive re-evaluation of the sunspot number. At the end of this process, the goal or expectation is that the solar and solar-terrestrial community will have a single, reliable, and vetted sunspot number time series with stated uncertainties. At the present juncture, the preponderance of evidence points to a time series that will more closely resemble the $R_{\mathrm{I}}$ series developed by Rudolf Wolf during the second half of the nineteenth century (and its update, Clette and Lefèvre 2016; Figure 4) than either the Hoyt and Schatten (1998a, 1998b) or the Usoskin et al. (2016) time series that were developed to replace it.

Appendix: Solar Activity Time Series

Table 2 Solar activity time series