1 Introduction

Violent solar eruptions in the form of coronal mass ejections (CMEs) and flares often cause pulsed disturbances propagating through the corona on a global scale. These CME- and flare-initiated disturbances cause a variety of effects in the corona, transition region, and chromosphere, as observed in the EUV-range, X-rays, radio-wavelength domain, and in the chromospheric and transition-region spectral lines. The longest known signatures are so-called Moreton waves, which are observed in the H\(\upalpha\) spectral line (Moreton 1960; Moreton and Ramsey 1960) and radio type II bursts (Payne-Scott, Yabsley, and Bolton 1947; Wild and McCready 1950). The physical explanation for these two phenomena was proposed in a series of papers by Uchida (1968), Uchida, Altschuler, and Newkirk (1973), and Uchida (1974) in terms of large-scale coronal shocks. A quarter of a century later, such global coronal disturbances were directly revealed in the EUV range, soft X-rays, the He i 1083 nm spectral line, and the radio-wavelength range (for references see Warmuth et al., 2004a; Vršnak et al., 2006; Olmedo et al., 2012), and were identified as sharp fronts ahead of CMEs in white-light coronagraphic images (e.g., Ontiveros and Vourlidas, 2009). In the past decade, the research in this field strongly intensified, resulting in many articles based on either the observational, theoretical, numerical, or a combined approach. A brief overview of recent research efforts can be found in, e.g., Section 8 of Klimchuk et al. (2009) and Section 9 of in van Driel-Gesztelyi et al. (2012), whereas detailed summaries of various aspects of the research on global coronal waves and wave-like disturbances are presented in reviews by, e.g., Warmuth (2007, 2010), Vršnak and Cliver (2008), Wills-Davey and Attrill (2009), Gallagher and Long (2011), Zhukov (2011), Patsourakos and Vourlidas (2012), and Liu and Ofman (2014).

Currently, there are several conflicting interpretations of these CME- or flare-related globally propagating disturbances, such as magnetohydrodynamic (MHD) fast-mode wave, MHD slow-mode wave, non-wave options (various forms of propagating magnetic-field restructuring), and “hybrid” wave/non-wave combinations. When the observational studies are combined with analytical considerations and numerical simulations, it becomes increasingly clear that most of these options occur in the solar atmosphere (cf. Warmuth and Mann, 2011; see also reviews by Warmuth 2010 and Liu and Ofman 2014). However, the most prominent coronal disturbances, which are frequently associated with H\(\upalpha\) Moreton waves and radio type II bursts, can be explained only in terms of large-amplitude fast-mode waves or shocks (e.g., Uchida, 1974; Warmuth et al., 2001, 2004a, 2004b; Vršnak et al., 2002b; Veronig, Temmer, and Vršnak, 2008; Patsourakos et al., 2009; Muhr et al., 2010, 2011; Patsourakos, Vourlidas, and Stenborg, 2010; Veronig et al., 2010, 2011; Grechnev et al., 2011; Kozarev et al., 2011; Long, DeLuca, and Gallagher, 2011; Ma et al., 2011; Kienreich et al., 2011; Warmuth and Mann, 2011; Asai et al., 2012; Patsourakos and Vourlidas, 2012; Shen and Liu, 2012a, 2012b; Temmer, Vršnak, and Veronig, 2013; Kienreich et al., 2013; Shen et al., 2013; Yang et al., 2013; Liu and Ofman, 2014). In such events, the so-called overexpansion, occurring in early stages of the eruption (see, e.g., Figure 6 in Vršnak et al., 2004), plays a significant role in the wave formation (e.g., Temmer et al., 2009; Patsourakos, Vourlidas, and Stenborg, 2010; Kienreich et al., 2011; Kozarev et al., 2011).

To provide the theoretical background and physical comprehension of such waves in general, the very basic characteristics of the formation of the large-amplitude wavefront by an explosively expanding three-dimensional (3D) piston and the evolution of the perturbation into a shock was studied analytically in several articles (see, e.g., Vršnak and Lulić, 2000a, 2000b; Žic et al., 2008; Temmer et al., 2009; Afanasyev and Uralov, 2011; Lulić et al., 2013). However, the most effective approach that can provide a comprehension of the formation and evolution of the eruption-driven large-amplitude waves under coronal conditions is numerical modeling, which is currently oriented in two directions. One type of simulations uses the initial configuration that closely reproduces the underlying coronal structure for a particular observed event. This approach is usually employed to simulate and analyze the initiation and propagation of a given coronal wave in a realistic coronal magnetic field environment (see, e.g., Wu et al., 2001; Cohen et al., 2009, 2010; Schmidt and Ofman, 2010; Downs et al., 2011, 2012; Schrijver et al., 2011; Selwa, Poedts, and DeVore, 2012, 2013; Wu, Wu, and Liou, 2013). The other type of simulations starts from a simplified initial magnetic configuration and considers only the most general characteristics of the eruption, aiming to infer the nature and the most basic characteristics of coronal waves that should be intrinsic to all events (see, e.g., Chen et al., 2002; Chen, Fang, and Shibata, 2005; Chen, Ding, and Fang, 2005; Wu et al., 2005; Pomoell, Vainio, and Kissmann, 2008; Wang, Shen, and Lin, 2009; Mei, Udo, and Lin, 2012; Hoilijoki et al., 2013, Wang et al., 2015).

Currently, the majority of numerical simulations is aimed exclusively at various aspects of the evolution of the coronal component of the disturbance, i.e., they focus on understanding the characteristics of the so-called EUV waves (for terminology see, e.g., Warmuth, 2007; Liu and Ofman, 2014), usually neglecting its consequences in the transition region and chromosphere. An exception is the numerical simulation presented by Chen, Ding, and Fang (2005), where the coronal eruption is set into a gravitationally stratified atmosphere that quite realistically reproduces the chromosphere, transition region, and corona. Based on the synthesized radiative output, the soft X-ray, EUV, and H\(\upalpha\) wave signatures were identified in this simulation. The soft X-ray and H\(\upalpha\) components moved at similar speeds, the H\(\upalpha\) signature lagging for a few tens of Mm behind the soft X-ray perturbation. Furthermore, a much slower EUV wave signature was also identified, as frequently found in observations (e.g., Shen and Liu, 2012b; Xue et al., 2013).

In this study, we analyze a numerical simulation in detail that is to a certain degree similar to that performed by Chen, Ding, and Fang (2005). The main objective is an in-depth quantitative analysis of the propagation of the coronal wave and the effects it causes in the transition region and chromosphere. In particular, we focus on:

  • the overall morphology and evolution of the complete process, from the initiation by the eruption up to the propagation in a quiet corona, considering different eruption dynamics and different background magnetic field configurations;

  • the role of the overexpansion in the wave formation and the late-phase signatures related to the relaxation of the atmosphere after the wave passage;

  • the relative kinematics of the coronal, transition region, and chromospheric signatures (i.e., EUV wave, He i wave, and Moreton wave);

  • the spatial and temporal evolution of the perturbation in the chromosphere, including the evolution of the amplitude and downward velocity of the chromospheric disturbance as a function of depth and time;

  • the dependence of the amplitude and downward velocity of the chromospheric disturbance on the coronal wave amplitude;

  • a comparison with an analytic consideration of the chromospheric disturbance characteristics and evolution;

  • a comparison with simulations that do not include the chromospheric layer; and

  • a comparison with the basic properties of the MHD wave formation by a cylindrical piston mechanism (see Lulić et al., 2013).

In Section 2 we describe the model. Our results are presented in Section 3, which is split into two subsections. The first presents a detailed morphological description of the event, the second is devoted to the in-depth analysis of the numerical results, which we performed separately for the horizontal propagation of the main coronal disturbance, downward propagation of the main perturbation in the chromosphere, and the secondary coronal effects. The results are discussed and conclusions drawn in Section 4.

2 The Model

In the following, a 2.5 D model is considered, meaning that all quantities are invariant along the \(z\)-coordinate, but the \(z\)-component of the magnetic field \(B_{z}(x,y)\ne0\) is included in the calculation. On the other hand, the \(z\)-component of the velocity (\(v_{z}\)) is always kept zero (\(v_{z}=0\)). Thus, the input and the basic output quantities are the density \(\rho\), the \(x\)- and \(y\)-component of the velocity, (\(v_{x}\), \(v_{y}\)), and all three components of the magnetic field, (\(B_{x}\), \(B_{y}\), \(B_{z}\)). Simulations were performed employing the Versatile Advection Code (VAC; Tóth, 1996; Goedbloed, Keppens, and Poedts, 2003). This numerical code was developed at the Astronomical Institute at Utrecht, in collaboration with the Institute for Plasma Physics, the Mathematics Department at Utrecht, and the Centrum Wiskunde and Informatica at Amsterdam. The code is based on the full set of MHD equations, including the gravity. It is suitable for the analysis of a broad variety of astrophysical phenomena, including MHD shock waves.

For the simulations we used a 2D numerical mesh containing \(995\times 995\) cells, supplemented by two ghost-cell layers at each boundary, which were used to regulate the boundary conditions (thus, the complete grid consists of \(999\times999\) cells). At the top, left, and right edges of the numerical box we applied continuous boundary conditions, meaning that gradients of all quantities were kept zero by copying the variable values from the edge of the mesh into the ghost cells. At the bottom of the numerical box, representing the solar photosphere, a fixed boundary condition was applied to reproduce the magnetic field line-tying in the inert photosphere. All quantities were normalized, so that distances are expressed in units of the numerical-box length (\(L=1\)), velocities are normalized to the background Alfvén speed \(v_{\mathrm{A0}}\), and time is expressed in terms of the Alfvén travel time over the numerical-box length (\(\tau_{\mathrm {A}}=L/v_{\mathrm{A0}}\)). We applied the approximation \(\beta=0\), where \(\beta\) is the plasma-to-magnetic pressure ratio. The origin of the coordinate system was set at the center of the bottom boundary.

Since this article is primarily focused on understanding the propagation of waves and shocks in the lowest layers of the solar corona and their effects on the solar chromosphere, special attention was paid to the vertical profile of the density. To reproduce the solar atmosphere, the numerical box was divided into three domains, corresponding to the chromosphere, transition region, and low corona. The density was set to \(\rho=1\) at the base of the corona, i.e., the top of the transition region. The lowest layer, representing the chromosphere, extends from \(y=0\) to \(y=0.1\). In the applied model-atmosphere, in this domain the density decreases for ≈ five orders of magnitude, following the exponential law. The next layer, representing the transition region (TR), extends from \(y=0.1\) to \(y=0.125\). Over this height range, we applied a linear density decrease of two orders of magnitude. Above \(y=0.125\) it extends the corona, whose density decreases exponentially from \(\rho=1\), where we applied a scale height 100 times larger than in the chromospheric layer. The vertical density profile is drawn in the main graph of Figure 1a. In the inset of Figure 1a we present our model atmosphere, scaled to the quiet-atmosphere model by Vernazza, Avrett, and Loeser (1981). The comparison shows that the model we applied in the simulation represents the chromosphere above the height of 600 km quite well, and it also fits the transition region. As we show below, this is a sufficiently good approximation, since the effects of the coronal shock passage become negligible below a height of \({\approx}\,1000~\mbox{km}\).

Figure 1
figure 1

The initial configuration (\(t=0\)): a) background vertical density profile, and b) radial profile of the flux-rope magnetic field (solid line – \(B_{z}\); dotted – \(B_{\phi}\)). The graph in the inset of a) compares our density profile, drawn as a solid line, with the density model by Vernazza, Avrett, and Loeser (1981), drawn as a dashed line.

Full size image

The basic initial magnetic field consists of two components. One of them is the axial magnetic field of the flux rope, whose axis is oriented in the \(z\)-direction and set at the height \(y_{0}\). This \(z\)-component of flux-rope magnetic field is defined as

$$ B_{z}(r)=\sqrt{B_{z0}^{2}-b\,r^{2}}, $$
(1)

where \(B_{z0}\) represents the initial magnetic field at the center of the flux rope located at \(x=0\), \(y=y_{0}\), \(r\) represents the local radial coordinate defined by \(r^{2}=x^{2}+(y-y_{0})^{2}\), while \(b(r)\) defines the field strength profile within the source region. In particular, we employed the form \(b=(B_{z0}^{2}-B_{z\mathrm {e}}^{2})/r_{\mathrm{e}}^{2}\), where \(r_{\mathrm{e}}\) is the initial flux-rope size and \(B_{z\mathrm{e}}\) represents the external magnetic field strength outside the source region (for details see Lulić et al., 2013).

The other flux-rope field component is the poloidal one, defined as

$$ B_{\phi}(r) = \frac{B_{\phi{\mathrm{e}}}}{2} \left[\sin\left(\frac{\pi r}{r_{\mathrm{e}}} - \frac{\pi}{2}\right) +1\right], $$
(2)

where \(B_{\phi{\mathrm{e}}}\) represents the initial poloidal field at the flux-rope boundary. Outside the flux rope (\(r>r_{\mathrm{e}}\)) we set \(B_{z\mathrm{e}}=0\), while the poloidal field is the potential field \(B_{\phi}=B_{\phi{\mathrm{e}}}r_{\mathrm{e}}/r\). The behavior of \(B_{z}(r)\) and \(B_{\phi}(r)\) is shown in Figure 1b.

The initial magnetic field configuration of the flux rope is not in equilibrium, which causes its rapid expansion. The impulsiveness of the expansion is regulated by applying different magnetic field strengths at the center of the flux rope. To facilitate the identification of the flux rope in the simulation snapshots, the density in the flux rope was taken to be ten times higher than in the ambient atmosphere. We note that as a result of the lower inertia, the upper parts of the flux rope are accelerated more than lower parts.

In the applied simulations the initial flux-rope height \(y_{0}\), the flux-rope radius \(r_{\mathrm{e}}\), the initial upward speed of the flux rope \(v_{y0}\), the initial poloidal field at the edge of the flux rope \(B_{\phi{\mathrm{e}}}\), and the central field strength \(B_{0}\) were varied in different runs. For the initial central magnetic field strength we applied the values \(B_{0}=5\), 6, 7, 8, 9, 20, and 50. The initial height was set to \(y_{0}=0.20\), 0.25, and 0.30, and for the initial upward speed we used \(v_{y0}=1\), 2, 3, 4, and 5. Various combinations of these input parameters provide an insight into how different forms of the eruption affect the characteristics of the eruption-associated large-scale wave. Simulations with high values of \(v_{y0}\) and low \(B_{0}\) reproduce eruptions where vertical dynamics dominates, while those with low values of \(v_{y0}\) and high \(B_{0}\) reproduce eruptions where the initial “overexpansion” dominates.

In Figure 2 different eruption types are depicted. In the events where the vertical dynamics dominates the lateral expansion (Figures 2a and b), the eruption generates a typical bow shock ahead of the flux rope. The low corona and transition layer are only weakly affected by the eruption, and there is practically no effect in the chromosphere, especially if the eruption starts from a larger height. In contrast, these regions are strongly affected by eruptions that are characterized by a strong lateral expansion and start from low heights (Figures 2c and d). Therefore we analyze below the outcome for such an expansion-dominated eruption in detail, applying \(y_{0}=0.2\), \(r_{\mathrm{e}}=0.1\), and \(v_{y0}=1\), in combination with \(B_{0}=10\) and 20, to obtain insight into how a degree of the expansion impulsiveness influences the formation and evolution of the eruption-driven low-coronal and chromospheric disturbance.

Figure 2
figure 2

Evolution of the coronal disturbance driven by different types of the eruption: a) and b) eruption dominated by vertical motion (weak flux-rope expansion); c) and d) eruption dominated by overexpansion. Two background coronal magnetic field configurations are considered: a) and c) purely potential arcade field (\(B_{y\mathrm{e}}=0\)); b) and d) helmet streamer configuration (\(B_{y\mathrm{e}}=1\)). The left, middle, and right columns show snapshots taken at \(t=0.02, 0.05, \mbox{and } 0.08\). White lines represent the magnetic field lines; the density is color-coded (logarithmic scale; \(\rho=\mathrm{e}^{\alpha}\), where \(\alpha\) is written in the displayed color-code scale. Input parameters are written at the top of each panel.

Full size image

All the runs performed with the above mentioned input combinations were repeated by adding a vertical background magnetic field to reproduce the overall helmet streamer that the flux rope is embedded in (see, e.g., Low and Hundhausen, 1995) and to decrease the inclination of the field lines in the low corona and chromosphere. This external field is antisymmetric with respect to \(x=0\), i.e., it has the same orientation as \(B_{\phi}\) at the edges of the flux rope and has a uniform value \(B_{y\mathrm{e}}\) over the numerical box, except at \(x=0\), where it vanishes. The overall configuration is similar to the lower parts of the helmet streamer structure, containing a vertical current sheet (CS) along \(x=0\) (Figures 2b and d). The CS causes the external magnetic field configuration to be initially not in equilibrium. As a result, a downflow is formed along the current sheet, which also causes the plasma inflow into the CS. However, the CS-related disturbance propagates relatively slowly in the \(x\)-direction, which means that throughout the time span that is included in the analysis, the CS-related effects stay within close vicinity of \(x=0\), which is evidenced by spatial profiles of the flow speed at different heights (to be presented in Section 3.2), showing no motion before the wavefront arrival. Consequently, the presence of the CS only affects the upward dynamics of the eruption and the evolution of the eruption-related coronal disturbance at its very summit. The horizontal acceleration of the flux-rope boundary in such a configuration (hereafter called helmet streamer configuration) is somewhat stronger than for \(B_{y\mathrm{e}}=0\) (hereafter called arcade configuration) because of the larger \(B_{y}\) field, i.e., the stronger \(j_{z}\times B_{y}\) force, where \(j_{z}\) is the electric current density in the flux rope. On the other hand, the deceleration of the boundary is subsequently stronger than in the arcade configuration because of a confining effect of the vertical field. Thus, the horizontal kinematics of the flux-rope boundary is somewhat different in the arcade and helmet streamer configurations. However, this difference affects the coronal-wave evolution only marginally (to be shown in Section 3.2). The evolution and kinematics of the low coronal signatures of the eruption-related disturbance is also affected by a different ambient Alfvén speed, which is higher in the helmet streamer configuration than in the arcade configuration.

The flux-rope expansion creates a large-amplitude disturbance in the surrounding corona, whose leading front steepens into a shock as a result of the nonlinear evolution of the wave (see Vršnak and Lulić (2000a) and references therein). At lower coronal heights the wave propagates as a quasi-perpendicular fast-mode magnetosonic wave (Chen, Ding, and Fang 2005). The passage of the wave over the more inert transition region layers and the chromosphere causes a delayed response of these regions, manifested mainly as a downward compression in the form of a downward propagating quasi-longitudinal fast-mode wave. In the following we focus on the horizontal propagation of the low-coronal segment of the wave and its effect on the transition region and the chromosphere to clarify the relationship between fast coronal waves and chromospheric Moreton waves.

3 Results

3.1 Morphology

In this section we study the evolution of the eruption and the wave in the arcade and the helmet streamer configurations in detail. This is shown in Figures 2c and d, respectively. Initially, at \(t=0\), the flux rope is centered at \((x;y)=(0.0;0.2)\) and has a radius of \(r_{\mathrm{e}}(0)=0.1\) (seen as enhanced density region in the \(t=0\) panels of Figure 2). As a result of the applied unstable initial magnetic field configuration, the flux-rope expansion starts immediately at \(t=0\). The expansion leads to a decrease of the flux-rope density and a weakening of the flux-rope magnetic field. On the other hand, the magnetoplasma in the flux-rope vicinity becomes compressed, i.e., an outward-propagating wave perturbation is created.

The wavefront segments in the region of the flux-rope summit and at low heights above the chromosphere propagate as a quasi-perpendicular fast-mode MHD wave (increased magnetic field component parallel to the wavefront in the downstream region). At heights \(y\approx0.2\,\mbox{--}\,0.4\), the wave is practically a fully perpendicular magnetosonic wave (note that there is always a certain wavefront segment exactly perpendicular to a magnetosonic wave). Figures 2c and d clearly show that the wave is much faster than the flux-rope expansion, which is a typical signature of a piston-driven wave (see, e.g., Vršnak, 2005; Warmuth, 2007).

In the case that reproduces the helmet streamer structure above the flux rope (\(B_{y\mathrm{e}}=1\); Figure 2d), the upward-propagating segment of the wavefront interacts with the vertical current sheet, which is seen as a thin vertical structure of increased density at \(x=0\). The interaction creates a very localized perpendicular shock at the wave summit and leads to a deformation (flattening) of the flux-rope summit. As mentioned in Section 2, the interaction only affects the evolution of the uppermost parts of the wavefront and the vertical dynamics of the flux rope. The low-coronal evolution of the wavefront and the lateral expansion of the flux rope is not affected by this interaction. This can be seen qualitatively by comparing Figures 2c and d, and it can be more rigorously checked by inspecting the spatial profiles of the flow speed at, e.g., \(y=0.2\) (to be presented in Section 3.2), which show no motion before the wavefront arrival.

At low coronal heights and in the transition region, the situation becomes more complicated for two reasons. First, the flux-rope expansion is much weaker at the very bottom of the rope due to higher inertia. Second, the field lines outside of the flux rope in the chromosphere are embedded in a very dense plasma. Both effects cause a strong deformation of the field lines in the transition region as the coronal wave propagates over it. To demonstrate this effect, we show in Figure 3 enlarged snapshots of the low-coronal wave propagation in the arcade configuration (left-column panels) and the helmet streamer configuration (right-column panels). The two upper rows show the shock propagation phase, the two bottom rows show the late-phase disturbance. We note that both options result in very similar morphological and evolutionary wave characteristics.

Figure 3
figure 3

Enlarged portion of snapshots (\(0 < x < 0.5\), \(0 < y < 0.3\)), depicting the evolution of the wave in the arcade configuration (left) and helmet streamer configuration (right) at low coronal heights, transition region, and chromosphere. Times are given in the insets. The white arrow marks the “echo” feature.

Full size image

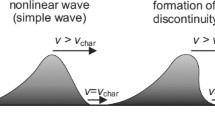
In the propagation phase the transition region is pushed down by the pressure excess in the shock downstream region, so its height decreases. The perturbation at a given point propagates downward, which can be seen as a downward propagation of field-line deformation. This propagation has the characteristics of a quasi-longitudinal fast-mode MHD shock. Eventually, the perturbation propagates into the chromosphere, but the effect weakens and slows down as it protrudes into the continuously denser chromospheric plasma (Figure 4). The front of the downward-propagating perturbation is depicted in Figure 4a by the black dashed line. Thus, the chromospheric perturbation (corresponding to a Moreton wave) lags behind the transition-region and coronal perturbation (corresponding to an EUV wave). This is fully consistent with the results presented by Vršnak et al. (2002b), where kinematics of sharp-wavefront EUV waves and the associated Moreton-wave signatures observed in the H\(\upalpha\) and the He i 1083 nm spectral line were compared. Note that the downward-propagating quasi-longitudinal disturbance can be approximately represented by the switch-on shock (see the sketch in Figure 4c).

Figure 4
figure 4

Enlarged portion (\(0< x<0.5\), \(0< y<0.15\)) of snapshots at \(t=0.1\) and 0.2, revealing the nature of the Moreton wave. a) Downward motion; the black dashed line depicts the downward-moving wavefront. b) An additional relaxation wave (white dashed line). c) Sketch: thin lines represent field lines, thick lines depict the shock (dashed lines correspond to the situation shown in a), while full lines represent the switch-on configuration).

Full size image

A certain time after the coronal wavefront passage, the relaxation of the system begins. This is most directly seen as a successive increase of the height of the transition region and chromosphere, which is depicted by the white dashed line in Figure 4b. Associated with the upward motion of the chromosphere and the transition region, we note in Figure 4b an upward-propagating deformation of the field lines with the characteristics of a switch-off slow-mode MHD shock (depicted by the white dashed line).

In the low corona, the relaxation stage in both the helmet streamer and the arcade configurations is characterized by the development of turbulent flows in the flux-rope volume (Figure 3, bottom panels). In close association with the relaxation of the chromosphere and the transition region, an interesting coronal feature appears in the form of a slowly traveling density compression, with only a small effect on the form of the magnetic field lines (indicated by arrows in Figure 3). This feature is similar to the “echo” feature noticed by Wang, Shen, and Lin (2009) and Wang et al. (2015) in their purely coronal-range simulation. The \(x\)-component of the velocity of this disturbance is significantly slower than that of the primary coronal wave. When the snapshots displayed in Figure 3 are compared, they show that the eruption in the arcade configuration propagated to a somewhat larger height than in the helmet streamer configuration because of the current-sheet effects in the latter case. Except for certain smaller differences, the echo feature appears to be quite similar in both configurations.

After the passage of a sharp coronal EUV wave associated with the Moreton wave, we therefore expect to observe the passage of a significantly slower perturbation, manifested mainly as a density compression that propagates upward and sidewise, and is associated with a slow upward relaxation of the chromosphere and transition region. As a result of its inclination and the spatial extent, this feature should be observed as a wide and diffuse EUV brightening propagating from the source region, and to do this much more slowly than the sharp coronal EUV wavefront associated with the Moreton wave.

3.2 Quantitative Analysis

After qualitatively describing the main morphological characteristics of the wave formation and evolution, we analyze in the following the simulation results from a quantitative point of view in more detail. First, we analyze the horizontal propagation of the primary disturbance, then the downward propagation of the associated chromospheric perturbation, and finally, the behavior of the secondary coronal disturbances.

3.2.1 Primary Disturbance: Horizontal Propagation

In the upper and middle panels of Figure 5 we present the evolution of the spatial profiles of the density \(\rho(x)\) and horizontal flow velocity \(v_{x}(x)\) at the height \(y=0.2\) for the helmet streamer configuration. We note that except for the numerical effects, the plasma ahead of the wave is at rest. In the bottom two panels we show the vertical component of the flow velocity \(v_{y}(x)\). Because of the symmetry, \(x<0\) is not displayed. The initial density in the flux rope is set to be ten times higher than the external density, the axial magnetic field at the rope center is set to \(B_{0}=20\), and the azimuthal field magnetic field at the rope surface to \(B_{\phi}=5\). In the left column, the early phase of the wave evolution is shown (formation phase), and the right column presents the freely propagating phase. The corresponding graphs for the arcade configuration (not displayed) show very similar patterns.

Figure 5
figure 5

Formation and horizontal propagation of the coronal shock at \(y=0.2\) (only \(x>0\) is shown) in the helmet streamer configuration (\(B_{y\mathrm{e}}=1\)): spatial profiles of the density (top) and horizontal component of the flow speed (middle). The left panels show the wave formation (growing wave amplitude), the right panels outline the propagation phase. In the bottom two panels, we present the vertical component of the flow speed at \(y=0.08\), showing the propagation of the Moreton wave and the chromospheric relaxation. Times are displayed in the insets; different time steps are used in the left and right panels.

Full size image

From the \(\rho(x)\) profiles we measured the propagation of the contact surface and the wavefront. First, we compared the kinematics of the wave signatures in the arcade and the helmet streamer configurations for \(B_{0}=20\). The outcome is presented in Figure 6. The kinematical graphs show basically the same behavior for the two configurations, the differences are primarily caused by the difference in the ambient coronal Alfvén speed, which is higher in the helmet streamer configuration because of the superposed \(B_{y\mathrm{e}}=1\) field. To a smaller extent, the differences are also caused by somewhat different eruption or expansion dynamics, as described in Section 2.

Figure 6
figure 6

Comparison of the wavefront \(x\)-direction kinematics in the arcade field configuration (\(B_{y\mathrm{e}}=0\); dotted lines) and the helmet streamer configuration (\(B_{y\mathrm{e}}=1\); solid lines), measured at three different heights (\(y=0.2\) – black, \(y=0.1\) – blue, and \(y=0.08\) – red). Gray lines represent a motion of the contact surface in the \(x\)-direction (denoted by “piston”) at the height of \(y=0.2\), i.e., at the initial height of the flux-rope center. Panel a) shows the distance–time curves \(x(t)\) of the wavefront leading edge; in panel b) the corresponding phase speeds \(w(t)\) and the piston speed \(v_{\mathrm{p}}(t)\) are displayed; in panel c) these speeds are presented as a function of distance \(w(x)\), \(v_{\mathrm {p}}(x)\); the ambient Alfvén speed \(v_{\mathrm{A}}(x)\) at the height of \(y=0.2\) is shown by thin black lines (dotted: \(B_{y\mathrm{e}}=0\); full: \(B_{y\mathrm{e}}=1\)).

Full size image

Next, we compare the kinematics of the wave driven by the \(B_{0}=20\) eruption in the helmet streamer configuration with a more gradual expansion, driven by \(B_{0}=10\) (all other parameters are kept unchanged). The kinematics are shown in Figure 7.

Figure 7
figure 7

The \(x\)-direction kinematics of the wavefront in the helmet streamer configuration (\(B_{y\mathrm{e}}=1\)), measured at three different heights for \(B_{0}=20\) (left) and \(B_{0}=10\) (right). The \(y\)-coordinate is written by the curves. Gray line represents the motion of the contact surface (denoted as “piston”) at the height of \(y=0.2\), i.e., at the initial height of the flux-rope center. Panels a) and b) show the distance–time curves \(x(t)\) of the wavefront leading edge (dashed lines) and the wave crest (solid lines). Panels c) and d) display the corresponding phase speeds \(w(t)\) and the piston velocity \(v_{\mathrm{p}}(t)\). In panels e) and f) these velocities are shown as a function of distance \(w(x)\), \(v_{\mathrm {p}}(x)\); the brown dotted line shows the ambient Alfvén speed at the height \(y=0.2\).

Full size image

The evolutionary time-line and the basic characteristics of the main signatures for the arcade configuration with \(B_{0}=20\) and the helmet streamer configuration with \(B_{0}=20\) and 10 are summarized in Tables 1 and 2, respectively. To transform the displayed normalized distances into those corresponding to the coronal environment, the displayed values need to be multiplied by the length \(\lambda\) (km) of the coronal element depicted by the numerical box. Analogously, the presented normalized velocities need to be multiplied by an assumed background Alfvén speed \(v_{\mathrm{A0}}\) (\(\mbox{km}\,\mbox{s}^{-1}\)). To transform the presented normalized times, they need to be multiplied by the Alfvén travel time \(\tau_{\mathrm{A}}~(\mbox{s}) =\lambda/v_{\mathrm{A0}}\). For example, we took for the background coronal Alfvén speed a value of \(v_{\mathrm{A0}}=300~\mbox{km}\,\mbox{s}^{-1}\) and for the numerical box a size of \(\lambda=600~\mbox{Mm}\), corresponding to an extended flux rope with a diameter of 120 Mm. This gives for the Alfvén travel time \(\tau _{\mathrm{A}}=\lambda/v_{\mathrm{A0}}=2000~\mbox{s}\). In this case, for \(B_{0}=20\), the shock forms after 60 s at a distance of 150 Mm, etc. For a more compact source region, e.g., taking \(\lambda =200~\mbox{Mm}\), which corresponds to a flux-rope diameter of 40 Mm, the shock forms at a distance of 50 Mm.

Table 1 Timing and the corresponding location of the most prominent features.
Full size table
Table 2 Basic characteristics of the most prominent features.
Full size table

The most prominent feature in Figure 5a is a sharp density peak propagating slowly in the \(x\)-direction, starting from \(x=0.1\). It represents the contact surface, i.e., the edge of the flux rope where the density pile-up forms as a result of the flux-rope expansion. This feature corresponds to the bright frontal rim of the CME. On the other hand, the density decreases over most of the flux rope because the flux rope expands, which represents the so-called core dimming that occurs after CME take-off.

The flux-rope expansion creates a wave ahead of the contact surface that becomes clearly recognizable at \(t\approx0.008\). In this phase, which is associated with the acceleration phase of the flux-rope expansion (see gray curves in Figures 6b and 7b), the wave amplitude increases and the wavefront steepens, forming a discontinuity (shock) at \(t\approx0.03\) at a distance of \(x\approx 0.25\) (compare in Figure 7a the time at which the wave crest catches up with the leading edge of the wave profile). We note that the wave propagates much faster than the contact surface (“piston”). The wave attains a maximum amplitude (the ratio of the downstream and upstream density, \(X\)) of \(X=2\) at \(t=0.036\) at a distance of \(x=0.3\) (the corresponding values for the arcade configuration are listed in Tables 1 and 2).

The lateral expansion of the flux-rope attains a maximum velocity of \(v_{x}^{\mathrm{max}}=3.11\) at \(t=0.018\). After this, it gradually slows down, stopping at \(t=0.046\), when the rope surface reaches a distance of \(x=0.17\). During the deceleration phase, a density depletion forms in the rear of the wave (denoted by “dip” in Figure 5b), presumably corresponding to the transient dimming that usually follows the bright coronal-wave signature. We note that the depth of this dip (\({\sim}\,20\,\mbox{--}\,30~\%\)) is considerably smaller than that of the core dimming (\({>}\,50~\%\)). Eventually, the flux-rope starts to retreat slowly. In this phase, the flow velocity associated with the wavefront decreases (Figure 5d), the density amplitude remains roughly constant (Figure 5b), and the flow velocity in the dip region becomes negative.

The horizontal propagation of the perturbation is analyzed in detail at the heights of \(y= 0.2\) (the initial height of the flux-rope center), \(y=0.25\) (the height of the flux-rope center at the time of the fastest lateral expansion), \(y=0.1\) (top of the chromosphere), and \(y=0.08\) (upper chromosphere). The wave kinematics at the heights of \(y=0.2\), \(y=0.1\), and \(y=0.08\) is displayed in Figure 7 in the form of \(x(t)\), \(w(t)\), and \(w(x)\) graphs, where \(w\) represents the wave phase speed. In addition, the kinematics of the flux-rope lateral expansion (denoted as “piston”, \(v_{\mathrm{p}}\)) is shown. Thin dashed and bold full lines represent the motion of the outermost element of the wave and the wave crest, respectively. The time when the bold line catches up with the thin dashed line marks the moment of the shock formation.

The results shown in the left column of Figure 7 are based on the simulation for the helmet streamer configuration with \(B_{0}=20\). In the right column, we present analogously the results for the simulation with \(B_{0}=10\) (all other input parameters are kept the same), representing a more gradual expansion – the piston attains a maximum speed of \(v_{\mathrm{p}}^{\mathrm{max}}=0.5\) at \(t=0.02\), in contrast to the expansion driven by \(B_{0}=20\), which attains \(v_{\mathrm {p}}^{\mathrm{max}}=3.11\) in about the same time, i.e., the expansion driven by \(B_{0}=20\) is more than six times more impulsive than that driven by \(B_{0}=10\).

A comparison of the left and right panels of Figure 7 very clearly shows that the wave propagates much faster in the former case. Furthermore, by checking the \(\rho(x)\) profiles, we find that the wave amplitude is considerably larger for \(B_{0}=20\). Consequently, as the wavefront is created more impulsively, the shock forms at a much shorter time and distance (compare Figure 7a and Figure 7b). In the former case, the shock forms at \(t=0.03\), after it traveled a distance of \(\Delta x=0.15\) from the initial flux-rope surface; in the latter case it is formed at \(t=0.07\), after it has traveled a distance of \(\Delta x=0.25\). For \(B_{0}=20\) the density jumps at the shock by a factor of two (Figure 5b), whereas the \(\rho (x)\) profiles for \(B_{0}=10\) (not shown) show a maximum density ratio of about \(X=1.2\). Consequently, the local Alfvén-speed Mach number (\(M_{\mathrm{A}}=w/v_{\mathrm{A}}\)) is much higher in the former case, which is directly seen in Figure 7e and f, where the local Alfvén speed \(v_{\mathrm{A}}(x)\) at \(y=0.2\) is shown. In the former case the highest value of the coronal-wave Mach number is around \(M_{\mathrm{A}}\approx2\), while in the latter case, the wave crest propagates at a speed only slightly higher than the local Alfvén speed most of the time. This is consistent with the Rankine–Hugoniot jump relations (\(M_{\mathrm{A}}^{2}=X(X+5)/2(4-X)\) for a perpendicular shock, with \(\beta=0\)).

Figures 7a and b clearly show that the chromospheric signatures of the wave are delayed after the coronal wave, or in other words, there is a spatial offset between the coronal wave and the Moreton wave. Taking for the numerical box size the value of \(\lambda=200~\mbox{Mm}\) (in Section 3.2.1 denoted as “compact source region”), we find a lag of \({\approx}\,50~\mbox{Mm}\), which roughly corresponds to the observed offsets (e.g., Vršnak et al., 2002b). The delay or offset depends on the considered chromospheric depth, which is also evident in Figure 4. The delay or offset is only partly caused by the inclination of the coronal wavefront (as interpreted by Vršnak et al., 2002b) – a physically more important effect is the inertia of the dense chromosphere. The inclination effect is comparatively more important at the highest chromospheric layers, while the latter effect dominates at deeper layers.

Figure 7e shows that the perturbation at \(y=0.1\) and \(y=0.08\) occurs already at \(x<0.1\), i.e., below the outer parts of the flux rope (see sixth row of Table 1). This is a consequence of the coronal wave shape or inclination, which is the effect of the radial expansion of the flux rope that creates flows with a considerable downward component in the lowest parts of the coronal wave.

Figures 7c and d show that at a given time the perturbation propagates at approximately the same speed at all levels (consistent with the observations presented by Asai et al. (2012) in their Figure 5, curve F2f), meaning that the black dashed line depicting the chromospheric perturbation front in Figure 4 practically translates into larger distances. Consequently, the offset between the coronal and chromospheric wavefronts remains approximately constant (see Figure 7a), which is consistent with observations (see, e.g., Figure 9 of Vršnak et al., 2006).

On the other hand, Figures 7e and f reveal that at a given distance \(x\), the chromospheric perturbation propagates more slowly than the coronal wave because the speed is lower at deeper layers. Furthermore, at \(y=0.1\) the perturbation propagates at a speed comparable with the local Alfvén speed at \(y=0.2\), while at \(y=0.08\) the propagation speed is considerably lower than the local Alfvén speed at \(y=0.2\). This has to be taken into account if Moreton waves are used to infer the coronal Alfvén speed and magnetic field (coronal seismology).

3.2.2 Primary Disturbance: Chromospheric Compression

We now present numerical results on the downward-propagating chromospheric perturbation in the helmet streamer configuration and compare them with an order-of-magnitude analytical consideration. In particular, we present the outcome of the simulations obtained by applying \(B_{0}=10\) and \(B_{0}=20\). The former option causes a perturbation that is too weak to result in an observable Moreton wave, while the latter case reproduces typical Moreton wave signatures very well. The results for the arcade configuration are quite similar; some smaller differences are mainly related to a different amplitude of the coronal wave and to a certain degree they also occur because the chromospheric field lines are differently inclined, and this inclination is somewhat stronger than in the helmet streamer configuration.

First, we present the outcome of the simulation run performed with \(B_{0}=20\). In Figure 8, the vertical component of the flow velocity (\(v_{y}\)) and the plasma density (\(\rho\)) is shown as a function of height (\(v_{y}(y)\), \(\rho(y)\)) at \(x=0.3\) for several discrete times. The coronal shock reaches this distance at \(t=0.035\) at a height of \(y=0.27\). As a result of the shock-front curvature and inclination, the top of the chromosphere at \(x=0.3\) is perturbed considerably later, at \(t=0.06\) (the orange curve in Figure 8). The arrival of the shock causes a downflow of \(v_{y}=-0.22\) in the uppermost chromospheric layer (the highest downward speed at the top of the chromosphere occurs closer to the source region, so that at \(x=0.1\) it amounts to \(v_{y}=-0.45\)). At \(t=0.14\) the perturbation at \(x=0.3\) reaches \(y=0.08\), and the flow speed is already reduced to \(v_{y}=-0.04\). At \(t=0.45\) the perturbation becomes \(y=0.06\) and the flow speed is only \(v_{y}=-0.01\), i.e., less than 5 % of the initial value at \(y=0.1\).

Figure 8
figure 8

Evolution of the disturbance at \(x=0.3\) for \(B_{0}=20\): a) \(y\)-component of the flow velocity presented as a function of \(y\) for several discrete times (written in the inset), b) density presented as a function of \(y\) (in the inset the region covering the upper chromosphere and lower corona are enlarged to resolve the propagation of the chromospheric perturbation, as well as the formation of the reflected wave (\(t>0.08\)).

Full size image

The same analysis was performed for \(B_{0}=10\) that causes a considerably more gradual source-region expansion. In this case the coronal shock reached a distance of \(x=0.3\) at \(t=0.052\) at a height of \(y=0.31\). The shock flank reached the top of the chromosphere at \(t=0.068\) at \(x=0.14\). At the distance of \(x=0.3\) the shock hit the chromosphere at \(t=0.105\), causing a downflow of \(v_{y}=-0.025\) in the uppermost chromospheric layer. The layer \(y=0.08\) was perturbed at \(t=0.24\) because the flow speed was reduced to \(v_{y}=-0.01\). At \(t=0.6\) the perturbation reached \(y=0.06\), and the flow speed was only \(v_{y}=-0.002\).

The simulation-based perturbation kinematics and amplitude for \(B_{0}=10\) and \(B_{0}=20\) are presented in Figure 9 by red pluses and blue circles, respectively. The transformation from dimensionless quantities was performed by taking \(h=2000~\mbox{km}\) for the height of the chromosphere and \(300~\mbox{km}\,\mbox{s}^{-1}\) for the background Alfveén speed.

Figure 9
figure 9

Chromospheric response to the coronal wave, measured at \(x=0.3\): a) downward wave-velocity \(w_{y}\) versus height, b) downward wave-velocity \(w_{y}\) versus time; c) maximum downward-flow velocity \(v_{y}\) versus height, d) height of the wave crest versus time. Numerical results are presented for \(B_{0}=20\) (blue circles) and \(B_{0}=10\) (red pluses). Analytical results, starting with approximately the same downward flow-speed, are shown by solid lines; red and blue lines represent results for \(X=1.07\) and \(X=1.4\), respectively.

Full size image

In the following, the numerical results for the downward propagation of the chromospheric perturbation are compared with an analytical consideration. To simplify the problem, we assumed that the magnetic field in the upper layers of the chromosphere is vertical and that the downward-propagating shockfront is horizontal, i.e., that the downward-propagating disturbance is represented roughly by a switch-on shock (see Figure 4c).

For the switch-on shock the downstream/upstream density compression ratio, \(\rho_{2}/\rho_{1}\equiv X\), is related to the shock Alfvén Mach number as (e.g., Priest, 1982; Vršnak et al., 2002a)

$$ \frac{w}{v_{\mathrm{A}}} \equiv M_{\mathrm{A}} = \sqrt{X} , $$
(3)

where \(v_{\mathrm{A}}=B_{1}/\sqrt{\mu\rho_{1}}\) is the upstream Alfvén speed and \(w\) is the shock speed. Denoting the rest-frame flow speed behind the shock front as \(v\) (i.e., the shock-rest-frame downstream flow speed equals to \(w-v\)), the mass conservation that reads \((w-v)\rho_{2} = w\rho_{1}\) can be written in the form

$$ \frac{v}{v_{\mathrm{A}}} \equiv V = \left(1-\frac{1}{X}\right )M_{\mathrm{A}}. $$
(4)

We note that \(V\) is equivalent to \(v_{y}\) in the numerical simulation.

To be consistent with the numerical simulation, in the following we assume that the ratio of the plasma to the magnetic field pressure is very low, i.e., we employ the \(\beta=0\) approximation. In this case the conservation of the momentum component in the direction of the shock propagation (Priest, 1982) becomes

$$ \frac{B_{2}^{2}}{2\mu} + \rho_{2}(w-u)^{2} = \frac{B^{2}}{2\mu} + \rho_{1} w^{2}, $$
(5)

where \(B\) and \(B_{2}\) represent the upstream and downstream magnetic field strength, respectively. After dividing the equation by \(\rho _{1}v_{\mathrm{A}}^{2}/2\), and using Equation (4), we obtain

$$ \frac{B_{\perp}}{B}\equiv\chi= \sqrt{2X-2}, $$
(6)

where \(B_{\perp}\) is the downstream magnetic field component perpendicular to the direction of the shock motion.

Taking into account that in the switch-on shock the magnetic field and the shock-rest-frame flow velocity in the upstream region are parallel to the direction of the shock propagation (i.e., they are both parallel to the shock normal), the conservation of the momentum component in the direction of the shock propagation and the magnetic flux conservation simplify to

$$ \rho_{2} v_{\perp} v_{\parallel} - \frac{ B_{\perp} B_{\parallel} }{\mu} = 0 $$
(7)

and

$$ v_{\parallel} B_{\perp} - v_{\perp} B_{\parallel} = 0, $$
(8)

respectively, where \(v_{\perp}\) and \(B_{\perp}\) denote the downstream flow and field components perpendicular to the shock normal, while \(v_{\parallel}\) and \(B_{\parallel}\) represent the downstream flow and field components parallel to the shock normal.

By combining Equations (7) and (8), we find

$$ \frac{v_{\perp}}{v_{\mathrm{A}}} \equiv V_{\perp} = \chi M_{\mathrm {A}}. $$
(9)

This means that for a given compression ratio \(X\), the shock Mach number can be found from Equation (3), which also provides the evaluation of the downstream flow speed in the shock-normal direction, \(V\), from Equation (4). After knowing \(X\), \(M_{\mathrm{A}}\), and \(V\), the ratio \(\chi\) can be evaluated by using Equation (6) and the ratio \(V_{\perp}\) from Equation (9). For a given value of the upstream Alfvén speed \(v_{\mathrm{A}}\), the dimensionless quantities \(M_{\mathrm{A}}\), \(V\), and \(V_{\perp}\) also provide the shock speed \(w=M_{\mathrm{A}}v_{\mathrm {A}}\), as well as the downstream flow speed components \(v_{\parallel }=Vv_{\mathrm{A}}\) and \(v_{\perp}=V_{\perp}v_{\mathrm{A}}\).

The presented consideration shows that the chromospheric kinematics of the shock front and the evolution of the associated plasma flow are governed by the dependence of the Alfvén speed on height, \(v_{\mathrm {A}}(h)\), and the evolution of the compression ratio \(X\). Considering this, we note that the influence of changing \(X\) is expected to be relatively weak, since the Alfvén Mach number depends on the square root of the compression ratio, which is limited to \(1< X<4\). Thus, changes of the shock speed and the flow speed related to changes of \(X\) are limited to within a factor of 2. On the other hand, since the chromospheric density changes with height for about five orders of magnitude (Vernazza, Avrett, and Loeser 1981) while the magnetic field does not change much (see, e.g., Gary (2001), and references therein), the change of the Alfvén speed is strong and it might be expected that the effect of the decreasing Alfvén speed dominates the effect of changing \(X\). In this context, we note that our numerical simulations show that the compression ratio does not change much (see, e.g., the inset in Figure 8b) during the shock propagation through the chromospheric layers. For the simulation with \(B_{0}=10\), the compression ratio decreases from \(X=1.09\) at the top of the chromosphere to 1.07 in the mid-chromosphere, while for the \(B_{0}=20\) simulation, it decreases from 1.5 to 1.3 in the same height range.

In Figure 9 we present the results based on Equations (3) and (4) for \(X= \mbox{const.}\), where the function \(v_{\mathrm{A}}(h)\) is derived using the same \(\rho(h)\) scaling as in the numerical simulations and taking \(B(h)= \mbox{const.} = 10~\mbox{gauss (G)}\). The values of \(X\) are chosen in such a way that the initial shock speed and the associated flow velocity at \(h=2000~\mbox{km}\) reproduce the values obtained in the numerical simulations. The presented graphs correspond well for the analytical and numerical results, in spite of the relatively crude approximation of the numerical configuration by the switch-on geometry and the \(X= \mbox{const.}\) approximation. The only slightly larger discrepancy can be found in the middle part of the \(h(t)\) curve for the \(B_{0}=20\) simulation (Figure 9d), where the difference in the shock height is in the range of 5 %. The discrepancy might be related to the employed \(X= \mbox{const.}\) approximation, since the applied value of \(X=1.4\) differs from the values in the numerical simulation (\(X=1.5\rightarrow1.3\)) by \({\pm}\,5~\%\).

Figure 9 shows that for relatively weak shocks like those analyzed above, the shock kinematics depends only weakly on the strength of the coronal disturbance, the latter intrinsically determining the initial compression ratio of the chromospheric perturbation. On the other hand, the initial flow-speed amplitude (Figure 9c) depends strongly on the coronal shock strength. However, its evolution is governed by the \(v_{\mathrm{A}}(h)\) dependence.

Finally, we note that we also compared the behavior of \(v_{\perp}\) and \(B_{\perp}\) based on Equation (9) with the numerical values of \(v_{x}\) and \(B_{x}\), respectively. This comparison also shows a good correspondence of the numerical and analytical results, being on the same level as for the quantities compared in Figure 9.

3.2.3 Secondary Perturbations

The downstream region of the coronal shock is characterized by a strong upflow in both the helmet streamer and the arcade configuration. It starts to develop when the coronal shock reaches the transition region and further amplifies when the perturbation hits the chromosphere. This is illustrated in Figure 8a, where the development of the vertical profile at \(x=0.3\) of the \(y\)-component of the flow velocity \(v_{y}(y)\) is presented for the helmet streamer configuration. The outcome for the arcade configuration is very similar – for the comparison, the simulation-based values analogous to those presented in the following for the helmet streamer configuration are shown in Tables 1 and 2. As a result of the curvature of the coronal shock, the shock in the vertical cut is seen as a downward- (and upward-) propagating shockfront, characterized by negative (positive) \(v_{y}\) in the shock downstream region (depicted by two arrows close to the abscissa of Figure 8a). When the shock enters into the transition region (\(t=0.052\)), the upflow starts forming in low coronal layers (see in Figure 8a the \(v_{y}(y)\) profile at \(t=0.06\)). The upflow forms a well-defined peak that moves upward at a speed of \(w_{y}\approx0.6\,\mbox{--}\,0.7\) and is characterized by a flow speed that increases to up to \(v_{y}\approx0.65\). Since the propagation of the peak is characterized by \(w_{y}\approx v_{y}\), it is not a wave, but just a convective flow.

In the phase during which the upflow speed is still enhancing, another upward-propagating shock forms between the expanding upflow-region and the coronal shockfront (denoted as “secondary shock” in Figure 8a). It becomes recognizable at \(t=0.08\) as a weak perturbation in the rear of the main coronal shock, at a height of \(y\approx0.3\) (marked by the dotted arrow in Figure 8a). Subsequently, it propagates upward as a growing simple-wave blast (for the terminology see, e.g., Landau and Lifshitz (1987) or Vršnak (2005)), being slightly faster than the main shock and lagging behind it for \(\Delta y\approx0.2\). Eventually, it fragments into several substructures (see the profile at \(t=0.12\)), forming an upward-propagating quasi-periodic wave-train at \(t>0.18\) in \(v_{y}(y)\). It should be noted that such wave trains are sometimes observed in association with EUV waves (see, e.g., Liu and Ofman (2014) and references therein).

The upward expansion of the upflow, starting already around \(t\approx 0.05\) (Figure 8a), is accompanied by its spreading in the \(x\)-direction (see the horizontal solid-line arrow at the right side of Figure 10a), tracking a horizontal propagation of the coronal shock. This perturbation is also associated with the outward propagation of the density compression (Figure 10d), associated with a gradual change of the horizontal flow speed \(v_{x}(x)\) (see the horizontal right-side segments of the profiles in Figure 10b, whose propagation is marked by the solid-line arrow). At \(y=0.2\), around \(t\approx0.14\), a new \(v_{x}(x)\) and \(B_{y}(x)\) steep disturbance forms in the upflow region (marked by a dotted arrow in Figures 10b and c), propagating in the \(x\)-direction at a mean phase speed of \(w\approx3\) (marked by the horizontal dashed-line arrow at the right side of Figures 10b and c), which is almost twice as slow as the primary wave. The highest speed of \(w_{\mathrm{max}}\approx4.5\) occurs at \(t=0.17\) when the wave reaches \(x=0.22\), which is almost twice as slow as \(w_{\mathrm{max}}=7.5\) found for the primary wave. Comparing the position of this horizontally propagating compression signature with Figure 3, we find that it corresponds to the echo feature. Amplitudes of this perturbation are \(v_{x}=0.5\,\mbox{--}\,0.6\) (variable), \(v_{y}=0.8\rightarrow0.4\) (continuously decreasing), and \(X=1.4\,\mbox{--}\,1.6\) (variable). We note that the traveling density compression develops a sharp peak at \(t=0.22\) (marked by a dotted arrow in Figure 10d), reaching the value of \(\rho\approx2\). Furthermore, we note that the compression region is followed by a density depletion, where the density is reduced to \(\rho\approx0.25\). Comparing the amplitude of this dip with the one that tracked the primary shock, we find that this new depletion is much deeper and shows a much more pronounced outward propagation. Thus, transient dimmings that track EUV waves are more likely to be caused by the depletion behind the secondary perturbation than by the primary one.

Figure 10
figure 10

Evolution of secondary perturbations at \(y=0.2\) in the helmet streamer configuration: a) vertical component of the flow velocity, \(v_{y}(x)\), b) horizontal component of the flow velocity, \(v_{x}(x)\), c) vertical component of the magnetic field \(B_{y}(x)\), and d) the density, \(\rho(x)\). The times for each curve are given in the legend shown in a) and c). The meaning of the arrows is explained in the main text. Fluctuations in the rear of the erupting arcade are confined within \(x<0.12\).

Full size image

To conclude, the upflow and its propagation in the form of an oblique wave are caused by partial reflection of the incoming coronal wave at the transition region and chromosphere – a part of the incoming wave enters into the chromosphere, and the rest is reflected back into the corona. Figure 10 reveals that in the reflected signature the frontal density compression is followed by a density depression in the transition region and in the lower layers of the corona. We conclude that this signature corresponds to a transient dimming behind the EUV wave.

No clearly recognizable echo feature is observed for \(B_{0}=10\); instead there is only a wave-train, best seen in the \(v_{x}(x)\) plots after \(t=0.14\). This implies that weak eruptions can produce only one observable disturbance, and that is the main wave, moving in such cases at a constant speed that is close to the local magnetosonic speed. Similarly, no echo signature is expected in eruptions where the vertical motion dominates the lateral expansion, such as those shown in Figures 2a and b. In both cases, no detectable Moreton wave is expected. On the other hand, eruptions characterized by a sufficiently strong overexpansion should produce a Moreton wave together with a fast primary EUV wave, and in addition, a slower EUV signature propagating behind the primary one, as sometimes observed (cf., Liu and Ofman (2014) and references therein).

4 Discussion and Conclusions

Our simulations reveal that even a model that considers a very simply configured eruption in a very simple environment results in a complex response of the surrounding atmosphere. Simulations reveal a rich variety of eruption-driven phenomena, reproducing nicely the typically observed eruption-associated signatures. A detailed analysis of simulations provides quantitative relations between the characteristics of the eruption and the evolution of the atmospheric response, and it reveals the physical nature of the various observed signatures.

The most prominent effect caused by the eruption is the primary perturbation, forming a fast-mode MHD shock that propagates in all directions ahead of the expanding source-region. It is important to note that the source region expansion is subsonic: according to Figure 7e, the maximum Alfvén Mach number of the source region was \(M_{\mathrm{A}}\approx0.5 \mbox{ and } 0.1\) for the simulations with \(B_{0}=20 \mbox{ and } 10\), respectively. Thus, the shock formation is caused by a nonlinear evolution of the large-amplitude perturbation front driven by a subsonically expanding piston (Vršnak and Lulić 2000a; Lulić et al. 2013). The amplitude and the steepness of the initial perturbation front is higher for a more impulsive piston expansion, so that the steepening of the front profile is faster than for a slower expansion. Consequently, the distance or time required for the shock formation is shorter for more powerful eruptions, and the shock amplitude is higher (Vršnak and Lulić, 2000a, 2000b; Vršnak, 2001). In a real coronal situation, the shock will not be formed if the expansion is too slow.

For the two analyzed source-region expansions in the helmet streamer configuration, which reach \(M_{\mathrm{A}}\approx0.5 \mbox{ and } 0.1\) within \(t\approx 0.02\), the shock forms at \(t=0.03 \mbox{ and } 0.07\) at a distance of \(x=0.25 \mbox{ and } 0.35\), respectively (see Table 1). Taking for the background coronal Alfvén speed a value of \(v_{\mathrm{A0}}=300~\mbox{km}\,\mbox{s}^{-1}\) and ascribing the numerical box a size of, e.g., \(\lambda=450~\mbox{Mm}\) (corresponding to the Alfvén travel time of \(\tau _{\mathrm{A}}=\lambda/v_{\mathrm{A0}}=1500~\mbox{s}\)), we find that the corresponding shock formation times (distances) are \(\tau=t\times\tau _{\mathrm{A}}=45~\mbox{s}\) (\(d=x\times \lambda=112~\mbox{Mm}\)) and 105 s (158 Mm), respectively. These numbers are consistent with the appearance of the coronal EUV waves (e.g., Warmuth and Mann, 2011), Moreton waves (e.g., Warmuth et al., 2004a) and the radio type II bursts (e.g., Vršnak, 2001).

After a phase where the coronal perturbation is driven by the expanding source region, the coronal wave continues its propagation or evolution as a freely propagating large-amplitude “simple wave”. Its kinematics is governed by the increasing size of the expanding wavefront, the evolution of the wave amplitude, and the change of the background Alfvén speed along the direction of propagation. In the situation where the background Alfvén speed decreases with distance (like in the studied simulation), the amplitude-decrease as a result of the wavefront expansion, and the nonlinear evolution of the perturbation profile that causes its broadening (see Section 102 in Landau and Lifshitz 1987) is compensated for by the effect of the Alfvén speed decrease, which tends to increase the wave amplitude. Thus, since the amplitude does not change much, the wave-speed decreases primarily because of the changing Alfvén speed. At larger distances, where the Alfvén speed is expected to be more or less constant, the wave should continue to slow down. However, in this situation, the deceleration is caused by the wave-amplitude decrease that now becomes effective due to the other two processes, i.e., the wave profile broadening and the increasing size of the expanding wavefront. When the amplitude becomes low, nonlinear effects become negligible and the wave continues to move at a speed approximately equal to the ambient Alfvén speed (or magnetosonic speed in the case of \(\beta\neq0\)). For a more gradual source region expansion (depicted by the \(B_{0}=10\) simulation), the nonlinear effects in the wave propagation are almost negligible from the very beginning because of the low amplitude of the initial coronal perturbation.

The pressure jump associated with the coronal shock passage impulsively exerts a downward force on the transition region and chromosphere, causing their compression. The perturbation propagates downward as a quasi-longitudinal MHD shock that can be well approximated by the switched-on shock of a constant density-compression amplitude. Thus, the kinematics is primarily determined by the vertical profile of the background Alfvén speed. Since the Alfvén speed decreases rapidly with the chromospheric depth and the density compression remains almost constant, the flow velocity associated with the downward-propagating shock rapidly decreases. A comparison of our simulations shows that if the flux-rope eruption is characterized by a sufficiently strong lateral expansion, it results in a disturbance that is strong enough to create an observable Moreton wave. On the other hand, less impulsive eruptions, as well as those with insufficient lateral expansion, cause a much weaker chromospheric perturbation that is not likely to be observed as a Moreton wave. In this case, maybe an asymmetric, i.e., nonradial, eruption is required to generate a Moreton wave on the erupting side of the flux rope. Thus, according to our results, eruptions showing the so-called overexpansion are the best candidates for creating Moreton waves. This might explain the relatively low occurrence rate of Moreton waves, if it is accepted that the overexpansion is a preferable condition for their formation.

The analysis of the perturbation kinematics at different heights (Figure 7) shows that the chromospheric perturbation (corresponding to a Moreton wave) lags behind the transition-region and coronal perturbation (corresponding to an EUV wave). This is fully consistent with the observations of the sharp-wavefront EUV waves associated with H\(\upalpha\) and He i Moreton waves presented by Vršnak et al. (2002b). The lag of the chromospheric signature is caused primarily by the time needed by the perturbation to protrude sufficiently deep into the chromosphere, and is only partly due to the inclination of the coronal wavefront.

After the passage of the primary coronal wave and the associated Moreton-wave chromospheric perturbation, a number of phenomena occur in the low corona. First, a weak transient density depletion occurs in the rear of the coronal disturbance. Then, a coronal upflow starts forming in the rear of the primary disturbance. The upflow expands upward and horizontally, which drives a secondary shock at the rear of the primary shock, propagating at a similar speed as the primary one, but with a smaller amplitude.

Eventually, the expansion of the upflow in both the arcade and the helmet streamer configurations creates another steep obliquely propagating wavefront (echo feature) that expands considerably more slowly than the primary coronal wave. The horizontal component of the phase velocity of this oblique disturbance in the case of the impulsive source-region expansion is found to be \(w_{x}\approx0.7 v_{\mathrm{A0}}\), while for the more gradual expansion it was not recognized in the simulations.

After the passage of a primary coronal EUV wave and the associated Moreton wave, we therefore expect to observe a passage of a significantly slower perturbation, but only if the eruption is characterized by a sufficiently strong lateral expansion. This secondary perturbation is manifested mainly as a density compression that propagates upward and sidewise and is followed by a slow upward relaxation of the lower corona, transition region, and chromosphere. Because of its inclination and the spatial extent, this feature should be observed as a wide and diffuse feature propagating from the source region at much slower speed than the sharp primary coronal EUV wavefront. In less powerful eruptions, this secondary perturbation is expected to be absent, so that the only observable disturbance should be the primary one, but without a detectable Moreton wave. It should move at a local Alfvén speed, i.e., should not show much deceleration when propagating through a quiet corona.

The density compression associated with the secondary disturbance is followed by a relatively strong density depletion, which corresponds to a transient dimming observed behind coronal waves. Eventually, the event gradually ends by an upward relaxation of the compressed chromospheric and transition-region layers.

To conclude, we showed that even a relatively simple 2.5 D numerical simulation, depicting just the most basic characteristics of an overexpanding flux rope in an idealized background atmosphere, provides an in-depth insight into the nature of various phenomena occurring as a consequence of the eruption. It directly relates properties of the eruption with the characteristics and evolution of the expanding large-amplitude coronal fast-mode MHD wave (observed as fast EUV coronal waves and radio type II bursts) and the related chromospheric downward-propagating quasi-longitudinal perturbation (resulting in a Moreton wave). Moreover, it reveals the nature of secondary effects such as coronal upflows, secondary shocks, various forms of wave-trains, delayed large-amplitude slow disturbances, transient coronal dimmings, and chromospheric relaxation.