1 Introduction

Predicting the effects of solar eruptions at the Earth is a scientific art in the making. Many different approaches have been developed worldwide, using analytical, numerical, or empirical techniques, to better understand the physics behind interplanetary coronal mass ejections (ICMEs), which should ultimately lead to space weather predictions on a routine basis with reasonable accuracy. The NASA Solar TErrestrial RElations Observatory (STEREO, Kaiser et al. 2008), launched in 2006 and consisting of two observatories leading and lagging the Earth’s orbit by 22.5° per year, plays a major role in these efforts. STEREO has been designed to enhance our ability to forecast ICME arrival times at Earth through more precise determination of ICME speeds and directions with both stereoscopic and single-spacecraft techniques, based on observations taken from outside the Sun–Earth line to eliminate projection effects (Gopalswamy et al. 2001; Schwenn et al. 2005) and filling the imaging gap between the Sun and 1 AU with the Heliospheric Imagers (HI) instruments (Eyles et al. 2009). The latter has also been achieved from within Earth’s orbit by the Solar Mass Ejection Imager (SMEI) instrument (Eyles et al. 2003).

An idea originally introduced by Sheeley et al. (1999) was used to predict directions and speeds of ICMEs (Davis et al. 2009) and corotating interaction regions (Rouillard et al., 2008) from HI images. This method makes use of a simple geometrical fact, which can be illustrated as follows: if someone throws a ball with constant velocity along a constant direction, an observer measuring the angle between himself, the thrower, and the ball as a function of time will notice deceptive decelerations or accelerations in the time-angle profile. The form of this function depends on the speed and direction of the ball with respect to the observer. Applied to ICMEs in any plane given by a position angle to solar north (e.g., the ecliptic plane), these profiles, known analytically for either point-like (fixed-Φ, FP, Sheeley et al., 1999; Kahler and Webb, 2007) or circular fronts (harmonic mean, HM, Lugaz, Vourlidas, and Roussev, 2009; Howard and Tappin, 2009), can be inversely fitted through a minimization process to observed profiles of the elongation angle of the ICME front from the Sun (e.g. Rouillard et al. 2009; Davis et al., 2009; Howard and Tappin, 2009; Tappin and Howard, 2009; Davies et al., 2009; Savani et al., 2009, 2010; Möstl et al., 2009, 2010, 2011; Lugaz, 2010).

We denote the techniques as FPF and HMF (for FP- and HM-Fitting). The FPF technique has been successfully applied in real time to an ICME in April 2010 (Davis et al. 2011), and to some other recent real-time events, and is a candidate for a technique to be used routinely on a future space weather mission at the L5 point in the Sun–Earth system (Gopalswamy et al. 2011) or on Solar Orbiter. In comparison to a numerical simulation, some biases have been found for FPF/HMF, mainly for cases where the ICME is either close to the limb or heading toward the observer (Lugaz, Roussev, and Gombosi 2011). Similarly to the preceding techniques, stereoscopic versions exist for FP (Liu et al. 2010a) and HM (Lugaz et al. 2010), relaxing the assumptions of constant speed and direction, though these techniques have not yet revealed strong deviations from radial propagation far from the Sun.

An improvement to the single-spacecraft techniques has been introduced by Davies et al. (2012; further called DA12), called self-similar expansion or SSE to convert elongation to distance. This is based on model 2 by Lugaz et al. (2010); DA12 made it suitable as a prediction tool through inverse fitting (SSEF). This model has great appeal because it solves some problems (see discussion by Möstl et al., 2011, further: MO11) which are intrinsic to the point-like or very wide front assumptions of FP and HM, respectively. It is especially useful for considerations of when and with what speed the ICME front will hit a planet, resulting in possible magnetic storms, or a spacecraft which makes in situ observations of the solar wind plasma and magnetic field parameters.

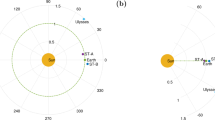
This short report aims to clarify the calculation of arrival times and speeds at a particular position in the heliosphere with the SSE model (DA12) or its stereoscopic version, model 2 in Lugaz et al. (2010). The assumption is that the ICME front can be approximated by a circle with constant angular width (see Figure 1). Our term “front” allows one to investigate either the speed and arrival time of the interplanetary shock wave or the front boundary of the magnetic flux rope or ejecta driving the shock. Given the position of a spacecraft with respect to the direction of the ICME apex (the point along the front with greatest heliospheric distance from the Sun), this model will lead to later arrival times and lower speeds, or even to no hit at all. In this way, we extend the work of MO11, who derived a similar arrival time correction for the HM model, which is a limiting case of SSE for large ICME width. The FP model can also easily be understood as the limiting case of SSE for negligible width. Clearly, in the real solar wind environment these idealized conditions may not even be roughly met, and distortions of the fronts will be likely. Also note that a spherical expanding front centered on the Sun (called “Point-P” by various authors) has the same heliocentric distance, everywhere, and corrections to speed and arrival time are not needed. However, to derive geometrically consistent arrival times and speeds with SSE or its triangulation version, it is necessary to use the formulas derived in this paper.

Figure 1
figure 1

The geometry of the SSE model. An observer looks along the tangent to a circular front at an elongation ϵ(t) to Sun center. The circle expands with constant angular half-width λ along a constant ICME propagation direction ϕ. Note that the full width of the ICME is 2λ.

Full size image

The analytical considerations we present here are not restricted to techniques used on HI instruments, but they provide a simple framework to assess the effects of an ICME hitting a target with its apex or flank. If the direction of an ICME is known from stereoscopic observations close to the Sun from various techniques (Thernisien, Vourlidas, and Howard 2009; Tappin and Howard 2009; Temmer, Preiss, and Veronig 2009; de Koning, Pizzo, and Biesecker 2009; Mierla et al. 2010; Byrne et al. 2010; Rodriguez et al. 2011), an educated guess can be made regarding the difference in heliospheric longitude between the ICME apex and the spacecraft or planet. A model for ICME propagation can then be used to extrapolate the arrival time and speed of the ICME apex to 1 AU (see, e.g., Gopalswamy et al., 2001; Vršnak and Gopalswamy, 2002; Schwenn et al., 2005; Siscoe and Schwenn, 2006; Vršnak et al., 2010; Maloney and Gallagher, 2010; Vršnak et al., 2012, this issue), which can subsequently be corrected for the longitude difference using the formulas presented here, given that the width of the ICME is known, or simply assumed.

The average width of a CME in coronagraph observations is about 50° (Yashiro et al. 2004) with considerable scatter around this value. Direct comparison of STEREO/HI movies to a rendered three-dimensional (3D) density model of a loop-like ICME revealed a true (deprojected) width of 70° (Wood, Howard, and Socker 2010) for one event. However, we are interested here in the angular extent of the ICME front along the line of sight (LOS) in a given plane (such as the ecliptic). Stereoscopic modeling assuming such a geometry by Lugaz et al. (2010) revealed half (full) widths in the ecliptic from 25 – 45° (50 – 90°), and observations of interplanetary shocks and their solar sources point to extents of up to 100° (Richardson and Cane 1993). Note also that the ICME angular extent along the LOS should depend upon its orientation with respect to the ecliptic plane (see, e.g., Liu et al., 2010b; Kilpua et al., 2011; Möstl et al., 2011).

We start by deriving the formulas in Section 2 and discussing them in comparison to the former FP and HM models. We then plot the effects on arrival time and speed predictions and discuss their significance in Section 3, and then conclude with comments on our assumptions and future work.

2 Derivation of Arrival Time and Speed for SSE

Figure 1 shows the geometry introduced by Lugaz et al. (2010) and elaborated by DA12. It is assumed that an observer looks along the tangent to a circular front propagating radially away from the Sun with constant angular width. The elongation-to-distance conversion for SSE can be derived as:

$$R_{\mathrm{SSE}}=\frac{d_o \sin({\epsilon(t)})(1+\sin\lambda )}{\sin(\epsilon (t)+\phi) +\sin\lambda} $$
(1)

with d o the radial distance of the observing spacecraft (called O) from the Sun, ϵ(t) the measured elongation angle as function of time, λ the angular half-width of the ICME, angle ϕ the propagation direction as measured from the observer, and \(R_{\mathrm {SSE}}\) the heliocentric distance of the ICME apex. For the large and small triangles in Figure 1 we can write:

(2)
(3)

We further need a relation between \(R_{\mathrm{SSE}}\) and r, the radius of the circle. Using \(R_{\mathrm{SSE}}=r+c\) and r=csinλ leads to:

$$ r (R_{\mathrm{SSE}}, \lambda)= \frac{R_{\mathrm{SSE}} \sin\lambda }{(1+ \sin\lambda)},$$
(4)

and can be understood as a radius of curvature, which is, however, coupled to the width λ. It also is a function of the apex position, and thus time, because the circle expands as the front propagates outwards. Using Equation (4) in Equation (3) and solving for a allows one to put a into Equation (2), and after some rearranging, Equation (1) is obtained. For completeness, the circle’s central heliocentric distance is:

$$c=\frac{R_{\mathrm{SSE}}(t)}{(1+\sin{\lambda})}.$$
(5)

By comparison, the HM model assumes a circle which is attached to the Sun at all times (Lugaz, Vourlidas, and Roussev 2009; Howard and Tappin 2009), and this simply corresponds to Equation (1) for the case of λ=90°:

$$R_{\mathrm{HM}}=\frac{2 d_o \sin{\epsilon(t)}}{\sin(\epsilon (t)+\phi) +1}. $$
(6)

If the width is negligible (λ=0°), the FP conversion for elongation to distance follows from Equation (1) (Sheeley et al., 1999):

$$R_{\mathrm{FP}}=\frac{d_o \sin{\epsilon(t)}}{\sin(\epsilon (t)+\phi)}. $$
(7)

We now ask ourselves: How far does the apex of the ICME front need to travel away from the Sun until the front hits the in situ spacecraft or planet I? Clearly, for a circular front this will always be greater than I’s heliocentric distance, d i . As seen from Figure 2, the ICME apex is separated at an angle Δ to I, so we make the following ansatz:

(8)
(9)

Using r=csinλ in Equation (8) results in:

$$ \alpha= \arcsin\biggl(\frac{\sin\Delta}{ \sin\lambda} \biggr).$$
(10)

Substituting Equations (10) and (4) into Equation (9) leads to:

$$R_{i\mathrm{SSE}}(\Delta, \lambda, d_i)=\frac{d_i \sin\Delta(1+\sin\lambda )}{\sin(\arcsin(\sin\Delta/ \sin\lambda)+\Delta)\sin\lambda}$$
(11)

Using trigonometric identities, this can be simplified to:

$$ R_{i\mathrm{SSE}}(\Delta, \lambda, d_i) = \frac{d_i (1+\sin\lambda )}{\cos \Delta+\sqrt{\sin^2 \lambda- \sin^2 \Delta}}$$
(12)

We designated this special distance as \(R_{i\mathrm{SSE}}\), because it is the heliocentric distance of the ICME apex at the arrival time t a when the spacecraft is hit by the front, as illustrated in Figure 2. Again, for HM with λ=90°, Equation (12) indeed reduces to:

$$R_{i\mathrm{HM}}=\frac{d_i}{\cos\Delta}, $$
(13)

similar to the one used by MO11. For FP, one may assume that a small spherical front is centered around the assumed point, so we simply have \(R_{i\mathrm{FP}}=d_{i}\).

Figure 2
figure 2

Similar to Figure 1, but now with an in situ spacecraft I situated at a heliocentric distance d i and at an angle Δ with respect to the ICME apex.

Full size image

2.1 Arrival Time

If we further assume that the ICME front travels with constant speed \(V_{\mathrm{SSE}}\) for all times when \(R_{\mathrm{SSE}}(t) > d_{i}\), we can express the arrival time correction \(t_{c\mathrm{SSE}}>0\) as:

$$ t_{c\mathrm{SSE}}=\frac{R_{i\mathrm{SSE}}(\Delta, \lambda,d_i)-d_i}{V_{\mathrm{SSE}}}.$$
(14)

This formula states how long the ICME apex must travel, after it has passed d i , until I is hit by the front. Here, \(V_{\mathrm{SSE}}\) can also be seen as an asymptotic speed given by an ICME propagation model.

For the SSE fitting technique (DA12), which results in constants for λ, ϕ, \(V_{\mathrm{SSE}}\), and the launch time \(t_{0\mathrm{SSE}}\), the arrival time at the spacecraft I can be expressed as:

$$ t_{a\mathrm{SSE}}=t_{0\mathrm{SSE}} +\frac{R_{i\mathrm{SSE}}(\Delta , \lambda, d_i)}{V_{\mathrm{SSE}}}.$$
(15)

One must understand that the launch time \(t_{0\mathrm{SSE}}\) is not determined from chromospheric or low coronal observations, but that it is rather a backprojection to the center of the Sun (where ϵ(t)=0) to obtain a time of reference for calculating \(t_{a\mathrm{SSE}}\) (see also MO11). It is assumed here that the speed \(V_{\mathrm{SSE}}\) is a constant for the range of elongation angles for which the time-elongation track, which is fitted with SSEF, is extracted from HI observations. Any earlier accelerations or decelerations of the CME closer to the Sun do not affect the calculation of \(t_{a\mathrm{SSE}}\). However, the launch time \(t_{0\mathrm{SSE}}\) will consequently be only a rough estimate of the real launch time of the CME in the corona.

Similarly, for the HM model the arrival time calculation can be written as:

$$ t_{a\mathrm{HM}}=t_{0\mathrm{HM}} +\frac{R_{i\mathrm{HM}}(\Delta,d_i)}{V_{\mathrm{HM}}},$$
(16)

which reduces with Equation (13) to an expression consistent with MO11 (their Equation B7).

Note that for SSE, not only is the arrival time well defined, but the prediction of whether or not a spacecraft or planet is hit by an ICME is given by the conditions λ>Δ (hit) and λ<Δ (no hit). This is much more precise compared to FP, where, strictly, a point never hits another point. Also, for HM, which corresponds to SSE for λ=90∘, the circle will always hit if the in situ spacecraft is inside the half-space given by ϕ±90∘.

2.2 Arrival Speed

Additionally, for an expanding circular front, every point along the front moves with a slower speed compared to the apex. Thus a prediction of a corrected arrival time should always include a corrected speed (see MO11). Because we assume radial propagation, the component of the velocity is always the radial component away from the Sun, and the others are zero. For self-similar expansion (SSE), the following relation must be valid because the speed must be proportional to distance along the front, so the shape does not change with time:

$$\frac{d_i}{R_{i\mathrm{SSE}}}=\frac{V_{i\mathrm{SSE}}}{V_{\mathrm{SSE}}},$$
(17)

Rearranging and substituting \(R_{i\mathrm{SSE}}\) from Equation (12) shows that the front at an angle Δ to the ICME apex moves with the following speed (\(V_{i\mathrm{SSE}}< V_{\mathrm{SSE}}\)) away from the Sun:

$$ V_{i\mathrm{SSE}} = V_{\mathrm{SSE}} \frac{ \cos\Delta+\sqrt{\sin^2 \lambda- \sin^2 \Delta} }{ (1+\sin\lambda)}.$$
(18)

Again, for λ=90°, Equation (18) reduces to:

$$V_{i\mathrm{HM}}=V_{\mathrm{HM}} \cos({\Delta})$$
(19)

as stated by MO11 for the HM case.

3 Plots for Arrival Time and Speed Corrections

In this section we explore the significance of the previously derived formulas by plotting the corrections for arrival time and speed for spacecraft positions along the ICME flank, for different sets of parameters. In Figure 3 we introduce five SSE fronts with angular half-widths of λ=[10,25,40,60,90]°. These values correspond to a radius of curvature which is equal to the radius r of the circle as given by Equation (4), of r=[0.086,0.211,0.321,0.433,0.5] AU for an apex distance of \(R_{\mathrm {SSE}}=1~\mbox{AU}\). We will also use \(V_{\mathrm{SSE}}=[400, 600, 800, 1000]~\mbox{km\,s}^{-1}\), covering typical ICME speeds observed in situ at 1 AU throughout a solar cycle (Richardson and Cane 2010).

Figure 3
figure 3

Illustration of five SSE fronts with different angular half-widths λ. The in situ observing spacecraft is positioned at an angle Δ to the ICME apex.

Full size image

3.1 Arrival Time

In Figure 4a, we plot the arrival time correction \(t_{c\mathrm{SSE}}\) given by Equation (14) as a function of Δ for an ICME speed of \(V_{\mathrm{SSE}}=400~\mbox{km\,s}^{-1}\) and the in situ spacecraft at Earth distance (d i =1 AU). This is done similarly to MO11 (their Figure 8b), but these authors restricted themselves to the HM case (λ=90°), which is the blue solid curve in Figure 4a. The functions for λ=[10,25,40,60]∘ each stop at the equivalent value for Δ, though only seen in the plot for λ=10°. This is because for Δ>λ the ICME does not hit the spacecraft, and \(t_{c\mathrm{SSE}}\) becomes imaginary. For smaller values of λ, a few degrees difference in Δ can lead to large differences in the arrival time, whereas for large λ values the curves become increasingly flatter. Also note that for λ=60∘ there is already almost no difference to HM, so the formulas mainly affect cases where small values of λ are combined with a Δ close to λ; i.e., the case for glancing encounters of ICMEs which are of small angular extent along the LOS. This is either the case for intrinsically narrow ICMEs or elongated flux-rope-like ICMEs which have a high inclination of their axis to the ecliptic plane.

Figure 4
figure 4

(a) The arrival time correction \(t_{c\mathrm{SSE}}\) assuming the ICME parameters \(V_{\mathrm{SSE}}=400~\mbox{km\,s}^{-1}\) and the in situ observer situated at d i =1 AU, for different values of the ICME half-width λ. (b) Similar to above, but for \(V_{\mathrm{SSE}}=600~\mbox{km\,s}^{-1}\), (c) \(V_{\mathrm{SSE}}=800~\mbox{km\,s}^{-1}\), (d) \(V_{\mathrm {SSE}}=1000~\mbox{km\,s}^{-1}\).

Full size image

Figures 4b, 4c, 4d show similar plots for \(V_{\mathrm{SSE}}=[600, 800, 1000]~\mbox{km\,s}^{-1}\), which allow one to quickly see (also useful for real-time assessments) how long the flank might be delayed for a given set of ICME parameters. As an example, one sees that, for an average width of an ICME shock front (a full width of 80° corresponding to λ=40°), the arrival time correction stays low (< 10 hours) for encounters within Δ<25°, but it quickly rises when Δ>25° and may easily delay the front arrival by one or even two days. We thus conclude that the arrival time for an ICME front approximated by SSE is increasingly hard to pinpoint at its flanks, where small errors in Δ may lead to large errors in the arrival time prediction.

3.2 Arrival Speed

For Figure 5 we repeated this analysis for the speed corrections. We use the same sets of parameters as in the previous section to insert in Equation (18). Note that \(V_{i\mathrm {SSE}}\) does not depend on d i , because the front always moves with constant speed, regardless of the heliospheric distance of I. Again, where Δ>λ the ICME does not hit the spacecraft. Clearly, the functional forms are governed by the same correction factor as compared to the arrival time in the previous section. Again, these plots are meant to be useful for looking up the effect of a glancing encounter for given parameters. For cases where Δ>30°, the arrival speed can be slower in the order of 100 – 200 km s−1 compared to the apex, showing that, for geometrically consistent calculations of arrival times and speeds, one must include these formulas because they lead to significant deviations from those inferred from the ICME apex.

Figure 5
figure 5

(a) The corrected ICME speed \(V_{i\mathrm{SSE}}\) at a longitudinal separation Δ between the ICME apex and the in situ target, assuming the ICME parameters \(V_{\mathrm{SSE}}=400~\mbox{km\,s}^{-1}\) and the given angular half-widths λ. (b) Similar to above, but for \(V_{\mathrm{SSE}}=600~\mbox{km\,s}^{-1}\), (c) for \(V_{\mathrm {SSE}}=800~\mbox{km\,s}^{-1}\), (d) for \(V_{\mathrm{SSE}}=1000~\mbox{km\,s}^{-1}\).

Full size image

4 Conclusions

Our aim was to show how arrival times and speeds can be analytically calculated for self-similar expanding (SSE) circular fronts with constant angular width. We have shown plots of the corrections for speeds and arrival times for an observer at 1 AU and typical ICME speeds at 1 AU. Clearly, this is useful for techniques which assume this geometry for application to observations by a single-spacecraft heliospheric imager (HI) instrument (SSEF, Davies et al., 2012) or two HIs (Lugaz et al. 2010), to forecast the effects of interplanetary coronal mass ejections at the Earth and other planets. However, it is also useful for any empirical/analytical technique which is used to calculate arrival times of ICMEs (summary by Siscoe and Schwenn, 2006; see also Vršnak et al., 2012, this issue, for the drag-based model). Assuming the SSE geometry leads to the following results: for glancing encounters of an ICME with a planet or spacecraft, the flank parts of an ICME might be delayed by one or – in extreme cases – two days, and speeds can be affected in the order of 100 to 200 km s−1. These corrections are both significant, given that arrival time predictions are usually in the order of ± 12 hours (see, e.g., Davis et al., 2011), and geoeffects of ICMEs are thought to be determined by the reconnection electric field −V r ×B z , depending on the plasma radial velocity component V r and the southward magnetic field component B z (see, e.g., Burton, McPherron, and Russell, 1975).

Further assumptions we used for the derived corrections are that after the apex of the front passed the heliocentric distance of the planet or spacecraft, i) the ICME propagates radially away from the Sun, and ii) it does so with constant speed. Clearly, in a structured solar wind, the ICME front might easily become distorted by the heliospheric current sheet, corotating interaction regions, or other ICMEs; thus one always must remember that the geometry used here is a highly idealized one. We also note that, in the SSE framework, the curvature of the front is coupled to the full width, leading to a rather rigid description of its shape. De-coupling the width from the curvature would be possible in an elliptical model (or a related geometry used by Savani et al., 2011), at the cost of introducing another free parameter. We leave these ideas for future studies.

Nevertheless, the expressions presented here allow one to check the results of SSEF against ICME in situ observations. Our aim is to use the presented formulas in connection with the SSEF technique and its limiting cases (FPF and HMF) to test the efficacy of using HIs as a prediction tool for real-time space weather forecasting by studying a larger number of events. To do so in a geometrically consistent way, the derived corrections will be applied to comparisons between ICME arrival times and speeds derived from STEREO/HI with SSEF and those observed in situ by various spacecraft, extending other studies using elongation-fitting techniques and their stereoscopic versions (Davis et al., 2009; Liu et al., 2010a, 2010b, 2011; Möstl et al., 2009, 2010, 2011; Lugaz et al., 2012).