1 Introduction

After the Green Revolution in India, agricultural productivity and overall food production has increased significantly in the country. Consequently, India had a surplus stock of cereals for the first time ever with a national focus on calorie support to all people, especially for those from lower income groups (MoSPI and WFP 2019). In the following decades, as the economy continued to grow, the country experienced a significant decline in poverty levels. Despite this remarkable feat, the rate of malnutrition in India remains stubbornly high. The food security together with enriched nutrition is among the greatest priority of the Government of India to achieve the Sustainable Development Goal 2 (UNDP 2015). In India, National Sample Survey Office (NSSO) of Ministry of Statistics and Program Implementation, Government of India is the nodal authority to collect Household Consumer Expenditure Survey (HCES) data for producing estimates related to different food insecurity indicators for both rural and urban sectors at the state and the national level. Despite being highly crucial, the estimates of food insecurity indicators along with the disparities in food consumption and nutrition intake are unavailable further down the state level viz. district or further level of disaggregation in India. In the present circumstances, the growing interests of the scientists, government organization, policy makers and public agencies are concentrated in obtaining the local level statistical synopses. These local level areas or domains, better known as small areas or small domains are formed by cross-classification of several demographic and topographic variables that includes small topographic areas (e.g. districts) or small demographic groups (e.g. land category, social groups, religion, age-sex groups) or cross classifying both. On the other hand, in the existing survey data viz. HCES of NSSO, the small areas may have very small or even zero sample sizes and direct estimation in such cases may lead to large sampling error. The SAE methodology provides a viable and cost effective solution this problem of small sample sizes (Rao and Molina 2015). The SAE methods borrow strength from other external data sources viz. areas, time periods etc. to generate precise and representative estimates.

The SAE methods are mostly based on model-based approaches and the main idea behind this is to make a link between the target variable and the auxiliary information through statistical models. This may leads to describe the model-based estimators for these small areas. The area level or the unit level models are generally used in SAE based on the availability of the level of auxiliary information. Area level models are utilized when the model covariates (e.g. census variables) are available only in aggregate. The Fay–Herriot model (Fay and Herriot 1979) is a widely used area level model in SAE that assumes area-specific survey estimates are available, and that these follow an area level linear mixed model with area random effects, Chandra (2013) and Chandra et al (2015). Extensive work may be found in the literature where researchers have dealt with the problem of small area estimation by applying the Fay–Herriot model. The uncertainty of model-based small area estimators was studied by Prasad and Rao (1990), Datta and Lahiri (2000), González-Manteiga et al. (2010), Datta et al. (2011). Rao and Yu (1994) extended the Fay–Herriot model with time series and cross-sectional data while Marhuenda et al. (2013) and Morales et al. (2015) studied the spatiotemporal version of the Fay–Herriot model. Fay (1987) and Datta et al. (1991) introduced the multivariate Fay–Herriot model and Benavent and Morales (2016) extended it by considering different covariance structure of the random effects.

Time and again, there is a need of estimating correlated measures like food insecurity, unemployment or poverty indicators. Multivariate models often take into account for the correlation of several variables and typically fit to this kind of situations (Benavent and Morales 2016). Unlike the Fay–Herriot model (Fay and Herriot 1979), the multivariate Fay–Herriot model (MFH) considers joint modelling of more than one target variable taking into consideration different covariance arrangements between the vectors of the target variables and the vector of random effects. Several small area applications for estimation poverty, food insecurity and other socio-economics parameters have also been described in Indian data, see for example, Anjoy et al. (2019), Chandra et al. (2011), Islam et al. (2019) and references therein. However, these applications are based on use of univariate small area modelling ignoring the correlation between related variables of interest. Moreover, surveys are generally multivariate in nature and collect more than one target variables (e.g., HCES of NSSO). In small area estimation problem where there is scarcity of sample size within the areas, exploitation of correlation between the variables can offer an advantage in producing the reliable estimates for small area parameters (Rao and Molina 2015).

An attempt has been made in this paper to produce district level estimates of disparities in food consumption and nutrient intake for rural areas of Uttar Pradesh through joint modelling of the three target variables related to disparities in food consumption and nutrient intake under a MFH model approach. Uttar Pradesh is the most populous state in the country as well as the most populous country subdivision in the world. The state accounts for about 16.16% of India’s and about 2.9% of world’s population with an area of 243,290 square km that equals to 6.88% of India’s total geographical area. It holds the third largest economy of the country but it has a large number of people living below the poverty line. The mainstream occupation of majority of population in the state is based on agriculture and according to the Population Census 2011 about 78% of the people reside in rural areas. Therefore, it seems reasonable to consider rural areas of Uttar Pradesh to generate the district level estimates of disparities in food consumption and nutrition status using SAE techniques. The rest of the paper is organized as follows. The HCES data and the population census data is described in Sect. 2. In Sect. 3 we introduced the MFH model while the result and discussion part is discussed in Sect. 4. Finally some important conclusions are drawn in Sect. 5.

2 Data and Model Specification

In this section, the primary sources of the data used in multivariate SAE application is introduced. We utilized the 2011–2012 HCES data of the NSSO for rural districts of Uttar Pradesh and the Population Census data of 2011. These data are used for estimating the disparities in food and nutrition intake at district level in Uttar Pradesh. The 2011–2012 HCES is the latest round of available survey being used of policy analysis in India. The NSSO survey data is not freely downloadable but it can be obtained from the NSSO, Ministry of Statistics and Programme Implementation, Government of India (http://mospi.nic.in/). The HCE surveys of NSSO is carried out at regular intervals as part of its “rounds” and normally a year is taken to be the duration of each of these “rounds”. A representative sample of households is randomly selected through a suitable sampling design and the surveys are carried out by interviewing the selected household. The entire geographical area of India is eventually covered through these surveys of NSSO. Stratified multi-stage random sampling is used as the sampling design in the 2011–2012 HCES. In this survey, districts are selected as strata with villages as first stage units and households as second stage units. The 2011–2012 HCES of NSSO is designed to generate reliable estimates at state and national level for both the rural and urban sectors of the country. But this survey data cannot directly be used to generate reliable estimates at district level, because within each district sample size is not large enough to provide district level estimates with adequate precision and reliability. Although, district is always being a very crucial part of the planning process in the country, there are no surveys conducted to produce district level estimates in India and this leads to limit the policy interventions at the district or even further lower level.

The 2011–2012 HCES data of the NSSO comprised 5915 households from the rural areas in 71 districts of Uttar Pradesh. The sample sizes of all the surveyed districts ranged from 32 to 128 with average of 83. This survey provides information on quantity and value of more than 142 food items with a reference period of last 30 days for a few food items and last 7 days for the rest food items for rural areas in Uttar Pradesh. Table 1 apparently reveals that these districts comprised relatively small sample sizes with an average sampling fraction of 0.00023. On account of the constraint of small sample size, it is not possible to produce precise and reliable direct estimates at district level and subsequently leads to producing large standard errors from this survey (Chandra et al. 2011 and Rao and Molina 2015). An attempt has been made in this paper to address this issue of small sample size in obtaining district level estimates from the 2011–2012 HCES data. The multivariate SAE approach has been adopted to handle this issue by incorporating relevant auxiliary information from 2011 Population Census data.

Table 1 Details of sample size, sampled food insecure households and sampling fraction in 2011–2012 HCES dataset
Full size table

To estimate the disparities in nutrient intakes, the suggested intake of food items has been transformed into calorie, fat and proteins. The quantities of food recorded as consumed by the household are converted into the equivalent amounts of energy, protein and fat on the basis of a Nutrition Chart largely based on an ICMR publication (Gopalan et.al. 1991) which gives the energy, protein and fat content per unit of different foods in the Indian diet. It needs to be said, however, that the actual intake of nutrients depends on how these foods are actually processed and/or cooked in the surveyed households, Government of India. (2014). Usually the amount of total calorie, protein and fat intake for any food item is calculated form the quantities consumed as reported by the sample households. One of the constraints of the NSSO statistics is that the records on meals intake is at the household level, therefore we can't encompass the element of intra-household disparities of food consumption. In our analysis all the estimates are averaged as per capita on the family degree. We have taken three target variables for jointly model the disparities in food consumption and nutrition level using multivariate SAE approach. The target variables at the household level in the 2011–2012 HCES data are Y1: Average calorie intake (Kcal), Y2: Average protein intake (Protein) and Y3: Average fat intake (Fat) per person per day. Average dietary energy intake per person per day in rural India is 2400 kilocalorie (Kcal), as defined by the Ministry of Health and Family Welfare, Government of India. This paper aims to estimate the disparities in food consumption and nutrition level of rural households in Uttar Pradesh by jointly model the target variables viz. Kcal, Protein and Fat at small area level.

3 Theoretical Framework

This section briefly describes SAE method applied in the estimation of district level inequality in distribution of food and nutrition security. Let the population is divided into D small areas or areas (districts in our application) and let there are M number of target variables of the study. Here D is the total number of small areas in the population while M is the number of target variables of the study. Throughout, a subscript \(d(d = 1,\,.\,.\,.,\,D)\) is used to index the quantities belonging to small area d and a subscript \(m(m = 1,\,.\,.\,.,\,M)\) is used to denote the target variable m under the study. Let \(y_{dm} (m = 1,\,.\,.\,.,\,M)\) be an unbiased direct survey estimator of an unobservable population parameter (for example, the population mean) \(Y_{dm}\) of the variable m for small area d. Let \({\mathbf{x}}_{dm}\) be a \(p_{m}\)-vector of known auxiliary variables for area d that are related to the population mean \(Y_{dm}\) for target variable m. These area-specific auxiliary variables are typically obtained from secondary data sources viz. the population census or administrative registers. Let us denote \({\varvec{Y}}_{d}\) be the d-vector population mean of target variables of the study and \({\mathbf{y}}_{d} = \left( {y_{1m} ,...,y_{dm} } \right)^{T}\) be a vector of direct survey estimators of \({\varvec{Y}}_{d}\). Following Benavent and Morales (2016), an area level Fay–Herriot model (Fay and Herriot 1979) for more than one target variables is

$${\varvec{y}}_{d} = {\varvec{Y}}_{d} + {\varvec{\varepsilon}}_{d} \,{\text{and }}{\varvec{Y}}_{d} = {\mathbf{X}}_{d} {{\varvec{\upbeta}}}{ + }{\mathbf{u}}_{d}$$
(1)

In SAE literature, this model in (1) is often referred to the multivariate version of the Fay–Herriot model. The first stage accounts for the sampling variability of the survey estimates \({\mathbf{y}}_{d}\) of true area means \({\varvec{Y}}_{d}\) and the second stage links the true area means \({\varvec{Y}}_{d}\) to a matrix of known auxiliary variables \({\mathbf{X}}_{d} = diag\left( {{\mathbf{x}}_{d1} ,\,\,.\,\,.\,\,.\,,\,{\mathbf{x}}_{dM} } \right)_{M \times p}\) with \(p = \sum\nolimits_{m = 1}^{M} {p_{m} }\). The model (1) can be written as an area-level random effect model given by

$${\mathbf{y}}_{d} = {\mathbf{X}}_{d} {{\varvec{\upbeta}}} + {\mathbf{u}}_{d} + {{\varvec{\upvarepsilon}}}_{d} ,\,d = 1, \ldots ,D$$
(2)

Here \({{\varvec{\upbeta}}} = \left( {{\mathbf{\beta^{\prime}}}_{1} ,\,\,.\,\,.\,\,.,\,{\mathbf{\beta^{\prime}}}_{m} } \right)^{\prime }_{p \times 1}\) and \({{\varvec{\upbeta}}}_{m}\) is a \(p_{m}\)- vector of unobservable fixed effect parameters. The vector of random area effects \({\mathbf{u}}_{d}\) are independent and identically distributed with \({\mathbf{u}}_{d} \mathop \sim\limits^{ind} N\left( {0\,,\,\,{\mathbf{V}}_{{u_{d} }} } \right)\) and vectors of independent sampling errors \({{\varvec{\upvarepsilon}}}_{d}\) follows \({{\varvec{\upvarepsilon}}}_{d} \sim N\left( {0\,,\,\,{\mathbf{V}}_{{\varepsilon_{d} }} } \right)\). The two errors \({\mathbf{u}}_{d}\) and \({{\varvec{\upvarepsilon}}}_{d}\) are independent of each other within and across areas with covariance matrices \({\mathbf{V}}_{{\varepsilon_{d} }}\) are known and \({\mathbf{V}}_{{u_{d} }}\) depend on unknown parameters \(\left( {\theta_{1} ,\,\,.\,\,.\,\,.,\,\,\theta_{M} } \right)\). Aggregating D-area-level models, the model (2) can be written in matrix form as

$${\mathbf{y}} = {\mathbf{X }}{{\varvec{\upbeta}}} + {\mathbf{Zu}} + {{\varvec{\upvarepsilon}}}$$
(3)

where \({\mathbf{y}} = {\text{col}}\left( {{\mathbf{y}}_{d} ;1 \le d \le D} \right)\) is the \(DM \times 1\) vector of direct survey estimates, \({\mathbf{X}} = {\text{col}}\left( {{\mathbf{X}}_{d} \,;\,1 \le d \le D} \right)\) is the \(DM \times p\) matrix of covariates, \(Z = {\text{col}}^{\prime } (Z_{d} ;\,1 \le d \le D)\) is the known covariates of dimension \(DM \times DM\) characterizing differences among the small areas, \({\mathbf{u}} = {\text{col}}\left( {{\mathbf{u}}_{d} \,;\,1 \le d \le D} \right)\) is the \(DM \times 1\) vector of random area effects and \({{\varvec{\upvarepsilon}}} = {\text{col}}\left( {{{\varvec{\upvarepsilon}}}_{d} \,;\,1 \le d \le D} \right)\) is the \(DM \times 1\) vector of sampling errors with \({\mathbf{u}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{u} } \right)\) and \({{\varvec{\upvarepsilon}}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{\varepsilon } } \right)\). In general, \({\mathbf{Z}}\) is given by a matrix whose dth column \({\mathbf{Z}}_{d}\),\(d = 1,\,.\,.\,.,\,D\), is an indicator variable which takes the value 1 if a unit is in area d and is zero otherwise. In particular, in model (3) \({\mathbf{Z}}\) is a diagonal matrix of order \(DM \times DM\). Moreover, it is assumed that the random area effects \({\mathbf{u}}\) are distributed independently of the sampling errors \({{\varvec{\upvarepsilon}}}\) with \({\mathbf{u}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{u} } \right)\) and \({{\varvec{\upvarepsilon}}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{\varepsilon } } \right)\) where \({\mathbf{V}}_{u} = {\text{diag}}\left( {{\mathbf{V}}_{ud} \,;\,1 \le l \le D} \right)\) is the covariance matrix of random area effects and \({\mathbf{V}}_{\varepsilon } = {\text{diag}}\left( {{\mathbf{V}}_{\varepsilon d} \,;\,1 \le l \le D} \right)\) is the matrix of design variances.

We now consider two particularizations of the model (3) to obtain model-based small area estimates. The First predictor based on univariate Fay–Herriot model (UFH) considers \({\mathbf{V}}_{{u_{d} }} = {\text{diag}}\left( {\sigma_{um}^{2} \,;\,1 \le m \le M} \right)\),\({\mathbf{V}}_{{\varepsilon_{d} }} = {\text{diag}}\left( {\sigma_{\varepsilon dm}^{2} \,;\,1 \le m \le M} \right)\), \(d = 1\,,\,.\,\,.\,\,.\,,\,D\) and we assume \(\sigma_{\varepsilon dm}^{2}\)’s are known. For the second predictor based on multivariate Fay–Herriot model (MFH), \({\mathbf{V}}_{{u_{d} }} = {\text{diag(}}\sigma_{um}^{2} ;1 \le m \le M)\), \(d = 1\,,\,.\,\,.\,\,.\,,\,D\) and we assume a known but not necessarily diagonal matrix \({\mathbf{V}}_{\varepsilon }\), i.e. sampling errors are not independent with each other in this case. For both the predictors, the number of unknown parameters to be estimated is equal to \(M\) with \(\theta_{m} = \sigma_{um}^{2} ,\,\,m = 1,\,\,.\,\,.\,\,.,\,M\). Under the model (3), \(E\left( {\mathbf{y}} \right) = {\mathbf{X }}{{\varvec{\upbeta}}}\) and \(Var\left( {\mathbf{y}} \right) = {\mathbf{V}}_{y} = {\mathbf{V}}_{u} + {\mathbf{V}}_{\varepsilon } = diag\left( {{\mathbf{V}}_{yd} \,;\,1 \le d \le D} \right)\), with \({\mathbf{V}}_{u} = {\mathbf{Z^{\prime}}}\,{\mathbf{V}}_{u} {\mathbf{Z}}\) and \({\mathbf{V}}_{yd} = {\mathbf{V}}_{ud} + {\mathbf{V}}_{\varepsilon d} \,,\,\,d = 1,\,\,.\,\,.\,\,.,\,\,D\). Here, \({\mathbf{V}}_{y}\) depends on \(M\) unknown variance component parameters given by \({{\varvec{\uptheta}}} = \left( {\theta_{1} ,\,\,.\,\,.\,\,.,\,\,\theta_{M} } \right)\) and the restricted maximum likelihood (REML) method is often used to estimate \({{\varvec{\uptheta}}}\)(Benavent and Morales 2016). Replacing the estimated values \({\hat{\mathbf{\theta }}}\) of parameters \({{\varvec{\uptheta}}}\) in \({\mathbf{V}}_{u}\) to obtain \({\hat{\mathbf{V}}}_{u} = {\mathbf{V}}_{u} ({\hat{\mathbf{\theta }}})\) and \({\hat{\mathbf{V}}}_{y} = {\hat{\mathbf{V}}}_{u} + {\mathbf{V}}_{\varepsilon }\), the multivariate version of empirical best linear unbiased predictors (EBLUP) of \({\varvec{Y}}\) is defined as

$$\hat{\user2{Y}}_{{{\text{MFH}}}} = {\mathbf{X}}{\hat{{\varvec{\upbeta}}}} + {\mathbf{Z}}{\hat{\mathbf{u}}}$$
(4)

Here, empirical the best linear unbiased estimator (BLUE) of \({{\varvec{\upbeta}}}\) and the EBLUP of \({\mathbf{u}}\) are obtained as \({\hat{{\varvec{\upbeta}}}} = \left( {{\mathbf{X^{\prime}}}\,{\hat{\mathbf{V}}}_{y}^{ - 1} {\mathbf{X}}} \right)^{ - 1} {\mathbf{X^{\prime}}}\,{\hat{\mathbf{V}}}_{y}^{ - 1} {\mathbf{y}}\) and \({\hat{\mathbf{u}}} = {\hat{\mathbf{V}}}_{u} {\mathbf{Z^{\prime}}}\,{\hat{\mathbf{V}}}_{y}^{ - 1} \left( {{\mathbf{y}} - {\mathbf{X}}{\hat{{\varvec{\upbeta}}}}} \right)\) respectively. In small area applications, the mean squared error (MSE) estimates are desirable to measure the precision of estimates and also to construct the confidence interval for the estimates. The MSE estimate of multivariate version of EBLUP (4) is obtained using the MSE estimation given by Benavent and Morales (2016).

4 Results and Discussions

4.1 Model Fitting

The auxiliary variables used in this analysis are taken from the 2011 Population Census of India. The multivariate SAE approach based on area level models were applied to obtain the small area estimates as these auxiliary variables are available only as counts at district level. In the 2011 Population Census data, a total of almost 30 such auxiliary variables are available for usage in this analysis. Prior to the determination of suitable covariates for multivariate SAE modelling, an exploratory data analysis has been done for selection of few auxiliary variables. Principal Component Analysis (PCA) was also employed to obtain composite scores for some selected sets of auxiliary variables. In particular, we performed PCA separately on two sets of auxiliary variables and all measured at district level. These two sets of auxiliary variables are noted as P1 and P2 below. The first set (P1) comprised the proportions of main cultivators by gender, proportions of main workers by gender and proportions of main agricultural laborers by gender. 44% of the variability in the P1 set was explained by the first principal component (P11) for P1 and explained variability was increased to 69% by adding the second principal component (P12). The second set (P2) comprised the proportions of marginal agriculture laborers by gender and the proportions of marginal cultivator by gender. 52% of the variability in the set P2 was explained by the first principal component (P21) for P2 and explained variability was increased to 90% by adding the second principal component (P22).

First, we fitted the MFH Model mentioned in Sect. 3 using direct survey estimates of Kcal, Protein and Fat as the three response variables and the four principal component scores P11, P12, P21, P22 with some other selected auxiliary variables from the 2011 Population Census data as suitable covariates. The final selected model included four covariates namely proportional scheduled caste population (SC), literacy rate (Lit), index for main worker population (P11) and index for marginal worker population (P21). Table 2 present the estimated regression parameters for the three response variables Kcal, Protein and Fat. Noting the signs of the estimates of regression parameters we conclude that districts having larger population proportion in covariates SC, Lit, and P11 and smaller population proportion in P21 covariate have greater Kcal intake. On the other hand, districts having larger population proportion in Lit, and P11 and smaller population proportion in covariates SC and P21 have greater Protein and Fat intake. The variance component parameter estimates for MFH model are given by \(\hat{\sigma }_{u1}^{2} = 6333.90\), \(\hat{\sigma }_{u2}^{2} = 7.74\) and \(\hat{\sigma }_{u3}^{2} = 20.04\). The MFH model is employed using four significant covariates to generate the estimates of disparities in food consumption and nutrition level (i.e. disparities in Kcal, Protein and Fat intake) at district level for rural areas in Uttar Pradesh. The 2011–2012 HCES data of NSSO 68th round and the 2011 Population Census data of India is utilized for this analysis. In what follows, some crucial diagnostic measures are described to examine the model assumptions and validate the empirical performances of the MFH model. Following Brown et al. (2001), two types of diagnostics measures are employed to verify model assumptions viz. (1) the model diagnostics, and (2) the small area estimates diagnostics. The other diagnostic measures are used to validate the reliability of the model-based multivariate small area estimates of Kcal, Protein and fat obtained by MFH model.

Table 2 Regression parameters, standard error and p-values for Kcal, Protein and Fat
Full size table

4.2 Diagnostic Measures

Now for each of the target variable, the corresponding random area specific effects under MFH model given in (3) are assumed to be normally distributed with zero mean and fixed variance \(\sigma_{um}^{2}\), \(m = 1,\,2,\,3\). The district level residuals are expected to be randomly distributed around zero if the assumptions of the underlying model are satisfied. The normality assumption can be examined by using normal probability (q-q) plot. Figure 1 demonstrates the normal probability (Q–Q) plots of district-level residuals for the three target variables viz. Kcal, Protein and Fat. Further, the Shapiro–Wilk test was also performed to assess the normality assumption of the district specific random effects. If a dataset does not possess normality then the p-value of the Shapiro–Wilk test will be <  < 0.05. The Shapiro–Wilk test is executed using the R function shapiro.test() and the summary of the test is given in Table 3. The p-values of the Shapiro–Wilk test were 0.475, 0.722 and 0.112 for Kcal, Protein and Fat respectively. Moreover, the Q–Q plot also provide evidence in favor of the model assumption of normality and the Shapiro–Wilk p-values are greater than 0.05 which leads to the conclusion that the district specific random effects are expected to be normally distributed.

Fig. 1
figure 1

Normal q-q plots of the district-level residuals for Kcal, Protein and Fat

Full size image
Table 3 Summary of Shapiro–Wilk test along with p-values of district-level residuals obtained under MFH model for Kcal, Protein and Fat
Full size table

The reliability as well as the validity of the model-based multivariate small area estimates are evaluated by considering a set of commonly used diagnostics measures. Following Brown et al. (2001) and Chandra et al. (2011), these diagnostics are based on the argument that model-based small area estimates should be (a) consistent with unbiased direct survey estimates, i.e., they should provide an approximation to the direct survey estimates that is consistent with these values being “close” to the expected values of the direct estimates; and (b) more precise than direct survey estimates, as evidenced by lower mean squared error estimates, i.e., the model-based small area estimates should have mean squared errors significantly lower than the variances of corresponding direct survey estimates. We have selected the following measures viz. the bias diagnostic, the percent coefficient of variation (CV) diagnostic and the 95 percent confidence interval (CI) diagnostic. In addition, we implemented a calibration diagnostic where the model-based estimates are aggregated to higher level and compared with direct survey estimates at this level, Chandra et al. (2011). Here direct estimates are defined as the survey weighted direct estimates.

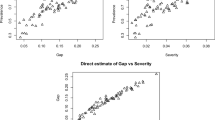
The bias diagnostic examine the validity whereas the CV and CI examine the precision of the model-based multivariate small area estimates. The bias diagnostic measure is established following the idea of Chandra et al. (2011). Being unbiased of the true values of the target population, the direct survey estimates’ regression on the true population values should appear to be linear and relate to the identity line. The regression of the direct survey estimates on the model-based small area estimates should be analogous if the model-based estimates are adjacent to these true population values. Therefore, the direct survey estimates in the y-axis vs. model-based estimates in the x-axis are plotted and we observed the departure of the model-based estimates from the fitted values of the regression line. The bias diagnostic plots are given in Fig. 2 in which direct survey estimates (Y-axis) are plotted against corresponding model based MFH estimates (X-axis) and tested for divergence of the fitted least squares regression line (thick line) from the line of equality Y = X line (thin line). Figure 2 reveals that the model-based small area estimates are not as much of extreme to the direct survey estimates, indicating the typical SAE outcome of shrinking more extreme values towards the average and the R2 value were given by 0.72, 0.74 and 0.77 for the target variable Kcal, Protein and Fat respectively. Overall, this bias diagnostic measures indicate that the model based multivariate small area estimates likely to be consistent with direct survey estimates.

Fig. 2
figure 2

Bias diagnostic plot with y = x line (thin line) and regression line (solid line) for Kcal, Protein and Fat consumption for rural areas in Uttar Pradesh: Model based MFH estimates versus direct estimates

Full size image

Next, we examined the magnitude to which the model-based multivariate small area estimates of Kcal, protein and Fat improved in precision than the UFH and direct estimates. Model-based multivariate small area estimates with small CVs are considered reliable. Table 4 presents a summary of percentage CVs of the direct estimates and the model-based multivariate small area estimates of the target variables Kcal, Protein and Fat. Figure 3 reports the District-wise root MSE while Fig. 4 presents the District-wise CV for the direct and MFH estimates for the all the three target variables. The CVs of the direct estimates are larger than the model based estimates for Kcal, Protein and Fat. Table 4 and Fig. 4, clearly indicate that direct estimates of all the three target variables are truly unstable with CVs ranging from 1.88 to 8.80% with a mean value of 3.87% for Kcal, 1.99–8.14% with a mean value of 3.94% for Protein and 3.42–18.02% with a mean value of 7.07% for Fat. On the other hand, the CVs of the model based estimates vary from 1.59 to 3.22% with a mean value of 2.40% for Kcal, 1.61–3.78% with a mean value of 2.44% for Protein and 2.98–8.56% with a mean value of 5.26% for Fat. The relative performance of the model based multivariate small area estimates for all the target variables has improved with decreasing sample sizes of the districts when compared to the direct estimates. Thus, these model based estimates are more precise and reliable and indicate the disparity in food and nutrition intake level much better than the direst estimates. Figure 5 displays the 95 percent confidence intervals (CIs) produced by direct and model based estimates while the corresponding widths of CIs are demonstrated in Fig. 6. It can be established from Figs. 5 and 6 that 95% CIs of the model based estimates are much narrower than that of the direct estimates. In addition, we also investigated the aggregation property of the district level estimates generated by model-based SAE method at higher level of aggregation (e.g., Regional and State level). The state-level estimates of Kcal, protein and fat is derived by

$$\hat{Y}_{i} = {{\sum\nolimits_{j = 1}^{D} {N_{j} \hat{Y}_{ij} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{j = 1}^{D} {N_{j} \hat{Y}_{ij} } } {\sum\nolimits_{j = 1}^{D} {N_{j} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{j = 1}^{D} {N_{j} } }}\quad i = 1,\,\,2,\,\,3\,{\text{and}}\,j = 1, \ldots ,D$$

where \(\hat{Y}_{ij}\) denote the estimate of Kcal, protein and fat intake for \(i = 1,\,\,2,\,\,3\) and district j with \(N_{j}\) being the population size of the jth district. We grouped the districts in four regions viz. Eastern, Western, Central, and Southern regions and examined the aggregation property. Regional and state level estimates of Kcal, protein and fat intake are reported in Table 5. When we compare the model-based SAE estimates with the direct estimates, we found that the SAE estimates are very close to the direct estimates in both the state and regional level.

Table 4 Summary of the distribution of percentage coefficients of variation (% CV) for the direct and model-based estimates of Kcal, Protein and Fat
Full size table
Fig. 3
figure 3

District specific (increased sample size) Root MSE of direct and MFH estimators of Kcal, Protein and Fat in Uttar Pradesh

Full size image
Fig. 4
figure 4

District specific percentage coefficient of variation (CV) of direct and MFH estimators of Kcal, Protein and Fat in Uttar Pradesh. Districts are arranged in increasing order of sample size

Full size image
Fig. 5
figure 5

District-wise 95% nominal confidence interval for the direct and model based MFH estimates for the Kcal, Protein and Fat intake in Uttar Pradesh. Districts are arranged in increasing order of direct estimates

Full size image
Fig. 6
figure 6

District-wise width of 95% nominal confidence interval for the direct and model based MFH estimates for the Kcal, Protein and Fat intake in Uttar Pradesh. Districts are arranged in increasing order of direct estimates

Full size image
Table 5 Aggregated level estimates of Kcal, Protein and Fat generated by different SAE methods
Full size table

Figures 7, 8, 9 demonstrate three maps indicating the MFH estimates of Kcal, Protein and Fat in different districts in the rural areas of Uttar Pradesh. These map provides the district-wise degree of inequality and reveals the distribution of the consumption of the food and nutrition intake. The results given in Tables 6, 7, 8 supplement these maps and report the district-wise direct and MFH estimates along with their 95% confidence interval and CV. The results of Kcal estimates indicates that the eastern region of Uttar Pradesh are having a low level of calorie intake while central part of Uttar Pradesh indicate highest level of calorie intake followed by western region. In case of Protein and Fat consumption, the results indicate an east–west divide in the distribution. For instance, western part of Uttar Pradesh seems to have high level of Protein and Fat intake while Eastern part indicate low level of Protein and Fat intake. These results may provide useful information to the policy maker for effective policy formulation and financial resolutions.

Fig. 7
figure 7

Model based MFH estimates showing the spatial distribution of Kcal consumption by District in Uttar Pradesh

Full size image
Fig. 8
figure 8

Model based MFH estimates showing the spatial distribution of Protein consumption by District in Uttar Pradesh

Full size image
Fig. 9
figure 9

Model based MFH estimates showing the spatial distribution of Fat consumption by District in Uttar Pradesh

Full size image
Table 6 Direct and MFH estimates along with 95% confidence interval (95% CI) and percentage coefficient of variation (CV) of Kcal by district in rural areas of Uttar Pradesh
Full size table
Table 7 Direct and MFH estimates along with 95% confidence interval (95% CI) and percentage coefficient of variation (CV) of Protein by district in rural areas of Uttar Pradesh
Full size table
Table 8 Direct and MFH estimates along with 95% confidence interval (95% CI) and percentage coefficient of variation (CV) of Fat by district in rural areas of Uttar Pradesh
Full size table

5 Conclusions

In this paper, we initially summarize the empirical best linear unbiased predictor under multivariate Fay-Harriot model (MFH) for small area means. We then applied the MFH method in the 2011–2012 HCES data of NSSO, India to estimate the disparities in food consumption and nutrition level and to produce spatial maps related to Kcal, Protein and Fat intake in the districts of rural areas in Uttar Pradesh, India. We used the 2011 Population Census of India to collect the auxiliary variables for this analysis. Efficient estimation of correlated measures like food insecurity, nutritional consumption disparities are often required multivariate modelling approach which takes into account for the correlation between the target variables. In this study, all the target variables are jointly modelled using multivariate SAE to capture the inherent correlation between them. The improvement over univariate method based estimation is achieved in terms of MSE and CV of the district level estimates of Kcal, Protein and Fat intake in rural sector of Uttar Pradesh, India. The nutrition intake across the districts of Uttar Pradesh can help to stimulate the discussion about the drivers of hunger in this state. The empirical results so obtained, were assessed by various diagnostic measures and revealed that the model-based multivariate SAE method defined by MFH provide significant gains in efficiency in obtaining district level estimates of Kcal. Protein and Fat which in turn measures the disparities in food consumption and nutrition level. The MFH estimates based spatial maps indicate the evidence of unequal distribution of food consumption and nutrition level across the districts of rural areas of Uttar Pradesh, India.

This analysis undoubtedly established the advantages of SAE approach to deal with the problem of small sample sizes in obtaining precise and cost effective disaggregate or local level estimates along with the confidence intervals from existing survey data. Moreover, this analysis also illustrates the benefit of using multivariate small area estimation over the univariate case by modelling the target variables jointly through multivariate Fay Harriot models. This study also reveals that large proportion of the rural sector of Uttar Pradesh’s population is undernourished and below the recommended calorie intake of Government of India. Therefore, there is a massive need to build up some accord on the standards for least calorie and nutrition intake necessity as these factors makes disarray with respect to the seriousness of craving and under-nourishment. In India, the surveys conducted by NSSO, Government of India are aimed to produce national and state level estimates which does not reflect the actual scenario at the micro level (e.g. district level). The Government of India is pacing considerable emphasis on micro level planning for achieving a balanced economic development including food security. The district is an important domain for planning process in the country and therefore availability of district level statistics is vital to monitoring of policy and planning. This study produces reliable statistics at district level through SAE techniques that can be used in prioritization and targeting of efforts and investments. By implementing SAE technique, we are able to address the small sample size problem in producing the cost effective and reliable disaggregate level estimates and confidence intervals from existing survey data by combining auxiliary information from different published sources with direct survey estimates. The estimates and spatial maps generated by this study can be used by different Departments and Ministries in Government of India as well as International organizations in their policy planning to formulate effective action plans relevant to sustainable development goal indicator 2.1.2—severity of food insecurity.