The Italian Regional Well-Being in a Multi-expert Non-additive Perspective

Abstract

This paper designs a multidimensional index of well-being for 20 Italian regions, based on a set of 41 indicators organized in an original hierarchical structure, a decision-tree whose four main pillars are Economy, Society, Environment and Health. Our novel approach combines the objective dimension of the evaluation (a comprehensive set of statistical indicators) within a flexible non-additive aggregation model (the Choquet integral) characterized with the preferences of informed Italian stakeholders. Adopting the Choquet integral allows us to overcome the well-known limitations embedded in the linear models, by assigning a weight (capacity) to any coalitions of dimensions, and by allowing a different degree of substitutability within each decision node in the tree. The weights and the parameters for the aggregation are elicited through a computer-based nominal group technique, a method which reduces the occurrences of drastically dissenting valuations and the potential expert-selection bias. Our results show that experts’ perception of synergies and redundancies is quite heterogeneous between levels and nodes in the tree. Moreover, well-being measures are much influenced by the degree of substitutability embedded in the experts’ preferences. Overall, the Italian picture looks more heterogeneous when analysed through the Choquet integral, with respect to a linear model.

1 Introduction

There is a wide consensus in the socio-economic literature on the need of broadening the scope of the analysis of well-being, stemming from the belief that focusing just on economic welfare does not allow to obtain a reliable and comprehensive picture of a territory’s quality of life. Less consensus is reached when debating whether such analysis should be aimed at synthesizing well-being in a single measure rather than at providing the reader with a dashboard of indicators (see, e.g., Stiglitz et al. (2009), Sirgy (2011), Dasgupta (2001), Nussbaum and Sen (1993), and Ivaldi et al. (2015) for a recent literature review).

Evaluating the quality-of-life of a territory in a single index requires, at first, the availability of a sufficient number of measurable variables which could represent the complexity of the matter. In order to arrive to a synthetic evaluation, an aggregation function is needed; moreover, the function’s parameters can be elicited from stakeholders preferences, rather than pre-determined by the researcher. The socio-economic literature highlighted that no unanimous method exists to perform such choices, pointing out numerous theoretical issues (Stiglitz et al. 2009; Ravallion 2011, 2012a; Klugman et al. 2011; Decancq and Lugo 2013; Maggino and Zumbo 2012), as well as empirical ones (Kasparian and Rolland 2012; Lefebvre et al. 2010; Saisana et al. 2005; Ravallion 2012b), and highlighting the need for transparency in designs and methods (Sen and Anand 1997).

This paper builds a composite measure of well-being for Italian regions, following an original approach which combines the objective dimension of the evaluation (a comprehensive set of statistical indicators) within a flexible non-additive aggregation model (the Choquet integral) characterized with the preferences of informed Italian stakeholders. We decided to investigate quality of life at a sub-national level, due to the high heterogeneity characterizing the Italian socio-economic framework, which cause the “national mean” of any indicator to be a weak representative of the underlying phenomenon.

Basing on the framework developed by Stiglitz et al. (2009), we propose a model of well-being in the form of a detailed hierarchical structure, a decision tree, characterized by multiple successive decomposition levels and ultimately based on 41 raw statistical indicators.¹ Our approach contributes to the existing literature on regional well-being, which is characterized by indices involving a reduced number of indicators and a compact conceptual framework (e.g., Murias et al. (2012), Silva and Ferreira-Lopes (2014), Schrott et al. (2012)): we offer the policy maker a flexible monitoring tool, which can be read as a wide dashboard of geographically comparable indicators, rather than as a group of sub-domains, domains, pillars, or as a synthetic index.

In order to aggregate dimensions we adopt the non-additive Choquet Integral (Grabisch 1996; Meyer and Ponthière 2011; Pinar et al. 2014), which has very rare applications on this topic, and allows us to avoid the limitations of the linear models (e.g., full substitutability between dimensions). With respect to existing examples of non-additive methods in the literature (Bourguignon and Chakravarty 2003; Klugman et al. 2011; Cherchye et al. 2007b; Murias et al. 2012; Lefebvre et al. 2010; Ivaldi et al. 2015; Mazziotta and Pareto 2015), the Choquet allows to evaluate the relevance (the weight) of any coalitions of indicators for every decision node in the tree. Its flexibility is thus particularly suited to evaluate the complex concept of well-being.

To obtain the value of the synthetic measure we involved 37 informed-stakeholders and submitted them with a number of fictional scenarios (made by combining possible values of each node’s dimensions), asking for a cardinal evaluation in terms of their conveyed level of well-being (Meyer and Ponthière 2011; Pinar et al. 2014; Despic and Simonovic 2000). Experts’ responses allowed us to estimate the aggregation function’s parameters through ordinarily least squared.

In order to collect stakeholders’ preferences we adopted—to our best knowledge, for the first time in this field—the Nominal Group Technique as the elicitation framework: a face-to-face consensus development method which reduces the occurrence of drastically dissenting valuations by requiring an individual rating of the scenarios, the assembly of participants, a facilitated group discussion, and finally the individual and confidential re-rating (Rubin et al. 2006; Harvey and Holmes 2012).

Results indicate that: (1) stakeholders preferences over well-being dimensions are generally non-compensative; yet (2) the degree of allowed compensability differs significantly among nodes in the tree. Moreover, (3) experts evaluations depict the Italian regional well-being as highly heterogeneous, yet the degree of heterogeneity varies across domains and sub-domains; and (4) although some dominance-conditions exist between regions, there are several territories whose index ranking and values are highly sensitive to different stakeholders’ preferences, resulting in frequent rank-reversal effects. On the matter of weighting the dimensions of well-being, (5) Health is generally given a higher weight than sustainability; furthermore, (6) among the latter node, Society and Economy have a stronger relative impact than Environment.

The remaining of the paper is organized as follows. Section 2 describe the conceptual framework, Sect. 3 discusses the normalization procedure, Sect. 4 reviews the non-additive Choquet Integral and the aggregation process, Season 5 describes the preference elicitation procedure. Season 6 presents the results, alongside with a comparison with the outcome of a benchmark linear model, while Season 7 offers a sensitivity analysis and a discussion over results and methods.

2 Conceptual Framework: The Well-Being “Tree”

Composite measurement has gained substantial attention from media and policy makers in the last decade, and that such trend is continuously growing.² Numerous theoretical and empirical attempts have been made, from governments to international institutions, to build synthetic well-being indicators that would go “beyond GDP” at national, regional or community levels (UNDP 2014; Anand and Sen 1994; European Commission 2009; UNDP 2010; Alkire and Santos 2010; OECD 2013, 2014). In Italy, two reports were recently published, on Sustainable and Fair well-being, by the National Institute of Statistics and the National Council of Economy and Labour (ISTAT and CNEL 2014), which do not include the creation of a synthetic indicator.³

Indeed, due to the complexity of the latent phenomenon and the issues of data availability, the literature on well-being measures in Europe is characterized of indices built on a small number of indicators and on a compact conceptual framework, both at the regional (e.g., Murias et al. (2012), Silva and Ferreira-Lopes (2014), Schrott et al. (2012)), and at the national level (e.g., Meyer and Ponthière (2011), Cherchye et al. (2007b), Lefebvre et al. (2010), Mazziotta and Pareto (2015), Ivaldi et al. (2015)).⁴

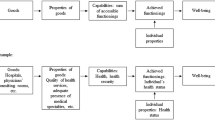
The concept of well-being operationalized in this paper takes the form of a hierarchic structure, whose multiple levels are characterized by a top-down decreasing degree of abstraction: well-being is decomposed into pillars, domains and sub-domains, ultimately basing on 41 “raw” statistical indicators. Such structure is the result of a joint work between scholars of the Ca’Foscari University of Venice and the Research Division of the Veneto Union of Chambers of Commerce (Unioncamere), and ideally draws from the conclusions of the French Commission on the Measurement of Economic Performance and social progress in 2009 (Stiglitz et al. 2009), and on the connected approaches to quality of life (Sirgy 2011).

The core part of our hierarchical structure is made of eight “domains” which cover aspects related to economic resources, labour market, education, safety, social capital, personal activities, environment and health. With respect to the Commission’s proposal, we split the leisure domain from the job-related one, since the former is semantically closer to the social dimension of life, while the latter is closer to the economic one. We also drop the governance dimension, since it is not a direct element of an individual quality of life. Figure 1 illustrates such structure.

Fig. 1

The Well-being hierarchical structure

In order to move from the eight domains to a unique measure, we aggregate them in four main “pillars” which represent the main components of well-being. Indeed, “Material Resources” and “Labour Market” constitute the Economic pillar, while “Education”, “Safety”, “Social Capital” and “Leisure” result in the Society pillar. The domains “Environment” and “Health” do not need further aggregation, and correspond to the remaining two pillars. Economic development, together with Social and Environmental conditions are usually considered as the three main components of a territory’s Sustainability levels, i.e. the capability of a socio-economic system to pursue and maintain economic growth without spoiling social and environmental resources for future generations (Pinar et al. 2014). Acting accordingly, we aggregate these pillars into a “Sustainability” dimension, which interacts with “Health” in constituting the final well-being node.

Within the “Economy” pillar, the node Material Resources has been disentangled into sub-domains conveying information on resource endowments, on inequality of resources as well as on the occurrence of deprivation conditions. Similarly, Labour Market is built of sub-domains related to unemployment conditions for the overall population, as well as for the weaker sectors of society (women and young population); finally, a third sub-domain capture the risk of social exclusion for the inactive population.

Within “Society”, the Education domain comprises sub-nodes on education attainments as well as on education opportunities, The node on Safety covers issues related to road-safety and crime-related safety. The Social Capital domain is disentangled into three sub-domains, following Donati (2014) and Putnam (2001). Primary Social capital refers to primary social relations (typically family-related), while Secondary Social capital covers the sphere of organized associations of civil society. Finally, the Generalized Social capital gathers information on Civic culture, and on public and political life participation.

The “Environment” dimension has three sub-nodes, related to urban open spaces (“green” areas), air-pollution conditions, and waste-management efforts.

“Health” sub-domains are focused on: (1) health-inequality, in order to spot the heterogeneity of morbidities and comorbidities between different socio-economic groups within a regional territory; (2) on “lifestyles”, with the aim of highlighting territories where health best-practices and health-rules are best (or worst) followed; and (3) on “health-levels”, i.e., the status-quo in term of regional health-outcomes. The latter sub-domain is, in turn, is further disentangled in three nodes targeted on longevity, mortality causes, and psycho-physical diseases. The former focuses on measures of life expectancy at various years and conditional to the absence of harsh functional and cognitive limitations. The second investigates the morbidity of specific diseases that lead to high proximity-to-death. The latter focuses on the occurrence of psychophysical diseases in the regional populations.

We now turn to discuss the 41 statistical indicators that constitute the grounds over which the “tree” takes form. It is important to stress that the choice of the raw variables is necessarily subjected to data-availability, while the design of the decision-tree is largely independent from such issues and mostly grounds on theoretical evaluations from the authors and the literature. After reviewing a vast set of database from numerous Italian and European sources, we concluded that regional data are rather un-equally distributed between thematic areas, in Italy and in Europe: while there are numerous indicators for domains as Material Resources, Labour Market, Health and Social Capital, relatively less regional information is accessible for Education, Security, Environment and Leisure. Moreover, some of the available indicators are not collected annually. It is for this reason that, as visible from Table 8, we decided not to establish a fixed number of variables per sub-domain. In some cases the sub-domain coincides with the indicator, and in general there are up-to four variables per sub-domain. “Appendix 1” provides a description of the 41 indicators included in the tree.

Given the aforementioned methodological issues, we are well aware that this set of variables does not fully, nor uniquely, comprise all the facets embedded in the well-being concept. Nevertheless, we believe it constitutes template coherent with the complexity of the latent factor, and it offers a distinctive alternative to more compact frameworks adopted in the existing literature. Indeed, our hierarchical structure allows the policy maker to investigate the measures of well-being at different levels of abstraction: on one side, a single index conveys a quick and comparable message on the quality of life in a region; on the other side, a palette of pillars, domains, sub-domains and, ultimately, raw indicators report information in an increasingly analytical fashion. Indeed, being able to identify the domains, or the sub-domains, that constitute a region’s strength and weaknesses can help the decision-maker in planning of future effective resources allocation. We believe that such an approach is itself a synthesis of the aforementioned debate on the opportunity of producing an aggregated index rather than a dashboard of indicators, and allows to exploit the strengths of both approaches.

3 Normalization

Raw indicators are usually observed and measured with different measurement units. Moreover, they might be alternatively positively or negatively related to the latent phenomenon. Hence, in order to ensure comparability and monotonicity of any aggregation function, each individual indicator must be normalized in such a way that its increase would never lead, ceteris paribus, to a decrease in the aggregated value. (see Giovannini et al. (2008) for a comprehensive discussion).

Our preferred specification is the min–max normalization function τ, widely used in the literature of multidimensional measures (Cherchye et al. 2007a; Chiappero-Martinetti and von Jacobi 2012; Murias et al. 2012; Lefebvre et al. 2010; Silva and Ferreira-Lopes 2014; Mazziotta and Pareto 2015; Pinar et al. 2014), in the Human Development Index (Anand and Sen 1994) and in the OECD Better Life (Boarini and D’Ercole 2013).

For each region i where an attribute x is observed at a time t, the corresponding normalized value is determined as:

$$ \tau_{ + }^{i,t} (x^{i,t} ) = \frac{{x^{i,t} - b_{ + } \hbox{min} (x)}}{{b_{ + } \hbox{max} (x) - b_{ + } \hbox{min} (x)}}\quad {\text{or}}\quad \tau_{ - }^{i,t} (x^{i,t} ) = \frac{{b_{ - } \hbox{min} (x) - x^{i,t} }}{{b_{ - } \hbox{max} (x) - b_{ - } \hbox{min} (x)}} $$

(3.1)

where τ ₊ is used when x is an attribute positively related to well-being (i.e., it is a “good”) and τ ₋ is used when x is an attribute negatively related to well-being (i.e., it is a “bad”).

The coefficients bmin _i and bmax _i are the highest and lowest values to be used as benchmarks for the x variable for region i. Regardless on how the benchmarks are defined, it is straightforward that, for x “good”, b₊max corresponds to a more desirable performance than b₊min, while the opposite is true for x “bad”. The min–max strategy rescales indicators into an identical range [0,1].

Before discussing the definition of such benchmarks, it is useful to highlight the link imposed by the min–max function between the original variable x and its normalized value τ(x), through the analysis of the partial derivative in (3.2):

$$ \frac{{\partial \tau_{ \pm }^{i} (x^{i} )}}{{\partial x^{i} }} = \pm \frac{1}{{b_{ \pm } \hbox{max} (x) - b_{ \pm } \hbox{min} (x)}} $$

(3.2)

The effect of a one-unit increment in x on the transformed τ (x) is constant, since the transformation function is linear, and depends solely on the benchmarks $b_{ \pm } { \hbox{max} }$ and $b_{ \pm } { \hbox{min} }$. The higher is their range, the weaker the marginal contribution.⁵ Thus, when (3.1) is adopted as normalization function, attention should be casted to the economic justification for the choice of such benchmarks, since they are the main drivers of the trade-offs lying behind any composite index built on these normalized data.

Following the existing literature in order to define the benchmarks, our preferred strategy would be to make them correspond to policy-target set by European or Italian institutions. Whenever such targets should not be available, we resort to adopt as benchmarks the best and worst practices observed in the European Union in the years 2000–2012 (see Table 1).

Table 1 Definitions of benchmarks for normalization function

Table 2 Scenario examples

Table 3 Example of a decision matrix with 9 scenarios made of four attributes (the “Society” node)

Table 4 Shapley values and Orness indices for main Index and Pillars

Table 5 Shapley values and Orness indices for Well-being domains

Table 6 Median values for Well-being, Sustainability and Health indices

Table 7 Median values for Economy, Society and Environment indices

This choice is driven by two issues on the min–max function that are worth stressing: (1) sensitivity to data-availability and variable distribution; and (2) the interpretation of the normalized values. As for the first issue, sensitivity to variables’ distribution, the presence of outliers in the observed variables would stretch the range over which the normalization is performed, therefore weakening the original variable‘s contribution to the overall index, through a reduction in its marginal effect on the normalized variable (3.2). In order to limit such occurrences and extend the exogeneity of the normalization function, references take into account performance observed in a wider set of territories than the one on which the analysis is focused (our alternative definition).

Secondly, it is important to discuss what should be the interpretation of the normalized values obtained from the data-driven min–max transformation. Consider a pair of indicators j, k (e.g., longevity and unemployment rate), and suppose that we observe (conveniently dropping the time index) x _j  = 76.5 years and x _k  = 14 % unemployment rate. The minimum observed level of longevity was 70,9 in Romania (2002) while the highest level was reached in Spain (2010) with 82.3 years. As for the unemployment rate, the range spans from 2.8% (Netherlands 2008) to 25% (Spain 2012). Implementing the min–max transformation (3.1), leads us to τ _j (76.5 years) = 0,5 and τ _k (14% unemployment-rate) = 0,5. Equality in the transformed values τ _j , τ _k implies that the two attributes j (longevity) and k (unemployment-rate) are equally satisfied in our quality of life framework. Whether it can also be interpreted as an equality in the levels of welfare “revealed” by the two variables, is debatable. Prudently, we could acknowledge that both values lie at equal distance between the observed-minimum and the observed-maximum in their respective data-series.⁶

To strengthen the economic interpretation of the normalization, we decided to use institutional-set goalposts (our preferred definition) in spite of observed values, whenever possible. Such policy benchmarks might be set by European or Italian institutions, in laws, regulations or policy targets (e.g., Europe 2020 or the Lisbon Strategy).⁷ When a policy target is available, the normalized variable conveys, at least partially, the extent to which a region is “far” from a desirable performance.⁸

The last two columns of Table 8 (“Appendix 1”) detail the benchmarks adopted in the normalization.

Table 8 Description of raw indicators

4 The Choquet Integral as Aggregation Function

After having defined the conceptual structure of the latent phenomenon, some set of preferences must be implemented in order to obtain, from the bottom to the top of the tree, a synthetic well-being index. Thus, for each decision-node a suitable aggregation operator has to be defined. Although a standard aggregation methodology for aggregated indices consists of linear aggregation, the preference independence assumption embedded in such models (i.e., full substitutability between dimensions) appears rather implausible when applied to well-being. Indeed, a region with average performances in the four pillars (economy, society, environment, health) would result in the same well-being level of one with top performance in two pillars and bad performance in the remaining two. If we suspect that there is a limit to the substitutability between dimensions, that is, if a mixed “bundle” of average performance is generally preferred to “extremes” bundles where dimensions score very high and very bad, the hypothesis of the linear model have weak economic justification. Hence, scholars have proposed composite monetary (e.g., Daly et al. (1994), Decancq and Schokkaert (2016)) and non-monetary, non-compensative measures, either using flexible CES frameworks (Bourguignon and Chakravarty 2003), geometric aggregation (Klugman et al. 2011), the Benefit of the Doubt approach (through Data Envelopment Analysis, see Cherchye et al. (2007b), Murias et al. (2012), Lefebvre et al. (2010)), factor analysis (Ivaldi et al. 2015) or variations of the arithmetic mean (Mazziotta and Pareto 2015).

In this paper, we adopt an alternative non-additive framework as the Choquet Integral, which has rarely been applied on this topic, and allows us to overcome some limitations embedded in the aforementioned literature (Meyer and Ponthière 2011; Pinar et al. 2014). The existing indices, indeed, are not meant to capture the specific degrees of substitutability, synergies or redundancies for any n-tuple of dimensions, nor to assign weights to coalitions of indicators (they rather do it for each of them separately). Our framework allows us to estimate such parameters and can prove informative in an intertwined context as the well-being measurement. In what follows we provide a brief description of the Choquet Integral and its properties, applied to our well-being framework. For a more detailed and specific analysis, we refer the reader to the works by Grabisch (1996), Grabisch et al. (2008), and Grabisch and Labreuche (2010).

Formally, each node in the tree is a set of criteria (also called attributes or dimensions). Taking a generic set N = {1, 2,…, n}, a non-additive measure is a monotone set function $\mu :2^{N} \to \left[ {0,1} \right]$, which assigns to every subset (coalition) of criteria a weight (measure) that is not necessarily the sum of the weights of any partition of it. Namely, if the measure of a coalition is greater (smaller) than the sum of the measures of their partitions, a synergic (redundant) interaction exists. To be an Aggregation Operator, the set function $\mu$ has to satisfy monotonicity and border conditions, such as:⁹

$$ \left\{ {\begin{array}{*{20}l} {\mu (\emptyset ) = 0} \hfill \\ {\mu (N) = 1} \hfill \\ {\forall S,T \subseteq N,S \subseteq T \subseteq N \Rightarrow \mu (S) \le \mu (T) \le 1} \hfill \\ \end{array} } \right. $$

(4.1)

Let $\left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be the normalized values of the criteria in the node N, and σ a permutation of indices such that $x_{{\left( {\sigma \left( 1 \right)} \right)}} \le \cdots \le x_{\sigma \left( N \right)}$, the Choquet integral with respect to $\mu$ is:

$$ C_{\mu } (x_{1} , \ldots ,x_{n} ) = \sum\limits_{i = 1}^{n} {x_{\sigma (i)} \left[ {\mu (A_{\sigma (i)} ) - \mu (A_{\sigma (i + 1)} )} \right]} $$

(4.2)

where $A_{{\left( {\sigma \left( i \right)} \right)}} = \left\{ {\sigma \left( i \right), \ldots ,\sigma \left( n \right)} \right\}, \forall i \in \left\{ {i = 1, \ldots ,n} \right\}$ and $A_{{\left( {\sigma \left( {n + 1} \right)} \right)}} = \emptyset$. The Choquet integral computes the aggregated values adding the marginal gains of each added attribute, starting from the minimum up to the maximum. In fact, all the criteria are satisfied at least with the value of the minimum, thus the weight of the universal set (equal to one) is applied to the minimum value of the normalized criteria. Subsequently the minimum criterion is cut off and the same procedure is applied to the remaining $n - 1$ criteria; to the minimum of these $n - 1$ criteria is assigned the value of the measure corresponding to this coalition, the (new) minimum is cut off, and the procedure continues until all the criteria are evaluated. Tuning the values of the measure, a wide range of preference structure can be implemented. A synergic effect can be represented by a super-additive measure, as a redundant effect can be obtained by a sub-additive measure. In the neutral case, the Choquet integral collapses into the weighted averaging. Anywise, it can be proved that the Choquet is a mean operator: that is, its value lies between the minimum and the maximum of its arguments.

Hence, the Choquet Integral allows for heterogeneous evaluations of quality of life, both within and between decision nodes: the evaluation for two territories which both have, in a given node, two dimensions with performance at 50% above the average and one at 50% below it, may differ depending on the nature of the poor-performing dimensions (e.g., for the Sustainability node, the penalization in the evaluation might depend on whether the worst condition pertains to the Economy or the Social component); moreover, since the Choquet Integral’s parameters are node-specific, the evaluation for nodes with similar distribution of their attributes’ performance may differ, depending on the subject area (e.g., whether we are evaluating Economic or Health issues).

A different, yet convenient, representation of the Choquet integral can be furnished using the so named Möbius values. In fact it can be showed that, being $\wedge$ the minimum operator:

$$ C_{m} (x_{1} , \ldots ,{\text{x}}_{n} ) = \sum\limits_{T \subseteq N} {m(T)\mathop \varLambda \limits_{i \in T} } x_{i} $$

(4.3)

where $m\left( S \right) = \sum\nolimits_{T \subseteq S} {\left( { - 1} \right)^{s - t} \mu \left( T \right),\forall S \subseteq N}$ are the Möbius representation of the non-additive measure $\mu$, and $s = card\left( S \right)$, $t = card(T$). The values of the Möbius representation can be positive in the case of synergic interaction, negative in the case of redundant interactions, null in absence of interaction (in average). The representation is bi-univocal, and the inverse transform is given by:

$$ \mu (T) = \sum\limits_{S \subseteq T} {m(S)} $$

(4.4)

Furthermore, the following conditions need to be satisfied (boundary and monotonicity):

$$ \left\{ {\begin{array}{*{20}l} {m(\emptyset ) = 0} \hfill \\ {\sum\limits_{T \subseteq N} {m(T) = 1} } \hfill \\ {\sum\limits_{\begin{subarray}{l} T \subseteq S \\ i \mathrel\backepsilon T \end{subarray} } {m(T) \ge 0\quad \quad \forall S \subseteq N,\forall i \in S} } \hfill \\ \end{array} } \right. $$

(4.5)

The parameters elicitation is simpler in the case of the Möbius representation and for this reason we decided to use this format and to elicit the Experts preference structure through an ad hoc questionnaire.¹⁰

4.1 Orness and Shapley Values

The Choquet Integral gives us the opportunity of analyzing the stakeholders’ responses from multiple perspectives.

The non-additive measure, or its Möbius representation, is also extremely informative as for the behavioral characteristic of the respondent. To this purpose we limit to mention the Orness index, together with the Shapley value.

The Orness index is computed for each decision node, taking values from 0 to 1, and measures the extent to which a respondent is close to the optimistic (rather than to the pessimistic) perspective (for a detailed approach, see e.g. Marichal (2004), from which we borrowed the notation). Higher values indicate that the aggregated Choquet evaluation for the node becomes closer and closer to the maximum value amongst the observed dimensions: i.e., the decision-maker believes that a good performance in one dimension more-than-compensates for a lower performance in another. The Orness index is given by:

$$ Orness(i) = \frac{1}{n - 1}\sum\limits_{T \subseteq N} {\frac{n - t}{t + 1}m(T)} $$

(4.6)

with n = card (N), t = card (T). At its apex, the Orness index is equal to 1 if the measure of all the singleton equals one, meaning that the satisfaction of at least one criterion is sufficient to guarantee the satisfaction of the aggregated index (the logical operator maximum). An index of 0.5 corresponds to linear preferences, with perfect substitutability between dimensions, while values below 0.5 indicate a tendency to imperfect-substitutability. At the lowest extreme, when the Orness is zero, no substitutability is allowed: the measure of all the coalitions is null (except for the set N), thus it is necessary that the value of all the criteria be high to obtain a high aggregated value (the logical operator minimum). The Orness index can be interpreted as a measure of a penalization for unbalanced values of the indicators, an approached developed, e.g., also in Mazziotta and Pareto (2015). With respect to the aforementioned approach, though, our penalization is node-specific, given that it depends on stakeholders’ evaluation, which is itself node-specific. Hence, the same heterogeneity in indicators’ performances can be penalized differently, depending on the context; in other words, the Choquet Integral accounts for the plausible hypothesis that the degree of social risk embedded in performances’ unbalance be deemed as higher for some contexts than for others.

The Shapley value measures the relative importance of each criterion in a node, they are non-negative, and sum up one (for a detailed description, we refer to Miranda and Grabisch (2009) and Grabisch et al. (2008), from which we borrow the notation). They should be interpreted at-the-margin: the Shapley value of a dimension is the average marginal gain obtained by adding that dimension to every coalition (in the node) that did not already include it. A higher value, thus, represents a higher relative importance. In terms of the Möbius representation of μ, the Shapley value of the ith criterion in a generic node is:

$$ Shapley(i) = \sum\limits_{T \subseteq N\backslash i} {\frac{1}{t + 1}m(T \cup i)} $$

(4.7)

4.2 Parameters’ Elicitation and Capacity Identification

For each node of the hierarchical tree a suitable measure needs to be elicited. Being $n$ the number of criteria in the node, we would need to elicit $2^{n - 2}$ values. Clearly the numerical complexity exponentially increases with $n$, and this can be a serious problem: too many questions become necessary, increasing the burden for the Decision Maker and the probability of inconsistencies. For this reason, a compromise between complexity and information capability is advisable. Indeed, this can be done by adopting a $k$-additive model, i.e. a non-additive measure where interactions are only possible for coalitions with cardinality less or equal to k (proposed by Grabisch (1997), to which we refer for futher details). A measure $\mu$ is k-additive if its Möbius representation satisfies $m\left( T \right) = 0$ $\forall T \subseteq N:$ $t > k$, with $t = card\left( T \right)$, and if it exists at least one subset $T$ with $card\left( T \right) = k$ such that $m\left( T \right) \ne 0$. If $k = 2$ we have a second order model (2-order model for brevity) and only n(n + 1)/2 parameters are required. We deemed a second order model as a good compromise between the topics’ complexity and the representation capability, and we applied it to our case study.

There are numerous methods for capacity identification in the literature, among which we recall the Least-squared, the Maximum-split, the Minimum variance, the Minimum distance, and other generalisations of the least-squares methods. We refer the reader to Grabisch et al. (2008) for a review of the aforementioned main approaches.

In this paper, we adopt the least-squares capacity-elicitation approach, and identify the values of the Möbius representation for each node in the tree from the answer given by an expert panel to a suitable designed questionnaire (described in details in Sect. 5). Namely, let us suppose that the questionnaire for a generic node N is submitted to an Expert. The questionnaire is formed by $M$ questions, each representing a hypothetical scenario (a case), being $\left[ {x_{1} \left( j \right), \ldots ,x_{n} \left( j \right)} \right]$ the vector of the normalized criteria values of the $j$-th scenario and $y\left( j \right)$ the corresponding evaluation, i.e. the answer to be fulfilled by the Expert.¹¹ The least-squares method aims at minimizing the average quadratic distance between the evaluations provided by the decision-maker and the overall values computed by means of the Choquet integral.

Thus the following quadratic optimization problem can be formulated:

$$ \begin{array}{*{20}l} {\mathop {\hbox{min} }\limits_{m(T)} \sum\limits_{j = 1}^{M} {(C_{m} (j) - y(j))^{2} } } \hfill \\ {s.t.} \hfill \\ {\sum\limits_{\begin{subarray}{l} T \subseteq S \\ i \in T \end{subarray} } {m(T) \ge 0\forall S \subseteq N,\forall i \in S} } \hfill \\ {\sum\limits_{T \subseteq S} {m(T) = 1} } \hfill \\ \end{array} $$

(4.8)

where $C_{m} \left( j \right), j = 1,..,M$ are the value of the $j$th case computed using the 2-order model. The unknown variables are the values of the second order non additive measure $m\left( T \right), T \subseteq N, card \left( T \right) \le 2$, and the problem is quadratic given that the Choquet integral $C_{m} \left( j \right)$ is linear w.r.t. measure values. This formulation is very general, and the constraints cardinality increases exponentially with $n$, making more difficult even a numerical solution. But limiting to a second order model, having in mind that $\left( T \right) = 0$ $\forall T \subseteq N, card \left( T \right) > 2$, the complexity is strongly reduced, and the quadratic optimization problem can be easily solved by standard techniques, at least until $n$ remains inside acceptable values. A Möbius representation for the node N is to be computed for each Experts involved in the elicitation.

Let us offer a simple applied example of the methodology used to identify the Möbius coefficients for a node consisting of two criteria (A, B), for which the scenarios 1a and 2a of Table 2 are submitted to the experts for an evaluation, under a 2-additive Choquet framework. Each criterion can take values from 0 to 1. Let us assume that an expert evaluates the first scenario with value 0.38, and the second with value 0.75.

Using (4.8) and (4.3), the minimisation problem can be written as follows:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{m(A),m(B),m(AB)} (0.3m(A) + 0.5m(B) + 0.3m(AB) - 0.38)^{2} \\ & \quad \quad+ (0.9m(A) + 0.4m(B) + 0.4m(AB) - 0.75)^{2} \\ & s.t. \\ & m(A) + m(B) + m(AB) = 1 \\ & m(A) \ge\, 0 \\ & m(B) \ge\, 0 \\ & m(A) + m(B) + m(AB) \ge 0 \\ \end{aligned} $$

where the last constraint is implicit in the first. The problem’s solution gives m(A) = 0.7, m(B) = 0.4, m(AB) = −0.1.

Note that the optimization problem involving scenarios 1a and 2a is strictly convex, and therefore has a unique solution. Anyway, as pointed out by Miranda and Grabisch (1999), the strict convexity of the problem (4.8) depends on the constraints. Namely, the matrix of the constraints’ coefficients (the scenario-questions posed to the experts) needs to satisfy some conditions on the ranking, with specific co-monotonicity conditions to be imposed on the questions. To clarify this point, we present a simple counter-example referred again to a node with two criteria (A, B), for which the scenarios 1b and 2b of Table 2 are submitted to the experts for an evaluation, under a 2-additive Choquet framework. Each criterion can assume values from 0 to 1. We also assume that an expert evaluates the first scenario with value 0.3, and the second with value 0.5.

Given the decision matrix and the responses, it is not possible to distinguish whether the decision maker is giving maximum importance to the first criterion or is adopting a “minimum-like” preference, thus assigning to each scenario the minimum value of the criteria. In other words, the solution to the corresponding optimisation problem (4.8) is not unique: namely, it has infinite solutions made by a linear combinations of the aforementioned two.

5 Stakeholders’ Preferences and Their Aggregation

As already explained, to estimate the parameters for the second-order Choquet Integral, scenarios depicting fictional societies are to be generated for each node in the tree, and evaluated in terms of their conveyed level of satisfaction.

As for any aggregation function, the parameters (in our case, the scenarios’ evaluations) can either reflect a preference structure elicited from some stakeholders group (e.g., field-experts, members of institutions, citizens), or being predetermined by the researcher herself, in a top-down fashion (Kim et al. (2015) and Decancq and Lugo (2013) produce a recent review of elicitation strategies). Although any set of preferences over a well-being index is arbitrary, in absence of a commonly accepted theoretical framework, it is our belief that eliciting actual experts’ preferences can provide stronger economic justification for the index premises, as well as boost the external validity of the results.

When asking a decision-maker to evaluate a scenario, her response will be the result of two intertwined factors, i.e., the general values that drive her decision, and the specific considerations that she may attach to single attributes included in the scenarios. Such factors can be sometimes hard to disentangle, and they both affect the scenarios’ evaluation. Moreover, some stakeholder may be not at ease with such evaluative process.

5.1 Stakeholders’ Selection and Sessions’ Set-Up

In order to tackle the aforementioned difficulties, we built four panels of stakeholders, one or each pillar in the well-being tree, with the requirement of having certified experience and knowledge, either applied or theoretical, on the issues at stake, as well as active actors of the public debate on the development of territorial policies. We tried to involve individuals with wide and heterogeneous backgrounds (within each pillar) in order to represent the highest number of perspectives on the same issues: each group gathered public officers, private managers and professionals, academic professors and social workers.

As for the experts’ number, we could not aim at creating statistical representative groups, but rather tried to select a rationalised sample of individuals. It’s important to recall that the higher the number of experts, the harder and slower the operationalization procedures while, at the same time, the higher the representative power. Given the selected elicitation framework (scenarios evaluation with Nominal-Group-Technique, which are described in the next paragraphs), we followed the literature recommendations (Delbecq et al. 1975) suggesting an ideal range that goes from 7 (minimum) to 12 (maximum) members for each group. A total of 37 experts were involved in the elicitation process, divided as follows: 9 experts for Economics, 10 experts for Society, 8 experts for Environment, 10 experts for Health.¹²

The well-being tree depicted in Fig. 1 requires us to determine the aggregation parameter for 15 nodes. As already stated, the lowest nodes of the tree (i.e., those involving raw indicators) are generated as the arithmetic average of the underlying indicators, with equal weight-distribution, therefore they are not included in the expert elicitation process. Each panel evaluates only the nodes belonging to their own pillar, plus the two top-nodes of the tree (nodes 1 and 2), which were submitted to all the experts. E.g., the Economics panel would tackle the nodes 3, 7, 8, as well as 1 and 2.

We gathered the panel-groups separately and provided them with a questionnaire for each decision-node involved in their expert are, plus the node “Sustainability” and “Well-being”. The questionnaires were provided sequentially, not at once, and computer-based, through a Wi-Fi network of laptops (one per each stakeholder) running a proprietary software.

5.2 Building Scenarios

The choice of evaluating the well-being conveyed by fictional scenarios (made by combining possible values of each node’s dimensions) has already been established in the literature (Meyer and Ponthière 2011; Pinar et al. 2014; Despic and Simonovic 2000), and provides an alternative to the standard strategy of asking for the “relative-weight” of each nodes’ dimension in a budget-allocation fashion (Chowdhury and Squire 2006; Hoskins and Mascherini 2009; Kim et al. 2015). The latter strategy is inherently inconsistent with the non-additive nature of our analysis, and was thus not adopted.

A computer-based questionnaire has been prepared, which includes a decision matrix for each decision-node in the tree. Following a procedure inspired from Despic and Simonovic (2000), the questionnaires included a list of possible scenarios described by the variables involved in the decision-node, where each variable could take four performance levels, i.e., highly positive (corresponding to a value of 1), positive (0.67), negative (0.34) and highly negative (0). As in Pinar et al. (2014), and contrary to what Despic and Simonovic (2000) suggest, no specific numerical definitions have been provided for such performance-levels, e.g., no specific numerical example has been made for a “highly positive” level of unemployment, and so on. Indeed, given the broad scope of the index and the variety of backgrounds which characterized each expert (even though the expert groups were pillar-specific, so that backgrounds’ variability is reduced), a more neutral setting has been preferred.

For each scenario, the stakeholder needed to fulfil the last column with a number in the range 0–10 where 0 represents a highly negative evaluation and 10 represents a highly positive one. Scenarios where all dimensions take the “best” or the “worst” levels are automatically assigned the highest or lowest score, respectively. Monotonicity was imposed as a ground rule for the stakeholders: if a scenario is strongly (weakly) dominated by another one, it must get a lower (or equal) evaluation. Each expert answered the questionnaires through a user-specific laptop provided by the elicitation-team. The following table provides an example, taken from the decision-node of the Society pillar (i.e., the aggregation of the Domains Education, Safety, Leisure and Social Network). The whole set of scenarios is reported in “Appendix 4” (Table 3).

Experts were made aware of the fact that, apart from the monotonicity assumption, no absolute “correct” or “wrong” answers existed, and that it would be sufficient for them to express evaluations coherent with their preferences on the issues at stake.

5.3 Method: The Nominal Group Technique

Facing the challenge to make the stakeholders interact within each group, we decided to use a consensus method as the nominal group technique (NGT). This methodology, never applied—to our best knowledge—to the topic of well-being evaluation, allows to stimulate group discussion, sharing ideas, highlighting common grounds as well as differences between stakeholders (on this technique, see the recent contribution by Rubin et al. (2006), Williams (2007), Bertin (2011) and Harvey and Holmes (2012)). A crucial feature of the NGT is that, although requiring the set-up of a discussion-group, it avoids the typical “group” dynamics, because the verbal communication between participants is minimized by the common set of rules (e.g., it is a group only in “nominal” terms). It is, therefore, an appropriate strategy to retrieve opinions and evaluations on issues that, because of their complexity, are difficult to be analyzed through quantitative methods or rigid decision-making models. Indeed, the NGT approach assumes that an aggregate representation of reality can be retrieved through comparison of individual experiences and individual representations. Moreover, unlike standard elicitation strategies, the NGT minimizes the occurrence of drastically dissenting valuations, which would require the adoption of statistical methods to generate an ex-post consensus and mitigate the potential bias resulting from the selection of panel members. Indeed, a re-rating of scenario is required whenever the heterogeneity of the first-round evaluation was too high (in our case, when the inter-quartile range is higher than 20). Nevertheless, the NGT does not impose a complete agreement to be achieved among experts, and each stakeholder has to produce a confidential answer to the submitted tasks.

Each session’s procedure can be summarized as follows:

• Each expert is provided with a seat and a laptop at the table. A member of the research-team embodies the role of the NGT leader. He introduces the participants to each evaluation session (one for each decision node), provides information, clarifies doubts and stimulates participants’ attention.

• For each aggregation node to be evaluated, instructions appear on the laptop screen through a specific software (the questionnaire was also provided in paper), with description of the attributes involved in the node. In this introductory stage of the session, such information are also read aloud by the NGT leader, who clarifies terms’ meanings and background issues that are connected to the decision node.

• Each expert provides an evaluation for every submitted scenario, without any communication between participants.

• A first results’ evaluation follows, where “consensus” is either acknowledged or not for each scenario. The lack of consensus is determined when the evaluations’ inter-quartile range has a value of 20 or higher.

• In the latter case, a discussion is initiated by the NGT leader, who asks each participant to state their views on the subject at stake. A second evaluation follows, only on the scenarios where consensus was not met, and following the same methods described above.

5.4 Aggregation of Experts Preferences

We set up an aggregation model which produces a synthetic index of well-being following a bottom-up methodology: the 41 normalized statistical indicators are aggregated amongst sub-domains (1), which are in turn aggregated in “domains” (2). Domains are synthesized in four Pillars (3), among which Economy Society and Environment are aggregated into Sustainability (4). The latter, together with pillar Health, constitutes the well-being index (5).

The first aggregation (1) is a simple average of the indicators’ normalized values. In the remaining steps, the Choquet Integral model is used, with the parameters elicited in the NGT sessions. In particular, a specific Choquet Integral is estimated for each expert and for each decision-node which she was asked to evaluate.

As already discussed, the stakeholders evaluated only the nodes pertaining to their expertise area, with the exceptions of the node at level 4 (“sustainability”) and 5 (“Well-Being”). Therefore, it would not be possible to create a single “representative expert” by averaging the Möbius measures from each expert. We resorted to a different strategy. The aggregation model for levels (2) and (3) randomly grouped, in 1000 rounds, 4 Experts, one per Pillar, thus generating a distribution of 1000 values for each sub-domain, domain and pillar. In each round, the values for the nodes at levels (4) and (5) have been generated with a Choquet Integral whose Möbius measures were the average of those expressed by the 4 decision-makers selected for steps (2) and (3).¹³

6 Results

6.1 Stakeholders Preferences: Substitutability and Relative Weights

Given the complexity of the topic at hand, we could expect experts’ evaluations to be, in general, characterized by an Orness index lower than 0.5. This would signal that some degree of synergy characterizes the dimensions involved, and that substitutability is lower than assumed by a linear model. Since the Orness index is expert- and node-specific, we present here the average value for each node, in order to convey some information on the expert group as a whole. Such values are reported in the second column of Table 4 for the main nodes in the tree, while the remaining ones are reported in Table 5. We can immediately notice that (1) Orness indices take always values lower than 0.5 and that (2) they are quite heterogeneous between nodes. This, again, shows the importance of eliciting actual preferences when trying to aggregate a multidimensional phenomenon. In particular, the Orness index is rather low (<0.35) for the well-being, the Economy and the Health nodes, as it appears that experts deem these nodes as the ones that need their sub-dimensions to perform all relatively well, in order to obtain a good overall synthetic performance. The revealed preferences, thus, signal that a linear approach for these nodes would not fit our stakeholders’ intrinsic view of the phenomena at stake. Adopting a standard linear model, rather than imposing a fix penalization rule, would introduce a top-down bias between researcher’s hypothesis and the stakeholders’ views.

The third column in Table 4 reports the average Shapley value expressed by the experts, for each node’s dimension. Results show that, again, it is quite common for the experts to allocate weights un-equally. The node “Well-being” is less affected by Sustainability (46% of the weight) than by Health (54%). Sustainability is, in turn, a synthesis of three main pillars (Economy, Society, and Environment) whose weights are slightly un-balanced in favor of the former two, with Environment being given an average weight of 29%. Therefore, even though the aggregation is non-linear and non-additive (so we could prudently say that the elicitation tends to give more importance to the Health pillar rather than to the remaining three ones. In evaluating the node “Economy”, experts allocate much more importance to Labor market issues (62%) than to Material resources (38%); similarly, among the dimensions of the Society Pillar, Education and Safety have weights which are consistent with an equal-allocation, while Leisure and Social Network are given a relatively lower and higher weight, respectively. Other heterogeneous weightings take place within the Environment node, where the issues of green areas (24%) have a sensibly lower impact than pollution (43%), and in the Health Pillar, where Health levels (longevity, mortality causes, the incidence of specific diseases) are allocated a relatively higher weight (44%), while inequality issues are have a relatively lower one (21%).

When looking at lower-level nodes, as the Domains for the Economy and Society Pillars (Table 5), the degree of compensativity increases, while the relative weights remain rather unequally distributed. The Orness indices for the two Domains of the Economy Pillar (Material Resources and Labour Market) still have Orness values below 0.5, while Domains in the Society are characterized by full substitutability (Education and Social Capital). This means that Stakeholders do not deem a strong balance of performance amongst dimensions in order to be particularly important for the satisfaction of these nodes. In the case of the Safety domain, Experts’ preferences tend even more to an “optimistic” view (the logical operator “maximum”).

As for the Shapley values, they are still highly unequally distributed within nodes: when evaluating “material resources” the priority is given to inequality issues, while for “labour market” there is a strong prevalence for the overall “unemployment” indicators, rather than for the conditions of specific population sectors. In evaluating “Education”, a vast majority of the weight goes to the scholarization conditions, rather than to school dropouts. As for “Safety” issues, the priority is given to “crime-related” safety rather than to “road safety”, while in the Social Capital area, the distribution of weights appear more balanced.

The full results for the elicited 2-additive Möbius measures are reported in “Appendix 3”.

6.2 Results for the Synthetic Index

In this section we will report, for each node in the tree, the median value of the 1000 simulations described in Sect. 5.4. We also compute a national average index (population-weighted), and the coefficient of variation of regional indices¹⁴ for each decision-node. Combining randomly the Experts involved in the evaluation, allows for an informative robustness analysis (discussed in Sect. 7) of the median indices built on such preference sets.

Table 6 present the results for the well-being index and its two main sub-dimensions, Sustainability and Health, for the year 2012. The indices’ values always range between zero and one due to the normalization of the underlying raw indicators. The overall Italian picture does not look positive, with regional indices being (1) highly heterogeneous and (2) rather poor.¹⁵ Except for Trentino-Alto Adige, with a median index of 0.78, regional well-being spans from a maximum of 0.62 in Veneto to a minimum of 0.27 in Calabria. The coefficient of variation is 0.27, meaning that the size of the standard deviation between regions accounts for 27% of the national average value.

The results are also strongly geo-characterized (see “Appendix 3” for a regional map of Italy). After the top two North-east regions, we find two from the Centre (Marche and Toscana, with values 0.61 and 0.58), the small Valle d’Aosta at 0.61, and further 6 regions from the Centre-North areas (Emilia-Romagna, Friuli-Venezia Giulia, Lombardia, Umbria, Liguria e Piemonte) between 0.58 and 0.49. Overall, the first 11 positions in the well-being table belong to Centre-North regions, while the remaining are Southern areas, with Lazio (the region of Rome) being a fourth-to-last exception. This ranking is coherent (although not equal) to recent results in regional studies (Murias et al. 2012). Such strong geographic spread is even worsened when one notices that, apart from the small Molise with a score close to Piemonte (0.46), the well-being index for the South drops to 0.43 for Sardegna, and all the way down to Calabria’s 0.27.

Table 6 also reports the aggregate measures for the Sustainability node and for the Health pillar, while the values for the Economy, Society and Environment Pillars (which constitute the Sustainability node) are reported in Table 7.

The Health pillars has the highest coefficient of variation (above 0.35), and the worst average score across the four (0.43), denoting the existence of a potential social risk from bad health: indeed, while there is no region with a high health index (except for Trentino), five territories fall below the level of 0.32. Such territories are from Southern Italy (Sicilia, Basilicata, Calabria, Abruzzo), plus the Centre region Lazio. In the Health dimension, the common Italian geo-characterization appears weaker, with two Souther Regions (Molise and Puglia around 0.47) in the top-ten, and Norhtern Liguria (0.45) and Piemonte (0.42) at lower levels.

The average evaluation on the Italian Sustainability conditions are slightly higher than for Health, with an average index of 0.54 and a much lower variability (coefficient of variation at 0.23). Indeed, regions are concentrated in a small range of values: after the most virtuous Trentino at 0.79, the following 9 territories lie between Veneto (0.67) and Abruzzo (0.60). Unlike for Health, the Italian picture of sustainability appears strongly geo-characterized, with Abruzzo being the only Southern region in the top-ten, and Liguria the only Northern one on a sensibly lower level (0.54)

When looking at single pillars, Society is the most virtuous one among the four, with the highest average value and the smallest dispersion across regions, while Economy has both a lower average value and a much higher variability. As for the Environment pillar, it is characterized by an average score (0.53) and a variability degree (0.24) lying in between those of Economy and Society. The usual geo-characterization of Italian regions is confirmed, yet two notable exceptions exist: Abruzzo takes the second position, with a score (0.79) close to the first-ranked Trentino (0.84). A substantial gap divides these territories from the lower ranked ones, with Lombardia (0.64) in the third position and other six regions lying above 0.6. Among the worst ranked we find mostly Southern areas, with Northern Liguria at the fifth-to-bottom place, with a score of 0.42.

Trentino—Alto Adige’s predominance in the overall well-being index reflects in a top performance in each of the 4 pillars. Indeed, a similar correspondence is visible (yet, to lower extents) for the group of runners-up Veneto, Marche, Valle d’Aosta, Toscana, although their rankings are sensibly different between Economy, Society, Environment and Health. Similarly, Southern regions are mostly concentrated at the bottom of each ranking.

Although well-being is linked with sound economic, environmental and health conditions, these results show how multidimensionality can sometimes challenge such view. Liguria occupies mostly mid-table positions, but scores very low in the Environment dimension. Emilia-Romagna’s performance in the Economic pillar is higher than the one scored by regions preceding it on the overall index. Similarly, Abruzzo’s very high score in the Environment pillar grants it a good ranking as of Sustainability, yet its well-being is relatively low. Both these regions have their overall indicator penalized by a relatively bad performance in the Health pillar, indeed a very bad one for Abruzzo. Similar effects can be found for Piemonte and Lazio and, on the opposite direction, for Marche. Non-additivity allows experts to adopt a non-compensative behaviour when evaluating such regional dashboards. Moreover, stakeholders’ severity is generally higher when the evaluation involves health-related matters (see the Orness index between Sustainability and Health in Table 4), hence the penalization (or the bonus) accorded to the aforementioned regions when computing the synthetic measure.

7 Discussion

7.1 Effects of Experts’ Subjectivity on Well-Being Evaluations

In order to gain further insights on the Italian framework, we look at the distribution of the well-being index coming from the multi-expert simulations (Sect. 6.2), and represent it through box-plots for each region (Fig. 2, where regions are sorted by their median index value). Such visualization technique is useful to evaluate experts’ consensus about a region’s value: the narrower a box, the higher the agreement on the region’s condition. What we notice is that boxes’ dimensions is noticeably heterogeneous, and at the same time not geographically driven: the agreement on Marche, Valle d’Aosta, Toscana, Friuli Venezia Giulia, Umbria, Molise, Sardegna and Sicilia is significantly higher than for Lombardia, Liguria, Piemonte, Basilicata, Lazio, Abruzzo and Calabria. Higher dispersion is symptomatic of the existence of conflicting performances across well-being dimensions, e.g., very bad in some pillar and very good in others. With respect to the well-being node, the focus is casted on its two components, namely, Sustainability and Health. By comparing Fig. 2 with Table 6, it results that regions with wider boxplots for well-being values are those where these two components obtain quite different values.

Fig. 2

Distribution of the Well-being index over 1000 simulations (regions ranked by highest median value)

When a territory has similar Sustainability and Health indices, experts’ evaluation will play a relatively little role in aggregating them into a synthetic well-being index (should the two dimensions have the same normalized value, this would automatically correspond to the synthetic index). Conversely, when they exhibit opposite performances, the matter of how to aggregate them becomes crucial, hence the high variance in the synthetic index. Regions as Lombardia, Liguria, Basilicata, Lazio and Abruzzo are good examples of occurrences where the Health performance is sensibly lower than the Sustainability one. In such cases, regardless of the weights attached to the dimensions, the evaluation of a “severe” expert would differ strongly from that of a “compensative” one. Although preferences were elicited following a consensus method as the NGT, differences in perceptions towards dimensions’ substitutability are still capable of generating volatility in well-being’s evaluation. Moreover, such analysis allows us to detect that, regardless of the stakeholders’ preferences, the well-being’s level of the Southern regions (except for Molise) is well below that of the Center-North ones (excluding Lazio). Indeed, looking at the box dimensions, one can verify that the interquartile range for Sardegna (and of the worse-off regions) is entirely below that of Piemonte (and of the better-off regions). Similar cutoffs are harder to identify within the Center-North group (except for Trentino), thus emphasising even more the gap between North’s and South’s values.

Finally, Fig. 2 allows to quickly spot the regions with heterogeneous performance across indicators, with respect to those with a more uniform dashboard. E.g., Abruzzo’s well-being evaluation spans from a first quartile at 0.24 and a third quartile at 0.40, reminding us of the precautionary attitude needed when facing multidimensional evaluations, and alerting us on the existence of opposite performances between the Sustainability and the Health pillars.

7.2 Comparison with a Linear Model

With respect to the standard linear model, the Choquet Integral allows synergies and redundancies to exist between dimensions. In order to appreciate the difference between these two aggregation strategies, and to perform a robustness check of our results, we re-estimate the hierarchical tree by aggregating nodes through a linear average of the normalized sub-nodes values. In order to coherently compare the methods, the linear average implements has weights corresponding to the Shapley values elicited from the Stakeholders (Table 4). We replicate the 1000 multi-expert simulation as described in the previous sections, and report the median values of the well-being index in Fig. 3, as well as the regions’ ranking (according to the median values of the index).

Fig. 3

Comparison of Well-being rankings and values between Choquet and linear models

The left-side graph shows that the linear model always introduces a positive bias in evaluating well-being across regions. The main reason for this relies in the highest severity allowed by the Choquet Integral in evaluating multiple dimensions at each decision node, in terms of lower compensativity. Moreover, the spread between the models’ indices is not uniform across regions, and reaches its maximum levels in Lombardia, Liguria, Molise, Basilicata, Lazio, Abruzzo and Calabria, where we already know there is a higher heterogeneity between the main components of well-being (Economy, Society, Environment, and Health). Such performances’ heterogeneity gets a weaker penalization in the linear model, where the shortcomings in one dimension can always be compensated by better performances in others. As a result, the distance in absolute terms between the best and the worst regions increases under the Choquet evaluation. Nevertheless, the regional well-being ranking is rather robust at varying methodologies (right-hand side graph in Fig. 3), with important exceptions. When switching from a linear to a Choquet model, Lombardia drops two positions, Abruzzo drops four, while Puglia and Campania gain two. As already noted, relative positions may switch within the North or the South groups, but the geographical disparities remain evident.

We can also investigate the difference between the two models at lower stages of the well-being tree. To this purpose, we concentrate on the results at the Pillar-level (Fig. 4).

Fig. 4

Comparison of rankings and values for Economy, Society, Environment and Health indices between Choquet and linear models

When switching from the Choquet Integral to the linear model, a positive bias is confirmed in each of the four dimensions. Yet, this spread is particularly small in the Economy pillar, signaling a rather homogeneous set of performances in the sub-domains across the regions.

The evaluation of the Society dimension is quite consistent between the two methods for numerous regions, yet it visibly differs for territories as Abruzzo, Lazio, Liguria, Lombardia, Molise, Piemonte, and Umbria. Although all these regions have relatively high performance in the Education and the Safety domains, the Choquet Integral values are driven down by some bad performance in the Leisure and, particularly, in the Social Network dimensions. Similarly, In the Environment area, regions as Basilicata, Calabria, Molise and Sicilia exhibit a spread between the two methods that exceeds 10 points in absolute values. Indeed, these regions obtain good scores in the sub-domain of air-pollution, but face shortcomings in the coverage of urban green areas and in the waste-recycling management. Because of the full substitutability hypothesis, the potential social risks embedded in such a heterogeneous dashboard are much less highlighted in the linear model.

Similar, and even stronger, spreads can be found by looking at the results of the Health Pillar. The non-additive measures are much lower than the linear ones for northern territories as Veneto, Lombardia, Liguria, and Piemonte, and southern ones as Sardegna, Sicilia, Basilicata, Calabria, and Abruzzo. Again, high heterogeneities characterize these regions within the Health sub-domains, hence the penalization by the stakeholders, whose preferences were generally more pessimistic in this field.

8 Conclusions

This paper built an original framework for measuring the Quality-of-life at regional level in Italy. We combined the need for a wide dashboard of indicators (organized in a hierarchical structure) with a non-additive aggregation model which allows for varying degrees of substitutability between well-being dimensions at each node in the tree. Furthermore, we set up a multi-expert elicitation strategy, using Nominal-group-technique, to characterize the aggregation function with the informed-opinions of local stakeholders. Results show that, indeed, stakeholders express different degrees of substitutability, depending on the well-being area under scrutiny, which are successfully modelled within the Choquet Integral but would not be captured in a standard linear aggregation model. Moreover, our analysis highlights that some territories have a highly unbalanced dashboard of indicators, which leads to higher penalization by the most severe stakeholders. Indeed, regions’ index ranking and values in the well-being and in several sub-domains can differ, depending on the set of preferences adopted, although a dominance-relationship exists between some Centre-North regions and some Southern ones.

Appendices

Appendix 1: Variables Description

Within the material-resources domain, we selected raw indicators of disposable equivalent household income per capita and of non-food household-expenditure for the “income-level” sub-node; for “inequality of resources” we adopted the Gini index, while for the “deprivation” sub-domain we used the Eurostat synthetic index of deprivation and the at-risk-of-poverty rate (with threshold fixed at 50% of median national disposable income). Within the “labour market” domain, the “unemployment” sub-domain includes rates of unemployment and long-term unemployment for the whole population; “society’s weakest” include indicators on women and youth labour-market participation; the “inactive” dimension includes the share of individuals not in employment, education or training. Within the “education” domain, the sub-node “scholarization” includes data on high-school and university degrees attainments, while “school accessibility” accounts for the school-dropouts as a share of the population aged 18–24. Within the “safety” domain, “road safety” is represented by the indicator on mortality for car accidents, while the “crime-related safety” includes both violent-crime and minor-crime indices. The “generalized social capital” is measured by the share of Italian “B-type” social cooperatives,¹⁶ the share of individuals aged 14+ who participate in cultural associations, the number of blood donors per 1.000 inhabitants and the 2008 general elections turnout. The “secondary social capital” encompasses indicators on the number of volunteering organizations per 10.000 inhabitants as well as the share of individuals aged 14+ who participated in volunteering activities. Finally, “primary social capital” includes data on the frequency of friends meeting in leisure time and on the share of individuals who provided free help to others. Within the “Environment” domain, the sub-node on “green cities” is an indicator of the green areas density in urban environments; “air pollution conditions” are measured through indicators of CO₂ emissions per capita and frequency of daily urban PM10 threshold trespassing; “waste-management” measures the share of recycling on total urban wastes. Within the Health domain, the “health inequality” node is constituted by a measure of inequality in morbidity between individuals in bad and in non-bad socioeconomic status, whose values go from 0 to 100, where 0 means low inequality (this measure is detailed in “Appendix 2”).

In the last two columns, benchmarks from a policy-target, are marked with a star “*”.

Appendix 2: The Health Inequality Index

The health inequality index is an average of six own-built inequality measures, showing the extent to which poor individuals are more (or less) prone than richer ones to be subjected to a number of risk-symptoms. The data used are regional micro-data on individuals medical and socio-economic status, from the survey PASSI (Progressi delle Aziende Sanitarie per la Salute in Italia), and cover six indicators (each one expressed as dichotomous variable: symptoms occurring vs non-occurring): diabetes, depression, smoking, scarce physical activity, drinking and bad diet. Data includes information on individuals economic conditions, through a question asking whether the respondent is able to make ends meet: (1) very easily; (2) rather easily; (3) rather hardly; (4) very hardly. We first generated a dichotomous variable for economic status (high or low conditions), joining together the categories (1) and (2), (3) and (4), respectively. For each symptom and each region, we then counted the individuals who declare to suffer from it, for each of the two economic status, thus obtaining a variable I_k,g (number of individuals affected by symptom k, in good economic conditions) and a variable I_k,b (number of individuals affected by symptom k, in bad economic conditions).

For each region i, we then computed the difference between I_k,g and I_k,b, and normalized it dividing it by the maximum observed difference across Italian regions, as in the following expression:

$$ HI_{k}^{i} = 1 - \frac{{\left| {I_{k,g}^{i} - I_{k,b}^{i} } \right|}}{{Max\left| {I_{k,g}^{i} - I_{k,b}^{i} } \right|}} $$

The kth Health Inequality index spans from a minimum of 0 (highest observed differences of k-symptom’s occurrence between socio-economic statuses) and 1 (lowest observed differences). The Health Inequality index included in the hierarchical tree is the simple average of the so-built six indices.

Appendix 3: Topographical Representation of Italian Regions

Appendix 4: Scenarios Submitted for Evaluation

See Tables 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18.

Table 9 Decision matrix for the “Quality of life” node

Table 10 Decision matrix for the “Sustainability” node

Table 11 Decision matrix for the “Economy” node

Table 12 Decision matrix for the “Material resources” node

Table 13 Decision matrix for the “Labour market” node

Table 14 Example of a decision matrix with 9 scenarios made of four attributes (the “Society” node)

Table 15 Decision matrix for the “Education” node

Table 16 Decision matrix for the “Safety” node

Table 17 Decision matrix for the “Social Network” node

Table 18 Decision matrix for the “Environment” node

Appendix 5: Möbius Measures Elicited from Stakeholders

Each of the boxes in Table 19 report the Möbius measure elicited from the stakeholders for each Pillar and Domain in the hierarchical tree. Since each stakeholder has its own Möbius measures, we report here the average measures across the experts that were involved in each node’s evaluation. The sign of the Möbius measures can be interpreted as detailed in Sect. 4.1.

Table 19 Möbius measures (2-additive) elicited from the NGT sessions (pillars and major nodes in capital letters)

It is interesting to notice that the great majority of the interactions between dimensions¹⁷ have a positive sign, thus conveying the existence of complementarity (or “synergy”) between them. This kind of information is coherent with the analysis of the Orness measures already described in Sect. 6: strong complementarity (i.e., low substitutability) is detected between Health and Sustainability (the well-being node), Labour Market and Material Resources (the Economy Pillar), between indicators of Unemployment and of Society’s weakest employment conditions (within the Labour market Domain), between Generalised and Primary Social Capital (Social Capital Domain), as well as between Air quality and Waste management within the Environmental Pillar, and between all the dimensions of the Health Pillar. Conversely, distinct substitutability is detected between the Economy and the Social Pillar (within the Sustainability node), between Secundary and Primary Social Capital (within the Social Capital Domain), between Road and Crime safety (Safety Domain), as well as between Waste management and Green areas (within the Environmental Pillar).

Appendix F: Results for Well-Being Domains

See Table 20.

Table 20 Well-being domains indices (Choquet integral), year 2012