1 Introduction

Willingness to pay is usually seen by economists as the most appropriate way to convert into monetary units the benefits that result from investments reducing the probability of death or disease (see for instance the influential contributions of Drèze 1962, Schelling 1968 and Mishan 1971). The measure has been exploited in several studies evaluating the effects of public policies increasing safety. For instance, the willingness to pay for improvements in road safety (Jones-Lee et al. 1985), for pesticide free food (Misra et al. 1991), for poison control centers (Phillips et al. 1997), for improved air quality (Carlsson & Johansson-Stenman 2000), for electronic waste recovering and recycling programs (Nixon & Saphores 2007) and for moving to a neighborhood with less violent crime (Bishop & Murphy 2011) have been assessed.

The theoretical foundations of the willingness to pay for reductions in the probability of death or disease have been introduced by Drèze (1962). Since then, a deeper understanding of the properties of this measure has been provided in the literature. For instance, Jones-Lee (1974) describes the form of the functional relationship between the willingness to pay for reductions in the probability of death and the size of these reductions. Jones-Lee (1974) also shows that the willingness to pay should rise with the baseline probability of death, a phenomenon termed the “dead anyway effect” by Pratt & Zeckhauser (1996). These authors also address the concentration of the risk in the population. Specifically, keeping the aggregate risk constant, Pratt & Zeckhauser (1996) determine if the willingness to pay for larger reductions in the probability of death concentrated on a small number of individuals is higher than the willingness to pay for smaller reductions in probability spread within a larger population. Hammitt (2000) examines the effects of the health status and of wealth on the willingness to pay for reductions in the probability of death (expressed as the value of statistical life). He indicates that the first effect depends on the way the marginal utility of wealth changes with health status. Assuming that additional wealth is more valuable in life than as a bequest, Hammitt (2000) also indicates that the value of statistical life increases as wealth rises if individuals are risk averse or risk neutral. Dachraoui et al. (2004) examine the effect of risk aversion on the willingness to pay for self-protection. They show that risk aversion increases (resp. decreases) this willingness to pay Footnote 1 only when the baseline probability of loss is above (resp. below) \(\frac {1}{2}\). Crainich et al. (2015) specify this relationship by showing that the willingness to pay to reduce the probability of disease is the product of the willingness to pay under risk neutrality and an adjustment factor that depends on both risk aversion and downside risk aversion. The impact of background risks on the willingness to pay for self-protection has been analyzed by Eeckhoudt & Hammitt (2001) and by Bleichrodt et al. (2003). Eeckhoudt & Hammitt (2001) examine how various sources of mortality affect the willingness to pay for reducing the probability of death while Bleichrodt et al. (2003) highlights the conditions under which the willingness to pay to reduce the probability of a given disease increases as the probability and severity of comorbidities rise. The impact of information about individuals’ heterogeneity on the willingness to pay for projects reducing the probability of death has been examined by Hammitt & Treich (2007) who show that when the reduction in the probability of death differs across individuals, the average willingness to pay decreases with information about individual risk change.

Our paper complements these theoretical developments by examining the effects that personalized health information should have on the average willingness to pay for disease prevention actions. The ever growing availability of personal health related information (due for instance to the development of genetic testing, to the multiplication of public health campaigns and to the increasing use of the internet for medical purposes) changes the way diseases are perceived by individuals and thus modifies their propensity to prevent them.Footnote 2 In this paper, we examine prevention actions reducing either the probability of disease or its severity (self-protection and self-insurance, respectively, in Ehrlich and Becker’s 1972 terminology) and focus on personal information about the baseline probability of disease (provided by genetic predisposition tests for instance).Footnote 3 With such information, individuals do not make medical decisions based on the prevalence of the disease (i.e. based on average information) but according to personal characteristics instead. Whether they learn that their intrinsic probability to develop a given disease is higher or lower than the prevalence of the disease, individuals’ willingness to pay for prevention should, in theory, be modified. Consequently, an interesting question related to the development of personalized health information is whether the willingness to pay for prevention based on the average information (i.e. in the absence of personalized information) is higher than the average willingness to pay for prevention with personalized information. In this paper we address this question, the answer to which determines how the relevance of a prevention program is affected by the development of genetic testing. Note that in contrast to Hammitt & Treich (2007), the heterogeneity we deal with is about the baseline probability of disease (i.e. because this is the information that genetic tests provide) and not about the reduction in the probability of death resulting from a public project.

In the first model developed in the paper, we show that personalized information about the probability of disease raises the average willingness to pay for self-protection (Section 2). We then show (Section 3) that the same information raises the average willingness to pay for self-insurance if the marginal utility of wealth rises with health. Section 4 concludes.

2 Average willingness to pay for self-protection

We suppose the population consists of individuals who are identical in every respect (initial wealth, severity of disease in case it occurs, preferences towards risk,...) with the exception of their baseline probability of disease which is determined by genetic predispositions. In the absence of genetic testing, this information is not available to individuals.Footnote 4 We examine the effect of the dissemination of this information through the development of genetic testing: individuals are supposed to switch from a situation where they are unaware of their intrinsic probability of disease (they just know the prevalence of the disease, i.e. the average probability in the population) to a situation where they know this probability. The question we address is whether the genetic information modifies the average willingness to pay for a prevention program that reduces the probability of disease.Footnote 5 We may expect individuals’ willingness to pay for such a program to change once they learn that their probability of developing the disease is higher or lower than what they expected. We analyze the way the genetic information changes individuals’ willingness to pay as well as the way it modifies the average willingness to pay for prevention.

We assume that individuals maximize their expected utility and derive utility from wealth (w) and health (h), hence u(w, h). The utility function is increasing and concave in both argumentsFootnote 6 (u 1(w, h) > 0, u 2(w, h) > 0, u 11(w, h) < 0 and u 22(w, h) < 0). No a priori assumption is made about the sign of u 12(w, h). A given disease occurs with a probability p and lowers the individual’s health status from h to h − m (where m denotes the severity of the disease).

As a result, the individuals’ expected utility is given by:

$$ \overline{EU}=(1-p)u(w,h)+pu(w,h-m) $$
(1)

Suppose that public authorities are considering the implementation of a prevention program reducing by Δ the probability of disease (an activity termed “self-protection” in the literature), so that the probability of disease is p − Δ instead of p. The individuals’ willingness to pay (denoted by v) for this program is implicitly defined by Eq. 2:

$$ (1-p)u(w,h)+pu(w,h-m)=(1-p+{\Delta} )u(w-v,h)+(p-{\Delta} )u(w-v,h-m) $$
(2)

In this expression, v corresponds to the wealth change which — when coupled with a reduction Δ in the probability of disease — keeps \( \overline {EU}\) constant.

We first determine the way v changes with p by using Eq. 2 and the implicit function theorem. We obtain:

$$ \frac{dv}{dp}\,=\,\frac{\left[ u(w,h)\,-\,u(w\,-\,v,h)\right] \,-\,\left[ u(w,h\,-\,m)\,-\,u(w\,-\,v,h\,-\,m) \right] }{(1\,-\,p\,+\,{\Delta} )u_{1}(w\,-\,v,h)\,+\,(p\,-\,{\Delta} )u_{1}(w\,-\,v,h\,-\,m)}\,=\,\frac{G}{ EU_{1}} $$
(3)

The denominator of Eq. 3 is positive since it corresponds to the expected marginal utility of wealth (denoted by E U 1). The numerator of Eq. 3 is denoted by G. Its sign depends on the comparison between the utility loss resulting from a wealth decrease (from w to w − v) in two health states: the perfect health state (h) and the disease state (h − m). When the reduction in wealth is more painful in the perfect health state (i.e. when u 12 > 0), G > 0 and the willingness to pay for the prevention program rises with the baseline probability of disease. The reverse holds when u 12 < 0. In short:

$$\frac{dv}{dp}\gtreqless 0\Longleftrightarrow u_{12}\gtreqless 0 $$

We now determine whether \(\frac {dv}{dp}\) changes at an increasing, constant, or decreasing rate with p. Using Eq. 3, we obtain:

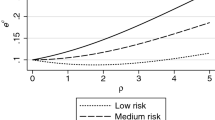
$$ \frac{\partial \left( \frac{dv}{dp}\right) }{\partial p}=\frac{ G[u_{1}(w-v,h)-u_{1}(w-v,h-m)]}{\left( EU_{1}\right)^{2}}\geq 0 $$
(4)

Note that our objective is to define the values taken by v for different levels of p. Since these levels of p do not result from changes in self-protection actions but are instead exogeneous (they result from the genetic information), we do not have to consider the way p modifies w.Footnote 7 The numerator of Eq. 4 is the product of two terms whose signs are identical. Specifically, both G = [u(w, h) − u(w − v, h)] −[u(w, h − m) − u(w − v, h − m)] and [u 1(w − v, h) − u 1(w − v, h − m)] are positive (resp. negative) if u 12 > 0 (resp. u 12 < 0). Therefore, while the sign of u 12 determines whether v is decreasing or increasing in p, the relationship is convex in both cases (it is linear when u 12 = 0). We then conclude from Eq. 4 that no matter the sign of u 12, \(\frac {dv}{dp}\) changes at an increasing rate with p. The relationship between the willingness to pay for self-protection (v) and the baseline probability of disease (p) is represented in Fig. 1a, b.

Fig. 1
figure 1

Willingness to pay for self-protection

Full size image

From there, using Jensen’s inequality, it is straighforward to show that whatever the distribution of p around its mean value \(\overline {p}\), \( E(v(p))\geq v(\overline {p}).\) That is, the willingness to pay for self-protection based on the average information (i.e when the individual probability is unknown) is lower than the average willingness to pay for prevention when the individual probability is known. As a consequence, the development of genetic predisposition tests should raise the benefits related to self-protection programs.

2.1 An extension: The efficiency of self-protection actions

The literature on disease prevention usually assumes that the efficiency of self-protection actions increases with the baseline probability of disease. This characteristic has not been taken into account in Section 2 where it was assumed that the reduction in the probability of disease resulting from self-protection was constant (and equal to Δ) whatever the baseline probability of disease. In this section, we address this property of self-protection actions by assuming instead that Δ = Δ(p) with 0 <Δ′(p) < 1 (i.e. the reduction in the probability of disease due to self-protection rises with the baseline probability of disease).

However, we must specify the probability function Δ(p) in such a way that the average reductions in the probability of disease before and after the genetic information are equal. We make this assumption in order to capture only the effect of the genetic information on the willingness to pay for self-protection. In other words, given this assumption, changes in the average willingness to pay for self-protection solely result from the information about the probability distribution and not from a larger or a lower average reduction in the probability of disease. In order to isolate a pure information effect, we thus assume Δ″(p) = 0. Using Jensen’s inequality, this assumption ensures that whatever the distribution of the probability of disease around its mean, self-protection has the same effect on the average reduction in the probability of disease.

As in Section 2, the initial expected utility is given by Eq. 1. The willingness to pay (denoted by y) for a reduction Δ(p) in the probability of disease is defined by:

$$ (1{\kern-.3pt}-{\kern-.3pt}p)u(w,h){\kern-.3pt}+{\kern-.3pt}pu(w,h-m)\,=\,(1{\kern-.3pt}-{\kern-.3pt}p{\kern-.3pt}+{\kern-.3pt}{\Delta} (p))u(w{\kern-.3pt}-{\kern-.3pt}y{\kern-.3pt},h)+(p{\kern-.3pt}-{\kern-.3pt}{\Delta} ({\kern-.3pt}p{\kern-.3pt}){\kern-.3pt})u(w-y{\kern-.3pt},{\kern-.3pt}h-m{\kern-.3pt}) $$
(5)

Expressing y as a function of p by using Eq. 5 and the implicit function theorem, we obtain:

$$ \frac{dy}{dp}\,=\,\frac{\left[ u(w,h)\,-\,u(w\,-\,y,h)\right] \,-\,(1\,-\,{\Delta}^{\prime }(p)) \left[ u(w,h\,-\,m)\,-\,u(w\,-\,y,h\,-\,m)\right] }{(1\,-\,p\,+\,{\Delta} (p))u_{1}(w\,-\,y,h)\,+\,(p\,-\,{\Delta} (p))u_{1}(w\,-\,y,h\,-\,m)}\,=\,\frac{K}{EU_{2}} $$
(6)

The denominator of Eq. 6 — denoted by E U 2 — corresponds to the expected marginal utility of wealth and is therefore positive. The numerator of Eq. 6 is denoted by K. From Eq. 3, we know that \(u_{12}\gtreqless 0\Longleftrightarrow \left [ u(w,h)-u(w-y,h)\right ] \gtreqless \left [ u(w,h-m)-u(w-y,h-m)\right ] \) (see Section 2). Since Δ′(p) > 0, we thus conclude that complementarity between wealth and health (i.e. a positive sign of the cross derivative u 12) implies K > 0 and, consequently that the willingness to pay for self-protection rises with the baseline probability of disease (\(u_{12}\geq 0\Rightarrow \frac {dy}{dp}>0\)). When Δ was constant with p (Section 2), u 12 > 0 was necessary and sufficient to reach this result. Since we assume Δ′(p) > 0 in this section, an extra incentive to implement self-protection actions is provided for individuals whose baseline probability of disease is higher. Therefore, u 12 ≥ 0 is now only sufficient for the willingness to pay for self-protection to rise with the baseline probability of disease.

Let us now determine the rate at which y changes with p. To do so, we must compute:

$$ \frac{\partial \left( \frac{dy}{dp}\right) }{\partial p}=\frac{\frac{dK}{dp} EU_{2}-K\frac{dEU_{2}}{dp}}{[EU_{2}]^{2}} $$
(7)

where:

$$K>0\text{ if }u_{12}\geq 0\text{ } $$
$$\frac{dK}{dp}={\Delta}^{\prime \prime }(p)\left[ u(w,h-m)-u(w-y,h-m)\right] =0 \text{ since }{\Delta}^{\prime \prime }(p)=0 $$
$$EU_{2}>0\text{ } $$
$$\frac{dEU_{2}}{dp}=(1-{\Delta}^{\prime }(p))\left[ u_{1}(w-k,h-m)-u_{1}(w-k,h) \right] \lesseqgtr 0\text{ if }u_{12}\gtreqless 0\text{ } $$

The easiest case to consider is u 12 ≥ 0 which leads to \(\frac { \partial \left (\frac {dy}{dp}\right ) }{\partial p}>0\) via K > 0 and \(\frac { dEU_{2}}{dp}<0\). Complementarity between wealth and health (u 12 ≥ 0) thus implies that the willingness to pay for self-protection rises at an increasing rate with the baseline probability of disease. Using Jensen’s inequality, it follows that the average willingness to pay rises with personalized information in that case.

The same conclusion holds when u 12 is sufficiently negative so that K < 0. Combined with \(\frac {dEU_{2}}{dp}>0\) (which follows from u 12 < 0), this leads to \(\frac {\partial \left (\frac {dy}{dp}\right ) }{\partial p}>0\) and personalized information about the baseline probability of disease increases the average willingness to pay for self-protection. Note that this conclusion is reinforced in these two situations when Δ″(p) > 0.

Finally, when u 12 is not too negative so that K > 0, we obtain that personalized information about the baseline probability of disease lowers the average willingness to pay for self-protection. This conclusion is reinforced when Δ″(p) < 0.

3 Average willingness to pay for self-insurance

We suppose in this section that the severity of disease can be reduced (its probability remaining constant) through another prevention action (termed “self-insurance”). We use again the methodology exploited in the previous section to determine whether the average willingness to pay for this type of prevention rises or falls as individuals become informed about their baseline probability of disease.

The individual expected utility is again given by Eq. 1. The willingness to pay (denoted by z) for a given reduction Ψ in the severity of the disease is implicitly obtained from Eq. 8:

$$ (1\,-\,p)u(w,h)\,+\,pu(w,h\,-\,m)\,=\,(1\,-\,p)u(w\,-\,z,h)\,+\,pu(w\,-\,z,h\,-\,m\,+\,{\Psi} ) $$
(8)

In Eq. 8, z corresponds to the wealth variation which — when coupled with the reduction Ψ (such that Ψ > 0) in the severity of the disease — leaves individuals at the constant expected utility \(\overline {EU}\).

Using Eq. 8 and the implicit function theorem, the way z changes with p is defined as follows:

$$ \frac{dz}{dp}=\frac{\left[ u(w,h)-u(w,h-m)\right] -\left[ u(w-z,h)-u(w-z,h-m+{\Psi} )\right] }{(1-p)u_{1}(w-z,h)+pu_{1}(w-z,h-m+{\Psi} )}= \frac{F}{EU_{3}} $$
(9)

The denominator of Eq. 9 is denoted by E U 3. It corresponds to the expected marginal utility of wealth and is therefore positive. The numerator of Eq. 9 is denoted by F. Its sign depends on the comparison between two health deteriorations evaluated at two wealth levels. Specifically, the first term of F (u(w, h) − u(w, h − m)) measures the effect of reducing the health status by m when the individual’s wealth is equal to w. The second term of F (u(w − z, h) − u(w − z, h − m + Ψ)) measures the effect of a smaller reduction in health (m − Ψ) which occurs at a lower wealth level (w − z). When the effect of health losses decreases as wealth falls (i.e. when u 12 > 0), the second term of F is lower than the first: the health reduction considered is lower and it occurs at lower wealth levels, it is therefore less painful. Formally, we have:

$$F=\left[ u(w,h)-u(w,h-m)\right] -\left[ u(w-z,h)-u(w-z,h-m)\right] +{\Psi} u_{2}(w-z,\alpha )\text{ } $$

with h − m < α < h − m + Ψ.

Since u 2 > 0 and \(u_{12}\gtreqless 0\Longleftrightarrow [u(w,h)-u(w,h-m)] \gtreqless [u(w-z,h)-u (w-z,h-m)]\), we thus obtain:

$$u_{12}\geq 0\Rightarrow \frac{dz}{dp}>0 $$

Let us now determine how \(\frac {dz}{dp}\) changes with p. To do so, we compute:

$$ \frac{\partial \left( \frac{dz}{dp}\right) }{\partial p}=\frac{\frac{dF}{dp} EU_{3}-F\frac{dEU_{3}}{dp}}{[EU_{3}]^{2}} $$
(10)

where:

$$F>0\text{ if }u_{12}\geq 0\text{ } $$
$$\frac{dG}{dp}=0\text{ } $$
$$EU_{3}>0\text{ } $$
$$\frac{dEU_{3}}{dp}=u_{1}(w-z,h-m+{\Psi} )-u_{1}(w-z,h)<0\text{ if }u_{12}\geq 0 $$

From Eq. 10, it follows that u 12 ≥ 0 is a sufficient condition to have \(\frac {\partial \left (\frac {dz}{dp}\right ) }{\partial p} >0 \) via F > 0 and \(\frac {dEU_{3}}{dp}<0\). Under this condition, the willingness to pay for self-insurance increases at an increasing rate with the baseline probability of disease (z is convex in p). Using Jensen’s inequality, this implies that the willingness to pay for self-insurance based on the average information (i.e. with no genetic information) is lower than the average willingness to pay for self-insurance with genetic information. Under u 12 ≥ 0, we can thus conclude that genetic predisposition tests, by providing personal information about the baseline probability of disease, raise the benefits of self-insurance programs.

In Section 2.1, we provided an extension to the basic model developed in Section 2 by assuming that the efficiency of self-protection actions increased with the baseline probability of disease. The same kind of extension could be provided here by assuming that the efficiency of self-insurance actions increases as the severity of the disease rises (i.e.Ψ(m) with Ψ′(m) > 0). However, this would not change the result obtained. Therefore, with no loss of generality, we only suppose that the efficiency of the self-insurance action does not change with the severity of the disease.

4 Conclusion

The paper evaluates how personalized information about the baseline probability of disease — the only source of heterogeneity in our model — modifies the average willingness to pay for disease prevention actions. This issue is of particular interest as the development of predisposition genetic tests will soon generalize this kind of information. The question we deal with is thus related to the way this information should modify the relevance of disease prevention programs.

Prevention actions that either reduce the probability of disease (self-protection) or reduce the severity of the disease (self-insurance) are analyzed. We show that personalized health information about the probability of disease raises the average willingness to pay for self-protection when the efficiency of self-protection is constant and independent of the baseline probability of disease. When the efficiency of self-protection actions rises with respect to the baseline probability of disease, the same conclusion is obtained about the effect of personalized information on the average willingness to pay for self-protection as long as the marginal utility of wealth does not fall with individuals’ health status (i.e. if u 12 ≥ 0), a preference that has been empirically supported by Viscusi & Evans (1990), Sloan et al. (1998) and Finkelstein et al. (2009)Footnote 8 among others. Under the same assumption about the cross derivative of the utility function, we also show that personalized information about the baseline probability of disease increases the average willingness to pay for self-insurance.

The effect of information on the relevance of disease prevention programs has been done here under the assumption that decision makers maximize their expected utility in a context of risk. Of course, it would be interesting to develop the same type of analysis for decision makers who follow other rules of behavior such as Yaari’s dual theory of risk (1987) or rank dependent expected utility.Footnote 9 Another potential and valuable extension would be to consider decision making under ambiguity. Ambiguity is very likely to prevail in the context of medical decision making (see e.g. Berger et al. 2013 for diagnostic or treatment decisions). Besides, in a recent paper, Snow (2011) addressed the effect of information on the relevance of disease prevention programsFootnote 10 and indicated that the intensity of prevention efforts (both self-protection and self-insurance) made by (ambiguity averse) individuals is higher in the presence of ambiguity than in its absence. By removing the ambiguity surrounding the probability of diseases, predisposition tests should thus make individuals less prone to making prevention efforts. However, while Snow (2011) focuses on a pure ambiguity effect by analyzing changes in the prevention effort made by similar individuals once the uncertainty about their probability of disease is removed, we evaluate the effect of the same information on the average willingness to pay of (ambiguity neutral) individuals differing in their baseline probability of disease. Our paper thus shows that the adoption of this different (and complementary) perspective leads to a qualification of the result obtained by Snow (2011).