Rationality on the rise: Why relative risk aversion increases with stake size

Abstract

How does risk tolerance vary with stake size? This important question cannot be adequately answered if framing effects, nonlinear probability weighting, and heterogeneity of preference types are neglected. We show that the observed increase in relative risk aversion over gains cannot be captured by the curvature of the value function. Rather, it is predominantly driven by a change in probability weighting of a majority group of individuals who weight probabilities of high gains more conservatively. Contrary to gains, no coherent change in relative risk aversion is observed for losses. These results not only challenge expected utility theory, but also prospect theory.

Risk is a ubiquitous feature of social and economic life. Many of our decisions, such as what trade to learn and where to live, involve risky consequences of great importance. Often these choices entail substantial monetary costs and rewards. Therefore, risk taking behavior under high stakes is a relevant area of economic research. The effect of stake size on risk tolerance has been debated since the early days of expected utility theory as economic theory is agnostic about the existence, direction and size of stake effects. In a classical paper, Markowitz (1952) surmised that risk preferences are likely to reverse from risk seeking over very small stakes to risk aversion over high stakes.

Markowitz did not test his conjecture experimentally, but abundant evidence has accumulated by now showing that relative risk aversion indeed rises with stake size. However, due to the limits of experimental budgets, the bulk of the studies addressing stake sensitivity are either based on quite limited payoff ranges or, when substantial payoffs are involved, on hypothetical choices (Hogarth and Einhorn 1990; Bosch-Domenech and Silvestre 1999; Kuehberger et al. 1999; Weber and Chapman 2005; Astebro et al. 2009). While experiments with payoffs in the range of a few dollars may not reveal the effective degree of risk tolerance over truly high stakes, results based on hypothetical choices may not be informative, either, as the literature on incentive effects suggests. A large body of experimental evidence shows that it makes a difference whether subjects respond to decision situations with hypothetical or real monetary consequences: In general, subjects tend to be relatively more risk averse when real money is at stake (Smith and Walker 1993; Wilcox 1993; Beattie and Loomes 1997; Camerer and Hogarth 1999). A striking example is provided by Holt and Laury (2002, 2005) who find that, contrary to their results on real payoffs, subjects’ risk aversion exhibited over hypothetical lotteries does not change with increasing stake size at all. Therefore, in order to be able to address the issue of stake sensitivity in a satisfactory way, experiments with real substantial payoffs are needed.

Not surprisingly, there are only a handful of experiments with substantial monetary incentives, typically conducted in developing countries (Grisley and Kellog 1987; Wik et al. 2004). Two prominent studies in this category, both of which investigate behavior over risky gains only, are Binswanger (1981) and Kachelmeier and Shehata (1992). Binswanger reports data on subjects from rural India with stakes amounting to a month’s average income. He reaches the same conclusion as Kachelmeier and Shehata who paid up to three month’s wages in Beijing, China: Relative risk aversion over gains increases significantly when stakes are raised from low payoffs to substantial ones. In agreement with these experimental findings field data on behavior in game shows, where prizes up to a million dollars can be won, also show that contestants tend to behave more conservatively when faced with higher stakes (Bombardini and Trebbi 2005; Andersen et al. 2006b; Baltussen et al. 2008; Post et al. 2008).¹ Therefore, the empirical evidence so far seems to confirm Markowitz’s conjecture of increasing relative risk aversion.

In decision situations with clearly defined monetary outcomes and objectively given probabilities, such as in controlled experimental settings with context, framing and response mode held constant, changes in risk taking behavior should only result from a change in the evaluation of outcomes and/or probabilities. Most economists would attribute this change in relative risk aversion to the characteristics of the utility for money, and would search for suitable functional forms that are able to accommodate this behavioral pattern. Little is known about the underlying forces of the increase in relative risk aversion, however. In particular, it is not clear whether the change in risk tolerance is actually a consequence of the way people value low versus high amounts of money or whether probability weighting is sensitive to stake size.

Most previous studies focused on the overall effect of stake size on risk taking, ignoring probability weighting. In their seminal contribution, Tversky and Kahneman (1992) already suspected that probability weights might be responsive to the level of outcomes, but they questioned whether increasing the complexity of decision theory was worth the costs of such an endeavor. Some preliminary findings indeed suggest that probability weights may be stake dependent (Camerer 1991). One of the few experimental studies that explicitly addressed this possibility is Kachelmeier and Shehata (1992). They find that there is an interaction effect of stake size with probability level, namely that stake-sensitivity is greater for smaller probabilities, but their data set is not sufficiently rich to draw any conclusions on the relative contributions of outcome valuation and probability weighting to the change in risk attitudes. Etchart-Vincent (2004), on the other hand, who directly investigates the stake dependence of probability weights under hypothetical losses does not detect any clear stake effect, which may be due to hypothetical bias discussed above. To summarize, relative risk aversion over real gains increases significantly with stake size. Whether utility for money or probability weighting is the driving force behind this change has not been systematically studied so far. Moreover, evidence on losses is scarce and not conclusive.

In order to close this gap, we analyze comprehensive choice data stemming from an experiment conducted in Beijing in 2005. The experimental subjects had to take decisions over substantial real monetary stakes with maximum payoffs amounting to more than an average subject’s monthly income. In total, subjects were presented with 28 lotteries over gains and another 28 otherwise identical lotteries framed as losses in order to be able to investigate the effect of increasing stake size on relative risk aversion in both decision domains. To disentangle the effects of stake size on the valuation of monetary outcomes and probability weighting, we estimated the parameters of a flexible sign- and rank-dependent decision model, which nests expected utility theory as a special case. Furthermore, as average estimates may gloss over potentially important differences in individual behavior we account for the existence of heterogeneous preference types. We estimated a finite mixture regression model, which assigns each individual to one of several distinct behavioral types and provides type-specific parameter estimates for the underlying decision model (El-Gamal and Grether 1995; Stahl and Wilson 1995; Houser et al. 2004). Its ability to parsimoniously characterize distinct behavioral types is probably the most attractive feature of finite mixture models.

The following results emerge from our analysis. First, at the level of observed behavior, we find a strong and significant difference between subjects’ evaluations of risky gains and losses. Whereas observed certainty equivalents over gains exhibit significantly increasing relative risk aversion, there is no coherent stake-dependent pattern in subjects’ behavior over the same lotteries presented as losses, implying a significant framing effect.

Second, model estimates show that, contrary to many economists’ expectations, value function parameters remain stable over increased stakes in both decision domains, implying that the observed increase in average relative risk aversion over gains cannot be explained by changing attitudes towards monetary outcomes. Rather, it can be predominantly attributed to a change in probability weighting. The probability weighting function for high gains is characterized by substantially lower probability weights over a wide range of probabilities than the respective function for low stakes, entailing less optimistic lottery evaluation and, thus, greater relative risk aversion at high stakes. This change is particularly pronounced for smaller probabilities for which the average decision maker tends to be risk seeking, corroborating the findings by Kachelmeier and Shehata (1992). In the loss domain, however, no such change in probability weights can be inferred from the estimates, consistent with the observed pattern of behavior.

Third, a model allowing for heterogeneity of preference types is clearly preferable to a representative-agent model. We find two distinct behavioral groups: The majority of about 73% of the subjects exhibit an inverted S-shaped probability weighting curve, whereas the minority can essentially be characterized as expected value maximizers. Furthermore, we show that the observed increase in average relative risk aversion over gains can exclusively be attributed to a change in behavior by the majority group of decision makers, who evaluate high-stake prospects more cautiously by putting lower weights on stated gain probabilities. In contrast, the minority type’s behavior is not affected by rising stakes at all.

Our results entail material consequences for decision theory as well as applied economics. The first two findings, the framing effect as well as the probability weighting function as carrier of changing risk attitudes, effectively rule out expected utility theory as a candidate for explaining increasing relative risk aversion. Since it is the probability weights that are responsible for the change in relative risk aversion, more flexible utility functions cannot adequately solve the problem of modeling increasing risk aversion. While the observed differences between the evaluation of gains and losses, in principle, lends support to sign-dependent decision models, such as prospect theory, stake dependence of probability weights, however, calls theories based on stake-invariant probability weights into question.

The third finding poses a challenge to type-independent models of choice under risk, which might be prone to aggregation bias. We show that the vast heterogeneity in individual risk taking behavior, typically found in choice data (Hey and Orme 1994; Gonzalez and Wu 1999; Cohen and Einav 2007), is substantive in the sense that a single preference model is unable to adequately describe behavior. If maximization of expected utility is accepted as normative standard of rational behavior the majority of the individuals clearly deviate from rationality. The heterogeneity of preference types may render policy recommendations based on average parameter estimates inappropriate when strategic interactions among market participants play a role. As the literature on individual irrationality and aggregate outcomes has shown (Haltiwanger and Waldman 1985, 1989; Fehr and Tyran 2005, 2008; Camerer and Fehr 2006), the mix of behavioral types may be crucial for the market outcome and, depending on the nature of the strategic interdependence, the behavior of even a minority of players may be decisive for the aggregate outcome. Furthermore, regulatory policy should be designed in such a way that it creates large benefits for those who make errors, while imposing little or no harm on those who are fully rational (Camerer et al. 2003). Obviously, total net benefits of a regulatory policy measure depend not only on the costs for the rational citizens and the benefits for the irrational ones, but also on the relative numbers of rational and irrational types in the population. Therefore, knowing the mix of behavioral types is important for designing cost efficient programs and regulations.

To the best of our knowledge, this is the first study that provides a systematic examination of stake effects on probability weights for real substantial payoffs. Neither are we aware of any other study that examines the relevance of framing and type heterogeneity for the impact of stakes on risk tolerance.

The remainder of the paper is structured as follows. Section 1 describes the experimental design and procedures. The decision model applied to the experimental data as well as the finite mixture regression model are presented in Section 2. The results of the estimation procedure are discussed in Section 3. Section 4 concludes the paper.

1 Experiment

In the following section, the experimental setup and procedures are described. The experiment took place in Beijing in November 2005. The subjects were recruited by flier distributed at the campuses of Peking University and Tsinhua University. Interested people had to register by email for one of two sessions conducted on the same day. Subjects were selected to guarantee a balanced distribution of genders and fields of study. In total, 153 subjects’ responses were analyzed.

The experiment served to elicit certainty equivalents for 56 two-outcome lotteries over a wide range of outcomes and probabilities.² Twenty-eight lotteries offered low-stake outcomes between 4 and 55 Chinese Yuan (CHN) with an expected payoff of about 16 CHN, approximately equal to the going hourly wage rate. Another 28 lotteries entailed high-stake outcomes from 65 to 950 CHN. Overall, payoffs spanned the range of 0.25 to approximately 60 hourly wages.³ The high-stake lotteries were constructed from the low-stake ones by inflating the outcomes by approximately the same factor such that reasonable integer numbers were obtained and the highest obtainable payoff amounted to a student’s monthly allowance, amounting to less than 1,000 CHN for the majority of students. Average total earnings per subject summed to approximately 323 CHN, including a show up fee of 20 CHN. Monetary incentives were substantial given the subjects’ average monthly disposable income of about 700 CHN.

Probabilities of the lotteries’ higher gain or loss varied from 5% to 95%. One half of the lotteries were framed as choices between risky and certain gains (“gain domain”); the same 28 decisions were also presented as choices between risky and certain losses (“loss domain”). For each lottery in the loss domain, subjects were provided with a specific endowment which served to cover their potential losses. These initial endowments rendered the expected payoff for each loss lottery equal to the expected payoff of an equivalent gain lottery. The set of gain lotteries is presented in Table 1.

Table 1 Gain lotteries (x ₁, p; x ₂)

Subjects were entitled to one random draw from their low-stake decisions and one random draw from their high-stake decisions. In order to preclude order effects, low-stake and high-stake lotteries were intermixed and appeared in random order in a booklet containing the decision sheets.

For each lottery, a decision sheet, such as presented in Fig. 1, contained the specifics of the lottery and a list of 20 equally spaced certain outcomes ranging from the lottery’s maximum payoff to the lottery’s minimum payoff. Subjects had to indicate whether they preferred the lottery or the certain payoff for each row of the decision sheet. The lottery’s certainty equivalent was then calculated as the arithmetic mean of the smallest certain amount preferred to the lottery and the subsequent certain amount on the list. For example, if a subject’s preferences corresponded to the small circles in Fig. 1, her certainty equivalent would amount to 13.5 CHN. This elicitation procedure has been widely used in the experimental literature (Tversky and Kahneman 1992). We chose this method because it is transparent, easy to understand and well suited for a paper-and-pencil experiment.⁴

Fig. 1

Design of the decision sheet

Before subjects were permitted to start working on the experimental decisions, they were presented with two hypothetical choices to become familiar with the procedure. Subjects could work at their own speed. The vast majority of them needed considerably less than 90 min to complete the experiment. After completion of the experimental tasks and a complementary socioeconomic questionnaire one of each subject’s low-stake as well as high-stake choices were randomly selected for payment. Subjects executed the random draws themselves and were paid in private afterwards.

2 Econometric model

This section discusses the specification of the econometric model, which is based on several building blocks: first, the basic decision model; second, the specification of stake dependence; third, assumptions on the error term; and finally, a finite mixture regression approach which accounts for heterogeneity in behavior. At the end of this section we also briefly discuss some of the issues typically encountered when estimating finite mixture regression models.

2.1 The basic decision model

The basic model of decision under risk should be able to accommodate a wide range of different behaviors. Sign- and rank-dependent models, such as cumulative prospect theory (CPT), capture robust empirical phenomena such as nonlinear probability weighting and loss aversion (Starmer 2000). Therefore, the flexible approach of CPT, lends itself to describing risk taking behavior. According to CPT, an individual values any binary lottery $\mathcal{G}_g=(x_{1g},p_g;x_{2g}), \ g \in \{1, \ldots, G\}$, where |x _1g | > |x _2g | , by

$$ v\left( \mathcal{G}_g \right)= v\left(x_{1g}\right) w\left(p_g\right) + v\left(x_{2g}\right)\left(1-w\left(p_g\right)\right) . $$

(1)

The function v(x) describes how monetary outcomes x are valued, whereas the function w(p) assigns a subjective weight to every outcome probability p. The lottery’s certainty equivalent $\hat{ce}_g$ can then be written as

$$ \hat{ce}_{g}= v^{-1}\left[ v\left(x_{1g}\right) w\left(p_g\right) + v\left(x_{2g}\right)\left(1-w\left(p_g\right)\right) \right] . $$

(2)

In order to make CPT operational we have to assume specific functional forms for the value function v(x) and the probability weighting function w(p). A natural candidate for v(x) is a sign-dependent power function

$$ v(x)= \left\{ \begin{array}{l@{{\kern6pt}}l} x^\alpha & \mbox{if } x \geq 0 \\ -(-x)^\beta & \mbox{otherwise,} \end{array} \right. $$

(3)

which can be conveniently interpreted and which has also turned out to be the best compromise between parsimony and goodness of fit in the context of prospect theory (Stott 2006). For this specification of the value function, a separate parameter of loss aversion, i.e. capturing that “losses loom larger than corresponding gains”, is not identifiable in our data.⁵ As Koebberling and Wakker (2005) point out, loss aversion should be interpreted as the difference between risk aversion with respect to mixed gambles, encompassing both gains and losses, and nonmixed gambles, confined to single-domain outcomes. Our lottery design comprises nonmixed gambles only and, therefore, the concept of loss aversion in this interpretation cannot be applied to our analysis.

A variety of functions for modeling probability weights w(p) have been proposed in the literature (Quiggin 1982; Tversky and Kahneman 1992; Prelec 1998). We use the linear-in-log-odds function⁶ introduced by Goldstein and Einhorn (1987) and applied by Lattimore et al. (1992):

$$ w(p) = \frac{\delta p^\gamma}{\delta p^\gamma+(1-p)^\gamma} , \ \delta \geq 0, \ \gamma \geq 0. $$

(4)

We favor this specification because it has proven to account well for individual heterogeneity (Wu et al. 2004)⁷ and its parameters have an intuitively appealing interpretation: The parameter γ largely governs the slope of the curve, whereas the parameter δ largely governs its elevation. The smaller the value of γ, the more strongly S-shaped is the curve. Thus, this parameter can be interpreted as a measure of departure from rationality if linear weighting is considered to be the standard for rationality. The parameter δ can be viewed as indicator of optimism: The larger the value of δ, the more elevated is the curve, ceteris paribus, i.e. the higher is the weight put on any probability. Linear weighting is characterized by γ = δ = 1. In a sign-dependent model, the parameters may take on different values for gains and for losses, yielding a total of six behavioral parameters to be estimated.

2.2 Stake dependence

In order to address our focal question of stake-size effects, we introduce a dummy variable HIGH into the basic decision model, such that HIGH = 1 if the lottery under consideration contains high-stake payoffs amounting to 65 CHN or more, and HIGH = 0 otherwise. Each one of the behavioral model parameters ω ∈ {α, β, γ′, δ′}, with γ′ and δ′ comprising the domain-specific parameters for the slope and the elevation of the probability weighting functions, is assumed to depend linearly on HIGH in the following fashion:

$$ \omega=\omega_0+\omega_{\rm HIGH} \times {\rm HIGH}, $$

(5)

with ω ₀ representing the respective low-stake parameter. This step adds another six behavioral parameters to the set of model parameters.

If relative risk aversion indeed changes with stake size, at least one of the coefficients of the high-stake dummy HIGH should turn out to be significantly different from zero. If the estimates of α _HIGH or β _HIGH were significant, the present model would be mis-specified, as the power function, used for estimation, cannot account for changing relative risk aversion. In this case, an alternative specification of the value function that can accommodate changing relative risk aversion would be called for. In particular, if the valuation of monetary outcomes is the driving force behind the observed change in risk tolerance over gains, α _HIGH should be negative, material in size and statistically significant.

2.3 Error specification

In the course of the experiment, risk taking behavior of individual i ∈ {1,...,N} was measured by her certainty equivalents ce _ig for a set of different lotteries $\mathcal{G}$. Since the behavioral model explains deterministic choice, an individual’s actual certainty equivalents ce _ig are bound to deviate from the predicted certainty equivalents $\hat{ce}_{g}$ by an error ε _ig , i.e. $ce_{ig}=\hat{ce}_{g}+\epsilon_{ig}$. There may be different sources of error, such as carelessness, hurry or inattentiveness, resulting in accidentally wrong answers (Hey and Orme 1994). The Central Limit Theorem supports our assumption that errors are normally distributed and simply add white noise.

Furthermore, we allow for three different sources of heteroskedasticity in the error variance. First, for each lottery subjects have to consider 20 certain outcomes, which are equally spaced throughout the lottery’s outcome range |x _1g  − x _2g |. Since the observed certainty equivalent ce _ig is calculated as the arithmetic mean of the smallest certain amount preferred to the lottery and the subsequent certain amount, the error is proportional to the outcome range, which has to be taken account of by the estimation procedure.

Second, since our approach models a representative agent’s behavior, an individual’s choices will most likely depart from the average prediction. As subjects may be heterogeneous with respect to their previous knowledge, their ability of finding the correct certainty equivalent as well as their attention span, we expect the error variance to differ by individual. Rather than imposing additional assumptions on the error distribution⁸ we estimate the standard deviations of the individual errors σ _ig directly by

$$ \sigma_{ig}=\xi_{i} \left|x_{1g}-x_{2g}\right|, $$

(6)

where ξ _i is an individual-specific parameter. As expected, ξ _i  = ξ is rejected by a likelihood ratio test with a p-value close to zero, favoring specification of individual errors.

Third, lotteries in the gain domain may be evaluated differently from the ones in the loss domain.⁹ Therefore, we additionally allow for domain-specific variance in the error term. Our assumption is justified by a likelihood ratio test which rejects that ξ _i are the same for gains and losses. These considerations imply that we control for all three types of heteroskedasticity in the estimation procedure, which adds two more parameters per individual, i.e. 153 parameters for gains and 153 parameters for losses, to the econometric model.

2.4 Accounting for heterogeneity

A suitable estimation procedure, such as maximum likelihood, yields estimates for the average values of the behavioral parameters θ = (α′,β′,γ′,δ′)′. If there is heterogeneity of a substantive kind, i.e. if there are several distinct data generating processes, a representative-agent model may be inferior to a model allowing for distinct types. For this reason, we estimate a finite mixture model which accounts for heterogeneity in a parsimonious way. The basic idea of the mixture model is assigning an individual’s risk-taking choices to one of C different types of behavior, each characterized by a distinct vector of parameters θ _c  = (α _c ′,β _c ′,γ _c ′,δ _c ′)′, c ∈ {1,...,C}. The estimation procedure yields estimates of the relative sizes of the different groups π _c , as well as the group-specific parameters θ _c of the underlying behavioral model.

In this paper we define groups across decision domains, i.e. each individual is classified on the basis of all of her choices over both gains and losses. In principle, one could analyze behavior over gains separately from behavior over losses. However, as we show in Appendix A, such an approach is inferior to an overall classification. Therefore, we define behavioral groups in a domain-independent way and estimate π _c jointly for gains and losses.¹⁰

Given our assumptions on the distribution of the error term, the density of type c for the i-th individual can be expressed as

$$ f\big(ce_i, \mathcal{G}; \theta_c, \xi_i \big)= \prod_{g=1}^{G}{ \frac{1}{\sigma_{ig}} \, \phi\left( \frac{ce_{ig}-\hat{ce}_{g}\big(\mathcal{G}_g;\theta_c\big)}{\sigma_{ig}} \right),} $$

(7)

where ϕ(·) denotes the density of the standard normal distribution and ξ _i accounts for individual-specific heteroskedasticity. Since we do not know a priori which group a certain individual belongs to, the relative group sizes π _c are interpreted as probabilities of group membership. Therefore, each individual density of type c has to be weighted by its respective mixing proportion π _c , which is unknown and has to be estimated as well. Taking the sum over the weighted type-specific densities yields the individual’s contribution to the model’s likelihood function $L(\Psi;ce, \mathcal{G})$. The log likelihood of the finite mixture regression model is then given by

$$ \label{equ:finmix} \ln {L} \left(\Psi; ce, \mathcal{G} \right) = \sum_{i=1}^{N}{ \ln \sum_{c=1}^{C}{\pi_c \, f\big(ce_i, \mathcal{G}; \theta_c, \xi_i\big)} }, $$

(8)

where the vector Ψ = (θ′₁,...,θ′ _C ,π ₁,..., π _C − 1, ξ ₁′,...,ξ _N ′)′ summarizes the parameters to be estimated.

2.5 Estimation

In order to deal with the issues of non-linearity and multiple local maxima encountered when maximizing the likelihood of a finite mixture regression model (McLachlan and Peel 2000), the iterative Expectation Maximization (EM) algorithm is the method of choice here (Dempster et al. 1977). This algorithm also provides an additional feature: It calculates, by Bayesian updating in each iteration, an individual’s posterior probability τ _ic of belonging to group c, given the fit of the model. These posterior probabilities τ _ic represent a particularly valuable result of the estimation procedure. Not only does the procedure endogenously assign each individual to a specific group, but it also supplies us with a method of judging classification quality. The τ _ic can be used to calculate a summary measure of ambiguity, such as the Normalized Entropy Criterion NEC (Celeux 1996), in order to gauge the extent of dubious assignments. If all the τ _ic of the final iteration are either close to zero or one, all the individuals are unambiguously assigned to one specific group and a low measure of entropy is observed.

Furthermore, entropy measures provide an additional criterion to discriminate between models with differing numbers of types. Since the finite mixture regression model is defined over a pre-specified number of groups, a criterion for assessing the correct number of groups is called for. Classical criteria, such as the Akaike Information Criterion AIC or the Bayesian Information Criterion BIC, trade off model parsimony against goodness of fit, but do not measure the ability of the mixture to provide well separated and nonoverlapping components, which, ultimately is the objective of estimating mixture models (Celeux 1996).

Various problems may be encountered when maximizing the likelihood function of a finite mixture regression model and, therefore, a customized estimation procedure has to be used, which can adequately deal with these problems. Details of the estimation procedure are discussed in Appendix C (see also Bruhin et al. 2007).

3 Results

In the following sections we investigate the stake-size sensitivity of observed risk taking behavior and present the estimates of the decision model assuming one homogeneous type of preferences. Furthermore, we show that substantive heterogeneity is present in our data and discuss the quality of the classification procedure as well as the number of distinct behavioral types identified in the data. Finally, we characterize these different types by their average behavioral parameters and discuss the effect of stake size on each group’s behavior.

3.1 Aggregate behavior

Result 1

On average, observed behavior exhibits the fourfold pattern of risk attitudes, predicted by prospect theory, for both low-stake and high-stake outcomes. Stake-specific behavior is subject to a strong framing effect, however: When gains are at stake, relative risk aversion increases with stake size at almost all levels of probability. In the loss domain no such clear picture emerges.

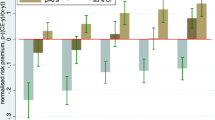
Support  In Fig. 2, observed risk taking behavior is summarized by the median relative risk premia RRP = (ev − ce)/|ev|, where ev denotes the expected value of a lottery’s payoff and ce stands for its certainty equivalent. RRP > 0 indicates risk aversion, RRP < 0 risk seeking, and RRP = 0 risk neutrality. The light gray bars in Fig. 2 represent the observed median RRP for low-stake lotteries, the dark gray ones represent the respective high-stake median RRP. The median relative risk premia RRP, sorted by the probability p of the higher gain or loss, show a systematic relationship with p. For both low stakes and high stakes, subjects’ choices display a fourfold pattern (Tversky and Kahneman 1992), i.e. they are risk averse for low-probability losses and high-probability gains, and they are risk seeking for low-probability gains and high-probability losses. Therefore, at first glance, average behavior is adequately described by a model such as CPT.

Fig. 2

Median relative risk premia by stake size

What the bar plots also reveal is that median relative risk premia differ substantially by stake level: When subjects’ preferences exhibit increasing relative risk aversion, we should observe different low-stake and high-stake RRP, namely, high-stake choices should be relatively less risk tolerant than low-stake choices. Inspection of Fig. 2 confirms that, in the gain domain, median high-stake choices are considerably less risk seeking for small probabilities and somewhat more risk averse for large probabilities than their median low-stake counterparts. For losses, the evidence is not so clear-cut, however. At some levels of probability, low-stake median RRP display relatively higher risk aversion than high-stake RRP, and at some other levels the reverse is true.

In order to judge whether the distributions of the stake-dependent RRP are significantly different from each other, we performed a series of Wilcoxon signed-rank tests for each level of probability, which yield the following results at the conventional level of significance of 5%: With the exception of the probability of 95%, all the low-stake RRP over gains are significantly smaller than the high-stake ones. We therefore conclude that there is a significant stake effect in the data on choices over gains: On average, people are relatively more risk averse for high gains than for low gains.

In the loss domain, no consistent picture emerges: Low-stake RRP are significantly smaller at three levels of probability (p ∈ { 0.10, 0.75, 0.95 }), significantly larger at one level (p = 0.05), and insignificantly different at the remaining three levels of probability (p ∈ { 0.25, 0.50, 0.90 }). Therefore, we conclude that there is no obvious systematic relationship between stake-size effect and level of probability for loss lotteries.

Our data show behavior consistent with nonlinear probability weighting, but also a substantial framing effect. Relative risk aversion increases with stake size, albeit only for gains. When subjects evaluate the same lotteries framed as losses rather than as gains, their relative risk aversion does not systematically increase. In fact, no coherent pattern of stake-dependent behavior under losses emerges. This sensitivity to framing, already visible at the level of observed behavior, clearly excludes expected utility theory from the list of eligible models for describing average risk taking behavior.

We now turn to one of our major concerns, namely, whether the change in relative risk aversion over gains can be attributed to a specific component of lottery evaluation.

Result 2

In the aggregate model, the estimated curvatures of the value functions do not significantly change with rising stakes.

Support  Table 2 contains the parameter estimates for the decision model discussed in Section 2. For the time being, we focus on the average parameter estimates displayed in columns (1) and (4), labeled “Pooled”. The curvature parameters of the value functions over low stakes are denoted by α₀ for gains and β₀ for losses.¹¹α_HIGH and β_HIGH represent the corresponding estimated coefficients of the high-stake dummy HIGH, measuring the change in curvature brought about by increased stake levels. For both domains, the estimates for α_HIGH and β_HIGH are small in size, and the bootstrapped standard errors, reported in parentheses below the respective point estimates, indicate that the coefficients are not significantly different from zero. Furthermore, when a restricted model with stake-invariant curvature parameters is estimated, the likelihood ratio test of the restricted model against the unrestricted one renders a p-value of 0.911. This test result implies that the hypothesis of equal curvatures over both ranges of outcomes cannot be rejected.

Table 2 Classification of behavior: overall behavioral types

If the valuation of monetary outcomes were the carrier of increasing relative risk aversion over gains, the estimates of α _HIGH would have to be negative, statistically significant and, presumably, quite sizable, since the specification of the value function as a power function can only accommodate constant relative risk aversion. As the estimation results show, however, this is not the case. Therefore, we conclude that changing attitudes towards monetary outcomes are not responsible for the observed increase in relative risk aversion. This finding also holds for alternative specifications of the value function that are sufficiently flexible to capture changing relative risk aversion, such as the expo-power function introduced by Saha (1993).

As the curvature of the value function is robust to stake size, the observed increase in relative risk aversion over gains has to be driven by the other component of lottery evaluation, probability weighting, as the next result confirms.

Result 3

At the aggregate, high-gain probability weights deviate significantly from low-gain probability weights. No substantial difference in stake-dependent probability weights results for losses.

Support  We first discuss our findings for the gain domain. A first indication of the stake sensitivity of probability weights for gains can already be found in the bar plots in Fig. 2. The differences in the observed stake-dependent RRP decrease markedly with increasing probability level, suggesting a substantial interaction effect.¹²

Inspection of column (1) of Table 2 confirms that the estimated change in the elevation of the curve, measured by δ _HIGH, is significantly negative and substantial in size, implying a major decrease in elevation from 1.304 to 0.913. Moreover, the change in the slope of the probability weighting function γ _HIGH is significantly positive (0.056), implying a slightly less strongly S-shaped curve for high stakes. The impact of these parameter changes on the shape of the probability weighting function can be examined in Fig. 3. The top panel of the figure shows, for each decision domain, the estimated probability weighting curves for low stakes, defined by HIGH = 0, plotted against the high-stake curves, defined by HIGH = 1. Evidently, the high-gain function is less elevated and slightly less strongly curved than the low-gain function, indicating a substantial decrease in probability weights.

Fig. 3

Average probability weights by stake size. Dashed lines: 95%-confidence bands based on the percentile bootstrap method

However, significant changes in single parameter estimates do not tell the whole story. Since the probability weights are a nonlinear combination of two parameters, inference needs to be based on γ and δ jointly. Therefore, the percentile bootstrap method (using 2,000 replications) was employed to construct the 95%-confidence bands for the difference in the low-stake and the high-stake probability weighting curves. In order to judge the overall effect of rising stakes on the shape of the probability weighting function, we inspect the bottom panel of Fig. 3, depicting the confidence bands for the stake-dependent differences in probability weights. Whenever a confidence band includes the zero line, the hypothesis of stake-invariant probability weights cannot be rejected. The graph on the left hand side for the gain domain, however, shows that the difference between low-gain probability weights and high-gain probability weights is indeed statistically significant over nearly the whole range of probabilities, mirroring our findings on the observed RRP. Therefore, we have conclusive evidence that the high-gain probability weighting curve departs significantly and substantially from the low-gain curve.

In the domain of losses, a totally different picture emerges. The top panel of Fig. 3 depicts practically overlapping low-loss and high-loss probability weighting curves. The high-loss curve is slightly less strongly S-shaped, which is also reflected in the significant parameter estimate for γ _HIGH in column (4) of Table 2, amounting to 0.045. However, this immaterial difference in the stake-dependent slope parameters does not imply a significant difference in the overall shape of the curves: The bottom panel of Fig. 3 shows that the 95%-confidence band for the difference in the stake-dependent probability weighting curves over losses includes the zero line practically for all levels of probability. This finding implies that, in choices framed as losses, stake effects are negligible, in line with the lack of any stake-dependent pattern diagnosed in the observed RRP.

Our findings demonstrate that probability weights are the carrier of changing risk tolerance observed in the domain of gains, and suggest that prospect theory, and for that matter many other decision theories which postulate stake-independent probability weighting, cannot adequately deal with risk taking choices involving major changes in stake levels.

3.2 Heterogeneous types of behavior

In the previous section we have only considered the evidence for the average decision maker. If there is heterogeneity in the population, in the sense that a single preference theory cannot adequately capture behavior, the parameter estimates of the pooled model may be misleading. For this reason, the analysis is extended to account for latent heterogeneity by estimating a finite mixture regression model.

So far we have not addressed the issue whether a finite mixture regression model is actually to be preferred over a single-component model in the first place, and what the number of groups C in the mixture model should be. In order to deal with these questions the researcher needs a criterion for assessing the correct number of mixture components. The literature on model selection in the context of mixture models is quite controversial, however, and there is no best solution.¹³ For this reason, rather than relying on a single measure, we examine several criteria with differing characteristics to get a handle on the problem of model selection: the AIC, the BIC as well as the NEC. According to these criteria, the model which minimizes the respective criterion value should be preferred.

Example 4

There is substantive heterogeneity in individual risk preferences rendering the aggregate model inferior to a mixture of two distinct types of behavior.

Support  We calculated AIC, BIC and NEC for three different model sizes, C ∈ {1,2,3 }, presented in Table 3.

Table 3 Model selection criteria

AIC and BIC are highest at C = 1, thus C > 1 is clearly favored over C = 1. As the NEC criterion is not defined for C = 1, Biernacki et al. (1999) argue in favor of a multi-component model if there is a C > 1 with NEC(C) ≤ 1, which clearly is the case here. Given the unanimous recommendation by all three criteria we conclude that a finite mixture model is superior to a representative-agent model.

With regard to the choice between C = 2 and C = 3, the three-group classification seems to be favored by the classical criteria but not by NEC. From the point of view of entropy two groups are sufficient to characterize behavior. As entropy is generally extremely low for both the two-group and three-group classifications, both models seem quite sensible. However, it can be shown that for C = 3 the majority type gets divided into two different subtypes exhibiting qualitatively similar parameter estimates whereas the minority type, which is quite distinct, remains stable in size as well as group membership.¹⁴ As the three-group classification does not offer additional material insights, we limit our discussion to C = 2.

The low value of NEC in our analysis indicates that nearly all the individuals can be unambiguously assigned to one of the two types. This clean segregation can also be inferred from the distributions of the posterior probabilities of group assignment in Fig. 4: τ _EUT denotes the posterior probability of belonging to the first group, which can be characterized, as we will demonstrate below, as expected utility maximizers (“EUT types”): The individuals’ posterior probabilities of being an expected utility maximizer are either close to one or close to zero for practically all the individuals. The histogram also shows that the EUT group encompasses a minority of the decision makers, whereas the other group represents a majority of approximately 73% of the subjects.

Fig. 4

Clean segregation

The subsequent group of results addresses the focal questions: How can these two different types be characterized? And in which way do they react to rising stake levels?

3.2.1 Minority behavior

Result 5

The minority type, constituting about 27% of the subjects, can essentially be characterized as expected value maximizers over both low- and high-outcome ranges.

Support  The estimates of the behavioral parameters for the minority type are displayed in columns (2) and (5) of Table 2. The relative group size of the minority type is estimated to be 0.266, matching the size of the corresponding bar in the histogram of Fig. 4.

In order to be able to characterize decisions as consistent with expected value maximization, both the value functions and the probability weighting functions are required to be linear. Turning to outcome valuation, we observe that α ₀ and β ₀ are not statistically distinguishable from one, as the standard errors reveal. Furthermore, the coefficients of the high-stake dummy are not significantly different from zero, indicating the robustness of the value function curvatures to increasing stake size. Therefore, we conclude that the value functions over both gains and losses are essentially linear and unresponsive to stake size.

Linearity of the second model component, probability weighting, holds if the parameter estimates for both γ and δ are equal to one. The low-stake parameter estimates for δ ₀ in columns (2) and (5) are not distinguishable from one, but the respective ones for γ ₀ are. However, inspection of the probability weighting curves in Fig. 5 confirms that departures from linear probability weighting are insubstantial. Furthermore, for both gains and losses, no stake-size effect is visible in slope or elevation of the probability weighting curves, as both γ _HIGH and δ _HIGH are insignificantly different from zero, and the 95%-confidence bands for the difference in the stake-dependent probability weighting curves include the zero line, as confirmed by the bottom panel of Fig. 5. These findings suggest that the minority type of decision makers behaves essentially as expected value maximizers, and therefore consistently with EUT. These conclusions, based on the estimation results, also bear out at the level of observed behavior. The EUT types’ median relative risk premia in the bottom panel of Fig. 6 are close to zero, indicating near risk neutrality for both low stakes and high stakes.

Fig. 5

Probability weights by stake size: EUT types. Dashed lines: 95%-confidence bands based on the percentile bootstrap method

Fig. 6

Type-specific median relative risk premia by stake size

Obviously, the minority’s behavior is robust over the whole outcome range and can, therefore, not account for increasing relative risk aversion observed in the aggregate data. As the next result shows, the second group of individuals, constituting approximately 73% of the subjects, exhibit a completely different set of behavioral parameter values.

3.2.2 Majority behavior

Result 6

The majority group’s behavior is characterized by nonlinear probability weighting. Whereas value function parameters remain stable over the whole outcome range in both decision domains, probability weights for gains do not. The low-gain probability weighting curve is characterized by significantly more optimistic weighting of probabilities than the high-gain curve. No such effect is present in the probability weighting curves for losses, however.

Support  The majority group, labeled “Non-EUT”, consists of about 73% of the individuals. As in the pooled model, value function parameter estimates of α_HIGH and β_HIGH are not significantly different from zero, as can be seen in columns (3) and (6) in Table 2. Again, the observed change in relative risk aversion over gains cannot be attributed to the valuation of monetary outcomes.

In order to examine the stake-specific probability weighting curves for the majority group we inspect the top panel of Fig. 7. Our findings on the majority group’s curves reflect the same patterns of stake sensitivity as the pooled ones do: For both gains and losses the curves are inverted S-shaped, and there is a major domain-specific difference. In the loss domain the stake-specific curves practically coincide, and their difference is not statistically significant, as the left hand side of the bottom panel of Fig. 7 confirms. In the gain domain, however, we find the high-stake probability weighting curve to be substantially less elevated than the low-stake one. This change is brought about by the significant stake sensitivity of the elevation parameter over gains, reflected by the estimate for δ _HIGH, − 0.344 (see column (3) in Table 2). The high-gain probability weighting function is also slightly less curved than the low-gain one, as γ _HIGH is estimated to be 0.058.

Fig. 7

Probability weights by stake size: non-EUT types. Dashed lines: 95%-confidence bands based on the percentile bootstrap method

The joint impact of these parameter changes is statistically significant, as the right hand side of the bottom panel of Fig. 7 shows. Therefore, we conclude that increasing relative risk aversion over gains is mainly attributable to the Non-EUT types’ behavior who weight high-gain probabilities significantly and substantially less optimistically than low-gain ones. These effects can also be traced back in the pattern of observed choices: The top panel of Fig. 7 displays a substantial stake-dependent difference, particularly over smaller probabilities, in the Non-EUT types’ median RRP, which is much more pronounced than the respective difference in the pooled data, shown in Fig. 2.

The results of the finite mixture regression demonstrate that there is substantive heterogeneity in risk taking behavior, which may be glossed over when focusing on a single-preference model. Only one distinct group of individuals is prone to changing risk tolerance when stakes are increased. These Non-EUT types tend to evaluate low-gain prospects significantly more optimistically than high-gain prospects. Thus, prospect theory, even though designed to explain non-EUT behavior, cannot account for this change in relative risk aversion.

4 Discussion and conclusions

This paper pursues three goals. First, it studies the effect of substantial real payoffs, framed as gains and losses, on risk taking. Second, the paper analyzes the influence of rising stakes on the components of lottery evaluation, i.e. on the value and probability weighting functions. Third, it examines heterogeneity in risk taking behavior over varying stake levels. With regard to the first objective, we find a significant and sizable increase in relative risk aversion when gains are scaled up. In the domain of losses, however, no such clear effect is present in the data. We can only speculate on the potential reasons for this finding. One possible explanation is the use of different rules and heuristics when losses are at stake. This interpretation is supported by the empirical regularity that probability weights for gains differ systematically from probability weights for losses (Abdellaoui 2000; Bruhin et al. 2007). Another possibility is the hypothetical nature of the losses in our experiment. Here, losses are effectively gains and only appear as losses due to the framing of the decisions. Such an interpretation is consistent with the absence of a clear stake effect for purely hypothetical losses in Etchart-Vincent (2004). In any case, as subjects evaluate lotteries differently depending on the lotteries being framed as gains or as losses, expected utility theory is effectively ruled out as a valid description of behavior.

Concerning the second objective, we presented evidence that the increase in relative risk aversion over gains can be mainly attributed to a move of the average probability weighting function towards less optimistic weighting, whereas attitudes toward monetary payoffs remain essentially stable. That probability weights are the carrier of changing risk attitudes raises the question of the driving force behind this change. Unfortunately, little is known empirically about potential determinants of probability weights. However, evidence is accumulating that probability weights are systematically affected by specific characteristics of the decision situation. Not only do they vary with stake size but they are also sensitive to the delay of uncertainty resolution: Abdellaoui et al. (2009) find that departure of the probability weighting function from linearity decreases with the delay of uncertainty resolution, resulting in an increase in risk tolerance over time (see also Noussair and Wu 2006).¹⁵

Recent generalizations of expected utility theory invoking emotions as rationale for probability weighting may offer a starting point for explaining the malleability of probability weights (Bell 1985; Gul 1991; Loomes and Sugden 1986; Wu 1999). Walther (2003), for instance, shows that an inverse S-shaped probability weighting function emerges endogenously from utility maximization when a decision maker’s utility depends not only on monetary payoffs but also on elation and disappointment anticipated to materialize at uncertainty resolution. In particular, over- and underweighting of probabilities is driven by the balance of elation proneness and disappointment aversion: The stronger is disappointment aversion relative to elation proneness, the broader will be the range of pessimistically weighted gain probabilities and vice versa.

Such an affect-based approach may provide a unifying explanation for the observed stake and delay dependence of probability weights if relative disappointment aversion significantly interacts with the context of the decision situation.¹⁶ In the case of stake dependence, it seems plausible that, when stakes increase substantially, anticipated feelings of disappointment get stronger relative to the elation one expects to feel when an advantageous low-probability event materializes. This effect would shift the probability weighting curve downwards and induce relatively higher risk aversion. With regard to uncertainty resolution the vividness of anticipated emotions might generally be lower for delayed lotteries than for immediately resolved ones, which would result in the probability weighting curve getting less strongly S-shaped.¹⁷ To our knowledge, the theory of affective utility has not been directly tested empirically.¹⁸ However, the study by Rottenstreich and Hsee (2001) may be interpreted as preliminary evidence for affect sensitivity of probability weights: The authors report that people tend to be less responsive to probabilities when they react to emotion-laden targets, such as a kiss by one’s favorite movie star or an electric shock, than they do in the case of comparatively pallid monetary outcomes. Moreover, van Winden et al. (2008) have recently shown that the intensity of hope and worry indeed decline with the delay of uncertainty resolution, supporting our conjecture.

Our results pose a number of potential problems to both theoretical and applied economics. As most theories of decision under risk typically assume separability of probability weights and outcome valuation, decision models may misrepresent risk preferences considerably when probability weights interact with the size of payoffs or other lottery characteristics in a material way. Our findings suggest that such an interaction with stake size is significant and substantial, which renders rank-dependent models, such as prospect theory, questionable when risk preferences over a wide range of outcomes are concerned. Models of affective utility, on the other hand, seem to be a promising point of departure but need to be extended to account for interaction effects as well.

In pursuing our third major objective, we demonstrated that there is substantive heterogeneity which can be parsimoniously characterized by two distinct behavioral types who either weight probabilities near linearly or nonlinearly with only the latter type exhibiting increasing relative risk aversion. Two clearly segregated groups of comparable size and characteristics were also found in two independent Swiss data sets (Bruhin et al. 2007) and, for choices over gains only, in a British data set (Conte et al. 2007), which suggests that this mix of preference types seems to be quite robust for the class of decisions studied here.

The question of heterogeneity is an important one in many economic contexts. For example, it drives the division of labor in organizations, the development of human capital and it may create strong selection of participants into particular markets. Moreover, heterogeneity may make the marginal individual quite different from the average one, which might be problematic for representative-agent models used in macroeconomics and finance (Camerer 2006; Cohen and Einav 2007). In addition, heterogeneity drives the market interactions of rational and boundedly rational agents. Theoretical and experimental work on market aggregation has shown that the mix of rational and irrational actors may be crucial for the aggregate outcome (Russell and Thaler 1985; Haltiwanger and Waldman 1985, 1989; Fehr and Tyran 2005, 2008). This literature demonstrates that whether individual mistakes would be erased or magnified depends on the nature of strategic interdependence. When behaviors are strategic complements, even a minority of players may be pivotal for the market outcome. Substantive heterogeneity is also important for economic policy. Regulatory policy should be designed in such a way that it creates large benefits for those who make errors, while imposing little or no harm on those who are fully rational. In order to be able to gauge a program’s total net benefits the regulator needs to know the mix of behavioral types. Therefore, knowing the composition of the population is important for designing cost efficient programs and regulations.

It is an open question whether nonlinear probability weighting should be considered as irrational. In Walther’s model of affective utility nonlinear probability weighting is a consequence of utility maximization and, thus, not irrational per se. However, there is evidence that anticipated emotions deviate significantly from experienced emotions, which drives a wedge between decision utility and experienced utility, the ultimate standard for welfare judgments (Kahneman et al. 1997; van Winden et al. 2008). If nonlinear probability weights are manifestations of systematic errors utility maximization is based on the wrong premises and, consequently, behavior is merely boundedly rational. Therefore, investigation into the mechanisms underlying the malleability of probability weights should be high on the list of priorities for future research. Moreover, many real world decisions involve substantial risky payoffs as well as delayed resolution of uncertainty which may have countervailing effects on risk tolerance. New carefully designed experiments are called for that vary stake size and delay in order to derive meaningful parameter estimates which are useful for applied economics. Finally, future research needs to examine the robustness of our results with respect to other characteristics of the decision situation, such as complexity. It may well be the case that parameter estimates as well as the mix of behavioral types will change when decision tasks become more complex.

Appendices

Appendix A: Domain-specific behavior

The main goal of estimating a finite mixture model is to classify each individual to one of C different behavioral types. Our econometric model, as specified in Eq. 8, requires that each individual belongs to only one behavioral type, even though the behavioral parameters of each type are domain specific and may be different for decisions framed as gains or as losses. This makes the model very flexible in classifying the individuals into types which may exhibit domain-specific behavioral patterns, but retains the individual as unit of classification.

However, one can also estimate the finite mixture model separately for each domain. In such a case, behavioral types are only characterized within their specific domain and, consequently, each individual will be classified into two types, one for decisions framed as gains and the other for decisions framed as losses. The (overall) log likelihood of such a specification,

$$ \begin{array}{lll} \ln \tilde{L}\big(\tilde{\Psi}; ce, \mathcal{G}\big) &=& \label{equ:domain} \left[ \sum_{i=1}^{N}{ \ln \sum_{c=1}^{C} \tilde{\pi}_c^{(w)} f\left({ce_i^{(w)}, \mathcal{G}^{(w)}; \tilde{\theta}_c^{(w)},\tilde{\xi}_i^{(w)}}\right)} \right]\\ &&+ \left[ \sum_{i=1}^{N}{ \ln \sum_{c=1}^{C} \tilde{\pi}_c^{(l)} f\left({ce_i^{(l)}, \mathcal{G}^{(l)}; \tilde{\theta}_c^{(l)},\tilde{\xi}_i^{(l)}}\right)} \right] \, , \end{array} $$

(9)

is completely separable into decisions framed as gains, (w), and decisions framed as losses, (l). Note that since the above model (9) does not nest the original model (8) we cannot test these two specifications against each other. Nevertheless, as Table 4 shows, the separated model achieves a lower log likelihood than the original model, the estimates of which are displayed in Table 2, even though it has one more parameter. It also results in a higher value of the BIC (−62,058 vs. −62,163). This shows that the above specification is clearly inferior to domain-independent typing.

Table 4 Classification of behavior: domain-dependent types

At the level of individual type assignment, the main difference between the domain-specific model and the domain-independent one is that 13 people, identified as overall EUT type, move to the Non-EUT group for gains, which explains the lower percentage of EUT types in the domain-specific model (19.5% vs. 26.6%).

Appendix B: Error parameter distribution

Fig. 8

Distributions of estimated $\hat{\xi_i}$ by domain

Appendix C: Estimation of the finite mixture regression model

As it is generally the case in finite mixture models, direct maximization of the log likelihood function

$$ \ln {L} \big(\Psi; ce, \mathcal{G} \big) = \sum_{i=1}^{N}{ \ln \sum_{c=1}^{C}{\pi_c \, f\big(ce_i, \mathcal{G}; \theta_c, \xi_i\big)} } $$

may encounter several problems, even if it is in principle feasible (for a general treatise see for example McLachlan and Peel (2000)). First, the highly non-linear form of the log likelihood causes the optimization algorithm to be rather slow or even incapable of finding the maximum. Second, the likelihood of a finite mixture model is often multimodal and, therefore, we have no guaranty that a standard optimization routine will converge towards the global maximum rather than to one of the local maxima.

However, if individual group-membership were observable and indicated by t _ic  ∈ {0,1} the individual contribution to the likelihood function would be given by

$$ \tilde{\ell}\big(\Psi_i; ce_i, \mathcal{G}, t_i \big) = \prod_{c=1}^{C} {\left[ \pi_c \, f\big(ce_i, \mathcal{G}; \theta_c, \xi_i \big) \right]^{t_{ic}}} $$

By using the above formulation and taking logarithms, the complete-data log likelihood function

$$ \ln { \tilde{L} } \big(\Psi; ce, \mathcal{G},t \big) = \sum_{i=1}^{N}{ \sum_{c=1}^{C}{t_{ic} \left[\ln{\pi_c} + \ln{f\big(ce_i, \mathcal{G}; \theta_c, \xi_i\big)} \right]} } $$

would follow directly. As relative group sizes sum up to one, their maximum likelihood estimates, $\hat{\pi}_c=1/N \sum_{i=1}^{N}{t_{ic}}$, would be given analytically by the relative number of individuals in the respective group. Furthermore, the maximum likelihood estimates of the group-specific parameters could be obtained separately in each group by numerically maximizing the corresponding joint density function which would simplify the optimization problem considerably.

The EM algorithm proceeds iteratively in two steps, E and M, while it treats the unobservable t _ic as missing data. In the E-step of the (k + 1)-th iteration the expectation of the complete-data log likelihood $\tilde{L}$, given the actual fit of the data Ψ ^(k), is computed. This yields, according to Bayes’ law, the posterior probabilities of individual group-membership

$$ \tau_{ic}\left(ce_i, \mathcal{G}; \Psi_i^{(k)} \right)= \frac{\pi_c^{(k)} \, f\left(ce_i, \mathcal{G}; \theta_c^{(k)}, \xi_i^{(k)} \right)} {\sum_{m=1}^{C}{\pi_m^{(k)} \, f\left(ce_i, \mathcal{G}; \theta_m^{(k)}, \xi_i^{(k)} \right)}} $$

which replace the unknown indicators of individual group-membership, t _ic .

Given $\tau_{ic}\left(ce_i, \mathcal{G}; \Psi_i^{(k)} \right)$, the complete-data log likelihood, $\tilde{L}$, is maximized in the following M-step which yields the updates of the model parameters,

$$ \pi_c^{(k+1)} = \frac{1}{N} \sum_{i=1}^{N}{\tau_{ic}\left(ce_i, \mathcal{G}; \Psi_i^{(k)} \right)}, $$

and

$$ \begin{array}{lll} \left( \theta_1^{(k+1)}, \ldots,\theta_C^{(k+1)} , \xi_1^{(k+1)},\ldots, \xi_N^{(k+1)} \right) &=&{\operatornamewithlimits{arg\,max}}_{\theta_1,\ldots,\theta_C, \xi_1,\ldots, \xi_N} \sum_{i=1}^{N}{\sum_{m=1}^{C}{\tau_{im}\left(ce_i, \mathcal{G}; \Psi_i^{(k)} \right) }}\\ &&{{\times\,\ln f\left(ce_i, \mathcal{G}; \theta_m^{(k)}, \xi_i^{(k)} \right)}}. \end{array} $$

As Dempster et al. (1977) show, the likelihood never decreases from one iteration to the next, i.e. $L \left(\Psi^{(k+1)}; ce, \mathcal{G} \right) \geq L \left(\Psi^{(k)}; ce, \mathcal{G} \right)$, which makes the EM algorithm converge monotonically towards the nearest maximum of the likelihood function regardless whether this maximum is global or just local. Therefore, one may apply a stochastic extension, the Simulated Annealing Expectation Maximization (SAEM) algorithm proposed by Celeux et al. (1996), in order to overcome the EM algorithm’s tendency to converge towards local maxima. In each iteration, there is a non-zero probability that the SAEM algorithm leaves the current optimization path and starts over in a different region of the likelihood function, which results in much higher chances of finding the global maximum. But this robustness against multimodality of the objective function comes at the cost of much higher computational demands.

As the EM algorithm is computationally highly demanding, even in its basic form, and tends to become tediously slow when close to convergence, our estimation routine relies on a hybrid estimation algorithm (Render and Walker 1984): It first uses either the EM or the SAEM algorithm and takes advantage of their robustness before it switches to the direct maximization of the log likelihood by the much faster BFGS algorithm.¹⁹ The estimation routine in this form turned out to be efficient and robust as it reliably converged towards the same maximum likelihood estimates regardless of the randomly chosen start values.