1 Introduction

There is a wide range of quantitative methods to assess the creditworthiness of loan applicants and to estimate probabilities of default (PD). As well-developed statistical models often outperform a subjective credit risk assessment (Sun 2007), quantitative methods are common in banks’ credit risk assessment. The most common parametric techniques are linear and quadratic discriminant analysis as well as generalized linear models such as logistic regression models (LRM). Besides these statistical-driven techniques, different non-parametric methodologies such as decision tree learning, genetic algorithms or neuronal networks can be distinguished (Chen and Chiou 1999; Yobas et al. 2000). The latter are often superior to parametric methods (Atiya 2001; Varetto 1998), but suffer from non-convex optimization problems. Apart from optimization problems, the indicator weighting often contradicts the economic default hypothesis associated with the financial ratios used as predictor variables. Other enhanced credit risk models take macroeconomic conditions in addition to firm-specific characteristics into account (Carling et al 2007; Butera and Faff 2006). The dynamic of macroeconomic conditions and a time lagged impact on firm-specific characteristics lead to a high complexity of these models.

Furthermore, all upper mentioned approaches are designed to specify the classifier by minimizing the classification error on training data. Schölkopf and Smola (2002) point out that empirical risk minimization does not imply low structural risk, i.e. a small classification error on unseen test data. Thus, regularization methods or outlier adjustments are necessary to ensure both unbiased classification and high generalization.

Support Vector Machines (SVM) are derived from the statistical learning theory and follow a structural risk minimization principle as shown by Boser et al. (1992) and Cortes and Vapnik (1995). To obtain classifiers, these powerful learning systems merge efficient algorithms from the optimization theory and elements of the statistical learning theory. Huang et al. (2004) underline the intersectional character of SVM by combining the advantages of theory-driven methods and data-driven machine learning methods. The basic idea of SVM is to define a hyperplane that geometrically separates binary classes. As demonstrated by Vapnik (2000), the optimal hyperplane is obtained by maximizing the margin between the data points of the two classes whereby a structural risk minimum is achieved. Nonlinear SVM classifiers apply kernel functions to map the data from the input space into a higher dimensional feature space, where an optimal separating hyperplane may be constructed (Schölkopf and Smola 2002). In contrast to other nonlinear classification methodologies like neural networks, the convexity of the underlying optimization problem is ensured.

The classification performance is often superior to other artificial intelligence approaches (e.g. neural networks or genetic algorithms) and classical statistical techniques (Ravi Kumar and Ravi 2007; Cristianini and Shawe-Taylor 2006; Abe 2005). This has been shown, for example, in bioinformatic applications, text categorization, e-mail spam detection, and general pattern recognition problems (Baesens et al. 2003). The central advantages of SVM include the geometrical representation of the classifier as a hyperplane, the formulation of a convex optimization problem that leads to a unique optimum, and the possibility to estimate an upper bound of the generalization error on unseen test data. The resulting classifier generalizes well even in high dimensional input spaces and under small training sample conditions. As the amount of available financial default data is typically small and often of low quality, this classifier seems particularly suitable for credit risk estimation, including default classification (Härdle et al. 2005) and PD estimation.

This paper gives a comprehensive introduction to SVM and compares the credit rating capabilities of a SVM classifier to a LRM regarding default classification and PD prediction. Chen et al. (2006) and Härdle et al. (2007) have shown a superior classification performance of the SVM. Little availability of accounting data from bankrupt companies and high variance of the derived financial ratios is a typical problem of credit risk prediction. Therefore, we particularly focus on the influence of high variance of the training data and small training sample conditions. Moreover, the empirical analysis is based on a large up-to-date data sample and in contrast to the aforementioned publications adequate statistical measurements are considered to evaluate classification as well as accuracy and reliability of the predicted probabilities of default.

The paper is structured as follows: Section 2 provides an introduction into the theory of SVM.Footnote 1 Section 3 describes the empirical research design including data set composition and the financial ratios used for default estimation. The results of default classification accuracy and goodness of PD prediction are presented in Sect. 4, followed by a conclusion in Sect. 5.

2 SVM classifier for credit scoring

Consider a given training data set \(\{({\bf x}_k, y_k)\}^{N}_{k=1}\) with input data \({\bf x}_{k}\in {\mathbb{R}}^{n}\) and dependent binary class labels y k  ∈ {−1, 1}, where default is denoted as y k  = 1 and non-default is denoted as y k  =  −1. The input data x k represents the observation of the n applied default indicator variables for company k.

According to Vapnik (1998), Hastie et al. (2001) and Schölkopf and Smola (2002) a separating hyperplane w Tφ(x) + b = 0 satisfies for a non-linear and separable case

$$ {\bf w}^{T}\varphi({\bf x}_{k})+b\geq+1 \quad \hbox{if} \quad y_k=1 $$
(1)
$$ {\bf w}^{T}\varphi({\bf x}_{k})+b\leq-1 \quad \hbox{if}\quad y_k=-1 $$
(2)

equivalent to

$$ y_{k}\left[{\bf w}^{T}\varphi({\bf x}_{k})+b\right] \geq 1 $$
(3)

with the weight vector w Tand the bias b. The resulting SVM classifier is

$$ y({\bf x})=\hbox{sgn}\left({\bf w}^{T}\varphi({\bf x})+b\right). $$
(4)

The function \(\varphi({\bf x}):X \rightarrow F\) is a non-linear map from the input space X to some high dimensional feature space F, where a linear separation is possible (Cristianini and Shawe-Taylor 2006). However, a perfect non-linear separation is not desirable in practical use, as it often leads to a low generalization ability.

For a non-separable case, it is necessary to introduce a slack variable ξ with ξ k  ≥ 0 ∀k to tolerate misclassification in the set of margin constraints. Thus, constraint (3) still holds for overlapping classes. Misclassification only occurs when ξ k  > 1. The classification constraint (3) follows as

$$ y_{k}\left[{\bf w}^{T}\varphi({\bf x}_{k})+b\right]\geq 1-\xi_{k}. $$
(5)

The decision function that classifies test data points results from the solution of the convex optimization problem

$$ \max_{{\bf w},b,\xi}C \Rightarrow \min_{{\bf w},b,\xi} \frac{1}{2}\|{\bf w}\|^2 $$
(6)
$$ \hbox{subject to}\quad y_{k}\left[{\bf w}^{T}\varphi({\bf x}_{k})+b\right] \geq 1-\xi_{k}, $$
(7)
$$ \xi_{k}\geq 0, \, k=1,\ldots,N $$
(8)

The equivalent objective function for the optimization problem (6) is considered as

$$ \min_{{\bf w},b,\xi} {\fancyscript{T}}_{P}({\bf w},\xi) = \frac{1}{2} {\bf w}^T{\bf w}+\gamma\sum_{k=1}^N\xi_{k} $$
(9)
$$ \hbox{subject to} \quad y_{k}\left[{\bf w}^{T}\varphi({\bf x}_{k})+b\right] \geq 1-\xi_{k}, $$
(10)
$$ \xi_{k} \geq 0, \, k=1,\ldots,N $$
(11)

where \(\frac{1}{2} {\bf w}^T {\bf w}\) maximizes the margin between the two classes and the separating hyperplane, while \(\gamma\sum_{k=1}^N\xi_{k}\) minimizes the classification error.

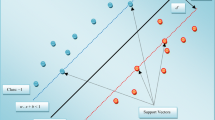
As illustrated in Fig. 1, the so-called soft-margin classifier is obtained by maximizing the margin C subject to the classification error. The classification error \(\sum_{k=1}^N\xi_{k}\) and the classifier capacity have to be controlled to ensure high generalization on unknown test data. The capacity is controlled via \(\frac{1}{2} {\bf w}^T{\bf w}\) (Schölkopf and Smola 2002). The higher the capacity, the more suitable is the selected classifier to separate the training data. However, as shown by Vapnik (1998) this does not guarantee a small test error and even increases the uncertainty of the test error. The tuning parameter γ is a positive real number that weights the influence of misclassification on the objective function \({\fancyscript{T}}_{P}({\bf w},\xi).\) The (primal) Lagrangian is considered as

$$ {\fancyscript{L}}({\bf w},b,\xi;\alpha,\nu)={\fancyscript{T}}({\bf w},\xi)-\sum_{k=1}^{N}\alpha_{k}\left(y_{k}\left[{\bf w}^{T}\varphi({\bf x}_{k})+b\right]-1+\xi_{k}\right)-\sum_{k=1}^{N}\nu_{k}\xi_{k} $$
(12)

with Lagrange multipliers α k  > 0,  ν k  > 0  ∀k. The solution function f(x) can be written as

$$ f({\bf x}) = {\bf w}^{T}\varphi({\bf x})+b $$
(13)
$$ =\sum_{k=1}^{N}\alpha_{k}y_{k}\varphi^{T}({\bf x})\varphi({\bf x}_{k})+b $$
(14)
Fig. 1
figure 1

Soft-margin SVM classifier for a non-separable case of overlapping classes. The solid line shows the separating hyperplane that is a linear decision boundary in the mapped feature space F. The maximal margin of width \(C=\frac{2}{\|{\mathbf{w}}\|}\) is represented by broken lines. ξ k is the distance of data points x k from the correct side of the maximal margin

Full size image

According to Vapnik (1998), Boser et al. (1992) no explicit construction of φ(x) is necessary. The solution function can be computed just by using inner products between a particular transformed test data point φ(x) and all transformed training data points φ(x k ). This computation in a huge (even infinite) dimensional feature space F is possible by application of a kernel function K(x, z), such that for all x, z ∈ X

$$ K({\bf x, z})=\varphi^{T}({\bf x})\varphi({\bf z}) $$
(15)

so that (14) follows as

$$ f({\bf x})=\sum_{k=1}^{N} \alpha_{k}y_{k}K({\bf x, x}_{k})+b. $$
(16)

The kernel function K(x, x k ) returns a real valued number characterizing the similarity of a particular test data point x and each training data point x k (Schölkopf and Smola 2002). As the default behavior of the training data and its similarity to the test data is known, a default prediction for the test data can be derived. In this paper, a radial basis kernel function

$$ K({\bf x, x}_k)={\rm exp}\left(-\frac{\|{\bf x}-{\bf x}_k\|^2}{\sigma^2}\right) $$
(17)

is implemented. This kernel function is a standard approach (Evgeniou et al. 2000) and achieves best accuracies on different benchmark data sets (van Gestel et al. 2004). However, the improvement of the statistical fitting leads to an intransparent classifier response, as the non-monotonic prediction of a nonlinear SVM may imply a non intuitive marginal impact of each default indicator that is in contrast to its underlying financial default hypothesis.

Suykens and Vandewalle (1999) propose a least-squares SVM (LS-SVM) classifier with a least-squares cost function and replace the inequality constraints by equality constraints. Hence (9) to (11) are modified into

$$ \min_{{\bf w},b,e} {\fancyscript{T}}_{P}({\bf w},e) = \frac{1}{2} {\bf w}^T{\bf w} + \gamma \frac{1}{2} \sum_{k=1}^Ne_{k}^{2} $$
(18)
$$ \hbox{subject to} \quad y_{k}\left[{\bf w}^{T}\varphi({\bf x}_{k})+b\right] = 1-e_{k} \, \forall k $$
(19)

where e k plays a similar role as the slack variable ξ k in the soft-margin SVM formulation (5). The LS-SVM simplify the solving of the optimization problem because of equality constraints and a linear Karush-Kuhn-Tucker system (Suykens et al. 2002). As computation is accelerated and performance comparable to other SVM formulations, we will use a LS-SVM classifier in the following analysis.

3 Data and methods

The data sample contains financial reports of 31,049 German companies from 2000 to 2006, thereof 1,112 companies had a default or failure to pay their credit obligations. The underlying financial reports are prepared in accordance with the German Accounting Standards (HGB) or the International Financial Reporting Standards (IFRS).

To ensure highest data quality, all financial ratios were calculated on the basis of verified balance sheets and income statements. The financial data were verified by comparing the published superordinated items of the balance sheet and income statement to checksums that were derived by aggregating the corresponding subordinated items. If these checksums exceeded the value of the published superordinated item by more than EUR 100, the corresponding financial data record was excluded from the study.

A particular financial data record of a company was labeled as default, if a credit event occurred within 2 years from the corresponding reporting date. The credit event was defined in accordance with the Basel Committee on Banking Supervision (2006). Thus, an obligor is denoted as default, if the payment of credit obligations is unlikely or past due more than 90 days. The default denotation, subject to the default horizon and default definition, is crucial for a comparison of performance studies on default classification and PD estimation.

The data was prepared as follows. In a first step the total data sample, including financial data and associated default information, was randomly partitioned into a training sample and a hold-out test sample. To avoid a biased training of the classifier, which might be due to external and non-financial variables such as industry, company size, report date, or legal form, we carefully prepared the training data. Each default data record was matched to a similar non-default data record (one-to-one-matching) regarding legal form, industry sector, date of the financial report, and company size.Footnote 2 Thus, the explanatory default information inherent in the training data is balanced.

The classifier was estimated on this matched training sample and tested on the non-matched test sample to evaluate its generalization ability. The data samples often contained several financial reports of the same company referring to different report dates. To avoid a bias due to different length or irregularity of time series, the training and test samples were composed as company-unique data samples.Footnote 3

In a second step, the total data sample was modified into a company-unique sample, that only contains the most recent financial data record of each default and non-default company. This representative sample of the global company portfolio, denoted as calibration sample, was used to estimate calibrated PD. The number of companies and financial reports available for the analysis are displayed in Table 1.

Classification and prediction of PD may be affected by a high variance of the data and a varying partitioning into training and test sample. To analyze the impact of variance and partitioning on classification and PD prediction, both was evaluated for alternative outlier adjustments and different training/test partitions (Table 2).

Table 1 Composition of total data samples over time horizon
Full size table
Table 2 Composition of data samples
Full size table

The outlier adjustment was implemented as a simple percentile-based elimination of outlier data. A data record (y k , x k ) was considered as outlier and excluded from the corresponding data sample, if

$$ {\bf x}^{ND}_{k}<P^{ND}_{\epsilon}\left({\bf x}^{ND}\right) \vee {\bf x}^{ND}_{k}>P^{ND}_{1-\epsilon}\left({\bf x}^{ND}\right) $$
(20)

and

$$ {\bf x}^{D}_{k}<P^{D}_{\epsilon}\left({\bf x}^{D}\right) \vee {\bf x}^{D}_{k}>P^{D}_{1-\epsilon}\left({\bf x}^{D}\right), $$
(21)

where \({\bf x}_k^{D}\,\left({\bf x}_k^{ND}\right)\) is the input data of the particular default (non-default) data record and \(P_{\epsilon}^{D}\,\left(P_{\epsilon}^{ND}\right)\) is the ε% percentile of the default (non-default) data. The higher the adjustment level ε, the more restrictive is the outlier adjustment and the lower is the variance of default and non-default data.

To analyze the impact of outliers on the classification of unseen test data, the training data was adjusted for outliers at different levels. The PD estimation may be affected by a biased classifier estimation and a biased calibration of the PD prediction. Therefore, the accuracy of the PD prediction was evaluated separately for adjusted training data and adjusted calibration data.

Both the SVM classifier and the LRM include the same financial ratios as default indicators to ensure a methodical performance evaluation. The considered default indicators were selected based on their univariate discrimination power measured by the area under the receiver operating characteristic curve.

As a large number of default explaining indicators allows only little performance gains due to mutual correlation and leads to the problem of the so-called curse of dimensionality, the number of applied variables has to be reduced (Theodoridis and Koutroumbas 2006). Therefore, the indicators were ranked according to their univariate discrimination power and the low performing ones were gradually eliminated until the Pearson correlation coefficient of the remaining financial ratios did not exceed 0.45. It should be noted that the Pearson correlation coefficient does not indicate complex non-linear relationships. These dependencies were not further considered because an approach that considers the wide universe of possible non-linear relationships might lead to the finding of spurious relations among the explaining variables. Hence, our approach might not capture all dependencies between the explaining variables but the critical effects of dependencies on model specification are accounted for.

Finally the following 5 indicators were chosen from a catalogue of original 19 financial ratios to model the credit risk of medium and large sized companies of the manufacturing, trading and service industry.

1. Cash flow return on investment:

\({\rm CFROI}=\frac{\text {Cash\;flow}}{\text {Total\;assets}}\)

2. Net debt ratio:

\({\rm NDR}=\frac{\text{Financial\;liabilities\;-\;Cash}}{\text{Capital employed}}\)

3. Interest coverage:

\({\rm IC}=\frac{{\rm EBITDA}}{\text{Interest expenses}}\)

4. Equity ratio:

\({\rm ER}=\frac{\text{Equity}}{\text{Total assets}}\)

5. Liability turnover:

\({\rm LT}=\frac{\text{Accounts\;payable}}{\text{Net sales}}\)

This set of ratios refers to profitability, capital structure and the relation of cash flow to net debt. Hence, a wide spectrum of credit risk related information of the balance sheet and the income statement is covered. The selected indicators are not appropriate for banks and insurance companies, because their financial reporting structure and business model fundamentally differs from the industries mentioned above. Therefore, financial institutions and small entities with less than EUR 5 million sales volume are not included in the data sample.

The comparison of the SVM classifier and a LRM was structured into three steps. First, the SVM classifier and the LRM were specified. Second, the classification performance of the SVM classifier and the LRM on the test sample was evaluated and compared using the test suggested by DeLong et al. (1988). Finally, the accuracy of the estimated PD of 25 equally sized rating classes was evaluated by the Brier score and its decompositions.

The probability of default π(x) is provided by the LRM

$$ \pi({\bf x})=\frac{{\rm exp}\left(\beta_0+\beta^T{\bf x}\right)}{1+{\rm exp}\left(\beta_0+\beta^T{\bf x}\right)} $$
(22)

with the coefficient vector βT = (β1, …, β n ) and the intercept β0. Coefficient vector and intercept were estimated by the maximum likelihood method implemented in the \(\hbox{MATLAB}^{\circledR}\) Statistics Toolbox.

The non-linear SVM classifier (16) was trained by the \(\hbox{MATLAB}^{\circledR}\) Bioinformatics Toolbox. The choice of the required kernel parameter σ and the margin control parameter γ is crucial. Because a global and unique optimum of the parameters cannot be obtained analytically, a range of values must be tried before an adequate parameter set can be selected (Schölkopf and Smola 2002; Cristianini and Shawe-Taylor 2006). The generalization parameter γ and the kernel parameter σ of the radial basis kernel were specified by selecting a parameter set that maximizes the classification accuracy on a randomly separated subset of the training sample. To obtain an adequate parameter set, the classification accuracy was evaluated for γ = 0, …, 25 and σ = 1, …, 60 in interval steps of 0.2. The SVM classifier was finally trained and tested with the specified adequate parameter set on the matched training sample and test sample.

A common criterion to measure classification accuracy is the area A under the receiver operating characteristic (ROC). The empirical ROC curve is a plot of the hitrate (correctly classified as default) HR(c) against the corresponding false alarm rate (falsely classified as default) FAR(c) for alternative cut-off values c. The cut-off values are used to classify observed data points x as default (y = 1) or non-default (y =  −1). The area under the ROC curve is equal to the probability

$$A=P(S_{ND}<S_{D}) + \frac{1}{2} P(S_{ND}=S_{D}).$$
(23)

The rating scores of default companies S D and non-default companies S ND are continuous random variables. Their underlying distribution results from the obtained classifier (Engelmann et al. 2003; Bamber 1975).

The classification accuracy of the SVM classifier and the LRM were compared by testing the difference of the two correlated areas under the ROC according to DeLong et al. (1988). We constructed this test as a one-tailed test with the null hypothesis that the areas under the ROC are equal, against the alternative hypothesis that the classification accuracy of the SVM classifier is superior to the LRM. The compared ROC curves were checked for intersection to make sure that the observed area under the ROC curve is an overall difference of classification performance for companies with higher and lower default risk.

$$ H_0: A_{\rm SVM}=A_{\rm LRM} $$
(24)
$$ H_1: A_{\rm SVM}>A_{\rm LRM} $$
(25)

Apart from classification accuracy, a reliable PD forecasting is very important for credit risk assessment. While classification focuses on the event of default and only allows for binary class assignments, pricing and rating of credit obligations require a measure to qualify the risk exposure. A ranking of credit obligations is only possible, when the underlying variable is at least ordinally scaled. Assuming a portfolio of non-default companies only, an evaluation of classification accuracy is not reasonable. However, the reliability of probability forecasts should certainly be considered, since an accurate grading of these companies according to their individual risk exposure requires an unbiased estimation of the PD. Furthermore, the banking regulation framework of the Basel Committee on Banking Supervision (2006) stresses the reliability issue as well as the classification performance.

The LRM (22) directly provides a probability of default π(x). However, due to the matching procedure, the estimated model implies an a-priori probability of default of about 50%. The necessary recalibration of the LRM and the transformation of the SVM classifier values into calibrated forecasts of PD is achieved by fitting a non-linear model

$$ \hat{p}(s)=\frac{1}{1+\alpha_1 {\rm exp}(\alpha_2 s)} $$
(26)

where \(\hat{p}\) is the estimated probability of default and s is the rating score provided by the LRM and the SVM classifier. The model parameters α1 and α2 are obtained by a non-linear fitting of the model.

The rating score s LRM provided by the LRM is given by

$$ s_{\rm LRM}=\hat{\beta}_0+\hat{\beta}^T{\bf x} $$
(27)

where \(\hat{\beta}_0\) and \(\hat{\beta}\) are the intercept and coefficient vector resulting from the maximum likelihood estimation of model (22). The SVM rating score s SVM is given by the SVM classifier (16) and thus

$$ s_{SVM}=\sum_{k=1}^{N}\alpha_{k}y_{k}K({\bf x, x}_{k})+b. $$
(28)

The estimation of model (26) was accomplished in two steps. First, all data records of the calibration sample were ordered by their issued rating score. The ordered sample is then segmented into 25 ranked and equally sized rating classes. Finally, the model (26) was estimated by a non-linear least squares regression of the average default frequency on the average rating score of all rating classes, whereby the default frequency was employed as an estimator of the PD.

A common measure to evaluate the PD prediction is the Brier score and its decomposed components (Hersbach 2000). The Brier score is defined as

$$ {\rm BS}=\frac{1}{N} \sum^{m}_{i=1}N_i\left[o_i\left(1-\hat{p}_i\right)^2+(1-o_i)\hat{p}^2_i\right] $$
(29)

where o i is the observed default frequency, \(\hat{p}_i\) is the estimated probability of default and N i is the size of rating class i = 1, …, m. The lower the Brier score, the better is the probabilistic prediction. In the case of equally sized rating classes, formula (29) can be simplified to

$$ {\rm BS}=\frac{1}{m} \sum^{m}_{i=1}\left[o_i\left(1-\hat{p}_i\right)^2+(1-o_i)\hat{p}^2_i\right]. $$
(30)

The Brier score (30) can be decomposed into the uncertainty of the default frequency U, the resolution RS and the reliability RL of the PD prediction:

$$ {\rm BS}={\rm RL}-{\rm RS}+U $$
(31)

The reliability

$$ {\rm RL}=\frac{1}{m} \sum^{m}_{i=1}\left[o_i-\hat{p}_i\right]^2 $$
(32)

is the mean squared prediction error. The lower the RL, the better is the accuracy of the PD prediction. The reliability concerning a particular rating class i can be measured by the logarithm of the relation of observed default frequency and the predicted PD

$$ {\rm LRL}_i=\ln(o_i)-\ln\left(\hat{p}_i\right) $$
(33)

that relativizes the prediction error to the estimated PD of rating class i. In this way, the prediction error is standardized and more easily comparable throughout all rating classes. As long as o i  > 0 holds for all i = 1, …, m, LRL i is well defined.

The resolution

$$ {\rm RS}=\frac{1}{m}\sum^{m}_{i=1}(o_i-o)^2, $$
(34)

is the average squared deviation of the observed default frequencies o i from the observed global default frequency o of the data sample. The higher the resolution, the better is the refinement and the reliability of the rating class assignment.

Assuming binomially distributed default events, the uncertainty of the default frequency U is equal to the variance of the global default frequency and given by

$$ U=o(1-o). $$
(35)

This last component of the Brier score is independent of the classifier and inherent in the data sample. Hence, Brier scores of classifiers always have to be compared on the basis of the same data sample.

4 Results

Table 3 shows the area under the ROC and its standard error \(\hat{\sigma}(A)\) of the SVM classifiers and the LRM. The last column results from the test of the difference of the two correlated areas according to DeLong et al. (1988), assuming an outperformance of the SVM classifier. It displays the probability of a false rejection of the null hypothesis (24). Engelmann et al. (2003) showed that asymptotic normality of A is approximately given for small samples with 50 defaults. As training and test sample include more than 100 default data points, normality may be assumed and the tests of the performance differences may be considered as reliable.

Table 3 Classification accuracy of the SVM classifier and the LRM
Full size table

The non-linear SVM classifier yields a significantly higher classification accuracy on the training and test sample for all alternative partition settings. The extent of outperformance differs from training to test sample. Regarding the classification of training data, the absolute difference of the two compared areas is nearly constant at about 7% and highly significant for all training and test partitions. However, regarding the classification of test data, this difference decreases from 6 to 4%, if the training partition is enlarged from 75 to 90% of the data sample. The smaller the training sample, the more superior is the classification performance of the SVM classifier.

The standard error \(\hat{\sigma}(A)\) decreases for larger training samples and increases for smaller test samples. The change of the standard error mainly result from a varying sample size. However, the standard errors of the estimated areas of the SVM classifier are smaller than those of the LRM for all partitioning settings. Despite a worsened confidence level due to an increasing standard error and a decreasing performance difference, the outperformance of the SVM classifier is still statistically significant at the 1% level.

The classification accuracies on a non-adjusted test sample for alternative outlier adjustments of the training sample are displayed in Table 4.

Table 4 Classification accuracy of the SVM classifier and the LRM (test data)
Full size table

While the classification performance of the SVM classifier on the test data is barely influenced, the classification performance of the LRM significantly increases as outliers are removed from the training data. In case of a small test sample, a more restrictive adjustment leads to a non-significant outperformance of the SVM classifier due to a higher standard error and a decreasing difference of the two compared areas under the ROC. However, in case of a small training sample, the outperformance of the SVM classifier is statistically significant for all outlier adjustment levels.

Obviously, outlier adjustments have a larger impact on the classification performance of a LRM. It can be concluded that the specification of the separating hyperplane is less biased by outliers than the estimation of the LRM. This underlines the generalization advantages of SVM classifiers. Furthermore, the SVM classifier yields a higher classification accuracy for smaller training sample sizes.

The comparison of the Brier scores of the PD prediction, including its decompositions reliability RL and resolution RS, are displayed in Table 5 for alternative outlier adjustments of the training data and in Table 6 for alternative outlier adjustments of the calibration data.

Table 5 Goodness of the estimation of the probability of default (adjusted training data)
Full size table
Table 6 Goodness of the estimation of the probability of default (adjusted calibration data)
Full size table

As the training data is adjusted for outliers, the prediction of PD by the SVM classifier is much more accurate for all test partitions and outlier adjustment levels ε. The lower Brier score results from a higher resolution and a highly superior reliability. A more restrictive adjustment of the training data improves the resolution of the LRM, but deteriorates its reliability. In contrast, the reliability and resolution of the SVM classifier is hardly affected. The Brier score of the SVM classifier based PD prediction is nearly constant for all outlier adjustment levels and test partitions, while the goodness of the LRM-based PD forecasts is worsened by a more restrictive adjustment.

As shown in Table 6, the SVM classifier also allows a more accurate prediction of PD, when the calibration data is adjusted for outliers. The variance of the default frequency decreases from 0.03453 to 0.03134 due to the exclusion of outliers from the calibration data. Hence, the lower Brier score mainly results from a sample-driven decrease in variance, but also from superior resolution and reliability of the PD prediction. A more restrictive adjustment of the calibration data improves the resolution and reliability of the LRM based PD forecasts. The reliability and resolution of the predicted PD based on the SVM classifier are hardly affected. Hence, the absolute outperformance of the SVM classifier in terms of resolution and reliability decreases.

Concerning the PD prediction, it may be summarized that the PD prediction based on the SVM classifier is obviously less biased by outliers, as already observed for classification. An accurate PD prediction by the LRM requires an outlier adjustment of the calibration data. In contrast, the adjustment of the training data improves the classification performance of the LRM, but worsens the goodness of PD forecasting. Surprisingly, a variation of the partitioning of training and test data hardly affects the goodness of probability prediction. This holds true for the SVM classifier and LRM.

Finally Fig. 2 illustrates the logarithmically standardized prediction error LRL i for all rating classes i. The PD forecasts based on the SVM classifier are much more reliable in most of the rating classes. The LRM leads to an overestimation of the probability of default in good rating classes and to an underestimation in bad rating classes. The plots of the estimated PDs and the observed default frequencies for a non-adjusted (a) and a 2% adjusted (b) calibration sample based on the LRM and the SVM classifier are illustrated in Figs. 3 and 4. The shape of the default frequency distribution and the curve of the estimated PD indicate that the rating score s provided by the SVM classifier leads to a better ranking order of default and non-default companies. The default frequencies were much better estimated by the PD forecasts based on the SVM classifier. Furthermore, the non-linear fitting of model (26) based on the rating score provided by the LRM is suboptimal, if the calibration data has a high variance and is not adjusted for outliers. In contrast, the SVM classifier allows a good fitting of model (26) for adjusted and non-adjusted calibration data.

Fig. 2
figure 2

Logarithmically standardized prediction error LRL i of all rating classes i = 1, …, 25 without any outlier adjustments. 75% of the data sample is allocated for training and 25% for testing

Full size image
Fig. 3
figure 3

Default frequency and estimated probability of default based on the LRM for an outlier adjustment at level ε = 0% (a) and ε = 2% (b). 75% of the data sample is allocated for training and 25% for testing

Full size image
Fig. 4
figure 4

Default frequency and estimated probability of default based on the SVM classifier for an outlier adjustment at level ε = 0% (a) and ε = 2% (b). 75% of the data sample is allocated for training and 25% for testing

Full size image

5 Conclusion

This paper shows that SVM classifiers are powerful learning systems which are suitable for default classification and the estimation of probabilities of default (PD). Our empirical results show that the theoretical advantages of SVM classifiers can be used to improve the accuracy of default classification and the reliability of PD prediction. The specification of an optimal separating hyperplane is obviously less sensitive to outliers than the maximum likelihood estimation of the LRM, and its classification performance and the PD prediction is superior, especially when sample size is limited. In contrast to the LRM, we found that the SVM classifier is more robust to a higher variance of the training and calibration data. Hence, SVM seem better suited for use with financial ratios, where variances are usually high and data availability often is a bottleneck. Although the parameterization and selection of the kernel function remains a very complex issue, we find that in sum, SVM classifiers are superior to LRM in default classification and default probability prediction.