Marriage as a commitment device

Abstract

Non-cooperative couples are inefficient. Cooperation raises the utility of both parents, and of each child, but does not guarantee efficiency. In the presence of credit rationing, a cooperative equilibrium may not exist outside marriage, because the main earner cannot credibly promise to compensate the main childcarer at some future date, and may not be able or willing to do so at front. By allowing the main childcarer to credibly threaten divorce if the main earner does not deliver the promised compensation when the time comes, marriage makes that promise credible, and thus increases the probability that a cooperative equilibrium will exist. In a separate-property jurisdiction, a reduction in the cost or difficulty of obtaining a divorce increases married women’s participation in the labour market. In a community-property one, it has no such effect.

1 Introduction

The question addressed by the present paper is not why are couples formed, but why do they marry. In developed countries until only a few decades ago, and in many developing ones still today, cohabitation without marriage attracted social stigma and legal discrimination, not only on to the couple, but also on to their offspring. In some developed countries, married couples enjoy certain residual legal and fiscal advantages over unmarried ones. But why do couples marry in countries where there is no discrimination against unmarried couples, or in favour of legally married ones? A number of different explanations have been put forward in the economics literature. Grossbard-Shechtman (1982), Rowthorn (2002), and Chiappori and Oreffice (2008), view marriage as a selection device, that helps improve the "match quality" of the union. Scott (2002) and Wickelgren (2009) view it as a commitment device, that encourages the parties to make efficiency-enhancing, couple-specific investments after marriage.

We also examine the commitment value of marriage, but focus on the efficiency-enhancing effects of division of labour between domestic (identified here with child raising) and income raising activities. Given that the person who specializes in the former will earn less than the one who specializes in the latter, neither party will agree to be the main childcarer without adequate compensation by the main earner. We show that, in the presence of credit rationing, an unmarried couple may not reach agreement on division of labour, because the prospective main earner cannot commit to compensate the prospective main childcarer at some future date, and may find it impossible or disadvantageous to carry out the compensation in full at front. If that is the case, the parties will not cooperate, and the resulting allocation will be inefficient. Otherwise, the parties will cooperate, but the allocation may still be inefficient (albeit less than without cooperation), because the marginal cost of compensating the main childcarer will rise faster than it would if the main earner could either borrow or postpone the payment. Marriage facilitates cooperation if the main childcarer can credibly threaten divorce, because it will then be in the main earner’s interest to compensate the former. This is the sense in which marriage may serve as a commitment device in the present context. Our approach allows us to relate the commitment argument to the matrimonial property regime, ¹ and to the cost of obtaining a divorce.

Section 2 of the present paper sets out and justifies the underlying assumptions. Section 3 characterizes an efficient allocation of domestic resources. Sections 4 examines the choice of game and the properties of the ensuing equilibrium in the absence of the marriage institution. Section 5 does the same in the presence of the marriage institution, and examines the decision to marry. Section 6 discusses the results in light of the evidence and draws some policy conclusions.

2 Assumptions

Our focus is on the union formed by a particular woman, f, and a particular man, m. To get to our point with a minimum of analytical complication, we assume that f and m are perfectly informed about each other’s characteristics, and about those of all alternative partners. This is justified by the fact that, in developed societies, marriage typically follows an extended period of search and cohabitation, but will prevent us from examining phenomena clearly connected with imperfect information such as separation while the children are still dependent on their parents. The perfect information assumption extends also to current (not necessarily future) divorce legislation and sentencing practice, ² but not to the economy as a whole (so much so, that f and m cannot borrow without collateral). We further assume that there is no exogenous premium on marriage, or penalty for unmarried cohabitation, and that culture plays no role in the gender division of labor. That is not entirely true in practice even in developed societies, but assuming it allows us to concentrate on the commitment issue.

There are two periods, labelled 1 and 2. In period 1, the couple can have children, and expend resources on them. In period 2, any children born in the previous period are independent adults. The woman has ultimate control over fertility. A child requires at least t ₀ units of specifically maternal time over the peri-natal period. Depending on school of pediatric thought, this minimum may be as short as 3 weeks, or as long as 3 years, but all our non-gender results survive if we set it equal to zero. Together with the fact that men cannot bear children, of which it is a reflection, this is the only natural asymmetry between the sexes to which we are going to admit. Any other asymmetry will be man-made. Above t ₀, the father’s time is a substitute for the mother’s. In most of the analysis we assume that it is a perfect substitute, but we will argue that allowing for imperfect substitutability makes no difference of substance to the results. Let t be the amount of time that a child receives from his or her parents in period 1 over and above t ₀. Given perfect substitutability,

$$ t=t_{f}+t_{m}, $$

(1)

where t _i is the amount of attention provided by parent i = f, m. Plausibly assuming that the length of time for which the mother cannot be replaced by the father is relatively short,

$$ t_{0}<t. $$

The child’s lifetime utility maximized conditionally on (c, t) is denoted by v(c, t), where v(.) is an indirect utility function, increasing and concave. Since c may include the services of professional child minders, concavity implies that bought-in child care is an imperfect substitute for parental attention.

Iyigun (2009) demonstrates the existence of a sorting equilibrium in which every agent is matched with an agent who has the same preferences. As our analysis starts where the matching process ends, we assume that the two parties to the match have the same preferences. Assuming descending altruism, the utility of partner i is written as

$$ U_{i}=u\left( a_{i1}\right) +u\left( a_{i2}\right) +\beta nv(c,t), \quad 0<\beta <1, $$

(2)

where $\left( a_{i1},a_{i2}\right)$ is i’s consumption stream, c the amount of money (or goods money can buy) that the parents jointly expend on each child, u(.) the instantaneous utility function, assumed increasing and concave, and β a measure of parental altruism. We will refer to v(c, t) as the quality, and n as the quantity, of children. Since the nv(c, t) term is common to both f’s and m’s utility, children are a local public good.³

As leisure does not figure in (2), i will throw any time that is left over from child-care activities inelastically on to the labor market. This assumption allows us to focus on the allocation of total work time between market (“labor”) and domestic (identified here with child-care) activities. Further assuming that this total is the same for both parties in each period,⁴ and normalizing it to unity, f’s and m’s period-1 labor supplies will be, respectively,

$$ L_{f}=1-\left( t_{0}+t_{f}\right) n $$

(3)

and

$$ L_{m}=1-nt_{m}. $$

(4)

Since L _i cannot be negative, $\left( n,t_{f},t_{m}\right)$ must be such that

$$ \left( t_{0}+t_{f}\right) n\leq 1 $$

and

$$ nt_{m}\leq 1. $$

We assume that neither of these restrictions is ever binding (i.e., that the opportunity-cost of looking after children is sufficiently high for neither parent to want to spend more than the whole of his or her total work time in this activity). In period 2, when the children no longer demand attention, the labor supply will be equal to unity for both parties.

When the union is formed, i is endowed with b _i units of capital and h _i units of human capital. The former is the fruit of previous saving or bequests, and can be borrowed against (if illiquid) or added to by saving. The latter may be partly a reflection of natural talent, and partly the outcome of previous educational investments or labor experience. Normalizing the rental price of human capital to unity, h _i is also i’s initial wage rate. A number of authors, including Mincer and Ofek (1982), Kunze (2002), and Manning and Petrongolo (2008), report evidence that the wage rate increases with the amount worked. This may be explained by saying that human capital accumulates with labor experience, or that employers face a fixed cost per employee. Allowing for either or both possibilities, we assume that i’s wage rate is

$$ w_{i1}=\left( 1+\alpha L_{i}\right) h_{i}, $$

in period 1, and

$$ w_{i2}=\left( 1+\alpha \right) \left( 1+\alpha L_{i}\right) h_{i} $$

in period 2, where α is a positive constant. Partner i then earns

$$ y_{i1}\left( L_{i}\right) \equiv w_{i1}L_{i} $$

(5)

in period 1, and

$$ y_{i2}\left( L_{i}\right) \equiv w_{i2} $$

(6)

in period 2. Notice that not only period-1, but also period-2 earnings are completely determined by the time allocation chosen in period 1, and that there are increasing returns to labor. The assumption that a unit of female human capital attracts the same rent as a unit of male human capital, and that the wage rates of two equally endowed persons increase with labor at the same rate irrespective of sex, implies absence of gender discrimination in the labor market. In the next section, we will briefly look at the implications of gender discrimination, and of allowing f and m to differ also in their ability to raise children.

Again because our story starts where the matching process ends, we take $\left( b_{i},h_{i}\right)$ as given. Having remarked that these endowments are, at least in part, the outcome of investments made before the union was formed, it stands to reason that those investments were carried out with a view to maximizing i’s chances of a good match,⁵ as well as of a good return in the labor market. Should we then impose any restriction on the possible values of $\left( b_{f},h_{f}\right)$ and $\left( b_{m},h_{m}\right)$? Developing an idea in Becker (1973), Lam (1988) demonstrates the existence and stability of matching equilibria characterized by either positive or negative assortative mating over human capital endowment and conventional assets. For his part, Masters (2008) shows that unions of equally attractive individuals are stable, while unions of unequally attractive ones are not. Allowing for chance and hormones to have their part in the matching process, we take $\left( b_{f},h_{f}\right)$ and $\left( b_{m},h_{m}\right)$ to be arbitrarily given, subject only to the restriction that f and m are equally attractive. Taking the latter to mean that f and m would have the same utility in the best alternative to the present match (and assuming, for simplicity, that this alternative is singlehood), we write the restriction in question as

$$ \hbox{max}_{s_{i}}\left\{ u\left( b_{i}+y_{i1}\left( 1\right) -s_{i}\right) +u\left( s_{i}r+y_{i2}\left( 1\right) \right) \hbox { s.t. }0\leq s_{i}\right\} =U^{S}, \quad i=f,m, $$

(7)

where s _i denotes i’s saving,⁶ and r is the interest factor. This leaves room for either positive or negative assortment over money and human capital endowments, and only rules out the possibility that a party is superior to the other on all scores.

Like most of the economics literature on the family or the couple, we assume that the cost of a full contingent contract, enforceable in an ordinary court of law, is prohibitively high. Once the couple is formed, the parties play a two-person game. In much of the literature, the choice of game is exogenous. Here, by contrast, it is endogenous, and depends on all the parameters of the model, including individual endowments and the legal environment. Both parties have power of veto over the choice of game, and on whether or not to marry. Each party has also the option of unilaterally withdrawing from the union if the couple is not married, or of petitioning a court for divorce if it is. In real life, many unions break down while the children are still dependent on their parents, or even before the children are born. The cause of these early separations is imperfect information about the present partner, or about the availability of alternative ones. Given our assumption that f and m know each other’s characteristics, and those of all alternative partners, however, separation in period 1 makes no sense. Had either party had a better alternative to the present match, he or she would have taken it in the first place. Separation may then make sense only in period 2, when the children are out of the way, and there are no more efficiency gains to be reaped.

3 Efficiency

We start by characterizing efficient allocations. A Pareto-optimal $\left( a_{f1},a_{f2},a_{m1},a_{m2},s,t_{f},t_{m},c,n\right)$ maximizes

$$ \Uplambda =\lambda U_{f}+\left( 1-\lambda \right) U_{m}, \quad 0\leq \lambda \leq 1, $$

(8)

for some λ, subject to (1–6), to the resource constraints,

$$ \sum_{i=f,m}\left[ a_{i}^{1}-b_{i}-y_{i1}\left( L_{i}\right)\right] +nc+s=0 $$

(9)

and

$$ \sum_{i=f,m}\left[ a_{i}^{2}-y_{i2}\left( L_{i}\right) \right] -sr=0, $$

(10)

and to

$$ 0\leq s, $$

(11)

where s is the couple’s joint savings.⁷ The parameter λ may be interpreted as f’s domestic welfare weight.

As U _i depends on t, not on its allocation between t _f and t _m , we can carry out the optimization in two steps. First, we find the $\left( t_{f},t_{m}\right)$ which minimizes the opportunity-cost of a child for each possible $\left( n,t\right) .$ Second, we look for the $\left(a_{f1},a_{f2},a_{m1},a_{m2},s,t,c,n\right)$ which maximizes $\Uplambda.$ The first step is illustrated in Fig. 1. The straight line with absolute slope equal to unity is an isoquant. The convex-to-the-origin curves with absolute slope

$$ -\frac{dt_{m}}{dt_{f}}=\frac{\left( 1+2\alpha \left[ 1-\left( t_{0}+t_{f}\right) n\right] \right) r+A}{\left[ 1+2\alpha \left( 1-nt_{m}\right) \right] r+A}\frac{h_{f}}{h_{m}}, $$

(12)

diminishing as t _m is substituted for t _f , are isocosts. The constant A is equal to $\alpha \left( 1+\alpha \right)$ if (11) is not binding, to 0 if it is binding. Convexity implies that the solution will be at a corner.

Fig. 1

Efficient division of labour

Let

$$ B\equiv \frac{\left[ 1+2\alpha \left( 1-nt_{m}\right) \right] r+A}{\left( 1+2\alpha \left[ 1-\left( t_{0}+t_{f}\right) n\right] \right) r+A}. $$

If

$$ h_{f}\leq Bh_{m}, $$

(13)

the opportunity-cost of a child is minimized by the traditional division of labor,

$$ t_{f}=t,\quad t_{m}=0. $$

(14)

Otherwise, it will be minimized by the liberated division of labor,

$$ t_{f}=0,\quad t_{m}=t. $$

(15)

As B cannot be less than unity, that opportunity-cost may be minimized by the traditional division of labor even if h _f is larger than h _m .

Proposition 1

Efficiency requires domestic division of labor according to personal comparative advantages. The man may have a comparative advantage in market work even if his earning capacity is initially lower than the woman’s.

This proposition stands even if we relax our assumptions concerning the technology of reproduction and the remuneration of labor. If we replace the assumption that t _m is a perfect substitute for t _f with the one that the former substitutes for the latter at a diminishing marginal rate, the isoquants become convex to the origin and the cost-minimizing allocation may then be interior. So long as t ₀ is positive, or h _f different from h _m , however, there will still be some specialization, because the isocosts will still be asymmetrical. Allowing for the possibility that not only the ability to raise money, but also the ability to bring up children increases with experience, will only make it more likely that the cost-minimizing time allocation is at a corner. Allowing for the possibility that the labor market discriminates against women (less pay for equal work and ability, or more limited career opportunities) would tip the scales further in favour of the traditional division of labor. Setting t ₀ equal to zero would remove the gender asymmetry, but not the need for partial or total specialization.

We now go on to finding the $\left( L_{f},L_{m},s,,c,n,t\right)$ which maximizes (8), subject to (9–11). If the borrowing constraint is binding, the solution will be only a “local” Pareto optimum, in the sense that the wider economy in which the household is immersed is not a Pareto optimum (that is the sense in which the expression “Pareto efficiency” is generally used in game theory). In either case, the solution will equate each child’s marginal rate of substitution (MRS) of t for c to the couple’s marginal opportunity-cost of providing attention, and each parent’s MRS of quantity for quality of children to the full cost of an extra child for the couple. It will also equalize the MRS of consumption in period 1 for consumption in period 2 across the parents. If (11) is not binding, the common value of this MRS will be equal to r (see Appendix, Sect 7.1).

4 Equilibrium without marriage

In the present section, we model behavior as if the marriage institution did not exist (that will be remedied in Sect. 5), and ask ourselves whether f and m would, or would not, cooperate. For simplicity, we identify cooperation with Nash bargaining (henceforth, NB), and non-cooperation with playing Cournot-Nash (CN). As both parties have right of veto over the choice of game, the couple will play NB if (after any appropriate money transfer) neither party would be better-off playing CN instead. If both parties are indifferent between the two games, they will spin a coin

4.1 Non-cooperation

If the couple plays CN, each party chooses its own time and income allocation. The woman chooses also the number of children. Let c _i be the amount of money that i spends on each child (i = f, m), so that

$$ c=c_{f}+c_{m}. $$

The woman then chooses $\left( a_{f1},a_{f2},s_{f},c_{f},t_{f},n\right)$ so as to maximize

$$ U_{f}=u\left( a_{f1}\right) +u\left( a_{f2}\right) +\beta nv\left( c_{f}+c_{m}, t_{f}+t_{m}\right) , $$

subject to her own budget constraints,

$$ a_{f1}+nc_{f}+s_{f}=b_{f}+y_{f1}\left( L_{f}\right) $$

(16)

and

$$ a_{f2}=rs_{f}+y_{f2}\left( L_{f}\right), $$

(17)

and to the borrowing constraint

$$ 0\leq s_{f}, $$

(18)

taking $\left( c_{m},t_{m}\right)$ as parameters.

The man chooses $\left( a_{m1},a_{m2},s_{m},c_{m},t_{m}\right)$ so as to maximize

$$ U_{m}=u\left( a_{m1}\right) +u\left( a_{m2}\right) +\beta nv\left( c_{f}+c_{m}, t_{f}+t_{m}\right), $$

subject to

$$ a_{m1}+nc_{m}+s_{m}=b_{m}+y_{m1}(L_{m}), $$

(19)

$$ a_{m2}=rs_{m}+y_{m2}(L_{m}) $$

(20)

and

$$ 0\leq s_{m}, $$

(21)

taking $\left( c_{f},t_{f},n\right)$ as parameters.

In Appendix, Sect 7.2 we demonstrate the following.

Proposition 2

If the parties play CN, the opportunity-cost of children will not be minimized, and the mother will free-ride on the father over the choice of the number of children. If the parties have the same endowments, they will share market and domestic work equally between them. Otherwise, they will specialize against their personal comparative advantages. The equilibrium will give the same utility to both parties, but will not be efficient. The quality of the children will be too low, because the couple will spend too little time, and relatively too much money, on each child. The quantity may be too large or too small.

Nothing of substance changes if m rather than f has ultimate control over fertility, and the father is thus the free-rider. If neither party has sole control of n, there will be no free-riding, but the allocation will be inefficient all the same, because each child will still be raised with the wrong mix of money and parental attention. We have already remarked that, given perfect information, it would make no sense for a couple to separate in period 1. In period 2, the parties will be indifferent between separating or staying together, because their utility level will be the same in either case.

4.2 Cooperation

The parties have a common interest in minimizing the opportunity-cost of children, and coordinating their decisions regarding the quantity and quality of the same. Having established that cost minimization requires division of labor, and given that the party who specializes in domestic work (henceforth, the "main childcarer") will earn, in both periods, less than the one who specializes in market work (henceforth, the "main earner") because y _i1(.) and y _i2(.) are increasing functions, neither party will be willing to do the former unless it receives adequate compensation from the other in period 1, or confidently expects to receive it in period 2. In period 2, however, it will be in the main earner’s interest to renege on any promise it may have made to the main childcarer in period 1. In the absence of a legally enforceable contract, any such promise will then lack credibility, and the compensation will have to be paid in full at front.

If a NB equilibrium exists, it maximizes

$$ N=\left( U_{f}-R_{f}\right) \left( U_{m}-R_{m}\right), $$

(22)

where R _i denotes i’s reserve utility (i = f, m), subject to the Utility Possibility Frontier (UPF),

$$ F\left( U_{f},U_{m}\right) \leq 0. $$

(23)

As i would not be willing to cooperate if it were better-off doing otherwise, R _i will be equal to i’s utility in the alternative CN equilibrium.⁸ In most applications of bargaining theory, the UPF is assumed to coincide with the efficiency locus, and thus to be symmetrical. If we made this assumption, a NB equilibrium would always exist, because the CN equilibrium is inefficient. As we will see, however, in our context, the UPF may lie inside the efficiency locus, and be asymmetrical.

Let x ₁ be a voluntary transfer (positive, negative or zero) from m to f in period 1. The UPF is traced by choosing $\left( a_{f1},a_{f2},a_{m1},a_{m2},s_{f},s_{m},x_{1},c,t,n\right) ,$ for each possible value of λ , so that it maximizes (8), subject to f’s and m’s budget constraints in the two periods, which now read

$$ a_{f1}+cn+s_{f}=b_{f}+y_{f1}\left( L_{f}\right) +x_{1}, $$

(24)

$$ a_{m1}+s_{m}+x_{1}=b_{m}+y_{m1}\left( L_{m}\right) $$

(25)

$$ a_{f2}=s_{f}r+y_{f2}\left( L_{f}\right), $$

(26)

and

$$ a_{m2}=s_{m}r+y_{m2}\left( L_{m}\right), $$

(27)

and to their credit constraints, (18) and (21). We have conventionally assigned the monetary cost of the children, cn, entirely to the mother. If x ₁ is positive, however, at least part of this cost will be effectively borne by the father.

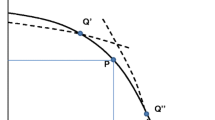
Let j denote the main childcarer, and k the main earner (j, k = f, m). We show in Appendix, Sect 7.3 that, if neither borrowing constraint were ever binding, the UPF would coincide with the efficiency locus. If that were the case, a NB equilibrium would exist, be efficient, and give the same utility to both parties. Otherwise, the UPF will be either steeper or flatter than the efficiency locus, and lie inside it. In Fig. 2, the continuous concave-to-the-origin curve, symmetrical around the 45° line, represents the efficiency locus. The convex-to-the-origin curves are contours of (22). The dashed curve, steeper than the efficiency locus, represents the UPF in the case where k is at least as tightly credit constrained as j for x ₁ = 0. In the opposite case, the UPF is flatter than the efficiency locus. Point C represents the CN equilibrium, and the threat-point of the NB game. Without credit rationing, the NB equilibrium would be at point B, on the efficiency locus, and on the 45° line. With credit rationing, such an equilibrium may not exist, because point C may lie inside the dashed curve. In the case pictured, it is at point B’, inside the efficiency locus and above the 45° line. In the opposite case, not pictured, the NB equilibrium would still lie inside the efficiency locus, but this time below the 45° line. Again in Appendix, Sect 7.3, we show that the first case is more likely if k = f, than if k = m.

Fig. 2

Cournot-Nash equilibrium. Nash-bargaining equilibrium without marriage, and with either separate-property or community-property marriage

Proposition 3

If neither party is credit constrained, an unmarried couple will play NB. The ensuing equilibrium will be efficient, and give the same utility to both parties. Otherwise, a NB equilibrium may not exist. If it does, it will be inefficient, and give one party higher utility than the other. The main earner is more likely to be the favoured party if the division of labor is the liberated, than if it is the traditional one.

Even if utilities are not equalized, f and m will still be indifferent between separating or staying together in period 2, because their utilities and period-2 incomes are not be affected by the decision.

5 Marriage

Let us now introduce the marriage institution. A marital union differs from a non-marital one in that it cannot be dissolved without court permission. In the event of dissolution (“divorce”), the court will decide how to split any assets held in common, and may also order one party to make a transfer to the other out of his or her own resources. Having argued that, under our assumptions, neither party will have an interest in ending the union in period 1, divorce may take place only in period 2, when the children are independent adults. In the present context, therefore, if a divorce court decides to treat one party better than the other, it will be on distributional, not child maintenance grounds.⁹ If a married equilibrium exists, and is different from the unmarried one, the couple will marry. If it does not exist, the couple will stay unmarried. If it coincides with the unmarried one, the couple will marry with probability one half (spin a coin).

Let γ be the cost (necessarily nonnegative) of obtaining a divorce. Let θ be the mandatory award (positive, negative or zero) that f would receive from m, in addition to half the value of any assets she might hold jointly with m, in the event of divorce. While γ is exogenous, θ is decided by the court. We consider two possibilities. The first is that the courts have a neutral stance, θ ≡ 0. The second is that they have an egalitarian stance,

$$ \theta =\theta \left( U_{m}-U_{f}\right) , \quad \theta \left( 0\right) =0, \theta^{\prime }>0. $$

(28)

The possibility that a court would deliberately set out to increase inequality between the former spouses seems too perverse to merit attention, and may be ruled out by law. As the CN equilibrium gives the same utility to both parties irrespective of marital status, marriage can make a difference only if the spouses play NB, and the courts have an egalitarian stance. We will then focus on that combination of hypotheses.

5.1 Separate property

In a separate-property jurisdiction, any income or assets a spouse generates or acquires in the course of marriage are that spouse’s personal property. The period-1 budget constraints are still (24) and (25). To allow for the possibility that marriage might lend credibility the main earner’s promise to compensate the main childcarer in period 2 rather than 1, however, we write the period-2 budget constraints as

$$ a_{f2}=s_{f}r+y_{f2}\left( L_{f}\right) +x_{2} $$

(29)

and

$$ a_{m2}+x_{2}=s_{m}r+y_{m2}\left( L_{m}\right), $$

(30)

where x ₂ is a voluntary transfer (positive, negative or zero) from m to f in period 2. The credit constraints remain (18) and (21). In addition to satisfying these restrictions, an equilibrium must now give each party at least as much period-2 consumption without as with divorce,

$$ s_{f}r+y_{f2}\left( L_{f}\right) +\theta -\gamma \leq a_{f2} $$

(31)

and

$$ s_{m}r+y_{m2}\left( L_{m}\right) -\theta -\gamma \leq a_{m2}, $$

(32)

or one of the spouses would petition for divorce. We will refer to (31) as f’s, and (32) as m’s divorce-threat constraint. At most one of these additional restrictions will be binding.

The threat-point is now the unmarried (CN or NB) equilibrium. The UPF is obtained maximizing (8) for each possible λ, subject to (18–21, 24, 25, and 29–32). We show in Appendix, Sect 7.4 that, if neither party were credit constrained at any point, the married UPF and the married NB equilibrium would coincide with the unmarried ones. By contrast, if k’s credit constraint is binding, and at least as tight as j’s for x ₁ = 0 as in Fig. 2, the married UPF, represented by the dot-and-dash curve, will be steeper than the unmarried one, represented by the dashed curve, and lie outside it (but still inside the efficiency locus), everywhere above the 45° line. In the opposite case, not pictured, where j’s credit constraint is binding, and tighter than k’s for x ₁ = 0, the married UPF will be flatter than the unmarried one, and lie inside it, everywhere above the 45° line. At and below that line, the married UPF will coincide with the unmarried one whatever the case. In the first case, marriage then expands the area inside the UPF, and thus increases the probability that a NB equilibrium exists. In Fig. 2, this equilibrium exists and is represented by point B ^SP. In the second case, marriage reduces the area under the UPF, but this does not have any effect on the probability of cooperation because, if a married NB equilibrium exists, it will lie on or below the 45° line, and thus coincide with the unmarried one. As already remarked, the first case is more likely for k = f than for k = m.

Notice that γ relaxes both divorce-threat constraints.¹⁰ Consequently, a reduction in γ would increase the probability of a married NB equilibrium in the case illustrated by Fig. 2, where the k is more tightly credit constrained than j, but would have no effect if neither party were credit constrained, or j more than k. A number of couples who would not have married at the higher γ would then marry at the lower one. Without marriage, some of these couples would have played CN. Having argued that the case where k is more tightly credit constrained than j is more likely if k = f than if k = m, it then follows that the share of married couples practising the liberated division of labor is decreasing in γ .

Proposition 4

If, without transfers, the main earner would be at least as tightly credit constrained as the main childcarer, separate-property marriage will raise the probability that a NB equilibrium exists, and make that equilibrium less inefficient if it does. In all other cases, separate-property marriage will make no difference. A reduction in the cost of obtaining a divorce raises the share of married couples where the woman is the main earner.

5.2 Community property

In a community-property jurisdiction, any income produced or assets acquired in the course of marriage are the couple’s joint property. In the event of divorce, a court will be called upon to split the assets held in common,

$$ p\equiv \left[ s-\left( b_{f}+b_{m}\right) \right] r, $$

in some way (therefore, in this case, θ will include the difference between f’s and m’s shares of p). An implication of community property is that the only way a party can make a transfer to the other while the marriage lasts is to pass some of its money endowment. Notice that the value of p would not be affected by such a move. Another implication is that a CN game is now out of the question, because neither spouse can hold on to what it earns. Therefore, a married couple can only play NB.

A couple married in such a jurisdiction faces the joint period-1 and period-2 budget constraints (9) and (10), and the joint credit constraint (11), instead of the individual budget and credit constraints it would face if it were either unmarried, or married in a separate-property one. The divorce-threat constraints are now

$$ \left( b_{f}+z\right) r+y_{f2}\left( L_{f}\right) +\frac{p}{2}+\theta -\gamma \leq a_{f2} $$

(33)

and

$$ \left( b_{m}-z\right) r+y_{m2}\left( L_{m}\right) +\frac{p}{2}-\theta -\gamma \leq a_{m2}, $$

(34)

where z denotes a voluntary asset transfer (positive, negative, or zero) from m to f in period 1. Notice that z does not figure in (9, 10) because it does not alter p, but does figure in (33, 34) because it affects individual post-divorce incomes. Notice also that, depending on initial capital endowments, either spouse (not necessarily the main earner as in separate-property marriage) may now be able to credibly threaten divorce.

The threat-point is again the unmarried (CN or NB) equilibrium. The UPF is derived by maximizing (8) for each possible λ, subject to (9–11) and (33, 34) . We show in Appendix, Sect 7.5 that, irrespective of whether the couple’s joint credit constraint is or is not binding, an allocation satisfying these restrictions will be efficient if and only if neither divorce-threat constraint is binding. It is then in f’s and m’s common interest to redistribute their pre-marital assets between them in such a way that neither of those constraints will be binding, and the married equilibrium will be efficient.¹¹ In the case illustrated by Fig. 2, the married equilibrium is represented by point B ^CP, on the efficiency locus, and above the 45° line. In the opposite case, not pictured, where j’s credit ration is initially tighter than k’s, the married equilibrium would lie below that line. Notice that, even in a community-property regime, the party favoured by the unmarried equilibrium is favoured also by the married one. If the unmarried equilibrium were at point B, the married one would coincide with it.

Proposition 5

Community-property marriage ensures the existence and efficiency of a cooperative equilibrium independently of the cost of obtaining a divorce. If neither party were credit constrained at the unmarried equilibrium, the married equilibrium would coincide with the unmarried one.

6 Discussion

Our results may be summarized as follows. A necessary but not sufficient condition for the domestic allocation of resources to be efficient is that the parties specialize to some extent in either income or child raising activities according to their personal comparative advantages. Given that a child requires at least a certain amount of specifically maternal time, the woman needs a larger human-capital endowment than the man to qualify for the main earner role on such grounds. Non-cooperative couples are inefficient, because the parties do not specialize according to comparative advantages, spend too little of their time and relatively too much of their money on each of their children, and may also have the wrong number of children (but we cannot say if too many or too few). Cooperation guarantees division of labor according to comparative advantages, and raises the utility of each child and of both parents, but does not guarantee efficiency. The first two parts of this last statement will not come as a surprise, but the third one may because Nash-bargaining games are usually constructed to have an efficient equilibrium. We have shown that this will not be the case if the main earner cannot credibly promise to compensate the main childcarer at some future date, and is either unable or unwilling to do so at front because of credit rationing. Marriage facilitates cooperation if it allows the main childcarer to credibly threaten divorce should the main earner renege on the promised compensation, and thus makes it in the main earner’s own interest to honour the promise. Separate-property marriage is more likely to have this effect if the woman is the main earner, than if the man is, but does not guarantee that a cooperative equilibrium will exist and be efficient. Community-property marriage does so in any case. In a separate-property jurisdiction a reduction in the cost or difficulty of obtaining a divorce raises the share of couples where the woman is the main earner. In a community-property one, it has no such effect.

Although obtained under the restrictive assumption that the parties are perfectly informed about each other’s and every alternative partner’s characteristics, these theoretical predictions appear to be consistent with the evidence. Chiappori et al. (2002) and Mazzocco (2007) test the hypothesis that the domestic allocation of resources is efficient. The former find that the hypothesis is not rejected by the data, but the latter finds that it is. Gemici and Laufer (2010) report that married couples specialize more than unmarried ones. Vernon (2010) finds that the traditional division of labor (the man is the main earner, the woman the main childcarer) is the prevalent pattern even in a developed country like the US. Nonetheless, Bureau of Labor Statistics (2004), Drago et al. (2004), and Stancanelli ((2007) report that, in the US as in other developed societies, the couples where the woman earns more than the man are a substantial minority (up to one in five). Gray (1998) estimates that the introduction of no-fault divorce legislation in the US induced married women to supply more labor in separate-property states, but not in community-property ones. The latter is disputed by Stevenson (2008), however, who attributes the matrimonial property effect to an omitted-variable error.

Our finding that the domestic allocation of resources may be inefficient (even if the parties cooperate!) raises questions about the empirical literature that seeks to estimate the distribution of consumption between the parties (the "sharing rule") under the assumption that the allocation is always efficient. Our other result, that a reduction in the cost or difficulty of getting a divorce may foster cooperation, and thus increase welfare, implies that divorce should be made cheap and easy. Giving unmarried couples the same rights as married ones, though desirable from other points of view, does not serve the same purpose because it does not induce domestic cooperation.

Appendix

1.1 Efficiency

The first-order conditions yield

$$ \frac{u^{\prime }\left( a_{i1}\right) }{u^{\prime }\left( a_{i2}\right) }=r+ \frac{\rho }{\mu }, $$

(35)

$$ \frac{v_{t}}{v_{c}}=-\left( y_{f1}^{\prime }+\frac{y_{f2}^{\prime }}{r+\frac{ \rho }{\mu }}\right) \frac{\partial L_{f}}{\partial t}-\left( y_{m1}^{\prime }+\frac{y_{f2}^{\prime }}{r+\frac{\rho }{\mu }}\right) \frac{\partial L_{m}}{ \partial t} $$

(36)

and

$$ \frac{v}{v_{c}}=c-\left( y_{f1}^{\prime }+\frac{y_{f2}^{\prime }}{r+\frac{ \rho }{\mu }}\right) \frac{\partial L_{f}}{\partial n}-\left( y_{m1}^{\prime }+\frac{\mu y_{f2}^{\prime }}{r+\frac{\rho }{\mu }}\right) \frac{\partial L_{m}}{\partial n}, $$

(37)

where μ is the Lagrange-multiplier of (10), necessarily positive, and ρ that of (11), positive if the couple is credit constrained, zero otherwise.

In view of (3, 4), and assuming that n is positive (or there would be no division of labour, and no gain from the union),

$$ \frac{\partial L_{f}}{\partial t}<0, \quad \frac{\partial L_{f}}{\partial n} <0\hbox { and }\frac{\partial L_{m}}{\partial t}=\frac{\partial L_{m}}{ \partial n}=0 $$

(38)

if $\left( h_{f},h_{m}\right)$ satisfies (13), and the division of labour is consequently (14),

$$ \frac{\partial L_{f}}{\partial t}=0,\quad \frac{\partial L_{f}}{\partial n} <0, \quad\frac{\partial L_{m}}{\partial t}<0\hbox { and }\frac{\partial L_{m}}{\partial n}<0 $$

(39)

if $\left( h_{f},h_{m}\right)$ violates (13), and the division of labour is then (15).

1.2 Cournot-Nash equilibrium

For i’s (i = f, m) first-order conditions on the choice of $\left( a_{i1},a_{i2},s_{i},c_{i},t_{i}\right) ,$

$$ u^{\prime }\left( a_{i1}\right) =\beta v_{c}, $$

(40)

$$ \frac{u^{\prime }\left( a_{i1}\right) }{u^{\prime }\left( a_{i2}\right) }=r+ \frac{\rho _{i}}{\mu _{i}} $$

(41)

and

$$ \frac{v_{t}}{v_{c}}=\left( y_{i1}^{\prime }+\frac{y_{i2}^{\prime }}{r+\frac{ \rho _{i}}{\mu _{i}}}\right) n, $$

(42)

where μ _i is the Lagrange-multiplier of i’s period-2 budget constraint, and ρ _i that of i’s credit constraint (i = f, m). Additionally, for f’s first-order condition on the choice of n, 

$$ \frac{v}{v_{c}}=c_{f}+\left( y_{f1}^{\prime }+\frac{y_{f2}^{\prime }}{r+ \frac{\rho _{f}}{\mu _{f}}}\right) \left( t_{0}+t_{f}\right). $$

(43)

Using (5, 6) and (40–42), we find that, at the CN equilibrium, a _f1 = a _m1, a _f2 = a _m2, μ _f  = μ _m , ρ _f  = ρ _m and U _f  = U _m . As f could always choose n = 0, and thus L _f  = 1, the common utility level will be at least equal to U ^S. In view of (3–6) and (43), we also find that

$$ \begin{aligned} &\left( 1+2\alpha \left[ 1-\left( t_{0}+t_{f}\right) n\right] +\frac{\mu \alpha \left( 1+\alpha \right) }{r\mu +\rho }\right) h_{f} \\ =&\left( 1+2\alpha \left( 1-nt_{m}\right) +\frac{\mu \alpha \left( 1+\alpha \right) }{r\mu +\rho }\right) h_{m}. \\ \end{aligned} $$

where μ is now used to denote the common equilibrium value of μ _f and μ _m , and ρ that of ρ _f and ρ _m , at the CN equilibrium. This tells us that, if h _f  = h _m and, consequently in view of (7), b _f  = b _m , f and m will split everything down the middle. Otherwise, the monetary cost of the children will be divided equally between them, but the parent with the larger human capital endowment will supply more child care, and less market work, than the one with the larger money endowment. In other words, the parties will specialize against their comparative advantages.¹² The opportunity-cost of the children will not be minimized in either case.

The equilibrium will be inefficient, even if ρ = 0, because the MRS of t for c is equated to each parent’s, rather than to the couple’s, marginal opportunity-cost of providing attention, and that of n for v to the full cost of an extra child for f, rather than for the couple. As the full cost for the couple is inefficiently large, however, we cannot be sure that f’s share of this cost will be smaller than the efficient total. Therefore, we cannot say in general whether n will be too large or too small.

1.3 Nash-bargaining equilibrium without marriage

From the first-order conditions, we find that, at each point of the UPF,

$$ \frac{u^{\prime }\left( a_{i1}\right) }{u^{\prime }\left( a_{i2}\right) }=r+ \frac{\rho _{i}}{\mu _{i}}, \quad i=f,m, $$

(44)

$$ \frac{v_{t}}{v_{c}}=-\left( y_{f1}^{\prime }+\frac{y_{f2}^{\prime }}{r+\frac{ \rho _{f}}{\mu _{f}}}\right) \frac{\partial L_{f}}{\partial t}-\left( y_{m1}^{\prime }+\frac{y_{m2}^{\prime }}{r+\frac{\rho _{m}}{\mu _{m}}} \right) \frac{\partial L_{m}}{\partial t} $$

(45)

and

$$ \frac{v}{v_{c}}=c-\left( y_{f1}^{\prime }+\frac{y_{f2}^{\prime }}{r+\frac{ \rho _{f}}{\mu _{f}}}\right) \frac{\partial L_{f}}{\partial n}-\left( y_{m1}^{\prime }+\frac{y_{m2}^{\prime }}{r+\frac{\rho _{m}}{\mu _{m}}} \right) \frac{\partial L_{m}}{\partial n}, $$

(46)

where μ _i is again the Lagrange-multiplier of i’s period-2 budget constraint, and ρ _i that of i’s credit constraint (i = f, m). As cooperative parents specialize according to their personal comparative advantages, the signs of $\frac{\partial L_{i}}{\partial t}$ and $\frac{\partial L_{i}}{\partial n}$ are those shown in (38) if the initial endowments satisfy (??), or those shown in (39) if they do not. If ρ _f  = ρ _m  = 0, (44–46) reduce to (35–37), and the allocation is then efficient at every point of the UPF. Otherwise, f’s intertemporal trade-off, $r+\frac{\rho _{f}}{\mu _{f}},$ will be different from m’s, $r+\frac{\rho _{m}}{\mu _{m}}.$ If that is the case, at some point or everywhere along the UPF, the allocation will be inefficient despite the fact that cooperative parents specialize according to their comparative advantages.

Let j denote the main childcarer, and k the main earner (j, k = f, m). As x ₁ becomes larger (more positive if k = m, more negative if k = f), U _j will rise relative to U _k , but k’s credit ration will become tighter relative to j’s. In the case where

$$ 0<\rho _{j}\leq \rho _{k}\quad\hbox{for}\,x_{1}=0, $$

(47)

the allocation will then become more inefficient. As the opportunity-cost of U _j in terms of U _k increases faster than it would if k could either borrow, or postpone the payment, the UPF will be steeper than the efficiency locus, and lie inside it, everywhere in the $\left( U_{j},U_{k}\right)$ plane. The case where

$$ 0<\rho _{k}\leq \rho _{j}\quad \hbox{for}\, x_{1}=0 $$

(48)

is more complicated. Up to the point where ρ _k  = ρ _j , any increase in the size of x ₁ will make the allocation less inefficient. The opportunity-cost of U _j in terms of U _k will then rise more slowly than it would if k were more tightly credit constrained than j, and the UPF will consequently be flatter than the efficiency locus, but still lie inside it. From that point onwards, we are back to the previous case. In view of (7) and (13) , $\left( b_{k}-b_{j}\right)$ will be negative if k = f, but can have any sign if k = m. In the absence of any information about $\left( b_{f},h_{f}\right)$ and $\left( b_{m},h_{m}\right)$, other than that they satisfy (7), and given that $\left(y_{k1}-y_{j1}\right)$ is positive anyway, the likelihood of (47) is then higher if we observe k = f, than if we observe k = m.

1.4 Nash-bargaining equilibrium with separate-property marriage

From the first-order conditions, we find that, at each point of the married UPF,

$$ \frac{u^{\prime }\left( a_{i1}\right) }{u^{\prime }\left( a_{i2}\right) }=r+ \frac{\rho _{i}}{\mu _{i}-\xi _{i}},\quad i=f,m, $$

(49)

$$ \frac{v_{t}}{v_{c}}=-\left( y_{f1}^{\prime }+\frac{y_{f2}^{\prime }}{r+\frac{ \rho _{f}}{\mu _{f}-\xi _{f}}}\right) \frac{\partial L_{f}}{\partial t} -\left( y_{m1}^{\prime }+\frac{y_{m2}^{\prime }}{r+\frac{\rho _{m}}{\mu _{m}-\xi _{m}}}\right) \frac{\partial L_{m}}{\partial t} $$

(50)

and

$$ \frac{v}{v_{c}}=c-\left( y_{f1}^{\prime }+\frac{y_{f2}^{\prime }}{r+\frac{ \rho _{f}}{\mu _{f}-\xi _{f}}}\right) \frac{\partial L_{f}}{\partial n} -\left( y_{m1}^{\prime }+\frac{y_{m2}^{\prime }}{r+\frac{\rho _{m}}{\mu _{m}-\xi _{m}}}\right) \frac{\partial L_{m}}{\partial n}, $$

(51)

where ξ _i denotes the Lagrange-multiplier of i’s divorce-threat constraint (i = f, m), and the other variables are defined as in the last section.

If neither divorce-threat constraint is binding (ξ _f  = ξ _m  = 0), these conditions reduce to (35–37), and the married UPF coincides with the unmarried one. Not so if either of these constraints is binding at some point. Given that only j’s divorce-threat constraint can be binding, k’s intertemporal trade-off remains $\left( r+\frac{\rho _{k}}{\mu _{k}}\right) ,$ but j’s becomes $\left( r+\frac{\rho _{j}}{\mu _{j}-\xi _{j}}\right)$. In view of (28), ξ _j  ≥ 0 as U _j  ≤ U _k . If (47) is true, the difference between k’s and j ’s intertemporal trade-offs is initially smaller, and the allocation less inefficient, than it would be without marriage. As x ₁ becomes larger, however, ξ _j decreases. Therefore, the married UPF is steeper than the unmarried one for all U _j  ≤ U _k , and lies outside it for all U _j  < U _k . By contrast, if (48) is true, the difference between the two trade-offs will be initially larger, and the allocation more inefficient, than it would be without marriage. As x ₁ becomes larger, ξ _j will again decrease, but the married UPF will now be flatter than the unmarried one for all U _j  ≤ U _k . In either case, the married UPF will coincide with the unmarried one for all U _j  ≥ U _k .

1.5 NB equilibrium with community-property marriage

For the first-order conditions, at each point of the married UPF,

$$ \frac{u^{\prime }\left( a_{i1}\right) }{u^{\prime }\left( a_{i2}\right) }= \frac{\mu r+\rho }{\mu -\xi _{i}}, \quad i=f,m, $$

(52)

$$ \frac{v_{t}}{v_{c}}=-\left( y_{f1}^{\prime }+\frac{\mu -\xi _{f}}{\mu +\rho } y_{f2}^{\prime }\right) \frac{\partial L_{f}}{\partial t}-\left( y_{m1}^{\prime }+\frac{\mu -\xi _{f}}{\mu +\rho }y_{m2}^{\prime }\right) \frac{\partial L_{m}}{\partial t} $$

(53)

and

$$ \frac{v}{v_{c}}=c-\left( y_{f1}^{\prime }+\frac{\mu -\xi _{f}}{\mu +\rho } y_{f2}^{\prime }\right) \frac{\partial L_{f}}{\partial n}-\left( y_{m1}^{\prime }+\frac{\mu -\xi _{f}}{\mu +\rho }y_{m2}^{\prime }\right) \frac{\partial L_{m}}{\partial n}, $$

(54)

where μ denotes the Lagrange-multiplier of the couple’s joint period-2 budget constraint, ρ that of their joint credit constraint, and ξ _i that of i’s divorce-threat constraint, i = f, m. As only one of ξ _f and ξ _m can be positive, and irrespective of whether the credit constraint is or is not binding, an allocation will then be efficient if and only if neither divorce-threat constraint is binding.