Developers, Herding, and Overbuilding

Abstract

Recent years have seen the most pronounced turbulence that real estate markets have ever experienced. There have been wild swings in prices, a wave of foreclosures, countless failed investments, and massive overbuilding. This paper will be primarily concerned with overbuilding. Of the many forces that may have combined to produce this situation, the paper will focus on rational overbuilding carried out by developers whose decisions are made under uncertainty. We will establish the possibility of both statistical and reputation-based herding. The former refers to developers learning from each other, and so tending to copy. The latter refers to developers copying each other in order to reduce the probability of a loss of reputation that can result from making an unconventional choice.

Introduction

Recent years have seen the most pronounced turbulence that real estate markets have ever experienced. There have been wild swings in prices, a wave of foreclosures, countless failed investments, and massive overbuilding.

This paper will be primarily concerned with overbuilding. The simplest way to see overbuilding is to look at inventories. As of January 2010, the stock of completed unsold new houses was 97,000, a decline from the peak of 199,000 in January 2008.¹ The magnitude of the inventory accumulation that occurred can be put into perspective by noting that the peak inventory numbers represent a 155% increase over May 2006 inventories, the month that the Case-Shiller twenty-city composite house price index peaked.² Furthermore, inventories in January 2010 had just returned to approximately late 2004 levels. Looking further back, January 2010 inventory levels were still 116% of their January 2000 levels.

An alternative way to look for overbuilding is to look at time-to-sale for completed new homes. This also increased markedly, from 3.7 months in May 2006, to 14.2 months in January 2010. For comparison, in the depths of the previous major housing downturn in the early 1990s, time-to-sale peaked at 8 months in June 1991. Yet another useful statistic is the months of supply of new and existing homes. As of January 2010 there was a 9.1 month supply new homes, and a 7.8 month supply of existing homes.³ The normal values are in the 4–5 month range. Of course, these are all indicators of what may be termed ex post overbuilding. Since few anticipated in 2005 that there would be a financial collapse and a very serious recession, it is not so surprising that the shocks that the economy suffered led to a situation with a large number of unsold homes and long times-to-sale.

However, some instances of overbuilding appear to have been carried out by well-informed agents in an environment where they might plausibly be thought to have known better. In contrast to the ex post overbuilding discussed above, arising from negative shocks, this is ex ante overbuilding in the sense that decisions were inefficient given the information available to the decision maker at the time the decision was made. Figure 1 plots housing units under construction and the supplies of existing and new houses over the January 2005–December 2007 time frame.⁴ As can be seen in the figure, the supply of existing houses rises over the entire period, and the supply of new houses begins to rise in the summer of 2005, specifically, in August 2005. The figure also illustrates that the number of houses under construction continues to rise until May/June 2006. Perhaps more interesting is Fig. 2, which plots houses under construction and two different homebuilder sentiment indexes: a general housing market index and an index of future sales expectations for single-family detached homes. As can be seen in the figure, both sentiment indexes peak in June 2005, while, as noted above, the rate of new construction continues to rise until May/June 2006. In fact, from Figs. 1 and 2, it is interesting to note that the rate of new construction does not return to its January 2005 level until July/August 2007. This is the case despite the fact that between May 2006 and July 2007, new home sales declined by 67%.⁵ Thus, not only did construction continue despite knowledge on the part of homebuilders that a market decline either was approaching or had begun, but the rate of construction actually rose.

Fig. 1

New houses under construction and months of supply of new and existing homes. Note: Data from U.S. Census Bureau, “Houses for Sale by Region and Months’ Supply at Current Sales Rate”; “Houses Sold and for Sale by Stage of Construction and Median Number of Months on Sales Market (since completion)”; U.S. Department of Housing and Urban Development, “U.S. Housing Market Conditions,” Various Issues

Fig. 2

New houses under construction and builder sentiment. Note: Data from U.S. Census Bureau, “Houses Sold and for Sale by Stage of Construction and Median Number of Months on Sales Market (since completion)”; U.S. Department of Housing and Urban Development, “U.S. Housing Market Conditions,” Various Issues

A similar pattern appears in Fig. 3, which shows stock prices of three major homebuilders. Examining the figure, it seems clear that the stock market foresaw potential trouble for homebuilders. As the figure illustrates, the homebuilder stock prices peaked in July 2005, which is consistent with a fairly widespread understanding that the housing market was approaching a peak. Examining the insider trading behavior of officers and directors of some homebuilders adds further support to the notion that homebuilders may have had concerns about the housing market in the summer of 2005. As noted in a New York Times article in October 2005 (Cresswell 2005), insider sales at the ten largest home builders by market value were 60% greater in 2005 than in 2004. All this information is, at the least, suggestive that homebuilders continued to build at relatively high rates beyond the point at which they, and investors, seemed to know that a decline in the housing market was a serious possibility.⁶

Fig. 3

Stock prices for KB homes (KBH), Toll Brothers (TOL), and Pulte Homes (PHM). Note: Data from Yahoo! Finance

There are many forces that could have combined to produce this recent episode of overbuilding. One force that has been at the center of explanations of recent turbulence has been irrational behavior on the demand side of the market (Case and Shiller 2003). This irrationality may involve adaptive expectations or animal spirits. If consumers believe that housing prices will rise, then the user cost of capital will be low, which can justify high and rising prices. High and rising prices, in turn, can justify extensive activity on the supply side. The irrationality of the expectations process means that the price increases cannot persist indefinitely. When prices ultimately fall, a substantial oversupply remains.

This paper, in contrast, will consider a supply side explanation that does not involve irrationality. It is important to be clear that we do not dispute the plausibility of the demand side irrationality explanation or the importance of other forces. However, given the behavior of homebuilders discussed above, we believe it is important to consider the supply side as well. Inasmuch as suppliers are more experienced than consumers, we also believe that in considering suppliers it is valuable to consider a model with full rationality. This paper will show that rational overbuilding can arise under imperfect information.⁷

The key motivation for our model is that there is a great deal of evidence suggesting that developers copy each other. For example, the first enclosed shopping center was built by Victor Gruen in 1956. As of 2007, it had spawned 1,110 imitators (International Council of Shopping Centers, Economist 2007). Similarly, Garreau (1992) makes it clear that the developers of edge cities are aware of each other, and are happy to copy each other’s good ideas. In his wonderfully detailed study of a new urbanist development, Rybczynski (2008) provides numerous examples of developers copying each other’s ideas. These range from the way that houses are arranged on a site down to the bricks that are used in construction.

It should not be surprising that developers are prone to copying each other. This practice is common across business activities, from the movies made in Hollywood, to the computer code that is written in the Silicon Valley, to the commodity future contracts that are issued in Chicago. In the case of real estate developers, there is almost no intellectual property protection for any particular development concept. This leaves room for imitators.

In the examples presented above, the implicit story was that developers tend to copy each other’s good ideas. However, there are other examples—just as salient as shopping centers, edge cities, and new urbanist designs—where developers seem to copy ideas that are not so clearly good. Streets have been laid without sidewalks in many rapidly growing parts of North America, which has been associated with poor health (Ewing et al. 2003; see the contrary view in Eid et al. 2008). Leaky condominiums have been built in rainy Vancouver, with significant damage ensuing (Lee and Somerville 2009). Houses are built in fire zones using wood shingles despite the risk (Shafran 2008). It is therefore important, once one has acknowledged the frequency of copying in general, to consider when developers will copy good ideas and when they will not. Put another way, it is important to consider the informational efficiency of development.

In this paper, we analyze a particular sort of information inefficiency, overbuilding in real estate. The analysis will be specified to apply most naturally to residential development, but the insights will be more general. The key activity in the model is a real estate project. The paper will show that two distinct but related sorts of herd behavior have the potential to lead to overbuilding. The first sort of herding is statistical in nature, where developers copy their predecessors because they learn from them. We establish the possibility of an information cascade in this context, where later developers fail to act according to their private information because the information that can be inferred from the behavior of early developers is sufficiently persuasive. The overbuilding that arises in this case is inefficient in an informational sense.

The paper also considers reputation-based herding. In this analysis, the probability of a project succeeding or failing depends on the location where it takes place. There are two types of agents in the model, developers and a bank that funds their activities. Our conception of developers focuses on their informational expertise. Specifically, each developer obtains a signal of a location for possible development. The developers are vertically differentiated, with good developers being more likely to have obtained signals of good locations. Projects require financing from the bank, but the bank does not observe the quality of developers or the signals that they receive. The bank must therefore infer the quality of a developer from past activity. In this analysis, the bank’s inference can be based on project outcomes and on project locations. Herding arises when developers choose locations other than those signaled in order to prevent the bank from updating its estimates of developer quality based on location. This results in multiple developers picking the same location. We establish that such herding can arise in plausible circumstances.

Both statistical and reputation-based herding are analyzed here as potential contributors to the overbuilding that took place in the recent housing boom. Put concretely, the two sorts of model offer explanations for why a developer in 2006 might have been willing to continue building despite having concerns about the future. In the statistical explanation, a developer might keep building despite concerns because other developers were continuing to build, suggesting that they did not share the same concerns. In the reputation explanation, a developer continues to build because of the possible reputation consequences of forgoing an ongoing boom in favor of an unconventional choice.

In both sorts of herding model, overbuilding takes place without being driven by demand-side irrationality. In the statistical model, it is rational for later developers to learn what they can from early developers, and it is this behavior that can lead to an informationally inefficient cascade of overbuilding. In the reputation model, the banks optimally fund, given their imperfect information. The developers optimally choose locations, given their private information regarding development locations and their recognition of the banks’ imperfect information. In both cases, uncertainty can lead to rational but inefficient overbuilding.⁸

Again, we do not claim that this is the only force that has been at work in the recent real estate cycle. There are, of course, too many papers on this topic to list even a small fraction of them here. To list just a few, Haughwout et al. (2008) and Foote et al. (2008) emphasize interactions between mortgage markets, the housing sector, and the larger economy. See Aizenman and Jinjarak (2009) for an exploration of the role of international flows of goods and financial assets, so-called “global imbalances.” See Glaeser et al. (2008) for an analysis of the price and quantity dimensions of bubbles, and see Ferreira et al. (2010) for a discussion of the implications of bubble on household mobility.

In identifying the herding tendency, our work is squarely in the tradition of research in financial economics. See, Chamley (2004) for a thorough introduction. Bikchandani et al. (1998), Bikhchandani and Sharma (2000), and Hirshleifer and Teoh (2003) are other useful reviews of the literature. Examples of recent work include Dasgupta and Prat (2006, 2008), and Cipriani and Guarino (2008). There are two key lines of research in this area. The first deals with information cascades, referred to as statistical herding by Banerjee (1992). The key early papers in this literature are Bikchandani et al. (1992) and Welch (1992). The other line of research deals with reputational herding. Scharfstein and Stein (1990) is seminal. They demonstrate that agent concerns regarding their reputations in the eyes of principals could lead them to ignore private information and imitate others. Both types of herd behavior—either statistical or reputational—have been demonstrated to arise in a wide range of settings, and for a variety of reasons. The paper that is most relevant to this one is DeCoster and Strange (1993), who consider reputational herding in location decisions. The present paper extends that analysis by considering cascades and also by working with models that are specified to capture key characteristics of real estate development.

In addition to shedding light on real estate dynamics, the paper’s analysis also contributes to the agglomeration literature. Regarding agglomeration, most explanations are based on either an increase in productivity associated with spatial concentration or an increase in consumption possibilities (Fujita and Thisse 2002; Duranton and Puga 2004; Rosenthal and Strange 2004). This paper’s connection with the agglomeration literature is simple: overbuilding is a sort of agglomeration. Our model shows that herding can arise from appropriate forms of imperfect information. Other models of uncertainty and agglomeration include Pascal and McCall (1980), who explore a tendency to imitate in location choices, Strange et al. (2006), who show that agglomeration can arise as a mechanism to promote adaptation to random shocks, and Berliant and Kung (2010), who demonstrate how the stratification of different types of workers can arise from information asymmetry.

The remainder of the paper is organized as follows. The first section presents a model of statistical herding, when developers copy each other because each is imperfectly informed and has the potential to learn. This is shown to have the potential to lead to overbuilding. The next section presents a simple version of the canonical reputation-based herding model applied to real estate development, where herding arises from reputation concerns. In the following section, a variation of the reputation-based herding model is presented that extends the analysis by showing they apply even when a developer knows he/she is good, and by explicitly analyzing the type of locations at which herding is more likely to occur. In the following section, a hybrid model is presented in which the incentives that lead to both statistical and reputation-based herding are present.

Statistical Herding and Overbuilding

Overview

This section will consider a statistical microfoundation for overbuilding. The force at work will be an information cascade, as considered by Bikchandani et al. (1992), and others (see, for instance the survey by Bikchandani et al. (1998), and the early seminal contributions by Banerjee (1992) and Welch (1992)). The key force at work here is that developers are imperfectly informed, each receiving noisy signals of the profitability of development, and so they can learn from each other’s choices. This can incline them to copy each other. The information cascade occurs when developers ignore their own signals about the state of the market in favor of the information implied by prior decisions. Such a cascade can be shown to arise when early decision makers receive the same signal, creating such a strong consensus that future agents do not act as suggested by their signals. The overbuilding that arises in this case is, therefore, inefficient in an informational sense.

Overbuilding is fundamentally an agglomeration issue. It is about building too much in a particular place and time. It is interesting to note in regard to the informational foundations of overbuilding that the idea of an imperfectly informed agent learning from another agent’s location choice pre-dates the recent research on information cascades in general. Pascal and McCall (1980) analyze a case where agents choose locations under uncertainty regarding the profits that locations will generate. They show that inference from predecessor decisions can lead to copying. They do not consider the possibility of an “agglomeration cascade,” with agents completely ignoring their own signals and the possible spread of bad information. They also do not consider overbuilding.

Model

Our goal here is to show the possibility of this sort of statistical herding leading to overbuilding. It is sufficient for our purposes to work with a very simple model. In it, developers choose sequentially whether to build in a particular market or elsewhere. The economic profit from choosing “elsewhere” is assumed without loss of generality to be 0. This is known. A developer’s profit from choosing to “build” equals V−F−C*n. F and C are positive constants, while n is the number of developers who also build in this city. V is a binomial random variable. With probability 1/2, V = V^H >0. With probability 1/2, V    =    0. Whether V will be high or low is unknown at the time of development. C is meant to capture primarily congestion costs, although it could also be interpreted to include the reduction in revenues associated with the entry of other developers. We will suppose below that developers incur only the congestion present at the time of their own decisions, not the congestion that will probabilistically ensue when later developers choose. There are a number of potential sources of congestion at the local level. A later developer may have more difficulty obtaining skilled construction workers or may experience longer permitting delays, for instance.

We also suppose that developers receive private information signals σ ∈ {σ ^L, σ ^H} regarding the profitability of building. Specifically, we suppose that ${\text{prob}}\left( {\left. {\sigma = {\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right) = \phi$, so the probability of receiving signal σ ^H conditional on the true state of nature being V = V^H equals ϕ. Likewise, ${\text{prob}}\left( {\left. {\sigma = {\sigma^{\text{L}}}} \right|{\text{V}} = 0} \right) = \phi$, so the probability of receiving signal σ ^L conditional on the true state of nature being V    =    0 is also assumed equal to ϕ. We suppose ϕ    >    1/2, which means that the signal is informative in the sense that a positive (negative) signal indicates that the state of nature is more likely than not good (bad). In addition, the signals received by different developers are assumed to be conditionally independent given the state of nature. Also, we suppose that each developer observes only her own signal, and the signals are assumed to be noncontractable. Finally, we assume the developers are identical except for their position in the sequence of location choices and the random signals that they receive.

Overbuilding as an Information Cascade

The key to the analysis below is that later developers can sometimes infer the signals that earlier developers have received. If there is a sufficiently strong consensus from early movers, then a later developer may choose to ignore her own signal. A developer deciding whether or not to build in a hot market like Phoenix in 2006, for instance, can infer the optimistic assessments of prior developers from their construction activity. Even if this late developer has information that suggests caution (a low state signal, in the context of the model), the developer may choose to develop anyway if there is a sufficiently strong consensus of prior movers. And this decision can be rational given the information that the developer has at the time of her decision.

We will establish the possibility of this sort of cascade in a stylized model of sequential development. The expected profit for the first developer choosing “build” is ${\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) - {\text{F}} - {\text{C}}$ if the developer receives the high state signal. ${\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right){{\text{V}}^{\text{H}}}$. By Bayes Rule, ${\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right) = \phi$. See the Appendix for details. The expected profit of the first developer upon receiving the high state signal thus equals ϕV^H−F−C. The expected profit for the first developer is ${\text{E}}\left( {\left. {\text{V}} \right|\sigma = \left. {{\sigma^{\text{L}}}} \right\} - {\text{F}} - {\text{C}}} \right.$ if the developer receives the low state signal. This equals $\left( {{1} - \phi } \right){{\text{V}}^{\text{H}}} - {\text{F}} - {\text{C}}$, since ${\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{L}}}} \right) = {\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{L}}}} \right){{\text{V}}^{\text{H}}}$ and by Bayes Rule, ${\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{L}}}} \right) = \left( {{1} - \phi } \right)$.

Our goal is to consider the possibility of an informational cascade in real estate development. There is, therefore, no reason for us to pay attention here to developers for whom the signal is not decisive. We will therefore suppose that the first developer is marginal in the sense that a developer will choose “build” if and only if she receives a good signal. This requires:

$$ \left( {{1} - \phi } \right){{\text{V}}^{\text{H}}} < {\text{F}} + {\text{C}} < \phi {{\text{V}}^{\text{H}}}. $$

(1)

Suppose that the first developer has, indeed, received the high signal.

Now consider how the second developer will respond to her own signal and to the behavior of the first developer. If the second developer also receives the high signal, then Bayesian updating gives the probability of the high state conditional on two developers having received the positive signal as ${\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right) * {\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)/{\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}}} \right) = {\phi^{{2}}}/\left[ {{ }{\phi^{{2}}} + {{\left( {{1} - \phi } \right)}^{{2}}}} \right]$. Again, see the Appendix for the details. Intuitively, the developer assigns a probability of the high state that is greater than φ, the probability that would be suggested by one developer’s having received a positive signal. This is because the developer can infer that the first developer has also received a positive signal, which increases the probability of the high state of nature. In this case, the expected profit from building for a second developer who has also received a high signal and who has inferred that the first developer has done the same will be

$$ {\phi^{{2}}}/\left[ {{\phi^{{2}}} + {{\left( {{1} - \phi } \right)}^{{2}}}} \right]{{\text{V}}^{\text{H}}} - {\text{F}} - {\text{2C}}. $$

(2)

Suppose instead that the second developer receives the low signal. In this case, updating gives the probability of the high state V = V^H as 1/2, with expected profits from building in this case equal to

$$ \left( {{1}/{2}} \right){{\text{V}}^{\text{H}}} - {\text{F}} - {\text{2C}}. $$

(3)

Again, we want the signal to be decisive. This requires that congestion costs are small enough so expected profits are positive if the second developer receives the high state signal but large enough that expected profits are negative if the second developer receives the low state signal. Using (2) and (3), this requires

$$ \left( {{1}/{2}} \right){{\text{V}}^{\text{H}}} < {\text{F}} + {\text{2C}} < \left[ {{\phi^{{2}}}/\left[ {{\phi^{{2}}} + {{\left( {{1} - \phi } \right)}^{{2}}}} \right]} \right]{{\text{V}}^{\text{H}}}. $$

(4)

Suppose that the second developer has also received the high signal.

All of this is preamble to the decision facing the third developer: if this developer observes that both predecessors have built but obtains a low signal, will the third developer make use of this new signal? If the answer to this question is no, then there will be an information cascade. Applying Bayes’ Rule here gives the posterior of ϕ.⁹ The expected profits from building are then

$$ \phi {{\text{V}}^{\text{H}}} - {\text{F}} - {\text{3C}}. $$

(5)

The third developer will therefore choose to build even when receiving the negative signal when

$$ {\text{F}} + {\text{3C}} < \phi {{\text{V}}^{\text{H}}}. $$

(6)

If (6) holds, along with (1) and (4), we have an information cascade. If such a cascade occurs, then later developers will have no information beyond what can be inferred from the decisions of the first two developers and their own signals. An important difference between this sort of agglomeration cascade and a pure information cascade is that congestion will eventually cause the cascade to stop. In this illustrative model, this will take place when

$$ \phi {{\text{V}}^{\text{H}}} - {\text{F}} - {\text{nC}} > 0, $$

(7)

and

$$ \phi {{\text{V}}^{\text{H}}} - {\text{F}} - \left( {{\text{n}} + {1}} \right){\text{C}} \leqslant 0. $$

(8)

At this level of congestion, the nth developer chooses to build despite receiving a low signal after observing two actions from which two high signals can be inferred. Developer n + 1 chooses not to build.

We now have the key result:

• Proposition 1. If conditions (1), (4), and (6) hold, then if developer 1 and developer 2 both receive the high-state signal σ ^H, then all successive developers will build through the level of n defined by (7) and (8).

• Proof: See above.

This sort of cascade will arise when the two high signals have sufficient inferential power that they outweigh a single low signal. This is easy to demonstrate in a model without congestion (i.e., Bikchandani et al. (1992)). In the case with congestion examined here, a necessary condition for an information cascade is that the gain from the second high signal (relative to a case with one high and one low signal) must outweigh the marginal congestion costs, C. The gain from the second signal is the difference

$$ {\text{E}}\left( {\left. {\text{V}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}},{\sigma_{{2}}} = {\sigma^{\text{H}}},{\sigma_{{3}}} = {\sigma^{\text{L}}}} \right) - {\text{E}}\left( {\left. {\text{V}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}},{\sigma_{{2}}} = {\sigma^{\text{L}}}} \right) = \left( {\phi - {1}/{2}} \right){{\text{V}}^{\text{H}}}. $$

(9)

This is the difference between the expected revenue given the three signals σ _i and the expected revenue given two mixed signals. The necessary condition for a cascade to take place is thus:

$$ \left( {\phi - {1}/{2}} \right){{\text{V}}^{\text{H}}} > {\text{C}}. $$

(10)

The information cascade that we have analyzed here is very different in its foundation from the development cascade analyzed in the classic Grenadier (1996) analysis. His model also has the result that overbuilding may arise when agents are rational. In his case, development cascades arise from competition between developers rather than from information spillovers. A developer may respond to a rival “build” decision by also choosing “build” because the value of an old building is diminished by the leader’s decision to build a new building. The current state of the market is common knowledge, and, thus, not inferred from the decisions of rivals.

Interpretation

It makes sense to pause at this point and clarify what has been shown and what has not. The model shows that it is possible to have a cascade of overbuilding as a result of developers making inferences on the uncertain state of the market from prior activity. This overbuilding is inefficient in the sense that developers do not take into account the value that successive developers would place on being able to infer the signals that previous developers had received. The model does not say at all that this sort of event is certain.¹⁰

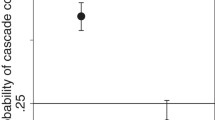
The specific event that we are interested in here is where early participants obtain incorrect optimistic signals and the activity that is justified by these signals encourages later actors to ignore their own correct pessimistic signals. In the context of the specific model above, the probability of the first two developers receiving high signals when the true state of nature is low equals (1− ϕ)². So if developers are very precise and receive signals that accurately reflect the state of the world 90% of the time, then the probability of an overbuilding cascade is only 1%. When they receive signals that are accurate 70% of the time, the probability of the cascade rises to 9%, nearly an order of magnitude, and a nontrivial number in its own regard. In the context of the highly stylized model presented here, we cannot, of course, say anything more about these specific numbers other than that they illustrate a real possibility.

This analysis can be extended in a straightforward way to a case where developers differ in quality. This extension will prove useful later in the paper when we deal with developer reputation, a situation where heterogeneity in quality is fundamental. Recall that ϕ is defined as the probability of correctly identifying the state of the world. In this case, therefore, we denote the quality of developer i by ϕ _i. Higher quality developers are thus more likely to receive signals that accurately reflect the state of the world. The condition for the signals of the first two developers being decisive, (1) and (4), become respectively

$$ \left( {{1} - {\phi_{{1}}}} \right){{\text{V}}^{\text{H}}} < {\text{F}} + {\text{C}} < {\phi_{{1}}}{{\text{V}}^{\text{H}}}. $$

(11)

and

$$ {\phi_{{1}}}\left( {{1} - {\phi_{{2}}}} \right)/\left[ {{\phi_{{1}}}\left( {{1} - {\phi_{{2}}}} \right) + \left( {{1} - {\phi_{{1}}}} \right){\phi_{{2}}}} \right]{{\text{V}}^{\text{H}}} < {\text{F}} + {\text{2C}} < {\phi_{{1}}}{\phi_{{2}}}/\left[ {{\phi_{{1}}}{\phi_{{2}}} + \left( {{1} - {\phi_{{1}}}} \right)\left( {{1} - {\phi_{{2}}}} \right)} \right]{{\text{V}}^{\text{H}}}. $$

(12)

(11) guarantees that the first developer will choose to build if and only if she receives the high state signal. (12) is a parallel condition for developer 2. The difference between these conditions and the prior parallel conditions with homogeneous developers is that (11) and (12) allow for developers to differ in quality. For instance, if developer 1 is known to receive highly accurate signals, then given a high value of ϕ ₁, a higher level of costs is required for developer 2 to be deterred by a negative signal. The cascade condition for the third developer becomes

$$ {\text{F}} + {\text{3C}} < \left[ {\left[ {{\phi_{{1}}}{\phi_{{2}}}\left( {{1} - {\phi_{{3}}}} \right)} \right]/\left[ {{ }{\phi_{{1}}}{\phi_{{2}}}\left( {{1} - {\phi_{{3}}}} \right) + \left( {{1} - {\phi_{{1}}}} \right)\left( {{1} - {\phi_{{2}}}} \right){\phi_{{3}}}} \right]} \right]{{\text{V}}^{\text{H}}}. $$

(13)

The term in brackets on the right side of (13) is the probability of a high state of nature given that developers 1 and 2 have received high signals, while developer 3 has received a low signal (see the Appendix). If (11), (12) and (13) hold, then developer 3 will choose to build if developers 1 and 2 have previously chosen to build.

The interesting case is when the better developers move first, with ϕ ₁ > ϕ ₂ > ϕ ₃. This case would seem to be least favorable to a cascade of overbuilding since the best information is made public through the decisions of these agents. This is only partly true. By (13), the assumption that ϕ ₃ is lower than ϕ ₁ or ϕ ₂ means that developer 3 is willing to ignore her own signal and follow the first two developers for higher values of C. A developer with a less accurate signal of the state of the world follows developers with better signals more readily. The sense in which this case is, indeed, less favorable to an overbuilding cascade is that there is a lower probability of the first two developers receiving incorrect signals. However, in the unlikely event that they do receive incorrect signals, their inherent superiority makes it more likely for developer 3 to copy them in the face of private information suggesting otherwise.

The big point of all of this is that this is an instance of rational behavior leading to informationally inefficient overbuilding. The overbuilding arises from developers copying each other in a situation when they should not. While this is certainly a logically coherent economic model of overbuilding, it does not fit so well with the evidence in the Introduction of developers building when it seems that they should have known that they should not do so. The next section will present a model of reputation-based herding that arguably fits these facts better.

Reputation-Based Herding

Overview

This section will present a simple model of reputation and overbuilding that complements the previous section’s statistical model. In this section, we will work with a highly stylized model designed to illustrate the key forces at work. We will extend the analysis in several ways later in the paper.

A developer’s reputation will be at the heart of the analysis. As with other sorts of entrepreneur, one of the key roles of real estate developers is to make decisions based on superior information about the markets in which they operate. Investors and their bank intermediaries have less information, and so they allocate project location decisions to developers, whose informational advantage enables them to make better choices. But investors are uncertain regarding the degree of any particular developer’s informational advantage. They must infer this from what developers do and how well they perform. Developer access to future financing may depend on this inference. This means that there are two elements to the payoffs that accrue to developers from making location choices: the direct payoffs that accrue from the choice itself and the indirect payoffs that arise from the effect of a developer’s choice on his reputation.

This section will show that developers will sometimes be forced to choose between direct payoffs and reputation. This tradeoff arises because a developer’s reputation depends in part on a comparison with other developers. This comparison can involve relative performance, with better performance suggesting a greater informational advantage. The comparison can also be based on relative decisions: if there is an underlying truth that some locations are better than others, then better informed developers will tend to behave similarly by choosing these locations. This creates incentives for developers to copy each other even when they know they should not in order to convince capital markets that they are well informed, thus leading to overbuilding.

A similar logic was expressed by Keynes, who wrote that “Worldly wisdom teaches it is better for reputation to fail conventionally than to succeed unconventionally.” (Keynes 1936, p. 158). This sort of reputation argument applies naturally to developer behavior during the recent housing boom. Imagine a developer who is choosing in 2006 between investing in a hot market like Phoenix or a more stable market like Fargo.¹¹ Suppose the developer considers Phoenix to be significantly overbuilt, while believing Fargo a market with growth potential. Suppose that a large number of other developers continue to build in Phoenix. By choosing Fargo instead, a developer would be revealing a tendency to think differently than the herd. Consistent with the Keynes quotation, this section’s key result is that being known to think differently may have an adverse effect on the developer’s reputation. This may affect access to financing for future projects, thus pushing the developer towards following the herd to Phoenix, despite the developer’s private misgivings. The safety that can be found with the herd can therefore help to explain the persistence of development booms even when developers should have known better.

Model

There are three agents in the model, two developers and a bank that finances their projects. The bank is meant to capture capital markets more generally. A developer must choose a location for a project. The project has uncertain returns. The distribution of these returns depends on the location that the developer chooses. We will suppose that there are a continuum of possible locations, each denoted by an address, a, which is formally a point on the real line. There is only one “good” location. If a developer picks the good location, then the probability of the project succeeding is α. All other locations are bad. If a developer picks a bad location, then the probability of succeeding is zero. A developer does not know for sure, however, if a given location is good or not.

Some developers are better than others at identifying good locations. Specifically there are two types, good and bad. The prior probability that any given developer is good is p. Each developer i receives a signal identifying a location for development, s_i.¹² A good developer always receives a signal of the good location. A bad developer always receives a signal of a bad location. The signal received by a developer is private information. Neither the bank nor the developer knows a developer’s type. Because of this, neither knows whether a particular location is good or not.

The bank finances developer projects with simple loans. If a project is successful, the bank earns principal and interest, and the developer earns a payoff of R. If two developers pick the same location, there is an additional congestion cost of C. As in the previous section, this can be interpreted as literal congestion (i.e., construction labor becomes more expensive) or as a reduction in price associated with moving down the demand curve. In this case, the payoff to a developer’s project, net of congestion, is R-C, which is assumed to be positive. Consistent with the informational advantage we attribute to developers, we suppose also that the bank does not know the values of R and C.¹³ If a project is unsuccessful, the developer earns a payoff of 0, and the bank incurs a total loss. Since only good developers can identify locations with a positive probability of success, the bank cares about the quality of the developers to whom it lends. We assume for simplicity that cash flows are not discounted. We suppose that the bank is willing to finance developers with a probability of being good equal to or greater than p, and that developers know this financing criteria. The developer assigns a value to continued financing equal to W. We will clarify this continuation value below.

Many of the simplifying assumptions above can be relaxed. There can be multiple good locations. Bad developers can have a positive probability of receiving a good signal, and projects at bad locations can succeed. All that is really needed is for the qualitative differences that we have assumed to hold. The strong assumptions have been made here because they allow us to characterize much more transparently the economics of reputation and herding in real estate markets.

Reputation-Based Herding and Overbuilding

The key complication in the analysis is that the developer choice of location given a signal and the bank’s updating of its estimate of developer quality must be mutually consistent in a perfect Bayesian equilibrium of the game.¹⁴ It is natural to begin by considering the possibility of an equilibrium in which the bank believes that developers always select signaled locations.

How would developers locate given these bank beliefs? It is a dominant strategy for the first developer to choose the location that was signaled, a₁ = s₁, since any other location guarantees project failure.¹⁵ If the second developer receives a signal of the same location, s₂ = a₁, then the second developer can infer that both developers are good. Picking a₂ = a₁ is dominant for the second developer in this case.

The interesting case is where the second developer receives a signal of a different location. If both developers were good, they would have received the same signals. Thus, when he observes that developer 1 must have received a different signal, developer 2 knows that either he, or developer 1, or both, is bad. Given this signal disagreement, developer 2 would update his estimate of the probability of himself being good to p/(1 +   p) < p. His posterior for developer 1 being good would also be p/(1 +   p) < p. However, the bank does not observe the signal disagreement. It can only infer a signal disagreement from location choices. This is crucial, since it means that developer 2 can prevent the bank from learning of the signal disagreement by copying developer 1’s location.

Suppose that the second developer selects his signaled location. In this case, if the developer succeeds, the bank assigns a posterior probability of one to the developer being good. If the developer fails, the bank’s posterior is $\left( {{1} - \alpha } \right){\text{p}}/\left( {{1} - \alpha {\text{p}}} \right) < {\text{p}}$.¹⁶ The developer will receive future financing in the former case but not in the latter.

All of this means that the expected payoff to the second developer from choosing the signaled location is:

$$ \alpha {\text{p}}/\left( {{1} + {\text{p}}} \right) \left[ {{\text{R}} + {\text{W}}} \right]. $$

(14)

(14) equals the current plus continuation payoffs if the developer is good (to which the developer assigns posterior probability p/(1 + p)) and the project succeeds (probability α). In the case where either the developer is bad or good but unlucky (fails at a good location), the current payoff is zero. In addition, the posterior estimate of developer quality falls below p, so the developer does not receive further financing, and the continuation value is also 0.

Suppose, in contrast, that the developer herds by following his predecessor. Under the hypothesized bank belief that developers follow their signals, the bank updates its estimate of developer 2’s quality to one, since the bank now believes that developer 2 has received the same signal as developer 1. Developer 2 continues to recognize the signal disagreement, and so assigns a probability of p/(1 + p) to developer 1 being good. This gives an expected payoff of

$$ \alpha {\text{p}}/\left( {{1} + {\text{p}}} \right)\left[ {{\text{R}} - {\text{C}}} \right] + {\text{W}}. $$

(15)

The cost term in (15) captures the congestion associated with overbuilding.

The second developer will make the herding choice if

$$ \left[ {{1} - \alpha {\text{p}}/\left( {{1} + {\text{p}}} \right)} \right]{\text{W}} - \alpha {\text{p}}/\left( {{1} + {\text{p}}} \right){\text{C}} > 0. $$

(16)

Herding dominates if the continuation value, W, is large enough. Clearly, if there were no continuation value at all, then there would be no value in building a reputation, so there would be no reason to forego current payoffs to ensure future funding. If we put more structure on W by supposing that it equals the value of just one more project, then the herding condition (16) is likely to hold. Allowing W to represent the value of the rest of a developer’s career further increases the value of herding in (16).

Suppose that (16) holds. We have shown that in this case, developer 2 will choose to copy developer 1 even when developer 2 has a private signal suggesting otherwise. In other words, developer 2 will choose to herd. However, all of the analysis that has led to this calculation has been based on the bank believing that all developers are selecting the locations that they have been signaled. This belief is thus not consistent with optimal developer behavior if (16) holds. Perfect Bayesian equilibrium requires both that developers choose optimally given bank beliefs (which holds) and that bank beliefs be consistent with developer choices (which does not hold if condition (16) is satisfied). This means that there can be no equilibrium where (16) holds and the bank believes that developers always locate according to their signals.

We have shown thus far that locating according to signals when the bank believes developers will do so is not consistent with perfect Bayesian equilibrium because developers will have an incentive to herd. To complete this part of the analysis, we must specify bank beliefs and developer strategies (locations as functions of signals, other developer locations, and bank beliefs) that are consistent with each other and thus with perfect Bayesian equilibrium.

What alternate bank beliefs would be consistent with equilibrium? Consider the following. If the developers pick the same location, then the bank supposes that the first developer has located according to signal and the second developer has simply copied the first developer, that is, engaged in herding. In this case, the bank believes that developer 2’s location is unrelated to his signal. We will show below that developer 2 will choose to herd, so this is the bank’s belief on-the-equilibrium-path. In order to completely characterize the bank’s belief and in order to establish that the developers are choosing optimally given the bank’s beliefs, we must also specify an off-the-equilibrium path belief that describes how the bank would interpret the second developer choosing a different location than the first. We suppose that if the second developer picks a different location, then the bank assumes that the second developer has chosen his signaled location.

In order for this bank belief (which includes both the on- and off-equilibrium path elements) to be consistent with perfect Bayesian equilibrium, developer 2 must actually want to choose a₁ regardless of signal.¹⁷ As before, under these beliefs, if s₂ = a₁, developer 2 chooses to locate at a₂ = a₁ whether or not (16) holds. If s₂    ≠    a₁, then herding is beneficial when (16) is met. Thus, the beliefs and strategies described above are consistent with perfect Bayesian equilibrium.

All of this can be summarized as follows:

• Proposition 2 If condition (16) holds, then there exists a perfect Bayesian equilibrium where developer 2 will choose the same location as developer 1 even when developer 2 receives a different signal.

• Proof: See above.

The equilibrium in Proposition 2 features overbuilding when the developers receive different signals. The overbuilding arises from the second developer’s reputation concerns. Specifically, the second developer herds to frustrate the bank’s ability to learn his true quality, resulting in overbuilding. A consequence is that the developer is assured of continued financing. The basic logic is that a strategy with a high probability of failing conventionally (with the herd) may have a higher expected payoff than a strategy with a low probability of failing unconventionally (alone).¹⁸

The source of overbuilding with the strategic herding analyzed here is different in important ways from the statistical herding described in “Statistical Herding and Overbuilding”. In both cases, uncertainty and learning are important. In the statistical case, developers overbuild because they do not know better. In the unfortunate case where the common wisdom is mistakenly that building is profitable, any one developer’s signal is insufficient to persuade the developer otherwise, and overbuilding arises. In this section’s strategic case, the developer’s do know better. They choose overbuilding because doing so has less reputation risk associated with it.

This section presented a simple reputation-based herding model applied to real estate development, in order to communicate the essential logic of such models and illustrate in a reasonably transparent way how reputation-based herding could result in overbuilding. The rest of the paper will be spent extending this model.

Fully-Informed Developers and Booms

Overview

The previous section presented a reputation-based model of overbuilding. The key result was that a rational developer who is uncertain of her own quality may choose to ignore the information contained in a private location signal and instead simply copy another developer’s decision, an instance of herding.

In the previous section’s model, developers do not know their own quality. When a developer observes a location decision from which it can be inferred that another developer has received a different signal, then the developer will revise down her estimate of her own quality. This puts the developer is a tricky situation: choose the signaled location or copy the other developer (herd). Choosing the signaled location puts the developer’s reputation at risk, since the bank learns from this that the developers received different signals and infers that one or both are bad. In the case where the developer fails alone, the bank will reduce its estimate of the developer’s quality. This is costly for the developer because future financing depends on the bank’s perception of the developer’s informational advantage. Copying the other developer avoids this reputation cost, but it incurs costs arising from inefficient overbuilding.

This section will extend this analysis in two ways. First, it will show that the equilibrium herding result does not depend on the developer not knowing her own quality, and thus having every reason to be concerned about the possibility of a negative reputational shock. The herding result proves, in fact, to be quite robust. A developer can rationally choose herding even when knowing with perfect certainty that she is good and in addition being endowed with perfect information regarding the attributes of alternative potential development locations.

Second, this section will show that herding is more likely at a location that is not unambiguously bad. Much of the overbuilding that took place during the recent housing boom was at sites that had strong fundamentals, such as warm weather locations like Florida and Arizona. The problem with this sort of overbuilding is not that developers are choosing bad locations but that developers are choosing locations that, while justifying a certain amount of activity, have been overdeveloped. This section will consider the differences between the overbuilding of good locations that accompanies booms and overbuilding at locations that are simply bad.

Model

This section’s analysis of fully informed developers and booms will involve an adaptation of the reputation model from the previous section. Most of the key model elements are the same: two developers, sequential decisions, a bank, and uncertain projects that may either succeed or fail.

There are several important differences. First, in order to simplify the updating, we will suppose now that there are many good locations. The implication is that the selection of different locations by developers does not provide any basis for bank inferences regarding developer quality. Bank updates of uniquely located developers must, therefore, be based on the success or failure of projects. As before, the probability of success at a good location is α. The probability of success at a bad location is now assumed to be β, 0 < β < α. Thus, even if developer 1 is bad, her project has a positive probability of success. Second, in this section we adopt an alternate approach to the costs of overbuilding. In order to achieve maximal transparency, we will suppose that overbuilding results in a lower probability of project success. This is in contrast to the linear congestion costs considered previously. This approach will allow us to characterize two quite different circumstances that might face a developer. In the first, developer 1 has picked an inferior (bad) location. We suppose in this case that the probability of success for developer 2 from herding at this location equals ε < β < α. In contrast, the location picked by developer 1 may be a reasonable location, but it may have been overbuilt. In this case, the probability of success for developer 2 from herding at this location is δ, with ε < δ < α. The distinction here is between herding at a boom location that has been developed beyond its optimal scale (i.e., Phoenix), or at a location with poor fundamentals (i.e., Frostbite Falls, Minnesota).

Most importantly, in this section we now suppose that the following developer (developer 2) is fully-informed. Specifically, developer 2 knows her type (good), and also knows whether developer 1’s location is good or bad. Since developer 2 is good, she always receives a signal identifying a good location (probability of project success equal to α). However, although developer 2 knows for sure that her signal is of a good location, the bank does not.

Fully-Informed Herding

We are interested in whether a fully-informed developer will have a tendency to herd. To avoid repetition, we will consider for now only the case where developer 1 has picked a bad location. In this case, developer 2 is choosing between her signaled location (a good location, probability of success α) and developer 1’s location (a bad one, probability of success for developer 2 of ε). We will consider the equilibrium bank beliefs from the previous section’s reputation model: if the two developers pick the same location, then the bank supposes that developer 1 has located according to signal and developer 2 has copied the first developer (i.e., herded, by picking a₁ regardless of her own signal). If developer 2 picks a different location, then the bank assumes that developer 2 has received a different signal (s₂ ≠ a₁). Given these beliefs, we then must determine the circumstances under which developer 2’s herding choice is optimal.

Focusing on the case where developer 2 knows that developer 1 has selected a bad location, developer 2 has two choices: copy the mistaken predecessor (choose a₂ = a₁ = s₁) or follow her own signal (choose a₂ = s₂). Given the bank’s beliefs, herding gives developer 2 an expected payoff equal to

$$ \varepsilon {\text{R}} + {\text{W}}. $$

(17)

As above, herding ensures continued financing. Given the bank beliefs, choosing the signaled location gives developer 2 an expected payoff of

$$ \alpha \left[ {{\text{R}} + {\text{W}}} \right]. $$

(18)

The first term is straightforward. The project succeeds with probability α, and so generates an expected current payoff equal to αR. The second term reflects the fact that the bank will finance future activities only if the project succeeds when developer 2 chooses a different location than developer 1. This is because it will assign a posterior quality estimate greater than p if developer 2 succeeds having chosen a distinct location (the posterior is $\alpha {\text{p}}/\left[ {{\text{p}}\alpha + \left( {{1} - {\text{p}}} \right)\beta } \right] > {\text{p}}$) and a posterior quality estimate less than p if developer 2 fails (with a posterior in this case of $\left( {{1} - \alpha } \right){\text{p}}/\left[ {{\text{p}}\left( {{1} - \alpha } \right) + \left( {{1} - {\text{p}}} \right)\left( {{1} - \beta } \right)} \right] < {\text{p}}$).¹⁹ From (17) and (18), the expected payoffs for developer 2 are greater from herding when

$$ \left( {{1} - \alpha } \right){\text{W}} - \left( {\alpha - \varepsilon } \right){\text{R}} > 0. $$

(19)

(19) defines the conditions under which a fully informed developer will choose to herd at a location that she knows to be bad, and, thus, to have a lower success probability A higher continuation value encourages herding as previously. In this case, however, for a fully-informed developer, if the developer were to always succeed (α = 1), then herding cannot occur. Even fantastically successful developers, however, will fail sometimes, even when they pick the right location, so we do not see α = 1 as an especially realistic case. The initial failure of Canary Wharf in London seems to be an apt example. The second term captures the loss in current value from choosing to herd at the bad location. If the difference in project success probabilities is not too large (α close to ε), this will strengthen the incentive to herd.

In sum, we have established a corollary to Proposition 2.

• Proposition 3: If (19) holds, requiring the continuation payoff to be large relative to congestion costs, then even if developer 2 is fully-informed (as described above), there is a perfect Bayesian equilibrium in which inefficient overbuilding will occur.

• Proof: see above.

Proposition 3 shows that herding is not simply about developers of uncertain quality trying to avoid being correctly identified as being poor risks. It is also about the possibility of having bad luck, which even the best decision makers may encounter. The herding in Proposition 3 arises because the developer wants to avoid the possibility of being falsely labeled a bad developer. The overbuilding that the herding results in is inefficient in both an informational sense (bank does not learn) and an allocative sense (construction in bad locations).

Herds and Booms

Thus far in this section, we have shown that even a fully-informed developer has an incentive to herd at a location that she knows is bad and, thus, offers a lower probability of success. We will now turn to consider a less extreme sort of overbuilding.

The motivation is that the most extreme overbuilding seems to take place in locations that have gone through booms built on plausible economic fundamentals. It is easy, for instance, to find boosters who extolled the Sun Belt. Our model distinguishes these boom locations by supposing that the probability of success (for a herding developer who is good with probability 1, and knows it) at an overbuilt boom location is greater than at a location that is simply bad (δ > ε).

Again, since we are concerned with the possibility of overbuilding, we will consider only the case where developer 2 is choosing to follow what he or she knows to have been a mistake by developer 1.²⁰ And again, we will maintain the bank beliefs outlined immediately above and earlier in the paper. We will then ask, under what conditions will a fully informed developer 2 choose to herd?

In this situation, the expected payoff from developer 2 following her signal remains as given by (18). The expected payoff from herding becomes

$$ \delta {\text{R}} + {\text{W}}. $$

(20)

Using (18) and (20), the expected payoffs are greater from herding when

$$ \left( {{1} - \alpha } \right){\text{W}} - \left( {\alpha - \delta } \right){\text{R}} > 0. $$

(21)

The basic effect thus remains. A high continuation value encourages it (the first term), as does a low cost in current expected payoffs (the second term). Comparing (21) with (19) is instructive. Because δ > ε, the second term in (21) is smaller in absolute value than the second term in (19). This means that herding is more likely in the overbuilt-boom situation. Since it is essentially a stylized fact that most overbuilding takes place in the aftermath of booms, we see this result as having empirical relevance.

Herds and Cascades

We have thus far focused on two related forces that can lead developers to overbuild. The first involves later developers learning from their predecessors. This can be beneficial for a later developer who obtains a better estimate of the state of the market from the actions of earlier movers. The cascade involves some initial learning, and then learning stops. The cascade is costly to later developers because it means that their inferences are based on relatively little information. The second force we have considered is the preservation of a reputation by copying predecessors. This deprives investors of information.

It is worth observing that although these forces are logically distinct, they could potentially both be at work. And if they are, they will reinforce each other. To see this, it is helpful to consider a slightly modified version of the cascade model from earlier in the paper. Consider a sequence of three developers. The first two developers are concerned only with the expected payoffs from the current investment, as in the statistical herding model analyzed above. This would be the case if their quality were known (e.g., if they were established developers). The third developer cares about both current and future activities. This developer has a quality unknown to the bank. As with the reputation model considered above, suppose that if the bank’s estimate of developer quality has become no worse, then the developer will be financed in the future, with a continuation value again given by W. The decisions are as in the statistical model from earlier in the paper: “build” or “locate elsewhere” based on a signal.²¹

We suppose that a good developer receives a signal as in the paper’s earlier statistical herding model. The conditional probability of receiving signal σ ^H conditional on the true state of nature being V = V^H is denoted ϕ    > 1/2. Similarly, the conditional probability of receiving signal σ ^L conditional on the true state of nature being V = V^L is also assumed equal to ϕ. For a bad developer, the signals are noise, with the probability of high- and low-state signals equaling ½ regardless of the true state of nature.

This analysis has been set up so that most of the cascade analysis goes through unchanged. There is no change to the conditions under which the first and second developers’ signals are meaningful, (1) and (4). Suppose that the bank’s beliefs are a slight modification of the perfect Bayesian equilibrium beliefs in the previous reputation analysis. If developers 1 and 2 have made the same decision (either “build” or “elsewhere”) and developer 3 makes the same decision as well, then the bank assumes that developer 3 is herding, that is, copying the predecessors. If developers 1 and 2 make different decisions (one chooses “build”; the other chooses “elsewhere”), then the bank assumes that developer 3 is acting as directed by his signal. Also, if developers 1 and 2 make the same choice but developer 3 makes a different one, then the bank again assumes that developer 3 is acting as directed by his signal.

The key result of this extension is that under these beliefs, herding is more likely to take place than in the paper’s initial simple cascade model. This is because in addition to a developer learning from predecessors (as in the earlier cascade model), the developer now must consider how the bank might learn from his development choice parallel to the paper’s previous reputation analysis.

We are concerned here with the overbuilding case, so suppose that developers 1 and 2 have chosen to build. By choosing to follow the predecessors even with a low-state signal (i.e., herding), developer 3 expects to earn

$$ \phi {{\text{V}}^{\text{H}}} - {\text{F}} - {\text{3C}} + {\text{W}}. $$

(22)

By assumption, the current expected payoff to developer 3 is zero from choosing “elsewhere.” The continuation value from choosing “elsewhere” (i.e., not herding) depends on how the bank might update its posterior regarding developer 3’s quality. This will depend on outcomes. The mechanics are slightly different than above, but the analysis is qualitatively the same. See the Appendix for details. The update will be based on what can be inferred about the developer’s quality from the realized state of nature. Suppose that the state of nature proves to be high. If developer 3 chooses “elsewhere” and the state is actually high, the posterior for developer 3 will be lower. Developer 3 will not receive future financing in this case. Suppose developer 3 chooses “elsewhere,” and the state is actually low. In this case, the bank’s posterior estimate of the quality of developer 3 will be greater than the prior, and developer 3 will be financed in the future. The probability of being in a high state given that developers 1 and 2 have received the high state signal while developer 3 has received the low state signal is ϕ as discussed earlier. Thus, the expected payoff from choosing “elsewhere” is zero (the first period payoff) plus (1    −    ϕ)W, the expected value of the reputation. This means that the condition under which developer 3 should follow the predecessors is the difference between (22) and (1    −    ϕ)W, which is

$$ \phi {{\text{V}}^{\text{H}}} - {\text{F}} - {\text{3C}} + \phi {\text{W}} > 0. $$

(23)

Because of the last term—the reputation effect—(23) is weaker than the condition under which expected profit is positive for the third developer in the basic cascade model. It is easy. It is easy to see that this makes successive developers more willing to herd as well.

There is one important additional difference between this analysis and the cascade model from earlier in the paper. In the pure cascade case, the amount of overbuilding is ultimately limited by congestion, as can be seen in (7) and (8) above. In this modified model, the parallel conditions for the arrest of overbuilding are

$$ \phi {{\text{V}}^{\text{H}}} - {\text{F}} - {\text{nC}} + \phi {\text{W}} > 0 $$

(24)

and

$$ \phi {{\text{V}}^{\text{H}}} - {\text{F}} - \left( {{\text{n}} + {1}} \right){\text{C}} + \phi {\text{W}} \leqslant 0. $$

(25)

Because of the reputation term, these correspond to more overbuilding.

In sum, when there is the potential for both statistical and reputational herding, herding is both more likely and more serious when it occurs.

Conclusions

This paper has shown that two kinds of herding by developers—statistical and reputation-based—can lead to overbuilding. The statistical herding arises because developers can learn from each other’s decisions. If early developers obtain inaccurate signals that a market is strong, this can lead to an information cascade where later developers choose to ignore their signals, leading to overbuilding. The reputational herding arises because developers want to frustrate bank attempts to discern their true quality or because they are afraid the bank will draw incorrect inferences regarding their quality, leading them to ignore their signals and overbuild in particular markets. In the former case, developers do not know any better than to overbuild. In the latter case, overbuilding is a fully-informed choice.

It is important to be clear that we are not claiming that the two types of herd behavior are always at work. Instead, the analysis suggests the possibility of herd behavior as a contributing factor to the overbuilding discussed in the Introduction. It is possible that overbuilding arising from irrational expectations of consumers might be moderated in the near future by the hard lessons of the recent boom and bust cycle. It is difficult to believe that households have not really learned that real estate is not necessarily as “safe as houses.”

In contrast, the overbuilding analyzed here arises from behavior that is entirely rational. In fact, herding can be optimal even for a developer who is certain that the common wisdom is fallacious, as illustrated above. The rationality of herding means that there are no lessons that agents can learn from recent events that would remove the herding incentives.

The analysis in the paper has been set out to explain the overbuilding that plagues some markets as of this writing. This is only one kind of imitation in real estate. The Introduction refers to other sorts, including copying the sorts of malls and communities that predecessors have built. In addition to offering a possible explanation for overbuilding, this paper’s analysis can explain these sorts of imitation as well.

It is important to recognize, however, that the imitation that this paper has generated depends on the model framework that has been employed. In this paper’s models, uncertainty encourages developers to copy each other, and so it can lead to overbuilding. The possibility of herding depends on solitary developers having low expected payoffs. In the statistical model, they had low expected payoffs because choosing a solitary location amounted to flouting the wisdom of the crowd. In the reputation model, they had low expected payoffs because selecting a unique location risked losing access to future financing, and, thus, continuation payoffs.

While this analysis is correct, there are situations where contradictory forces are at work to raise the expected payoff to solitary activity. Effinger and Polborn (2001) consider a situation with what they call “anti-herding.” Their model deals with reputation-based strategic herding rather than information cascades and statistical herding. Experts may want to avoid revealing signals that they think differently in order not to risk their reputations. However, if the expected value of being better than other experts is sufficiently high, they may want to reveal that they think differently. In the strongest (“anti-herding”) situation, they actually choose to locate away from their own and their rival’s signals in order to reduce the risk of being thought of as an ordinary expert. Their model is couched in a model of Bertrand competition where there is little value to expertise that is broadly distributed.

This sort of effect can be brought into the paper’s reputation analysis through the continuation payoff. Instead of supposing that developers who are of a reservation quality are funded and obtain W, suppose that the continuation payoff is given by the function W(ρ), an increasing function of the posterior probability of being good as perceived by the bank, ρ. Now suppose that the bank believes that developers locate according to their signals. In the case of signal disagreement, the second developer has expected earnings of

$$ \alpha {\text{p}}/\left( {{1} + {\text{p}}} \right) \left[ {{\text{R}} + {\text{W}}\left( {1} \right)} \right] $$

(26)

from locating as directed by her signal. The developer’s expected earnings are

$$ \alpha {\text{p}}/\left( {{1} + {\text{p}}} \right)\left[ {{\text{R}} - {\text{C}}} \right] + {\text{W}}\left( \rho \right) $$

(27)

from herding. Herding and thus overbuilding is chosen when

$$ {\text{W}}\left( \rho \right) - \alpha {\text{p}}/\left( {{1} + {\text{p}}} \right)\left[ {{\text{C}} + {\text{W}}\left( {1} \right)} \right] > 0. $$

(28)

In this case, the locate-as-signaled equilibrium can now be viable if the payoffs of being recognized as high quality are high enough. This is in addition to the previously discussed effect of congestion costs, which discourage herding. Overbuilding is, therefore, less likely with this modification to payoffs.

In the case of real estate, this situation could be manifested in the best developers being granted more credit. To the extent that this results in better-informed agents making more decisions, this would also reduce the statistical tendency for overbuilding.

There is an additional situation in which the tendency for overbuilding may not be present. Because we are interested in exploring the forces that have led to overbuilding, we have focused much of the analysis on situations where early decisions to build or agglomerate are imitated, leading to excess supply. It is important to recognize that the analysis in the paper goes through essentially identically for the inverse case, the one where the early decisions that are imitated are not to build or to agglomerate but instead to wait or to disperse. The forces considered here can potentially, therefore, explain not just the excesses of a boom but also the negative excesses of the bust, a silent herd.

Appendix

This Appendix contains additional detail on the Bayesian updating of developer quality.

Section III

The expected profit for the first developer choosing “build” is ${\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) - {\text{F}} - {\text{C}}$ if the developer receives the high state signal. Since revenues are either V^H or 0, ${\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right){{\text{V}}^{\text{H}}}$. By Bayes Rule, ${\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {\sigma = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right){\text{prob}}\left( {\sigma = {\sigma^{\text{H}}}} \right)/{\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)$. By assumption, prob(V = V^H)    =  1/2. The unconditional probability of receiving the good signal is ${\text{prob}}\left( {\sigma = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {\sigma = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right){\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right) + {\text{prob}}\left( {\sigma = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = 0} \right){\text{prob}}\left( {{\text{V}} = 0} \right) = \phi * \left( {{1}/{2}} \right) + \left( {{1} - \phi } \right) * \left( {{1}/{2}} \right) = {1}/{2}$. Thus, ${\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right) = \phi$, so we have ${\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) = \phi {{\text{V}}^{\text{H}}} - {\text{F}} - {\text{C}}.$

Suppose that the first developer has behaved as if she has received the high state signal. If the second developer receives the high signal, then we have by Bayes’ Rule

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad * {\text{ prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)/{\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad = {\phi^{{2}}} * \left( {{1}/{2}} \right)/\left[ {\left( {{1}/{2}} \right)\left[ {{\phi^{{2}}} + {{\left( {{1} - \phi } \right)}^{{2}}}} \right]} \right] = {\phi^{{2}}}/\left[ {{\phi^{{2}}} + {{\left( {{1} - \phi } \right)}^{{2}}}} \right]} \hfill \\ \end{array} $$

(A.1)

If the second developer receives the low signal, we have

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{L}}}} \right) = {\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad * {\text{ prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)/{\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = \phi * \left( {{1} - \phi } \right) * \left( {{1}/{2}} \right)/\left[ {\phi * \left( {{1} - \phi } \right)} \right] = {1}/{2}} \hfill \\ \end{array} $$

(A.2)

If the third developer observes that both predecessors have built but obtains a negative signal, the probability of the high state is by Bayes’ Rule equal to:

$$ \begin{array}{*{20}c} {{{\text{prob}}{\left( {{\text{V}} = {\text{V}}^{{\text{H}}} \left| {\sigma _{1} = } \right.\sigma ^{{\text{H}}} \cap \sigma _{2} = \sigma ^{{\text{H}}} \cap \sigma _{3} = \sigma ^{{\text{L}}} } \right)}}} \hfill \\ {\quad \quad \quad \quad { = {\text{prob}}{\left( {\sigma _{1} = \sigma ^{{\text{H}}} \cap \sigma _{2} = \sigma ^{{\text{H}}} \cap \sigma _{3} = \sigma ^{{\text{L}}} \left| {{\text{V}} = {\text{V}}^{{\text{H}}} } \right.} \right)}}} \hfill \\ {\quad \quad \quad \quad {*{\text{prob}}{\left( {{\text{V}} = {\text{V}}^{{\text{H}}} } \right)}/{\text{prob}}{\left( {\sigma _{1} = \sigma ^{{\text{H}}} \cap \sigma _{2} = \sigma ^{{\text{H}}} \cap \sigma _{3} = \sigma ^{{\text{L}}} } \right)}}}\hfill \\ {\quad \quad \quad \quad { = \phi ^{2} *{\left( {1 - \phi } \right)}*{\left( {1/2} \right)}/{\left( {1/2} \right)}{\left[ {\phi ^{2} {\left( {1 - \phi } \right)} + {\left( {1 - \phi } \right)}^{2} \phi } \right]}}} \hfill \\ {\quad \quad \quad \quad { = \phi ^{2} {\left( {1 - \phi } \right)}/{\left[ {\phi ^{2} {\left( {1 - \phi } \right)} + {\left( {1 - \phi } \right)}^{2} \phi } \right]} = \phi .}} \hfill \\ \end{array} $$

(A.3)

In the case where developers differ in quality, the probability of a high state of nature when developers 1 and 2 have received positive signals and developer 3 has received a negative signal is

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right) = {\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}} \cap {\sigma_{{3}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)/{\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = \left[ {{\phi_{{1}}}{\phi_{{2}}}\left( {{1} - {\phi_{{3}}}} \right)} \right]/\left[ {{\phi_{{1}}}{\phi_{{2}}}\left( {{1} - {\phi_{{3}}}} \right) + \left( {{1} - {\phi_{{1}}}} \right)\left( {{1} - {\phi_{{2}}}} \right){\phi_{{3}}}} \right].} \hfill \\ \end{array} $$

(A.4)

Section IV

In this section, we have assumed that there are multiple good locations. This means that updating will be based only on whether projects succeed or fail when the developers have picked different locations. If the second developer selects a distinct location and succeeds, the probability of the developer being good is

$$ \begin{array}{*{20}c} {{{\text{prob}}{\left( {{\text{developer}}\;2\;{\text{is}}\;{\text{good}}\left| {{\text{developer}}\;2\;{\text{succeeds}}} \right.} \right)}}} \hfill \\ {\quad \quad \quad { = {\text{prob}}{\left( {{\text{developer}}\;2\;{\text{succeeds}}\left| {{\text{developer}}\;2\;{\text{is}}\;{\text{good}}} \right.} \right)}}} \hfill \\ {\quad \quad \quad {*{\text{prob}}{\left( {{\text{developer}}\;2\;{\text{is}}\;{\text{good}}} \right)}/{\text{prob}}{\left( {{\text{developer}}\;2\;{\text{succeeds}}} \right)}}} \hfill \\ {\quad \quad \quad { = \alpha *{\text{p}}/{\left[ {{\text{p}}\alpha + {\left( {1 - {\text{p}}} \right)}\beta } \right]} > {\text{p}}}} \hfill \\ \end{array} $$

(A.5)

If the second developer selects a distinct location and fails, the probability of the developer being good is

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {\left. {\text{developer 2 is good}} \right|{\text{developer 2 fails}}} \right)} \hfill \\ {\quad \quad \quad = {\text{prob}}\left( {\left. {\text{developer 2 fails}} \right|{\text{developer 2 is good}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {\text{developer 2 is good}} \right)/{\text{prob}}\left( {\text{developer 2 fails}} \right)} \hfill \\ {\quad \quad \quad = \left( {{1} - \alpha } \right){\text{p}}/\left[ {{\text{p}}\left( {{1} - \alpha } \right) + \left( {{1} - {\text{p}}} \right)\left( {{1} - \beta } \right)} \right] < {\text{p}}.} \hfill \\ \end{array} $$

(A.6)

Section V

Suppose that the high state of nature is realized. If developer 3 chooses “elsewhere” and developers 1 and 2 both choose build, then the bank’s posterior estimate of developer 3’s quality is:

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {\left. {\text{developer 3 is good}} \right|{\text{V}} = {{\text{V}}^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}} \cap {\sigma_{{3}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{developer 3 is good}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {\text{developer 3 is good}} \right)/{\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{p}}\left( {{1} - \phi } \right) * \left( {{1}/{2}} \right)/\left[ {\left( {{1}/{2}} \right)\left[ {{\text{p}}\left( {{1} - \phi } \right) + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right]} \right] = {\text{p}}\left( {{1} - \phi } \right)/\left[ {{\text{p}}\left( {{1} - \phi } \right) + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right] < {\text{p}}} \hfill \\ \end{array} $$

(A.7)

Similarly, if developers 1 and 2 both choose build and the low state of nature is realized, and developer 3 has received the low-state signal, the bank’s posterior for developer 3 is:

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {\left. {\text{developer 3 is good}} \right|{\text{V}} = {{\text{V}}^{\text{L}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{L}}} \cap {\sigma_{{3}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{developer 3 is good}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {\text{developer 3 is good}} \right)/{\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{L}}} \cap {\sigma_{{1}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{p}}\phi * \left( {{1}/{2}} \right)/\left[ {\left( {{1}/{2}} \right) \left[ {{\text{p}}\phi + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right]} \right] = {\text{p}}\phi /\left[ {{\text{p}}\phi + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right] > {\text{p}}.} \hfill \\ \end{array} $$

(A.8)