High-order PLS path model with qualitative external information

Abstract

A common situation in the analysis of latent constructs is the availability of external information about the data which could affect the model parameters’ estimation. In this paper a procedure for isolating these information based on the orthogonal projectors in the frame of second order PLS-PM is presented. An application to a case study in the field of the measurement of the subjective quality of work will show the way of functioning and the results obtained from the proposed procedure.

1 Introduction

A frequent scenario which occurs in the analysis of psychometric data is the one in which: (a) the theoretical concept is hierarchical in nature, and it might then be decomposed in sub-dimensions according to a multiple level structure; (b) additional information about units and/or variables are available and they could potentially be relevant for the analysis of the theoretical concept.

As concerns the former aspect, a well-known procedure for estimating the parameters related to latent hierarchical relations, based on the partial least squares path model (PLS-PM) method, has been proposed in literature: the repeated indicators (or hierarchical component) approach Lohmöller (1989). The latter aspect is rooted in the tradition of the External Information Analysis proposed in Yanai (1970).

In the present study, the method of orthogonal projectors is proposed for additively decomposing the original data matrix into two matrices, one representing the external information component and the other one of residuals (that part of data which is not explained by the external information). The high-order PLS estimation is then applied to the original and residual matrices.

This approach allows to analyze the hierarchical latent structure and interpreting it according to different sources of variation.

The paper is organized as follows: in Sects. 2 and 3 the high-order PLS approach and the External Information Analysis are shown. A case study is presented in Sect. 4 in order to illustrate an application of the proposed method.

2 PLS-PM algorithm

In the following sections we introduce the PLS-PM estimation procedure and the formalization of the high-order PLS-PM considering as example a second-order model.

2.1 PLS-PM estimation procedure

The PLS-PM is the most suitable tool for the investigation of relations with a high level of abstraction. Proposed for the first time by Herman Wold to be used in multivariate analysis, the basic PLS algorithm was subsequently extended for its application in the structural equation modelling (SEM) in 1975 Wold (1975) by Wold himself. An extensive review on PLS approach is given in the Handbook of PLS Esposito Vinzi et al. (2010). The model-building procedure can be thought of as the analysis of two conceptually different models. While the measurement (or outer) model specifies the relationships of the observed variables with their (hypothesized) underlying (latent) constructs, the structural (or inner) model then specifies the causal relationships among latent constructs, as posited by some theory. The two sub-models are the following:

$$\begin{aligned} {\varvec{\xi }}_{(m,1)}&= \mathbf{{B}}_{(m,m)} {\varvec{\xi }}_{(m,1)} + {\varvec{\tau }}_{(m,1)} \nonumber \\ \mathbf{{x}}_{(p,1)}&= {\varvec{\Lambda }}_{(p,m)} {\varvec{\xi }}_{(m,1)} + {\varvec{\delta }}_{(p,1)} \end{aligned}$$

(1)

where the subscripts $m$ and $p$ are the number of, respectively, the latent (LVs) and the manifest variables (MVs) in the model, while the letters $\varvec{\xi }$, $\mathbf {x}$, $\mathbf {B}$, $\varvec{\Lambda }$, $\varvec{\tau }$ and $\varvec{\delta }$ indicates LVs and MVs vectors, the path coefficients linking the LVs, the factor loading linking the MVs to the LVs, and the errors terms of the model. The observations taken on n units, for the p variables, are collected in the centered data matrix $\mathbf {X}_{(n,p)}$.

The parameters estimation (Ciavolino and Al-Nasser 2009; Ciavolino 2012) follows a double approximation of the $(n,1)$ vectors of scores corresponding to the LVs $\varvec{\xi }_j$ (with $j=1, ...,m$). The external estimation of $\varvec{\xi }_j$, named $\mathbf {y}_j$, is obtained as the product of the block of MVs $\mathbf {X}_j$ (considered as the matrix units for variables) by the outer weights $\mathbf {w}_j$ (which represent the estimation of measurement coefficients, $\varvec{\Lambda }$). The internal estimation, $\mathbf{z}_j$, is obtained as the product of the external estimation $\mathbf {y}_j$ and the inner weights $\mathbf {e}_j$. According to the hypothesized relationship among MVs and LVs, outer weights are computed as:

$$\begin{aligned} \mathbf{w}_j = \mathbf{X}_j^{'} \mathbf{z}_j \end{aligned}$$

for Mode A (reflective relationship), and:

$$\begin{aligned} \mathbf{w}_j = (\mathbf{X}_j^{'} \mathbf{X}_j)^{ - 1} \mathbf{X}_j^{'} \mathbf{z}_j \end{aligned}$$

or Mode B (formative relationship). The inner weights $\mathbf {e}_j,i$, are defined through the correlations between $\mathbf {y}_j$ and the connected $\mathbf {y}_i$, with $i\ne j$. The estimation of the inner weights follow three different schemes:

• the sign of the correlation between each pair of external estimations $\mathbf {y}_i$ and $\mathbf {y}_j$ (centroid scheme);

• the correlation between each pair of $\mathbf {y}_j$ (factorial scheme);

• the multiple regression coefficient among $\mathbf {y}_j$ (path weighting scheme).

The PLS algorithm starts by initializing outer weights to one for the first MV of each LV; then, the parameters estimation is performed, until convergence, by iteratively computing:

• 1. external estimation, $\mathbf {y}_j=\mathbf {X}_j \mathbf {w}_j$;

• 2. internal estimation, $\mathbf {z}_j=\sum _j \ne i \mathbf {e}_{j,i} \mathbf {y}_j$;

• 3. outer weights estimation, with Mode A or B.

The causal paths among LVs (the coefficients in the B matrix) may be obtained through Ordinary Least Squares (OLS) method.

2.2 Second-order PLS-PM

Wold’s original design of PLS path modelling does not consider higher-order latent variables, where some or all the MVs are assumed to be also linked to a higher-order factor, interpreting what the lower order LVs have in common and what makes them correlated. On this basis, a special procedure for the case of hierarchical constructs has been proposed by Lohmöller Lohmöller (1989), the so-called Hierarchical Component Model or Repeated Indicators Approach, which is the most popular approach when estimating higher-order constructs through PLS. The procedure is very simple: the second-order factor is directly measured by the observed variables previously used for the first-order factors. Although this approach repeats the number of MVs used, the model can be estimated by the standard PLS algorithm Reinartz et al. (2004). The manifest indicators, measuring each first-order LV, are simply repeated in order to represent the higher-order construct. Because of its simplicity, this approach is the most used by researchers who want to model higher-order constructs with PLS. A disadvantage of this approach is a possibly biasing of the estimates by relating variables of the same type together through PLS estimation Ciavolino and Nitti (2013). According with Rajala and Westerlund (2010), the Repeated Indicators approach could be applied provided that all the measurement relationships are modelled as reflective.

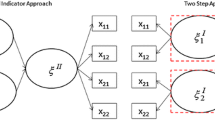
The measurement and the path coefficients’ matrices assume, in this case, a particular structure, that will be described through an example. Let us suppose that a model has two first-order LVs $\varvec{\xi }^I=(\xi ^{I}_1,\xi ^{I}_2)'$, and one second-order LV $\xi ^{II}$ (the superscripts are used for distinguishing the order of the LVs in the model). The first-order and the second-order LVs can be formalized in a single vector as follow: $\varvec{\xi }=(\xi ^{I}_1,\xi ^{I}_2,\xi ^{II})'$. Each of the first-order LVs is measured by two MVs ($x_1$-$x_2$ and $x_3$-$x_4$, respectively), while the high-order LV reflects on the four MVs, as sketched in Fig. 1.

Fig. 1

Second-order path diagram

The observed data matrix X is thus made up by $2p=8$ columns and the coefficients matrices are set as follows:

$$\begin{aligned} \mathbf {\varvec{\Lambda }}_{(8,3)}=&\begin{bmatrix} \varvec{\varLambda }^I_{(4,2)}&\quad \mathbf 0 _{(4,1)}\\ \mathbf 0 _{(4,2)}&\quad \varvec{\varLambda }^{II}_{(4,1)} \end{bmatrix} =\begin{bmatrix} {\lambda }^I_{11}&\quad 0&\quad 0 \\ {\lambda }^I_{21}&\quad 0&\quad 0\\ 0&\quad {\lambda }^I_{32}&\quad 0 \\ 0&\quad {\lambda }^I_{42}&\quad 0\\ 0&\quad 0&\quad {\lambda }^{II}_{53} \\ 0&\quad 0&\quad {\lambda }^{II}_{63}\\ 0&\quad 0&\quad {\lambda }^{II}_{73} \\ 0&\quad 0&\quad {\lambda }^{II}_{83} \end{bmatrix}&\mathbf {B}_{(3,3)}=&\begin{bmatrix} 0&\quad 0&\quad {\beta }_{13} \\ 0&\quad 0&\quad {\beta }_{23}\\ 0&\quad 0&\quad 0 \end{bmatrix} \end{aligned}$$

(2)

As the number of MVs is doubled, the matrix $\varvec{\varLambda }$ of the measurement coefficients has dimension ${(2p,m)}$, which in our example is (8,3). For the first $p$ (1 to 4) rows, a measurement coefficient ${\lambda }$ is provided when a link from the first-order LV to the MV holds, and 0 elsewhere. In the last $p$ rows (5–8), the replicated MVs are linked to the second-order LV by setting a ${\lambda }$ in the third column. As concerns the matrix B of the path coefficients, it is constrained to have ${\beta }$s only in correspondence of the path coefficients linking ${\xi }^{II}_2$ to the two first-order LVs. Then, using the parameter matrices 2 to define the second-order form, the model in the Eq. 1 becomes:

$$\begin{aligned} \varvec{\xi }_{(3,1)}&= \mathbf{{B}}_{(3,3)} {\varvec{\xi }}_{(3,1)} + {\varvec{\tau }}_{(3,1)} \nonumber \\ \mathbf{{x}}_{(4,1)}&= {\varvec{\Lambda }}^{I}_{(4,2)} {\varvec{\xi }}^{I}_{(2,1)} + {\varvec{\delta }}^{I}_{(4,1)}\nonumber \\ \mathbf{{x}}_{(4,1)}&= {\varvec{\Lambda }}^{II}_{(4,1)} {\xi }^{II} + {\varvec{\delta }}^{II}_{(4,1)} \end{aligned}$$

(3)

Note that, in the measurement (2nd and 3rd) equations of model (3), the dependent variables are the same: from here the name of “repeated indicators” approach.

3 External information analysis

External information can be used in the high-order model defined in the previous paragraph to take into account characteristics about the units or about the variables Takane and Shibayama (1991). Some examples can be considered as belonging to a specific group for the units (for example, in the case of persons: age, sex, education; in the case of firms: sector of activity, juridical status), or to define categorization of the variables (as those underlying the same concept, socio-demographic and measures). The external information can be formalized by defining orthogonal projectors and ortho-complementary projectors for the rows and for the columns. Let consider a matrix $\mathbf {X}$ with $p$ variables, and two matrices: $\mathbf {U}$, for the external information on the rows, with $n$ rows and $q$ columns; $\mathbf {C}$ of the external information on the columns, with $p$ rows and $r$ columns.

The method decomposes the original data into several components, those that can be explained, and those that would be independent of the external information Yanai (1970). The introduction of the external information in the data is made by using the mathematical concept of the projection. Let define the quantity:

$$\begin{aligned} \mathbf {P}_U = \mathbf {U} (\mathbf {U}' \mathbf {U})^{-1} \mathbf {U}' \end{aligned}$$

(4)

The square matrix $(n,n)$ $\mathbf {P}_U$ is symmetric and idempotent: $\mathbf {P}_U = \mathbf {P}^{'}_U$ and $\mathbf {P}_U = \mathbf {P}^{2}_U$, so allowing directly the expression of the projection. Following the least squares principle, the matrix $\mathbf {X}$ can be decomposed into the following components:

$$\begin{aligned} \mathbf {X} = \mathbf {P}_U \mathbf {X} + \mathbf {Q}_U \mathbf {X} = (\mathbf {U} (\mathbf {U}' \mathbf {U})^{-1} \mathbf {U}') \mathbf {X} + (\mathbf {I} - \mathbf {U} (\mathbf {U}' \mathbf {U})^{-1} \mathbf {U}') \mathbf {X} \end{aligned}$$

(5)

where $\mathbf {I}$ is the identity matrix and $\mathbf {Q}_U =( \mathbf {I} - \mathbf {P}_U )$ is the ortho-complementary projector, such that $\mathbf {P}_U \mathbf {Q}_U=\mathbf {0}$. Premultiplying by $\mathbf {X}'$ and $1/n$ we obtain the covariance matrix:

$$\begin{aligned} \begin{aligned}&Cov(X,X)=\frac{1}{n} \mathbf {X}' \mathbf {X}= \frac{1}{n} \mathbf {X}' \mathbf {U} (\mathbf {U}' \mathbf {U})^{-1} \mathbf {U}' \mathbf {X} + \\&\quad + \frac{1}{n} (\mathbf {X}' \mathbf {X} - \mathbf {X}' \mathbf {U} (\mathbf {U}' \mathbf {U})^{-1} \mathbf {U}' \mathbf {X}) \end{aligned} \end{aligned}$$

which can be rewritten as follows:

$$\begin{aligned} \begin{aligned}&Cov(X,X)=Cov(X,U) Cov(U,U)^{-1} Cov(U,X)+\\&\qquad +[ Cov(X,X) - Cov(X,U) Cov(U,U)^{-1} Cov(U,X)] =\\&\quad =Cov(X,X|P_{U})+Cov(X,X|Q_{U}) \end{aligned} \end{aligned}$$

By performing a Principal Component Analysis (PCA) on $Cov(X,X|P_{U})$ we obtain components which relate to the external information, while performing the PCA on $Cov(X,X|Q_{U})$ we obtain components free of the external information. Moreover, the extracted eigenvalues reflect the part of the variability related to the effect of the external information given by the fact that the sum of the eigenvalues of $Cov(X,X|P_{U})$ and $Cov(X,X|Q_{U})$ is equal to the sum of the eigenvalues of $Cov(X,X)$.

The same consideration can be done on the matrix $\mathbf {C}$, related to the external information on the columns, obtaining the following $(p,p)$ projector:

$$\begin{aligned} \mathbf {P}_C= \mathbf {C} (\mathbf {C}' \mathbf {C})^{-1} \mathbf {C}' \end{aligned}$$

(6)

In case $\mathbf {X}$ is in standardized form, $Cov(X,X)$ is the correlation matrix and the total variance (the sum of the eigenvalues) is equal to $p$ (the number of variables). Taking into account the information about the columns, the matrix of the measurements $\mathbf {X}$ can be decomposed according to the following relationship:

$$\begin{aligned} \mathbf {X} = \mathbf {P}_U \mathbf {X} \mathbf {P}_C + \mathbf {Q}_U \mathbf {X} \mathbf {P}_C + \mathbf {P}_U \mathbf {X} \mathbf {Q}_C + \mathbf {Q}_U \mathbf {X} \mathbf {Q}_C \end{aligned}$$

(7)

where the matrix $\mathbf {Q}_C =(\mathbf {I} - \mathbf {P}_C)$ is the ortho-complementary projector of $\mathbf {P}_C$, such that $\mathbf {P}_C \mathbf {Q}_C=\mathbf O$. Each term has a precise statistical meaning in it; in particular:

• $\mathbf {P}_U \mathbf {X} \mathbf {P}_C$ indicates the effect of row and column information,

• $\mathbf {Q}_U \mathbf {X} \mathbf {P}_C$ is the effect of column information without the effect of the row one,

• $\mathbf {P}_U \mathbf {X} \mathbf {Q}_C$ is the effect of row information without the column ones,

• $\mathbf {Q}_U \mathbf {X} \mathbf {Q}_C$ is the part which disregards external information.

A particular case of a projector can be defined by considering a dummy variable, or a collection of dummy variables, defining the orthogonal projector for the units. Let define $\mathbf {P}_U$ as a dummy matrix projector, where each column represents a group and each row has value one when the unit is a member of the group and zero otherwise. $\mathbf {Q}_U =(\mathbf {I} - \mathbf {P}_U)$ is the ortho-complementary projector. In this case the matrix $\mathbf {P}_U \mathbf {X}$ reports the mean values of each group, or, in case of standardized matrix, the deviation of the class mean from the total mean. The matrix $\mathbf {Q}_U \mathbf {X}$ is the residual matrix of the values from the total mean.

3.1 High-order PLS-PM with external information

Our idea is the integration of a high-order PLS-PM with the external information, in order to improve the interpretation of the results. The proposal is the use of the repeated indicators approach for the definition of the model, by using, both at first and at second level, matrices that integrate and leave out external information. In this case the external information regard just the observations, and the matrix of the external information on the variables is an identity matrix $\mathbf {P}_C = \mathbf {I}$. As a result the formula (7) is reduced to formula (5). By defining $\mathbf {P}_U \mathbf {X}= \mathbf {PX}$ and $\mathbf {Q}_U \mathbf {X}= \mathbf {QX}$ we can rewrite the formula as follow:

$$\begin{aligned} \mathbf {X} = \mathbf {PX} + \mathbf {QX} \end{aligned}$$

(8)

We will estimate two models: the first model, that uses as indicators the dataset $\mathbf {X}$ and will be the reference model to evaluate the latent and the links among the variables; the second model, which uses as indicators the dataset $\mathbf {QX}$ to evaluate the change in the latent structure when the observed data are depurated from the qualitative external information.

4 Organizational justice case study

One greatly important dimension of the subjective quality of work is the organizational justice, measured from the psychological point of view with the fairness perception. The organizational justice can be detected in relation to many different aspects of work, related to two sub-dimensions: distributive justice and procedural justice (Paul (2006); Tortia (2008); Jones and Martens (2009)). The distributive justice relies on the perceived fairness of one’s outcome with respect to the input/output ratio; it can be distinguished into individual distributive fairness (related to stress, responsibility and effort of worker) and others distributive fairness (related with wages of colleagues and superiors). Instead, the procedural justice concerns the perceived fairness of the formal allocation process, measured by procedural fairness, expressed by the availability of information on worker activity and organisation goals, and interactional fairness, as the attention to workers’ needs and proposals. Walumbwa et al. Walumbwa et al. (2009) considered the effects of procedural and distributive justice on the feeling of inclusion or belongingness to a particular organization, and studied the effects of interactional justice on the quality of the leader-member exchange relationships with their immediate superiors. Their final hypothesis is that organizational identification and leader-member exchange relationships have a heavy effect on the job performance, via the moderator effect of the voluntary learning behaviour of employees. Therefore, the theoretical path model is reported in Fig. 2 where the LVs are Organizational Justice (second-order), Distributive and Procedural Justice (first-order), and the MVs are Distributive Fairness Individual and Others (linked to the Distributive Justice) and Procedural and Interactional Fairness (linked to the Procedural Justice).

Fig. 2

Second-order PLS-PM path diagram

4.1 Data collected

The dataset used in our study derive from the $ICSI {2007}$ (Indagine sulle Cooperative Sociali Italiane, 2007), a survey that concerns 320 social cooperatives sampled from the Istat-Census 2003 database of the Italian National Institute of Statistics, with 4,134 paid workers that in 2007 answered the questionnaire designed by academic experts in economic and organisation fields with the aim to investigate the objective and subjective quality of work in the non-profit sector (Carpita (2009);Depedri et al. (2010)). Following the route in the organizational research previously outlined, for the organizational justice dimension we have considered the following four multi-item ordinal scales included in the $ICSI {2007}$ questionnaire:

• DISTRIBUTIVE FAIRNESS - INDIVIDUAL: “Do you think that your overall pay is fair compared with ...”

  5 items: (i) Stress, (ii) Responsibility, (iii) Effort, (iv) Training, (v) Loyalty

  Response Scale:

  1 = Much less than fair, 2, ..., 4 = Fair, ..., 6, 7 = Much more than fair

• DISTRIBUTIVE FAIRNESS - OTHERS: “Do you think that your overall pay is fair compared with ...”

  4 items: (i) Wage others, (ii) Wage Colleagues, (iii) Wage Superiors, (iv) Co-operative Resources

  Response Scale:

  1 = Much less than fair, 2,..., 4 = Fair,..., 6, 7 = Much more than fair

• PROCEDURAL FAIRNESS: “How much you agree with the following statements? Your firm give to you...”

  5 items: (i) Information, (ii) Equality, (iii) Targets, (iv) Guidelines, (v) Respect

  Response Scale:

  1 = Strongly disagree, 2,..., 6, 7 = Strongly agree

• INTERACTIONAL FAIRNESS: “Your supervisor or your superiors are fair with respect to ...”

  6 items: (i) Listening, (ii) Advice, (ii) Working needs, (iv) Attention, (v) Personal needs, (vi) Availability

  Response Scale:

  1 = Definitely not, 2,..., 4 = Neither yes nor no,..., 6, 7 = Definitely yes.

In order to lighten the subsequent analysis, we considered the unidimensional measures of the four fairness sub-dimensions summarizing the original 20 items contained in the $ICSI {2007}$ dataset, obtained by a previous Rasch Analysis Carpita and Golia (2012). This procedure is aimed at reducing the complexity of the model and the number of parameters that must be estimated, and allows for separation between reliability studies and more substantive research Oberski and Satorra (2013).

The reliability of these measures, estimated with the Person Reliability Index Linacre (2012), are 0.89 and 0.74 for Individual and Other Distributive Fairness respectively, 0.80 for Procedural Fairness and 0.79 for Interactional Fairness. These measures had been used in other analyses, to assess their validity as drivers of the job satisfaction Carpita and Vezzoli (2012).

In this study we consider the cooperatives as the statistical units of analysis, using the averages of the four Rasch measures as organizational fairness perceptions of their paid workers¹. To ensure a suitable coverage level, we have considered the subset of 175 social cooperatives with more than 40 % of randomly sampled respondent paid workers: these are 1,898 of all the 3,088 (61.5 %) paid workers of the 175 cooperatives.

As qualitative external information we have considered the following three organization’s characteristics, that were informative in other previous studies on the $ICSI {2007}$ dataset (Manisera (2011); Carpita and Golia (2012))²:

• Class of paid workers. The social cooperatives have been distinguished according to the number of paid workers and grouped into two categories: less than 20 workers (65.7 %) and 20 or more workers (34.3 %).

• Geographical area. The social cooperatives from Northern (58.3 %), Central (12 %) and Southern (29.7 %) Italy are differentiated in order to determine the effects due to the location.

• Juridical status. The social cooperatives of “Type A” (65.7 %) and “Type B” (34.3 %) have been distinguished, being the former mainly oriented at providing health, social and/or educational services, and the latter at integrating disadvantaged people into the labour market.

In order to explore the structure of the collected data, the joint use of the PLS-PM and the External Analysis method have been implemented. This combined analysis is aimed at revealing the extent to which removing the effect of the qualitative information about the cooperatives can modify the latent structure of the Organizational Justice second-order construct.

4.2 Results

A preliminary Principal Component Analysis (PCA) showed the effect of introducing the external information in the data. The PCA has been performed on the three matrices $\mathbf {X}$ (containing the four Rasch measures), $\mathbf {PX}$ (the effects of the external information on units) and $\mathbf {QX}$ (that part of data excluding the external information); the scree-plot reporting the respective eigenvalues is shown in Fig. 3.

Fig. 3

Variance explained by each PC for the three datasets in (8)

For the matrix of the raw data, $\mathbf X$, the sum of the eigenvalues is equal to 4 (the total variance of the four standardized variables). Most of the variability is accounted for by the first principal component (eigenvalue = 2.28), while the second eigenvalue is slightly higher than 1. For the data matrix of the external information $\mathbf {PX}$ the sum of the eigenvalues is 0.666, which means that the percentage of variance explained by the three organization’s characteristics is equal to 16.7 %. For the residual matrix $\mathbf {QX}$ the sum of the eigenvalues is equal to 3.334 (proportion of variance 83.3 %). The sum of the first eigenvalues of $\mathbf {PX}$ and $\mathbf {QX}$ is almost equal to the first eigenvalue of $\mathbf {X}$: the projection of $\mathbf {X}$ on the external information reduce the variance explained by the first principal component of $\mathbf {X}$.

Figure 4 shows the projections of the 175 observations (cooperatives) and of the four variables (fairness perceptions) on the first two principal components of $\mathbf X$, $\mathbf {PX}$ and $\mathbf {QX}$ respectively. Note that scatterplots of $\mathbf X$ and $\mathbf {QX}$ on the left looks like very similar. Instead, the observations of $\mathbf {PX}$ are restricted to be the averages related to the external informations (there are $2 \cdot 3 \cdot 2 - 1 = 11$ points, as we haven’t cooperatives of type B with more then 20 workers in the south of Italy).

Fig. 4

PCA for the three datasets in (8)

For the variables on the two-dimensional projection on the right, we observe that the four fairness variables in $\mathbf {X}$ and expecially in $\mathbf {QX}$ are well separated as aspected; for the PX matrix, procedural and interactional-O fairness are nearly the same on the first PC.

Table 1 reports the reliability measures and the variance explained by each construct over the two models. No remarkable differences are found for the R² values: the second-order construct is able to capture around the 60–70 % of the variability in the first-order LVs for both models. The same consideration holds for communality, which is the variability in the block of items explained by the corresponding LV. Both composite reliability and Cronbach’s alpha measures are more than satisfactory within the two models, showing an high internal consistency of the latent constructs.

Table 1 Variance explained and reliability indices for the second-order PLS-PM with the X and the QX datasets

Once the reliability is assessed, the very core of the PLS-PM results are the measurement and the path coefficients estimates, which are reported, respectively, in the left and the right part of Table 2. No substantial differences occur in the measurement coefficients estimates and the two models lead to little differences in the path coefficients expressing the effect of the second-order LV on the first-order dimensions of organizational justice. The effects observed on the original data matrix are reduced when the data are filtered from the external information.

Table 2 Measurement and path coefficients estimated for the second-order PLS-PM with the X and the QX datasets

5 Conclusions and further remarks

In the analysis of latent constructs the researcher can benefit from considering external information which characterizes the observations and/or the variables under investigation. The integration of such features in the model is useful in evaluating their impact on the model itself.

The present work illustrates a procedure for deflating the data matrix based on an orthogonal projection of its rows (the statistical units) and its columns (the variables). The proposal is thus the implementation of the PLS-PM on the matrix obtained as a “residual” of the projection.

An application in the field of the measurement of the subjective quality of work allowed to highlight the results that can be achieved in the case of external information of a qualitative nature. The procedure can be easily extended to the case of quantitative external information on units and variables under analysis. A further aspects which has to be deepened by future analysis is that of interactions among factors related to the qualitative information.