Time-varying tandem queues with blocking: modeling, analysis, and operational insights via fluid models with reflection

Abstract

In this paper, we develop time-varying fluid models for tandem networks with blocking. Beyond having their own intrinsic value, these mathematical models are also limits of corresponding many-server stochastic systems. We begin by analyzing a two-station tandem network with a general time-varying arrival rate, a finite waiting room before the first station, and no waiting room between the stations. In this model, customers that are referred from the first station to the second when the latter is saturated (blocked) are forced to wait in the first station while occupying a server there. The finite waiting room before the first station causes customer loss and, therefore, requires reflection analysis. We then specialize our model to a single station (many-server fluid limit of the $G_t/M/N/(N +H)$ queue), generalize it to k stations in tandem, and allow finite internal waiting rooms. Our models yield operational insights into network performance, specifically on the effects of line length, bottleneck location, waiting room size, and the interaction among these effects.

1 Introduction

Blocking is an important phenomenon in service, computer, communication, and manufacturing systems (for example, [10, 62]). This has motivated our paper, in which we analyze several stochastic models of time-varying tandem queues with blocking. For each such model, we develop and prove its fluid limit in the many-server regime: System capacity (number of servers) increases indefinitely jointly with demand (arrival rates). We adopt a fluid framework since it yields accurate approximations for time-varying models, which are otherwise notoriously intractable. In fluid models, entities that flow through the system are animated as continuous fluid, and hence the system dynamics can be captured by differential equations. There is ample literature justifying that fluid models accurately approximate heavily loaded service systems [42, 46, 48, 49, 59, 75, 77].

The models we focus on (flow lines) have been researched for decades [5, 6, 41, 53]; our research takes the analysis to the new territories of time-varying environments and many-server stations. Such general models are also applicable in modeling healthcare environments and the bed-blocking phenomenon [21, 36, 56, 58, 65, 69, 81] in particular. This phenomenon occurs when a patient remains hospitalized after treatment completion due to lack of beds in a more appropriate facility (for example, a rehabilitation or geriatric ward). In that case, the patient occupies/blocks a hospital bed and thus prevents the admittance of another patient from the Emergency Department (ED); this may block the ED as well. Blocking in healthcare systems is pervasive (see [14]) between surgery rooms, recovery rooms, and internal wards.

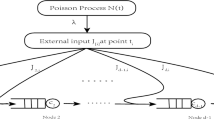
Our basic model (Sect. 2) is a network with two queues in tandem (Fig. 1), where the arrivals follow a general time-varying counting process. There is a finite waiting room before the first station and no waiting room between the two stations. There are two types of blocking in this network. The first occurs when the first station is saturated (all its servers are occupied and its waiting room is full), and therefore, arriving customers must leave the system (are blocked); such customer loss is mathematically captured by reflection. The second type of blocking occurs when the second station is saturated (all its servers are busy); in this case, customers who complete their service at the first station are forced to wait there while still occupying their server. Such a mechanism is known as blocking after service (BAS) or manufacturing blocking [10, 15]; and here, as it turns out (see [81]), an appropriate state representation renders reflection unnecessary for capturing this type of blocking. A real system that is naturally modeled by such two queues in tandem is an ED feeding a hospital ward; servers here are hospital beds.

Using the Functional Strong Law of Large Numbers for all our stochastic models, we establish the existence and uniqueness of fluid approximations/limits. These are first characterized by differential equations with reflection, which are then transformed into differential equations with no reflection but rather with discontinuous right-hand side (RHS) [24]; the latter are easier to implement numerically. The accuracy of our fluid models is validated against stochastic simulation, which amplifies the simplicity and flexibility of fluid models in capturing the performance of time-varying overloaded networks.

The two-station network is both specialized and extended. First, we derive a fluid limit for the $G_t/M/N/(N+H)$ queue that seems, to the best of our knowledge, already new. Next, in Sect. 3, we analyze the more general network with k queues in tandem and finite waiting rooms throughout—both before the first station and in-between stations. It is worth noting that our models cover all waiting room options at all locations: finite positive, infinite, or zero (no waiting allowed) and that reflection arises only due to having a finite waiting room before the first station.

Finally, in Sect. 4, we provide operational insights regarding the performance of time-varying tandem queues with finite buffers. Due to space considerations, in this paper we chose to calculate performance measures from the customer viewpoint: throughput, number of customers, waiting times, blocking times, and sojourn times; performance is measured at each station separately as well as overall within the network. (One could also easily accommodate server-oriented metrics, such as occupancy levels or starvation times.) Calculations of the above customer-driven measures provide insights into how network characteristics affect performance: We focus on line length (number of queues in tandem), bottleneck location, size of waiting rooms, and their joint effects.

1.1 Literature review

Despite the fact that time-varying parameters are common in production [38, 55] and service systems [23, 29], such as in healthcare [4, 17, 80], research on time-varying models with blocking is scarce. We now review the three research areas most relevant to this work.

Tandem queueing models with blocking Previous research on tandem queueing networks with blocking has focused on steady-state analysis for small networks [2, 28, 37], steady-state approximations for larger networks [9, 13, 19, 26, 58, 62, 67, 68, 71], and simulation models [14, 18, 21, 34, 54].

Several papers have analyzed tandem queueing networks with an unlimited waiting room before the first station and a blocking-after-service mechanism between the stations. In [7], the steady state of a single-server network with two stations in tandem was analyzed. In this model, the arrival process was Poisson and there was no waiting room between stations. The transient behavior of the same network was analyzed in [63]. The model in [7] was extended in [5] to an ordered sequence of single-server stations with a general arrival process, deterministic service times, and finite waiting room between the stations. The author concluded that the order of stations and the size of the intermediate waiting rooms do not affect the sojourn time in the system. We extend the analysis in [5] to time-varying arrivals, a finite waiting room before the first station, exponential service times, and a different number of servers in each station. We show how the order of stations does affect the sojourn time and how it interacts with the waiting room capacity before the first station.

The system analyzed in [7] was generalized in [6] under blocking-before-service (BBS) (or k-stage blocking mechanism) in which a customer enters a station only if the next k stations are available. A tandem queueing network with a single server at each station and no buffers between the stations was analyzed in [35]; the service times for each customer are identical at each station. In [73], heuristics were developed for ordering the stations in a tandem queueing network to minimize the sojourn time in the system. In this setting, each station has a single server and an unlimited waiting room. Simulation was employed in [18] to analyze work in process (WIP) in serial production lines, with and without buffers in balanced and unbalanced lines. The results of [27] were extended in [52] for analyzing tandem queueing networks with finite capacity queues and blocking. In that work, the author estimated the asymptotic behavior of the time customer n finishes service at Station k, as n and k become large together. Single-server flow lines with unlimited waiting rooms between the stations and exponential service times were investigated in [53]. The authors derived formulas for the average sojourn time (waiting and processing times). In our models, in addition to having time-varying arrivals, many-server stations, and finite waiting rooms, the sojourn time also includes blocking time at each station.

Fluid models with time-varying parameters Fluid models were successfully implemented in modeling different types of service systems. These models cover the early applications for post offices [57], claims processing in social security offices [70], call centers [1, 29], and healthcare systems [17, 80, 81]. Fluid models of service systems were extended to include state-dependent arrival rates, and general arrival and service rates [76, 77]. Time-varying queueing models were analyzed for setting staffing requirements in service systems with unlimited waiting rooms, by using the offered load heuristics [29, 78, 79].

Time-varying heavy-traffic fluid limits were developed in [48, 49] for queueing systems with exponential service, abandonment, and retrial rates. Accommodating these models for general time-varying arrival rates and a general independent abandonment rate was done in [42] for a single station, and for a network in [43]. These models were extended to general service times in [44,45,46].

Heavy-traffic approximations for systems with blocking have focused on stationary loss models [11, 12, 66]. An approximation for the steady-state blocking probability, with service times being dependent and non-exponential, was developed in [39]. A recent work in [40] focused on stabilizing blocking probabilities in time-varying loss models. In our paper, we contribute to this research area by developing a heavy-traffic fluid limit for time-varying models with blocking.

Queueing models with reflection Queueing models with reflection were analyzed in [30] for an assembly operation by developing limit theorems for the associated waiting time process. There it was shown that this process cannot converge in distribution and thus is inherently unstable. This model is generalized in [72] by assuming finite capacities at all stations and developing a conventional heavy-traffic limit theorem for a stochastic model of a production system. The reflection analysis detailed in [16, 31] for a single station and for a network is extended in [50, 51] for state-dependent queues. Loss systems for one station with reflection were analyzed in [25, 74]. More recently, [64] solved a generalized state-dependent drift Skorokhod problem in one dimension, which is used to approximate the transient distribution of the M / M / N / N queue in the many-server heavy-traffic regime.

1.2 Contributions

As we see it, the main contributions of this paper are the following:

• 1. Modeling We analyze a time-varying model for k many-server stations in tandem, with finite waiting rooms before the first station and between the other stations. This covers, in particular, the case of infinite or no waiting rooms, which includes the $G_t/M/N/(N+H)$ queue. For all these models, we derive a unified fluid model/approximation, which is characterized by a set of differential equations with a discontinuous right-hand side [24].

• 2. Analysis of the stochastic model We introduce a stochastic model for our family of networks in which, as usual, the system state captures station occupancy (for example, (4–5), for $k=2$). It turns out, however, that a state description in terms of non-utilized servers is more amenable to analysis (7–8). Indeed, it enables a representation of the network in terms of reflection, which yields useful properties of the network reflection operator (for example, Lipschitz continuity).

• 3. Analysis of the fluid model Through the Functional Strong Law of Large Numbers, we derive a fluid limit for the stochastic model with reflection in the many-server regime. Using properties of the reflection operator, we solve for the fluid limit, which allows it to be written as a set of differential equations without reflection. This fluid representation is flexible, accurate and effective, hence, easily implementable for a variety of networks.

• 4. Operational insights Our fluid model yields novel operational insights for time-varying finite-buffer flow lines. Specifically (Sect. 4), via numerical experiments, we analyze the effects on network performance of the following factors: line length, bottleneck location, size of the waiting room, and the interaction among these factors.

2 Two stations in tandem with finite waiting room

We now develop a fluid model with blocking for two stations in tandem, as illustrated in Fig. 1. In Sect. 3, we further extend this model for a network with k stations in tandem and finite internal waiting rooms between the stations.

Fig. 1

Two tandem stations with a finite waiting room before the first station

This FCFS system is characterized, to a first order, by the following (deterministic) parameters:

• 1. Arrival rate $\lambda (t)$, $t \ge 0$, to Station 1.

• 2. Service rate $\mu _{i} > 0$, $i=1,2$.

• 3. Number of servers $N_{i}$, $i=1,2$.

• 4. Transfer probability p from Station 1 to Station 2, $0 \le p \le 1$ (i.e., with probability p, a customer will be referred to Station 2 upon completion of service at Station 1);

• 5. Finite waiting room H at Station 1; there is no waiting room at Station 2 ($H=0$ is allowed; in this case, customers join the system only if there is an idle server in Station 1).

The stochastic model is created from the following stochastic building blocks, all of which are assumed to be independent:

• 1. External arrival process $A= \{A(t), t\ge 0\}$; A is a counting process, in which A(t) represents the external cumulative number of arrivals up to time t; here

  $$\begin{aligned} {\mathbb {E}}A(t)= \int _0^t{\lambda (u) \, \mathrm {d}u},\quad t\ge 0. \end{aligned}$$

  (1)

  A special case is the non-homogeneous Poisson process, for which

  $$\begin{aligned} A(t)= A_0\left( \int _0^t{\lambda (u)\, \mathrm {d}u}\right) , \quad t \ge 0, \end{aligned}$$

  where $A_{0}(\cdot )$ is a standard Poisson process (unit arrival rate).

• 2. “Basic” nominal service processes $D_{i}= \{D_{i}(t), t \ge 0\}$, $i=1,2,3$, where $D_{i}(t)$ are standard Poisson processes.

• 3. The stochastic process $X_{1}=\{X_{1}(t), t \ge 0\}$, which denotes the number of customers present at Station 1 that have not completed their service at Station 1 at time t.

• 4. The stochastic process $X_{2}=\{X_{2}(t), t \ge 0\}$, which denotes the number of customers present at Station 1 or 2 that have completed service at Station 1, but not at Station 2, at time t.

• 5. Initial number of customers in each state, denoted by $X_{1}(0)$ and $X_{2}(0)$.

A customer is forced to leave the system if Station 1 is saturated (the waiting room is full, if a waiting room is allowed) upon its arrival. We assume that the blocking mechanism between Station 1 and Station 2 is blocking after service (BAS) [10]. Thus, if upon service completion at Station 1, Station 2 is saturated, the customer will be forced to stay in Station 1, occupying a server there until a server at Station 2 becomes available. This mechanism was modeled in [81] for a network with an infinite waiting room before Station 1. In our case, however, to accommodate customer loss, we must use reflection in our modeling and analysis.

Let $Q = \{Q_{1}(t),Q_{2}(t), t \ge 0\}$ denote a stochastic queueing process in which $Q_{1}(t)$ represents the number of customers at Station 1 (including the waiting room) and $Q_{2}(t)$ represents the number of customers in service at Station 2 at time t. The process Q is characterized by the following equations:

$$\begin{aligned} Q_1(t) =&\,X_1(t) + B(t),\\ Q_2(t) =&\,X_2(t) \wedge N_2, \end{aligned}$$

where $B(t)=(X_2(t)-N_2)^+$ represents the number of blocked customers in Station 1, and

$$\begin{aligned} X_1(t)&= X_1(0)+ \int _0^t{1_{\left\{ X_1(u-) + (X_2(u-)-N_2)^+ < \,N_1+H\right\} } \,\mathrm {d}A(u)}\nonumber \\&\quad - D_1\left( p\mu _1 \int _0^t{\left[ X_1(u) \wedge (N_1-B(u))\right] } \, \mathrm {d}u\right) \nonumber \\&\quad - D_3\left( (1-p)\mu _1 \int _0^t{\left[ X_1(u) \wedge (N_1-B(u))\right] } \, \mathrm {d}u\right) ,\nonumber \\ X_2(t)&= X_2(0) + D_1\left( p\mu _1 \int _0^t{\left[ X_1(u) \wedge (N_1-B(u))\right] }\, \mathrm {d}u\right) \nonumber \\&\quad - D_2\left( \mu _2 \int _0^t{\left[ X_2(u) \wedge N_2\right] } \, \mathrm {d}u\right) ; \quad t \ge 0. \end{aligned}$$

(2)

Here, $1_{\{x\}}$ is an indicator function that equals 1 when x holds and 0 otherwise. The second right-hand term in the first equation of (2) represents the number of arrivals that entered service up to time t. As noted in [51], an inductive construction over time shows that (2) uniquely determines the process X. Observe that $X_1(t) + (X_2(t) - N_2)^+ = N_1+H$ implies that the first station is blocked until the next departure.

2.1 Representation in terms of reflection

First, we rewrite (2) by using the fact that

$$\begin{aligned} \begin{aligned}&\int _0^t{1_{\left\{ X_1(u-) + (X_2(u-)-N_2)^+ < \,N_1+H\right\} } \, \mathrm {d}A(u)}\\&\ \ \ \ \ \ \ \ \ = A(t) - \int _0^t{1_{\left\{ X_1(u-) + (X_2(u-)-N_2)^+ = \,N_1+H\right\} } \, \mathrm {d}A(u)} ; \end{aligned} \end{aligned}$$

(3)

here, the last right-hand term represents the cumulative number of arrivals to Station 1 that were blocked because all $N_1$ servers were busy and the waiting room was full.

Now, we rewrite (2) and (3):

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{bmatrix} X_1(t) \\ X_1(t)+ X_2(t) \end{bmatrix} = \begin{bmatrix} Y_1(t) - L(t) \\ Y_2(t) - L(t) \end{bmatrix} \le \begin{bmatrix} N_1+H \\ N_1+N_2+H \end{bmatrix}, \quad t \ge 0,\\ \mathrm {d}L(t) \ge 0, L(0)=0,\\ \int _0^\infty {1_{\{X_1(t) + (X_2(t) - N_2)^+ < \, N_1+H\}} \, \mathrm {d}L(t)}=0, \end{array}\right. } \end{aligned}$$

(4)

where

$$\begin{aligned} Y_1(t)&= X_1(0) + A(t) - D_1\left( p\mu _1 \int _0^t{\left[ X_1(u) \wedge (N_1-B(u))\right] }\, \mathrm {d}u\right) \nonumber \\&\ \ \ - D_3\left( (1-p)\mu _1 \int _0^t{\left[ X_1(u) \wedge (N_1-B(u))\right] } \,\mathrm {d}u\right) ,\nonumber \\ Y_2(t)&= X_1(0) + X_2(0) + A(t) - D_3\left( (1-p)\mu _1 \int _0^t{\left[ X_1(u) \wedge (N_1-B(u))\right] } \, \mathrm {d}u\right) \nonumber \\&\ \ \ - D_2\left( \mu _2 \int _0^t{[X_2(u) \wedge N_2]} \, \mathrm {d}u \right) ,\nonumber \\ L(t)&= \int _0^t{1_{\{X_1(u-)+(X_2(u-)-N_2)^+ = \, N_1+H\}} \, \mathrm {d}A(u)}. \end{aligned}$$

(5)

Figure 2 (left) geometrically illustrates the reflection in (4). The region for $X_1$ and $X_2$ is limited by the two blue lines. Arrivals are lost when the system is on the blue lines. The system leaves the state $X_1=N_1+H$ when a service is completed at Station 1. The system leaves the state $X_1+X_2=N_1+N_2+H$ when a service is completed at Station 2.

Fig. 2

Geometrical representation of the reflection. On the left—in terms of X, and on the right—in terms of R

The last equation of (4) is a complementary relation between L and X: $L(\cdot )$ increases at time t only if $X_1(t) + (X_2(t) - N_2)^+ = N_1+H$. We justify this by first substituting the last equation of (5) in the last equation for L(t) of (4), which yields the following:

$$\begin{aligned} \begin{aligned} \int _0^\infty \! {1_{\{X_1(t) + (X_2(t) - N_2)^+ < \, N_1+H\}} \cdot 1_{\{X_1(t-)+(X_2(t-)-N_2)^+ = \, N_1+H\}} \, \mathrm {d}A(t)}=0. \end{aligned} \end{aligned}$$

(6)

Now, if (6) does not hold, there must be a time when, at state $N_1$, a service completion and an arrival occur simultaneously. However, when $X_1+(X_2-N_2)^+ = N_1+H$, the next departure will occur according to an exponential random variable; hence, by the independence of the building blocks, an arrival occurs simultaneously with a departure with probability 0.

We simplify (4), so that the reflection will occur on the axes, by letting

$$\begin{aligned} R_1(t)&= N_1 + H - X_1(t), \\ R_2(t)&= N_1 + N_2 + H - \left( X_1(t) + X_2(t)\right) = R_1(t) + N_2 - X_2(t), \quad t \ge 0. \end{aligned}$$

Note that $R_1(t)$ represents the non-utilized space in Station 1 at time t, namely the blocked servers, the idle servers, and the available waiting room space. When all $N_1$ servers are occupied and the waiting room is full, $R_1(t)$ includes the blocked servers at Station 1. When all $N_1$ servers are occupied but the waiting room is not full, $R_1(t)$ includes the blocked servers and the available waiting room space. When some of the $N_1$ servers are idle, $R_1$ includes the sum of the idle servers, the blocked servers, and the available waiting room space. The function $R_2(t)$ represents the available space in the system at time t. Hence, when the $N_1+N_2$ servers are occupied, $R_2(t)$ includes the available waiting room space. When only the $N_2$ servers are occupied but not all $N_1$ servers are occupied, $R_2(t)$ includes the idle servers in Station 1 and the available waiting room space. Finally, when Station 2 is not full, $R_2(t)$ includes the idle servers in Stations 1 and 2 and the available waiting room space.

The functions $R_1$ and $R_2$ give rise to the following, equivalent to (4):

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \begin{bmatrix} R_1(t) \\ R_2(t) \end{bmatrix} = \begin{bmatrix} {\tilde{Y}}_1(t) + L(t) \\ {\tilde{Y}}_2(t) + L(t) \end{bmatrix} \ge 0, \quad t \ge 0,\\ \mathrm {d}L(t) \ge 0, L(0)=0,\\ \int _0^\infty {1_{\{R_1(t) \wedge R_2(t) \,> \, 0\}} \, \mathrm {d}L(t)}=0, \end{array}\right. } \end{aligned} \end{aligned}$$

(7)

where

$$\begin{aligned}&{\tilde{Y}}(t) = \begin{bmatrix} {\tilde{Y}}_1(t) \\ {\tilde{Y}}_2(t) \end{bmatrix} = \begin{bmatrix} N_1 + H - Y_1(t) \\ N_1+N_2+ H - Y_2(t) \end{bmatrix} ; \end{aligned}$$

(8)

the last line in (7) is derived from

$$\begin{aligned}&\int _0^t{1_{\left\{ X_1(t)+(X_2(t)-N_2)^+ < \, N_1 + H\right\} } \, \mathrm {d}L(t)} = \int _0^t{1_{\left\{ N_1 + H - X_1(t)> (X_2(t)-N_2)^+ \right\} } \, \mathrm {d}L(t)}\\&\quad = \int _0^t{1_{\left\{ R_1(t) - (R_1(t)-R_2(t))^+> \,0 \right\} } \, \mathrm {d}L(t)} = \int _0^t{1_{\left\{ R_1(t) \wedge R_2(t) > \,0 \right\} } \, \mathrm {d}L(t)}. \end{aligned}$$

The processes ${\tilde{Y}}_1$, ${\tilde{Y}}_2$, and L (see (7)) can be stated in the “language” of R:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{Y}}_1(t) &{}= R_1(0) - A(t) + D_1\left( p\mu _1\int _0^t{\left[ (N_1 + H - R_1(u)) \wedge (N_1-B(u))\right] } \, \mathrm {d}u\right) \\ &{} \ \ \ +\,D_3\left( (1-p)\mu _1\int _0^t{\left[ (N_1 + H - R_1(u)) \wedge (N_1-B(u))\right] }\, \mathrm {d}u\right) , \\ {\tilde{Y}}_2(t) &{}= R_2(0) - A(t) + D_3\left( (1-p)\mu _1\int _0^t{\Big [\big (N_1 + H - R_1(u)\big ) \wedge \big (N_1-B(u)\big )\Big ]} \, \mathrm {d}u\right) \\ &{} \ \ \ +\,D_2\left( \mu _2\int _0^t{\left[ N_2 \wedge \big (R_1(u) - R_2(u)+ N_2\big )\right] }\, \mathrm {d}u\right) ,\\ L(t) &{}= \int _0^t{1_{\{R_1(u-) \wedge R_2(u-) \,= \, 0\}} \, \mathrm {d}A(u)}. \end{array}\right. } \end{aligned}$$

Here, $B(u) = \big (R_1(u) - R_2(u)\big )^+$ in terms of R.

Figure 2 (right) presents the direction of reflection in terms of R. When the process hits the boundary of the positive quadrant, L increases. This increase causes equal positive displacements in both $R_1$ and $R_2$ as necessary to keep $R_1 \ge 0$ and $R_2 \ge 0$, which drives L in the diagonal direction, presented in Fig. 2.

From (7), we see that $L(t) \ge - {\tilde{Y}}_1(t)$ and $L(t) \ge -{\tilde{Y}}_2(t)$. Therefore, $L(t) \ge \big (-{\tilde{Y}}_1(t) \vee -{\tilde{Y}}_2(t)\big ) = -\big ({\tilde{Y}}_1(s) \wedge {\tilde{Y}}_2(s)\big )$, and

$$\begin{aligned} L(t) = \sup _{0 \le s \le t} \left( -\left( {\tilde{Y}}_1(s) \wedge {\tilde{Y}}_2(s)\right) \right) ^+. \end{aligned}$$

Note that this solution is applicable even though ${\tilde{Y}}$ depends on R (see [50] for details, though recall that they do not cover blocking).

2.2 Fluid approximation

We now develop a fluid limit for our queueing model through the Functional Strong Law of Large Numbers (FSLLN). We begin with (7) and scale up the arrival rate and the size of the system (servers and waiting room) by $\eta >0$, $\eta \rightarrow \infty$. This parameter $\eta$ will serve as an index of a corresponding queueing process $R^{\eta }$, which is the unique solution to the following Skorokhod representation:

$$\begin{aligned} {\left\{ \begin{array}{ll} R_1^{\eta }(t) = {\tilde{Y}}_1^{\eta }(t) + L^{\eta }(t) , \\ R_2^{\eta }(t) = {\tilde{Y}}_2^{\eta }(t) + L^{\eta }(t), \end{array}\right. } t \ge 0, \end{aligned}$$

where

$$\begin{aligned}&\begin{bmatrix} {\tilde{Y}}_1^\eta (\cdot ) \\ {\tilde{Y}}_2^\eta (\cdot ) \end{bmatrix}\nonumber \\&= \begin{bmatrix} R_1^{\eta }(0) - A^{\eta }(\cdot ) + D_1\left( p\mu _1\int _0^{\cdot }{\left[ (\eta N_1 +\eta H - R_1^{\eta }(u))\wedge (\eta N_1 - B^{\eta }(u))\right] } \, \mathrm {d}u\right) \\ +\,D_3\left( (1-p)\mu _1\int _0^{\cdot }{\left[ (\eta N_1 +\eta H - R_1^{\eta }(u))\wedge (\eta N_1 - B^{\eta }(u))\right] } \, \mathrm {d}u\right) \\ R_2^\eta (0) - A^{\eta }(\cdot ) + D_3\left( (1-p)\mu _1\int _0^{\cdot }{\left[ (\eta N_1 +\eta H - R_1^{\eta }(u))\wedge (\eta N_1 - B^{\eta }(u))\right] } \, \mathrm {d}u\right) \\ + \,D_2\left( \mu _2\int _0^{\cdot }{\left[ \eta N_2 \wedge (R_1^{\eta }(u) - R_2^{\eta }(u)+ \eta N_2) \right] } \, \mathrm {d}u\right) \end{bmatrix}. \end{aligned}$$

Here, $A^{\eta }= \{\eta A(t), t\ge 0\}$ is the arrival process under our scaling; thus,

$$\begin{aligned} {\mathbb {E}}A^{\eta }(t)= \eta \int _0^t{\lambda (u) \, \mathrm {d}u},\quad t\ge 0. \end{aligned}$$

We now introduce the scaled processes $r^{\eta } = \{r^{\eta }(t), t\ge 0\}$, $l^{\eta } = \{l^{\eta }(t), t\ge 0\}$ and $b^{\eta } = \{b^{\eta }(t), t\ge 0\}$ by

$$\begin{aligned} r^{\eta }(t) = \eta ^{-1} {R^{\eta }(t)}, \quad l^{\eta }(t) = \eta ^{-1} {L^{\eta }(t)} \quad \text {and} \quad b^{\eta }(t) = \eta ^{-1} {B^{\eta }(t)}, \end{aligned}$$

respectively; similarly, ${\tilde{y}}_1^{\eta } = N_1+H - y_1^{\eta }$ and ${\tilde{y}}_2^{\eta } = N_1+H + N_2 - y_2^{\eta }$. Then, we get that

$$\begin{aligned}&\begin{bmatrix} {\tilde{y}}_1^\eta (\cdot ) \\ {\tilde{y}}_2^\eta (\cdot ) \end{bmatrix} \nonumber \\&= \begin{bmatrix} r_1^{\eta }(0)- \eta ^{-1} A^{\eta }(\cdot ) + \eta ^{-1} D_1\left( \eta p\mu _1 \int _0^{\cdot } \left[ (N_1 + H - r_1^{\eta }(u))\wedge (N_1 - b^{\eta }(u))\right] \, \mathrm {d}u \right) \\ + \,\eta ^{-1} D_3\left( \eta (1-p)\mu _1 \int _0^{\cdot } \left[ (N_1 + H - r_1^{\eta }(u))\wedge (N_1 - b^{\eta }(u))\right] \, \mathrm {d}u \right) \\ r_2^\eta (0) - \eta ^{-1} A^{\eta }(\cdot ) + \eta ^{-1} D_3\left( \eta (1-p)\mu _1 \int _0^{\cdot }\left[ (N_1 + H - r_1^{\eta }(u))\wedge (N_1 - b^{\eta }(u))\right] \, \mathrm {d}u\right) \\ + \,\eta ^{-1} D_2\left( \eta \mu _2\int _0^{\cdot } \left[ N_2 \wedge (r_1^{\eta }(u) - r_2^{\eta }(u)+ N_2)\right] \, \mathrm {d}u\right) \end{bmatrix}. \end{aligned}$$

(9)

The asymptotic behavior of $r^{\eta }$ is described in the following theorem, which we prove in Appendix A.

Theorem 1

Suppose that

$$\begin{aligned} \left\{ \eta ^{-1} A^\eta (t),\, t \ge 0 \right\} \rightarrow \left\{ \int _0^t \lambda (u) \hbox {d}u,\, t \ge 0 \right\} u.o.c. \quad as \quad \eta \rightarrow \infty , \end{aligned}$$

and ${r^{\eta }(0)} \rightarrow r(0)$ a.s., as $\eta \rightarrow \infty$, where r(0) is a given nonnegative deterministic vector. Then, as $\eta \rightarrow \infty$, the family $\{r^{\eta }\}$ converges u.o.c. over $[0, \infty )$, a.s., to a deterministic function r. This r is the unique solution to the following differential equation (DE) with reflection:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} r_1(t) = r_1(0) - \int _0^t \left[ \lambda (u) - \mu _1 ((N_1 +H - r_1(u))\wedge (N_1-b(u)) )\right] \, \mathrm {d}u + l(t) \ge 0,\\ &{} r_2(t) = r_2(0) - \int _0^t \left[ \lambda (u) - (1-p)\mu _1 ((N_1 + H - r_1(u))\wedge (N_1-b(u)))\right] \, \mathrm {d}u \\ &{} \qquad \qquad + \int _0^t \left[ \mu _2 (N_2 \wedge (r_1(u) - r_2(u)+ N_2))\right] \, \mathrm {d}u + l(t)\ge 0,\\ &{} \mathrm {d}l(t) \ge 0, l(0)=0,\\ &{} \int _0^\infty {1_{\{r_1(t) \wedge r_2(t) \,> \, 0\}}\, \mathrm {d}l(t)}=0; \end{array}\right. } \end{aligned}$$

(10)

where $b(t)= \big (r_1(t) - r_2(t)\big )^+$, $t \ge 0$.

Returning to our original formulation (4), (10) can in fact be written in terms of $x(\cdot )$ for $t \ge 0$ as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} x_1(t) = x_1(0) + \int _0^t \left[ \lambda (u) - \mu _1 (x_1(u) \wedge (N_1-b(u)))\right] \, \mathrm {d}u - l(t) \le N_1 + H,\\ &{} x_1(t) + x_2(t) = x_1(t) + x_2(0) + \int _0^t \left[ p\mu _1 (x_1(u) \wedge (N_1-b(u))) - \mu _2 (N_2 \wedge x_2(u))\right] \, \mathrm {d}u \\ &{} \qquad \qquad \qquad \qquad \le N_1 + N_2 + H,\\ &{} \mathrm {d}l(t) \ge 0, l(0)=0,\\ &{} \int _0^\infty {1_{\{x_1(t)+(x_2(t)-N_2)^+ < \,N_1+H\}} \, \mathrm {d}l(t)}=0. \end{array}\right. } \end{aligned}$$

(11)

The function x will be referred to as the fluid limit associated with the queueing family $X^{\eta }$, where $X^{\eta } = (X_1^{\eta },\, X_2^{\eta }) = (\eta N_1 +\eta H - R_1^{\eta },\, R_1^{\eta } - R_2^{\eta } + \eta N_2)$.

The following proposition provides a solution to (11); see Appendix B for details. As opposed to (11), this solution (12) is given by a set of differential equations with discontinuous RHS but without reflection. Thus, implementing (12) numerically is straightforward via recursion, which would not be the case with (11).

Proposition 1

The fluid limit approximation for X in (2) is given by

$$\begin{aligned} x_1(t)&= x_1(0) - \mu _1\int _0^t \! \left[ x_1(u) \wedge (N_1-b(u))\right] \, \mathrm {d}u \nonumber \\&\quad + \int _0^t \!\left[ 1_{\{x_1(u)< \, N_1+H\}} \cdot 1_{\{x_1(u) + x_2(u)< \, N_1 + N_2+H\}} \cdot \lambda (u) \right] \,\mathrm {d}u \nonumber \\&\quad + \int _0^t \!\left[ 1_{\{x_{1}(u) = N_{1}+H\}} \cdot 1_{\{x_1(u) + x_{2}(u)< N_1 + N_{2} + H \}} \cdot \left[ \lambda (u) \wedge l_1^*(u) \right] \right] \,\mathrm {d}u \nonumber \\&\quad + \int _0^t \!\left[ 1_{\{x_{1}(u) < N_{1} + H\}} \cdot 1_{\{x_1(u) + x_{2}(u) = N_1 + N_2 + H \}} \cdot \left[ \lambda (u) \wedge l_2^*(u) \right] \right] \, \mathrm {d}u \nonumber \\&\quad + \int _0^t \left[ 1_{\{x_{1}(u) = N_{1}+H\}} \cdot 1_{\{x_1(u) + x_{2}(u) = N_1 + N_2+ H \}} \cdot \left[ \lambda (u) \wedge l_1^*(u) \wedge l_2^*(u)\right] \right] \, \mathrm {d}u,\nonumber \\ x_2(t)&= x_2(0) + \int _0^t \left[ p \mu _1 (x_1(u) \wedge (N_1-b(u))) - \mu _2 (x_2(u) \wedge N_2) \right] \, \mathrm {d}u, \end{aligned}$$

(12)

where

$$\begin{aligned} l_1^*(u)&= \mu _{1} N_{1},\\ l_{2}^*(u)&= \mu _2 N_2\ + (1-p)\mu _{1} \left( x_{1}(u) \wedge (N_{1} - b(u))\right) ,\\ b(u)&= (x_2(u) - N_2)^+. \end{aligned}$$

We now introduce the functions $q_{1}$ and $q_2$ that denote the number of customers at Station 1 (including the waiting room) and the number of customers in service at Station 2, respectively:

$$\begin{aligned} q_1(t)&= x_{1}(t) + b(t); \\ q_2(t)&= x_2 \wedge N_2. \end{aligned}$$

Remark 1

Our model can be used to analyze the $G_{t}/M/N/(N+H)$ queueing system. By assuming $N_2=\infty$ and $b=0$, the network can be reduced to a single station ($N_1=N$ and $\mu _1=\mu$). In that case, the fluid limit q for the number of customers in the system is given by

$$\begin{aligned} q(t)&= q(0)+ \int _0^t \left[ \lambda (u) - (\lambda (u) - \mu N )^+ \cdot 1_{\{q(u) = N+H\}} -\mu (q(u)\wedge N) \right] \,\mathrm {d}u. \end{aligned}$$

Remark 2

Abandonments from the waiting room can occur when customers have finite patience. This is a prevalent phenomenon in service systems and healthcare in particular (for example, customers that abandon the Emergency Department are categorized as Left Without Being Seen (LWBS) [3, 8]). Such abandonments can be added to our model by following [49, 60]. In particular, let $\theta$ denote the individual abandonment rate from the waiting room. Thus, the term $\theta \int _0^t [x_1(u)+b(u)-N_1]^+\, \mathrm {d}u$ should be subtracted from the right-hand side of $x_1(t)$ in (12); here, $[x_1(t)+b(t)-N_1]^+$ represents the number of waiting customers at Station 1 at time t.

2.3 Numerical examples

To demonstrate that our proposed fluid model accurately describes the flow of customers, we compared it to a discrete stochastic simulation model. In that model, service durations were randomly generated from exponential distributions. Customers arrive according to a non-homogeneous Poisson process that was used to represent a process with a general, time-dependent arrival rate. We note that simulating a general time-varying arrival process ($G_t$) is not trivial [32, 47]. In [44], the authors introduce an algorithm that is based on the standard equilibrium renewal process (SERP). This algorithm is implemented in [61] to approximate the general inter-arrival times for the phase-type distribution.

The fluid equations in (12) were solved recursively, by discretizing time. Figure 3 shows the comparison between the proposed fluid model and the average simulation results for two scenarios. In the first (left plot), $N_1=200$, $N_2=150$, $H=50$, $\mu _1 = 1/10$, $\mu _2=1/20$, $p=1$, $q_1(0)=q_2(0)=0$ and $\lambda (t)= 2t$, $0 \le t \le 120$. In the second (right plot), $N_1=30$, $N_2=60$, $H=10$, $\mu _1 = 1/10$, $\mu _2=1/90$, $p=1$, $q_1(0)=q_2(0)=0$, and $\lambda (t)= t$, $0 \le t \le 60$.

We calculated the simulation standard deviations, averaged over time and over 500 replications. For the first scenario, the standard deviations were 0.657 for the number of customers in Station 1 with a maximal value of 4.4, 0.558 for the number in Station 2 with a maximal value 4.2, and 0.585 for the number of blocked customers with a maximal value of 4.462. To conclude, the average difference between the simulation replications and their average is less than one customer.

Fig. 3

Total number in each station–fluid formulation versus simulation for two scenarios. The fluid model curves overlap the simulation curves

3 Multiple stations in tandem with finite internal waiting rooms

We now extend our model to a network with k stations in tandem and finite internal waiting rooms, as presented in Fig. 4. The notation remains as before, only with a subscript i, $i=1,\dots ,k$, indicating Station i. Moreover, we denote the transfer probability from Station i to Station $i+1$ as $p_{i,i+1}$. Before each station i, there is Waiting Room i of size $H_i$. The parameter $H_i$ can vary from 0 to $\infty$, inclusive. A customer that is referred to Station i, $i >1$, when it is saturated waits in Waiting Room i. If the latter is full, then the customer is blocked in Station $i-1$ while occupying a server there, until space becomes available in Waiting Room i.

Fig. 4

Multiple stations in tandem with finite internal waiting rooms

The stochastic model is created from the following stochastic building blocks, which are assumed to be independent: the external arrival process $A= \{A(t), t\ge 0\}$, as was defined in (2), processes $D_{i}= \{D_{i}(t), t \ge 0\}$, $i=1,\ldots ,2k-1$, where $D_{i}(t)$ are standard Poisson processes, and $X_{i}(0)$, $i=1,\dots ,k$, the initial number of customers in each state.

As before, the above building blocks will yield a k-dimensional stochastic process, which captures the state of our system. The stochastic process $X_{1}=\{X_{1}(t), t \ge 0\}$ denotes the number of arrivals to Station 1 that have not completed their service at Station 1 at time t, and the stochastic process $X_{i}=\{X_{i}(t), t \ge 0\}$, $i=2,\dots ,k$, denotes the number of customers that have completed service at Station $i-1$, but not at Station i at time t. The stochastic process $B_{i}=\{B_{i}(t), t \ge 0\}$, $i=1,\dots ,k-1$, denotes the number of blocked customers at Station i waiting for an available server in Station $i+1$.

Let $Q = \{Q_{1}(t),Q_{2}(t),\ldots ,Q_{k}(t), t \ge 0\}$ denote the stochastic queueing process in which $Q_{i}(t)$ represents the number of customers at Station i (including the waiting customers) at time t. The process Q is characterized by the following equations:

$$\begin{aligned} \begin{aligned} Q_1(t) =&\,X_1(t) + B_1(t); \\ Q_i(t) =&\,\big [X_i(t) + B_i(t)\big ] \wedge (N_i+H_i), \quad i=2,\dots , k-1;\\ Q_k(t) =&\,X_k(t) \wedge (N_k+H_k), \quad t \ge 0. \end{aligned} \end{aligned}$$

(13)

Here,

$$\begin{aligned} X_1(t)&= X_1(0)+ A(t) - D_1\left( p_{12}\cdot \mu _1 \int _0^t{\left[ X_1(u) \wedge \left( N_1-B_1(u)\right) \right] } \, \mathrm {d}u\right) \nonumber \\&\quad - D_{k+1}\left( (1- p_{12}) \cdot \mu _1 \int _0^t {\left[ X_1(u) \wedge \big (N_1-B_1(u)\big )\right] }\,\mathrm {d}u\right) \nonumber \\&\quad - \int _0^t{1_{\left\{ X_1(u-) + B_1(u-) = \,N_1+H_1\right\} } \, \mathrm {d}A(u)},\nonumber \\ X_i(t)&= X_i(0) + D_{i-1}\left( p_{i-1, i} \cdot \mu _{i-1} \int _0^t \left[ X_{i-1}(u) \wedge \left( N_{i-1} - B_{i-1}(u)\right) \right] \, \mathrm {d}u \right) \nonumber \\&\ \ \ \ - D_{i}\left( p_{i, i+1}\cdot \mu _i \int _0^t \left[ X_i(u) \wedge \left( N_i - B_i(u)\right) \right] \, \mathrm {d}u\right) \nonumber \\&\ \ \ \ - D_{k+i}\left( (1-p_{i, i+1})\cdot \mu _i \int _0^t \left[ X_i(u) \wedge \left( N_i - B_i(u)\right) \right] \, \mathrm {d}u \right) , i=2,\dots ,k-1,\nonumber \\ X_k(t)&= X_k(0) + D_{k-1}\left( p_{k-1,k} \cdot \mu _{k-1} \int _0^t \left[ X_{k-1}(u) \wedge \left( N_{k-1} - B_{k-1}(u)\right) \right] \, \mathrm {d}u \right) \nonumber \\&\quad - D_{k}\left( \mu _k \int _0^t \big [X_k(u) \wedge N_k \big ] \hbox {d}u \right) , \nonumber \\ B_i(t)&= \left[ X_{i+1}(t) + B_{i+1}(t) - N_{i+1}-H_{i+1}\right] ^+, i=1,\dots , k-2,\nonumber \\ B_{k-1}(t)&= \left[ X_{k}(t) - N_{k} - H_{k}\right] ^+. \end{aligned}$$

(14)

Note that although $B_{i}(t)$, $i=1,\dots ,k-1$, is defined recursively by $B_{i+1}(t)$, it can be written explicitly for every i. For example, when $k=3$, we get that $B_{1}(t) = [X_{2}(t) + [X_{3}(t) - N_{3}-H_3]^+ - N_{2}-H_2]^+$. An inductive construction over time shows that (14) uniquely determines the processes X and B.

By using similar methods as for the two-station network in Sect. 2, with more cumbersome algebra and notation, we establish that x, the fluid limit for the stochastic queueing family $X^{\eta }$, is given, for $t \ge 0$, by

$$\begin{aligned} x_1(t)&= x_1(0) - \mu _1\int _0^t{\left[ x_1(u) \wedge \left( N_1-b_1(u)\right) \right] \,\mathrm {d}u}\nonumber \\&\quad + \sum _{m=0}^{k} \,\sum _{\begin{array}{c} A \subset \{1,\ldots ,k\}:\\ \, |A|=m \end{array}}\int _0^t\Bigg [\prod _{\begin{array}{c} j \in A \end{array}} 1_{\left\{ \sum _{i=1}^j x_i(u) = \, \sum _{i=1}^j (N_i+H_i)\right\} }\nonumber \\&\quad \times \prod _{\begin{array}{c} j \in \{1,\ldots ,k\}\cap {\bar{A}} \end{array}}1_{\left\{ \sum _{i=1}^j x_i(u) < \, \sum _{i=1}^j (N_i+H_i)\right\} } \Big [\lambda (u)\wedge \bigwedge _{\begin{array}{c} y \in A \end{array}} l_y^*(u)\Big ]\Bigg ]\,\mathrm {d}u,\nonumber \\ x_i(t)&= x_i(0) + \int _0^t\Big [p_{i-1,i}\cdot \mu _{i-1} \left( x_{i-1}(u) \wedge \left( N_{i-1} - b_{i-1}(u)\right) \right) \nonumber \\&\quad -\mu _{i} \left( x_{i}(u) \wedge \left( N_{i} - b_{i}(u)\right) \right) \Big ] \,\mathrm {d}u, \quad i=2,\ldots ,k-1,\nonumber \\ x_k(t)&= x_k(0) + \int _0^t\Big [p_{k-1,k}\cdot \mu _{k-1} \left( x_{k-1}(u) \wedge \left( N_{k-1} - b_{k-1}(u)\right) \right) \nonumber \\&\quad -\mu _{k} \left( x_{k}(u) \wedge N_{k}\right) \Big ] \,\mathrm {d}u, \end{aligned}$$

(15)

where

$$\begin{aligned}&l_1^*(u) = \mu _{1} N_{1},\nonumber \\&l_{n}^*(u) = \mu _{n} N_{n} + \sum _{j=1}^{n-1}(1-p_{j,j+1})\mu _{j} \left( x_{j}(u) \wedge \left( N_{j} - b_{j}(u)\right) \right) , n=2,\dots ,k,\nonumber \\&b_i(t) = \left[ x_{i+1}(t) + b_{i+1}(t) - N_{i+1} - H_{i+1}\right] ^+, i=1,\dots , k-2,\nonumber \\&b_{k-1}(t) = \left[ x_{k}(t) - N_{k}- H_{k}\right] ^+. \end{aligned}$$

The term in the second line of (15) is a generalization of the last four terms in the expression for $x_1(t)$ in (12), when $k=2$.

For each summand and j, if $\sum _{i=1}^j x_i(u) = \sum _{i=1}^j N_i+H_i$, the corresponding $l_{j}(u)$ will appear in the product. The term $l_{j}(u)$ represents the departure rate from Station j when the waiting room and Stations $1,\dots ,j$ are full (i.e., $\sum _{i=1}^j x_i(u) = \, \sum _{i=1}^j(N_i+H_i)$). The two first summations account for all combinations of $l_j(u)$, $j \in \{1,\dots ,k\}$.

We now introduce the functions $q_{i}(t)$, $i=1,\dots , k$, which denote the number of customers at Station i at time t and are given by

$$\begin{aligned} q_1(t) =&\,x_1(t) + b_1(t);\\ q_i(t) =&\,\left[ x_i(t) + b_i(t)\right] \wedge \left( N_i+H_i\right) , \quad i=2,\dots , k-1;\\ q_k(t) =&\,x_k(t) \wedge \left( N_k + H_k\right) . \end{aligned}$$

Remark 3

A special case for the model analyzed in Sect. 3 is a model with an infinite sized waiting room before Station 1 ($H = \infty$). In this case, since customers are not lost and no reflection occurs, both the stochastic model and the fluid limit are simplified. This special case is in fact an extension of the two-station model developed in [81].

4 Numerical experiments and operational insights

In this section, we demonstrate how our models yield operational insights into time-varying tandem networks with finite capacities. To this end, we implement our models by conducting numerical experiments and parametric performance analysis. Specifically, we analyze the effects of line length, bottleneck location, and size of the waiting room on network output rate, number of customers in process, as well as sojourn, waiting, and blocking times. The phenomena presented were validated by discrete stochastic simulations.

In Sects. 4.1, 4.2, we focus on and compare two types of networks. The first has no waiting room before Station 1 ($H=0$), and in the second there is an infinite sized waiting room before Station 1 ($H=\infty$). Sects. 4.3, 4.4 are dedicated to buffer-size effects (H varies).

The model we provide here is a tool for analyzing tandem networks with blocking. Some observations we present are intuitive and can easily be explained; others, less trivial and possibly challenging, are left for future research.

4.1 Line length

We now analyze the line length effect on network performance. We start with the case where all stations are statistically identical and their primitives independent (i.i.d. stations). This implies that the stations are identical in the fluid model; in Sect. 4.2, we relax this assumption.

The arrival rate function in the following examples is the sinusoidal function

$$\begin{aligned} \lambda (t) = {\bar{\lambda }} + \beta \sin (\gamma t),\quad t \ge 0, \end{aligned}$$

(16)

with average arrival rate ${\bar{\lambda }}$, amplitude $\beta$, and cycle length $T = 2\pi /\gamma$.

Figure 5 presents the time-varying input and output rates from the network, as the number of stations increases from one to eight. In both types of networks ($H=0$ and $H=\infty$), the variation in the output rate diminishes and the average output rate (over time) decreases as the line becomes longer. When $H=0$, due to customer loss and blocking, the variation is larger and the average output rate is smaller.

Fig. 5

Line length effect on the network output rate with k i.i.d. stations, the sinusoidal arrival rate function in (16) with ${\bar{\lambda }}=9$, $\beta =8$ and $\gamma =0.02$, $N_i=200$, $\mu _i=1/20$ and $q_{i}(0)=0$, $\forall i \in \{1,\dots ,k\}$. Five networks of different length are considered

Figure 6 shows the time-varying number of customers in each station in a network with eight stations in tandem. When $H=0$ (left plot), due to customer loss, the average number of customers is smaller, while the variation is larger, compared to the case when $H=\infty$. In fact, only about 70$\%$ of arriving customers were served when $H=0$, compared to the obvious 100$\%$ when $H=\infty$.

Fig. 6

Total number of customers in each station in a network with eight i.i.d. stations and the sinusoidal arrival rate function in (16) with ${\bar{\lambda }}=9$, $\beta =8$ and $\gamma =0.02$, $N_i=200$, $\mu _i=1/20$, and $q_{i}(0)=0$, $i = 1,\dots ,8$

Observe that the same phenomenon of the variation and average output rate decreasing as the line becomes longer (Fig. 5) also occurs when stations have ample capacities to eliminate blocking and customer loss. In these cases, system performance reaches its upper bound. Here, the output from one station is the input for the next one. In [20], an analytic expression was developed for the number of customers in the $M_t/G/\infty$ queue with a sinusoidal arrival rate as in (16). In particular, the output rate from Station 1 is given by

$$\begin{aligned} \delta _1(t) = {\bar{\lambda }} + \beta \left( \frac{\mu ^2}{\mu ^2+\gamma ^2} \sin (\gamma t) - \frac{\gamma \mu }{\mu ^2+\gamma ^2} \cos (\gamma t)\right) , \quad t \ge 0. \end{aligned}$$

(17)

We now extend this analysis to tandem networks with ample capacity and hence no blocking (tandem networks with an infinite number of servers). Specifically, we consider (17) as the input rate for the second station and calculate the output rate from it, and so on for the rest of the stations. Consequently, the output rate from a network with i, $i=1,2,\ldots$, i.i.d. stations in tandem and exponential service times is given by the following expression:

$$\begin{aligned} \delta _i(t) = {\bar{\lambda }} + \beta \left( C_1^{(i)} \sin (\gamma t) - C_2^{(i)} \cos (\gamma t)\right) , \quad t \ge 0, \end{aligned}$$

(18)

where

$$\begin{aligned}&C_1^{(1)} = A_1, \quad C_2^{(1)} = B_1,\nonumber \\&A_i = \frac{\mu _i^2}{\mu _i^2+\gamma ^2}, B_i = \frac{\gamma \mu _i}{\mu _i^2+\gamma ^2}, \quad i=1,\ldots , k, \nonumber \\&C_1^{(i)} = C_1^{(i-1)}\, A_i - C_2^{(i-1)}\,B_i, C_2^{(i)} = C_1^{(i-1)}\, B_i + C_2^{(i-1)}\,A_i,\quad i=2,\ldots , k. \end{aligned}$$

(19)

Figure 7 demonstrates that, in the special case of no blocking and sinusoidal arrival rate, our results are consistent with those derived in [20]. Using (18) and (19), one can verify that the amplitude of the output rate decreases as the line becomes longer.

Fig. 7

Input and output rates from networks with k i.i.d. stations—fluid model (solid lines) versus values from (18) (dashed lines). The sinusoidal arrival rate function in (16) with ${\bar{\lambda }}=9$, $\beta =8$ and $\gamma =0.02$, $N=200$, $\mu =1/20$, and $q_{i}(0)=0$, $\forall i \in \{1,\dots ,k\}$. Five networks of different length are considered. Once the system reaches steady state, the curves from the fluid model and the analytic formula overlap

When capacity is lacking, blocking and customer loss prevail. Analytical expressions such as (18) do not exist for stochastic models with blocking, which renders our fluid model essential for analyzing system dynamics.

4.2 Bottleneck location

In networks where stations are not identical, the location of the bottleneck in the line has a significant effect on network performance. In our experiments, we analyzed two types of networks ($H=0$ and $H=\infty$), each with eight stations in tandem. In each experiment, a different station is the bottleneck; thus, it has the least processing capacity $0.3\,\upmu$N, while the other stations are i.i.d. with processing capacity $\upmu$N. Figure 8 presents the total number of customers in each station when the bottleneck is located first or last. In both types of networks, the bottleneck location affects the entire network.

Fig. 8

The bottleneck location effect on the total number of customers in each station. For the bottleneck station, j, $N_j=120$, $\mu _j=1/40$. For the other stations, $i=1,\dots ,8$, $i \not = j$ $N_i=200$, $\mu _i=1/20$, $q_{m}(0)=0$, $m=1,2,\dots ,8$, and $\lambda (t) = 2t$, $0\le t\le 40$

Figure 9 presents the total number of blocked customers in each station when the last station is the bottleneck. When $H=\infty$, blocking begins at Station 7 and surges backward to the other stations. Then, the blocking is released in reversed order: First in Station 1 and then in the other stations until Station 7 is freed up. In contrast, when $H=0$, blocking occurs only at Station 8. The blocking does not affect the other stations since Station 7 is not saturated, due to customer loss.

Fig. 9

Number of blocked customers in each station when the last station (Station 8) is the bottleneck. $N_i=200$, $\mu _i=1/20$, $i=1,\dots ,7$, $N_8=120$, $\mu _8=1/40$. $q_{m}(0)=0$, $m=1,\dots ,8$, and $\lambda (t) = 2t$, $0\le t\le 40$. On the left, the curves for Stations 1–6 are zero and overlap

4.3 Waiting room size

We now examine the effect of waiting room size before the first station. Figure 10 presents this effect on a network with four i.i.d. stations in tandem, as the size of the waiting room before the first station increases from zero to infinity. The left plot in Fig. 10 presents the total number of customers in the network, and the right plot presents the network output rate. The effect of the waiting room size on these two performances is similar. As the waiting room becomes larger, fewer customers are lost, and therefore the total number of customers in the network and the output rate increase.

Fig. 10

Waiting room size effect on the total number of customers (left plot) and on the output rate (right plot) in a network with four i.i.d. stations, where $N_i=200$, $\mu _i=1/20$, $q_{i}(0)=0$, $i=1,2,3,4$, and $\lambda (t) = 2t$, $0\le t\le 40$

4.4 Sojourn time in the system

It is of interest to analyze system sojourn time and the factors that affect it. We begin by analyzing a network with two stations in tandem. Figure 11 presents the effect of the waiting room size and the bottleneck location on average sojourn time and customer loss. When there is enough waiting room to eliminate customer loss, the minimal sojourn time is achieved when the bottleneck is located at Station 2. This adds to [5] and [7], who found that the order of stations does not affect the sojourn time when service durations are deterministic and the number of servers in each station is equal. When the waiting room is not large enough to prevent customer loss, there exists a trade-off between average sojourn time and customer loss. The average sojourn time is shorter when the bottleneck is located first; however, customer loss, in this case, is greater. Explaining in detail this phenomenon requires further research.

Fig. 11

The effects of waiting room size and bottleneck location on sojourn time and customer loss in a tandem network with two stations, where $q_{m}(0)=0$, $m=1,2$, and $\lambda (t) = 20$, $0 \le t\le 100$. In the bottleneck station, j, $N_j=120$, and $\mu _j=1/40$; in the other station, i, $N_i=200$, and $\mu _i=1/20$

Fig. 12

The effects of waiting room size and bottleneck location on the average sojourn time in a tandem network with eight stations. Here, $q_{m}(0)=0$, $m=1,\dots ,8$, and $\lambda (t) = 20$, $0 \le t\le 100$. In the bottleneck station, j, $N_j=120$, and $\mu _j=1/40$; in all other stations, $i=1,2,\dots ,8$, $i \not = j$, $N_i=200$, and $\mu _i=1/20$

We conclude with some observations on networks with k stations in tandem. Figure 12 presents the average sojourn time for different bottleneck locations and waiting room sizes. When the waiting room size is unlimited, the shortest sojourn time is achieved when the bottleneck is located at the end of the line. Conversely, when the waiting room is finite, the shortest sojourn time is achieved when the bottleneck is in the first station. Moreover, when the waiting room is finite, the sojourn time, as a function of the bottleneck location, increases up to a certain point and then begins to decrease. This is another way of looking at the bowl-shaped phenomenon [18, 33] of production line capacity. In the recent example, the maximal sojourn time is achieved when the bottleneck is located at Station 6; however, other examples show that it can happen at other stations as well. To better understand this, one must analyze the components of the sojourn time—namely, the waiting time before Station 1, the blocking time at Stations $1,\dots ,7$, and the service time at Stations $1,\dots ,8$. Since the total service time was the same in all the networks, we examined the pattern of the sojourn time is governed by the sum of the blocking and waiting times. Figure 13 presents each of these two components. The average waiting time (right plot) decreases as the bottleneck is located farther down the line. However, the blocking time (left plot) increases up to a certain point and then starts to decrease. To better understand the non-intuitive pattern of the average blocking time, one must analyze the components of the blocking time. In this case, it is the sum of the blocking time in Stations $1,\dots ,7$. Figure 14 presents the blocking time in each station and overall when $H=0$. The blocking time in Station i, $i=1,\dots ,7$, equals zero when Station i is the bottleneck, since its exit is not blocked. Further, it reaches its maximum when Station $i+1$ is the bottleneck. The sum of the average blocking time in each station yields the total blocking time and its increasing–decreasing pattern.

Fig. 13

The effects of waiting room size and bottleneck location on the average blocking time (left plot) and the average waiting time (right plot). The summation of the waiting time, blocking time, and service time yields the sojourn times presented in Fig. 12

Fig. 14

Average blocking time in each station and overall when $H=0$

Appendices

Appendix A: Proof of Theorem 1

Let T be an arbitrary positive constant. Using the Lipschitz property (Appendix C) and subtracting the equation for r in (10) from the equation for $r^{\eta }$ in (9) yields that

$$\begin{aligned}&\left||r_1^{\eta } - r_1\right||_T \vee \left||r_2^{\eta } - r_2\right||_T \le G\Bigg [ \left| r_1^{\eta }(0) - r_1(0)\right| + \Bigg \vert \Bigg \vert \int _0^{\cdot }{\lambda (u)\,\mathrm {d}u} - \eta ^{-1}A^{\eta }(\cdot )\Bigg \vert \Bigg \vert _T\nonumber \\&+ \Bigg \vert \Bigg \vert \eta ^{-1}D_1\left( \eta p\mu _1\int _0^{\cdot }{\left[ \Big (N_1 + H - r_1^{\eta }(u)\Big )\wedge \Big (N_1-b^{\eta }(u)\Big )\right] }\,\mathrm {d}u\right) \nonumber \\&- p\mu _1\int _0^{\cdot }{\left[ \left( N_1 + H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) \right] \,\mathrm {d}u}\Bigg \vert \Bigg \vert _T \nonumber \\&+ \Bigg \vert \Bigg \vert \eta ^{-1}D_3\left( \eta (1-p)\mu _1\int _0^{\cdot }{\left[ \left( N_1 + H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) \right] }\,\mathrm {d}u\right) \nonumber \\&- (1-p)\mu _1\int _0^{\cdot }{\left[ \Big (N_1 + H - r_1^{\eta }(u)\Big )\wedge \left( N_1-b^{\eta }(u)\right) \right] \,\mathrm {d}u}\Bigg \vert \Bigg \vert _T\nonumber \\&+ \Bigg \vert \Bigg \vert \mu _1 \int _0^{\cdot }\left[ \Big (N_1 + H - r_1^{\eta }(u)\Big )\wedge \left( N_1-b^{\eta }(u)\right) \right. \nonumber \\&\left. - \left( N_1 + H - r_1(u)\right) \wedge \Big (N_1-b(u)\Big )\right] \,\mathrm {d}u\Bigg \vert \Bigg \vert _T\Bigg ] \,\vee \nonumber \\&G \Bigg [\left| r_2^{\eta }(0) - r_2(0)\right| + \left|| \int _0^{\cdot }{\lambda (u)\,\mathrm {d}u} - \eta ^{-1}A^{\eta }(\cdot )\right||_T \nonumber \\&+ \Bigg \vert \Bigg \vert \eta ^{-1}D_3\Bigg (\eta (1-p)\mu _1\int _0^{\cdot }{\left[ \left( N_1 + H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) \right] }\,\mathrm {d}u\Bigg ) \nonumber \\&- (1-p)\mu _1\int _0^{\cdot }{\left[ \left( N_1 + H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) \right] \,\mathrm {d}u}\Bigg \vert \Bigg \vert _T \nonumber \\&+ \Bigg \vert \Bigg \vert \eta ^{-1}D_2\left( \eta \mu _2\int _0^{\cdot }{\left[ N_2 \wedge (r_1^{\eta }(u) - r_2^{\eta }(u) + N_2)\right] }\,\mathrm {d}u\right) \nonumber \\&- \mu _2\int _0^{\cdot }{\left[ N_2 \wedge (r_1^{\eta }(u) - r_2^{\eta }(u) + N_2)\right] \, \mathrm {d}u}\Bigg \vert \Bigg \vert _T\nonumber \\&+ \Bigg \vert \Bigg \vert (1-p)\mu _1 \int _0^{\cdot }\left[ \left( N_1 + H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) \right. \nonumber \\&\left. -\left( N_1 + H - r_1(u)\right) \wedge \left( N_1-b(u)\right) \right] \,\mathrm {d}u\Bigg \vert \Bigg \vert _T \nonumber \\&+ \Bigg \vert \Bigg \vert \mu _2\int _0^{\cdot }\left[ \left( N_2 \wedge \big (r_1^{\eta }(u) - r_2^{\eta }(u) + N_2\big )\right) \right. \nonumber \\&\left. - \left( N_2 \wedge (r_1(u) - r_2(u)+N_2)\right) \right] \,\mathrm {d}u \Bigg \vert \Bigg \vert _T\Bigg ], \end{aligned}$$

(20)

where G is the Lipschitz constant.

The first, second, sixth, and seventh terms on the right-hand side converge to zero by the conditions of the theorem. For proving convergence to zero of the third, fourth, eighth, and ninth terms, we use Lemma 1 in Appendix D. By the FSLLN for Poisson processes,

$$\begin{aligned} \sup _{0 \le u \le t}\left| \eta ^{-1}D(\eta u)- u\right| \rightarrow 0, \quad \forall t \ge 0 \quad a.s. \end{aligned}$$

Note that the functions $p\mu _1\int _0^{t}{\left[ \left( N_1+H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) \right] }\,\mathrm {d}u$ and $\mu _2\int _0^{t}{\left[ N_2 \wedge \Big (r_1^{\eta }(u) - r_2^{\eta }(u) + N_2\Big )\right] \,\mathrm {d}u}$ are bounded by $p\mu _1 \cdot (N_1 + H) \cdot T$ and $\mu _2 \cdot N_2 \cdot T$, respectively, for $0 \le p \le 1$ and $t \in [0, T]$. This, together with Lemma 1, implies that the third, fourth, eighth, and ninth terms in (20) converge to 0.

We get that

$$\begin{aligned}&\left||r_1^{\eta } - r_1\right||_T \vee \left||r_2^{\eta } - r_2\right||_T \nonumber \\&\le \left[ \epsilon _1^{\eta }(T) + G\mu _1 \left||\int _0^{\cdot }{\left[ \left( N_1 + H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) - \left( N_1 + H - r_1(u)\right) \wedge \left( N_1-b(u)\right) \right] }\,\mathrm {d}u\right||_T \right] \, \vee \nonumber \\&\Bigg [\epsilon _2^{\eta }(T) + G (1-p)\mu _1 \left||\int _0^{\cdot }{\left[ \left( N_1 + H - r_1^{\eta }(u)\right) \wedge \left( N_1-b^{\eta }(u)\right) - \left( N_1 + H - r_1(u)\right) \wedge \left( N_1-b(u)\right) \right] }\,\mathrm {d}u\right||_T \nonumber \\&\ \ \ +G\mu _2\left||\int _0^{\cdot }{{\left[ N_2 \wedge (r_1^{\eta }(u) - r_2^{\eta }(u) + N_2)\right] - \left[ N_2 \wedge (r_1(u) - r_2(u) + N_2)\right] \,\mathrm {d}u}}\right||_T \Bigg ] \nonumber \\ \le&\left[ \epsilon _1^{\eta }(T) +G\mu _1 \left||\int _0^{\cdot }{\left[ r_1^{\eta }(u) - r_1(u) \right] }\,\mathrm {d}u\right||_T +G\mu _1 \left||\int _0^{\cdot }{\left[ b^{\eta }(u) - b(u)\right] }\,\mathrm {d}u\right||_T\right] \, \vee \nonumber \\&\quad \Bigg [\epsilon _2^{\eta }(T)+ G(1-p)\mu _1 \left||\int _0^{\cdot }{\left[ r_1^{\eta }(u) - r_1(u) \right] }\,\mathrm {d}u\right||_T \nonumber \\&\quad +G(1-p)\mu _1 \left||\int _0^{\cdot }{\left[ b^{\eta }(u) - b(u)\right] }\,\mathrm {d}u\right||_T \nonumber \\&\ \ \ + G\mu _2\left||\int _0^{\cdot }{{\left[ r_1^{\eta }(u) - r_1(u) \right] \,\mathrm {d}u}}\right||_T + G\mu _2 \left||\int _0^{\cdot }{{\left[ r_2^{\eta }(u) - r_2(u)\right] \,\mathrm {d}u}}\right||_T\Bigg ] \nonumber \\ \le&\left[ \epsilon _1^{\eta }(T) + G\mu _1 \int _0^{T}{\left||r_1^{\eta } - r_1\right|| _u}\,\mathrm {d}u +G\mu _1 \int _0^{T}{\left||b^{\eta } - b\right||_u\,\mathrm {d}u}\right] \, \vee \nonumber \\&\Bigg [\epsilon _2^{\eta }(T)+G\mu _1 \int _0^{T}{\left||r_1^{\eta } - r_1 \right||_u\,\mathrm {d}u} +G\mu _1 \int _0^{T}{\left||b^{\eta } - b\right||_u\,\mathrm {d}u} \nonumber \\&\ \ \ + G \mu _2\int _0^{T}{{\left||r_1^{\eta } - r_1\right||_u\,\mathrm {d}u}} + G\mu _2 \int _0^{T}{{\left||r_2^{\eta } - r_2\right||_u\,\mathrm {d}u}}\Bigg ], \end{aligned}$$

(21)

where $\epsilon _1^{\eta }(T)$ bounds the sum of the first four terms on the right-hand side of (20), and $\epsilon _2^{\eta }(T)$ bounds the sum of the sixth to ninth terms; these two quantities $\epsilon _1^{\eta }(T)$ and $\epsilon _2^{\eta }(T)$ converge to zero, as $\eta \rightarrow \infty$. The second inequality in (21) is obtained by using the inequalities $| a \wedge b - a \wedge c | \le | b-c |$ and $| a \wedge b - c \wedge d | \le | a-c | + |b-d|$ for any a, b, c, and d. The third equality in (21) is because $0\le p \le 1$.

We now use

$$\begin{aligned} \int _0^{T}{\left||b^{\eta } - b\right||_u\,\mathrm {d}u}&= \int _0^{T}{\left||\left( r_1^{\eta } - r_2^{\eta }\right) ^+ - \left( r_1 - r_2\right) ^+\right||_u\,\mathrm {d}u} \nonumber \\&= \int _0^{T}{\left||r_1^{\eta } - r_1^{\eta } \wedge r_2^{\eta } - r_1 + r_1 \wedge r_2\right||_u\,\mathrm {d}u} \nonumber \\&\le \int _0^{T}{\Big [\left||r_1^{\eta } - r_1\right||_u +\left||r_1^{\eta } \wedge r_2^{\eta } - r_1 \wedge r_2\right||_u\Big ]\,\mathrm {d}u} \nonumber \\&\le \int _0^{T}{\Big [2\left||r_1^{\eta } - r_1\right||_u +\left||r_2^{\eta } - r_2\right||_u\Big ]\,\mathrm {d}u}\nonumber \\&= 2\int _0^{T}{\left||r_1^{\eta } - r_1\right||_u\,\mathrm {d}u} + \int _0^{T}{\left||r_2^{\eta } - r_2\right||_u\,\mathrm {d}u}. \end{aligned}$$

(22)

From (21) and (22), we get that

$$\begin{aligned}&\left||r_1^{\eta } - r_1\right||_T \vee \left||r_2^{\eta } - r_2\right||_T\nonumber \\&\le \left[ \epsilon _1^{\eta }(T) \vee \epsilon _2^{\eta }(T)\right] + G\left( 3 \mu _1 + \mu _2\right) \int _0^{T}{\left||r_1^{\eta } - r_1\right||_u\,\mathrm {d}u} + G\left( \mu _1 \vee \mu _2\right) \int _0^{T}{\left||r_2^{\eta } - r_2\right||_u\,\mathrm {d}u}\nonumber \\&\le \left[ \epsilon _1^{\eta }(T) \vee \epsilon _2^{\eta }(T)\right] + 2G\left( 3\mu _1 \vee \mu _2\right) \left[ \int _0^{T}{\left||r_1^{\eta } - r_1\right||_u\,\mathrm {d}u} + \int _0^{T}{\left||r_2^{\eta } - r_2\right||_u\,\mathrm {d}u}\right] \nonumber \\&\le \left[ \epsilon _1^{\eta }(T) \vee \epsilon _2^{\eta }(T)\right] + 4G\left( 3\mu _1 \vee \mu _2\right) \left[ \int _0^{T}{\left||r_1^{\eta } - r_1\right||_u\,\mathrm {d}u} \vee \int _0^{T}{\left||r_2^{\eta } - r_2\right||_u\,\mathrm {d}u}\right] \nonumber \\&\le \left[ \epsilon _1^{\eta }(T) \vee \epsilon _2^{\eta }(T)\right] + 4G\left( 3\mu _1 \vee \mu _2\right) \left[ \int _0^{T}{\left||r_1^{\eta } - r_1\right||_u \vee \left||r_2^{\eta } - r_2\right||_u\,\mathrm {d}u}\right] . \end{aligned}$$

(23)

The first equality in (23) is obtained by using the inequality $(a+b) \vee (c+d) \le a \vee c + b \vee d$, for any a, b, c, and d. Applying Gronwall’s inequality [22] to (23) completes the proof for both the existence and uniqueness of r.

Appendix B: Proof of Proposition 1

We begin by proving that the solution for (11) satisfies, for $t \ge 0$,

$$\begin{aligned} l(t)&= \int _0^t{1_{\left\{ x_1(u) \ge \, N_1+H\right\} }\cdot 1_{\left\{ x_1(u)+ x_2(u)< N_1 + N_2+H\right\} }\left[ \lambda (u) - l_1(u)\right] ^{+} \,\mathrm {d}u} \, \nonumber \\&\quad + \int _0^t{1_{\left\{ x_1(u) < \, N_1+H\right\} }\cdot 1_{\left\{ x_1(u)+ x_2(u) \ge N_1 + N_2+H\right\} }\left[ \lambda (u) - l_2(u)\right] ^{+} \,\mathrm {d}u}\nonumber \\&\quad + \int _0^t{1_{\big \{x_1(u) \ge \, N_1+H\big \}}\cdot 1_{\big \{x_1(u)+ x_2(u) \ge N_1 + N_2 + H\big \}}} \Big [\lambda (u) - l_1(u) \wedge l_2(u) \Big ]^{+} \,\mathrm {d}u, \end{aligned}$$

(24)

where

$$\begin{aligned}&l_1(u) = \mu _{1} \left( x_{1}(u) \wedge \left( N_{1} - b(u)\right) \right) ;\\&l_{2}(u) = \mu _2 \left( x_2(u) \wedge N_2\right) + (1-p)\mu _{1} \left( x_{1}(u) \wedge \left( N_{1} - b(u)\right) \right) . \end{aligned}$$

In order to prove this, we substitute (24) in (11) and show that the properties in (11) prevail. We begin by substituting (24) in the first line of (11). Using $(a-b)^+=[a-a\wedge b]$, for any a, b, we obtain

$$\begin{aligned} x_1(t)&= x_1(0) + \int _0^t{\left[ \lambda (u)- \mu _1 \left[ x_1(u) \wedge \left( N_1-b(u)\right) \right] \right] \,\mathrm {d}u}\\&\quad - \int _0^t{1_{\left\{ x_1(u) \ge N_1 + H\right\} }\cdot 1_{\left\{ x_1(u) + x_2(u)< N_1 + N_2 + H\right\} }\left[ \lambda (u) - \lambda (u) \wedge l_1(u)\right] \,\mathrm {d}u} \\&\quad - \int _0^t{1_{\left\{ x_1(u) < \, N_1+ H\right\} }\cdot 1_{\left\{ x_1(u)+ x_2(u) \ge N_1 + N_2 + H\right\} }\left[ \lambda (u) - \lambda (u) \wedge l_2(u)\right] \,\mathrm {d}u}\\&\quad - \int _0^t{1_{\left\{ x_1(u) \ge \, N_1 + H\right\} }\cdot 1_{\left\{ x_1(u)+ x_2(u) \ge N_1 + N_2 + H\right\} }} \left[ \lambda (u) -\lambda (u) \wedge l_1(u) \wedge l_2(u)\right] \,\mathrm {d}u, \end{aligned}$$

and therefore,

$$\begin{aligned} x_1(t)&= x_1(0) + \int _0^t\Big [1_{\left\{ x_1(u)< \, N_1+ H\right\} } \cdot 1_{\left\{ x_1(u) + x_2(u)< \, N_1 + N_2 + H\right\} } \cdot \lambda (u)\nonumber \\&\quad - \mu _1 \left[ x_1(u) \wedge \left( N_1-b(u)\right) \right] \Big ]\,\mathrm {d}u \nonumber \\&\quad + \int _0^t{\left[ 1_{\left\{ x_{1}(u) \ge N_{1} + H\right\} } \cdot 1_{\left\{ x_1(u) + x_{2}(u)< N_1 + N_{2}+ H \right\} } \cdot \left( \lambda (u) \wedge l_1(u) \right) \right] \,\mathrm {d}u}\nonumber \\&\quad + \int _0^t{\left[ 1_{\left\{ x_{1}(u) < N_{1}+H\right\} } \cdot 1_{\left\{ x_1(u) + x_{2}(u) \ge N_1 + N_2 + H \right\} } \cdot \left( \lambda (u) \wedge l_2(u)\right) \right] \,\mathrm {d}u}\nonumber \\&\quad + \int _0^t\left[ 1_{\left\{ x_{1}(u) \ge N_{1}+H\right\} } \cdot 1_{\left\{ x_1(u) + x_{2}(u) \ge N_1 + N_2+H \right\} } \cdot \left( \lambda (u) \wedge l_1(u) \wedge l_2(u)\right) \right] \,\mathrm {d}u;\nonumber \\ x_2(t)&= x_2(0) + \int _0^t{\left[ p \mu _1 \left[ x_1(u) \wedge \left( N_1-b(u)\right) \right] - \mu _2 \left( x_2(u) \wedge N_2 \right) \right] \,\mathrm {d}u}. \end{aligned}$$

(25)

Clearly, the properties in the third and fourth lines in (11) prevail. It is left to verify that the first and second conditions prevail. This is done by the following proposition.

Proposition 2

The functions $x_1(\cdot )$ and $x_1(\cdot ) + x_2(\cdot )$ as in (25) are bounded by $N_1 + H$ and $N_1+N_2 + H$, respectively.

Proof

First, we prove that the function $x_1(\cdot )$, as in (25), is bounded by $N_1+H$. Assume that, for some t, $x_1(t) > N_1+H$. Since $x_1(0) \le N_1+H$ and $x_1$ is continuous (being an integral), there must be a last ${\tilde{t}}$ in [0, t], such that $x_1({\tilde{t}}) = N_1+H$ and $x_1(u) > N_1+H$, for $u \in [{\tilde{t}}, t]$. Without loss of generality, assume that ${\tilde{t}}=0$; thus $x_1(0) = N_1+H$ and $x_1(u) > N_1+H$ for $u \in (0, t]$. From (25), we get that

$$\begin{aligned} x_1(t)&= N_1+H +\int _0^t{\left[ 1_{\left\{ x_{1}(u) + x_2(u) < N_1 + N_2+H\right\} }\cdot \left( \lambda (u) \wedge l_1(u) \right) \right] \,\mathrm {d}u}\, \\&\quad + \int _0^t{\left[ 1_{\left\{ x_{1}(u) + x_{2}(u) \ge N_1 + N_2+H\right\} }\cdot \left( \lambda (u) \wedge l_1(u) \wedge l_2(u)\right) \right] \,\mathrm {d}u}\\&\quad - \mu _1 \int _0^t{\left[ x_1(u) \wedge \left( N_1-b(u)\right) \right] \,\mathrm {d}u}\\&\le N_1 +H+ \int _0^t{\left[ l_1(u) - \mu _1 \left[ x_1(u) \wedge \left( N_1-b(u)\right) \right] \right] \,\mathrm {d}u}=N_1+H, \end{aligned}$$

which contradicts our assumption and proves that $x_1(\cdot )$ cannot exceed $H_1+N_1$.

What is left to prove now is that the function $x_1(\cdot ) + x_2(\cdot )$ is bounded by $N_1+N_2$. Without loss of generality, assume that $x_1(0) + x_2(0) = N_1 + N_2+H$ and $x_1(u) + x_2(u) > N_1 + N_2+H$ for $u \in (0, t]$. This assumption, together with $x_1 \le N_1+H$, yields that $x_2 > N_2$; hence, from (25), we get that

$$\begin{aligned}&x_1(t) +x_2(t)\\&\quad = N_1 + N_2 + H \int _0^t{\left[ 1_{\left\{ x_{1}(u) \ge N_{1}+N_1\right\} } \cdot \left( \lambda (u) \wedge l_1(u) \wedge l_2(u)\right) \right] \,\mathrm {d}u}\\&\qquad + \int _0^t{\left[ 1_{\left\{ x_{1}(u) < N_{1}+H\right\} } \cdot \left( \lambda (u) \wedge l_2(u)\right) \right] \,\mathrm {d}u}\\&\qquad - \int _0^t{\left[ (1-p)\mu _1 \left( x_1(u) \wedge \left( N_1-b(u)\right) \right) + \mu _2 \left( x_2(u) \wedge N_2 \right) \right] \,\mathrm {d}u}\\&\quad \le N_1 + N_2 + H +\int _0^t\left[ l_2(u) - (1-p)\mu _1 \left( x_1(u)\wedge \left( N_1-b(u)\right) \right) \right. \\&\qquad \left. - \,\mu _2 \left( x_2(u) \wedge N_2 \right) \right] \,\mathrm {d}u\\&\quad = N_1+N_2+H, \end{aligned}$$

which contradicts the assumption that $x_1(t) + x_2(t) > N_1 + N_2 + H$ and proves that $x_1(\cdot )+x_2(\cdot )$ is bounded by $N_1+N_2+H$. $\square$

By the solution uniqueness (Proposition 3), we have established that x, the fluid limit for the stochastic queueing family $X^{\eta }$ in (2), is given by (25).

The following two remarks explain why (25) is equivalent to (12):

• 1. After proving that $x_1(\cdot ) \le N_1 + H$ and $x_1(\cdot ) + x_2(\cdot ) \le N_1 + N_2 + H$ in Proposition 2, the indicators in (24) can accommodate only the cases when $x_1(\cdot ) = N_1 + H$ and $x_1(\cdot ) + x_2(\cdot ) = N_1 + N_2+ H$.

• 2. When $x_1(u)=N_1+H$ and $x_1(u)+x_2(u) < N_1+N_2+H$, $x_2(u) < N_2$, and hence $b(u)=0$ and $l_1(u) = l_1^*(u)$. Alternatively, when $x_1(u)< N_1+H$ and $x_1(u)+x_2(u) = N_1+N_2+H$, $x_2(u) > N_2$, and therefore $l_2(u)=l_2^*(u)$.

Appendix C: Uniqueness and Lipschitz property

Let $C \equiv C[0,\infty ]$. We now define mappings $\psi : C^2 \rightarrow C$ and $\phi : C^2 \rightarrow C^2$ for $m \in C^2$ by setting

$$\begin{aligned} \psi (m)(t)&= \sup _{0 \le s \le t} \left( -\Big (m_1(s) \wedge m_2(s)\right) \Big )^+; \\ \phi (m)(t)&= m(t) + \psi (m)(t)\begin{bmatrix} 1\\ 1 \end{bmatrix}, \quad t \ge 0. \end{aligned}$$

Proposition 3

Suppose that $m \in C^2$ and $m(0) \ge 0$. Then, $\psi (m)$ is the unique function l, such that

• 1. l is continuous and non-decreasing with $l(0)=0$,

• 2. $r(t) = m(t) + l(t) \ge 0$ for all $t \ge 0$,

• 3. l increases only when $r_1=0$ or $r_2=0$.

Proof

Let $l^*$ be any other solution. We set $y=r_1^* - r_1 = r_2^* - r_2 = l^* - l$. Using the Riemann–Stieltjes chain rule [31, Ch. 2.2]

$$\begin{aligned} f(y_t)=f(y_0) + \int _0^t f'(y) \,\mathrm {d}y, \end{aligned}$$

for any continuously differentiable $f: R \rightarrow R$. Taking $f(y) = y^2/2$, we get that

$$\begin{aligned} \frac{1}{2}\left( r_i^*(t) - r_i(t)\right) ^2 = \int _0^t (r_i^*-r_i)\,\mathrm {d}l^* + \int _0^t (r_i-r_i^*)\,\mathrm {d}l. \end{aligned}$$

(26)

The function $l^*$ increases when either $r_1^*=0$ or $r_2^*=0$. In addition, $r_1 \ge 0$ and $r_2 \ge 0$. Thus, either $(r_1^*-r_1)\,\mathrm {d}l^* \le 0$ or $(r_2^*-r_2)\,\mathrm {d}l^* \le 0$. Since $r_1^*-r_1 = r_2^*-r_2$, both terms are non-positive. The same principles yield that the second terms in both lines on the right-hand side of (26) are non-positive. Since the left-hand side $\ge 0$, both sides must be zero; thus, $r_1^*=r_1$, $r_2^*=r_2$, and $l^*=l$. $\square$

Proposition 4

The mappings $\psi$ and $\phi$ are Lipschitz continuous on $D_o[0,t]$ under the uniform topology for any fixed t.

Proof

We begin by proving the Lipschitz continuity of $\psi$. For this, we show that for any $T >0$ there exists $C \in R$ such that

$$\begin{aligned} \left||\psi (m) - \psi (m')\right||_T \le C\Big [\left||m_1-m'_1\right||_T \vee \left||m_2-m'_2\right||_T\Big ], \end{aligned}$$

for all $m, m' \in D_0^2$.

$$\begin{aligned}&\left||\psi (m) - \psi (m')\right||_T \nonumber \\&\quad = \left||\sup _{0 \le s \le \cdot } \Big (-\big (m_1(s) \wedge m_2(s)\big )\Big )^+ - \sup _{0 \le s \le t} \Big (-\big (m'_1(s) \wedge m'_2(s)\big )\Big )^+\right||_T \nonumber \\&\quad \le \left||\sup _{0 \le s \le \cdot } \left| \big (m_1(s) \wedge m_2(s)\big ) - \big (m'_1(s) \wedge m'_2(s)\big )\right| \right||_T\nonumber \\&\quad = \left|| \big (m_1 \wedge m_2\big ) - \big (m'_1 \wedge m'_2\big )\right||_T \le 2\Big [\left||m_1-m'_1\right||_T \vee \left||m_2-m'_2\right||_T\Big ]. \end{aligned}$$

(27)

The last inequality derives from

$$\begin{aligned} m_1(t) \wedge m_2(t) = \big (m_1(t)-m'_1(t) +m'_1(t)\big ) \wedge \big (m_2(t)-m'_2(t) +m'_2(t)\big ); \end{aligned}$$

therefore,

$$\begin{aligned} m_1(t) \wedge m_2(t) \le m'_1(t) \wedge m'_2(t) + \left||m_1-m'_1\right||_T + \left||m_2-m'_2\right||_T, \\ m_1(t) \wedge m_2(t) \ge m'_1(t) \wedge m'_2(t) - \left||m_1-m'_1\right||_T - \left||m_2-m'_2\right||_T, \end{aligned}$$

and

$$\begin{aligned} \left| m_1(t) \wedge m_2(t) - m'_1(t) \wedge m'_2(t)\right| \le \left||m_1-m'_1\right||_T + \left||m_2-m'_2\right||_T, \end{aligned}$$

which yields

$$\begin{aligned} \left||m_1(t) \wedge m_2(t) - m'_1(t) \wedge m'_2(t)\right||_T&\le \left||m_1-m'_1\right||_T + \left||m_2-m'_2\right||_T \\&\le 2 \left( \left||m_1-m'_1\right||_T \vee \left||m_2-m'_2\right||_T\right) . \end{aligned}$$

Our next step is proving the Lipschitz continuity of $\phi$. For this, we show that for any $T >0$ there exists $C \in R$ such that

$$\begin{aligned} \left||\phi _1(m) - \phi _1(m')\right||_T \vee \left||\phi _2(m) - \phi _2(m')\right||_T \le C\Big [\left||m_1-m'_1\right||_T \vee \left||m_2-m'_2\right||_T\Big ], \end{aligned}$$

for all $m, m' \in D_0^2$.

We begin with the left-hand side:

$$\begin{aligned}&\left||\phi _1(m) - \phi _1(m')\right||_T \vee \left||\phi _2(m) - \phi _2(m')\right||_T \\&= \left||m_1(t) + \psi (m)(t) - m'_1(t) - \psi (m')(t)\right||_T \vee \\&\qquad \left||m_2(t) + \psi (m)(t) - m'_2(t) - \psi (m')(t)\right||_T\\&= \left||m_1(t) - m'_1(t) + \psi (m)(t) - \psi (m')(t)\right||_T \vee \\&\qquad \left||m_2(t) - m'_2(t) + \psi (m)(t) - \psi (m')(t)\right||_T \\&\le \left||m_1(t) - m'_1(t)\right||_T + \left||\psi (m)(t) - \psi (m')(t)\right||_T \vee \\&\qquad \left||m_2(t) - m'_2(t)\right||_T + \left||\psi (m)(t) - \psi (m')(t)\right||_T \\&\le \left||m_1-m'_1\right||_T \vee \left||m_2-m'_2\right||_T + \left||\psi (m)(t) - \psi (m')(t)\right||_T \\&\le 3 \left( \left||m_1-m'_1\right||_T \vee \left||m_2-m'_2\right||_T \right) , \end{aligned}$$

where the last inequality is derived from (27). $\square$

Appendix D: Lemma 1

Lemma 1

Let the function $f_{\eta }(\cdot ) \rightarrow 0$, u.o.c. as ${\eta } \rightarrow \infty$. Then, $f_{\eta }(g_{\eta }(\cdot )) \rightarrow 0$, u.o.c. as ${\eta } \rightarrow \infty$, for any $g_{\eta }(\cdot )$ that are locally bounded uniformly in $\eta$.

Proof

Choose $T>0$, and let $C_{T}$ be a constant such that $\left| g_{\eta }(t)\right| \le C_{T}$, for all $t \in [0, T]$. By the assumption on $f_{\eta }(\cdot )$, we have $\Vert f_\eta \Vert _{C_T} \rightarrow 0$ as $\eta \rightarrow \infty$. It follows that $\Vert f_\eta (g_\eta (\cdot ))\Vert _T \rightarrow 0$ as $\eta \rightarrow \infty$, which completes the proof. $\square$