Consumer learning, switching costs, and heterogeneity: A structural examination

Abstract

This paper develops and estimates a model of forward-looking consumer learning with switching costs using household level scanner data from a frequently purchased product category. This is novel because current models of consumer purchase behavior assume that only one of these types of dynamics is present, not both at the same time. My model estimates support the presence of both learning and switching costs in this product category. The estimates show that before consuming new products, consumers are unsure of their tastes for them, and subsequently learn their tastes by purchase and consumption of new products. Switching costs are large, comprising roughly 30 percent of the cost of a medium sized package of the product. Additionally, the model incorporates very rich individual level unobserved heterogeneity in price sensitivities, tastes, and switching costs, and the amount by which consumers learn. To show that my model produces different implications than a model with learning or switching costs only, I estimate two more specifications, one without each type of dynamics, and simulate counterfactuals that are of interest to managers and policymakers. I find that intertemporal elasticities are underestimated when either type of dynamics is left out, by as much as 90%. Informative advertising is also affected by the presence of switching costs, although the direction of the bias is not signed. Leaving out dynamics also has a large impact on long-term elasticities, which are used by antitrust policymakers to evaluate the impact of mergers. When learning is ignored, cross elasticities are underestimated by as much as 45%. When switching costs are ignored, both own and cross elasticities are underestimated.

1 Introduction

Consumer dynamics such as consumer learning by experience and switching costs have played an important role in industrial organization and marketing for many years. Models of consumer purchase behavior in frequently purchased product categories typically include only one or the other type of dynamics. This paper develops and estimates a model of consumer purchase behavior which combines these two types of dynamics into a single model. The model is estimated using household level scanner data on a frequently purchased product category, and the estimates show that both learning and switching costs play a significant role in demand dynamics. Additionally, I demonstrate that leaving out one or the other type of dynamics can result in significant biases in model predictions that are of interest to managers and policymakers, such as the impact of introductory promotions and long-term price elasticities.

In models of consumer learning by experience, individuals are assigned a permanent taste, or match value, for each available product. A consumer learns about her taste for a product by purchasing and consuming it. This makes purchasing the product a dynamic decision, since the consumer’s decision to experiment with a new product is an investment that will pay off if the consumer likes the product and purchases it again in the future. Learning produces state dependence in consumer purchase behavior: a consumer’s prior purchases will impact her current decisions, because they impact what she believes about her tastes for currently available products. In marketing, learning has been offered as an explanation for state dependence for a long time (Givon and Horsky 1979). Structural approaches, which estimate the parameters of consumer utility functions, such as beliefs about tastes for new products, have been applied to several different product categories.¹

An alternative way of capturing state dependence in consumer purchase behavior is to model switching costs: one assumes consumers know their true tastes for all available products, but that there is a cost of switching between products. A popular way to specify switching costs in frequently purchased products is to include a parameter in a consumer’s utility that lowers it if she purchases a product that is different from her previous choice. Switching costs in markets for frequently purchased goods arise due to consumer-specific investment in a product. This investment can be psychological, as discussed in Klemperer (1995)’s pioneering paper on switching costs. The article argues that brand loyalty can create switching costs, which means that switching costs can play a role in many consumer packaged goods markets. Indeed, models incorporating switching costs of this type have seen widespread use in the empirical marketing literature for frequently purchased products.²

In contrast, in the model of this paper consumers are forward-looking, learn about new products and have costs of switching between products. The model is estimated on household level scanner data of laundry detergent purchases, where three new products are introduced during the period when the data was collected. Learning can be empirically separated from switching costs through differences in the effect of having made a first purchase of a new product on a consumer’s current purchase relative to the effect of having used a product in the previous purchase event. The model estimates show that consumers display a significant amount of uncertainty about their tastes for new products before they purchase them. The average cost of switching products, when measured in 1985 dollars, is roughly 1.35, about 30% of the cost of an average sized package of detergent.³

To show how the implications of my model differ from models which do not include either learning or switching costs, I estimate two restricted versions of the model that do not include one or the other form of dynamics. I then run three counterfactual simulations to assess the differences between these models. Two of these quantify consumer response to introductory promotional behavior: I compare the impact of short term introductory price discounts on future market shares across all three models, and the impact of introductory informative advertising on market shares in the full model to those of the model without switching costs. Relative to the model with learning and switching costs, the no learning model underpredicts the impact of short-term introductory price discounts by as much as two to three times. This happens because learning and switching costs can reinforce each other. A consumer who purchases a new product, believing her match value for it is high, will develop a cost of switching away from it even if she learns her actual taste for the product is low. The model with no switching costs also underpredicts the longer term impact of temporary price discounts on longer term shares: price discounts induce more current purchases, and when switching costs are present it takes longer for consumers to switch away once the discount has ended. I find that the model with only learning mispredicts the impact of introductory informative advertising on new product market shares and revenues, although the direction of the bias can be either positive or negative. The results of these counterfactual experiments have managerial importance: in markets where both of these dynamics are present, leaving out one type of dynamics will lead to incorrect predictions about the impact of promotions. They will also be of interest to industrial organization economists who seek to understand the role of information in markets where switching costs may be present: by ignoring switching costs, researchers will misestimate firms’ incentives to use introductory advertising.

I also compute a counterfactual that is of interest to policymakers: the long term price elasticities implied by each model. Own and cross-price elasticities are used by competition authorities to assess the impact of mergers. I find that in both the learning only and switching cost only models, own and cross price elasticities elasticities are usually underestimated by leaving out dynamics by as much as 90%. Thus, if competition authorities are examining a merger in a market where both switching costs and learning are present, ignoring either type of dynamics will lead to an underprediction of the impact of the merger on prices. This exercise is in the spirit of recent research in industrial organization which has shown that econometric models which ignore dynamics can lead to incorrect policy implications (for an example, see Hendel and Nevo 2006). This paper then takes this idea one step further, and shows that even if demand dynamics are modeled, mis-specifying those dynamics can still lead to serious biases.

Biases may also result from failing to model unobserved heterogeneity. As an example of this sort of bias, suppose that consumers are heterogeneous in their sensitivities to price discounts. If, as is common in practice, there are introductory price discounts on new products, price sensitive consumers will purchase the new products initially, and switch away from them to something else when their prices rise. This behavior is also what one would expect if consumers were learning about the new product, and some of them found they disliked it. Thus, ignoring unobserved heterogeneity could lead to overestimates in the amount of learning. To account for this potential bias, I model continuously distributed unobserved heterogeneity in consumer tastes, price sensitivities, switching costs, prior beliefs, and the amount by which consumers learn.

The presence of unobserved consumer heterogeneity raises computational issues in estimation. As discussed above, in my model consumers are forward-looking and take into account the effect of learning and other sources of dynamics on their future utility. Estimating models where consumers are forward-looking is extremely computationally burdensome, and as a result most papers that that have tackled these problems have been parsimonious in how they specify consumer heterogeneity, if it is modeled at all.⁴ To tackle this problem, I employ a newly developed Bayesian estimation procedure which makes it possible to estimate dynamic discrete choice models with consumer heterogeneity in a reasonable amount of time (the procedure in this paper is similar to those discussed in Imai et al. 2009 and Norets 2009b).⁵ A related contribution of this paper is that I include unobserved heterogeneity in consumer uncertainty about future match values: some consumers may be very sure about how much they will like a new product, and some may be less so. As far as I am aware, prior work on learning has assumed that the amount of uncertainty about new products is constant across consumers. In Section 3.3, I demonstrate that if one observes multiple new product introductions, it is possible to identify unobserved heterogeneity in the amount by which consumers learn. I find evidence of unobserved heterogeneity in consumer learning.

Another estimation issue arises due to the significant amount of coupon use that is observed in the data set - consumers use a coupon in roughly half of all purchase events. Previous papers in dynamic estimation have not included coupons, because including coupon usage as a right hand side variable raises serious endogeneity concerns: the researcher only observes coupons for products that were purchased, but not for products the consumer did not choose. Thus, coupons for non-purchased products must be treated as latent unobservables and integrated out during estimation, adding significantly to computational time (for an example of this correction in the estimation of static demand models, see Erdem et al. 1999). Not including coupons at all creates measurement error in prices, which will lead to biased estimates of price sensitivities. The estimation procedure I use allows me to easily incorporate coupon usage.

Before turning to the body of the paper, I note that the implications derived in this paper could easily arise in other product categories. A wide variety of other products where learning and switching costs play a role were cited above, and it is not difficult to conceive of others. For example, it is very likely that both learning and switching costs play a role in computer operating systems, a market which has been the subject of a number of high profile antitrust cases. Additional examples of markets where switching costs play an important role are discussed in Farrell and Klemperer (2007); some examples are cellular phones, credit cards, cigarettes, air travel, online brokerage services, automobile insurance, and electricity suppliers. It is certainly conceivable that consumer learning could also play a role in these markets. For example, in cellular phone markets consumers will likely learn about aspects of their provider’s service after signing a contract with them. Cellular phone contracts often penalize consumers for switching providers, which creates switching costs and makes the decision to invest in a plan a forward-looking one.

1.1 Related literature

Characterizing state dependence in demand as learning dates back to at least Givon and Horsky (1979), a paper which estimates the parameters of three models of state dependence: a linear learning model, which is presented as a reduced form model of slow learning; a Markov model, which is interpreted as a model of fast learning; and a Bernoulli model of brand choice, which is analogous to a static discrete choice model. The paper finds support for all three models, depending on the product category in question. The modeling approach, while informative about the time series process which best characterizes demand, does not distinguish between different structural models which could underlie that process. For example, fast learning may imply transition probabilities in choices which are consistent with the Markov model. However, switching costs will do this as well. Without controlling for a consumer’s first purchase event of a new product and time-varying exogenous variables such as prices, it is difficult to separate these different sources of demand dynamics. The structural approach taken in my paper addresses this concern.

A paper that examines an issue similar in spirit to my paper is Moshkin and Shachar (2002), which distinguishes between two different models of state dependence in demand: a model of asymmetric information, and a pure switching cost model. The paper estimates a model where each consumer’s behavior may be explained by one model or the other using television viewing data, finding that most consumers’ behavior is better explained by the learning model rather than the traditional switching costs model. There are a number of important differences between Moshkin and Shachar (2002)’s work and mine. First, the model of learning is different: firms offer new products every period and consumers learn via search rather than through experience; learning through experience is important for goods that are repeatedly purchased. Second, consumers are myopic in the model of Moshkin and Shachar (2002), which is probably a reasonable assumption for television viewing choices; however, as I have argued above, when consumers are learning by experience modeling forward-looking behavior is key. Modeling forward-looking behavior is a more difficult problem computationally. Third, my model is more flexible: in Moshkin and Shachar (2002) consumers are designated to display either learning, or switching costs, but not both behaviors at the same time as my model allows. Because I model unobserved heterogeneity in both switching costs and learning, my model nests that of Moshkin and Shachar (2002) as a special case.

There are also examples of models which nest learning and switching costs being applied to markets for services. Israel (2005) proposes and estimates a model of consumer learning and lock-in for an automobile insurance company. Very recent work by Goettler and Clay (2010) estimates a structural model of learning and switching costs on tariff choice data for an online grocer. Both of these papers are important contributions to our understanding about demand dynamics, but they differ in both the questions they answer and the complexity of the modeling approach. Most importantly, these papers provide evidence on these dynamics in the demand for services; I am the first to find evidence for both types of dynamics in a frequently purchased product category, which are the subject of a significant amount of interest in marketing and industrial organization. Also, there are a number of complications which arise when modeling learning with switching costs in packaged goods markets. In the two previous papers, the consumer learning process and the decision process is much simpler: there is a single service, and consumers are learning about their preference to use the service. In the case of Israel (2005), consumers are deciding whether or not to stay with the auto insurance company; in Goettler and Clay (2010)’s case they are deciding between three different tariff schedules for the grocer. Because these papers examine demand for a single product, it is impossible for them to compute some of the counterfactuals I do, such as cross-price elasticities. Including multiple products also adds significantly to the computational difficulty of the exercise. In my model, there are 30 different products, and three new products for consumers to learn about, making the model’s state space much larger.⁶ Finally, neither paper characterizes the biases that arise from leaving out one or the other type of dynamics by estimating restricted models.

2 Data set

2.1 Discussion of the scanner data

The data set I am using is A.C. Nielsen supermarket scanner data on detergent purchases in the city of Sioux Falls, South Dakota between December 29, 1985 and August 20, 1988. This data is particularly useful for identifying consumer learning and switching costs for two reasons: first, since this data is a panel of household purchases, it allows one to track individual household behavior over time. Second, during the period that this data was collected, three new brands of liquid laundry detergents were introduced to the market: Cheer in May 1986, Surf in September 1986 and Dash in May 1987. Households that participated in this study were given magnetic swipe cards, and each time the household shopped at a major grocery or drugstore in the city, the swipe card was presented at the checkout counter. Additionally, households that participated in the study filled out a survey containing basic demographic information.

During the time the data set was collected three large companies dominate the market: Procter and Gamble (Dash, Cheer, Era, Tide), Unilever (Wisk, Surf) and Colgate-Palmolive (Fab, Ajax). During this period, laundry detergents were available in two forms: liquids and powders. Market shares of all the brands used in the analysis are shown in Fig. 1. Smaller brands of each type I group into an Other category. Liquid detergents comprise roughly fifty percent of all units sold. Additionally, well known brands, such as Wisk and Tide, have high market shares.

Fig. 1

Market shares of major detergent brands

Table 1 shows the market shares of selected brands of liquids over different periods of time. It is notable that for all three new products, their market share tends to be significantly higher in the first 12 weeks after introduction than it is for the remainder of the sample period. This fact is consistent with learning, since the option value of learning induces consumers to purchase new products early. However, it is also consistent with consumer response to introductory pricing. The average prices of different brands at different periods of time are shown in the same table, underneath the shares. There are two noteworthy facts in this table. First, prices of the new brands Cheer and Surf tend to be lower in the first 12 weeks after introduction than they are later on in the data. This fact suggests that we should be aware of possible biases due to consumer heterogeneity: for example, price sensitive consumers could purchase the new products initially when they are cheap, and switch away from them as they get more expensive, which could be mistaken for learning. Second, when Cheer is introduced to the market by Procter and Gamble, the price of Wisk, a popular product of Unilever, goes down. Similarly, when Unilever’s Surf is new, Procter and Gamble’s Tide drops in price. Cheer and Surf have been successful products since their introductions, but Dash was discontinued in the United States in 1992. One possible reason for this is that Dash was more of a niche product: it was intended for front-loading washers, which constituted about 5% of the market at the time.

Table 1 Market shares, average prices: selected liquid brands at different periods

Table 2 summarizes household level information that is relevant to learning and brand choice. The first panel summarizes the number of purchase events that are observed for each household. As will be discussed in further detail below, separating out learning from switching costs will require observing a time series of purchases for each household. The fact that the average number of observed purchases is 22 is heartening. The next panel in the table shows the number of different brands a household is ever observed to purchase. 75% of households purchase at least 3 different products, and the median household purchases 4. The third panel of the table shows the fraction of households who ever make a purchase of one of the new products. It is notable that, even though the new products are heavily discounted on their introduction, and there is potentially value to learning about them, most households never purchase the products. One explanation for this is that most households have a favorite product, and the value of learning about a new product is not high enough to induce them to experiment. It is also possible that switching costs make it less likely consumers will experiment with a new product. Consumers who purchase the new product usually make their first purchase during the first 12 weeks after the product’s introduction, as shown in the fourth panel. The fact that consumers disproportionately make their first purchases soon after the product’s introduction is consistent with there being value to learning about the new product. Household switching behavior also provides evidence for learning, and this is shown in the last panel of the table. A purchase event is denoted as a switch if a household purchases a different product in their subsequent purchase. The panel shows the fraction of purchases of each new product where a switch occurs, split up by whether the purchase is a household’s first purchase of the product, or non-first purchase. For all three products, households are much more likely to switch to something else after their first purchase, as opposed to later purchases. This is consistent with household experimentation: after a household’s first purchase, the household learns how much they like the product. If they dislike it, they switch to something else. Households who make second purchases tend to like the product and will be more likely to repurchase it. A caveat is that these statistics are only suggestive of the presence of learning. The last statistic could also reflect consumer heterogeneity in price sensitivities. Since we observe introductory pricing for the new products, most consumers’ first purchases will occur when the product is on discount. Price sensitive consumers will purchase the products when they are cheap and will subsequently switch away from them. More sophisticated tests for the presence of learning which allow the researcher to account for unobserved heterogeneity are discussed in Osborne (2006). Evidence of learning in this data set is found in that work. The approach taken in this paper is also able to identify learning in the presence of consumer heterogeneity.

Table 2 Summary statistics: household purchase behavior

2.2 An overview of the laundry detergent market prior to 1988

The fact that the three new products were liquid detergents was not a coincidence, and to see why it is useful to briefly discuss the evolution of this industry. The first powdered laundry detergent for general usage to be introduced to the United States was Tide, which was introduced in 1946. Liquid laundry detergents were introduced later: the popular brand Wisk was introduced by Unilever in 1956. The market share of liquid laundry detergents was much lower than powders until the early 1980’s. The very successful introduction of liquid Tide in 1984 changed this trend, and detergent companies began to introduce more liquid detergents. Product entry in this industry is costly: an industry executive quoted the cost of a new product introduction at 200 million dollars (Cannon et al. 1987). Industry literature suggests a number of reasons for the popularization of liquids during this time: first, low oil and natural gas prices, which made higher concentrations of surfactants⁷ more economical; second, a trend towards lower washing temperatures; third, increases in synthetic fabrics; fourth, on the demand side, an increased desire for convenience. In the third and fourth points, liquids had an advantage over powders since they dissolved better in cold water, and did not tend to cake or leave powder on clothes after a wash was done.

The fact that new liquids were being introduced at this time suggests that learning could be an important component of consumer behavior. Many consumers may not have been familiar with the way liquids differed from powders, and they might learn more about liquids from experimenting with the new products. Further, there may be learning across the different brands of liquids. For example, using liquid Tide might not give consumers enough information to know exactly how liquid Cheer or Surf will clean their clothes. Learning about these products could be important for consumers to know how well these products will work for a number of reasons. First, laundry detergents are fairly expensive and the household will use the product for a long period of time, so the cost of making a mistake is not trivial. Second, consumers may have idiosyncratic needs which require different types of detergents. As an example, a consumer whose wardrobe consists of bright colors will likely prefer to wash in cold water, where liquids are more effective.

3 Econometric model

3.1 Specification of consumer flow utility

Below I describe the elements of my model of consumer learning and switching costs. In my structural econometric model an observation is an individual consumer’s purchase event of a package of liquid or powdered laundry detergent. In the following discussion, I index each consumer with the subscript i, and number the purchase events for consumer i with the subscript t. The dependent variable in this model is the consumer’s choice of a given size of one of the 30 different laundry detergents listed in Fig. 1.⁸ I index each product with the variable j, and each size with of the product with s.⁹ In a particular purchase event t for consumer i, not all of the choices may be available. I denote the set of products available to consumer i in purchase t as J _it . I assume that a consumer’s period utility is linear, as in traditional discrete choice models. The period, or flow utility for consumer i for product-size (j, s) ∈ J _it on purchase event t is assumed to be

$$ \begin{array}{rll} && u_{ijst}(S_{it-1},\alpha_i,p_{ijt},c_{ijt},\beta_i,x_{ijt},\eta_i, y_{ijt-1},\varepsilon_{ijt}) \\ &&{\kern6pt}= \Gamma_{ij}(S_{ijt-1},y_{ijt-1}) + \xi_{is} + \alpha_i (p_{ijst}-\alpha_{ic} c_{ijt}) + \beta_i x_{ijt} + \eta_i y_{ijt-1} + \varepsilon_{ijst}, \end{array} $$

(1)

where Γ _ij (s _{ijt − 1}, y _{ijt − 1}) is consumer i’s match value, or taste, for product j. A consumer’s match value with a product is a function of the two state variables s _{ijt − 1} and y _{ijt − 1}. The variable y _ijt is a dummy variable that is 1 if consumer i chooses product j in purchase event t, so y _{ijt − 1} keeps track of whether consumer i chose product j in her previous purchase event. The state variable s _ijt keeps track of whether consumer i has ever purchased product j prior to purchase event t, and it evolves as follows:

$$ s_{ijt}= s_{ijt-1} + 1\{ s_{ijt-1} = 0 \mbox { and } y_{ijt-1} = 1 \}. $$

(2)

For the 27 established products, I assume that consumer match values do not change over time, so Γ _ij (s _it − 1, y _it − 1) = γ _ij . For identification purposes, I normalize every consumer’s match for powder All (product 1) to 0. For the three new products, I assume that the evolution of the consumer’s permanent taste is as follows:

$$ \begin{array}{rll} \Gamma_{ij}(s_{ijt-1},y_{ijt-1})&=&\gamma_{ij}^0 \mbox{ if } s_{ijt-1} = 0, \mbox{ and } y_{ijt-1} = 0 \\ \Gamma_{ij}(s_{ijt-1},y_{ijt-1})&=&\gamma_{ij} \mbox{ if } s_{ijt-1} = 1, \mbox{ or } y_{ijt-1} = 1. \end{array}$$

(3)

The consumer’s match value for the new product is $\gamma_{ij}^0$ if the consumer has never purchased the product before, and it is γ _ij once she has. For the three new products, $\gamma_{ij}^0$ is consumer i’s prediction of how much she will like product j before she has made her first purchase of it. γ _ij is her true match with the product.

I assume that

$$ \gamma_{ij} \sim N\big(\gamma_{ij}^0, \sigma_{ij}^2\big), $$

(4)

where $\sigma_{ij}^2$ is consumer i’s uncertainty about her true taste for product j. I allow $\sigma_{ij}^2$ to vary with the household i’s income and size as follows:

$$ \sigma_{ij}^2 = \sigma_{\max} \frac{\exp( \sigma_{0ij} + \sigma_{1j} \ln(INC_i) + \sigma_{2j} \ln(SIZE_i))}{1+\exp( \sigma_{0ij} + \sigma_{1j} \ln(INC_i) + \sigma_{2j} \ln(SIZE_i))}. $$

(5)

Note that there is unobserved heterogeneity in $\sigma_{ij}^2$ as well as observed heterogeneity: σ _0ij varies across individuals and accounts for unobserved heterogeneity. INC _i is a variable that varies from 1 to 4, where the four possible categories correspond to the four income groups in Table 3. Household size, the variable SIZE _i , also varies from 1 to 4 and is defined similarly. Note that $\sigma_{ij}^2$ is always positive and bounded above by σ _max, which I assume is equal to 10.¹⁰

Table 3 Distributions of household demographics

The parameter α _i is consumer i’s price sensitivity. I also allow this parameter to vary with household income and size as follows,

$$ \alpha_i = \alpha_{\max} \frac{\exp( \alpha_{0i} + \alpha_{1} INC_i + \alpha_{2} SIZE_i)}{1+\exp( \alpha_{0i} + \alpha_{1} INC_i + \alpha_{2} SIZE_i)}, $$

(6)

where α _max is set to −500. α _i is assumed to always be negative and, like $\sigma_{ij}^2$, it is bounded. p _ijst is the price in dollars per ounce of size s of product j in the store during purchase event t, and the variable c _ijt is the value of a manufacturer coupon for product j that consumer i has on hand in purchase event t, also measured in dollars per ounce. The parameter α _ic is consumer i’s sensitivity to coupons. I assume that α _ic lies between 0 and 1, and that

$$ \alpha_{ic} = \frac{\exp(\alpha_{0ic})}{1+\exp(\alpha_{0ic})}, $$

(7)

where α _0ic lies on the real line.

In Eq. 1, β _i is a vector that measures consumer i’s sensitivity to other variables, x _ijt . The first and second elements of the x _ijt vector are dummy variables which are equal to 1 if product j is on feature or display, respectively. The third element is a dummy variable that is 1 if purchase event t occurs in the first week after the introduction of Cheer, and j is Cheer. The fourth is the same thing for the second week of Cheer, the fifth for the third and so on up to the fourteenth week after the Cheer introduction. The next element is a dummy variable that is 1 if purchase event t occurs in the third week after the introduction of Surf, and j is Surf. The next 11 elements are the same thing for weeks 4 to 14 after the Surf introduction. The next 14 elements of the vector are the same time-product dummy variables for the Dash introduction. These time dummy variables are included to capture the effect of unobserved introductory advertising for the new products.

The consumer’s utility in purchase event t is increased by η _i if she purchases the same product that she did in purchase t − 1. Note that the parameter η _i and the function Γ(s _{ijt − 1}, y _{ijt − 1}) allow two different sources of dynamics in consumer behavior: consumer’s previous product choices can affect her current utility. One way in which a consumer’s past product choices affect her current product choice is through the Γ(s _{ijt − 1}, y _{ijt − 1}) function: this is learning. If she has never purchased the new product j prior to purchase event t, her taste for this product is her expected taste, $\gamma_{ij}^0$, whereas if she has purchased it at some point in the past I assume that she knows her true taste for the product, γ _ij . The learning process I estimate in this paper is simpler in one dimension than the learning process which has been used in some other recent papers which estimate structural learning models, such as Erdem and Keane (1996) and Ackerberg (2003). In my learning process, consumers learn their true taste for the new product immediately after consuming it, while the previously cited papers model learning as a Bayesian updating process, which allows the learning to take place over several periods. Although my specification is more restrictive in this sense, I believe this restriction is reasonable for two reasons. First, consumers use laundry detergent several times in between purchases. The median number of weeks between purchases is 8, and consumers likely use laundry detergent on a very regular basis, at least once per week. Thus, in between purchases consumers will have had 8 or more consumption experiences with each product. This means that if a consumer purchases a new product for the first time, by her second purchase it is reasonable to assume that most or all of her uncertainty about the product will have been resolved. Thus, even if the underlying learning process is not a one shot model, the one shot model likely provides a very good approximation to the amount of learning that occurs between purchases. Secondly, both Erdem and Keane (1996) and Ackerberg (2003) actually find that consumers learn their tastes for the new products very quickly: their estimates suggest that most consumer uncertainty is resolve after one purchase. Hence, my assumption is consistent with their findings. Even with one shot learning, my model is still very complex. Making the learning process a slower Bayesian updating process would make the estimation even more cumbersome, and for the reasons given above would not likely change the results very much. Additionally, my model of learning is more sophisticated than those of the previously cited papers in a different dimension: I allow for continuously distributed unobserved heterogeneity in both the mean of consumer priors, and the variances. In contrast, both of the previously cited papers assume that consumer priors are the same for all consumers. Thus, my model allows for some consumers to be more sure of their ex-ante true tastes than others, and for some consumers to expect to like the new products more than others. I think this is an interesting innovation; as I will discuss below, the effectiveness of promotions for new products will depend on consumers’ initial beliefs and hence it will be important to model them flexibly.

The term η _i accounts for the dynamic behaviors of switching costs or variety-seeking. If η _i  > 0, consumer i’s utility is greater if she consumes the same product twice in a row. Thus, a positive η _i induces a switching cost (Pollack 1970; Spinnewyn 1981). An alternative way to model switching costs would be to subtract a positive η _i from all products except the one that was previously chosen; since utility functions are ordinal and there is no outside good in this model, these two formulations are equivalent. As discussed in the introduction, switching costs have been found to be an important part of demand for consumer packaged goods. They could arise due to brand loyalty developing over time; an alternative explanation for switching costs in packaged goods markets is that they may proxy for costs of recalculating utility if a consumer decides to switch products. A consumer who is shopping for a large number of products and is pressed for time may more easily recall her utility for the product she last purchased, which would bias her to repurchase it. If η _i  < 0, the consumer will prefer to consume something different than her previous product choice: I label this as variety-seeking (McAlister and Pessemier 1982). Variety-seeking is not likely an important behavior in laundry detergent markets, but I allow it in the model for the sake of generality. As with the price coefficient and consumer uncertainty, I allow both observed and unobserved heterogeneity in η _i :

$$ \eta_i = \eta_{i0} + \eta_{1} INC_i + \eta_{2} SIZE_i. $$

(8)

Last, the ε _ijst is an idiosyncratic taste component that is i.i.d. across i, j, s and t, and has a logistic distribution. I assume this error is observed to the consumer but not the econometrician and is independent of the model’s explanatory variables and the individual’s utility parameters such as α _i and β _i .

I model unobserved heterogeneity in a significant number of the individual-level parameters. In trial runs of the model, I found it was difficult to identify unobserved heterogeneity in many of the smaller brands, so I only model unobserved heterogeneity in 13 of the 30 brands. I also allow for unobserved heterogeneity in $\gamma_{ij}^0$’s, the α _0i ’s, the feature and display variables, the intercept of the switching costs parameter η _i0, and the σ _0ij ’s. Denote the vector of population-varying individual level parameters for consumer i listed previously as θ _i , and the vector of individual level parameters with the γ _ij ’s for the three new products removed as $\tilde{\theta}_i$. I assume that $\tilde{\theta}_i \sim N(b,W)$ across the population, where W is diagonal.¹¹ This assumption means that the household’s uncertainties about tastes for the new products, $\sigma_{ij}^2$’s, and the price sensitivities α _i ’s will be transformations of normals as shown in Eqs. 5 and 6. Their distribution is Johnson’s S _B distribution, which is discussed in Johnson and Kotz (1970), page 23. The parameters which do not vary across the population are the γ _ij ’s with small shares, the coefficients on household demographics for the learning parameters, the price sensitivities and the switching costs, which are σ _1j and σ _2j , α _1j and α _2j and η ₁ and η ₂ respectively, and a group of parameters which capture consumer expectations of future coupons c _ijt . These latter parameters will be discussed further in the next section. I denote the vector of population-fixed parameters as θ.

A feature of the model that the reader may have noted is that there is no outside good. This means that if the prices of all products were to increase, the total amount of laundry detergent sold would not decrease. In reality, if the price of all detergents increased significantly, consumers would either switch to a substitute, or wash their clothes less often. Since substitutes for detergent are not readily available, one would expect a quantity response. However, it seems probable that quantity response would be inelastic: most consumers likely do laundry on a regular basis, once or twice a week. Thus, if a price increase in a product is observed, consumers will likely switch to another brand, rather than washing their clothes less. In this paper, I only consider partial equilibrium counterfactuals, that is, the impact of changing the price of one product on consumer switching, holding fixed the prices of other products. Since this is going to lead to brand switching, rather than overall quantity reduction, not modeling an outside good should not impact the implications I examine. This issue would be a greater concern if I was calculating market equilibria, though. An additional concern is that leaving out the outside good, which in this case is consuming less detergent, could impact my parameter estimates. Hendel and Nevo (2006) shows that if consumer utility is linear in tastes for brands, and discounting is low, then the consumer’s quantity decision and the brand choice decision can be modeled separately. These are both true in the model I have discussed, which alleviates this concern. A final issue I wish to note is that although I have not modeled usage, I have modeled quantity choice. An alternative approach would be to model brand choice conditional on size choice, or to construct an average price for each brand. I choose to model size choice because the prices of sizes vary over time, and a consumer who prefers a certain brand may choose a different size than they normally would if that size happens to be on sale. Thus, modeling size choice in this way avoids potential measurement error in prices.

3.2 Consumer dynamic optimization problem

I assume consumers are forward-looking¹² and in each purchase event they maximize the expected discounted sum of utility from the current purchase into the future. The consumer’s expected discounted utility in purchase event t is

$$ \begin{array}{rll} &&{\kern-24pt} V(\Sigma_{it};\theta_i,\theta) \\ && {\kern-14pt} = \max\limits_{\Pi_i} E \left[ \sum\limits_{\tau=t}^\infty \delta^{\tau-t} u_{ijs\tau}(S_{i\tau-1},p_{ij\tau},c_{ij\tau},x_{ij\tau}, y_{ij\tau-1},\varepsilon_{ij\tau},\theta_i) | \Sigma_{it}, \Pi_i; \theta_i, \theta \right], \end{array}$$

(9)

where Π _i is a set of decision rules that map the state in purchase t, Σ _it , into actions, which are the y _ijt ’s in purchase event t. The parameter δ is a discount factor, which is assumed to equal 0.95.¹³ The function V(Σ _it ; θ _i , θ) is a value function, and is a solution to the Bellman equation

$$ \begin{array}{rll} V(\Sigma_{it};\theta_i,\theta) &=& E_{\varepsilon_{ijt}} \left[ \max\limits_{(j,s) \in J_{it}} \big\{ u_{ijst}(S_{it-1},p_{ijt},c_{ijt},x_{ijt}, y_{ijt-1},\varepsilon_{ijt},\theta_i)\right. \\ && {\kern50pt}\qquad \quad\left. \vphantom{\max_{(j,s) \in J_{it}}} +\, \delta E V(\Sigma_{it+1};\theta_i,\theta) \big\}\right]. \end{array} $$

(10)

The state vector in purchase event t, Σ _it , has the following elements: the S _{ijt − 1}’s for the new products, the y _{ijt − 1}’s for all 30 products, the prices of all products, p _ijt , the set of available products, J _it , and a new state variable n _t , which will be discussed later.

The expectation in front of the term V(Σ_it + 1; θ _i , θ) in Eq. 10 will be taken over the distributions of future variables, which are

• i) the true tastes for new products the consumer has never purchased, as in Eq. 4,

• ii) future prices,

• iii) future coupons, and

• iv) future product availabilities.

For reasons of computational tractability that will be discussed in the next section, I assume that consumers have naive expectations about future x _ijt ’s, which are the feature, display, and time dummies. By this I mean that consumers expect all these variables to have future levels of zero. A result of this assumption is that these variables do not have to be included in the state space.¹⁴

I account for consumer expectations about future prices p _ijst and product availability J _it in the following way. I estimate a Markov transition process for prices and availability from the data on a store-by-store basis, using a method similar to Erdem et al. (2003) which I will briefly summarize. A detailed description of the estimation can be found in the paper’s Technical Appendix, Section 3, which is available on request from the author. I assume that consumers’ actual expectations about these variables are equal to this estimated process. This process captures consumer expectations about the values prices will take when they run out of detergent and need to purchase it again. In the data, the number of weeks between purchases is clustered between 6 and 8 weeks. I assume that all consumers expect to make their next purchase in exactly 8 weeks, which is the median interpurchase time. Additionally, prices tend to be clustered at specific values, so the transition process for prices is modeled as discrete/continuous. I model the probability of a price change for a product conditional on its price 8 weeks ago, previous prices for other products, and whether a new product was recently introduced as a binary logit. Conditional on a price change, the probability of a particular value of the new price is assumed to be lognormal given the previous week’s prices in the same store and whether a new product introduction recently occurred. Note that there almost 150 possible brand-size combinations, which makes the state space of prices very large. To reduce the size of the state space, the Markov process for prices is only estimated on the most popular sizes of liquids and powders. The prices of other sizes are assumed to be a function of the prices of the popular sizes.

An important part of the price process is that we observe introductory pricing for the new products. I assume consumers understand that the prices of new products will rise after their introduction, so I include a dummy variable in both the price transition logit and regression which is 1 for the first 12 weeks after the introduction of Cheer, a separate dummy variable which is 1 for the first 12 weeks after the introduction of Surf, and one for the first 12 weeks after Dash’s introduction. Allowing for introductory pricing in this way will complicate the state space. To see why, consider a consumer who purchases a laundry detergent on the week of Cheer’s introduction. Suppose further that this person purchases detergent every 8 weeks, and she knows exactly when she will make her future purchases. This person’s next purchase will occur in 8 weeks, when the price of Cheer is still low. Her next purchase after that will occur in 16 weeks, when the price process is in its long run state. The number of purchase events before the consumer enters the long run price state will be a state variable, which I denote as n _t . Because I assume that all households expect to make their next purchase in 8 weeks, n _t will take on 2 values: 1 if the consumer’s purchase occurs within the first 4 weeks after the new product introduction, and zero anytime afterward.

For the state variable J _it , I estimate the probability of each detergent being available in a given calendar week for a given store separately using a binary logit. As was the case with prices, the process for availability is only estimated for the most popular sizes of each product, and so the only part of J _it that is a true state variable are the availabilities of these products. This means I estimate 30 logits, one for each product, where one of the regressors is whether the product was available 8 weeks ago. The availabilities of less popular sizes are assumed to be a function of the availability of the popular sizes. I assume that the introductions of new products are a surprise to consumers, so this aspect of the state space is not taken into account by my availability estimation. A result of this assumption is that consumers will recalculate their value functions after each new product introduction: there will be a value function for after the Cheer introduction, a new one after the Surf introduction, and another one after the Dash introduction. Hence, there will be three times where it will be possible for n _t to be equal to 1, right after the introduction of each new product.

I treat consumer expectations about future coupons, which are the c _ijt ’s, differently than future prices. I specify a process for the distribution of coupons and estimate the parameters of this process along with the other model parameters. I assume that the future c _ijt ’s are composed of two random variables: a binary random variable $\overline{c}_{ijt}$ which is 1 if consumer i receives a coupon for product j in purchase t, and a random variable v _ijt which is the value of the coupon received. Denote probability of a consumer having a coupon on hand and available for use for product j as p _cj . If a consumer receives a coupon for product j, the value of that coupon, which I denote as v _ijt , is multinomial and drawn from the empirical density of coupon values. Coupon values are clustered at certain numbers (such as 50 cents, 60 cents, or 1 dollar), so I calculate the probability of getting a particular coupon value for a particular brand in a period¹⁵ by tabulating the number of redeemed coupons of that value for that brand in that period, and dividing by the total number of redeemed coupons for that product in that period.

The last part of the state space is the process on the state variables summarizing purchase history, S _{ijt − 1} and y _{ijt − 1}. Because these state variables are influenced by consumer choices, it is instructive to examine how we compute the value functions as these parts of the state space change. Suppose first that S _{ijt − 1} = 0 for some product j. If the consumer decides to purchase product j for the first time, then S _ijt will be zero and y _ijt will be 1. When we construct the next period value function we will integrate out the consumer’s true taste for product j, conditional on $\gamma_{ij}^0$ and $\sigma_{ij}^2$. Let γ be a random variable with the distribution of true tastes for product j, where $f(\gamma|\gamma_{ij}^0,\sigma_{ij}^2)$ is $N(\gamma_{ij}^o,\sigma_{ij}^2)$, and denote θ _i (γ) as the vector of individual level parameters for consumer i with her true taste draw for product j replaced by γ. Denote v _ikst + 1(γ) as consumer i’s utility for size s of product k in purchase event t + 1 as a function of γ, minus the logit error ε _ijst + 1:

$$ \begin{array}{rll} \mbox{Product } k = j : v_{ikst+1}(\gamma) &=& \gamma +\xi_{is}- \alpha_i (p_{ikst+1}-\alpha_{ic} c_{ikt+1}) + \eta_i y_{ikt} \\ [4pt] && +\, \delta EV(\Sigma_{it+2};\theta_i(\gamma),\theta) \\ \mbox{Product } k \neq j : v_{ikst+1}(\gamma) &=& \Gamma_{ik}(S_{ikt},y_{ikt}) + \xi_{is} - \alpha_i (p_{ikst+1} - \alpha_{ic} c_{ikt+1}) + \eta_i y_{ikt} \\ [4pt] && +\, \delta EV(\Sigma_{it+2};\theta_i(\gamma),\theta). \end{array} $$

(11)

Consumer i’s expected value function in purchase event t + 1, at her first purchase of product j (S _ijt  = 0 and y _ijt  = 1) will be

$$ \begin{array}{rll} E V(\Sigma_{it+1};\theta_i,\theta) &= &E_{c_{it+1}} E_{p_{it+1}|p_{it}} E_{J_{it+1}|J_{it}} \\ && \times \left[ \int_{\gamma_{ij}} \ln\! \left( \sum\limits_{(k,s) \in J_{it+1}} \!\exp(v_{ikst+1}(\gamma_{ij}))\! \right)\!\! f\big(\gamma_{ij}|\gamma_{ij}^0,\sigma_{ij}^2\big)\,d \gamma_{ij} \right]. \end{array} $$

(12)

When the consumer has purchased product j in the past, such as at state space points S _ijt  = 1 and y _ijt  = 1 or S _ijt  = 1 and y _ijt  = 0, the value function will be defined similarly, but will be simpler: the consumer’s utility for all products given in Eq. 11 will be a function of the true taste γ _ij rather than γ and the value function in Eq. 12 will not include the integral over γ. Note that even if consumer i knows her true taste for all 3 new products (S _ijt  = 1 for all these products), there will still be dynamics in demand arising from the η _i . The consumer will take into account the fact that her purchase today will change y _ijt , and affect her utility in period t + 1.

3.3 Model identification

The identification argument can be summarized in two steps. First, one considers the period after most or all of the learning has occurred. During this period, it is possible to identify the distribution of consumer heterogeneity, and the distribution of consumer switching costs or variety-seeking. Once these distributions are known, the parameters which quantify learning will be identified from ways in which consumer behavior in the first few periods deviates from a model with no learning. For simplicity, assume that we are examining a market with one new product introduction, similar to the market analyzed with the simple model in Section 3. Assume further that we see each consumer for a long period of time (recall that the average number of purchases that is observed for each consumer is 22). Although the estimation procedure I am using is likelihood-based, for brevity I will discuss it in the context of method of moments estimation. Thus, I will consider which moments in the data will be necessary to solve for the model’s parameters. This is sufficient to show that the likelihood-based estimates are identified since the likelihood-based estimator, if it is correctly specified, is consistent and will converge to the same value as the method of moments estimator.

First, consider the period after most or all of the learning has occurred. In the long run, there will be no learning: since the distribution of the idiosyncratic error, ε _ijst , has infinite support, at some point in time everyone in the market will purchase the new product at least once. After every consumer has experimented with the new product, the only dynamics left in demand will be the switching costs or variety-seeking captured by the η _i ’s. At this point we are left with separately identifying the distribution of η _i ’s and the distribution of the non-dynamic coefficients in the consumer’s flow utility: consumer tastes for established products, consumer price sensitivities, and the distribution of the coefficients for the x _ijt ’s, the β _i ’s.

Consider first the task of identifying η _i for an individual consumer. The η _i causes state dependence in her demand: a consumer’s choice in purchase event t − 1 will affect her choice today. Chamberlain (1985) has argued that state dependence can be identified through the effect of previous exogenous variables on today’s purchase probabilities. As an example, consider the effect of a price cut for Tide in purchase event t − 1 on the probability of consumer i purchasing Tide in purchase event t. If the price cut has no effect of this probability, then η _i  = 0. If the price cut increases the probability that the consumer purchases Tide in purchase event t, then η _i  > 0 and the consumer has a switching cost. If the price cut decreases the probability of the consumer purchasing Tide in purchase event t, then η _i  < 0 and the consumer is a variety-seeker. If we observe consumer i for a long period of time, and there is variation in the time series path of prices the consumer observes, then it should be possible to infer the size of the consumer’s η _i .

Once the η _i distribution has been identified, we are left with identifying the heterogeneity of the non-dynamic coefficients in the consumer’s flow utility. Identification of this part of consumer heterogeneity is straightforward and will come through the effect of variation in purchase event t exogenous variables on purchase event t purchase probabilities.

Now consider the periods right after the new product introduction, when we will need to identify consumer uncertainty, $\sigma_{ij}^2$, and consumers’ expected tastes for the new products, $\gamma_{ij}^0$. In my model I allow these parameters to vary across the population, but to get a feel for identification it is easier to start with the case where there is no heterogeneity. Hence, for the next few paragraphs I will drop the i subscript. First, consider the identification of $\sigma_j^2$. This parameter will be identified from the change over time in the likelihood a consumer repurchases the new product. In particular, it can be shown that for any value of the discount factor and for any value of η _i , among consumers whose previous purchase was the new product, the share of consumers who repurchase the product increases over time if σ ² > 0.¹⁶ This is because initially the consumers whose previous purchase was the new product consist mostly of consumers who are experimenting; later it consists mostly of consumers who like the new product. The share of consumers who repurchase the new product is an increasing function of the population variance in tastes for the new product. Immediately following the new product introduction, this share will reflect the population variance in expected tastes, the $\gamma_{ij}^0$’s (which for the moment we have assumed to have zero variance). As consumers learn, the population variance in tastes will be increased by $\sigma_j^2$. Since consumers’ taste draws will be taken from more extreme ends of the taste distribution, those who purchase the new product will tend to have higher taste draws after the learning has occurred and will be more likely to repurchase it. An increase in $\sigma_j^2$ will increase the share of consumers who repurchase the new product in periods after all learning has occurred. Hence, $\sigma_j^2$ can also be identified from the difference between the share of consumers who repurchase the new product immediately following the new product introduction and the share of consumers who repurchase the new product after all learning has occurred: the greater this difference, the greater is $\sigma_j^2$. Note that although the η _i parameter also impacts the likelihood of repurchasing a new product, η _i is constant over time so it will not cause the repurchase rate to change over time. Thus, learning and switching costs are separately identified.¹⁷

The identification of the mean of $\gamma_j^0$ and its variance is straightforward when $\sigma_j^2$ is constant across the population. First, note that in the period after the learning occurs, we can identify the distribution of true tastes for the new product. The mean of the population distribution of tastes for the new product will be the same as the mean of the $\gamma_i^0$ distribution. The variance in the distribution of true tastes for the new product is the variance of $\gamma_j^0$ plus $\sigma_j^2$. We can identify $\sigma_j^2$ using the share difference moment or from the change in the share of consumers who repurchase the new product. The variance of $\gamma_j^0$ will simply be the variance in the population distribution of true tastes minus the $\sigma_j^2$.

Last I consider identification of unobserved heterogeneity in $\sigma_j^2$. Unobserved heterogeneity in $\sigma_j^2$ can be identified if I assume that it is the same across j’s, and I observe multiple new product introductions. In particular, assume that $\sigma_j^2$ is specified as

$$ \sigma_j^2 = 5\frac{\exp\big(\sigma_{0j}+\sigma_{1j}'D_i+ \varepsilon_{i,\sigma}\big)}{1+\exp\big(\sigma_{0j}+\sigma_{1j}'D_i+\varepsilon_{i,\sigma}\big)}, $$

(13)

where ε _i,σ is a mean zero error term. We want to estimate the variance of ε _i,σ, which I denote $\sigma_\sigma^2$. An argument for the identification of this variance can be made by extending the argument for the identification of $\sigma_j^2$ in the case where there is no heterogeneity. Consider two groups of consumers: those who purchased Cheer prior to the introduction of Surf, and those who did not. We can estimate a value of $\sigma_{\rm Surf}^2$ for each of these groups of consumers from the change over time in the repurchase share within each group. If $\sigma_\sigma^2$ is zero, then the two estimates of $\sigma_{\rm Surf}^2$ will be the same, because there is no heterogeneity in $\sigma_{\rm Surf}^2$. However, if $\sigma_\sigma^2$ is positive, then all else equal those consumers who purchased Cheer will have higher values of $\sigma_{\rm Cheer}^2$ than those who did not. Because $\sigma_{\rm Surf}^2$ is positively correlated with $\sigma_{\rm Cheer}^2$ through ε _i,σ, the estimate of $\sigma_{\rm Surf}^2$ will be higher for the consumers who bought Cheer than for the consumers who did not. The difference between these two estimates will rise the higher is $\sigma_\sigma^2$.

The argument presented above for separating learning from switching costs is not dependent on the learning being one shot learning or the switching costs occurring in only one period. Other learning papers have allowed the learning process to be a multi period Bayesian learning process. However, even in these learning models, consumers eventually learn their taste for the new products. One simply needs a long enough time series to allow the impact of the learning to decrease. One could also allow the switching cost to last for more than one period: it could be allowed to build over time. The identification argument outlined above would remain unchanged, except that after the learning had died one could use exogenous variables from periods prior to the previous purchase to identify the switching cost. Thus, observing more time periods after the learning has died out will aid in identifying switching costs that build over time.

4 Estimation procedure

The model is estimated on a subsample of 550 households. The original data set contains 1,693 households in total. Roughly 600 of the households were dropped due to data issues, and a 50 percent random subsample of the remaining households was kept for estimation. The random sampling was done to ease computational burden. The model takes roughly one week to run due to its complexity. I note that my sample is similar in size to that used in other dynamics papers that estimate models similar to this one: for example, Erdem and Keane (1996) includes 167 households, and Hendel and Nevo (2006) includes 221. Details on the construction of the data set are discussed in the Technical Appendix, Section 1.

4.1 Coupon parameters

Before I discuss in detail the estimation procedure, I wish to discuss an issue that arises in estimation due to the inclusion of coupons. In the full model, I assume that the price of a product j to a consumer is the shelf price, p _ijst , minus the value of a coupon c _ijt . Coupons present an estimation difficulty: in my data set, I only observe whether a consumer has a coupon for the particular product that she purchases in a given purchase event. We do not observe whether the consumer has a coupon for any other products at that time. I overcome this problem by treating any coupons for products that the consumer did not choose as unobservables.

I assume that for each purchase event every coupon c _ijt for a non-purchased product (one for which y _ijt  = 0) received by the consumer is drawn from the same distribution as consumer expectations about future coupons that is described in Section 3.2; hence, consumer expectations about future coupons are rational. To summarize the notation developed in that section, recall that the c _ijt for a non-purchased product is composed of two random variables, the binary random variable $\overline{c}_{ijt}$ which is 1 if the consumer receives a coupon for product j, and v _ijt , which is the value of the coupon received. Then the variable c _ijt is equal to $\overline{c}_{ijt}v_{ijt}$, and the vector of population-fixed parameters, θ, contains the parameters p _cj . Note that because these coupon parameters must be between zero and one, they are transformations of underlying parameters. Each p _cj is equal to $\exp(\tilde{p}_{cj})/(1+\exp(\tilde{p}_{cj}))$, where $\tilde{p}_{cj}$ lies in the real line.

This specification is a first approximation to solving the problem of unobserved coupons and represents a step forward from most papers that estimate discrete choice dynamic programming problems. The procedure I use is similar to Erdem et al. (1999), who also propose a discrete distribution for the probability a consumer has a coupon on hand for a non-purchased product, and estimate the parameters of the distribution. Note that there is more than one explanation for why a consumer might have or not have a coupon on hand for a non-purchased product. It could be that no coupon was available for the product, or it could be that a coupon was available but the consumer found it too costly to search for it and cut it out. The scanner data does not contain information on coupon availability and how likely a consumer was to search for coupons, so there is no way to separate these explanations. There is also a subtle endogeneity issue that could arise with coupon use: consumers could be more likely to search for coupons for products for which they have high tastes. I do not take this source of endogeneity into account, and to my knowledge this problem has not been addressed in scanner data research.

4.2 Estimation algorithm

I estimate the structural model described in the previous section using Markov Chain Monte Carlo, which is abbreviated as MCMC. MCMC methods are Bayesian methods, which differ from classical methods in that they do not involve maximizing or minimizing a function. In models with high dimensional unobserved heterogeneity, like the one I have specified, maximization of a likelihood function can be numerically difficult. Bayesian procedures proceed differently: the researcher must specify a prior on the model parameters and then repeatedly draw new parameters from their posterior distribution conditional on the observed data.¹⁸

Drawing from the posterior is made easier using an MCMC procedure called Gibbs sampling, which involves breaking the model’s parameter vector into different blocks, where each block’s posterior distribution, conditional on the other blocks and the observed data, has a form that is convenient to draw from. Gibbs sampling proceeds by successively drawing from each parameter block’s conditional posterior. This procedure results in a sequence of draws which converge to draws from the joint distribution of all the model parameters. The initial draws in the sequence are discarded, and remaining draws from the converged distribution are used to calculate statistics of model parameters, such as mean or variance.¹⁹ My underlying demand model is the random coefficients logit model, with two differences: the coupon parameters and the value function solution. Thus, the setup for my Gibbs sampler is very similar to that used to estimate the random coefficients logit model. This estimator is well understood and is described in Train (2003), pp. 307–308.

To form the conditional posterior distributions for the blocks of parameters it is necessary to impose a prior distribution on some of the model parameters. I assume flat priors on θ and the $\tilde{p}_{cj}$’s, a normal prior on b which I denote k(b), and inverse gamma priors on the elements of the diagonal matrix W, which I denote as IG(W). The posterior distribution of the model parameters will depend on the parameters’ prior distribution and the probability of the data given the parameters. The priors on b and W are assumed to be non-informative, so that k(b) has zero mean and infinite variance. The prior on W is also chosen to be non-informative, so that the scale is set to 1 and the degrees of freedom approaches 1. The posterior distribution of the model parameters will depend on the parameters’ prior distribution and the probability of the data given the parameters.

The probability a consumer chooses a particular product in purchase event t, given her preferences and the values of observables, can be expressed using a simple logit formula. Denote d _ijst as the variable that is 1 if consumer i chooses size s of product j in purchase event t. Denote d _it as the vector of observed d _ijst ’s, c _it as the vector of c _ijt ’s, x _it as the vector of x _ijt ’s and v _ijst as the consumer’s flow utility minus the logit error. The probability of the consumer’s choice in purchase event t will be

$$ Pr(d_{it}|\theta_i,\theta,\Sigma_{it},c_{it},x_{it}) = \sum_{(j,s) \in J_{it}} d_{ijst} \frac{\exp(v_{ijst} + \delta EV(\Sigma_{it+1};\theta_i,\theta))}{\sum_{(k,l) \in J_{it}}\exp(v_{iklt} + \delta EV(\Sigma_{it+1};\theta_i,\theta))}. $$

(14)

Denote g(θ _i |b, W) as the density of an individual level θ _i and Pr(c _it |θ) as the probability of a particular c _it . Then the posterior density of the parameters is proportional to

$$ \begin{array}{rll} \Lambda(\theta_i \forall i, b\!,\! W, c_{it} \forall i \mbox{ and } t, \theta)\! &\propto & \!\prod\limits_{i=1}^I\! \left[ \prod\limits_{t=1}^{T_i} \left\{ Pr(d_{it}|\theta_i,\theta,\!\Sigma_{it},c_{it},x_{it}) Pr(c_{it}|\theta) \right\}\! g(\theta_i|b\!,\!W) \!\right] \\ && \cdot\, k(b)IG(W) \end{array} $$

(15)

I draw from this posterior in 5 different blocks, where each block has a functional form that is convenient to draw from. I will describe these formulas briefly in the next few paragraphs. More details on the specifics of the Gibbs steps are given in detail in the Technical Appendix.

The first block draws θ _i for each household conditional on the d _it ’s, the c _it ’s, b and W. Because of the assumption that the error term is logit, the conditional posterior likelihood of a particular vector of θ _i is proportional to $\prod_{t=1}^{T_i} \left\{ Pr(d_{it}|\theta_i,\theta,\Sigma_{it},c_{it},x_{it}) \right\} g(\theta_i|b,W)$. This distribution is not conjugate, which means that the Metropolis-Hastings algorithm (see Technical Appendix, Section 2 for the steps I use to implement this) must be used in this step.²⁰

In the second step, I draw a new vector of fixed parameters, θ. The posterior distribution of θ conditional on θ _i , the $\overline{c}_{ijt}$’s, v _it and the d _it ’s is

$$ \prod_{i=1}^I \prod_{t=1}^{T_i} \left\{ Pr(d_{it}|\theta_i,\theta,\Sigma_{it},c_{it},x_{it}) Pr(c_{it}|\theta) \right\}. $$

(16)

This distribution is also not conjugate and the Metropolis-Hastings algorithm must be used to draw from it.

The third step draws a new b vector conditional on $\tilde{\theta}_i$ for i = 1, ...I and W. The conditional posterior distribution for b is normal, so this step is straightforward. Similarly, the conditional posterior of the elements of W given $\tilde{\theta}_i$ for i = 1, ...I and b are inverse Gamma, which is straightforward to draw from. For unobserved coupons, each $\overline{c}_{ijt}$ is drawn separately across households, products and purchase events, and has a Bernoulli posterior distribution conditional on v _it , θ _i , θ and d _it .

Because one draws parameters out of conditional posteriors, initial parameter draws may be influenced by the starting points. To avoid this, it is common practice to drop the initial draws. I run the estimator for 20,000 iterations, and drop the first 10,000 draws. A more detailed discussion of convergence is presented in the Technical Appendix, Section 5.

4.3 Value function solution

The method of Imai et al. (2009) and Norets (2009b) works in conjunction with the Gibbs sampler to obtain a solution of the value function. In this section I will broadly describe how I solve for the value function in Eq. 14 and how the method works. The innovation of this new method is that discrete choice dynamic programming problem is solved only once, along with the estimation of the model parameters.

Recall that in the Gibbs sampling algorithm described in the previous section, we draw a sequence of model parameters that converges to draws from the parameters’ joint distribution. The basic idea of the value function solution method can then be broken up into two steps. First, at a particular point g in sequence, draw small number of values of the unobservable and calculate expected utility at all state space points. The expected utility and the current parameter value are then retained for use in later iterations of the MCMC sequence. In order to calculate expected utility at some point g in the sequence, it is necessary to have an approximation of the value function at the current parameter value. In the second step, the value function is calculated as a weighted average of previously retained expected utilities, where the weights are kernel densities of the difference between the current parameter and the previous saved parameters. In actual implementation these steps are performed in reverse order: first the value function is interpolated at the current parameter draw, and then the expected utilities are calculated. However, I believe it is easier to understand the algorithm by looking at the steps in the order I have laid them out, rather than the order in which they are executed. In the following paragraphs I will describe these two steps in greater detail.

Consider the first step, which is to draw some values of the model’s unobservables and calculate expected utility. This calculation is done at points in the state space, Σ = (s, p, J, y, n), and the expected utilities and current parameter value are retained. There are two different sets of unobservables which are unobserved to the consumer at the time she makes her purchase decision, and must be integrated out when the value function is formed: the ε _ijst ’s, and the consumer’s future tastes for products she has not yet purchased, the γ _ij ’s. Integrating out the ε _ijst ’s does not require numerical approximation: because of the assumption that they are logit errors, the consumer’s expected utility has a closed form solution, conditional on θ _i , θ, and future coupons. This is not true when we integrate out the future γ _ij ’s and c _ijt ’s, so these must be approximated numerically. As an example, let us consider constructing an analogue to the consumer’s expected value function in Eq. 12, which is the value at state space point s _j  = 0, y _j  = 1 for some new product j. First I draw L = 10 draws from the true taste distribution for product j, which is $N(\gamma_{ij}^0,\sigma_{ij}^2)$, and from the coupon distribution implied by θ. To calculate the expected utility, we need to calculate first each consumer’s exact utility (ignoring the logit error) at each product at simulation l. Denote the lth taste draw as $\gamma_{ij}^l$ and the lth coupon draw as $c_{ij}^l$, and denote $\theta_i^l$ as the vector of θ _i with the consumers true taste for product j (γ _ij ) taken out and replaced with the simulated tastes ($\gamma_{ij}^l$). Assume that we have an approximation of the expected value function at point n of the sequence for next period’s state space point, Σ′ = (s′, p′, J′, y′, n′), which I will denote as $E_{(p',J')|(p,J)}V_n(s',p',J',y',n';\theta_i^l,\theta)$.²¹ Then the consumer’s utility for product j at simulation l, $v_{ij}^l$, will be

$$ \begin{array}{rll} \mbox{Product } k = j : v_{iks}^l & = & \gamma_{ik}^l + \xi_{is} - \alpha_i (p_{ks} - \alpha_{ic}c_{ik}^l) + \eta_i y_k \\ & & +\, \delta E_{(p',J')|(p,J)}V_n(S',p',J',y',n';\theta_i^l,\theta) \\ \mbox{Product } k \neq j : v_{iks}^l &= & \gamma_{ik}(S_k) +\xi_{is} - \alpha_i (p_{ks} - \alpha_{ic}c_{ik}^l) + \eta_i y_k \\ & & +\, \delta E_{(p',J')|(p,J)}V_n(S',p',J',y',n';\theta_i^l,\theta), \end{array} $$

(17)

which corresponds to Eq. 11.

Her expected utility for purchasing product j for the first time (state space point y _j  = 1, s _j  = 0) at the individual i’s θ _i is then calculated as

$$ \hat{EV}_g(S,p,J,y,n;\theta_i,\theta) = \frac{1}{L} \sum\limits_{l=1}^L \ln \left( \sum\limits_{(k,s) \in J } \exp(v_{iks}^l) \right). $$

(18)

The second step of the algorithm is to calculate the approximation of the value function at the parameter draw for the current point in the sequence, g. Denote consumer i’s individual level parameters at this iteration as θ _i,g, the population-fixed parameters as θ _g , and the vector of θ _i,g stacked on θ _g as $\overline{\theta}_{i,g}$. Recall that at each point in the sequence, the expected utilities calculated in the first step are retained along with the parameter draws. Assume that at iteration g we have retained N(g) previous parameter draws and expected utilities, and we want to calculate the expected value function at θ _i,g. This is then calculated as

$$ \begin{array}{rll} &&{\kern-6pt}E_{(p',J')|(p,J)} V_g(s,p,J,y,n,\theta_{i,g},\theta_g) \\ &&{\kern12pt}= \frac{ \sum_{r=1}^{N(g)} \left[ \hat{EV}_r(s,p,J,y,n;\theta_{i,r},\theta_g) \right] k( (\overline{\theta}_{i,g} - \overline{\theta}_i^r)/h_k ) }{ \sum_{i=1}^{N(g)} k( (\overline{\theta}_{i,g} - \overline{\theta}_{i,r})/h_k ) }, \end{array} $$

(19)

where k(·) is a kernel density function and h _k is a bandwidth parameter, and $\hat{EV}_r(s,p,J,y,n;\theta_{i,r},\theta)$ is the rth retained expected utility.²² The approximated value function is used to calculate the utilities in Eq. 17.²³

5 Estimation results

Estimates of selected model parameters are shown in Table 4.²⁴ Recall that the coefficients of consumer i’s flow utility are broken up into two groups: those that vary across the population, denoted θ _i , and those that are fixed across the population, denoted θ. The population-varying coefficients are normally distributed across the population with mean b and diagonal variance matrix W. The Markov Chain Monte Carlo estimator produces a simulated posterior distribution of b, W, and the fixed parameters, θ. The columns of estimates under the heading “Mean” shows the means and standard deviations (shown in parentheses) of the simulated posterior density for each element of b; similarly, the columns of estimates under the heading “Variance” shows the mean and standard deviation of the simulated posterior for W.²⁵ Estimates of parameters that are fixed across the population, θ, are shown under the “Mean” heading; the corresponding entries under the “Variance” heading are dashed for these parameters. Although the numbers in the table are means and standard deviations of parameter posterior densities, they can be interpreted in the same way as the estimated coefficients and standard errors that are produced by classical methods.

Table 4 Selected parameter estimates of b, θ, and W (utility function)

The first 8 rows show the estimated tastes for some of the established products.²⁶ The All Powder product is normalized to 0, so the taste parameters capture a consumer’s utility relative to this product. Mean taste parameters for popular brands such as Powder or Liquid Tide are positive. Furthermore, most of the mean taste parameters are statistically significant, except for some smaller brands such as Oxydol or Dynamo. The variances are quite large as well, ranging from about 2.2 to about 4.5, indicating a significant amount of unobserved heterogeneity in tastes. Consumer heterogeneity in tastes is very important in this market, which is consistent with these products being experience goods. It is also consistent with important heterogeneity in factors such as the types of fabrics in a household’s wardrobe, the types of soils and stains that need to be cleaned, the water temperature used, the household’s washing machine quality, and the types of scents the household prefers.

The next six rows show consumer responses to prices, coupons, feature and display variables. The parameter for consumer price sensitivities is constructed in the same way as for the learning parameters (Eq. 6). The population average value of the price coefficient is about − 104, with a standard deviation of 26, indicating that there is substantial heterogeneity in price sensitivity.²⁷ The parameter on household income is negative and significant, which is intuitive. The parameter for household size, however, is not precisely estimated. The estimate of the coupon sensitivity parameter is about 5. Recall that the coupon sensitivity coefficient that enters the consumer flow utility, α _ic , is a transformation of α _0ic , $\frac{\exp(\alpha_{0ic})}{1+\exp(\alpha_{0ic})}$ (Eq. 7). This means that the coupon sensitivity is very close to one. The feature and display variables are both positive and precisely estimated.

5.1 Estimated consumer uncertainty and switching costs

I now turn to the estimates of the parameters that are of primary interest in this paper, those pertaining to learning and switching costs. The learning parameters are shown in the third block of parameters in Table 4. Recall that for each new product, consumers have a prediction of their taste for it, $\gamma_{ij}^0$, and uncertainty about their taste, $\sigma_{ij}^2$. The first three rows of this block of coefficients shows the estimated distribution of predicted tastes for each new product. On average, consumers expect to like Surf the best, then Cheer, and then Dash the least. The population variances of these parameters are large, especially for Cheer and Dash, indicating that there is a significant amount of variation in consumers’ prior beliefs about these products.

The next lines show estimates of the parameters pertaining to consumer uncertainty. Recall that I model both observed and unobserved heterogeneity in learning, where the unobserved heterogeneity is persistent within a consumer, across products (see Eq. 13). For simplicity of presentation, when I estimate the model I use the following specification for consumer uncertainty

$$ \sigma_j^2 = 5\frac{\exp(\sigma_{0i}+\sigma_{\rm 0,Surf}\textbf{1}\{j = Surf \}+\sigma_{\rm 0,Dash}\textbf{1}\{j = Dash\} +\sigma_{1j}'D_i)}{1+\exp(\sigma_{0i}+\sigma_{\rm 0,Surf}\textbf{1}\{j = Surf \}+\sigma_{\rm 0,Dash}\textbf{1}\{j = Dash\} +\sigma_{1j}'D_i)}, $$

(20)

which is equivalent to that of Eq. 13. σ _0i represents the intercept for Cheer; the intercept for Surf is σ _0i  + σ _{0, Surf}, and similarly for Dash.²⁸ The variance of the intercept term, σ _0i , is large, indicating there is unobserved heterogeneity in learning that is not being captured by income or household size. The impact of household size on learning is always negative, indicating larger households are more certain about their true tastes for new products than smaller ones, although this effect is not precisely estimated for Cheer. The impact of household income is also negative for Cheer and Surf, but not for Dash.

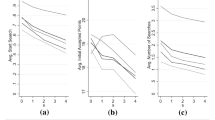
To see what the population distribution of consumer uncertainty looks like, in the two top panels and the bottom-left panel of Fig. 2, I show kernel density plots of the estimated σ _ij parameters.²⁹ Consumers are more uncertain of their true tastes for Surf than for Cheer, and are most uncertain for Dash. In all the products, there is a significant amount of heterogeneity in learning across the population.

Fig. 2

Estimated population distributions of learning and switching cost parameters

The variance in true tastes for these products will be a function of both the variance in the prior, and the mean and variance of the learning parameter. If the amount of learning is small, most of the variance in true tastes will be comprised of the variance in priors. To see this, notice that the true taste $\gamma_{ij} = \gamma_{ij}^0 + \sigma_{ij}z_{ij}$, where z _ij is a standard normal random variable that is independent of both $\gamma_{ij}^0$ and σ _ij .³⁰ Using the decomposition of variance formula, the variance of the true taste can be written as

$$ \begin{array}{rll} V(\gamma_{ij}) & = & V(\gamma_{ij}^0) + E_{z_{ij}}(V(\sigma_{ij})z_{ij}^2) + V_{z_{ij}}(E(\sigma_{ij})z_{ij}) \\ & = & V(\gamma_{ij}^0) + V(\sigma_{ij}) + E(\sigma_{ij})^2. \end{array} $$

The percentage of the variance in true tastes that is due to learning is therefore $(V(\sigma_{ij}) + E(\sigma_{ij})^2)/V(\gamma_{ij})$. For Cheer, this percentage is about 30%; for Surf, is is about 82%, and for Dash, it is about 87%. For all three products, the amount of learning is significant when measured in this way.

The estimated parameters related to switching costs are shown in the last three rows of the table. The intercept is large and positive, suggesting that most consumers have high switching costs. Larger households incur smaller switching costs, while the impact of household income on switching costs appears negligible. The bottom right panel of Fig. 2 shows the estimated population distribution of switching costs. Most households display switching costs, although a small proportion—roughly 8%—are estimated to be variety-seeking (negative switching costs). An estimate of the disutility of switching costs to the consumer can be made by dividing the switching cost parameter by the price coefficient. This average of this ratio is about 2.1 cents per ounce. The modal package size for liquid detergents is 64 ounces, which suggests the disutility from switching costs are about $1.35, roughly 30 percent of the price of a bottle of detergent.

I present another exercise which quantifies the importance of learning in Table 5. First, consider the first three rows of the table. The first column shows the predicted market shares at the estimated parameter values. To compute these shares I simulate consumer purchases under the estimated taste distributions.³¹ The next column shows the result of the simulation after setting consumer priors about the new products equal to their true tastes for the new products.³² The third column shows the percentage change in the product’s market shares. The results show that removing learning increases the overall market shares of the new products. The absolute increase in share is small, but the percentage increase can be large.

Table 5 Effect of removing learning on new product market share (full model)

Changing the amount of learning in this way also can have a different impact on the short run market shares of a new product as opposed to the long run shares due to the option value of learning. The simulated increase in share due to removing learning is shown in the bottom three rows of the table. Although the short run absolute increase in share is larger than the long run increase, it is smaller in percentage terms. To see why the long and short run response to learning can be different in Fig. 3 I plot the estimated population distribution of tastes for Cheer before and after all learning has occurred. The thinner distribution is the population distribution of predicted means for Cheer (the $\gamma_i^0$’s), or the tastes for consumers who have not yet learned about Cheer. This distribution is normal with mean of 1.7 and variance of 1.4 (Table 4). The flatter one is the population distribution of true tastes for Cheer, which are tastes after learning has occurred. This distribution is normal, and has mean of 1.7, and a variance of 2, which is the variance specified in Eq. 21.

Fig. 3

Estimated taste distributions for cheer, before and after learning

When there is no learning, a consumer will make a first purchase of Cheer when her taste draw is such that her utility from purchasing Cheer is greater than any other product. In the figure, the line labeled “No Learning Cutoff” shows the cutoff for a consumer with average values of tastes for all products, assuming no switching costs, prices for all products are the same (and consumers expect them to stay the same), and the error terms are set to zero.³³ The share of consumers who will choose Cheer will be those whose taste draw is to the right of this line. Under full information, this share will be the red shaded area, which is the area under the dotted true taste curve to the right of the “No Learning Cutoff” line.

Figuring out the share of consumers who purchase the new product when there is learning is more complicated, because consumers are forward-looking and there is an option value of learning. All else equal, a higher option value of learning will result in more experimentation. The reason for this is that the cutoff in the presence of learning is equal to the no learning cutoff plus the option value of learning—it is always to the left of the no learning cutoff. This new cutoff is shown in the figure with the line labeled “Learning Cutoff”. The mass of consumers who experiment with the new product will be the area under the expected tastes distribution, which is shaded in black on the figure. If this black shaded area is smaller than the red shaded area, then informing consumers of their true match values will cause an increase in the product’s short run market share, even when accounting for the future value of learning. This is why removing learning increases the short run shares.

In the intermediate run, the effect of giving consumers their true taste draws can be even greater. The consumers who will be affected by this will be those who have not yet experimented. The consumers who have experimented will tend to be those who have a high option value of learning, so the consumers who will be left will have a low option value of learning. Their behavior will be similar to that of consumers do not learn, which means that the mass of consumers who purchase the new product when there is learning will be approximately those consumers to the left of the “No Learning Cutoff” line under the expected taste distribution. When consumers are informed of their true tastes, the increase will be the difference between this probability and the mass of consumers to the left of the line under the true taste distribution. This increase is greater than the difference between the mass of consumers who experiment when there is value to learning, and the mass of consumers who purchase when they are informed of their true taste. This explains why the percentage increase in long run share is larger than that of the short run share.

5.2 Managerial implications

This section examines two questions: what is the impact of introductory price promotions and introductory advertising on product revenues and market shares in my model of learning and switching costs? Second, if managers were to ignore the presence of switching costs or learning, how would their predictions about the impact of these marketing variables differ? In order to answer the second question, I estimated two restricted models: one where switching costs were set to zero, and one where it was assumed that consumers knew their tastes for all the new products beforehand.³⁴ For brevity, parameter estimates for these restricted models are not shown in the body of the paper, however, they are shown in the Technical Appendix, Section 6. There are a few qualitative differences between the estimates which are important to discuss.

The estimated taste coefficients and coefficients on switching costs look broadly similar for the full model and the switching costs only. This is consistent with the argument made in Section 3.3 regarding the identification of these parameters. I argued that consumer taste distributions and switching cost coefficients will be identified from longer run behavior. In the no learning model, the first few periods after the new product introduction will have some impact on the estimates, but most of the model’s identification will come from longer run behavior since we observe consumers for a long period of time after the product introductions. Although the estimates of these model parameters are similar, these two models make very different predictions about the impact of introductory price discounts and long term price elasticities, which will be discussed in Section 5.3.

In contrast to the switching costs only model, the model with only learning produces very different parameter estimates than the full model. In particular, the taste variances produced by the model are larger, often by a factor of two or three. The reason this result is produced is that when switching costs are not modeled, all observed tenure in brand choice is attributed to taste heterogeneity.

We now turn to the first counterfactual, which measures the impact of a temporary price cut on current and future market shares. Estimates of this impact, expressed in terms of elasticities, are shown in Table 6. To compute this elasticity, I hold prices fixed over time at their average values (outside the period in which the promotion occurs) and assume that no features, displays or couponing occurs. I then solve for each consumer’s value function, assuming beliefs are that prices will be fixed at their average values forever. I then simulate purchases for ten periods, where each consumer makes a single purchase every period. Since the modal interpurchase time is 8 weeks, each period can be thought of occurring approximately every two months.

Table 6 Counterfactual: impact of price cuts in periods 1, 3 and 5

The first row and first column of the table shows the impact of a one period price cut that occurs in period 1 on Cheer’s period one market share.³⁵ Note that this a partial equilibrium counterfactual: I assume that competitor prices do not respond to the temporary price cut. There is a large response in the period the price cut occurs: a 1% price cut generates a 6% increase in the quantity of Cheer sold. The next row shows how this price cut impacts period 2 quantity. The impact on period 2 quantity is still substantial: a 1% percent price cut generates a 0.84% increase in second period quantity. The intertemporal impact dies out quickly, however: after five or six periods, quantity sold is very close to that with no price cut. The next two columns of the table show the impact of the price cut if it occurs in period 3 or period 5, respectively. When I compute this counterfactual, I simulate purchases for the periods prior to the price cut, and I assume that the price cut occurs unexpectedly. This means that consumers have time to purchase the new product and learn about it prior to the price cut. My results indicate that the price cut becomes less effective at building both present and future market shares the later it is introduced. This is a result of the fact that consumers learn over time, and learning and switching costs reinforce each other. When consumers learn and have switching costs, some consumers who purchase the product and receive a low match value with it continue to purchase it due to the switching cost. As time goes on and the amount of learning occurring in the population decreases, the intertemporal impact of the price cut decreases as well. The impact of the price cut in the period during which it occurs drops because the option value of learning can rise in the presence of switching costs.³⁶ The intuition behind this is that if a consumer receives a good match value for the new product and has switching costs, it is less likely she will have to switch in the future, making the option value of learning larger. This provides an alternative explanation for why we observe introductory pricing of the new products to the idea that firms recognize dynamics and are pricing with them in mind. It may be that firms are myopic and simply observe that short run demand elasticity is falling, and raise their prices in response. The rows below Cheer show the impact of a similar price cut for Surf and Dash. The results are similar for these two products.

It is interesting to contrast the bias that occurs from using model estimates which do not account for learning or switching costs. The fourth, fifth and sixth columns show the impact of the price cut under the model parameters produced by the switching costs only model. The impact of the temporary price cut on current shares is smaller when there is no learning. This occurs because when there is no learning, there is no option value of learning. The option value of learning makes the new product more attractive to consumers, and the price cut more effective at building current share. The intertemporal effect is also smaller: as noted in the previous paragraph, this is due to the fact that learning combined with switching costs can reinforce each other when temporary price cuts occur. Note that the bias from not modeling learning can be significant: for Cheer, the intertemporal elasticity is underestimated by as much as 65%. The own (short term) elasticity is underestimated by as much as 55%. Similar results are obtained for Surf; for Dash, the intertemporal elasticities are often smaller, although the differences are less stark.

The last three columns show the results for the model with no switching costs. The impact of a price cut during the period it occurs can be greater or smaller than the model with learning and switching costs. This ambiguity is likely driven by two effects which work against each other. First, taste variances are estimated to be higher in the model without switching costs, which will tend to drive own price elasticities towards zero. However, the lack of switching costs will tend to drive price elasticities away from zero, counteracting this effect. The overall impact of leaving out switching costs on the short term effect of the price cut is therefore ambiguous. In contrast, the effect on intertemporal elasticities is clear. They are significantly lower, due to the lack of switching costs. The impact of the price cut on future market shares is not zero, however, due to the presence of learning. The price cut induces some consumers to purchase the new product, and those who have good matches with it continue to purchase it for a long time. However, it appears that the effect of learning alone on intertemporal elasticities is small.

The second counterfactual, shown in Table 7, demonstrates the effect of informative advertising on the short run and intermediate run market shares for the new products. The market shares are simulated in the same way as the price cut counterfactuals. The informative advertising is modeled as follows: when the new product is introduced, I assume that every consumer receives a signal a _ij about their true match value for the new product which is normally distributed with mean γ _ij and variance $\sigma_{aj}^2$. I assume that consumers update their expected true taste, $\gamma_{uij}^0$, and the variance of their true taste distribution, $\sigma_{uij}^2$, using a Bayesian updating rule (see DeGroot 1970, pg. 166–167):

$$ \begin{array}{rll} \gamma_{uij}^0 & =& \frac{\frac{\gamma_{ij}^0}{\sigma_{ij}^2} + \frac{a_{ij}}{\sigma_{aj}^2}}{\frac{1}{\sigma_{ij}^2} + \frac{1}{\sigma_{aj}^2}} \\ \sigma_{uij}^2 & =& \frac{1}{\frac{1}{\sigma_{ij}^2}+\frac{1}{\sigma_{aj}^2}} \end{array} $$

(21)

For each product, I assume that the signal variance $\sigma_{aj}^2$ is one half of the estimated population variance. This counterfactual is simulated using the results of the full model and the model with no switching costs.

Table 7 Counterfactual: effect of informative advertising

The simulated market shares are shown in the first ten rows of Table 7. Informative advertising increases the market shares of all three products. The increase is largest for Dash and smallest for Cheer, which is consistent with the estimated learning parameters being largest for Dash and smallest for Cheer (Fig. 2). Because consumers are very uncertain about Dash, which was a niche produce, informative advertising is very effective at increasing its market share. Revenues for all three products also increase.

The results of the learning only model are shown in the fourth, fifth, and sixth columns. The impact of the advertising is different, in part because this model produces different estimates of consumer uncertainty. In the no learning model, the average uncertainty for Cheer is 1.43, for Surf it is 0.44, and for Dash it is 1.59. The impact of the advertising on the time series behavior of market shares is also different, and this is due to the fact that switching costs are zero. In the model with switching costs, the impact of the informative advertising is smaller in the initial periods as opposed to later periods. This happens because, before the new product is introduced, consumers have been using one of the older products, and it takes time for them to overcome this switching cost and purchase the new product. In contrast, in the model with no switching costs, the impact of the advertising is large at first, but then it drops over time as consumers who purchase the new product find they dislike it and switch away from it.

5.3 Long term price elasticities

In Table 8 I compute the empirical price elasticities implied by the full model, the switching costs only model, and the learning only model. The price elasticities are computed in a method similar to how I computed the impacts of price cuts in the counterfactual exercises from the previous section. First, I compute the market shares for ten periods, holding the prices of all products fixed over time at their averages. Then, I cut the price of all sizes of one of the products by ten percent for all ten periods, and compute the percentage change in the product’s market share, divided by ten. Note that this type of price elasticity is not simply the impact of a 1 period price cut on the product’s market share. When I compute the market shares at the lower price, consumers expect the lower price to last forever, and adjust their value functions accordingly.

Table 8 Counterfactual: long term empirical price elasticities

The first column of the table shows the impact of a long term price cut for Cheer Liquid on Cheer Liquid, Wisk Liquid, Tide Liquid, and Tide Powder. I show the simulated for the first period only, but the findings I will discuss below hold in later periods. The own price elasticity of Cheer for a permanent price cut in Cheer is − 4.93, and cross-price elasticity of a price cut on Cheer for Wisk’s quantity in period 1 is 0.20. Note that when I computed the elasticities in the first column, I assumed that Surf and Dash were not available, and that there was learning in Cheer. The second, third, and fourth columns show the impacts of long term price cuts in Surf Liquid, Dash Liquid, and Tide Liquid respectively. For the Tide Liquid price cut, I assume that all products are available, and that there is learning in Dash. The own price elasticity of the new products are estimated to be significantly larger than in the case of temporary price cuts. This is likely due to the fact that the price cuts are affecting consumers’ future utility through the switching costs and the learning, in addition to their current utility. The cross-elasticities of demand are roughly between 10% and 46%.

The results for the no learning model are shown in the fifth through eighth columns. The own price elasticities for the new products are somewhat lower, although the difference is small. The impact on cross-price elasticities is larger: when learning is ignored, the cross elasticities between new and established products generally drops, the magnitude of the drop being as large as 45%. This happens because the option value of learning makes new products more attractive; a price cut on a new product will be more likely to draw customers away from old products in the presence of learning.

The impact of ignoring switching costs is shown in the final three columns. Interestingly, the own price elasticities of all products are estimated to be much smaller, and the cross price elasticities are smaller as well. This finding seems counterintuitive—because switching costs make it more difficult to switch between products, one might expect own and cross price elasticities to rise when the switching costs are removed. There are two forces that will tend to move the elasticities in the opposite direction. First, the estimated taste variances are larger in the no switching costs model, which compensates for the lack of switching costs somewhat. Second, there is a dynamic effect, which is a result of the fact that this price cut is a long term price cut. When there is a long term price cut on a product with switching costs, that product becomes more attractive to consumers because they realize that the price of the product will be low in the future, and therefore they will be less likely to incur the switching cost in the future. The fact that the dynamics are driving this finding becomes obvious when one compares this finding to the impact of the one period price cut in Table 6. There, the impact of a one period price cut on current demand was sometimes larger in the no switching costs model, and sometimes smaller, and there was no systematic pattern. Because the price cut only occurred for a single period, the dynamic aspect did not come into play. The magnitude of the bias in long term elasticities is significant: it is as much as 30% for the own elasticities, and as much as 45% on the cross elasticities.

One reason that computing these elasticities correctly is important is that own and cross-price elasticities are used by the Federal Trade Commission and the US Department of Justice to evaluate the competitive impact of mergers. Cross-price elasticities are an input into unilateral effects analysis, where agency personnel examine whether a producer of several products could profitably raise the price of one (or some) of them post-merger. As an example, suppose that all the laundry detergents analyzed in this paper were produced by different firms, and a merger between Cheer and Wisk was announced. A unilateral effects analysis would ask whether the producer of both products would find it profitable to raise the price of Cheer, for example. If Cheer and Wisk were very similar products, then many consumers of Cheer would switch to Wisk, which would mitigate the impact of the price increase on the merged firm’s profits. Clearly, the higher the cross-price elasticity between the two products is, the larger will be the unilateral effect. Above I have demonstrated that leaving out learning or switching costs has a significant impact on estimated cross-price elasticities. This means that it is very important to correctly characterize the sources of dynamics in demand in order to make correct inferences about the impact of mergers.

6 Conclusions and extensions

This paper estimates a novel model of learning and switching costs, finding evidence for both types of dynamics. By estimating restricted version of the model and computing counterfactuals that are relevant to managers and policymakers, I demonstrate that a model of learning and switching costs has different economic implications than a model with only switching costs and a model with only learning. In my model, consumers are forward-looking, and I allow a rich distribution of heterogeneity in consumer tastes, price sensitivities, consumer expectations of true match values, and the type of alternative dynamics.

There are a number of extensions for this research that would be useful. First, this paper abstracts from the supply side: for example, the counterfactuals I compute are partial equilibrium counterfactuals and do not account for competitor responses. It would be interesting to examine the model’s supply side implications: for example, we might be interested in knowing the impact of learning on the ease of new product entry, or on equilibrium pricing behavior. It would be interesting to know how the different models explored in these papers might lead researchers to different conclusions. One way to perform this kind of exercise would be to take the demand systems as given, solve for the market equilibria implied by each model, and compute comparative statics. This sort of exercise has been performed in markets with switching costs in Dubé et al. (2008). In this paper, the computation of the market equilibrium is tractable because switching costs are the only source of dynamics, and consumers are not forward-looking (Dubé et al. (2008) argue that the problem with forward-looking consumers is similar to the problem with myopic ones, when firms prices follow a Markov process.). Solving the model with forward-looking consumers who learn their match values for new products is a more difficult task.