Quantum zero correlation linear cryptanalysis

Abstract

The advent of large-scale quantum computers would greatly threaten the security of current cryptosystems. It is urgent to investigate how quantum computing will affect the security of symmetric cryptosystems. Since the security of symmetric schemes heavily depends on the development of cryptanalytic tools, studying the applications of quantum algorithms to classical cryptanalytic tools is critical. To this end, we study quantum zero correlation linear cryptanalysis and propose two quantum algorithms for finding zero correlation linear hulls of Feistel ciphers and SPN ciphers, respectively. We prove that, as long as the attacked block ciphers satisfy certain algebraic conditions, the linear approximations output by the proposed algorithms have zero correlation with a probability close to one. The proposed algorithms have polynomial-time quantum complexity and do not require any quantum or classical query to the attacked block ciphers. Compared to the classical zero correlation linear cryptanalysis, the quantum version has the advantage for extending the number of rounds of zero correlation linear approximations.

1 Introduction

Entanglement is very important to perform computations and communications through particles, which behave according to quantum mechanics. Entanglement is used to create channels for quantum communications [1, 2]. Zidan’s model is quantum computing model based on entanglement strength that is used for solving untraditional problems in quantum computers [3]. The advent of large-scale quantum computers would have a huge impact in many fields. The advent of large-scale quantum computers would have a huge impact in many scientific fields. There is no doubt that cryptography will be greatly threatened. In terms of public-key cryptography, using Shor’s algorithm [4] an adversary with a quantum computer can break any public-key cipher that is based on factorization or discrete logarithm problem, such as RSA, which is widely used in secure communication on the Internet. In terms of symmetric cryptography, Grover’s algorithm can provide a quadratic speedup for any exhaustive key search [5], and using Simon’s algorithm [6] quantum adversaries can break the 3-round Feistel structure [7] and the Even–Mansour cipher [8], which have been proved secure in classical computing model.

The superior capability of quantum computers to process information originates in the superposition principle of states. When a quantum computer processes n qubits, one operation actually operates on $2^n$ pieces of data at the same time. This parallel property enables some problems that are difficult to solve in electronic computers to be effectively solved in quantum computers. The research and development of quantum computers has made steady progress over the past 20 years. Although we are still a long way from realizing a truly universal quantum computer, every advance in quantum computing threatens the currently widely used cryptosystems. In 2016, the National Institute of Standards and Technology (NIST) has released an announcement to solicit, evaluate and standardize public-key cryptographic algorithms against quantum attacks, which marking the arrival of the post-quantum cryptography era. Investigation of the quantum security of classical cryptographic schemes is urgently required.

In recent years, there has been a amount of research aimed at using quantum algorithms to attack symmetric ciphers. A representative example is the quantum algorithm for element search in unordered data sets proposed by Grover in 1996 [5], which has a quadratic speedup over the corresponding classical algorithm. Using Grover’s algorithm, any exhaustive search attack can achieve a quadratic speedup. This suggests that in the post-quantum world, the key lengths of symmetric cryptosystems need to be doubled to maintain equivalent ideal security. Simon’s algorithm [6] also plays an important role in symmetric cryptanalysis. Given a two-to-one periodic Boolean function, Simon’s algorithm can find its period by querying the function in superposition O(n) times (n is the length of the function’s input), while the classical algorithm needs $2^{n-1}+1$ classical queries for the worst case. In 2010, Kuwakado and Morii constructed a polynomial-time quantum distinguisher of the 3-round Feistel structure based on Simon’s algorithm [7]. Subsequently, they used Simon’s algorithm again to extract the key of the Even–Mansour scheme [8]. These two examples showed that symmetric algorithms that are proven secure in classical computing model may be broken by quantum adversaries. Santoli et al. extended the results in [7], proving that there is still an efficient quantum distinguisher when the round functions of the 3-round Feistel cipher are not permutations [9]. In the same paper, they also proposed a quantum forgery attack to the CBC-MAC scheme. Almost simultaneously, Kaplan et al. also extended the results in [7] with a different approach [10] and exploited Simon’s algorithm to attack authentication modes such as PMAC and GMAC. Leander and Alexander combined Simon’s algorithm and Grover’s algorithm to propose a quantum key-recovery attack on the FX structure [11]. Inspired by their work, Dong et al. combined the 3-round quantum distinguisher of Feistel cipher proposed in [7] with Grover’s algorithm to perform a key-recovery attack on the Feistel cipher [12]. Afterwards, they further applied this method to the generalized Feistel structure (GFS) [13]. In EUROCRYPT 2020, Jaques et al. further studied the quantum computing complexity of the attack to AES using Grover’s algorithm and obtained a better query complexity [14].

Although there have been many interesting results, in contrast to public-key cryptography, the ability of quantum adversaries to attack symmetric cryptosystems is not very clear. The currently proposed quantum attacks to symmetric schemes are relatively scattered, and we cannot yet generate a criterion or consensus for evaluating whether a symmetric algorithm can resist quantum attacks like public-key cryptography.

In symmetric cryptography, the designers usually justify the security of the ciphers by proving its resistance against various known cryptanalytic tools. The security of symmetric schemes heavily depends on the development of cryptanalytic tools; thus, it is critical to study the power of cryptanalytic tools when they are combined with quantum algorithms. Zhou, Q. firstly considered applying quantum algorithms to differential cryptanalysis [15]. They applied Grover’s algorithm to the key recovery stage of differential cryptanalysis and obtained a quadratic speedup. After that, Kaplan et al. further applied Grover’s algorithm to the key recovery stage of various differential and linear cryptanalysis and applied the results to the LAC and KLEIN algorithms [16]. In EUROCRYPT 2020, Hosoyamada et al. proposed a quantum collision attack on AES-MMO and Whirlpool hash functions using differential characteristics [17]. In ASIACRYPT 2020, Dong et al. applied quantum algorithms to truncated differential attack and attacked AES-MMO, AES-MP and -512 algorithms [18]. In this paper, we focus on the zero correlation linear cryptanalysis, which has become a very effective tool for attacking block ciphers since it was proposed by Bogdanov and Rijmen [19]. Zero correlation linear cryptanalysis exploits the existence of linear approximations with zero correlation to distinguish block ciphers from random permutations. We apply Simon’s algorithm to zero correlation linear cryptanalysis and propose a quantum algorithm for finding the linear approximations with zero correlation.

There are two quantum security models established for evaluating the security of cryptographic primitives: the Q1 model and the Q2 model [20]. A Q2 adversary can execute quantum operations and can query cryptographic oracles with quantum superpositions of classical inputs to receive the superpositions of corresponding outputs. In contrast, a Q1 adversary collects data classically and processes them with quantum operations. He can execute quantum operations but only make classical queries. The Q1 model has lower requirements on the adversary’s ability and is more in line with the actual attack scenarios in the post-quantum world.

In this paper, we study the zero correlation linear cryptanalysis in quantum computing model and propose two quantum algorithms for finding zero correlation linear hulls of Feistel ciphers and SPN ciphers, respectively. The proposed quantum algorithms first transform the problem of finding zero correlation linear hulls into the problem of finding impossible differentials and then use Simon’s algorithm to find the impossible differentials. Our quantum algorithms have following advantages:

• We have proved that, as long as the attacked Feistel or SPN ciphers satisfy certain algebraic conditions, the probability that the linear approximations output by the quantum algorithms have zero correlation is close to 1.

• The main difficulty in classical zero correlation linear cryptanalysis is to extend the number of rounds of zero correlation linear hulls. Even if we can find zero correlation linear hulls with a small number of rounds by observation, as the number of rounds increases, the number of active S-boxes will increase and the overall encryption function will be more complicated, and thus, the difficulty of finding zero correlation linear hulls will increase dramatically. The quantum algorithms proposed in this paper treat multiple rounds of the block cipher as a black box when applying Simon’s algorithm, ignoring the internal structures of the cipher. The increase in the number of rounds does not necessarily lead to an increase in the difficulty of finding zero correlation linear hulls. Therefore, the proposed algorithms have an advantage over the classical zero correlation linear cryptanalysis for extending the number of rounds of zero correlation linear approximations.

• The complexity of the proposed algorithms is polynomial-time. Only polynomial qubits are required, and executing the algorithms needs only polynomial universal gates. Moreover, the proposed algorithms do not require any quantum or classical query to the block ciphers and thus can be executed under the $Q_1$ model, which has lower requirements on the attacker’s ability and is more in line with the actual attack scenarios in the post-quantum world.

2 Preliminaries

We first briefly recall the notations and results about symmetric cryptanalysis and quantum computing that will be used in this paper.

2.1 Symmetric cryptanalysis

Let n denote a positive integer and ${\mathbb {F}}_2$ denote the finite field of characteristic two. ${\mathbb {F}}_2^n$ is a n-dimension vector space over ${\mathbb {F}}_2$. The SPN and Feistel structures are two most widely used structures in the design of block ciphers.

SPN cipher A cipher with substitution-permutation network (SPN) structure iterates some SP-type round functions for achieving confusion and diffusion. A function is called SP-type, if it can be decomposed into a substitution layer, which consists of multiple nonlinear transformations (S-boxes), followed by a linear transformation. Specifically, the input of a SP-type function $F:{\mathbb {F}}_2^{s\times t}\rightarrow {\mathbb {F}}_2^{s\times t}$ is first divided into t segments $x=(x_1,x_2,\cdots ,x_{t})$, and each segment $x_i$ has s bits; then, t nonlinear transformations $S_i$’s are applied to $x_i$’s to obtain a vector $y=(S_1(x_1),S_2(x_2),\cdots ,S_{t}(x_{t}))\in {\mathbb {F}}_2^{s\times t}$. At last, a linear transformation P is applied to y and Py is the final output of F. An iteration of the SPN structure is shown in Fig. 1.

Feistel cipher The plaintext of a Feistel cipher with a blocksize of 2n is divided into two parts $(L_0,R_0)\in {\mathbb {F}}_2^n\times {\mathbb {F}}_2^n$. Suppose the number of rounds is r. The encryption process is to iterate the following transformation r times:

$$\begin{aligned} \left\{ \begin{array}{l} L_{i+1}=F_{i+1}(L_i)\oplus R_i\\ R_{i+1}=L_i\\ \end{array} \right. ,\quad 0\le i\le r-1, \end{aligned}$$

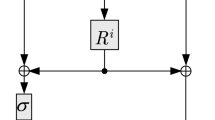
where $F_{i+1}:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2^n$ is the $(i+1)$-th round function, and $L_i$, $R_i\in {\mathbb {F}}_2^n$. The output of E is defined as the output of the r-th iteration. The $(i+1)$-th iteration is shown in Fig. 2. In the following, we focus on the case where $F_i$’s are SP-type functions.

Fig. 1

An iteration of a SPN cipher

Fig. 2

An iteration of a Feistel cipher

Zero correlation linear cryptanalysis Zero correlation linear cryptanalysis is an important cryptanalytic tool for attacking block ciphers developed by Bogdanov and Rijmen [19]. Let $a=(a_1,\cdots ,a_n), b=(b_1,\cdots ,b_n)\in {\mathbb {F}}_2^n$, the inner product of a and b is defined as

$$\begin{aligned} a\cdot b\triangleq a_1b_1\oplus a_2b_2\oplus \cdots \oplus a_nb_n, \end{aligned}$$

where $\oplus$ denotes the exclusive-or operation. Given a Boolean function $f:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2$, the correlation of f is defined as:

$$\begin{aligned} c(f(x))\triangleq \frac{\#\{x\in {\mathbb {F}}_2^n|f(x)=0\}-\#\{x\in {\mathbb {F}}_2^n|f(x)=1\}}{2^n}=\frac{1}{2^n}\sum _{x\in {\mathbb {F}}_2^n}(-1)^{f(x)}, \end{aligned}$$

where the notation “#” denotes the number of elements in a set. Given a vector function $F:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2^k$, the correlation of a linear approximation with a n-bit input mask a and a k-bit output mask b is defined as:

$$\begin{aligned} c(a\cdot x\oplus b\cdot F)\triangleq \frac{1}{2^n}\sum _{x\in {\mathbb {F}}_2^n}(-1)^{a\cdot x\oplus b\cdot F(x)}. \end{aligned}$$

If $c(a\cdot x\oplus b\cdot F)=0$, then $a\rightarrow b$ is said to be a zero correlation linear hull of F. For any vector $a\ne \varvec{0}$, it is obvious that $c(a\cdot x)=0$, thus $a\rightarrow \varvec{0}$ is always a zero correlation linear hull of F. When F is a permutation over ${\mathbb {F}}_2^n$, for any $b\ne \varvec{0}$, we have $c(b\cdot F(x))=0$. In this case, $\varvec{0}\rightarrow b$ is also a zero correlation linear hull of F. It is notable that the concept “zero correlation” has no relation to quantum correlation phenomena; the former is a mathematical concept, while the latter is a physical concept.

Let E be a block cipher with $R=r+t$ rounds, and $E^{(r)}$ denote the round-reduced variant of E. Namely, $E^{(r)}$ is the cipher that only iterates the first r rounds of E. Zero correlation linear attack exploits the fact that $E^{(r)}$ has a linear approximation with a correlation of exactly zero. This property allows us to detect some non-random behavior of $E^{(r)}$ and thus can be used to distinguish the round-reduced cipher $E^{(r)}$ from a random permutation. Zero correlation linear cryptanalysis is composed by two phases. In the first phase, the adversary finds a linear approximation $a\rightarrow b$ of $E^{(r)}$ that has zero correlation. In the second phase, the adversary uses the found zero-correlation linear hull to recovery the subkey of the last t rounds of E. Specifically, for each possible subkey, he partially decrypts all the ciphertexts by t rounds and then computes the correlation of the linear approximation $a\rightarrow b$ of $E^{(r)}$. For wrong guesses of the subkey, the output obtained by decrypting the ciphertexts by t rounds can be regarded as the output of a random function; therefore, the probability that the correlation happens to be zero is negligible, while the correlation computed by correct subkey must be zero. The adversary uses this difference to filter out the correct key.

Impossible differential cryptanalysis Given a vector function $F:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2^k$, the probability of a differential $\varDelta x\rightarrow \varDelta y$ with an input difference $\varDelta x$ and an output difference $\varDelta y$ is defined as:

$$\begin{aligned} p(\varDelta x \rightarrow \varDelta y)\triangleq \frac{\#\{x\in {\mathbb {F}}_2^n|F(x)\oplus F(x\oplus \varDelta x)=\varDelta y\}}{2^n}. \end{aligned}$$

If the differential probability $p(\varDelta x \rightarrow \varDelta y)$ is equal to zero, then $\varDelta x\rightarrow \varDelta y$ is called an impossible differential of F.

Similar to zero correlation linear cryptanalysis, impossible differential cryptanalysis also exploits some non-random property of the round-reduced cipher $E^{(r)}$. Like the zero correlation property, impossible differential can also be used to distinguish the cipher $E^{(r)}$ from a random permutation. Impossible differential attack is composed by two phases. In the first phase, the adversary finds an impossible differential of the round-reduced cipher $E^{(r)}$, and in the second phase, the adversary uses the found impossible differential to sieve the subkey of the last t rounds. For each possible subkey, the adversary partially decrypts all ciphertexts by t rounds and computes the output differences, then excludes the keys that cause the impossible differential.

Structure and dual structure In symmetric cryptanalysis, when searching for zero correlation linear hulls or impossible differentials, we often only exploit the existence of a mask (difference) of an S-box instead of the specific value of the mask (difference), such as the attacks to Camellia [21, 22] and AES [19, 23]. This means that if the S-boxes are replaced with some other transformations, the distinguishers still work. Based on this observation, Bing Sun et al. defined the notion of structure [24].

Definition 1

(Structure [24]) Suppose $E:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2^n$ is a block cipher with S-boxes as its basic nonlinear components:

• (1) A structure ${\mathcal {E}}^E$ is defined as a set of all block ciphers $E'$ which is exactly the same as E except that the S-boxes can take all possible transformations on the corresponding domains.

• (2) Suppose $a,b\in {\mathbb {F}}_2^n$. If for any $E'\in {\mathcal {E}}^E$, $a\rightarrow b$ is a zero correlation linear hull (impossible differential) of E, $a\rightarrow b$ is called a zero correlation linear hull (impossible differential) of ${\mathcal {E}}^E$.

As mentioned previously, the zero correlation linear hulls and impossible differentials of Camellia and AES algorithms that have been found so far are in fact the zero correlation linear hulls and impossible differentials of ${\mathcal {E}}^{Camellia}$ and ${\mathcal {E}}^{AES}$.

For SPN and Feistel ciphers, Bing Sun et al. also defined the notion of dual structure. They proved that there is a link between the impossible differentials of a structure and the zero correlation linear hulls of its dual structure. We will exploit this link to design quantum algorithms for finding zero correlation linear hulls.

Definition 2

(Dual Structure [24]) Let ${\mathcal {E}}_{SP}$ be an SPN structure with a linear transformation P. Then, the dual structure ${\mathcal {E}}_{SP}^{\bot }$ of ${\mathcal {E}}_{SP}$ is defined as ${\mathcal {E}}_{S(P^{-1})^T}$. That is, the ciphers in ${\mathcal {E}}_{SP}^{\bot }$ are the same as the ciphers in ${\mathcal {E}}_{SP}$ except that P is replaced by $(P^{-1})^T$.

Let ${\mathcal {F}}_{SP}$ be a Feistel structure with SP-type round functions whose linear transformation is denoted by P. Let $\sigma$ be the operation that exchanges the left and right halves of a vector. Then, the dual structure ${\mathcal {F}}_{SP}^{\bot }$ of ${\mathcal {F}}_{SP}$ is defined as $\sigma {\mathcal {F}}_{P^{T}S}\sigma$. That is, the ciphers in ${\mathcal {F}}_{SP}^{\bot }$ are the same as the ciphers in ${\mathcal {F}}_{SP}$ except that their round functions first execute the linear transformation $P^T$ and then execute the S-boxes, and the operation $\sigma$ is additionally added before the first round and after the last round of the cipher.

Figures 1 and 2 are exactly one iteration of the cipher in a SPN structure and a Feistel structure, respectively. Figure 3 shows an iteration of a cipher in the dual structure of a SPN structure, and Fig. 4 shows an iteration of a cipher in the dual structure of a Feistel structure.

Fig. 3

An iteration of a cipher in ${\mathcal {E}}^{\bot }_{SP}$

Fig. 4

An iteration of a cipher in $\mathcal {F}^{\bot }_{SP}$

2.2 Quantum Simon’s algorithm

The quantum algorithms proposed in this paper need to call Simon’s algorithm as a subroutine. Simon’s algorithm was proposed by Simon in 1994 [6] and realized an exponential speedup compared to classical algorithms. It solves the problem: given a Boolean function $F:\{0,1\}^n\rightarrow \{0,1\}^m$ that satisfies that there is a vector $s\in \{0,1\}^n$ such that

$$\begin{aligned}{}[F(x)=F(y)]\Leftrightarrow [x\oplus y\in \{0^n,s\}],\,\,\,\forall x,y\in \{0,1\}^n, \end{aligned}$$

find the period s. The Boolean functions that have such a period are said to satisfy Simon’s promise. Classical algorithms require $\Omega (2^{n/2})$ classical queries to F in order to find s, while Simon’s algorithm requires only O(n) quantum queries. Given the access to the quantum oracle which computes F in superpositions, Simon’s algorithm simply repeats the following subroutine:

• 1. Prepare the initial state $|0^n\rangle |0^m\rangle$ with $(n+m)$ qubits, then execute the Hadamard operator $H^{\otimes n}$ on the first register to obtain the state

  $$\begin{aligned} \frac{1}{\sqrt{2^n}}\sum _{x\in \{0,1\}^n}|x\rangle |0^m\rangle . \end{aligned}$$

• 2. Make a quantum query to F to obtain the state $\frac{1}{\sqrt{2^n}}\sum _{x\in \{0,1\}^n}|x\rangle |F(x)\rangle$.

• 3. Use the computational basis to measure the second register, giving a value F(z). The first register is according collapsed to the state $\frac{1}{\sqrt{2}}(|z\rangle +|z\oplus s\rangle )$.

• 4. Apply the Hadamard operator $H^{\otimes n}$ again to the first register and obtain the state

  $$\begin{aligned} \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2^n}}\sum _{y\in \{0,1\}^n}(-1)^{y\cdot z}[1+(-1)^{y\cdot s}]|y\rangle . \end{aligned}$$

• 5. Use the computational basis to measure this state. Since any $|y\rangle$ in this state that satisfies $y\cdot s=1$ has amplitude 0, the measurement result must be a vector y such that $y\cdot s=0$.

Repeating steps 1–5 for O(n) times, one can obtain $n-1$ independent vectors that are orthogonal to s, and then, it is easy to recover s by basic linear algebra.

Since any quantum circuit can be expressed in terms of gates in some universal set of unitary gates [25], we assume the quantum circuit realizing F is composed of gates in an universal gate set and denote the number of universal gates as $|F|_Q$. Running Simon’s subroutine once needs 2n single-qubit Hadamard gates and $|F|_Q$ additional universal gates. Therefore, running Simon’s algorithm on F needs a total of $O(2n^2+n|F|_Q)$ universal gates and $n+m$ qubits.

3 Quantum zero correlation linear cryptanalysis of Feistel ciphers

In this section, we will propose a quantum algorithm that is used to find zero correlation linear hulls of the Feistel ciphers. Bing Sun et al. have proved that, for the Feistel structures with SP-type round functions, an impossible differential of their dual structure can be used to derive a zero correlation linear hull of them. According to this fact, the idea of the proposed algorithm is to first use Simon’s algorithm to find impossible differentials of the dual structures and then use them to derive the zero correlation linear hulls of the original structure.

3.1 Quantum algorithm for finding zero correlation linear hulls of the Feistel ciphers

Suppose $F_{SP}$ is a Feistel cipher with SP-type round functions. Denote the structure of $F_{SP}$ as ${\mathcal {F}}_{SP}$ and its dual structure as ${\mathcal {F}}_{SP}^{\bot }$. We now present a quantum algorithm for finding zero correlation linear hulls of $F_{SP}$. More precisely, the proposed algorithm finds zero correlation linear hulls that are independent of the choices of the S-boxes, i.e., zero correlation linear hulls of ${\mathcal {F}}_{SP}$. Most cryptanalytic results using zero correlation linear cryptanalysis or impossible differential cryptanalysis are independent of the details of the S-boxes [19, 21,22,23]. If S-boxes are replaced by some other transformations in the ciphers, the corresponding cryptanalytic results usually remain the same. According to [24], the zero correlation linear hulls of a Feistel structure with SP-type round functions can be derived by the impossible differentials of its dual structure. Therefore, the problem of finding zero correlation linear hulls can be transformed into the problem of finding impossible differentials. Our quantum algorithm first searches for the impossible differentials of ${\mathcal {F}}_{SP}^{\bot }$ and then uses them to derive zero correlation linear hulls of $F_{SP}$.

To find the impossible differentials of ${\mathcal {F}}_{SP}^{\bot }$, let $F_{SP}^{\bot }$ be the cipher exactly the same as $F_{SP}$ except that its round functions first apply the linear transformation $P^{T}$, then apply nonlinear transformations $S_i$’s, and the operation $\sigma$ is additionally added before the first round and after the last round of the cipher. Namely, $F_{SP}^{\bot }=\sigma F_{P^{T}S}\sigma$. Obviously $F_{SP}^{\bot }\in {\mathcal {F}}_{SP}^{\bot }$. In fact, we find the impossible differentials of the structure ${\mathcal {F}}_{SP}^{\bot }$ by searching for impossible differentials of the cipher $F_{SP}^{\bot }$. If the structure ${\mathcal {F}}_{SP}^{\bot }$ has an impossible differential $\varDelta x\rightarrow \varDelta y$, then $\varDelta x\rightarrow \varDelta y$ is also an impossible differential of $F_{SP}^{\bot }$. Generally, a well-defined block cipher has only a few impossible differentials. Therefore, in this case if we find an impossible differential of $F_{SP}^{\bot }$, it has a high probability of being $\varDelta x\rightarrow \varDelta y$. Even if we obtain multiple results when searching for the impossible differentials of $F_{SP}^{\bot }$, we only need to randomly choose new bijective transformations to replace the S-boxes in $F_{SP}^{\bot }$, apply quantum algorithm to find the impossible differentials of the new cipher again, and then compute the intersection of the impossible differential sets of these two ciphers to obtain $\varDelta x\rightarrow \varDelta y$.

The key is how to find impossible differentials of the cipher $F_{SP}^{\bot }$. Since $F_{SP}^{\bot }=\sigma F_{P^{T}S}\sigma$, it is equivalent to finding impossible differentials of $F_{P^{T}S}$. In [26], the authors applied quantum algorithms to miss-in-the-middle technique to find impossible differentials. We adopt similar idea, but use Simon’s algorithm to find probability-1 differentials instead of the algorithm proposed in [26]. Specifically, we find impossible differentials of $F_{P^{T}S}$ by connecting two differentials with probability 1 that do not match where they meet. Suppose $F_{P^{T}S}$ has r rounds and its block size is 2n. For any $v\in \{1,2,\cdots ,r-1\}$, we divide $F_{P^{T}S}$ into two parts $F_{P^{T}S}=F^{\bot }_{(r-v)}\cdot F^{\bot (v)}$, where $F^{\bot (v)}$ corresponds to the first v rounds of $F_{P^{T}S}$ and $F^{\bot }_{(r-v)}$ corresponds to the last $r-v$ rounds of $F_{P^{T}S}$. Let ${\mathcal {K}}_v^1$, ${\mathcal {K}}_v^2$ denote the key spaces of $F^{\bot (v)}$ and $F^{\bot }_{(r-v)}$, respectively. As shown in Fig. 5, if $(\varDelta x_1,\varDelta x_2)\rightarrow (\varDelta y_1,\varDelta y_2)$ is a probability-1 differential of $F^{\bot (v)}$, $(\varDelta x'_1,\varDelta x'_2)\rightarrow (\varDelta y'_1,\varDelta y'_2)$ is a probability-1 differential of $F^{\bot \, (-1)}_{(r-v)}$ (the inverse function of $F^{\bot }_{(r-v)}$) and $(\varDelta y_1,\varDelta y_2)\ne (\varDelta y'_1,\varDelta y'_2)$, then $(\varDelta x_1,\varDelta x_2)\rightarrow (\varDelta x'_1,\varDelta x'_2)$ is an impossible of $F_{P^{T}S}$, and thus, $(\varDelta x_2,\varDelta x_1)\rightarrow (\varDelta x'_2,\varDelta x'_1)$ is an impossible differential of $F_{SP}^{\bot }$.

Fig. 5

Connect two probability-1 differentials to obtain an impossible differential of $F_{SP}^{\bot }$

The only remaining problem is how to find probability-1 differentials of a block cipher. Recall that Simon’s algorithm can be used to find the periods of Boolean functions that satisfy the Simon’s promise. Kaplan et al. have proved that Simon’s promise can be relaxed [10]. Even if a periodic function does not satisfy the Simon’s promise, as long as it satisfies some more relaxed condition, Simon’s algorithm can still find its period with a probability close to 1. Suppose $F:{\mathbb {F}}_2^{2n}\rightarrow {\mathbb {F}}_2^{2n}$ is a block cipher, and $\varDelta x\rightarrow \varDelta y$ is a probability-1 differential of F. Namely,

$$\begin{aligned} F(x)\oplus F(x\oplus \varDelta x)=\varDelta y \end{aligned}$$

holds for all $x\in {\mathbb {F}}_2^{2n}$. Define a new function

$$\begin{aligned} G:{\mathbb {F}}_2^{2n}\times {\mathbb {F}}_2^{2n}&\rightarrow {\mathbb {F}}_2^{2n}\\ (x,y)&\rightarrow F(x)\oplus y, \end{aligned}$$

then for all $x,y\in {\mathbb {F}}_2^{2n}$, we have

$$\begin{aligned} G(x\oplus \varDelta x,y\oplus \varDelta y)=F(x\oplus \varDelta x)\oplus (y\oplus \varDelta y)=F(x)\oplus y=G(x,y). \end{aligned}$$

Therefore, $\varDelta x\rightarrow \varDelta y$ is a probability-1 differential of F if and only if $(\varDelta x,\varDelta y)$ is a period of G. This means that, to find the probability-1 differentials of a block cipher F, we only need to apply Simon’s algorithm to the constructed function G to obtain its periods. However, we should note that, when we say “compute the value F(x)”, it actually means to compute $F_k(x)$. The ciphertext is computed under a specific secret key k. Thus, the attacker actually needs to find probability-1 differentials of $F_k(x)$. Since the attacker has no knowledge of k, he cannot execute the unitary operator of $F_k(x)$ when calling Simon’s algorithm on G. To solve this problem, we only need to treat the key as a part of the function’s input. Suppose the key space of F is ${\mathbb {F}}_2^m$. Define the function

$$\begin{aligned} {\hat{F}}:{\mathbb {F}}_2^m\times {\mathbb {F}}_2^{2n}&\rightarrow {\mathbb {F}}_2^{2n}\\ (k,x)&\rightarrow F_k(x), \end{aligned}$$

then the construction of the function ${\hat{F}}$ is completely public and thus the attacker can execute the corresponding unitary operator of it. When the attacker uses the aforementioned method to search for the probability-1 differentials of ${\hat{F}}$, he only needs to limit the first m bits of the input difference to be zero, namely limit the m-bit vector $\varDelta k$ in the probability-1 differential $(\varDelta k,\varDelta x)\rightarrow \varDelta y$ of ${\hat{F}}$ to be the zero vector, then $\varDelta x\rightarrow \varDelta y$ will be a probability-1 differential of $F_k$ regardless of the value of k. In consideration of this, the function G should be defined accordingly as

$$\begin{aligned} G:{\mathbb {F}}_2^{m}\times {\mathbb {F}}_2^{2n}\times {\mathbb {F}}_2^{2n}&\rightarrow {\mathbb {F}}_2^{2n}\\ (k,x,y)&\rightarrow F_k(x)\oplus y. \end{aligned}$$

In Sect. 3.2, we will prove that, if $(0^m,\varDelta x,\varDelta y)$ is a period of G, then $\varDelta x\rightarrow \varDelta y$ is a probability-1 differential of $F_k$ no matter what value k takes.

Based on the ideas discussed above, we propose a quantum algorithm for finding zero correlation linear hulls of the Feistel ciphers as following:

The step 5 in the algorithm ZCLHofFei is to find the probability-1 differentials of $F^{\bot (v)}$ and put them into the set $A_v^1$. Suppose $((\varDelta x_1,\varDelta x_2),(\varDelta y_1,\varDelta y_2)\big )$ ($\varDelta x_1,\varDelta x_2,\varDelta y_1,\varDelta y_2\in {\mathbb {F}}_2^n$) is a solution of the linear equations (1), then $(0^{m_1},\varDelta x_1,\varDelta x_2,\varDelta y_1,\varDelta y_2)$ is actually an output obtained by applying Simon’s algorithm on $G_v^1$, and thus, it is a period of $G_v^1$. Therefore, $(\varDelta x_1,\varDelta x_2)\rightarrow (\varDelta y_1,\varDelta y_2)$ is a probability-1 differential of $F_k^{\bot (v)}$. Similarly, the step 6 is to find probability-1 differentials of $F^{\bot (-1)}_{(r-v)}$ and put them into the set $A_v^2$. The steps 7–11 compare all the differentials in $A_v^1$ and $A_v^2$ to find non-trivial probability-1 differential pairs that do not match in the middle, then connect the unmatched differential pairs to obtain impossible differentials of $F_{P^{T}S}$. Since $F_{SP}^{\bot }=\sigma F_{P^{T}S}\sigma$, swapping the left and right halves of both the input differences and output differences of $F_{P^{T}S}$’s impossible differentials gives impossible differentials of $F_{SP}^{\bot }$. Step 9 puts the impossible differentials of $F_{SP}^{\bot }$ into the set H. The step 13 randomly chooses new bijective transformations to replace the S-boxes in $F_{SP}^{\bot }$ and then repeats the previous process on the new cipher to find its impossible differentials and puts them into the set L. Since $N=H\cap L$, the differentials in N are impossible for both $F_{SP}^{\bot }$ and the new cipher with random S-boxes. Therefore, any $(\varDelta x_2,\varDelta x_1)\rightarrow (\varDelta x'_2,\varDelta x'_1)$ in the set N has high probability of being an impossible differential of the dual structure ${\mathcal {F}}_{SP}^{\bot }$. We will prove in Section 3.2 that this means $(\varDelta x_2,\varDelta x_1)\rightarrow (\varDelta x'_2,\varDelta x'_1)$ is a zero correlation linear hull of ${\mathcal {F}}_{SP}$. It is notable that in steps 5 and 6 it is possible to get the same measurement result multiple times, but we do not need the $c(m_1+4n)$ results in step 5 or the $c(m_2+4n)$ results in step 6 to be non-identical. They only need to be independent and identically distributed random variables.

Running Simon’s subroutine in the steps 5 and 6 requires performing the corresponding unitary operators of function $G_v^1$ and $G_v^2$. The unitary operator $U_{G_v^1}$ of $G_v^1$ is defined as

$$\begin{aligned} U_{G_v^1}:\sum _{k,x,y,z}c_{k,x,y,z}|k\rangle |x\rangle |y\rangle |z\rangle \rightarrow \sum _{k,x,y,z}c_{k,x,y,z}|k\rangle |x\rangle |y\rangle |z\oplus G_v^1(k,x,y)\rangle . \end{aligned}$$

Since $G_v^1(k,x,y)=F_k^{\bot (v)}(x)\oplus y$, the attacker can execute $U_{G_v^1}$ by first performing the unitary operator

$$\begin{aligned} U_{F^{\bot (v)}}:\sum _{k,x,z}c_{k,x,z}|k\rangle |x\rangle |z\rangle \rightarrow \sum _{k,x,z}c_{k,x,z}|k\rangle |x\rangle |z\oplus F_k^{\bot (v)}(x)\rangle \end{aligned}$$

on the first, second and fourth registers, then applying 2n CNOT gates on the third and fourth registers. The quantum circuit of $U_{G_v^1}$ is shown in Fig. 6. Because the construction of $F^{\bot (v)}(k,x)$ is public, the operator $U_{F^{\bot (v)}}$ is available to the attacker. The operator $U_{G_v^2}$ can be implemented similarly.

Fig. 6

Quantum circuit to implement $U_{G_v^1}$

3.2 Analysis of the algorithm ZCLHofFei

In this subsection, we first prove the validity of the algorithm ZCLHofFei by deducing its probability of success and then analyze its complexity. Before proving the validity of the algorithm ZCLHofFei, we need to define some parameters. Suppose that m, n are two positive integers and $F:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2^m$ is a Boolean function. Let D(F) denote the set of all probability-1 differentials of F. That is,

$$\begin{aligned} D(F)=\{(a,b)\in {\mathbb {F}}_2^n\times {\mathbb {F}}_2^m|F(x\oplus a)\oplus F(x)=b, \forall x\in {\mathbb {F}}_2^n\}. \end{aligned}$$

For an arbitrary Boolean function $F:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2^m$ we can define the following parameter

$$\begin{aligned} \epsilon (F):=\frac{1}{2^n}\max _{\begin{array}{c} (a,b)\in {\mathbb {F}}_2^n\times {\mathbb {F}}_2^m\\ (a,b)\notin D(F) \end{array}}|\{x\in {\mathbb {F}}_2^n|F(x)\oplus F(x\oplus a)=b\}|. \end{aligned}$$

(3)

This parameter is defined as, for any vector (a, b) that is not a probability-1 differential of F, the maximum possible proportion of x in ${\mathbb {F}}_2^n$ that satisfies $F(x)\oplus F(x\oplus a)=b$. It measures how close the vectors not in D(F) can be to be a probability-1 differential of F. Obviously $0\le F<1$. The smaller the value of $\epsilon (F)$, the easier it is to distinguish F’s probability-1 differentials from the other vectors.

For an arbitrary block cipher $E:{\mathbb {F}}_2^n\rightarrow {\mathbb {F}}_2^n$ with r rounds, we define the parameter

$$\begin{aligned} {\hat{\epsilon }}(E)\triangleq \max \{\epsilon (E^{(v)}),\epsilon (E_{(r-v)}^{(-1)})|1\le v\le r-1\}, \end{aligned}$$

where $E^{(v)}$ denotes the first v rounds of E, $E_{(r-v)}^{(-1)}$ denotes the inverse function of the last $r-v$ rounds of E, and $\epsilon (E^{(v)}),\epsilon (E_{(r-v)}^{(-1)})$ are defined as in Eq.(3). For any $v\in \{1,2,\cdots ,r-1\}$, $E^{(v)}$ and $E_{(r-v)}$ are both round-reduced versions of E. By the definition of $\epsilon (\cdot )$, for a block cipher E the parameter ${\hat{\epsilon }}(E)$ actually describes the distance between the probability-1 differentials of all reduced versions of E and the other vectors. The smaller the value of ${\hat{\epsilon }}(E)$, the more distant the other vectors are from being probability-1 differentials of an reduced version of E.

The following theorem justifies the validity of the algorithm ZCLHofFei.

Theorem 1

Suppose that $F_{SP}$ is a Feistel cipher with SP-type round functions and there exists a constant p such that ${\hat{\epsilon }}(F_{SP}^{\bot })\le p<1$. If running the algorithm ZCLHofFei on $F_{SP}$ with a parameter c (c is chosen such that ($\frac{1+p}{2})^c<\frac{1}{2}$) outputs a set N, then the probability that the linear approximations in N are zero correlation linear hulls of $F_{SP}$ is close to 1.

Proof

We divide the proof into two parts:

Part(I) In this part, we prove that the probability of all differentials in N being impossible differentials of ${\mathcal {F}}_{SP}^{\bot }$ is close to 1. (Every $(\varDelta x_2,\varDelta x_1)\rightarrow (\varDelta x'_2,\varDelta x'_1)\in N$ can be viewed both as a linear approximation and as a differential.)

Consider the set $A_v^1$ obtained in the step 5 of the algorithm ZCLHofFei. For any $((\varDelta x_1,\varDelta x_2),(\varDelta y_1,\varDelta y_2))$ in $A_v^1$, it holds that $(0^{m_1},(\varDelta x_1,\varDelta x_2),(\varDelta y_1,\varDelta y_2))$ is a solution of the following linear equations:

$$\begin{aligned} \left\{ \begin{array}{l}(k,x,y)\cdot u^{(1)}=0\\ (k,x,y)\cdot u^{(2)}=0\\ \cdots \\ (k,x,y)\cdot u^{(c(m_1+4n))}=0\\ k=0^m. \end{array} \right. \end{aligned}$$

Thus, it can be viewed as an output of Simon’s algorithm on $G_v^1$, except that the first $m_1$ bits are additionally required to be zero. Even though $G_v^1$ does not satisfy Simon’s promise, it satisfies the relaxed condition proposed in [10]. Specifically, for $v=1,\cdots ,r-1$, let $S(G_v^1)$ denote the set of all periods of $G_v^1$. Since ${\hat{\epsilon }}(F_{SP}^{\bot })\le p<1$, it holds that

$$\begin{aligned}&\max _{\begin{array}{c} (\varDelta k,\varDelta x,\varDelta y)\in {\mathbb {F}}_2^{m_1+2n+2n}\\ (\varDelta k,\varDelta x,\varDelta y)\notin S(G_v^1) \end{array}}\frac{|\{(k,x,y)|G_v^1(k,x,y)\oplus G_v^1(k\oplus \varDelta k,x\oplus \varDelta x,y\oplus \varDelta y)=\mathbf {0}\}|}{2^{m_1+4n}}\\ =&\frac{1}{2^{m_1+2n}}\max _{(\varDelta k,\varDelta x,\varDelta y)\notin D(F^{\bot (v)})}|\{(k,x)|F^{\bot (v)}(k,x)\oplus F^{\bot (v)}(k\oplus \varDelta k,x\oplus \varDelta x)=\varDelta y\}|\\ =&\epsilon (F^{\bot (v)})\le p. \end{aligned}$$

This means $G_v^1$ satisfies the relaxed condition of Theorem 1 in [10]; then, by the Theorem 1 in [10], $(0^{m_1},(\varDelta x_1,\varDelta x_2),(\varDelta y_1,\varDelta y_2))$ is a period of $G_v^1$ with a probability at least $1-(2(\frac{1+p}{2})^c)^{m_1+4n}$. When $(0^{m_1},(\varDelta x_1,\varDelta x_2),(\varDelta y_1,\varDelta y_2))$ is a period of $G_v^1$, for any $k\in {\mathbb {F}}_2^{m_1}$, any $(x_1,x_2)\in {\mathbb {F}}_2^{n}\times {\mathbb {F}}_2^{n}$, it holds that

$$\begin{aligned}&F^{\bot (v)}_k((x_1,x_2)\oplus (\varDelta x_1,\varDelta x_2))\oplus F^{\bot (v)}_k(x_1,x_2) \\ =&F^{\bot (v)}_k((x_1,x_2)\oplus (\varDelta x_1,\varDelta x_2))\oplus (\varDelta y_1,\varDelta y_2)\oplus F^{\bot (v)}_k(x_1,x_2) \oplus (\varDelta y_1,\varDelta y_2)\\ =&G_v^1\big (k,(x_1,x_2)\oplus (\varDelta x_1,\varDelta x_2),(\varDelta y_1,\varDelta y_2)\big )\oplus G_v^1(k,(x_1,x_2),{\varvec{0}})\oplus (\varDelta y_1,\varDelta y_2)\\ =&(\varDelta y_1,\varDelta y_2). \end{aligned}$$

This means for every key $k\in {\mathbb {F}}_2^{m_1}$, $(\varDelta x_1,\varDelta x_2)\rightarrow (\varDelta y_1,\varDelta y_2)$ is a probability-1 differential of $F^{\bot (v)}_k$. Therefore, except for a probability of $(2(\frac{1+p}{2})^c)^{m_1+4n}$, every $((\varDelta x_1,\varDelta x_2),(\varDelta y_1,\varDelta y_2))$ in $A_v^1$ satisfies that $(\varDelta x_1,\varDelta x_2)\rightarrow (\varDelta y_1,\varDelta y_2)$ is a probability-1 differential of $F^{\bot (v)}_k$. By a similar derivation, we can prove that, except for a probability of $(2(\frac{1+p}{2})^c)^{m_2+4n}$, every $((\varDelta x'_1,\varDelta x'_2),(\varDelta y'_1,\varDelta y'_2))$ in $A_v^2$ satisfies that $(\varDelta x'_1,\varDelta x'_2)\rightarrow (\varDelta y'_1,\varDelta y'_2)$ is a probability-1 differential of $F^{\bot (-1)}_{(r-v),k}$. According to the process of generating the set H (the step 9), for any $(\varDelta x_2,\varDelta x_1)\rightarrow (\varDelta x'_2,\varDelta x'_1)\in H$, it holds that $(\varDelta x_1,\varDelta x_2)\rightarrow (\varDelta x'_1,\varDelta x'_2)$ is an impossible differential of $F_{P^{T}S}$ with a probability at least $1-2(2(\frac{1+p}{2})^c)^{4n}$. Since $F_{SP}^{\bot }=\sigma F_{P^TS}\sigma$, the probability that there exists a differential in H that is not an impossible differential of $F_{SP}^{\bot }$ is at most $2(2(\frac{1+p}{2})^c)^{4n}$. Similarly, the probability of differentials in L not being impossible differentials of the new cipher obtained by replacing the S-boxes in $F_{SP}^{\bot }$ with random transformations is at most $(2(\frac{1+p}{2})^c)^{4n}$. For a well-defined block cipher that has an impossible differential dependent on the construction of S-boxes, the probability that the impossible differential still has zero probability after replacing the S-boxes with random transformations is negligible. Since $(\frac{1+p}{2})^c<\frac{1}{2}$, the value $2(2(\frac{1+p}{2})^c)^{4n}$ decreases exponentially to 0 as n increases. Therefore, the probability that the differentials in N being impossible of ${\mathcal {F}}_{SP}^{\bot }$ is close to 1.

Part(II) In this part, we prove that, for any $(a_0,a_1)\in {\mathbb {F}}_2^{2n}$, $(a_r,a_{r+1})\in {\mathbb {F}}_2^{2n}$, if $(a_0,a_1)\rightarrow (a_r,a_{r+1})$ is an impossible differential of the dual structure ${\mathcal {F}}^{\bot }_{SP}$, then it is also a zero correlation linear hull of the structure ${\mathcal {F}}_{SP}$. The conclusion of Theorem 1 can be obtained by combining the proofs of part (I) and (II). Theorem 1 in [24] has proved the exact inverted conclusion: an impossible differential of ${\mathcal {F}}_{SP}$ is also a zero correlation linear hull of its dual structure ${\mathcal {F}}^{\bot }_{SP}$. We adopt the same idea of the proof in [24], but because the positions of ${\mathcal {F}}_{SP}$ and ${\mathcal {F}}^{\bot }_{SP}$ are reversed, we need to construct S-boxes of ${\mathcal {F}}^{\bot }_{SP}$ differently.

It is sufficient to prove that, for any $(a_0,a_1)\rightarrow (a_r,a_{r+1})$, if there exists $F\in {\mathcal {F}}_{SP}$ such that $c((a_0,a_1)\cdot x\oplus (a_r,a_{r+1})\cdot F(x))\ne 0$, then there exists $F^{\bot }_r\in {\mathcal {F}}^{\bot }_{SP}$ such that the differential probability $p((a_0,a_1)\rightarrow (a_r,a_{r+1}))>0$. Suppose ${\mathcal {F}}_{SP}$ has t S-boxes each round, and the input of each S-box has s bits ($st=n$). Assume that $(a_0,a_1)\rightarrow (a_r,a_{r+1})$ is a linear approximate of some $F\in {\mathcal {F}}_{SP}$ with nonzero correlation. Denote the S-boxes in the i-th round as $S_i=(S_{i,1},S_{i,2},\cdots ,S_{i,t})$ ($i=1,\cdots ,r$), where $S_{i,j}$ is the j-th S-box. There exists a linear characteristic of F with nonzero correlation:

$$\begin{aligned} (a_0,a_1)\rightarrow (a_1,a_2)\rightarrow \cdots \rightarrow (a_{i-1},a_i)\rightarrow \cdots \rightarrow (a_r,a_{r+1}), \end{aligned}$$

where $a_i\in {\mathbb {F}}_2^n$. Since for any $d\ne a_iP^T$, $c(d\cdot x\oplus a_i\cdot (xP))=0$. The input mask of the linear transformation P must be $a_iP^T$ (as shown in Fig. 7). Denote the input masks of the S-boxes $S_i=(S_{i,1},S_{i,2},\cdots ,S_{i,t})$ as $b_i=(b_{i,1},b_{i,2},\cdots ,b_{i,t})$. Let $a_iP^T=((a_iP^T)_1,(a_iP^T)_2,\cdots ,(a_iP^T)_t)$, where $(a_iP^T)_j\in {\mathbb {F}}_2^s$ is the output mask of the j-th S-box. We have $b_i\oplus a_{i-1}=a_{i+1}$. Since for any $a\ne \mathbf {0}$, $a\rightarrow \mathbf {0}$ is a zero correlation linear hull, it holds that for any i, j such that $(a_iP^{T})_j=\mathbf {0}$, we have $b_{i,j}=\mathbf {0}$.

Fig. 7

Linear propagation of $F\in {\mathcal {F}}_{SP}$

Fig. 8

Differential propagation of $F^{\bot }_r$

Now for any $(x_L,x_R)=(x_{L,1},\cdots ,x_{L,t},x_{R,1},\cdots ,x_{R,,t})\in ({\mathbb {F}}_2^s)^t\times ({\mathbb {F}}_2^s)^t$, we construct a r-round cipher $F_r^{\bot }\in {\mathcal {F}}_{SP}^{\bot }$ such that

$$\begin{aligned} F_r^{\bot }(x_L,x_R)\oplus F_r^{\bot }(x_L\oplus a_0,x_R\oplus a_1)=(a_{r},a_{r+1}), \end{aligned}$$

which means $p((a_0,a_1)\rightarrow (a_r,a_{r+1}))>0$. Suppose $F_r^{\bot }=\sigma {\bar{F}}_r\sigma$, where ${\bar{F}}_r\in {\mathcal {F}}_{P^TS}$ and r denotes the number of rounds. The key is how to construct ${\bar{F}}_r$.

First consider the case where $r=1$. We define ${\bar{F}}_1$: for $j=1,2,\cdots ,t$: if $(a_1P^T)_j=\varvec{0}$, define $S_{1,j}$ as an arbitrary possible transformation on ${\mathbb {F}}_2^s$, and if $(a_1P^T)_j\ne \varvec{0}$, define

$$\begin{aligned} S_{1,j}(x_{L,j})=x_{L,j}\quad S_{1,j}(x_{L,j}\oplus (a_1P^T)_j)=x_{L,j}\oplus b_{1,j}, \end{aligned}$$

then

$$\begin{aligned} {\bar{F}}_1(x_L,x_R)\oplus {\bar{F}}_1(x_L\oplus a_1,x_R\oplus a_0)=(a_0\oplus b_1,a_1)=(a_2,a_1). \end{aligned}$$

Figure 8 shows the differential propagation of ${\bar{F}}_r$. Assume that we have constructed ${\bar{F}}_{r-1}$ such that ${\bar{F}}_{r-1}(x_L,x_R)\oplus {\bar{F}}_{r-1}(x_L\oplus a_1,x_r\oplus a_0)=(a_r,a_{r-1})$. Denote the output of ${\bar{F}}_{r-1}$ as $(y_L,y_R)=(y_{L,1},\cdots ,y_{L,t},y_{R,1},\cdots ,y_{R,t})$. We define ${\bar{F}}_{r}$: the first $r-1$ rounds are the same as ${\bar{F}}_{r-1}$, and for $j=1,2,\cdots ,t$, if $(a_rP^T)_j=\varvec{0}$ the S-box $S_{r,j}$ is an arbitrary possible transformation on ${\mathbb {F}}_2^s$; otherwise, the S-box $S_{r,j}$ is defined as follows:

$$\begin{aligned} S_{r,j}(y_{L,j})=y_{L,j}\quad S_{r,j}(y_{L,j}\oplus (a_rP^T)_j)=y_{L,j}\oplus b_{r,j}. \end{aligned}$$

Then, it holds that ${\bar{F}}_r(x_L,x_R)\oplus {\bar{F}}_r(x_L\oplus a_1,x_R\oplus a_0)=(a_{r-1}\oplus b_r,a_r)=(a_{r+1},a_r)$. Since $F_r^{\bot }=\sigma {\bar{F}}_r\sigma$, $(a_0,a_1)\rightarrow (a_r,a_{r+1})$ is a differential of $F_{r}^{\bot }$ with nonzero probability. $\square$

The condition ${\hat{\epsilon }}(F_{SP}^{\bot })\le p<1$ in Theorem 1 means that, for any vector (a, b) that is not probability-1 differential of any reduced version F of $F_{SP}^{\bot }$, only a limited proportion ($\le p$) of x satisfies

$$\begin{aligned} F(x\oplus a)\oplus F(x)=b. \end{aligned}$$

That is, (a, b) cannot be too close to be a probability-1 differential of any reduced version of $F_{SP}^{\bot }$. Theorem 1 states that, under this condition, all linear approximations output by the algorithm ZCLHofFei are zero correlation linear hulls of $F_{SP}$ with a probability close to 1.

Next we analyze the quantum complexity of the algorithm ZCLHofFei. The algorithm ZCLHofFei does not require querying any quantum or classical oracle. When applying the Simon’s subroutine, the attacker can execute the unitary operators of $G_v^1$ and $G_v^2$ on his own. We usually analyze the complexity of quantum algorithms from three aspects: the number of qubits required, the number of universal quantum gates in the corresponding circuit and the amount of classical calculations. In the following, we analyze the complexity of the algorithm ZCLHofFei from these three aspects.

The number of qubits Running Simon’s algorithm on $G_v^1$ once needs $m_1+6n$ qubits, and running Simon’s algorithm on $G_v^2$ once needs $m_2+6n$ qubits. Let m denote the sum of the lengths of the subkeys in all rounds of $F_{SP}$, then $m_1+m_2=m$. Since the qubits can be reused every time the Simon’s algorithm is executed, running the algorithm ZCLHofFei requires at most $m+6n$ qubits.

The number of universal gates Running Simon’s subroutine on $G_v^1$ once needs to perform $2(m_1+4n)$ single-qubit Hadamard gates and $|G_v^1|_Q$ additional universal gates, where $|G_v^1|_Q$ denotes the amount of universal gates required to execute the unitary operator of $G_v^1$ as explained in Section 2.2. Thus, running Simon’s algorithm on $G_v^1$ for $c(m_1+4n)$ times costs a total of $c(m_1+4n)(2m_1+8n+|G_v^1|_Q)$ universal gates. Similarly, running Simon’s algorithm on $G_v^2$ for $c(m_2+4n)$ times needs a total of $c(m_2+4n)(2m_2+8n+|G_v^2|_Q)$ universal gates. Therefore, the total number of universal gates required by the algorithm ZCLHofFei is:

$$\begin{aligned}&\sum _{v=1}^{r-1}\big [c(m_1+4n)(2m_1+8n+|G_v^1|_Q)+c(m_2+4n)(2m_2+8n+|G_v^2|_Q)\big ]\\ \le&c(m+4n)\sum _{v=1}^{r-1}(2m_1+2m_2+16n+|G_v^1|_Q+|G_v^2|_Q)\\ \overset{*}{=}&c(m+4n)\sum _{v=1}^{r-1}(2m+16n+|F_{P^TS}|_Q)\\ =&c(r-1)(m+4n)(2m+16n+|F_{P^TS}|_Q), \end{aligned}$$

which is a polynomial of m and n. The equation $(*)$ holds since

$$\begin{aligned} |G_v^1|_Q+|G_v^2|_Q=|F_k^{\bot (v)}|_Q+|F_{(r-v)k}^{\bot (-1)}|_Q=|F_k^{\bot (v)}|_Q+|F_{(r-v)k}^{\bot }|_Q=|F_{P^TS}|_Q. \end{aligned}$$

In other words, running the algorithm ZCLHofFei requires executing the unitary operator of the cipher $F_{P^TS}$ for $c(r-1)(m+4n)$ times and additional $c(r-1)(m+4n)(2m+16n)$ universal gates.

The amount of classical calculations The main classical calculations in the algorithm ZCLHofFei are to solve systems of linear equations. Solving a system of linear equations with s variables and t equations requires $O(s^2t)$ calculations. For every $v\in \{1,2,\cdots ,r-1\}$, solving linear equations (1) needs $O((m_1+4n)(4n)^2)$ classical calculations, and solving linear equations (2) needs $O((m_2+4n)(4n)^2)$ classical calculations. Therefore, the total amount of classical calculations required is $O(16(m+8n)n^2r)$.

4 Quantum zero correlation linear cryptanalysis of the SPN ciphers

In this section, we propose a quantum algorithm for finding zero correlation linear hulls of the SPN ciphers. Similar to the case of attacking the Feistel ciphers, the proposed quantum algorithm first calls Simon’s algorithm to find impossible differentials of the dual structure and then uses the found impossible differentials to derive zero correlation linear hulls of the original structure.

4.1 Quantum algorithm for finding zero correlation linear hulls of SPN ciphers

Suppose $E_{SP}$ is a SPN cipher. Denote the structure of $E_{SP}$ as ${\mathcal {E}}_{SP}$ and its dual structure as ${\mathcal {E}}_{SP}^{\bot }$. The quantum algorithm we will propose actually finds zero correlation linear hulls of the structure ${\mathcal {E}}_{SP}$. It first finds impossible differentials of the dual structure ${\mathcal {E}}_{SP}^{\bot }$ and then uses them to derive zero correlation linear hulls of ${\mathcal {E}}_{SP}$.

Let $E_{SP}^{\bot }$ be the cipher exactly the same as $E_{SP}$ except that the linear transformation P is replaced by $(P^{-1})^T$. That is, $E_{SP}^{\bot }=E_{S(P^{-1})^T}$. Obviously, $E_{SP}^{\bot }\in {\mathcal {E}}_{SP}^{\bot }$. If the structure ${\mathcal {E}}_{SP}^{\bot }$ has an impossible differential $\varDelta x\rightarrow \varDelta y$, then $\varDelta x\rightarrow \varDelta y$ is also an impossible differential of $E_{SP}^{\bot }$. Thus, we can find impossible differentials of the structure ${\mathcal {E}}_{SP}^{\bot }$ by searching for the impossible differentials of the cipher $E_{SP}^{\bot }$. Generally, a well-defined block cipher has only a few impossible differentials. Even if we obtain multiple results when searching for the impossible differentials of $E_{SP}^{\bot }$, we can exclude the differentials that are not impossible differentials of ${\mathcal {E}}_{SP}^{\bot }$ by randomly choosing new bijective transformations to replace the S-boxes in $E_{SP}^{\bot }$ and verifying whether these differentials are also impossible differentials of the new cipher.

Fig. 9

Connecting two probability-1 differentials gives an impossible differential of $E_{SP}^{\bot }$

We use miss-in-the-middle technique to find impossible differentials of $E_{SP}^{\bot }$. Suppose $E_{SP}^{\bot }$ has r rounds and the block size is n. For any $v\in \{1,2,\cdots ,r-1\}$, we divide $E_{SP}^{\bot }$ into two parts $E_{SP}^{\bot }=E^{\bot }_{(r-v)}\cdot E^{\bot (v)}$, where $E^{\bot (v)}$ corresponds to the first v rounds of $E_{SP}^{\bot }$, and $E^{\bot }_{(r-v)}$ corresponds to the last $r-v$ rounds of $E_{SP}^{\bot }$. Let ${\mathcal {K}}_v^1$, ${\mathcal {K}}_v^2$ denote the key spaces of $E^{\bot (v)}$ and $E^{\bot }_{(r-v)}$, respectively. As shown in Fig. 9, if $\varDelta x\rightarrow \varDelta y$ is a probability-1 differential of $E^{\bot (v)}$, $\varDelta x'\rightarrow \varDelta y'$ is a probability-1 differential of $E^{\bot \, (-1)}_{(r-v)}$ (the inverse function of $E^{\bot }_{(r-v)}$) and $\varDelta y\ne \varDelta y'$, then $\varDelta x\rightarrow \varDelta x'$ is an impossible differential of $E_{SP}^{\bot }$.

As in the case of attacking the Feistel ciphers, we use Simon’s algorithm to find probability-1 differentials of $E^{\bot (v)}$ and $E^{\bot }_{(r-v)}$. Since the secret key is unknown to the attacker, we need to consider the key as a part of the function’s input when calling Simon’s algorithm. By doing this, the periodic function is public and known to the attacker, and thus, its corresponding unitary operator can be executed by the attacker.

Based on these ideas, we propose a quantum algorithm for finding zero correlation linear hulls of the SPN ciphers as follows:

The step 5 in the algorithm ZCLHofSPN is to find probability-1 differentials of $E^{\bot (v)}$ and put them into the set $A_v^1$. Suppose $(\varDelta x,\varDelta y)$ ($\varDelta x, \varDelta y\in {\mathbb {F}}_2^n$) is a solution of the linear equations (4), then $(0^{m_1},\varDelta x,\varDelta y)$ is actually an output obtained by applying Simon’s algorithm on $G_v^1$, and thus, it is a period of $G_v^1$. This means that $\varDelta x\rightarrow \varDelta y$ is a probability-1 differential of $E^{\bot (v)}$. Similarly, the step 6 is to find the probability-1 differentials of $E^{\bot (-1)}_{(r-v)}$ and put them into the set $A_v^2$. The steps 7–11 compare all the differentials in $A_v^1$ and $A_v^2$ and connect the unmatched differential pairs to obtain impossible differentials of $E_{SP}^{\bot }$. The step 13 randomly chooses new bijective transformations to replace the S-boxes in $E_{SP}^{\bot }$ and then repeats the previous process on the new cipher to find its impossible differentials and puts them into the set L. The differentials in N are impossible for both $E_{SP}^{\bot }$ and the new cipher with random S-boxes. Therefore, any $\varDelta x\rightarrow \varDelta x'$ in the set N has a high probability of being an impossible differential of the dual structure ${\mathcal {E}}_{SP}^{\bot }$. The proof of Theorem 2 will show that this means $\varDelta x\rightarrow \varDelta x'$ is a zero correlation linear hull of ${\mathcal {E}}_{SP}$.

4.2 Analysis of the algorithm ZCLHofSPN

In this subsection, we first prove the validity of the algorithm ZCLHofSPN and then analyze its complexity. The following theorem justifies the validity of the algorithm ZCLHofSPN.

Theorem 2

Suppose $E_{SP}$ is a SPN cipher and there exists a constant p such that ${\hat{\epsilon }}(E_{SP}^{\bot })\le p<1$. If running the algorithm ZCLHofSPN on $E_{SP}$ with a parameter c (c is chosen such that ($\frac{1+p}{2})^c<\frac{1}{2}$) outputs a set N, then the probability that the linear approximations in N are zero correlation linear hulls of $E_{SP}$ is close to 1.

Proof

By a derivation similar to the proof of Theorem 1, we can prove that the probability of all differentials in N being impossible differentials of ${\mathcal {E}}_{SP}^{\bot }$ is close to 1. (Note that every $\varDelta x\rightarrow \varDelta y\in N$ can be viewed both as a linear approximation and as a differential.) We omit the proof of this part for simplicity. In the following we prove that, for any $a_0,a_r\in {\mathbb {F}}_2^{n}$, if $a_0\rightarrow a_r$ is an impossible differential of the dual structure ${\mathcal {E}}^{\bot }_{SP}$, then it is also a zero correlation linear hull of the structure ${\mathcal {E}}_{SP}$. This will complete the proof. Theorem 2 in [24] has pointed out this link between zero correlation linear hulls of a SPN structure and impossible differentials of its dual structure, but the authors did not present the proof. To prove this, we only need to prove the inverse negation proposition: for any $a_0\rightarrow a_r$, if there exists $E\in {\mathcal {E}}_{SP}$ such that $c(a_0\cdot x\oplus a_r\cdot E(x))\ne 0$, then there exists $E^{\bot }_r\in {\mathcal {E}}^{\bot }_{SP}$ such that the differential probability $p(a_0\rightarrow a_r)>0$.

Suppose ${\mathcal {E}}_{SP}$ has t S-boxes in each round, and the input of each S-box has s bits ($st=n$). Assume that $a_0\rightarrow a_r$ is a linear approximate with nonzero correlation of some $E\in {\mathcal {E}}_{SP}$. Denote the S-boxes in the i-th round of E as $S_i=(S_{i,1},S_{i,2},\cdots ,S_{i,t})$ ($i=1,\cdots ,r$), where $S_{i,j}$ is the j-th S-box. Then, there exists a linear characteristic of E with nonzero correlation:

$$\begin{aligned} a_0\rightarrow a_1\rightarrow \cdots \rightarrow a_{i-1}\rightarrow \cdots \rightarrow a_r, \end{aligned}$$

where $a_{i-1}$ is the input mask of the i-th round. Let $a_{i-1}=(a_{i-1,1},a_{i-1,2},\cdots ,$ $a_{i-1,t})$, where $a_{i-1,j}\in {\mathbb {F}}_2^s$, then $a_{i-1,j}$ is the input mask of the j-th S-box $S_{i,j}$ in the i-th round (as shown in Fig. 10). Since for any $d\ne a_iP^T$, we have $c(d\cdot x\oplus a_i\cdot (xP))=0$. The input mask of P must be $a_iP^T$. Therefore, the output mask of S-boxes must be $a_iP^T$. Let $a_iP^T=((a_iP^T)_1,(a_iP^T)_2,\cdots ,(a_iP^T)_t)$. For $j=1,\cdots ,t$, $(a_iP^T)_j$ is the output mask of $S_{i,j}$.

Fig. 10

Linear propagation of $E\in {\mathcal {E}}_{SP}$

Fig. 11

Differential propagation of $E^{\bot }_r\in {\mathcal {E}}_{SP}^{\bot }$

Now for any $x=(x_1,x_{2}\cdots ,x_{t})\in ({\mathbb {F}}_2^s)^t$, we construct a r-round cipher $E_r^{\bot }\in {\mathcal {E}}_{SP}^{\bot }$ such that

$$\begin{aligned} E_r^{\bot }(x)\oplus E_r^{\bot }(x\oplus a_0)=a_{r}, \end{aligned}$$

which means $p(a_0\rightarrow a_r)>0$.

First consider the case where $r=1$. We define $E_1^{\bot }$: for $j=1,2,\cdots ,t$: if $a_{0,j}=\varvec{0}$, define $S_{1,j}$ as an arbitrary possible transformation on ${\mathbb {F}}_2^s$, and if $a_{0,j}\ne \varvec{0}$, define

$$\begin{aligned} S_{1,j}(x_j)=x_{j}\quad S_{1,j}(x_{j}\oplus a_{0,j})=x_{j}\oplus (a_1P^{T})_j, \end{aligned}$$

then

$$\begin{aligned} E_1^{\bot }(x)\oplus E_1^{\bot }(x\oplus a_0)=a_1P^{T}\cdot (P^{-1})^T=a_1. \end{aligned}$$

Figure 11 shows the differential propagation of $E_r^{\bot }$. Assume we have constructed $E_{r-1}^{\bot }$ such that $E_{r-1}^{\bot }(x)\oplus E_{r-1}^{\bot }(x\oplus a_0)=a_{r-1}$. Denote the output of $E_{r-1}^{\bot }$ as $y=(y_{1},y_{2},\cdots ,y_{t})\in ({\mathbb {F}}_2^s)^t$. We define $E_r^{\bot }$: the first $r-1$ rounds are the same as $E_{r-1}^{\bot }$, and for $j=1,2,\cdots ,t$, if $a_{r-1,j}=\varvec{0}$ the S-box $S_{r,j}$ is an arbitrary possible transformation on ${\mathbb {F}}_2^s$, otherwise, the S-box $S_{r,j}$ is defined as follows:

$$\begin{aligned} S_{r,j}(y_{j})=y_{j}\quad S_{r,j}(y_{j}\oplus a_{r-1,j})=y_{j}\oplus (a_rP^{T})_j. \end{aligned}$$

Then, it holds that $E_r^{\bot }(x)\oplus E_r^{\bot }(x\oplus a_0)=(a_rP^{T})\cdot (P^{-1})^T=a_r$. Thus, $a_0\rightarrow a_r$ is a differential of $E_r^{\bot }$ with nonzero probability. $\square$

Theorem 2 states that, as long as a SPN cipher $E_{SP}$ satisfies the condition that ${\hat{\epsilon }}(E_{SP}^{\bot })\le p<1$ for some constant p, then all linear approximations output by the algorithm ZCLHofSPN applied on $E_{SP}$ are its zero correlation linear hulls with a probability very close to 1.

The algebraic condition ${\hat{\epsilon }}(E_{SP}^{\bot })\le p<1$ means that, for any vector (a, b) that is not probability-1 differential of any reduced version E of $E_{SP}^{\bot }$, only a limited proportion ($\le p$) of x satisfies

$$\begin{aligned} F(x\oplus a)\oplus F(x)=b. \end{aligned}$$

That is, it is not too difficult to distinguish the probability-1 differentials of the reduced versions of $E_{SP}^{\bot }$ with the other vectors. For any SPN cipher satisfying this condition, the algorithm ZCLHofSPN can efficiently find its zero correlation linear hulls with a probability close to 1.

Next we analyze the quantum complexity of the algorithm ZCLHofSPN. The algorithm ZCLHofSPN does not require any quantum or classical query. We still analyze the complexity from three aspects: the number of qubits required, the number of universal quantum gates and the amount of classical calculations.

The number of qubits Running Simon’s algorithm on $G_v^1$ once needs $m_1+3n$ qubits, and running Simon’s algorithm on $G_v^2$ once needs $m_2+3n$ qubits. Let $m=m_1+m_2$. Since the qubits can be reused, running the algorithm ZCLHofSPN requires at most $m+3n$ qubits.

The number of universal gates Running Simon’s subroutine on $G_v^1$ once needs to perform $2m_1+4n$ single-qubit Hadamard gates and $|G_v^1|_Q$ additional universal gates. Therefore, running Simon’s algorithm on $G_v^1$ for $c(m_1+2n)$ times needs a total of $c(m_1+2n)(2m_1+4n+|G_v^1|_Q)$ universal gates. Similarly, running Simon’s algorithm on $G_v^2$ for $c(m_2+2n)$ times needs a total of $c(m_2+2n)(2m_2+4n+|G_v^2|_Q)$ universal gates. The total number of universal gates required by the algorithm ZCLHofSPN is

$$\begin{aligned}&\sum _{v=1}^{r-1}\big [c(m_1+2n)(2m_1+4n+|G_v^1|_Q)+c(m_2+2n)(2m_2+4n+|G_v^2|_Q)\big ]\\ \le&c(m+2n)\sum _{v=1}^{r-1}(2m_1+2m_2+8n+|G_v^1|_Q+|G_v^2|_Q)\\ =&c(m+2n)\sum _{v=1}^{r-1}(2m+8n+|E_{SP}^{\bot }|_Q)\\ =&c(r-1)(m+2n)(2m+8n+|E_{SP}^{\bot }|_Q), \end{aligned}$$

which is a polynomial of m and n. In other words, running the algorithm ZCLHofSPN requires executing the unitary operator of the cipher $E_{SP}^{\bot }$ for $c(r-1)(m+2n)$ times and additional $c(r-1)(m+2n)(2m+8n)$ quantum universal gates.

The amount of classical calculations The main classical calculations in the algorithm ZCLHofSPN are to solve systems of linear equations. For every $v\in \{1,2,\cdots ,r-1\}$, solving linear equations (4) needs $O((m_1+2n)(2n)^2)$ classical calculations, and solving linear equations (5) needs $O((m_2+2n)(2n)^2)$ classical calculations. Therefore, the total amount of classical calculations required is $O((4m+16n)n^2r)$.

It is notable that, as long as an attacker obtains a zero correlation linear hull, whether it is computed by himself with a quantum computer or provided by someone else, he can use it to search the key even when he has no quantum computer. Thus, if some party use the proposed quantum algorithms in this paper to find some zero correlation linear hulls of a cipher and post them online, then other attackers without a quantum computer are also able to use them to find the secret key of the cipher.

Zero correlation linear cryptanalysis is one of the most commonly used tools for attacking block ciphers. The classical methods of finding zero correlation linear hulls can be summarized in two ways. One is to manually analyze the structures and mathematical properties of a specific block cipher and then derive the zero correlation linear hulls. The main difficulty of this method is to extend the number of rounds of the zero correlation linear hulls. Even if we can find a zero correlation linear hull with a small number of rounds by observation, as the number of rounds increases, the number of active S-boxes will increase and the overall encryption function will become more complicated; therefore, the difficulty of finding zero correlation linear hulls will increase sharply. Thus, this method can work only for a few block ciphers, such as CAST-256, SM4, and the number of rounds of the found zero correlation linear hull is usually not large enough to completely break the entire block cipher. Compared with this method, the algorithms ZCLHofFei and ZCLHofSPN convert finding zero correlation linear hulls into finding impossible differentials and treat multiple rounds of the block cipher as a black box, ignoring internal structures when applying Simon’s algorithm. Using this method, the increase in the number of rounds does not necessarily lead to an increase in the difficulty of finding zero correlation linear hulls. Therefore, the algorithms ZCLHofFei and ZCLHofSPN have an advantage over the classical zero correlation linear cryptanalysis for extending the number of rounds of zero correlation linear approximations. The second method of finding zero correlation linear hulls in classical zero correlation linear cryptanalysis is to exhaustive search using computers. The exhaustive search can be applied to most block ciphers. However, the computational complexity of searching for zero correlation linear hulls is exponential in the security parameter n. Compared with this method, our quantum algorithms take advantage of the natural parallelism of quantum computing so that the complexity of the search is only polynomial, and the quantum algorithms can be widely applied to the Feistel and SPN ciphers. We can say that it makes up for the shortcomings of the above two classical methods. Moreover, the algorithms ZCLHofFei and ZCLHofSPN do not require any quantum or classical query to the block ciphers, and thus can be executed under the $Q_1$ quantum attack model, which has lower requirements on the attacker’s ability and is more in line with the actual attack scenarios in the post-quantum world.

5 Conclusion

In this paper, we study quantum zero correlation linear cryptanalysis and propose two quantum algorithms for finding zero correlation linear hulls of Feistel ciphers and SPN ciphers, respectively. To justify the validity of the proposed algorithms, we prove that, as long as the attacked block ciphers satisfy certain algebraic conditions, the linear approximations output by the proposed algorithms have zero correlation with a probability close to 1. We also analyze the complexity of the proposed algorithms. Only polynomial qubits and universal gates are required, and executing the algorithms does not require any quantum or classical query to the block ciphers. They can be executed under the $Q_1$ model. Since the proposed quantum algorithms treat multiple rounds of the block cipher as a black box ignoring the internal structures of the cipher, they have an advantage over the classical zero correlation linear cryptanalysis for extending the number of rounds of zero correlation linear approximations.

Facing the threat posed by quantum computers, the cryptographic community must prepare quantum-resistant cryptographic schemes for the arrival of post-quantum era. The security of symmetric cryptosystems is always argued by proving its resistance against various known cryptanalytic tools, such as linear cryptanalysis and differential cryptanalysis, and thus heavily depends on the development of cryptanalytic tools. Therefore, studying the power of classical cryptanalytic tools when they are combined with quantum algorithms is critical for designing quantum-secure symmetric ciphers. Our research on the applications of quantum algorithms to zero correlation linear cryptanalysis, which is a very effective tool for attacking block ciphers, shows the advantages of quantum computing in symmetric cryptanalysis.

6 Discussion

There are many related directions worthy of further research. First, we can consider combining the quantum algorithms for finding zero correlation linear hulls proposed in this paper with Grover’s algorithm. Apply Grover’s algorithm to the key-recovery stage of zero correlation linear cryptanalysis and then evaluate the complexity of a complete quantum zero correlation linear attack. Second, under the premise of not reducing the success probability, how to improve the complexity of the proposed algorithms is also worth further investigating. Finally, the applications of quantum algorithms to other classical cryptanalytic tools, such as truncated differential and integral cryptanalysis, are also a valuable direction for research. We believe that the research in symmetric quantum cryptanalysis contributes to a better understanding of how quantum computing affects the security of symmetric ciphers and provides theoretical support for designing quantum-secure symmetric algorithms.