1 Introduction

Quantum-enhanced metrology aims to exploit quantum features of atoms and light such as entanglement, for measuring unknown physical quantities with precision going beyond the classical limit [1, 2]. Parameter estimation with N independent (unentangled) probes yields a precision of \(1/\sqrt{N}\), the so-called standard quantum limit [3]. Entangling the probes, however, can in principle offer a quadratic enhancement in precision, i.e., reach the Heisenberg limit with precision 1 / N [4, 5]. Such strategies have been experimentally realized in optical interferometry [6–8] with exciting applications for the detection of gravitational waves [9, 10]. Moreover, the same quantum enhancement principle can be utilized in atomic spectroscopy [11, 12] where the spin-squeezed states have been employed for improving frequency calibration precision [13–15].

Unfortunately, quantum systems are inevitably influenced by their environments, which reduces or even cancels the superiority that the quantum entanglement or squeezing provides in the processes of parameter estimation [16–19]. Thus the robustness of quantum protocols against various quantum noises becomes very important, and many researches relevant to this point have been done [20, 21]. Especially, people recently have found an interesting protocol [22] that the collaboration between non-Markovian memory effect and classical driving can dramatically preserve QFI of the phase parameter encoded in one qubit system and thus preserve the precision of quantum parameter estimation from the impact of environmental noises. A minor flaw is that the protocol was designed only in the case of independent probes, which did not utilize the role of quantum entanglement and thus only works within the framework of standard quantum limit. In this paper, we try to generalize the protocol to the case of quantum entangled probes and examine its validity. Considering the complexity of the generalization process, we only take two- and three-atom entangled states as the exemplary examples in the numerical simulations. The generalization to the case with more atoms is straightforward.

We will mainly concentrate on the protection of QFI of the phase parameter encoded in entangled states, because QFI characterizes the amount of information about the true value of the estimated parameter and its inverse gives the lower bound of the accuracy limit. Large QFI about the estimated parameter means high estimation accuracy, giving that the lower bound is tight. As comparison, we also study the protection of the corresponding entangled states. Because protection of QFI is in principle different from that of quantum states, the former is a kind of local protection that only protects the information of the estimated parameter, but the latter protects all the information encoded in a quantum state. We find that the behaviors of the two protections in the case of weak drivings have essential differences, but for suitably strong drivings, both the QFI and the quantum states can be protected effectively.

The paper is organized as follows. In Sect. 2, we introduce the systematic approach for treating an open quantum system with N two-level atoms, each interacting with individual environments and driven independently by classical fields. And in Sects. 3 and 4, we then use it to numerically study the evolutions of QFI and fidelity, paying particular attention to the protections of QFI and the corresponding entangled states. Finally, the conclusions are arranged in Sect. 5.

2 Model

Consider N two-level atoms, each interacting with its own zero-temperature bosonic reservoir modeled by an infinite chain of quantum harmonic oscillators and driven by a classical field. According to the theory of open quantum systems, if the evolution for the reduced density of atom j is described by the map \(\varepsilon _{j}\), then the evolution of the total open quantum system can be written as

$$\begin{aligned} \varepsilon (\rho )=\varepsilon _{j}^{\otimes N}(\rho ). \end{aligned}$$
(1)

Note that here \(\rho \) is the density matrix of the N atoms and in general it is an entangled state. This equation shows that single quantum map \(\varepsilon _{j}\) is the basis for studying the dynamics of the whole open quantum system.

Let \(\omega _{j0}\) and \(\omega _{j \mathrm{L}}\) be the frequencies of the transition and the classical driving field for atom j, then the Hamiltonian for atom j plus its environment, in the rotating frame with frequency \(\omega _{j \mathrm{L}}\), may be written as [22]

$$\begin{aligned} H_{j}= & {} \frac{\Delta _{j}}{2}\sigma _{j\mathrm{z}}+\varOmega _{j}\sigma _{j\mathrm{x}}+\sum _{k}\omega _{jk}b^{\dagger }_{jk}b_{jk}\nonumber \\&\quad \,+\,\sum _{k}(g_{jk}b_{jk}\sigma _{j+}{\hbox {e}}^{\mathrm{i}\omega _{j \mathrm{L}}}+\mathrm{H.C.}), \end{aligned}$$
(2)

where \(\sigma _{j\mathrm x}\), \(\sigma _{j\mathrm z}\) are the Pauli operators and \(\sigma _{j+}\), \(\sigma _{j-}\) the atomic inversion operators, \(\omega _{jk}\), \(b_{jk}\) and \(b_{jk}^{\dagger }\) are, respectively, the frequency, annihilation and creation operators for the k-th harmonic oscillator of the reservoir coupled to the atom j. \(\Delta _{j}=|\omega _{j0}-\omega _{j\mathrm L}|\) is the frequency detuning between atom j and its driving field, and \(\varOmega _{j}\) is the Rabi frequency of the driving field which is assumed to be real. The atom couples to its environment via the interaction of Jaynes–Cummings model with coupling strength \(g_{jk}\).

Introducing the dressed bases

$$\begin{aligned} |E_{j}\rangle= & {} \cos \frac{\eta _{j}}{2}|e_{j}\rangle +\sin \frac{\eta _{j}}{2}|g_{j}\rangle , \nonumber \\ |G_{j}\rangle= & {} -\sin \frac{\eta _{j}}{2}|e_{j}\rangle +\cos \frac{\eta _{j}}{2}|g_{j}\rangle , \end{aligned}$$
(3)

where \(\eta _{j}=\arctan (2\varOmega _{j}/\Delta _{j})\), \(\{|g_{j}\rangle ,|e_{j}\rangle \}\) are the eigenbase of atom j, and \(\{|G_{j}\rangle ,|E_{j}\rangle \}\) the eigenbase of the first two terms on the right hand side of Eq. (2), then the Hamiltonian can be simplified as

$$\begin{aligned} H'_{j}= & {} \frac{\omega _{{j}\mathrm D}}{2}\rho _{j\mathrm{z}}+\sum _{k}\omega _{jk}b^{\dagger }_{jk}b_{jk}\nonumber \\ \quad&+\,\cos ^{2}\frac{\eta _{j}}{2}\sum _{k}\left( g_{jk}b_{jk}\rho _{j+}{\hbox {e}}^{{i}\omega _{j \mathrm{L}}}+\mathrm{H.C.}\right) , \end{aligned}$$
(4)

where \(\omega _{j\mathrm{D}}=\sqrt{\Delta _{j}^{2}+4\varOmega _{j}^{2}}\) is the dressed frequency, and the new Pauli operators are defined as \(\rho _{j\mathrm{z}}=|E_{j}\rangle \langle E_{j}|-|G_{j}\rangle \langle G_{j}|\), \(\rho _{j\mathrm{+}}=|E_{j}\rangle \langle G_{j}|\). Note that in the deduction the rotating-wave approximation has been used and thus the condition \(\varOmega _{j}\ll \omega _{j0}, \omega _{j\mathrm{L}}\) must be met. Employing the trait of Jaynes–Cummings model and for the vacuum Lorentzian environment, the evolution governed by this Hamiltonian in the dressed base can be written as [22]

$$\begin{aligned} |G_{j}\rangle \otimes |0_{j}\rangle\rightarrow & {} |G_{j}\rangle \otimes |0_{j}\rangle , \nonumber \\ |E_{j}\rangle \otimes |0_{j}\rangle\rightarrow & {} \xi _{j}(t)|E_{j}\rangle \otimes |0_{j}\rangle +\sqrt{1-\xi _{j}^{2}(t)}|G_{j}\rangle \otimes |1_{j}\rangle , \end{aligned}$$
(5)

where \(|0_{j}\rangle \) and \(|1_{j}\rangle \) denote, respectively, the vacuum and one-photon states of the environment coupled to atom j. The parameter \(\xi _{j}(t)\) is defined as

$$\begin{aligned} \xi _{j}(t)={\hbox {e}}^{-M_{j}t/2}\left[ \cosh \left( \frac{K_{j}t}{4}\right) +\frac{2M_{j}}{K_{j}}\sinh \left( \frac{K_{j}t}{4}\right) \right] , \end{aligned}$$
(6)

with \(K_{j}=\sqrt{4M_{j}^{2}-2\gamma _{j0}\lambda _{j}(1+\cos \eta _{j})^{2}}\), \(M_{j}=\lambda _{j}+\mathrm{i}\Delta _{j}-\mathrm{i}\delta _{j}-\mathrm{i}\omega _{j\mathrm D}\). Here \(\delta _{j}\) is the detuning between the Bohr frequency of atom j and its environmental center frequency, \(\lambda _{j}\) defines the spectral width and \(\gamma _{j0}\) is the decay rate of atom j in free space.

Equation (5) describes the evolution of atom j in the dressed base, but our purpose is to find the evolution in the original bare base. Now we assume that the atom j plus its environment in the bare base have an initial state \(|\psi (0)\rangle =(\alpha |g_{j}\rangle +\beta |e_{j}\rangle )|0_{j}\rangle \) with the atomic initial state

$$\begin{aligned} \rho _{j}=\left[ \begin{array}{cc} |\alpha |^{2} &{}\quad \alpha \beta ^{*} \\ \alpha ^{*}\beta &{}\quad |\beta |^{2} \\ \end{array} \right] . \end{aligned}$$
(7)

By use of the evolution of Eq. (5), we easily find the reduced state of atom j at time t in the bare base to be,

$$\begin{aligned} \rho _{j}(t)= & {} \left[ \begin{array}{cc} |\alpha a_{j}+\beta b_{j}|^{2} &{} \quad (\alpha a_{j}+\beta b_{j})(\alpha b_{j}+\beta c_{j})^{*} \\ (\alpha b_{j}+\beta c_{j})(\alpha a_{j}+\beta b_{j})^{*} &{}\quad |\alpha b_{j}+\beta c_{j}|^{2} \\ \end{array} \right] \\+ & {} \left[ \begin{array}{cc} |\alpha e_{j}+\beta f_{j}|^{2} &{} \quad -(\alpha e_{j}+\beta f_{j})(\alpha d_{j}+\beta e_{j})^{*} \\ -(\alpha d_{j}+\beta e_{j})(\alpha e_{j}+\beta f_{j})^{*} &{}\quad |\alpha d_{j}+\beta e_{j}|^{2} \\ \end{array} \right] , \end{aligned}$$

where \(a_{j}=\xi _{j}(t)\sin ^{2}\frac{\eta _{j}}{2}+\cos ^{2}\frac{\eta _{j}}{2}\), \(b_{j}=[\xi _{j}(t)-1]\sin \frac{\eta _{j}}{2}\cos \frac{\eta _{j}}{2}\), \(c_{j}=\xi _{j}(t)\cos ^{2}\frac{\eta _{j}}{2}+\sin ^{2}\frac{\eta _{j}}{2}\), \(d_{j}=\sqrt{1-\xi _{j}^{2}(t)}\sin ^{2}\frac{\eta _{j}}{2}\), \(e_{j}=\sqrt{1-\xi _{j}^{2}(t)}\sin \frac{\eta _{j}}{2}\cos \frac{\eta _{j}}{2}\), \(f_{j}=\sqrt{1-\xi _{j}^{2}(t)}\cos ^{2}\frac{\eta _{j}}{2}\). Thus the map \(\varepsilon _{j}\) that acts on the atom j may be expressed as

$$\begin{aligned} \varepsilon _{j}(\rho _{j})=E_{j0}\rho _{j}E_{j0}^{+}+E_{j1}\rho _{j}E_{j1}^{+}, \end{aligned}$$
(8)

with Kraus operators

$$\begin{aligned} E_{j0}=\left[ \begin{array}{ll} a_{j} &{}\quad b_{j} \\ b_{j} &{}\quad c_{j} \end{array} \right] ,\quad E_{j1}=\left[ \begin{array}{ll} e_{j} &{}\quad f_{j} \\ -d_{j} &{}\quad -e_{j} \end{array} \right] . \end{aligned}$$
(9)

This map that acts on a single atom, along with Eq. (1), allow us in principle to deal with the dynamics of an open quantum system with arbitrary number of atoms when they expose in the independently dissipative environments and driven by classical fields individually.

3 Protection of QFI

In this Section, we study the evolution of QFI of the phase parameters encoded in multi-atom entangled states and examine whether the method proposed in [22] for the protection of QFI can still be valid in the case of quantum entangled probes. To this end, let us shortly review the notion of QFI firstly. The problem of determining the optimal measurement scheme for a particular estimation scenario is non-trivial. Fortunately, QFI provides us a useful tool for estimating the precision of a parameter measurement. The famous quantum Cramér–Rao theorem [23], \(\Delta ^{2}\phi \ge 1/(\nu F_{\phi })\), presents the lower bound of the mean-square error of the unbiased estimator for the parameter \(\phi \). Here \(\nu \) denotes the number of repeated experiments, and the QFI is defined through the symmetric logarithmic derivative as \(F_{\phi }=\mathrm{Tr}(\rho _{\phi }L_{\phi }^{2})\) with \(\partial \rho _{\phi }/\partial \phi =(L_{\phi }\rho _{\phi }+\rho _{\phi }L_{\phi })/2\). By diagonalizing the density matrix as \(\rho _{\phi }=\sum _{n}\lambda _{n}|\psi _{n}\rangle \langle \psi _{n}|\), one can write the QFI as [24]

$$\begin{aligned} F_{\phi }=\sum _{n}\frac{(\partial _{\phi }\lambda _{n})^{2}}{\lambda _{n}}+2\sum _{n\ne m}\frac{(\lambda _{n}-\lambda _{m})^{2}}{\lambda _{n}+\lambda _{m}} |\langle \psi _{n}|\partial _{\phi }\psi _{m}\rangle |^{2}, \end{aligned}$$
(10)

where the first and the second summations involve all sums but \(\lambda _{n}\ne 0\) and \(\lambda _{n}+\lambda _{m}\ne 0\), respectively.

Now we can clarify the problem of protection of QFI for entangled atomic states exposing in noisy environments. We will take the maximal entangled states of two and three atoms as the exemplary examples. Let us begin with the following two-atom entangled states

$$\begin{aligned} |\varPsi \rangle= & {} \frac{1}{\sqrt{2}}\left( |00\rangle +{\hbox {e}}^{\mathrm{i}\phi }|11\rangle \right) , \end{aligned}$$
(11)
$$\begin{aligned} |\varPhi \rangle= & {} \frac{1}{\sqrt{2}}\left( |01\rangle +{\hbox {e}}^{\mathrm{i}\phi }|10\rangle \right) , \end{aligned}$$
(12)

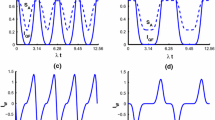
where the phase \(\phi \) is the parameter to be estimated. Though these two states have equivalent coherence from the point of view of the resource theory of coherence [25], they have different asymmetries under time translations [26]. Especially the state \(|\varPhi \rangle \) is more robust than \(|\varPsi \rangle \) in dissipative environments [27]. Employing the results presented in the previous Section, i.e., expressions of Eqs. (1) and (8), we can easily get the time evolutions of these two states. Then the QFI of the phase parameter \(\phi \) encoded in these states can be evaluated via Eq. (10). Due to the complexity of expressions, we thus omit the analytical results and only present the numerical simulations. In Fig. 1a, we plot the evolution of QFI as the dimensionless time \(\gamma _{0}t\) for the case of balanced driving, i.e., \(\varOmega _{1}=\varOmega _{2}\). Through out this paper without special instructions, we always set \(\Delta _{j}=\delta _{j}=0\) and \(\lambda _{j}=0.05\gamma _{0}\) (\(\gamma _{0}\) is assumed to be the same for every atom) for numerical simulations, and the QFI is evaluated at point \(\phi =\pi /2\). It is shown that the evolutions of QFI for the states \(|\varPsi \rangle \) and \(|\varPhi \rangle \) are similar, except for the larger values of QFI for state \(|\varPhi \rangle \) than \(|\varPsi \rangle \) in the cases of no or weak driving fields, which originate from the robustness of \(|\varPhi \rangle \) in the noisy environments [27]. It is clear QFI increases quickly with the increment of Rabi frequencies and acquires good protection when \(\varOmega _{1}=\varOmega _{2}=2\gamma _{0}\). In Fig. 2, we plot the evolution of QFI for the cases of non-balanced driving fields, i.e., \(\varOmega _{1}\ne \varOmega _{2}\), where the upper panel is for state \(|\varPsi \rangle \) and the lower panel for state \(|\varPhi \rangle \). The key feature of this plot is that QFI could not be protected effectively if one of the driving fields that act on the two atoms vanishes or is very weak, no matter how strong the other driving field is (please see Fig. 2a, d, b, e). Only when both the two driving fields become suitably large, can the QFI be protected effectively (red lines in Fig. 2c, f).

Fig. 1
figure 1

Evolution of QFI of the phase parameter versus dimensionless time. The left is for the two atomic states \(|\varPsi \rangle \) (blue lines) and \(|\varPhi \rangle \) (red lines), and the right is for the three atomic state \(|\Upsilon \rangle \). Where \(\Delta _{j}=\delta _{j}=0\), \(\lambda _{j}=0.05\gamma _{0}\), and \(F_{\phi }\) is evaluated at \(\phi =\pi /2\) (Color figure online)

Full size image
Fig. 2
figure 2

Time evolution of QFI of the phase parameter under non-balanced driving for states \(|\varPsi \rangle \) (upper panel) and \(|\varPhi \rangle \) (lower panel), where \(\Delta _{j}=\delta _{j}=0\), \(\lambda _{j}=0.05\gamma _{0}\), and \(F_{\phi }\) is evaluated at \(\phi =\pi /2\)

Full size image

In order to demonstrate the validity of the results for entangled states with more atoms, we consider the case that the phase parameter \(\phi \) is encoded in the GHZ state of three atoms,

$$\begin{aligned} |\Upsilon \rangle =\frac{1}{\sqrt{2}}(|000\rangle +{\hbox {e}}^{\mathrm{i}\phi }|111\rangle ). \end{aligned}$$
(13)

The evolution of QFI of the phase parameter for this state, under the considered model, is shown in Fig. 1b. It is clear that the QFI could not be protected effectively as long as one of the driving fields that act on the three atoms vanishes, no matter how strong the other driving fields are. However, when all the driving fields are not zero and reach certain degrees of strength, then the QFI can be protected effectively (red line in Fig. 1b). We believe that this result is correct for systems with more than three atoms, though we have not revealed the numerical simulations.

In the above discussions, we always assume \(\Delta _{j}=0\), i.e., the classical driving fields are resonant with the transition of atoms. For this design, the effect of the protection of QFI, under given strength of driving fields, is the best. For non-resonant driving, the QFI decreases with the increment of detuning \(\Delta _{j}\). This result is shown in Fig. 3 for the states of Eqs. (11) and (12) of two atoms, where we set \(\gamma _{0}t=50\), \(\delta _{j}=0\), \(\lambda _{j}=0.05\gamma _{0}\) and assume \(\Delta _{1}=\Delta _{2}=\Delta \).

Fig. 3
figure 3

Evolution of QFI of the phase parameter versus dimensionless detuning \(\Delta _{j}/\gamma _{0}\) for the two-atom states \(|\varPsi \rangle \) (left) and \(|\varPhi \rangle \) (right), where \(\delta _{j}=0\), \(\lambda _{j}=0.05\gamma _{0}\), \(\gamma _{0}t=50\), and \(F_{\phi }\) is evaluated at \(\phi =\pi /2\)

Full size image

4 Protect of quantum states

From the discussions of previous Section, we see that the introduction of suitable classical driving fields can effectively protect QFI of the phase parameter encoded in entangled states from damage of environmental noises. This protection is of course local, because it only protects the information about a certain parameter encoded in a quantum state. Now we wonder whether the whole quantum state is also protected? We answer this question by inspecting the evolution of fidelity of the quantum state itself. Fidelity is used to describe the similarity between two quantum states. For convenience, we here define it as \(F=\langle \psi (0)|\rho (t)|\psi (0)\rangle \) with \(|\psi (0)\rangle \) being the initial state and \(\rho (t)\) the evolutional state at time t. In Fig. 4a, we plot the time evolution of fidelity for the initial states of Eqs. (11) and (12) of two-atom system in the case of balanced driving, where the parameters are set to be the same as in Fig. 1a for the purpose of comparison. We can see on the one hand that the evolutions of fidelity and QFI are not consistent. Firstly for zero driving (\(\varOmega _{1}=\varOmega _{2}=0\)), the QFI for initial state \(|\varPhi \rangle \) is always greater than that for \(|\varPsi \rangle \), but the evolution of fidelity is just opposite, and the shapes of the evolutional curves for QFI and fidelity are also not consistent. Next, the evolutions of fidelity and QFI in the case of weak driving fields are also not consistent. For example, the evolutions of QFI for states \(|\varPhi \rangle \) and \(|\varPsi \rangle \) with \(\varOmega _{1}=\varOmega _{2}=0.2\gamma _{0}\) in Fig. 1a take on clearly separable after some time, but the corresponding evolutions of fidelity in Fig. 4a do not occur similar phenomenon. On the other hand however, for suitably large driving fields where the QFI is protected effectively, then the fidelity also acquires good protection (see the curves with \(\varOmega _{1}=\varOmega _{2}=2\gamma _{0}\) in Figs. 1a and 4a).

Fig. 4
figure 4

Time Evolution of fidelity: The left is for the two atomic states \(|\varPsi \rangle \) (blue lines) and \(|\varPhi \rangle \) (red lines), and the right is for the three atomic state \(|\Upsilon \rangle \). Where the parameters are the same as in Fig. 1 (Color figure online)

Full size image
Fig. 5
figure 5

Time evolution of fidelity under non-balanced driving for states \(|\varPsi \rangle \) (upper panel) and \(|\varPhi \rangle \) (lower panel), where the parameters are the same as in Fig. 2

Full size image

In Fig. 5, we plot the time evolution of fidelity for the initial states of Eqs.(11) and (12) in the case of non-balanced driving, where the parameters are set to be the same as in Fig. 2. From this figure, we can see a similar phenomenon as QFI that if one of the driving fields vanishes or is very weak, then the fidelity could not be protected effectively, no matter how strong the other driving is. Only when both the two driving fields reach suitable values, can the fidelity be protected effectively. In addition, by comparing this figure with Fig. 2, we see clearly that the evolutions of fidelity and QFI for this non-balanced driving cases are also not consistent, especially classical driving may sometimes reduces the fidelity (Fig. 5a) which never happens for QFI. However for large driving fields where QFI is protected effectively (red lines in Fig. 2c, f), then the fidelity also gains good protection (red lines in Fig. 5c, f).

We also study the time evolution of fidelity of the three-atom state \(|\Upsilon \rangle \) as in Fig.4b, where the parameters are set to be the same as in Fig. 1b. By comparing, we conclude the similar results: The evolutions of fidelity and QFI are not consistent for weak drivings, but they can be protected effectively when the driving fields that act on all atoms become suitably large. If one of the driving fields vanishes or is very weak, the fidelity could not be protected effectively.

At the end of this section, we point out that the classical driving fields may play important roles in the operation of states of open quantum systems. For example, they can be used to control quantum entanglement [28] and geometric quantum correlation [29], including improving quantum entanglement and controlling its sudden death, controlling the sudden transition of geometric quantum correlation and lengthening its frozen time. Unfortunately, these results were drawn only in the case of single mode environment. Our model has taken into account the effect of multi-mode environment and thus is more realistic. Our research further enriches the application of classical driving fields in the controlling of open quantum systems.

5 Conclusions

In conclusion, we have provided a systematic method for treating the dynamics of a multi-atom system embedded in the independently dissipative environments and driven individually by classical fields. We have simulated numerically the evolutions of QFI and fidelity for the given quantum systems with two and three atoms. We have found that both the QFI of the phase parameters encoded in entangled atomic states and the quantum states themselves can be protected effectively when all the classical fields that drive the atoms reach suitable strength. However, if one of the driving fields vanishes or is very weak, then the protection is seriously restricted and even possibly becomes worse for the maintaining of fidelity. This also implies that balanced driving is the best. We have also shown in the text that the resonant driving (the frequency of classical field equals that of atomic transition) is the most effective.

The protection of QFI of phase parameters encoded in multi-atom entangled states is of very importance, because it directly relates to the problem of quadratic enhancement in precision of quantum parameter estimation, comparing to the case of non-entangled probes. Though our research is the straightforward extension of the previous work based on one atom to multi-atom entangled states, the research itself is meaningful. In fact, entangled systems can take on some characteristics that do not bear for non-entangled one.

The protection of QFI is in principle different from that of quantum states, the former is a kind of local protection which only protects the information of the parameter to be estimated, and the latter is a whole protection which protects all the information encoded in quantum states. Our research suggests that the behaviors of the two protections in the case of weak driving have essential differences: Classical driving is always beneficial to the protection of QFI of phase parameters (see Figs. 1, 2, 3), but to the protection of quantum states it is not always the thing (Figs. 4, 5). However, for suitably strong driving, both QFI and quantum states can be protected effectively.