Introduction

Consider a randomized clinical trial in which an intervention X shows a significant effect on an outcome Y. A question that invariably comes to investigators’ minds is: How and why does the intervention produce the effect, or, more specifically, can the effect of X on Y be attributed to its effect on some intermediate variable Z standing between the two? The reasons we are concerned with such questions are both scientific and practical. Scientifically, mediation tells us “how nature works” and, practically, it enables us to predict behavior under a rich variety of conditions and interventions. For example, an investigator interested in preventing Y may wish to assess the extent to which Y could be prevented by changing an intermediate variable, Z, standing between X and Y, or modifying some intermediate process between X and Z (Bullock et al. 2010; MacKinnon 2008, Ch. 2).

For the past few decades the analysis of mediation has been dominated by linear regression paradigms, most notably the one advanced by Baron and Kenny (1986), which can be stated as follows: To test the contribution of a given mediator Z to the effect of X on Y, first regress Y on X and estimate the regression coefficient R YX , to be equated with the total effect. Second, include Z in the regression and estimate the partial regression coefficient R YX ·Z when Z is “controlled for” (or “conditioned on” or “adjusted for”). The difference between the two slopes, R YX  − R YX ·Z , would then measure the reduction in the total effect due to controlling for Z and should quantify the effect mediated through Z.

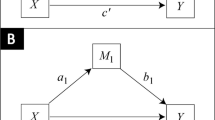
The intuition behind this scheme is demonstrated in Fig. 1a which shows a linear structural equation model governing the causal relationships between X, Y, and Z. If the total effect of X on Y through both pathways is τ = α + βγ, by adjusting for Z, we sever the Z-mediated path and the effect will be reduced to α. The difference between the two regression slopes gives

$$ \tau - \alpha = \beta\gamma $$
(1)

and the product βγ is what we expect the z-mediated effect to be.

Fig. 1
figure 1

a A single mediator Z contributing β × γ to the overall effect. b Multiple mediators, each contributing β i × γ i . The error terms, ϵ 1, ϵ 2, ϵ 3 represent factors omitted from the analysis

Full size image

Alternatively, one can venture to estimate β and γ independently of τ. This is done by first estimating the regression slope of Z on X to get β, then estimating the regression slope of Y on Z controlling for X, which gives us γ; multiplying the two slopes together gives us the mediated effect βγ. The scheme generalizes naturally to multi-path models, as shown in Fig. 1b which represents an opportunity to intervene on three mediating variables, or any subset thereof. The difference between the total effect τ and the effect measured after adjusting for mediator Z i gives the extent to which the indirect path through Z i contributes to the overall effect, τ. Again, this can be estimated either by the difference-in-coefficients or product-of-coefficients method.

The validity of these two methods depends of course on the assumption that the error terms, ϵ 1, ϵ 2, and ϵ 3, are uncorrelated because, otherwise, some of the structural parameters α, β and γ would not be estimable by regression analysis and both the difference-in-coefficients and product-of-coefficients methods would produce biased results. In randomized trials, where ϵ 1 can be identified with the randomization device, we are assured that ϵ 1 is uncorrelated with ϵ 2 and ϵ 3 and, so, the regressional estimates of τ and β will be unbiased. However, randomization does not remove correlations between ϵ 2 and ϵ 3 and, if such exist, adjusting for Z will create spurious correlation between X and Y which will be added to τ and would prevent the proper estimate of γ or α. In other words, the regression coefficient R YZ ·X would no longer equal γ and the difference R YX  − R ZX R YZ ·X would no longer equal α. This follows from the fact that “controlling” or “adjusting” for Z in the analysis (by including Z in the regression equation) does not physically disable the paths going through Z; it merely matches samples with equal Z values, and thus induces spurious correlations among other factors in the analysis (see Cole and Hernán 2002; Pearl 1998; VanderWeele and Vansteelandt 2009).Footnote 1 Such correlations cannot be detected by statistical means and, so, theoretical knowledge must be invoked to identify the sources of these correlations and, if possible, control for common causes (so called “confounders”) of Z and Y.Footnote 2 Remarkably, the regressional estimates of the difference-in-coefficients and the product-of-coefficients will always be equal.Footnote 3

This approach to mediation (often associated with Baron and Kenny) has two major drawbacks. One (mentioned above) is its reliance on the untested assumption of uncorrelated errors, and the second is its reliance on linearity and, in particular, on a property of linear systems called “effect constancy” (or “no interaction”): The effect of one variable on another is independent on the level at which we hold a third. This property does not extend to nonlinear systems; the level at which we control Z would in general modify the effect of X on Y. For example, if the output Y requires both X and Z to be present, then holding Z at zero would disable the effect of X on Y, while holding Z at a high value would enable the latter.

As a consequence, additions and multiplications are not self-evident in nonlinear systems. It may not be appropriate, for example, to define the indirect effect in terms of the “difference” in the total effect, with and without control. Nor would it be appropriate to multiply the effect of X on Z by that of Z on Y (keeping X at some level)—multiplicative compositions demand their justifications. Indeed, all attempts to define mediation by generalizing the difference and product strategies to nonlinear system have resulted in distorted and irreconcilable results (Glynn 2012; MacKinnon et al. 2007a, b; Pearl 2011a).

This paper describes a general estimation formula, first derived in Pearl (2001), which removes these nonlinear barriers and avails mediation analysis to a wide range of new applications, especially those involving categorical data and highly nonlinear processes. The first limitation, the requirement of error independence (or “no unmeasured confounders,” as it is often called) will remain intact, and should be kept in mind throughout our discussion.Footnote 4 Our focus in the sequel, however, will be on crossing the linear-to-nonlinear barrier, using the same causal assumptions that support the standard linear analysis of Baron and Kenny (1986).

Total, Direct and Indirect Effects

Consider the nonlinear version of the mediation model, as depicted in Fig. 2. In the most general case, the corresponding structural equations would have the form:

$$ x = F_1(\epsilon_1) \qquad z = F_2(x,\epsilon_2) \qquad y = F_3(x,z,\epsilon_3) $$
(2)

where X, Y, Z are discrete or continuous random variables, F 1, F 2, and F 3 are arbitrary functions, and ϵ 1, ϵ 2, ϵ 3 represent omitted factors which are assumed to be mutually independent yet arbitrarily distributed. Aside from this qualitative independence assumption, the model also hypothesizes the direction of causal influences, which are often discernible from temporal information or theoretical knowledge. Notably, the model allows for the existence of millions of unobserved subprocesses that make up the functions F 1, F 2, and F 3; these do not alter questions concerning the mediating role of Z.

Fig. 2
figure 2

A generic model depicting mediation through Z with no confounders

Full size image

Since the functions F 1, F 2, and F 3 are unknown to investigators, mediation analysis commences by first defining total, direct and indirect effects in terms of those functions and, then, expressing them in terms of the available data, which we assume is given in the form of random samples (x, y, z) drawn from the joint probability distribution P(x, y, z).

Total Effect

Among the three types of effects considered here, the easiest to define and estimate is the total effect, TE 0,1 which measures the change in Y produced by a unit change in X, say from X = 0 to X = 1. The status of Z need not be specified in this definition, since Z is allowed to track the changes in X and, so, we have for the total effect:

$$ TE_{0,1} (\epsilon_2,\epsilon_3) =F_3[1, F_2(1, \epsilon_2),\epsilon_3] - F_3[0, F_2(0, \epsilon_2),\epsilon_3] $$

where ϵ 2 and ϵ 3 are expected to vary from individual to individual. At the population level, we will define the total effect TE 0,1 to be the expectation of the difference above taken over ϵ 2 and ϵ 3, which (assuming independent errors) gives:

$$ TE_{0,1} = E(Y|X=1) - E(Y|X=0) $$
(3)

where E(Y|X = 1) is the expected value of Y when X equals 1. This difference is none other but the regression slope of Y on X, commonly estimated by OLS, which provides an unbiased estimate of the total effect regardless of the functional form of F 2 and F 3 (p. 72 Pearl 2009).

More generally, however, if we are interested in the total effect of a transition from X = x to X = x′, where x and x′ are any two levels of X (say two dosage levels of a drug), we write:

$$ TE_{x,x'} = E(Y|X=x') - E(Y|X=x). $$
(4)

Clearly, in nonlinear systems, both the baseline X = x and the endpoint X = x′ may play a role in affecting the change of Y.

Controlled and Natural Direct Effects

The idea of estimating the direct effect of X on Y by controlling for Z is applicable to nonlinear models as well since, assuming ϵ 2 and ϵ 3 are independent, conditioning on Z simulates the physical action of “fixing” or “setting” Z at a constant value, z, thus preventing X from transmitting its change along the mediating path X → Z → Y. The resulting estimand is called the “controlled direct effect” (Pearl 2001; Robins and Greenland 1992):

$$ CDE(z) = E(Y| X=1, Z=z) - E(Y| X=0, Z=z) $$
(5)

which is the regression slope of Y on X keeping Z constant at z.Footnote 5

However, the question arises: at what value should we set Z? As remarked earlier, different settings of Z would yield different results. For example, assume that X stands for a drug taken to cure a disease Y. As a side effect, X also stimulates the secretion of an enzyme Z that hastens the process through which the drug acts on the disease. If we fix Z at a high level, the drug will appear highly efficacious, while if we fix Z at a low level, the drug will have only a meager effect. The question remains therefore, at what value of Z should we conduct our analysis if we wish to evaluate the direct effect of the drug on the disease, unmediated by Z?

One can report, of course, the value of CDE(z) for each level Z = z, and let the user choose the value that matches the intervention policy under consideration. In many cases, however, the policy informed by the direct effect is not one where Z is set to a uniform level for all units in the population but, rather, one where the sensitivity of Z to X is suppressed or enhanced, not Z itself. Taking the enzyme example above, a policy maker may be interested in the benefit of developing a cheaper drug, identical to the one studied, but lacking the potential to stimulate enzyme secretion. Absent the mediating effect of Z, the efficacy of the new drug will be determined by whatever level Z attains naturally in the population, varying from individual to individual, not set uniformly by external control.

Under such settings, it is more meaningful to define a notion of direct effect called natural, that does not require setting Z uniformly over the population, but lets it vary from individual to individual. This notion, denoted NDE x,x′(Y) is defined as the expected change in Y induced by changing X from x to x′ while keeping all mediating factors constant at whatever value they would have obtained under X = x, before the transition from x to x′ (Robins and Greenland 1992; Pearl 2001).Footnote 6 This definition of direct-effect invokes the phrase: “at whatever value they would have obtained” which is counterfactual, and thus circumvents ideological prohibitions, upheld by some statisticians, against attributing mediation to nonmanipulable variables (Pearl 2000, 2011b). At the same time, because of its counterfactual character, the natural direct effect cannot be given direct empirical test; there is no way to rerun history and measure subjects response under conditions they have not actually experienced. It has been shown nevertheless (Pearl 2001) that, for the confounding-free model of Fig. 2, the natural direct effect can be estimated from population dataFootnote 7 and is given by:

$$ \begin{array}{rll} &&NDE_{x,x'} (Y) \\ &&\quad= \sum\limits_z [E(Y|X=x',Z=z)-E(Y|X=x,Z=z)]\\ &&\qquad\times\, P(Z=z|X=x) \end{array} $$

or, using a short-hand notation, we write:

$$ NDE_{x,x'}(Y) = \sum\limits_z [E(Y|x',z) -E(Y|x,z)] P(z|x).$$
(6)

The intuition is simple; the natural direct effect is the weighted average of the controlled direct effect, using the pre-transition distribution P(z|x) as a weighting function. Equation 6 can be estimated by a two-step regression, as will be shown in the sequel.

Indirect Effects

Remarkably, the counterfactual definition of the natural direct effect can be turned around and provide an operational definition for the indirect effect—a concept shrouded in mystery and controversy, because it is impossible, by controlling any of the variables in the model, to selectively disable the direct link from X to Y so as to let X influence Y solely via indirect paths. Therefore the indirect effect has no “controlled” interpretation.

The indirect effect, IE, of the transition from x to x′ is defined as the expected change in Y affected by holding X constant, at X = x, and changing Z (for each individual) to whatever value it would have attained had X been set to X = x′. Formally, this counterfactual definition reads:

$$ \begin{aligned}[b] IE_{x,x'}(Y) ={}& E[F_3(x, F_2(x', \epsilon_2), \epsilon_3)]\\ &- E[F_3(x, F_2(x, \epsilon_2), \epsilon_3)] \end{aligned} $$
(7)

which is similar to the definition of the natural direct effect (footnote 6) save for exchanging x with x′ in the first term.

Assuming again the confounding-free model of Fig. 2, the indirect effect defined in Eq. 7 can be reduced to an estimable expression (Pearl 2001), given by:

$$ IE_{x,x'}(Y) = \sum\limits_z E(Y|x,z)[P(z|x')-P(z|x)]. $$
(8)

The intuition here is quite different and unveils a nonparametric version of the product-of-coefficients strategy. The term E(Y|x, z) plays the role of γ in Fig. 1a, for it specifies how Y responds to Z for any fixed x, and the difference P(z|x′) − P(z|x) plays the role of β, for it captures the impact of the transition from x to x′ on the probability of Z. We see that what was a simple product operation in linear systems is here replaced by a composition operator that involves summation over all values of Z.

Equation 8 provides a general formula for mediation effects, applicable to any nonlinear system, any distribution, and any type of variables. Moreover, the formula is readily estimable by regression. Owing to its generality and ubiquity, I have referred to this expression as the “Mediation Formula” (Pearl 2009, 2010).

Not surprising, owed to the nonlinear nature of the model, the relationship between the total, direct and indirect effects is non-additive. The total effect TE of a transition is in fact the difference (not the sum) between the direct effect and the indirect effect of the reverse transition. Formally,

$${TE}_{x,x'}(Y) = NDE_{x,x'}(Y) - IE_{x', x}(Y). $$
(9)

where IE x′,x (Y) stands for the indirect effect of the transition from X = x′ to X = x. In linear systems, where reversal of transitions amounts to negating the signs of their effects, we have IE x,x′ = βγ(x′ − x) = − IE x′,x and the standard additive formula prevails. In general, however, additivity is a rare occurrence and it is the difference formula in Eq. 9 that governs the relation between the total, direct and indirect effects of the transition from x to x′.

In the rest of the paper, we will drop the letter ‘N’ from the acronym NDE, with the understanding that DE stands for the natural direct effect estimand given by Eq. 6, and use the acronyms TE, DE and IE for the total, direct and indirect effects, respectively.

The Mediation Formula: A Simple Solution to a Thorny Problem

This subsection demonstrates how the Mediation Formula of Eq. 8 can be applied in assessing mediation effects in nonlinear models. We will use the standard mediation model of Fig. 2, where all error terms are assumed to be mutually independent, with the understanding that adjustment for appropriate sets of covariates W may be necessary to achieve this independence (see footnote 7), that Z may represent a vector of variables, and that integrals should replace summations when dealing with continuous variables (Imai et al. 2010a).

The Mediation Formula (8) represents the average increase in the outcome Y that the transition from X = x to X = x′ is expected to produce absent any direct effect of X on Y. When the outcome Y is binary (e.g., recovery, or hiring) the ratio (1 − IE/TE) represents the fraction of responding individuals that is owed to direct paths, while (1 − DE/TE) represents the fraction owed to Z-mediated paths. (A response is “owed” to a path if it would not have occurred were it not for the mechanism represented by that path.) These two groups are not necessarily mutually exclusive as can be seen in our enzyme example; individuals who respond only in the presence of both the enzyme and the drug should owe their response to both the direct and indirect paths. In linear systems, where the two fractions correspond to 1 − βγ/ τ and 1 − α/ τ, respectively, they add up to one (see Eq. 1) and the latter goes by the name “proportion mediated” (MacKinnon 2008, p. 82).

Estimating Mediation Effects

The Mediation Formula (8) tells us that IE depends only on the conditional expectation of Y, not on its distribution. It calls therefore for a two-step regression which, in principle, can be performed nonparametrically. In the first step we estimate the conditional expectation

$$ g(x,z) = E(Y|x,z) $$
(10)

for every (x, z) cell. In the second step we fix x and regard g(x, z) as a function g x (z) of Z. We now estimate the conditional expectation of g x (z), conditional on X = x′ and X = x, respectively, and take the difference

$$ IE_{x,x'}(Y) = E_{Z|X}[g_x(z)|x'] - E_{Z|X}[g_x(z)|x]. $$
(11)

Nonparametric estimation is not always practical. When Z consists of a vector of several mediators, the dimensionality of the problem might prohibit the estimation of E(Y|x, z) for every (x, z) cell, and the need may arise to use parametric or semi-parametric approximations. We can then choose an appropriate parametric form for E(Y|x, z) (e.g., linear, logit, probit), estimate the parameters separately (e.g., by regression or maximum likelihood methods), insert the parametric approximation into Eq. 8 and estimate its two conditional expectations (over z) to get the mediated effect (VanderWeele 2009).

Both parametric and nonparametric methods will be demonstrated in the next three subsections.

The Linear Case

Let us examine what the Mediation Formula yields when applied to the linear version of our model, shown in Fig. 1a:

$$ \begin{aligned}[b] &x = a_0 + \epsilon_1, \quad z = b_0 + \beta x + \epsilon_2, \\ &y = c_0 + \alpha x + \gamma z + \epsilon_3 \end{aligned} $$
(12)

with ϵ 1, ϵ 2, and ϵ 3 uncorrelated, zero-mean error terms and a 0, b 0, c 0 the regression intercepts. Computing the conditional expectation in Eq. 8 gives E(Y|x, z) = c 0 + αx + γz, and yields

$$ IE_{x,x'}(Y) = \sum\limits_z (c_0 + \alpha x + \gamma z ) [P(z|x')-P(z|x)] $$
$$ = \gamma [E(Z|x') - E(Z|x)]$$
(13)
$$ = (x'-x) (\beta \gamma) = (x'-x) (\tau - \alpha) $$
(14)

where τ is the slope of the total effect;

$$ \tau = (E(Y|x')-E(Y|x))/(x'-x) = \alpha + \beta \gamma. $$
(15)

We thus obtained the standard expressions for indirect effects in linear systems, which can be estimated either as a difference τ − α of two regression coefficients or as a product βγ of two regression coefficients (see MacKinnon et al. 2007b). These two strategies do not generalize to nonlinear systems (Pearl 2011a) as will be shown next.

Linear Models with Interaction

To understand the difficulty, assume that the correct model behind the data contains a product term xz in the equation for y:

$$ y = c_0 + \alpha x + \gamma z+ \delta xz + \epsilon_3, $$

a nonlinear model explored by many researchers (Jo 2008; Judd and Kenny 1981; Kraemer et al. 2008; MacKinnon 2008). Further assume that we correctly account for this added term and, through diligent analysis on a large data set, we obtain accurate estimates of all parameters in this model. It is still not clear what combinations of parameters measure the direct and indirect effects of X on Y, or, more specifically, how to assess the fraction of the total effect that is explained by mediation and the fraction that is owed to mediation.Footnote 8 In linear analysis, the former fraction is captured by the product βγ/ τ, the latter by the difference (τ − α)/τ (Eq. 14) and the two quantities coincide. In the presence of interaction, however, each fraction demands a separate analysis.

To witness, substituting the nonlinear equation in Eqs. 4, 6 and 8 and assuming x = 0 and x′ = 1, yields the following decomposition:

$$ \begin{aligned} DE_{0,1} & = \alpha + b_0 \delta, \quad IE_{0,1} = \beta \gamma \\ TE_{0,1} & = \alpha + b_0 \delta + \beta (\gamma + \delta) = DE_{0,1} + IE_{0,1} + \beta \delta \end{aligned} $$

We conclude that the portion of output change for which mediation would be sufficient is IE 0,1 = βγ, while the portion for which mediation would be necessary is TE 0,1 − DE 0,1 = βγ + βδ. In other words, the strength of mediation as measured by the size of the indirect effect, βγ, is not the same as that measured by subtracting the direct effect, β(γ + δ). The difference, βδ, is caused by the interaction term δxy and is not affected by α. We further note that, if two populations differ only in the β parameter, they will have the same direct effect, DE, but will differ in the difference TE − IE. The former measures the portion explained by the direct effect and the latter the portion owed to the direct effect. These conclusions are not readily discernible from the structural equations without the guidance of the Mediation Formula and, indeed, they have not been addressed in previous analyses of this interaction model (Jo 2008; Judd and Kenny 1981, 2010; Kraemer et al. 2008; MacKinnon 2008; Judd and Kenny 2010).

We note that, due to interaction, a direct effect can be sustained even when the parameter α vanishes, and a total effect can be sustained even when both the direct and indirect effects vanish. This illustrates that estimating parameters in isolation tells us little about the effect of mediation and, more generally, mediation and moderation are intertwined; each mediator can act as a moderator and each moderator, if affected by X, must act as a mediator as well. Although the degree of moderation can be assessed separately from that of mediation, it is not necessary to base the assessment of one on the assumption that the other is absent, as suggested by some writers (Baron and Kenny 1986; Kraemer et al. 2008).Footnote 9

If the policy evaluated aims to prevent the outcome Y by way of weakening the mediating pathways, the target of analysis should be the difference TE − DE, which measures the highest prevention potential of any such policy. This maximum will be realized when the mediating path is totally suppressed, thus reducing the total effect from TE to DE, hence the difference TE − DE. If, on the other hand, the policy aims to prevent the outcome by weakening the direct pathway, the target of analysis should shift to IE, for TE − IE measures the highest preventive potential of this type of policy.

The Binary Case

The power of the Mediation Formula shines in studies involving categorical variables. To illustrate, we consider the case where all variables are binary; generalizations to multi-valued variables are straightforward. The low dimensionality of the binary case permits a nonparametric solution and an explicit demonstration of how mediation can be estimated directly from the data.

Assume that the observed data is given by Table 1. The factors E(Y|x, z) = g x,z and E(Z|x) = h x can be readily estimated, as shown in the two right-most columns of Table 1 and, when substituted in Eqs. 4, 6 and 8, yield

$$ DE = (g_{1,0}-g_{0,0})(1-h_0) + (g_{1,1}-g_{0,1})h_0 $$
(16)
$$ IE = (h_1-h_0)(g_{0,1}-g_{0,0}) $$
(17)
$$ \begin{array}{rll} TE & =& g_{1,1} h_1 + g_{1,0}(1-h_1)\\ &&-[g_{0,1} h_0 +g_{0,0}(1-h_0)] \end{array} $$
(18)

We see that logistic or probit regression is not necessary; simple arithmetic operations suffice to provide a general solution for any data set, regardless of the data-generating process.

Table 1 Computing the Mediation Formula from empirical data, for the model in Fig. 2, with X, Y, Z binary
Full size table

Numerical Example

To anchor these formulas in a concrete example, let us assume that X = 1 stands for a drug treatment, Y = 1 for recovery, and Z = 1 for the presence of a certain enzyme in a patient’s blood which appears to be stimulated by the treatment. Assume further that the data described in Tables 2 and 3 were obtained in a randomized clinical trial and that all omitted factors (ϵ 2 and ϵ 3 in Fig. 2) are judged to be independent. Our research question is what role does Z play in transmitting the action of X on Y, or, more specifically, to what extent does enhanced secretion of enzyme assist the remedial action of the drug on recovery.

Table 2 The percentage of patients carrying an enzyme (Z = 1) among treatment and non-treatment groups
Full size table
Table 3 The percentage of patients cured in each treatment-enzyme group
Full size table

To further motivate the example, we note that the question above is far from being hypothetical, but comes up often in planning and decision making. For example, suppose someone proposes the development of a much cheaper drug, equal in all respects to the one under study, save for lacking any effect on enzyme production. To determine the cost-benefit tradeoffs of the proposed development, we ask what reduction in efficacy, TE − DE, is expected from the proposed new drug.

Substituting this data into Eqs. 16–18 yields:

$$ \begin{aligned} DE & \!=\! (0.40\!-\!0.20)(1\!-\!0.40) \!+\! (0.80\!-\!0.30) 0.40 \\ &= 0.32 \\ IE & = (0.75-0.40)(0.30-0.20) = 0.035 \\ TE & = 0.80 \times 0.75 + 0.40 \times 0.25 \\ &\quad -(0.30 \times 0.40 + 0.20 \times 0.10) = 0.46 \\ IE/TE & = 0.07 \qquad DE/TE = 0.696 \\ 1- DE/TE &= 0.304 \end{aligned} $$

We conclude that 30.4% of all recoveries is owed to the capacity of the treatment to enhance the secretion of the enzyme,Footnote 10 while only 7% of recoveries would be sustained by enzyme enhancement alone. The enzyme seems to act more as a catalyst for the healing process of X than having a healing action of its own. The policy implication of such a study would be that efforts to develop a cheaper drug, identical to the one studied, but lacking the potential to stimulate enzyme secretion would face a reduction of 30.4% in recovery cases. More decisively, proposals to substitute the drug with one that merely mimics its stimulant action on Z but has no direct effect on Y are bound for failure; the drug evidently has a beneficial effect on recovery that is independent of, though enhanced by, enzyme stimulation.

It is instructive at this point to unfold the intuition behind the IE formula (Eq. 8 or 17) as reflected in our numerical example. Our task is to evaluate the fraction of recoveries that would be sustained solely by the drug enhancement of enzyme secretion absent any other effect the drug may have on the outcome. Table 2 reveals that, under no drug condition, a subject carrying the enzyme has a (0.30 − 0.20) greater chance of recovering than one without the enzyme. Table 3 shows that the drug increases the proportion of the former subjects by (0.75 − 0.40). Therefore, multiplying the increase in enzyme counts (0.75 − 0.40) by the increase in cure rate (0.30 − 0.20) gives IE = 0.035, which is about 7% of the total effect (TE).

Relations to Traditional Approaches

Conventional methods do not define direct and indirect effects in nonlinear settings where the underlying process is unknown, nor do they agree on a principle for defining those effects when the process is known. MacKinnon (2008, Ch. 11), for example, analyzes categorical data using logistic and probit regressions and constructs effect measures using products and differences of the parameters in those models. These measures are not compatible with the causal interpretation of effect measures, even when the parameters are precisely known; IE and DE may be extremely complicated functions of those regression coefficients (Pearl 2011a). Fortunately, those coefficients need not be estimated at all; mediation measures can be estimated directly from the data (Eqs. 16–18), circumventing the parametric analysis altogether.

Attempts to extend the difference and product heuristics to nonparametric analysis have encountered ambiguities that the Mediation Formula can now resolve.

The product-of-coefficients heuristic advises us to multiply the unit effect of X on Z

$$ C_\beta = E(Z|X=1)- E(Z|X=0) = h_1-h_0 $$

by the unit effect of Z on Y given X,

$$ \begin{aligned} C_\gamma &= E(Y|X=x, Z=1)- E(Y|X=x, Z=0) \\ &= g_{x,1}-g_{x,0} \end{aligned} $$

but does not specify on what value we should condition X. Equation 17 resolves this ambiguity: C γ should be conditioned on X = 0 in order for the product C β C γ to yield the correct mediation measure, IE.

The difference-in-coefficients heuristics instructs us to estimate the direct effect coefficient

$$ \begin{aligned} C_\alpha &= E(Y|X=1, Z=z)- E(Y|X=0, Z=z) \\ &= g_{1,z}-g_{0,z} \end{aligned} $$

and subtract it from the total effect, but does not specify on what value we should condition Z. Equation 16 determines that we should condition on both Z = 0 and Z = 1 and take their weighted average, using h 0 = P(Z = 1|X = 0) as the weighting function.

To summarize, the Mediation Formula dictates that, in calculating IE, we should condition on both Z = 1 and Z = 0 and average while, in calculating DE, we should condition on only one value, X = 0, and no average need be taken.

The difference and product heuristics are both legitimate, with each seeking a different effect measure. The difference-in-coefficients heuristics, leading to TE − DE, seeks to measure the fraction of the response for which mediation was necessary. The product-of-coefficients heuristics, leading to IE, seeks to estimate the fraction of response for which mediation would be sufficient. The former informs policies aimed at suppressing mediating pathways; the latter informs those aimed at suppressing direct pathways.

In addition to providing causally sound estimates for mediation effects, the Mediation Formula also enables researchers to evaluate analytically the effectiveness of various parametric specifications relative to any assumed model (Imai et al. 2010a; Pearl 2011a). This type of analytical “sensitivity analysis” could not be applied to mediation analysis, owing to the absence of an objective target quantity that captures the notion of indirect effect in nonlinear systems, free of parametric assumptions. The Mediation Formula of Eq. 8 explicates this target quantity.

The power of the Mediation Formula was recognized by Glynn (2012), Hafeman and Schwartz (2009), Imai et al. (2010a) Kaufman (2010) Mortensen et al. (2009), Petersen et al. (2006), VanderWeele (2009) and VanderWeele and Vansteelandt (2009). Imai et al. (2010c) have further shown that nonparametric identification of mediation effects allows for a flexible estimation strategy and illustrate this with various nonlinear models, quantile regressions, and generalized additive models. Imai et al. (2010b) describe an implementation of these extensions using a convenient R package. Sjölander (2009) provides bound on DE in cases where the confounders between Z and Y cannot be controlled.

The ability of the Mediation Formula to carry us across the linear-nonlinear barrier may suggest that, similar to traditional path analysis in linear systems, we can now assess (nonparametrically) the mediating effect of any chosen path or a bundle of paths in a causal diagram (Alwin and Hauser 1975; Bollen 1989). This turned out not to be the case. Avin et al. (2005) showed that there are many bundles of paths (i.e., subgraphs) in a graph G whose mediation effects cannot be assessed from either observational or experimental studies, even in the absence of unobserved confounders. They proved that the mediation effect of a subgraph SG is estimable if and only if it contains no “broken fork,” that is, a path p 1 from X to some vertex W, and two paths, p 2 and p 3, from W to Y, such that p 1 and p 2 are in SG and p 3 is in G but not in SG.

Clearly, a broken fork condition cannot occur in the graph of Fig. 1b, which enables us to assess the mediation effect of any subset of {Z 1, Z 2, Z 3}. However, if we add the arrow Z 3 → Z 2, then the effect contributed by the path X → Z 3 → Z 2 → Y would not be estimable, because removing the path p 3: Z 3 → Y from the evaluated subgraph, creates a “broken fork.” The controlled direct effect, in contrast, is always estimable when there are no unmeasured confounders and, for any graph and any subset Z, it is given by the truncated-factorization formula (Pearl 2009, p. 72).

Conclusions

Traditional methods of mediation analysis have been limited to linear models or semi-linear regression models, and have produced distorted estimates of “mediation effects” when applied to nonlinear models, or models with categorical variables. This paper offers a causally sound alternative that asymptotically ensures bias-free estimates while making no assumption on the distributional form of the underlying process.Footnote 11

We distinguished between proportion of response cases for which mediation was necessary and those for which mediation would have been sufficient. Both measures play a role in mediation analysis, and are given here a formal representation through the Mediation Formula. This formula is estimable by ordinary regression and provides an objective measure of the extent to which an effect is mediated through a given mediating path, independent of the method chosen for estimating that effect. While the validity of the formulas rests on the same assumptions that are required for standard linear analysis (i.e., no unmeasured confounders), their general appeal to nonlinear systems, continuous and categorical variables, and arbitrary complex interactions render them a powerful tool for the assessment of causal pathways in many of the health related sciences.