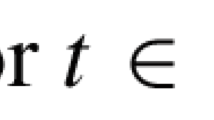Existence of positive solutions of delay dynamic equations

Abstract

In this article we study the existence of positive solutions for a dynamic equations on time scales. The main tool employed here is the Schauder’s fixed point theorem. The asymptotic properties of solutions are also treated. The results obtained here extend the work of Dorociakova and Olach (Tatra Mt Math Publ 43:63–70, 2009). Three examples are also given to illustrate this work.

1 Introduction

In 1988, Stephan Hilger [9] introduced the theory of time scales (measure chains) as a means of unifying discrete and continuum calculi. Since Hilger’s initial work there has been significant growth in the theory of dynamic equations on time scales, covering a variety of different problems; see [6,7,8, 12] and references therein.

Let $\mathbb {T}$ be a time scale such that $t_{0}\in \mathbb {T}$. In this article, we are interested in the analysis of qualitative theory of positive solutions of delay dynamic equations. Motivated by the papers [1,2,3,4,5, 8, 10, 11, 13] and the references therein, we consider the following delay dynamic equation

$$\begin{aligned} x^{\triangle }\left( t\right) +p\left( t\right) x^{\sigma }\left( t\right) +q\left( t\right) x\left( \tau \left( t\right) \right) =0,\,\,t\ge t_{0}, \end{aligned}$$

(1.1)

Throughout this paper we assume that $p:[t_{0},\infty )\cap \mathbb {T} \rightarrow \mathbb {R}$ and $q:[t_{0},\infty )\cap \mathbb {T}\rightarrow \left( 0,\infty \right)$ are rd-continuous, $\tau :\mathbb {T\rightarrow T}$ is increasing so that the function $x\left( \tau \left( t\right) \right)$ is well defined over $\mathbb {T}$. We also assume that $\tau :[t_{0},\infty )\cap \mathbb {T} \rightarrow [0,\infty )\cap \mathbb {T}$ is rd-continuous, $\tau (t)<t$ and $\lim _{t\rightarrow \infty }\tau (t)=\infty$. To reach our desired end we have to transform (1.1) into an integral equation and then use Schauder’s fixed point theorem to show the existence of solutions which are bounded by positive functions. The asymptotic properties of solutions are also treated.

The organization of this paper is as follows. In Sect. 2, we introduce some notations and definitions, and state some preliminary material needed in later sections. We will state some facts about the exponential function on a time scale as well as the Schauder’s fixed point theorem. For details on Schauder theorem we refer the reader to [14]. In Sect. 3, we establish our main results for positive solutions by applying the Schauder’s fixed point theorem. In Sect. 4, we present the asymptotic properties of solutions. In Sect. 5, we give three examples to illustrate our results. The results presented in this paper extend the main results in [8].

2 Preliminaries

A time scale is an arbitrary nonempty closed subset of real numbers. The study of dynamic equations on time scales is a fairly new subject, and research in this area is rapidly growing (see [1,2,3,4,5, 10, 11, 13] and papers therein). The theory of dynamic equations unifies the theories of differential equations and difference equations. We suppose that the reader is familiar with the basic concepts concerning the calculus on time scales for dynamic equations. Otherwise one can find in Bohner and Peterson books [6, 7, 12] most of the material needed to read this paper.

Definition 2.1

([6]). A function $f:\mathbb {T}\rightarrow \mathbb {R}$ is called rd-continuous provided it is continuous at every right-dense point $t\in \mathbb {T}$ and its left-sided limits exist, and is finite at every left-dense point $t\in \mathbb {T}$. The set of rd-continuous functions $f:\mathbb {T}\rightarrow \mathbb {R}$ will be denoted by

$$\begin{aligned} C_{rd}=C_{rd}(\mathbb {T)=}C_{rd}(\mathbb {T}, \mathbb {R} \mathbb {)}. \end{aligned}$$

Definition 2.2

([6]). For $f:\mathbb {T}\rightarrow \mathbb {R}$, we define $f^{\Delta }(t)$ to be the number (if it exists) with the property that for any given $\varepsilon >0$, there exists a neighborhood U of t such that

$$\begin{aligned} \left| \left( f(\sigma (t)\right) -f(s))-f^{\Delta }(t)\left( \sigma (t)-s\right) \right| <\varepsilon \left| \sigma (t)-s\right| \text { for all }s\in U. \end{aligned}$$

The function $f^{\Delta }:\mathbb {T}^{k}\rightarrow \mathbb {R}$ is called the delta (or Hilger) derivative of f on $\mathbb {T}^{k}$.

Definition 2.3

([6]). A function $p:\mathbb {T}\rightarrow \mathbb {R}$ is called regressive provided $1+\mu (t)p(t)\ne 0$ for all $t\in \mathbb {T}$. The set of all regressive and rd-continuous functions p :  $\mathbb {T} \rightarrow \mathbb {R}$ will be denoted by $\mathcal {R}=\mathcal {R}(\mathbb {T}, \mathbb {R} \mathbb {)}$. We define the set $\mathcal {R}^{+}$ of all positively regressive elements of $\mathcal {R}$ by

$$\begin{aligned} \mathcal {R}^{+}=\mathcal {R}^{+}(\mathbb {T}, \mathbb {R} \mathbb {)=\{}p\in \mathcal {R}:1+\mu (t)p(t)>0,\ \forall t\in \mathbb {T}\}. \end{aligned}$$

Definition 2.4

([6]). Let $p\in \mathcal {R}$, then the generalized exponential function $e_{p}$ is defined as the unique solution of the initial value problem

$$\begin{aligned} x^{\Delta }(t)=p(t)x(t),\,\,x(s)=1,\text { where }s\in \mathbb {T}\text {.} \end{aligned}$$

An explicit formula for $e_{p}(t,s)$ is given by

$$\begin{aligned} e_{p}(t,s)=\exp \left( \int _{s}^{t}\xi _{\mu (v)}(p(v))\Delta v\right) ,\text { for all }s,t\in \mathbb {T}, \end{aligned}$$

with

$$\begin{aligned} \xi _{h}(v)=\left\{ \begin{array} [c]{ll} \frac{\log (1+hv)}{h}&{}\text { if }h\ne 0,\\ v&{}\,\,\text { if }h=0, \end{array} \right. \end{aligned}$$

where $\log$ is the principal logarithm function.

Lemma 2.5

([6]). Let $p,q\in \mathcal {R}$. Then

• (i) $e_{0}(t,s)\equiv 1$ and $e_{p}(t,t)\equiv 1$,

• (ii) $e_{p}(\sigma (t),s)=(1+\mu (t)p(t))e_{p}(t,s)$,

• (iii) $\frac{1}{e_{p}(t,s)}=e_{\ominus p}(t,s)$ where, $\ominus p(t)=-\frac{p(t)}{1+\mu (t)p(t)}$,

• (iv) $e_{p}(t,s)=\frac{1}{e_{p}(s,t)}=e_{\ominus p}(s,t)$,

• (v) $e_{p}(t,s)e_{p}(s,r)=e_{p}(t,r)$,

• (vi) $\left( \frac{1}{e_{p}(\cdot ,s)}\right) ^{\Delta }=-\frac{p(t)}{e_{p}^{\sigma }(\cdot ,s)}$.

Lemma 2.6

([1]). If $p\in \mathcal {R}^{+}$, then

$$\begin{aligned} 0<e_{p}(t,s)\le \exp \left( \int _{s}^{t}p(v)\Delta v\right) ,\ \forall t\in \mathbb {T}. \end{aligned}$$

The proof of the main results in the next section is based upon an application of the following Schauder’s fixed point theorem.

Theorem 2.7

(Schauder’s fixed point theorem [14]). Let $\Omega$ be a closed, convex and nonempty subset of a Banach space X. Let $S:\Omega \rightarrow \Omega$ be a continuous mapping such that $S\Omega$ is a relatively compact subset of X. Then S has at least one fixed point in $\Omega$. That is there exists an $x\in \Omega$ such that $Sx=x$.

3 Existence of positive solutions

In this section we shall investigate the existence of positive solutions for equation (1.1). The main result is in the following theorem.

Theorem 3.1

Suppose that for $t\ge t_{0}$

$$\begin{aligned} 1<k_{1}\le k_{2},\,\,p(t)+k_{1}q(t)\ge 0, \end{aligned}$$

and

$$\begin{aligned} {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{1}q(s)\right) \right] \Delta s&\ge \log k_{1},\nonumber \\ {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{2}q(s)\right) \right] \Delta s&\le \log k_{2}. \end{aligned}$$

(3.1)

Then equation (1.1) has a solution which is bounded by positive functions.

Proof

We choose $T\ge t_{0}+\tau (T)$ and set

$$\begin{aligned} u(t)&=\exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{2}q(s)\right) \right] \Delta s\right) ,\\ v(t)&=\exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{1}q(s)\right) \right] \Delta s\right) ,\quad t\ge T. \end{aligned}$$

Let $C_{rd}\left( \left[ t_{0},\infty \right) , \mathbb {R} \right)$ be the set of all bounded rd-continuous functions with the norm

$$\begin{aligned} \left\| x\right\| =\sup _{t\ge t_{0}}\left| x(t)\right| <\infty . \end{aligned}$$

Then $C_{rd}\left( \left[ t_{0},\infty \right) , \mathbb {R} \right)$ is a Banach space. We define a close, bounded and convex subset $\Omega$ of $C_{rd}\left( \left[ t_{0},\infty \right) , \mathbb {R} \right)$ as follows

Define the map $S:\Omega \rightarrow C_{rd}\left( \left[ t_{0},\infty \right) , \mathbb {R} \right)$ as follows

$$\begin{aligned} (Sx)(t)=\left\{ \begin{array} [c]{ll} \exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+q(s)\frac{x(\tau (s))}{x^{\sigma } (s)}\right) \right] \Delta s\right) ,&{}t\ge T,\\ 1, &{}\tau (T)\le t\le T. \end{array} \right. \end{aligned}$$

We shall show that for any $x\in \Omega$ we have $Sx\in \Omega$. For every $x\in \Omega$ and $t\ge T$ we get

$$\begin{aligned} (Sx)(t)\le \exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{1}q(s)\right) \right] \Delta s\right) =v(t). \end{aligned}$$

Furthermore for $t\ge T$ we have

$$\begin{aligned} (Sx)(t)\ge \exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{2}q(s)\right) \right] \Delta s\right) =u(t). \end{aligned}$$

For $t\in \left[ \tau (T),T\right]$ we obtain $(Sx)(t)=1$. Further for every $x\in \Omega$ and $\tau (t)\ge T$ we get

$$\begin{aligned} (Sx)(\tau (t))&=\exp \left( {\displaystyle \int _{T}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+q(s)\frac{x(\tau (s))}{x^{\sigma } (s)}\right) \right] \Delta s\right) \nonumber \\&=(Sx)(\sigma (t))\exp \left( {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+q(s)\frac{x(\tau (s))}{x^{\sigma } (s)}\right) \right] \Delta s\right) . \end{aligned}$$

(3.2)

With regard to (3.1) and (3.2) we have

$$\begin{aligned} (Sx)(\tau (t))&\le (Sx)(\sigma (t))\exp \left( {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{2}q(s)\right) \right] \Delta s\right) \\&\le k_{2}(Sx)(\sigma (t)),\quad \tau (t)\ge T, \end{aligned}$$

and

$$\begin{aligned} (Sx)(\tau (t))&\ge (Sx)(\sigma (t))\exp \left( {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{1}q(s)\right) \right] \Delta s\right) \\&\ge k_{1}(Sx)(\sigma (t)),\quad \tau (t)\ge T. \end{aligned}$$

For $\tau (T)\le \tau (t)\le T$ we obtain $(Sx)(\tau (t))=1$. Thus we have proved that $Sx\in \Omega$ for any $x\in \Omega$.

We now show that S is continuous. Let $x_{i}\in \Omega$ be such that $x_{i}\rightarrow x$ as $i\rightarrow \infty$. Because $\Omega$ is closed, $x\in \Omega$. For $t\ge T$ we have

$$\begin{aligned}&\left| (Sx_{i})(t)-(Sx)(t)\right| \\&\quad =\left| \exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+q(s)\frac{x_{i}(\tau (s))}{x_{i}^{\sigma }(s)}\right) \right] \Delta s\right) \right. \\&\qquad \left. -\exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+q(s)\frac{x(\tau (s))}{x^{\sigma } (s)}\right) \right] \Delta s\right) \right| . \end{aligned}$$

So we conclude that

$$\begin{aligned} \lim _{i\rightarrow \infty }\left\| Sx_{i}-Sx\right\| =0. \end{aligned}$$

This means that S is continuous.

The family of functions $\left\{ Sx:x\in \Omega \right\}$ is uniformly bounded on $\left[ \tau (T),\infty \right)$. It follows from the definition of $\Omega$. This family is also equicontinuous on $\left[ \tau (T),\infty \right)$. Then by Arsela–Ascoli theorem the $S\Omega$ is relatively compact subset of $C_{rd}\left( \left[ t_{0}, \infty \right) , \mathbb {R} \right)$. By Theorem 2.7 there is an $x_{0}\in \Omega$ such that $Sx_{0}=x_{0}$. We see that $x_{0}$ is a positive solution of the Eq. (1.1). The proof is complete. $\square$

Corollary 3.2

Suppose that $k>1$, $p(t)+kq(t)\ge 0$ and

$$\begin{aligned} {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+kq(s)\right) \right] \Delta s=\log k,\quad t\ge t_{0}. \end{aligned}$$

Then Eq. (1.1) has a solution

$$\begin{aligned} x(t)=\exp \left( {\displaystyle \int _{T}^{t}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+kq(s)\right) \right] \Delta s\right) , \quad t\ge T. \end{aligned}$$

4 Asymptotic properties

In this section some asymptotic properties of positive solutions of (1.1) are treated.

Theorem 4.1

Suppose that $0<\alpha <1$, $p(t)+\alpha q(t)\ge 0,$ $t\ge t_{0}$ and

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{k-\alpha }\int _{\tau (t)}^{\sigma (t)}\xi _{\mu (s)}\left[ (k-\alpha )q(s)\right] \Delta s>\max _{k>1}\frac{\log k}{k-\alpha }. \end{aligned}$$

(4.1)

Then Eq. (1.1) has not a positive solution x with the property

$$\begin{aligned} x(\tau (t))\ge kx^{\sigma }(t), \,\,t\ge T\ge t_{0},\,\, k\in \left( 1,\infty \right) . \end{aligned}$$

Proof

Assume to the contrary that (1.1) has a positive solution x with the property $x(\tau (t))\ge kx^{\sigma }(t),$ $t\ge T\ge t_{0}$ for some $k\in \left( 1,\infty \right)$. Then

$$\begin{aligned} x^{\Delta }(t)+q(t)\left[ -\alpha x^{\sigma }(t)+x(\tau (t))\right]&\le 0,\nonumber \\ x^{\Delta }(t)+q(t)\left[ -\alpha +\frac{x(\tau (t))}{x^{\sigma }(t)}\right] x^{\sigma }(t)&\le 0,\nonumber \\ x^{\Delta }(t)+q(t)\left[ k-\alpha \right] x^{\sigma }(t)&\le 0,\nonumber \\ x^{\Delta }(t)e_{q(k-\alpha )}(t,s)+x^{\sigma }(t)q(t)\left[ k-\alpha \right] e_{q(k-\alpha )}(t,s)&\le 0,\quad t\ge T. \end{aligned}$$

(4.2)

Integrating the last inequality we get

$$\begin{aligned}&{\displaystyle \int _{\tau (t)}^{\sigma (t)}} \left( x(v)e_{q(k-\alpha )}(v,s)\right) ^{\Delta }\Delta v \begin{array} [c]{c} \le \end{array} 0,\\&\frac{x(\tau (t))}{x^{\sigma }(t)} \begin{array} [c]{c} \ge \end{array} e_{q(k-\alpha )}(\sigma (t),\tau (t)),\\&\frac{x(\tau (t))}{x^{\sigma }(t)} \begin{array} [c]{c} \ge \end{array} \exp \left( \int _{\tau (t)}^{\sigma (t)}\xi _{\mu (s)}\left[ (k-\alpha )q(s)\right] \Delta s\right) ,\quad t \begin{array} [c]{c} \ge \end{array} T. \end{aligned}$$

With regard to condition (4.1) there exists a constant $c>0$ such that

$$\begin{aligned} \frac{1}{k-\alpha }\int _{\tau (t)}^{\sigma (t)}\xi _{\mu (s)}\left[ (k-\alpha )q(s)\right] \Delta s\ge c>\max _{k>1}\frac{\log k}{k-\alpha },\quad t\ge t_{1}\ge T. \end{aligned}$$

(4.3)

Then we obtain

$$\begin{aligned} \frac{x(\tau (t))}{x^{\sigma }(t)}\ge \exp \left( (k-\alpha )c\right) =c_{1},\quad t\ge t_{1}, \end{aligned}$$

where $c_{1}>k$. Repeating this process by using (4.2) we get

$$\begin{aligned} \frac{x(\tau (t))}{x^{\sigma }(t)}\ge \exp \left( (c_{i}-\alpha )c\right) =c_{i+1},\quad t\ge t_{i+1}, \end{aligned}$$

(4.4)

where $c_{i+1}>c_{i},$ $i=1,2,\ldots$, since $(c_{i}-\alpha )c>\log c_{i}$. We see that $c_{i}\rightarrow \infty$ as $i\rightarrow \infty$. On the other hand for given $\epsilon >0$ and sufficiently large i we have

$$\begin{aligned} c_{i+1}<c_{i}+\epsilon ,\quad (c_{i}-\alpha )c=\log c_{i+1}\le \log (c_{i}+\epsilon ),\quad c\le \frac{\log (c_{i}+\epsilon )}{c_{i}-\alpha }, \end{aligned}$$

which is a contradiction with (4.3) far small $\epsilon >0$.

According to (4.3) for arbitrary $t\ge t_{1}$ we can choose $t^{*}>t$ such that

$$\begin{aligned}&\int _{\tau (t^{*})}^{\sigma (t)}\xi _{\mu (s)}\left[ (k-\alpha )q(s)\right] \Delta s\ge \frac{c}{2}(k-\alpha )\text { and }\int _{\sigma (t)}^{\sigma (t^{*})}\xi _{\mu (s)}\left[ (k-\alpha )q(s)\right] \Delta s\\&\quad \ge \frac{c}{2} (k-\alpha ). \end{aligned}$$

For Lemma 2.6 we have

$$\begin{aligned} \int _{\tau (t^{*})}^{\sigma (t)}q(s)\Delta s\ge \frac{1}{k-\alpha }\int _{\tau (t^{*})}^{\sigma (t)}\xi _{\mu (s)}\left[ (k-\alpha )q(s)\right] \Delta s\ge \frac{c}{2}, \end{aligned}$$

and

$$\begin{aligned} \int _{\sigma (t)}^{\sigma (t^{*})}q(s)\Delta s\ge \frac{1}{k-\alpha } \int _{\sigma (t)}^{\sigma (t^{*})}\xi _{\mu (s)}\left[ (k-\alpha )q(s)\right] \Delta s\ge \frac{c}{2}. \end{aligned}$$

Then

$$\begin{aligned} -x^{\Delta }(t)\ge -\alpha q(t)x^{\sigma }(t)+q(t)x(\tau (t)), \end{aligned}$$

Integrating the inequality from $\tau (t^{*})$ to $\sigma (t)$ and then from $\sigma (t)$ to $\sigma (t^{*})$ and using the non increasing character of x we obtain

$$\begin{aligned} x(\tau (t^{*}))-x^{\sigma }(t)&\ge \int _{\tau (t^{*})}^{\sigma (t)}q(s)x(\tau (s))\Delta s-\alpha \int _{\tau (t^{*})}^{\sigma (t)} q(s)x^{\sigma }(s)\Delta s\\&\ge \int _{\tau (t^{*})}^{t}q(s)x(\tau (s))\Delta s-\alpha \int _{\tau (t^{*})}^{\sigma (t)}q(s)x(s)\Delta s\\&\ge \frac{c}{2}x(\tau (t))-\frac{c\alpha }{2}x(\tau (t^{*})),\\ x(\tau (t^{*}))&\ge \frac{c}{2+c\alpha }x(\tau (t)),\quad t\ge t_{1}. \end{aligned}$$

Further we have

$$\begin{aligned} x^{\sigma }(t)-x^{\sigma }(t^{*})&\ge \int _{\sigma (t)}^{\sigma (t^{*} )}q(s)x(\tau (s))\Delta s-\alpha \int _{\sigma (t)}^{\sigma (t^{*} )}q(s)x^{\sigma }(s)\Delta s\\&\ge \int _{\sigma (t)}^{t^{*}}q(s)x(\tau (s))\Delta s-\alpha \int _{\sigma (t)}^{\sigma (t^{*})}q(s)x(s)\Delta s\\&\ge \frac{c}{2}x(\tau (t^{*}))-\frac{c\alpha }{2}x^{\sigma }(t),\\ x^{\sigma }(t)&\ge \frac{c}{2+c\alpha }x(\tau (t^{*})),\quad t\ge t_{1}. \end{aligned}$$

It follows that

$$\begin{aligned} x^{\sigma }(t)\ge \frac{c}{2+c\alpha }x(\tau (t^{*}))\text { and } x(\tau (t^{*}))\ge \frac{c}{2+c\alpha }x(\tau (t)),\quad t\ge t_{1}. \end{aligned}$$

Hence we have

$$\begin{aligned} \frac{x(\tau (t))}{x^{\sigma }(t)}\le \left( \frac{2+c\alpha }{c}\right) ^{2},\quad t\ge t_{1.} \end{aligned}$$

This is contradiction with (4.4). The proof of Theorem 4.1 is complete. $\square$

5 Examples

Example 5.1

Consider the delay dynamic equation on $\mathbb {T=}\,\, h\mathbb {Z}=\left\{ hk,\ k\in \mathbb {Z}\right\}$ where $h>1$,

$$\begin{aligned} x^{\Delta }(t)+\frac{3}{10h}x^{\sigma }(t)+\frac{1}{6h}x(t-h)=0,\ \ \ t\ge h. \end{aligned}$$

(5.1)

If we take $k_{1}=\frac{3}{2}$ and $k_{2}=6$, we get

$$\begin{aligned}&{\displaystyle \int _{\sigma (t)}^{t-h}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{1}q(s)\right) \right] \Delta s\\&= {\displaystyle \int _{t-h}^{t+h}} \frac{1}{h}\log \left[ 1+h\left( \frac{3}{10h}+\frac{3}{2}\frac{1}{6h}\right) \right] \Delta s\\&=\frac{1}{h}\log \left( \frac{31}{20}\right) {\displaystyle \int _{t-h}^{t+h}} \Delta s\\&=2\log \left( \frac{31}{20}\right) \ge \log k_{1}, \end{aligned}$$

and

$$\begin{aligned}&{\displaystyle \int _{\sigma (t)}^{t-h}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{2}q(s)\right) \right] \Delta s\\&= {\displaystyle \int _{t-h}^{t+h}} \frac{1}{h}\log \left[ 1+h\left( \frac{3}{10h}+6\frac{1}{6h}\right) \right] \Delta s\\&= {\displaystyle \int _{t-h}^{t+h}} \frac{1}{h}\log \left( \frac{23}{10}\right) \Delta s\\&=2\log \left( \frac{23}{10}\right) \le \log k_{2}. \end{aligned}$$

Then all conditions of Theorem 3.1 are satisfied and Eq. (5.1) has a solution which is bounded by functions

$$\begin{aligned} u(t)&=\exp \left( {\displaystyle \int _{h}^{t}} \frac{1}{h}\log \left( \frac{23}{10}\right) \Delta s\right) =\exp \left( \log \left( \frac{23}{10}\right) \left( \frac{t-h}{h}\right) \right) ,\\ v(t)&=\exp \left( {\displaystyle \int _{h}^{t}} \frac{1}{h}\log \left( \frac{31}{20}\right) \Delta s\right) =\exp \left( \log \left( \frac{31}{20}\right) \left( \frac{t-h}{h}\right) \right) ,\quad t\ge h. \end{aligned}$$

Example 5.2

Consider the delay dynamic equation on $\mathbb {T=Z},$

$$\begin{aligned} x^{\Delta }(t)+(1-\log 2)x^{\sigma }(t)+\frac{\log 2}{16}x(t-3)=0,\quad t\ge 3. \end{aligned}$$

(5.2)

If we take $k=16$, we have

$$\begin{aligned}&{\displaystyle \int _{\sigma (t)}^{t-3}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+kq(s)\right) \right] \Delta s\\&= {\displaystyle \int _{t-3}^{t+1}} \log \left[ 1+\left( 1-\log 2+16\frac{\log 2}{16}\right) \right] \Delta s\\&=4\log 2=\log k,\quad t\ge 3. \end{aligned}$$

Then all conditions of Corollary 3.2 are satisfied and Eq. (5.2) has a solution

$$\begin{aligned} x(t)=\exp (-\log 2(t-3)),\quad t\ge 3. \end{aligned}$$

Example 5.3

Consider the delay dynamic equation on $\mathbb {T= \mathbb {R} },$

$$\begin{aligned} x^{\Delta }(t)+\frac{1}{7t}x(t)+\frac{2}{7t}x\left( \frac{2}{3}t\right) =0,\quad t\ge 1. \end{aligned}$$

(5.3)

If we take $k_{1}=\frac{6}{5}$ and $k_{2}=3$ we obtain

$$\begin{aligned} {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{1}q(s)\right) \right] \Delta s&= {\displaystyle \int _{\frac{2}{3}t}^{t}} \left( \frac{1}{7s}+\frac{6}{5}\frac{2}{7s}\right) ds\ge \log k_{1},\\ {\displaystyle \int _{\sigma (t)}^{\tau (t)}} \xi _{\mu (s)}\left[ \ominus \left( p(s)+k_{2}q(s)\right) \right] \Delta s&= {\displaystyle \int _{\frac{2}{3}t}^{t}} \left( \frac{1}{7s}+3\frac{2}{7s}\right) ds\le \log k_{2}. \end{aligned}$$

Then all conditions of Theorem 3.1 are satisfied and Eq. (5.3) has a positive solution.