Multiple access interference cancelation technique in optical CDMA systems

Abstract

This paper presents a simple and efficient multiple access interference (MAI) cancelation technique in optical code division multiple access (OCDMA) system. The proposed technique is based on hybrid frequency shift keying (FSK) with an enhanced modified prime code as a signature sequence for coding techniques. Coherent FSK modulation along with incoherent demodulation using Arrayed-Waveguide Grating has been examined in the transceiver structure. In the proposed technique, a reference signal is constructed by using one of the addressed spreading sequences, and MAI cancelation is performed by subtracting the reference signal from the received signal of the desired user. The performance of the proposed FSK-OCDMA system is compared with the performance of the existing pulse position modulation (PPM)–OCDMA system. The simulation results reveal that the bit-error rate performance of the proposed technique is superior to the performance of the pulse position modulation (PPM) technique. Also, the results indicate that the proposed technique is very power efficient, and when the bit rate is constant, the network capacity can be expanded to accommodate a large number of simultaneous active users with low error rate. Moreover, the proposed technique simplifies the hardware of the receiver design.

1 Introduction

Nowadays, OCDMA systems are highly interesting as they offer several advantages such as high speed, huge bandwidth, asynchronous accesses with no waiting time, privacy, secure transmissions, ability to support variable bit rates and bursty traffic. Moreover, they provide high scalability of the optical network [1]. However, the main problem of OCDMA is the MAI, which is the ultimate limit for the system performance [2].

Several MAI cancelation techniques have been proposed in OCDMA systems such as the optical parallel interference cancelation (OPIC) technique [3]. The grouping property of modified prime sequences has been utilized as a means of interference cancelation in optical PPM-CDMA systems. Despite the excellent results achieved with this technique, it suffers from the receiver complexity problem. Also, the special properties of modified prime codes (MPCs) were utilized for interference cancelation in synchronous PPM-OCDMA systems. Unfortunately, this comes at the price of a more complexity in receiver architecture.

Both PPM and FSK are two popular modulation techniques in OCDMA networks. The PPM technique has been reported as an efficient technique to enhance the performance of the system, but it has some limitations for increasing the pulse position multiplicity $M$. Increasing $M$ gives a better performance, but adds more complexity to the system design.

In this paper, an interference cancelation technique is presented and analyzed using hybrid FSK-OCDMA (coherent modulation and incoherent demodulation) with an EMPC as a signature sequence. Due to the various prime code families introduced in [4], it has been noticed that the code length and accordingly correlation properties still need to be enhanced. Coherent FSK modulation along with incoherent demodulation using AWG is examined in the transceiver structure.

In the suggested technique, a reference signal is constructed using one of the addressed spreading sequences, and MAI cancelation is performed by subtracting the reference signal from the received signal of the desired user. The main objectives are to achieve more MAI cancelation, to get lower BER, and to simplify the receiver design as compared to that of the PPM technique.

M-array FSK modulation is characterized by the modulation index. By the variation of modulation index, different FSK modulation formats can be realized. The differences between FSK formats are reflected in the optical signal spectra, whereby a smaller modulation index enables more compact optical spectra. FSK is privileged by high-phase noise insensitivity and high-power efficiency. So, we have exploited these features and implemented a simple interference cancelation technique using hybrid FSK-OCDMA with an EMPC as a signature sequence.

M-array FSK allocates $M$ symbols to the corresponding $M$ wavelengths; whereas M-array PPM allocates the symbols to the slot positions. The modulated signal is then transmitted after being multiplied by the spreading code in the OCDMA via optical tapped delay lines (OTDLs). Then, the optical pulse sequences transmitted from users are multiplexed in the star passive optical network (SPON) couplers, and hence transmitted over fiber to the destination. At the receiver, in order to obtain the intended data from the received data, de-spreading is performed in a de-correlator, which consists of an OTDL with inverse tap coefficients. Then, the desired data are extracted in the demodulator based on the modulation technique.

In M-array PPM, the probability of overlapping pulses can be reduced by increasing the number of symbols $M$, because each symbol is allocated to a corresponding one slot among $M$ slots. On the other hand, for the proposed technique, $\log _2 M$encoded bits of data are assigned to $M$ frequencies (wavelengths) for all users as a result of M-array source coding. Therefore, this leads to a higher spectral efficiency, no wavelength-assignment, and a fewer set of wavelengths [5]. Since the number of slots in a frame is independent of the number of symbols, the bit rate of FSK does not decrease as the number of symbols increases. When the number of slots in a frame is $j$ (which corresponds to the repetition index of the tunable laser diode), the bit rate of M-array FSK becomes $M/j, ( j < M )$, times higher than that of M-array PPM. Also, the probability of having interference for M-array FSK is $1/{\left( {jM} \right) }$, while the corresponding probability for M-array PPM is $1/M$. Hence, the probability of having interference is reduced with FSK. That is why the FSK is adopted in the proposed approach.

This paper is organized as follows. Section 2 is dedicated for the proposed transceiver architecture. The BER performance analysis is discussed in Sect. 3. The simulation results and the discussion are given in Sect. 4. Finally, the concluding remarks are highlighted in Sect. 5.

2 Proposed transceiver architecture

A simple MAI cancelation technique in OCDMA systems is presented. It is based on a hybrid FSK technique and incorporates an EMPC as a signature sequence. Coherent FSK modulation along with incoherent demodulation using AWG is examined in the transceiver structure.

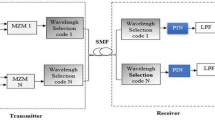
Figure 1 shows the signaling format for an M-array FSK pulse series assuming $M = 4$, where four wavelengths from $\lambda _0\,\hbox {to}\,\lambda _3$ are assigned to contain 2-bit information such as 00, 01, 10 and 11, respectively. $j$ is the repetition index, which corresponds to the number of slots between two subsequent transmitted optical pulses by a tunable laser diode (TLD). At the transmitter of the proposed transceiver illustrated in Fig. 2, the data are divided into frames, each frame consists of $j$ slots, and each slot consists of $P^{2}+2P$ chips. When $j>1$, one slot is selected for data transmission among $j$ slots in a frame. The subsequent data are placed on the same slot positions in the following frames. The data are placed on the desired slot in a frame, and then it is inputted to the TLD encoder as shown in Fig. 2, where we consider a step-tunable mode-locked laser diode with a 100 GHz repetition rate [6]. At the encoder block, a passive OTDL is used to make the CDMA encoding at the incoming 100 GHz feasible [7].

Fig. 1

Signaling format for M-array FSK-OCDMA system

Fig. 2

OCDMA Transceiver with MAI cancelation

The TLD emits the optical pulse with a certain wavelength corresponding to the data at certain chip positions in a slot coming from the coherent FSK modulator. Note that the optical pulses with other wavelengths are not emitted. The optical pulse is time spread in multiple chip positions corresponding to the ‘1s’ of the spreading code by the encoder consisting of OTDLs in the CDMA encoder. Then, this desired user’s signal is transmitted together with the signals of the other users in the star passive optical network (SPON).

The proposed technique is similar to the existing PPM counterpart; however, the main difference is that only one of the spreading sequences, which has a data-free component of the desired signal is used as a reference signal, and the cancelation is performed by subtracting the reference signal from the received signal of the desired user at each wavelength. The reference signal is used to cancel the interference for all users.

It is noticed that the total number of subscribers increases to $P^{2}-1$ instead of $P^{2}-P$ in the PPM counterpart. This makes the system operation faster because it has to compare the received signal with only one reference not $P$ references and also makes the receiver structure simpler because the OTDLs configurations in the reference branches are simplified into one instead of $P$. We allocate the first spreading code sequence in the first group to the intended user ($U_{1})$ and use the Pth spreading code as a reference signal. $C_{01}$ and $C_{0P}$ denote as the corresponding optical correlators for the main and reference branches, respectively.

In Fig. 2, the transmitted signal with $M$ wavelengths on the SPON is separated incoherently into $M$ signals with different wavelengths $\lambda _0 , \lambda _1,\ldots \lambda _{M-1}$ by AWG de-multiplexer [8]. We assume an ideal AWG, and hence, no interference between adjacent wavelengths occurs. The received signals are separated by $M$ wavelengths, and each is split into two parts passing through $C_{01}$ and $C_{0P}$, respectively. Also, the data of $U_{1}$ with wavelength $\lambda _0$ are assumed to be in slot 0. Hence, in slot 0 with other wavelengths, there are only interference components of other users in other groups except for group 1 due to the orthogonal sequences in each group. Other slots with $\lambda _0$ assigned to $U_{1}$ have the data component of $U_{1}$ and interference components. Now, since the main branch produces ‘data + interference + noise’, while the reference branch produces ‘interference + noise’, the interference and noise can be canceled out by subtracting the reference signal from the components of $U_{1}$ at all slots. Ideally, only the signal component of $U_{1}$ with wavelength $\lambda _0$ is kept in slot 0, and there are no components in the other slots. For the other wavelengths, there are no components in all slots, since $U_{1}$ has only components with $\lambda _0$. In practice, since the outputs of the photo-detectors (PDs) follow a Poisson process, and the PDs used in the branches have the same characteristics, they add similar amount of thermal and shot noise to the signals; accordingly, it can be assumed that the noises are also canceled out after subtraction. The outputs of $\hbox {C}_{01}$ and $C_{0P}$ for wavelength $\lambda _m$ and slot $s$ are converted from optical signal to electrical signal through the PDs. The outputs of $C_{01}$ and $C_{0P}$ are denoted as $Y_{m,s} (1), Y_{m,s} (P), m\in \{0,\ldots ,M-1\}, s\in \{0,\ldots ,j-1\}$, respectively. Since we have focused on slot 0 and assigned $\lambda _0$ to $U_{1}$, hence $m=0$ and $s = 0$. After the interference cancelation per wavelength, the signal with the highest power is selected by the maximum likelihood (ML) detector, while the signal with the lowest power is represented by 0. Then, the corresponding data are obtained from the M-array FSK detector unit.

3 BER performance analysis

From Figs. 1 and 2 of the signaling format and the proposed MAI cancelation, respectively, to get the BER for this system, we assume that the characteristic of the PDs follow the Poisson process, i.e., the number of photons has a Poisson distribution [12]. The signal power of the desired user with $\lambda _m$ in slot $s$ and the reference signal, $Y_{m,s} (i), i \in \{1, P\}$ after PD is given by:

$$\begin{aligned}&Y_{m,s} (i)=Z_{m,s} (i)+I_{m,s} (i) m \in \{ 0,1,\ldots ,M-1\}, \nonumber \\&s\in \{0,1,\ldots ,j-1 \} \end{aligned}$$

(1)

where $Z_{m,s}(i)$ is the user signal power, and $I_{m,s}(i)$ is the interference power.

The cross-correlation between the first and $x$th user, $C_{1,x}$, of the same group is equal to zero due to the employed signature sequence code. Thus, $U$ users $(0\le U\le P-2)$ in the first group do not affect the photon count of the first user. The Probability Density Function (PDF) of the random variable $U$ is given by [9]:

$$\begin{aligned} P_u \{U=u\}=\frac{\left( {\begin{array}{l} P^{2}-2P+1 \\ K-u \\ \end{array}} \right) \left( {\begin{array}{l} P-2 \\ u-1 \\ \end{array}} \right) }{\left( {\begin{array}{l} P^{2}-P-1 \\ K-1 \\ \end{array}} \right) } \end{aligned}$$

(2)

where $u\in \{ u_{\mathrm{min}},\ldots ,u_{\mathrm{max}} \}, \,u_{\mathrm{max}} =\mathrm{min} (K, P-1) \,\hbox {and}u_{\mathrm{min}} =\mathrm{max} ( 1, K-(P-1 )^{2})$. $K$ refers to the number of simultaneous active users.

Let us define the random variable $k_{m,s}$ to be the number of users, who are in groups other than the first group, and have a pulse in the $s$th slot with wavelength $\lambda _m$. The probability that $l_{m, s}$ users have a pulse in the $s$th slot with wavelength $\lambda _m$ is $1/{(jM)}$ and the probability of having no pulse is $1-1/{(jM)}$. Then, the PDF of $k_{m,s}$ can be expressed as:

$$\begin{aligned} P_u \{k_{m, s} =l_{m, s} \left| {U=u\}\left( \begin{array}{l} k-u \\ l_{m,s} \\ \end{array} \right) } \right. . \left( {\frac{1}{jM}} \right) ^{l_{m,s} }.\left( {1-\frac{1}{jM}} \right) ^{K-u-l_{m,s} }\end{aligned}$$

(3)

When user 1 has an optical pulse with wavelength $\lambda _m$ in the $s$th slot $(b_{m,s}^1 =\{m,s\})$, the expected value of the random variable $Z_{m,s} (i), i\in \{1, P\}$ is expressed as:

$$\begin{aligned} \bar{{Z}}_{m,s} (i)=\left\{ {\begin{array}{ll} \frac{(P+2). Q. T_c }{2} &{} \hbox {if}\,b_{m,s}^1 =\{m,s\} \\ 0 &{} \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$

(4)

where $T_c$ is the chip-duration. When we take the fiber attenuation coefficient $\alpha$ into consideration, the average number of received photon count per pulse $Q$ can be expressed as [10]:

$$\begin{aligned} Q=\frac{\xi P_W }{h f}.\frac{e^{-\alpha L}}{P+2}\approx \mu .\frac{\mathrm{ln}\, M}{P+2} \end{aligned}$$

(5)

where $P_W$ is the transmitted peak power per symbol, $\xi$ is the quantum efficiency of the PDs, $h$ is Blank’s constant, $L$ is the fiber length, $f$ is the optical frequency, $\mu$ is the average number of photons per pulse (photons/nat) [11], and $\mu =P_u / (h.f.\mathrm{ln}\,M). P_u$ is the received signal power, and it is given as $P_u =\xi . P_W . e^{-\alpha L}$.

The experimental values for these parameters are listed in Table 1.

Table 1 Link parameters

The expected value of the random variable $\bar{{I}}_{m,s} (i), i\in \{1, P\}$ can be expressed as:

$$\begin{aligned} \bar{{I}}_{m,s} (i)=l_{m,s} . Q. T_c \end{aligned}$$

(6)

From Eqs. (4) and (6), the expected value of $Y_{m,s} (i), i\in \{1, P\}$ is expressed as:

$$\begin{aligned} \bar{{Y}}_{m,s} (i)=\left\{ {\begin{array}{ll} \frac{(P+2+l_{m,s} ). Q. T_c }{2} &{}b_{m,s}^1 =\{m,s\} \\ \frac{l_{m, s} . Q. T_c }{2} &{} \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$

(7)

The strategy of the suggested idea for MAI cancelation consists in a subtraction process after the PDs between the reference signal and user 1. Since both PDs have the same characteristics; the signals suffer from the same shot noise, which cancels out after subtraction. The signal after subtraction is given by:

$$\begin{aligned} \tilde{Y}_{m,s} =\bar{{Y}}_{m,s} (1)-\bar{{Y}}_{m,s} (P) \end{aligned}$$

(8)

Since user 1 has an optical pulse with wavelength $\lambda _0$ at slot 0, the symbol-error occurs when $\tilde{Y}_{j,0} (1)\ge \bar{{Y}}_{0,0} (1), (j\ne 0)$. Suppose that $P_{E}$ denotes the symbol-error rate, and then the BER $\left( {P_b } \right)$ is expressed as [11]:

$$\begin{aligned} P_b \le \frac{M}{2(M-1)}.\sum _{u=u_{\mathrm{min} } }^{u_{\mathrm{max}} } {P_{_E } } .P_u \{U=u\} \end{aligned}$$

(9)

where:

$$\begin{aligned} P_E&=\sum _{j=0}^{M-1} {P_u } \{ \tilde{Y}_{j,0} \ge \tilde{Y}_{0,0} \left| { U=u,k_{0,0} } \right. =l_{0,0} ,\ldots ..,k_{M-1,0} \nonumber \\&=l_{M-1,0} , b_{m,s}^1 =\{0,0\}\}\nonumber \\&\quad \times P_u \{k_{0,0} =l_{0,0} , k_{1,0} =l_{1,0} , b_{m,s}^1 =\{0,0\}\left| {U=u\}} \right. \nonumber \\&\le (M-1) \sum _{l_{0,0} =0}^{k-u} {\sum _{l_{1,0} =0}^{k-u-l_{0,0} } {P_u } } [\tilde{Y}_{1,0} \ge \tilde{Y}_{0,0} \left| U=u, k_{0,0} =l_{0,0} ,k_{1,0} \right. \nonumber \\&=l_{1,0} ,b_{m,s}^1 =\{0,0\}\}\times P_u \{k_{0,0} =l_{0,0} ,k_{1,0} =l_{1,0} ,b_{m,s}^1 \nonumber \\&=\{0,0\} \left| {U=u\}\le \sum _{l_{0,0} =0}^{k-u} {\sum _{l_{1,0} =0}^{k-u-l_{0,0} } {P_u } } } \right. \{k_{0,0} =l_{0,0} ,k_{1,0}\nonumber \\&=l_{1,0} \left| {U=u\}\times \Phi (u,l_{m,0} } \right. ) \end{aligned}$$

(10)

and

$$\begin{aligned} \Phi (u,l_{m,0} )&= (M-1).P_u \{\tilde{Y}_{1,0} \ge \tilde{Y}_{0,0} \left| {U=u,k_{0,0} } \right. \nonumber \\&= l_{0,0} ,k_{1,0} =l_{1,0} ,b_{m,s}^1 =\{0,0\} \end{aligned}$$

(11)

The upper pounded $\Phi (u,l_{m,0} )$ is then given by [11]:

$$\begin{aligned}&\Phi (u,l_{m,0} )\le (M-1). \nonumber \\&E [z^{\bar{{Y}}_{1,0} (1)-\bar{{Y}}_{1,0} (P)\ge \bar{{Y}}_{0,0} (1)-\bar{{Y}}_{0,0} (P)} \left| {U=u, k_{0,0}=l_{0,0} , k_{1,0} } \right. =l_{1,0} ,\nonumber \\&b_{m,s}^1 =\{0,0\}] \end{aligned}$$

(12)

Where:

$z (z>1\,\hbox {an\,integer})$ denotes the number of optical interference pulses in slot 0 and E [.] refers to the expected value and by using the Chernoff bound $\Phi (u,l_{m,0} )$ can be expressed as:

$$\begin{aligned}&\mathrm{ln} \Phi (u,l_{m,0} )\le -\mathrm{ln} (M-1)\nonumber \\&\quad -\bar{{Y}}_{1,0} (1) (1-z)-\bar{{Y}}_{1,0} (P) (1-Z^{-1})\nonumber \\&\quad -\bar{{Y}}_{0,0} (1) (1-Z^{-1}) -\bar{{Y}}_{0,0} (P) (1-Z)+\bar{{Z}}_{0,0} (1) (1-z)\nonumber \\ \end{aligned}$$

(13)

Let $z-1=\rho (\rho >0\,\hbox {and\,integer} )$, we have then$1-z^{-1}\le 1 , \hbox {while}\,\rho -\rho ^{2}\le 0$. Hence, by considering new boundaries, we get this lower bound equation [11]:

$$\begin{aligned} 1-z^{-1}\ge \rho -\rho ^{2} \end{aligned}$$

(14)

From Eqs. 4, 7, 14 in Eq. 13, we get:

$$\begin{aligned} \mathrm{ln} \Phi (u,l_{m,0} )\!\le \! \!-\!\mathrm{ln} (M\!-\!1)\exp \left\{ {\!-\!\frac{Q. (P+2)^{2}}{4.(P+2+l_{0,0} +l_{1,0} )}} \right\} \nonumber \\ \end{aligned}$$

(15)

Then, we get the upper bound symbol-error probability $P_{E}$ as:

$$\begin{aligned}&P_E \le (M-1). \sum _{l_{0,0} =0}^{k-u} {\sum _{l_{1,0} =0}^{k-u-l_{0,0} } {P_u } } \{k_{0,0} \nonumber \\&\quad =l_{0,0} ,k_{1,0} =l_{1,0} ,b_{m,s}^1 =\{0,0\}\left| { U=u\}} \right. \end{aligned}$$

(16)

Finally from the above equations, we get the total upper-bounded probability of error $P_b$ as:

$$\begin{aligned}&P_b \le \frac{M}{2}\sum _{u=u_{\mathrm{min} } }^{u_{\mathrm{max}} } {\sum _{l_{0,0} =0}^{k-u} {\sum _{l_{1,0} =0}^{k-u-l_{0,0} } { \left( {\begin{array}{l} k-u-l_{0,0} \\ l_{1,0} \\ \end{array}} \right) } } } .\left( {\frac{1}{j.M}} \right) ^{l_{1,0} }.\nonumber \\&\qquad \times \left( {1-\frac{1}{j.M}} \right) ^{k-u-l_{0,0} -l_{1,0} }.\nonumber \\&\exp \left\{ -\frac{\rho }{2}.\frac{Q.(P+2)}{2}\right\} \times \left( {\begin{array}{l} k-u \\ l_{0,0} \\ \end{array}} \right) .\left( {\frac{1}{j.M}} \right) ^{l_{0,0} }.\left( {1-\frac{1}{j.M}} \right) ^{k-u-l_{0,0} }\nonumber \\&\qquad \times \frac{\left( {\begin{array}{l} P^{2}-2P+1 \\ k-u \\ \end{array}} \right) .\left( {\begin{array}{l} P-2 \\ u-1 \\ \end{array}} \right) }{\left( {\begin{array}{l} P^{2}-P-1 \\ k-1 \\ \end{array}} \right) } \end{aligned}$$

(17)

4 Simulation results and discussion

Our simulations have been carried out using Matlab. The simulated computer results clarified in Figs. 3, 4 and 5 indicate the relation between the BER performance and the average number of photons per pulse $\mu$ for both the proposed MAI canceler using FSK and the existing PPM techniques at $M = 4, 8\,\hbox {and}\,16$, respectively. These figures are the outcome of the simulations with the link parameters in Table 1. We have investigated the performance at a prime number $P =13$ with different values for the M-array FSK keying such as at $M = 4, 8,\,\hbox {and}\,16$. Also, we have studied different values for the repetition index $(j)$ such as $j = 1, 2\,\hbox {and}\,3$. The numerical results of the proposed MAI canceler using the FSK-OCDMA technique have been compared with PPM-OCDMA counterpart. In these simulations, we have assumed all interfering users are present, i.e., full load.

Fig. 3

Variation of BER performance with $\mu$ at $M = 4$

Fig. 4

Variation of BER performance with $\mu$ at $M = 8$

Fig. 5

Variation of the BER performance with $\mu$ at $M =16$

The simulated computer results reveal that the FSK-OCDMA is more power efficient than PPM technique. For instance, at $M = 8$, the BER reaches $10^{-9}$ and it is improved more at $M = 16$ under less average number of photons per pulse $\mu$. Also, it is clear that the repetition index $j$ can also enhance the performance of the FSK –OCDMA technique. The higher the repetition index, the better the system performance gained. For instance, for $M = 8$, at $\mu = 100$, the BER for FSK with $j = 3$ is $4.7\times 10^{-11}$. When $j = 2$, the BER is $2.1\times 10^{-9}\,\hbox {and it is } 1.6\times 10^{-7}$ at $j = 1$; while BER is $2.2\times 10^{-6}$ for the PPM technique. Also we have noticed that the higher the modulation index $M$, the more superior the performance gained in terms of a lower BER for both the FSK and PPM techniques.

The simulated computer results in Figs. 6, 7 and 8 illustrate the relation between the bit-error probability with the number of simultaneous users $K$, for both the FSK receiver and the PPM receiver at $M = 4, 8\,\hbox {and}\,16$, respectively. It is clear from these figures that the FSK technique outperforms the PPM, especially for a higher repetition index $j$ and higher order $M$.

Fig. 6

BER versus $K$ at $M = 4$

Fig. 7

BER versus $K$ at $M = 8$

Fig. 8

BER versus $K$ at $M =16$

Moreover, we have checked the effect of changing the average number of photons per pulse $\mu$ for both cases of FSK and PPM techniques as shown in Figs.  9, 10, 11, 12, 13 and 14. It is clear that the higher the average number of photons per pulse, the better the performance gained.

Fig. 9

BER versus $K$ at $M = 4$ and $\mu = 50$

Fig. 10

BER versus $K$ at $M = 4$ and $\mu =200$

Fig. 11

BER versus $K$ at $M = 8$ and $\mu = 50$

Fig. 12

BER versus $K$ at $M = 8$ and $\mu = 200$

Fig. 13

BER versus $K$ at $M =16$ and $\mu = 50$

Fig. 14

BER versus $K$ at $M = 16$ and $\mu = 100$

The results reveal that the technique based on FSK provides a better performance than that of the PPM technique for mitigating the effect of MAI in the OCDMA system. The reason is that in the PPM, the probability of having interference is reduced by increasing the number of slots (corresponding to the number of symbols) in the time domain. On the contrary, in the FSK, the probability of having interference is reduced by using both the number of wavelengths (corresponding to the number of symbols) and repetition index. When the chip rate is constant, in order to decrease the probability of having interference in the PPM technique, the number of slots has to be increased, which results in a larger frame length and a lower bit rate. Alternatively, in the FSK technique, the frame length depends only on the repetition index which is smaller than $M$ as indicated in Fig. 1 for signaling format. In addition, the system capacity can be expanded by growth in the repetition index $j$. By increasing the number of wavelengths $M$, the probability of having interference can therefore be further reduced in the FSK system with a shorter frame length than that of the PPM. Accordingly, FSK can attain higher bit-rate transmissions than PPM. The bit rates $R_b$, for FSK and PPM systems are given as [9, 11]:

$$\begin{aligned} R_b&= \frac{\log _2^M }{j.T_c .(P^{2}+2P)}, M-array\,FSK-OCDMA\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} R_b&= \frac{\log _2^M }{M.T_c .(P^{2}+2P)}, M-array\,PPM-OCDMA\nonumber \\ \end{aligned}$$

(19)

5 Conclusion

In this paper, a simple and efficient MAI cancelation technique using hybrid FSK technique has been presented and analyzed. This technique of modulation incorporates a good coding scheme that respects the requirements of MAI cancelation, using the EMPC as a signature sequence with the FSK technique. The coherent FSK modulation along with incoherent demodulation using AWG in the transceiver structure has been examined. As a result, the cancelation technique along with FSK-OCDMA system, as compared with existing technique of PPM-OCDMA, has more enhancements in the system performance under the same given conditions. It was observed that from the simulated computer results, the cancelation method, as compared with the existing PPM technique, has provided a lower error rate and a higher bit rate. Moreover, the results revealed that the FSK technique is very power efficient, and when the bit rate is constant, its network capacity can be expanded to accommodate a large number of simultaneous active users with low error rate. In addition, the proposed technique could simplify the hardware of the receiver structure.