Introduction

In continuum theory, the elastic deformation of isotropic powder and porous materials is described by Hooke’s law. The theoretical effective bulk (K) and shear (μ) moduli are found by solving two boundary-value problems of elasticity for a representative cell of a discontinuous material subject to triaxial compression and pure shear. The cell is a body of simple shape with a cavity. The well-known models [1–3] assume that the volume of the material skeleton of the cell is equal to the volume of the solid phase V m, and the volume of the cavity is equal to the volume of pores V p. In such models with initial density ρ0, the cell is a mechanically stable structure that resists deformation and its elastic moduli are nonzero (K(ρ0) > 0 and μ(ρ0) > 0). However, loose powder materials start deforming under arbitrarily low loads, i.e., their elastic moduli must be infinitesimal (K(ρ0) → 0 and μ(ρ0) → 0) and the continuum model must reflect their discrete structure.

Powder materials deform via the contact interaction of particles. Microscopic stresses and strains are concentrated near the contact surfaces of particles and abruptly decrease with distance from them. As a result, plastic deformation starts in the zones where elastic stresses and strains are concentrated, and just a portion (V d < V m) of the total volume V m of particles undergoes plastic deformation.

The idea of elastic and plastic volumes in the solid phase of powder and porous bodies is widely used in the discrete contact [4] and continuum [5, 6] models of plastic deformation. The discrete contact model describes the inhomogeneity of the deformation of the solid phase by associating the fields of microscopic stresses and strains only with a portion (active volume) of the entire volume of the solid phase [4]. With this hypothesis, the compaction equations provide a good fit to experimental data. In this connection, we propose here a continuum theory to describe the elastic and plastic properties of powder materials based on the physical hypotheses and structural models of discrete contact theory.

Approaches and models

Powder and porous materials are bimodulus materials, i.e., their elastic moduli depend on the stress mode [7], which is most clearly manifested as a difference between the tensile and compressive elastic moduli. Powder and porous materials are deformed for compaction, usually under predo inantly compressive stresses in closed volumes. The results obtained here are related to the compression of such materials.

A plasticity condition for powder materials based on Bal’shin’s structural model [4] and describing the contact interaction of particles was proposed in [8]. A deformable unit volume of a particle is a cylinder with one base being the contact area. A plastically deformable powder body as a whole is a system of volume V d of chaotically oriented cylinders contacting by bases. This system undergoes homogeneous tension/compression deformation. Prior to plastic deformation, the volume V d is in an elastic state. By analogy with plastic properties, we assume that the resistance to elastic deformation and the elastic properties of powder and porous materials are determined only by the elastic properties of the volume V d.

To find the effective bulk modulus K, we assume that the powder body is a ball and the equivalent representative cell is a spherical shell with surface area equal to that of the ball. In the models [1–3], the volume of the spherical shell is set equal to the volume V m of the solid phase, and the volume of cavity V p = V – V m, where V is the total volume of the powder body. The volume fraction of the shell is equal to the relative density of the powder: V m/V = ρ. In our model, the volume of the shell is equal to V d, and the volume of cavity V p = V – V d. Then the volume fraction of the shell is equal to the relative deformable volume: V d/V = α. The modulus K can be found by comparing the solutions of elastic problems for the ball and the spherical shell under hydrostatic compression. The expression for K is derived by replacing the relative density ρ in formula (14) of [2] by α. After appropriate transformations, we get

$$ K = \frac{4}{3}{\upmu_0}\frac{{\left( {1 + {\upnu_0}} \right)\upalpha }}{{2\left( {1 - 2{\upnu_0}} \right) + \left( {1 + {\upnu_0}} \right)\left( {1 - \upalpha } \right)}}, $$
(1)

where μ0 and ν0 are the shear modulus and Poisson’s ratio of the solid phase.

To find the effective shear modulus μ, we assume that the powder body is a cube subject to pure shear, and the equivalent representative cell is a cube with a cubic cavity [3, 9]. Averaging the microscopic stresses and strains over the solid phase of the porous body, according to [3, 9], we obtain

$$ \upmu = \uprho {\upmu_0}. $$
(2)

If the averaging is over the volume V d, then it is necessary to replace ρ in (3) by α:

$$ \upmu = \upalpha {\upmu_0}. $$
(3)

In the elastic case, the parameter α corresponds to the effective elastic moduli and can be defined as the effective volume of the solid phase. In the plastic case, α is the fraction of the plastically deformable volume of the solid phase.

To establish the functional relationship between the deformable volume V d and the density of the powder, it is necessary to solve complicated boundary-value problems for determining the distribution of stresses and strains in the ensemble of contacting particles of various shape. This can be avoided by compacting the powder [4]. The following dependence of α on ρ for this model was proposed in [10]:

$$ \upalpha = {\uprho^n}\frac{{\uprho - {\uprho_0}}}{{1 - {\uprho_0}}};\quad n = \frac{{2 - \uprho - {\uprho_0}}}{{1 - {\uprho_0}}}, $$
(4)

where ρ0 is the initial (bulk) relative density of the powder.

While the powder is loose (ρ = ρ0), the parameter α and the moduli K and μ are equal to zero, i.e., the powder does not resist deformation. This is how the model describes the initial (loose) state of powders. When ρ > ρ0, the powder undergoes either elastic or plastic deformation, depending on the level of macroscopic stresses.

Note that formulas (4) describe the plastic volume formed only by the compaction of powder and porous materials. This model does not describe the variation in plastic volumes with the load at constant density.

Experimental validation

We compared theoretical and experimental values of Young’s modulus E of a compacted copper powder with ρ0 = 0.3 [4]. The modulus E is calculated by the formula

$$ E = \frac{{9K\upmu }}{{3K + \upmu }}. $$
(5)

We also calculated the moduli by the theoretical formulas given in [2]:

$$ K = \frac{4}{3}{\upmu_0}\frac{{\left( {1 + {\upnu_0}} \right){\uprho^3}}}{{2{\uprho^2}\left( {1 - 2{\upnu_0}} \right) + \left( {1 + {\upnu_0}} \right)\left( {1 - \uprho } \right)}},\;\upmu = {\uprho^2}{\upmu_0}, $$
(6)

and in [11]:

$$ K = \frac{2}{3}{\upmu_0}\frac{{1 + {\upnu_0}{\uprho^2}}}{{1 - 2{\upnu_0}{\uprho^2}}}{\uprho^{{{2} \left/ {\uprho } \right.}}},\;\upmu = {\uprho^{{{2} \left/ {\uprho } \right.}}}{\upmu_0}. $$
(7)

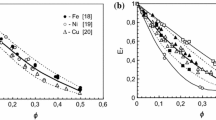
Figure 1 shows theoretical and experimental dependences of the ratio of modulus E for compacted copper powder to the modulus E 0 for cast copper on the porosity θ = 1 – ρ. It can be seen that formulas (6) overestimate Young’s modulus, whereas formulas (7) are in good agreement with the experimental data.

Fig. 1
figure 1

Relative Young’s modulus versus porosity θ of copper powder: 1) formula (4); 2) formula (6); 3) formula (7); circles = experiment [4]

Full size image

Unlike powders consisting of disperse particles, a porous body is a continuous matrix with pores. Theoretically, the elastic moduli of such materials must be zero at zero density (ρ = 0). Experiments, however, discovered that the elastic moduli of porous materials become zero or nearly zero at nonzero density. For example, according to [12], the elastic moduli of porous materials become infinitesimal at ρ = 0.227. Porous materials are produced by partial sintering of powders after cold compaction. In turn, the initial density of a powder before compaction is bulk density, while the effective volume α of a porous sintered material is calculated assuming that its initial density ρ0 is equal to bulk density. This conclusion is confirmed by experimental data in [12] where zero values of elastic moduli of sintered iron obtained by extrapolation correspond to the bulk density of iron powder. In the literature, however, one can find mainly the densities of sintered materials and very rarely the bulk density of powders. The initial density ρ0 can be defined as follows.

In our model, the elastic properties of a discontinuous body are determined by the volume α. At low porosity, pores are isolated from each other by the solid phase. As the volume of pores increases, the cross-section of the material skeleton decreases. Let the volume α become zero once open porosity has formed. If the pores are equal spheres, the maximum closed porosity θmax = 0.74, which corresponds to the close packing of balls with highest density. Therefore, in the absence of information on the bulk density of porous sintered materials, we can assess the initial density at which the elastic properties start showing up from the volume fraction θmax of the skeleton as ρ0 = 1 – θmax = 0.26. For nonspherical pores and for spherical pores of various size, ρ0 can be different.

The theory of elastic properties of sintered materials was experimentally validated in two cases: ρ0 = 0 and ρ0 = 0.26. Figures 2 and 3 show theoretical and experimental dependences of the relative Young’s and shear moduli of sintered nickel and iron on their porosity. Formula (6), which averages the microscopic properties over the solid phase, works well for porosities of up to 10%. The empirical formula (7) is in good agreement with experimental data in the examined range of porosity. The proposed model also describes well the elastic moduli of porous sintered materials, the best agreement with the experimental data being in the case of ρ0 = 0.26.

Fig. 2
figure 2

Relative Young’s modulus versus porosity θ of porous nickel (a) and porous iron (b): 1) formula (6); 2) formula (7); 3 and 4) formula (4) with ρ0 = 0 and ρ0 = 0.26, respectively; circles = experiment [11, 12]

Full size image
Fig. 3
figure 3

Relative shear modulus versus porosity θ of porous iron: 1) formula (6); 2) formula (7); 3 and 4) formula (4) with ρ0 = 0 and ρ0 = 0.26, respectively; circles = experiment [12]

Full size image

Let us discuss the plastic properties of powder materials. The mathematical description of the plastic deformation is based on the plasticity condition mentioned above. Loose powders plastically deform via both plastic shear of particles and slip of contacting particles. The plasticity condition proposed in [13] accounts for the dual mechanism and local nature of the deformation of particles:

$$ \frac{{{\upsigma^2}}}{{2\uppsi }} + \frac{{{T^2}}}{\upvarphi } = \upalpha {\left( {{c_0} - f\upsigma } \right)^2}\;\,{\text{for}}\;\upsigma < {\upsigma^*}; $$
(8a)
$$ \frac{{{\upsigma^2}}}{{2\uppsi }} + \frac{{{T^2}}}{\upvarphi } = \upalpha \uptau_{s0}^2\;\,{\text{for}}\;\upsigma \geq {\upsigma^*}, $$
(8b)

where σ is the average macroscopic stress; T is the intensity of macroscopic shear stresses; c 0 is the shear coalescence constant; f is the coefficient of internal friction; τs0 is the yield stress in shear of particle material; σ* is the average macroscopic stress at which the plastic deformation of particles begins. The plasticity conditions (8a) and (8b) describe the process of compaction via slip of particles and via plastic deformation of particles, respectively. Unlike the models [14], the right-hand side of Eqs. (8) includes α instead of ρ.

The functions ψ and φ in (8) are the ratios of the moduli K and μ to the shear modulus μ0 of the solid phase:

$$ \uppsi = \frac{K}{{2{\upmu_0}}};\;\upvarphi = \frac{\upmu }{{{\upmu_0}}}. $$
(9)

In [13], the elastic moduli were determined considering the elastic deformation of the entire solid phase. Since the deformation of the solid phase is of local nature, the moduli K and μ must be expressed in terms of the effective volume α. In the plastic case, the solid phase is considered incompressible (ν0 = 0.5), and we obtain the following expressions for ψ and φ from (1) and (3):

$$ \uppsi = \frac{2}{3}\frac{\upalpha }{{1 - \upalpha }};\;\upvarphi = \upalpha . $$
(10)

Various expressions for the functions ψ(ρ) and φ(ρ) are used in the models describing the elastic deformation of the entire solid phase [15]. In what follows, we will use the best-known expressions proposed by Skorokhod [1, 16]:

$$ \uppsi = \frac{2}{3}\frac{{{\uprho^3}}}{{1 - \uprho }};\;\upvarphi = {\uprho^2}, $$
(11)

and by Koval’chenko [11]:

$$ \uppsi = \frac{1}{6}\frac{{2 + {\uprho^2}}}{{1 - {\uprho^2}}}{\uprho^{{{2} \left/ {\uprho } \right.}}};\;\upvarphi = {\uprho^{{{2} \left/ {\uprho } \right.}}}. $$
(12)

The plasticity condition in the space of the stress tensor describes the loading surface of the powder body. An analysis of the canonical form of Eqs. (8a) shows [13] that the loading surface is either an ellipsoid, or a hyperboloid, or a paraboloid, depending on the structural condition of the powder. Under parabolic and hyperbolic plasticity, bulk strain rate e > 0 at any stress σ < σ* and the powder is loosened [13]. Powders are commonly deformed for the purpose of compaction. The process of compaction is described by elliptic plasticity conditions. Therefore, we will deal with elliptic plasticity for both σ < σ* and σ ≥ σ*. In this case, the constitutive equations are as follows [13]:

$$ {\upsigma_{ij}} = \frac{{2{c_0}\sqrt {\upalpha } }}{{\sqrt {{2\uppsi {e^2} + 2\uppsi \upvarphi F{H^2}}} }}\left[ {\left( {\frac{1}{{2F}} - \frac{1}{3}\upvarphi } \right)e{\updelta_{ij}} + \upvarphi {e_{ij}}} \right] - \frac{{\upalpha f}}{F}{c_0}{\updelta_{ij}}\;{\text{for}}\;\upsigma < {\upsigma^*}; $$
(13a)
$$ {\upsigma_{ij}} = \frac{{2{\uptau_{s0}}\sqrt {\upalpha } }}{{\sqrt {{2\uppsi {e^2} + \upvarphi {H^2}}} }}\left[ {\left( {\uppsi - \frac{1}{2}\upvarphi } \right)e{\updelta_{ij}} + \upvarphi {e_{ij}}} \right]\;{\text{for}}\;\upsigma \geq {\upsigma^*}, $$
(13b)

where e is the bulk strain rate; H is the shear strain rate intensity; F is the density and internal friction function defined by

$$ F = \frac{1}{{2\uppsi }} - \upalpha {f^2}. $$
(14)

The system of equations of plasticity for compressible materials is supplemented with the continuity equation

$$ \frac{{d\uprho }}{{dt}} + \uprho e = 0. $$
(15)

The plastic deformation of particles of metal powders is accompanied by the strain hardening of the solid phase. The shear strain rate intensity w depends on the invariants of strain rates of the powder body in the volumes α or ρ as follows [8, 16]:

$$ w = \frac{1}{{\sqrt {\upalpha } }}\sqrt {{2\uppsi {e^2} + \upvarphi {H^2}}}; \;\,w = \frac{1}{{\sqrt {\uprho } }}\sqrt {{2\uppsi {e^2} + \upvarphi {H^2}}} . $$
(16)

The equivalent plastic strain ε iα averaged over the deformable volume can be found by integrating (16) over t:

$$ {\upvarepsilon_{i\upalpha }} = \frac{1}{{\sqrt {3} }}\int\limits_0^t {w\,dt} . $$
(17)

If strain hardening obeys a power law, the yield stress σ s0 for the solid phase is defined by

$$ {\upsigma_{s0}} = {\upsigma_{0.2}} + B\upvarepsilon_{i\upalpha }^m. $$
(18)

where σ0.2 and σ s0 are the offset yield strength and the tensile yield stress, respectively; B and m are hardening constants. The shear yield stress and the compressive yield stress are related by \( {\uptau_{s0}} = {{{{\upsigma_{s0}}}} \left/ {{\sqrt {3} }} \right.} \).

Since the theory of plasticity is phenomenological, it is necessary to determine some material constants experimentally. For powder materials, estimates of these constants will depend on the deformation model and density functions ψ and φ. These functions may be either theoretical or experimental. Theoretical functions usually include only one structural parameter (porosity). However, the mechanical properties of powders are strongly dependent on particle size and morphology, production method, etc. These factors can be integrally incorporated into experimental density functions. In [15], it was shown that experimental density functions are different for different materials. Therefore, there can be no universal theoretical formulas for all porous bodies. Determining experimental density functions in each specific case is difficult and costly. It is thus reasonable to specify the functions ψ and φ and to determine the effective properties of the solid phase from experimental data.

For powder materials, it is first necessary to find the average stress σ* at which interparticle slip completes and the plastic deformation of particles of the solid phase begins. The stress σ* can be determined from the coordinates of the salient points of a linearized experimental compaction curve [17]. This method, however, requires high experimental accuracy and a great number of data points. It is therefore desirable to simplify, whenever possible, the general model, keeping physical consistency and mathematical accuracy. One of such simplifications is the following. The plastic deformation of particles begins after the highest density of packing is reached and further compaction via movement of particles becomes impossible. The stage of plastic deformation of particles for commercial powders begins in the range ρ* = 0.7–0.76 [17] which includes the highest relative density (ρ = 0.74) of the close packing of monodisperse spheres. We can assume that the plastic deformation of particles begins at ρ* = 0.74. Then the relative density (ρ ≥ ρ* = 0.74) rather than the average stress (σ* ≥ σ) should be limited.

The phenomenological constants were determined from the results reported in [18] for the true compaction pressure for metal powders in a closed die without contact friction. To determine the phenomenological constants for both stages of compaction, we need experimental data on compaction of powders from bulk density to relative density of no less than ρ = 0.9. However, only aluminum powder was compacted to ρ ≈ 0.92 in the experiment [18]. The maximum relative density of copper, iron, and nickel powders reached in [18] is ρ = 0.65–0.73.

The true pressure of compaction to high density was calculated as follows. The compaction curves for the true pressure p z are shifted to the left from the compaction curve for the total pressure p zΣ, the shift Δp z  = p zΣ – p z increasing with density [18]. An analysis of the compaction curves for aluminum powder under true [18] and total [19] pressure shows that Δp z (ρ) is described by a power equation:

$$ \updelta {p_z} = A{\left( {\uprho - {\uprho_0}} \right)^n}. $$
(19)

Thus, the approximating formula (19) can be obtained from compaction curves for true and total pressure in the range of low densities. Then, by extrapolating (19) to the range of high densities, it is possible to find Δp z and p z . Validation of the approach for aluminum powder against experimental data for true [18] and total [19] pressure shows that the extrapolated and experimental values of true pressure differ by no greater than 5%. Likewise, extrapolated values of the true pressure of compaction to high density for copper, iron, and nickel powders were obtained from compaction curves for true [18] and total [4, 20, 21] pressure.

When powders are compacted in closed cylindrical dies without friction, the radial and hoop strains are equal to zero (ε2 = ε3 = 0) and the principal stresses are equal (σ2 = σ3). The formulas for the phenomenological constants were derived from the constitutive equations (13). The values of c 0 and f were found by the least-squares method from the equation

$$ {p_z} = \frac{{{c_0}\sqrt {\upalpha } }}{{\sqrt {{\uppsi F}} }}\sqrt {{\frac{1}{{2F}} + \frac{2}{3}\upvarphi }} + \frac{{\upalpha f}}{F}{c_0}. $$
(20)

The initial yield stress σ s0 at relative density ρ* = 0.74 was calculated by the formula

$$ {\upsigma_{s0}} = \frac{{3{p_z}}}{{\sqrt {{6\upalpha \uppsi + 4\upalpha \upvarphi }} }}. $$
(21)

The offset yield strength σ0.2(p) of powder particles was set equal to σ s0. The phenomenological constants of powders under the plasticity condition (8) for α = ρ and density functions (11) and (12) were determined in a similar way. Table 1 summarizes the calculated results and the properties of cast materials [22].

Table 1 Phenomenological Constants of Powder and Cast Materials
Full size table

The effective hardening parameters B and m of the solid phase can be obtained by fitting an experimental curve σ s0(ε iα). Let us examine the possibility of using the hardening parameters of a cast material. A polycrystalline particle of a powder has a high initial yield strength σ0.2(p) (Table 1).

Then, at the beginning of plastic deformation, a particle can be considered a deformed cast material with cumulative plastic strain intensity ε i(c). Let the particle be strain-hardened in the same way as a cast material during plastic deformation above ε i(c). The yield stress σ s0 of the solid phase is related to the hardening parameters of the cast material as follows:

$$ {\upsigma_{s0}} = {\upsigma_{0.2\left( {\text{c}} \right)}} + B{\left( {{\upvarepsilon_{i\left( {\text{c}} \right)}} + {\upvarepsilon_{i\upalpha }}} \right)^m}, $$
(22)

where ε i(c) is the equivalent plastic strain of the cast material hardened to the level of the yield strength σ0.2(p) of the powder material and expressed in terms of σ0.2(p) and σ0.2(c):

$$ {\upvarepsilon_{i\left( {\text{c}} \right)}} = {\left( {\frac{{{\upsigma_{0.2\left( {\text{p}} \right)}} - {\upsigma_{0.2\left( {\text{c}} \right)}}}}{B}} \right)^{\frac{1}{m}}}. $$
(23)

The equivalent plastic strain ε iα in (22) can be found from expressions (15)–(17):

$$ {\upvarepsilon_{i\upalpha }} = \frac{1}{{\sqrt {3} }}\int\limits_{{\uprho_0}}^\uprho {\sqrt {{\frac{{2\uppsi }}{\upalpha } + \frac{{4\upvarphi }}{{3\upalpha }}\frac{{d\uprho }}{\uprho }}} } . $$
(24)

Theoretical and experimental compaction curves for powders in a closed die are shown in Fig. 4. The calculations used the plasticity condition (8) with density functions (10) and the equality α = ρ with density functions (11) and (12). The compaction via interparticle slip is described well by the formulas with the density functions (10) and (12). The results obtained with the density functions (11) are in poor agreement with the experimental data. Real powders in loose state begin to be compacted under arbitrarily low pressure, whereas the calculation for α = ρ predicts finite initial compaction pressure. This is because of the limitation of the physical model in which the entire solid phase deforms. The compaction by plastic deformation of particles was described using the hardening parameters of cast materials (Table 1) and the law of hardening (22). The results obtained with the density functions (10) are in best agreement with the experimental data for all powders. Thus, the simplified model of plastic deformation of powders based on the plasticity condition (8) provides a good fit to experimental compaction curves. This allows reducing the number of phenomenological parameters in the model and the labor intensity of the experiment.

Fig. 4
figure 4

Fitting of compaction curves for aluminum (a), copper (b), iron (c), and nickel (d) powders compacted in a closed die: 1) density functions (10); 2) α = ρ, density functions (11); 3) α = ρ, density functions (12); circles = experiment [18] and extrapolation of (19)

Full size image

The calculated values of the phenomenological constants confirm the leading role of the density functions in the description of the plastic properties of powder materials. These functions define the density dependence of the elastic moduli and the limiting elastic state of a powder. Accordingly, the validity of the plasticity condition for powder materials depends on the description of the limiting elastic state. The density functions (10) and (12) accurately describe the elastic moduli, which ensures the correct description of the plastic deformation of powders.

The data on compaction in a closed die were used to determine the phenomenological constants of powder materials. The continuum plastic model of powder materials was validated against test data on isostatic pressing and deposition in a high–pressure chamber. These processes permit exact analytic solutions and involve no contact friction.

Figure 5 shows theoretical compaction curves for isostatically pressed copper powder. The phenomenological parameters were obtained by fitting compaction curves for powders pressed in a closed die (Table 1). The experimental data points lie below the theoretical compaction curves plotted using the plasticity condition (8) for α = ρ and density functions (12) and lie above the curves plotted using the density functions (11). The results obtained with the density functions (10) are in best agreement with the experimental data.

Fig. 5
figure 5

Compaction curves for isostatically pressed copper powder: 1) density functions (10); 2) α = ρ, density functions (12); 3) α = ρ, density functions (11); circles = experiment [20]

Full size image

Theoretical curves describing deposition in a high-pressure chamber can be found in [15]. An iron powder already compacted to relative density ρ0 = 0.89 was subject to deposition. The relative density exceeds the limiting relative density (ρ = 0.7–0.76) at which compaction via interparticle slip is still possible. This is why the plasticity condition (8b) was used. Use was also made of the yield strength σ0.2(p) of iron powder and the hardening parameters of cast iron (Table 1). Since the samples for deposition in a chamber were preliminarily pressed in a closed die, the first to be determined was the cumulative equivalent plastic strain ε iα in the solid phase of a sample compacted in a closed die from ρ* = 0.74 to ρ = 0.89. Then the process of deposition in a high-pressure chamber was studied.

Figure 6 shows theoretical and experimental curves of axial stress σ1 versus axial strain ε1. It can be seen that the results calculated with theoretical density functions are in better agreement with the experimental data than the results obtained in [15] based on experimental density functions. Our model is more accurate than the calculation for α = ρ with the density functions (12). The theoretical curve of relative density ρ versus axial strain ε1 (Fig. 7) is also in good agreement with the experimental data. The sole exception is the case of chamber pressure p = 630 MPa in which the calculations [15] based on experimental density functions are in better agreement with experiment than our model.

Fig. 6
figure 6

Axial stress versus axial strain for iron powder deposited in a high-pressure chamber for r = 315 (a), 472.5 (b), and 630 (c) MPa: 1) density functions (10); 2) α = ρ, density functions (12); 3) calculated data [15], circles = experiment [15]

Full size image
Fig. 7
figure 7

Relative density versus axial strain for iron powder deposited in a high-pressure chamber for r = 315 (a), 472.5 (b), and 630 (c) MPa: 1) density function (10); 2) α = ρ, density function (12); 3) calculated data [15]; circles = experiment [15]

Full size image

The results on deposition in a high-pressure chamber suggest that the accuracy of the continuum model describing the plastic properties of powder materials is sufficient for practical purposes. For most calculation cases, the theoretical density functions (10) provide a better agreement with experiment than the empirical formulas used in [15].

Conclusions

Based on the physical hypotheses of the discrete-contact model, we have developed a continuum model that describes the elastic and plastic properties of isotropic powder materials during compaction and takes into account the inhomogeneous deformation of the solid phase. The inhomogeneity of the stress–strain state of the solid phase is described by associating the fields of microscopic stresses and strains with its effective volume rather than with the entire solid phase. Therefore, the elastic moduli and density functions are expressed in terms of the effective or deformable volume of the solid phase. The model shows good agreement with experimental data on the elastic properties and compaction via plastic deformation of powder materials.