Introduction

As the demand for timber, food and other tree products grows, tree plantations are expanding globally and their economic and environmental impacts are increasing. To improve productivity and sustainability of plantations we need to understand the cycling of energy, water, carbon and nutrients through them. The measurements and modelling that are required must account for spatial variations at a range of scales. Some of the data used for calculation of mass balances or modelling is spatially averaged at large scales due to characteristics of the method. For example, gas exchange measurements using flux towers integrate processes over the upwind area, and measurements of stream hydrology and water quality integrate processes in catchment areas. However, some of the measurements that are required for calculating mass balances or parameterising and testing models must be made at ‘point’ scale (eg. root or soil parameters determined on samples with dimensions of ~0.01–1 m). These data need to take into account variation at large scales due to landscape features such as soil type and topography, but must also account for variability at the scale of individual trees. It is important to account for small-scale variation in data because there can be as much variation at the scale of an individual tree as at larger scales (eg. Anuar et al. 2008; Law et al. 2009). Therefore the number and location of sampling or measurement points must be chosen carefully. Furthermore, in order to model plantation functions accurately, these small-scale patterns must either be mathematically described, or averaged in a representative manner. Average values may be derived by combining samples or by calculating means from multiple measurements. Tree-scale variation may be random or systematically related to the planting configuration (Whelan and Anderson 1996).

In this paper we consider the theoretical and practical aspects of accounting for systematic tree-scale lateral variations in plant, soil and hydrological parameters that are related to planting configuration and management regimes. Tree plantations are often planted on an equilateral triangular spacing, in order to maximise exploitation of light and soil resources. While trees are young, their canopies and roots extend in a more-or-less circular pattern, However, as they mature, canopies and root systems tend to overlap (IAEA 1975; Zaharah et al. 1989). Important parameters that have more-or-less radial distribution include the biomass of canopy and root system, and related parameters such as light interception and water uptake. While many tree and soil-related parameters are radially distributed, other parameters have different spatial patterns. For example, management practices such as harvesting traffic or fertiliser application usually occur along avenues, resulting in linear patterns of parameters such as soil density and nutrient content. In this paper we focus on oil palm (Elaeis guineensis Jacq.), one of the most important and rapidly expanding crops in tropical regions (Sayer et al. 2012).

The importance for sampling of this systematic tree-scale variation in plant and soil parameters in tree crops, including oil palm, has been recognised for a long time (Tinker 1960; Brown 1999) and several approaches have been employed to account for it. For example, it is common for soil samples to be taken separately from several visibly distinct management zones, both in plantation monitoring programs (Rankine and Fairhurst 1998; Brown 1999) and in process studies. If those results are to be used to estimate plantation-wide quantities, then the spatial pattern and extent of the zones must also be recorded. That has been done in some studies (eg. Lamade et al. 1996; Haron et al. 1998; Nelson et al. 2006; Frazão et al. 2013; Goodrick et al. in press) but not all. In another approach, some studies have employed tree-scale grid sampling designs (eg. Squire 1984; Adachi et al. 2006). If appropriate grid dimensions are used, then results from these studies can be scaled up to give plantation-wide values. Finally, some have sampled in a radial pattern (eg. Ruer 1967; Schroth et al. 2000; Banabas et al. 2008; Nodichao et al. 2011; Frazão et al. 2013) and, assuming the parameters measured are in fact radially distributed, these data can also be used for scaling up. Despite recognition of the importance of tree-scale variability for scaling up, there has been no systematic description of the various approaches and procedures possible.

The aim of this work was to define logical and practical sampling and calculation methods that account for systematic tree-scale lateral variation in plantations having equilateral triangular spacing. Such definitions will help inform sampling programs in future studies that entail scaling up from point samples or measurements. They will also help identify current sampling procedures that are not representative and should be improved. Here, we propose that there are essentially three approaches; patch, radial and grid, and we examine the way in which the latter two can be used to account for variability, using throughfall, root biomass and soil respiration measurements in mature oil palm plantations. We also define a) the dimensions of the minimum sampling area to account for tree-scale variability (ie. the ‘tree unit’ or fractions thereof), b) methods to delineate the tree unit in the field, and c) methods for calculating spatially-averaged values for the tree unit.

Materials and methods

Accounting for tree-scale variability: the tree unit

The oil palm crop is normally planted in equilateral triangular spacing (~ 9 m apart), with linear arrangement of harvest paths and frond piles (where pruned fronds are placed) in alternating rows (von Uexküll et al. 2003). A circle around each stem, with radius ~1–2 m, is kept weed-free to facilitate harvesting. Harvesting and other traffic moves along the harvest paths, and amendments such as fertilisers and palm oil mill by-products (eg. ‘empty fruit bunches’) are placed in various, but systematic, configurations (Goh et al. 2003). The effects of these systematic variations in plant and soil factors, brought about by plant architecture and management practices, tend to become more pronounced from planting time to felling time ~25 years later. At replanting time the spatial patterns of soil properties might be obliterated, smeared or reinforced, depending on the felling/poisoning technique used and the new planting configuration. In replantings the planting points are usually off-set from the previous ones, or the relationship between planting points of the old and new plantings may change altogether if spacing is changed. So, while the spatial patterns of soil and plant parameters differ with location and time, there are normally considerable systematic spatial variations in parameters. Therefore, sampling design is important.

A plantation may be represented as a repeating pattern of units. In the case of plantings with equilateral triangular spacing, the most compact and logical unit is a hexagon centred on a planting point, with the perimeter being the mid-point between the central and surrounding trees, ie. the Voronoi cell or Thiessen polygon of each tree (Fig. 1). A rectangular unit could also be, and has been, used to represent such a plantation (eg. Squire 1984; Adachi et al. 2006), but its dimensions do not match the plantation geometry as closely as a hexagon. The area of the tree unit (A h ), whether a hexagon or a rectangle, can be calculated from the tree spacing (S) by

Fig. 1
figure 1

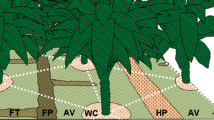
Section of an oil palm plantation with equilateral triangular spacing, showing: 7 trunks; the hexagonal ‘tree units’; the triangle that is the smallest repeating unit for radial patterns (in bold); typical patch patterns (frond pile, harvest path and weeded circle surface management zones); simple shapes that can be measured to estimate the area of the patches (horizontal hatching in central tree unit); an example of a contour line for a tree-related parameter, eg. extent of the canopy, whose radius depends on tree age (dashed lines); distribution of throughfall collection drums used in the throughfall case study (diagonally hatched circles in top-left tree unit); and a triangular sampling grid covering the half-hexagon that is the repeating unit for the patch pattern shown. Dots show the sampling points of the grid, with dimension H (white dots), H/2 (white and grey dots) and H/4 (white, grey and black dots), where H = length of the hexagon’s side. The distribution of fertiliser may or may not correspond with the surface management zones shown

Full size image
$$ {A}_h=\frac{\sqrt{3}}{2}{S}^2 $$
(1)

In the field, the tree unit can be delineated using ropes and no measurements. Ropes are strung between the trunks of the central tree’s 6 neighbours (Fig. 2). Note that the ropes are tied around each tree such that the rope-line between each tree aligns with the centre of the tree. In practice, we tied loose loops around each tree and joined them with a rope, which was then tightened. If one or more of the tree’s neighbours is missing, then a braced stake can be substituted for the missing trunk. Where the ropes cross over, at the six apices of the hexagon, the ropes are loosely attached to each other (to allow some slippage) in order to easily define the intersection point and thus true position of each apex.

Fig. 2
figure 2

Section of a plantation, showing how the hexagon palm unit at the centre (bold) may be set out using ropes (full lines) strung between the trunks (circles) of the 6 surrounding palms. The measurements shown, taken inside the approximately hexagonal palm unit, can be used to define the palm unit’s actual shape and area. Note that y1 = w4, y2 = x4 and y3 = y4

Full size image

While the area of a regular hexagon, representing the plantation as a whole, can be calculated by Eq. 1, a particular tree unit being sampled in the field may not be a perfect hexagon. Its area (A p ) can be calculated using 9 measurements made in the field, and summed for the 4 triangles created within the hexagon, by

$$ {A}_p={\displaystyle \sum_{i=1}^4\left(\frac{1}{4}\sqrt{{\left({w}_i^2+{x}_i^2+{y}_i^2\right)}^2-2\left({w}_i^4+{x}_i^4+{y}_i^4\right)}\right)} $$
(2)

based on Heron’s formula for the area of a triangle, where w i , x i and y i are the measurements shown in Fig. 2.

In order to account for spatial variability at the tree scale, which depends on the parameter being measured (Tinker 1960; Brown 1999), the tree unit can be examined in essentially three different ways; patch, radial or grid.

Variation in patches or zones

Visually distinct patches or zones may be delineated and sampled separately. The most obvious zones in the ‘tree unit’ of oil palm plantations are the trunk, weeded circle surrounding the trunk, frond pile and harvest path, which make up approximately 0.3–0.4, 10–15, 7–12 and 5–15 % of the total plantation area, respectively. The remaining area, usually the largest proportion of total area (approximately 60–70 %), has been variously termed ‘between other zones’, ‘inter-row’ or ‘avenue’, with the latter two terms usually including the harvest path. The dimensions of the management zones can be calculated by approximating the shapes as circles, rectangles and triangles and measuring the appropriate dimensions (Fig. 1).

Sampling by management zone is conceptually simple but, to ensure its representativeness, careful attention must be given to measurement of zone dimensions and placement of sampling points. The zone sampling concept assumes uniformity within zones, which is not the case. For example, while no data is available, we can assume that the effect of organic inputs on soil properties is greater at the centre of the frond pile, where inputs are highest, than near the edge. Another disadvantage of sampling by visible zones is that the influence of invisible factors, such as the history of fertiliser application, is not taken into account.

Variation with radial pattern

If the patterns being considered are radial (eg. canopy-related), then the smallest repeating unit can be reduced from the hexagon ‘tree unit’ to one twelfth of the hexagon, ie. the 30° triangle shown in Fig. 1, which we hereafter call the elemental triangle. The sides of the elemental triangle have lengths T, T/cos30° and T.tan30°, where T = S/2. Complete or high-resolution sampling of the elemental triangle will cover systematic radial variability, including overlapping radial patterns from surrounding trees. However, it may be difficult to sample the elemental triangle in a representative way, so a simpler approximation is to measure the radial distribution of the parameter (z) and integrate it radially over the area of the elemental triangle, ie. calculate the volume (V) of an object whose base is the elemental triangle and whose height (z) is described by a radial distribution around the centre of the tree unit. The volume of this object can be useful in itself, such as for calculation of throughfall volume, or it can be divided by the area of the elemental triangle to calculate the average value \( \left(\overline{z}\right) \)of a radially distributed parameter across the tree unit, and hence the plantation. Compared to high-resolution sampling of the elemental triangle, this approach, using a radial distribution, has the advantage of being mathematically described and hence amenable for modelling processes. It is also possible to calculate confidence limits for the quadratic regression and use them to calculate confidence limits for V and hence \( \left(\overline{z}\right) \).

We now derive an equation to calculate the volume of an object whose base is the elemental triangle and whose height, z, is radially distributed around the centre of the hexagon. We use the case where the radial distribution of the parameter z can be described by the quadratic relationship

$$ z={z}_0+ at+b{t}^2 $$
(3)

in which z 0 , a and b are constants and t is radial distance from the centre of the hexagon. The volume of the object can be derived by initially considering a differential volume and then integrating. The differential volume considered is based on a differential area (A) multiplied by the height z. The differential area is given in polar coordinates by

$$ dA= td\theta dt $$
(4)

The differential volume is then given by

$$ dV= ztd\theta dt $$
(5)

This, with the quadratic height model, gives

$$ dV=\left({z}_0+ at+b{t}^2\right) td\theta dt $$
(6)

In the case of parameters such as throughfall, the area of the trunk must be subtracted from the elemental triangle’s base area, so we allow for that in the derivation by subtracting the area of the trunk inside the elemental triangle. Integrating over this adjusted base area, which is bounded by angles θ = 0 and π/6 and bounded radially by t = t i (the radius of the trunk) and T/cosθ, gives

$$ V={\displaystyle {\int}_0^{\frac{\pi }{6}}{\displaystyle {\int}_{t_i}^{\frac{T}{ \cos \theta }}\left({z}_0+ at+b{t}^2\right) tdtd\theta}} $$
(7)

Performing the first integration,

$$ V={\displaystyle {\int}_0^{\frac{\pi }{6}}\left[\left(\frac{z_0{T}^2}{2{ \cos}^2\theta }+\frac{a{T}^3}{3{ \cos}^3\theta }+\frac{b{T}^4}{4{ \cos}^4\theta}\right)-\left(\frac{z_0{t}_i^2}{2}+\frac{a{t}_i^3}{3}+\frac{b{t}_i^4}{4}\right)\right]} d\theta $$
(8)

Which then gives

$$ V={\displaystyle {\int}_0^{\frac{\pi }{6}}\left(\frac{z_0{T}^2}{2{ \cos}^2\theta }+\frac{a{T}^3}{3{ \cos}^3\theta }+\frac{b{T}^4}{4{ \cos}^4\theta}\right)} d\theta -\frac{\pi }{6}\left(\frac{z_0{t}_i^2}{2}+\frac{a{t}_i^3}{3}+\frac{b{t}_i^4}{4}\right) $$
(9)

Solving the integral term by term gives, for the case where the radial distribution of z is described by a quadratic equation,

$$ V=\frac{z_0{T}^2}{2\sqrt{3}}+\frac{a{T}^3}{6}\left[ \ln \left(\sqrt{3}\right)+\frac{2}{3}\right]+\frac{10b{T}^4}{36\sqrt{3}}\kern2pt -\frac{\pi }{6}\left[\frac{z_0{t}_i^2}{2}+\frac{a{t}_i^3}{3}+\frac{b{t}_i^4}{4}\right] $$
(10)

The method can readily be extended to include cases where the radial height distribution is given by a higher order polynomial. In the case where the radial distribution of z can be described by a cubic relationship,

$$ z={z}_0+ at+b{t}^2+c{t}^3 $$
(11)

in which z 0 , a, b and c are constants and t is radial distance from the centre of the hexagon. The differential volume is then given by

$$ dV=\left({z}_0+ at+b{t}^2+c{t}^3\right) td\theta dt $$
(12)

Integrating over the area of the elemental triangle (minus area of trunk), which is bounded by angles θ = 0 and π/6 and bounded radially by t = t i (the radius of the trunk) and T/cosθ, gives

$$ V={\displaystyle {\int}_0^{\frac{\pi }{6}}{\displaystyle {\int}_{t_i}^{\frac{T}{ \cos \theta }}\left({z}_0+ at+b{t}^2+c{t}^3\right) tdtd\theta}} $$
(13)

Performing the first integration gives

$$ V={\displaystyle {\int}_0^{\frac{\pi }{6}}\left[\left(\frac{z_0{T}^2}{2{ \cos}^2\theta }+\frac{a{T}^3}{3{ \cos}^3\theta }+\frac{b{T}^4}{4{ \cos}^4\theta }+\frac{c{T}^5}{5{ \cos}^5\theta}\right)-\left(\frac{z_0{t}_i^2}{2}+\frac{a{t}_i^3}{3}+\frac{b{t}_i^4}{4}+\frac{c{t}_i{}^5}{5}\right)\right]} d\theta $$
(14)

Performing the second integration gives, for the case where the radial distribution of z is described by a cubic equation,

$$ V=\frac{z_0{T}^2}{2\sqrt{3}}+\frac{a{T}^3}{6}\left[ \ln \left(\sqrt{3}\right)+\frac{2}{3}\right]+\frac{10b{T}^4}{36\sqrt{3}}+\frac{c{T}^5}{5}\left[\frac{17}{36}+\left(\frac{3}{16}\right) \ln (3)\right]-\frac{\pi }{6}\left[\frac{z_0{t}_i{}^2}{2}+\frac{a{t}_i{}^3}{3}+\frac{b{t}_i{}^4}{4}+\frac{c{t}_i{}^5}{5}\right] $$
(15)

For the entire hexagonal area (tree unit), the volume is 12 V. The spatially averaged value of z over the tree unit, and hence the plantation, is given by

$$ \overline{z}=\frac{12V}{A_h-\pi {t}_i^2} $$
(16)

In order to measure the radial distribution of a parameter, either of two approaches may be taken. It is preferable, for regression analysis, to spread sampling points (with samples measured separately) evenly along a radial transect. To allow for the effects of overlapping canopies, at least two transects should be taken, one on either side of the elemental triangle. The other approach is for the number of samples or measurements to increase with radius, in proportion to the area represented at that radius, thus weighting the accuracy of determination according to area. That approach is described in the grid sampling section below.

Variation with any pattern: the grid approach

Parameters that are distributed in patches, radially, randomly or in any other pattern (eg. influenced by overlapping patch and radial distribution patterns), may be accounted for by sampling on a grid with appropriate resolution. Applying a grid to a hexagon shape is done most simply and uniformly using an equilateral triangular pattern. If the spatial pattern of a parameter of interest is radial or linear, as is the case for many tree- and management-related parameters in oil palm plantations, then a half-hexagon, aligned perpendicular to the linear patterns, is sufficient to account for the systematic variation (Fig. 1). An equilateral triangular sampling grid can be set up at different levels of resolution. The number of sampling points in a grid covering the half-hexagon (n 0.5 ), in which the length of the hexagon’s side is H and the distance between sampling points is H/u, is given by

$$ {n}_{0.5}={\left(u+1\right)}^2+u\left(u+1\right)/2 $$
(17)

Thus a half-hexagon sampling grid with dimension H has 5 sampling points, one with dimension H/2 has 12 points, one with H/4 has 35 points (Fig. 1), and one with H/8 has 117 points. If the grid covers the whole hexagon, then the number of sampling points (n) is given by

$$ n=2{n}_{0.5}-\left(2u+1\right) $$
(18)

Note that H is related to tree spacing (S) by

$$ H=S \cos 30{}^{\circ}/2 $$
(19)

A grid with dimension H does not cover management zones in a representative way, as few or no points are in the ‘between other zones’ area, which usually covers the largest proportion of the plantation. On the other hand, a grid with dimension H/8 gives more points than would be practical to sample.

The pattern of sampling and analyses within the half-hexagon grid can be decided depending on the purpose and budget. If a sample from each point is to be analysed, then the data can be used to produce a map, examine variability or to calculate a spatial average. In order to calculate a correct spatial average, a value can be calculated for each of the component triangles, by taking the average of each of the apex values. Then the average of all triangle values is calculated. That is what we have done here. If however, a spatial average is all that is required, then samples can be combined and analysed as one. In this case, different amounts of sample from each point must be combined in order to obtain a truly representative sample; one portion for all internal points, 1/3 of a portion for obtuse apices (white dots on right hand edge of diagram, Fig. 1), 1/6 of a portion for acute apices (top and bottom white dots, Fig. 1) and ½ of a portion for the remaining peripheral points. Alternatively, instead of taking samples at the grid points, samples can be taken in the centre of each triangle defined by the grid and combined in equal portions. This method gives 48 sampling points for a half-hexagon having a H/4 grid. These methods assume that the sample taken adjacent to the stem represents the point in the centre of the stem.

If a sampling grid is required for a radially distributed parameter (eg. related to canopy or root system), then the grid described above can be reduced from the half-hexagon described above to 1/6th of the hexagon (an equilateral triangle with apices at three of the white stars in Fig. 1). Taking a sample or measurement at the centre of each of the component equilateral triangles (whatever the resolution of the grid) will result in a sample or data set that is spatially weighted correctly for the radially distributed parameter, assuming that the sampling grid has sufficient resolution to representatively sample the radial gradient. Samples may be combined or measurements may be averaged in order to obtain a representative mean value. If the radial pattern of distribution is desired, then the value of the parameter at each sampling point is plotted against the distance from the tree centre.

In the field, a triangular sampling grid, covering the tree unit hexagon or half-hexagon, can be set up with ropes and no measurements. First, the tree unit perimeter is laid out using ropes, as described above. Then the grid points are located using intersecting lines of sight across marks made on the perimeter ropes (at H/u spacing), and marked on the ground using stakes.

Case study data collection

We examined the radial and grid sampling approaches for characterising spatial variability using data for throughfall, root biomass and soil respiration. Throughfall is important as it is the primary (although not only) determinant of infiltration and soil water balance, and it is often used to calculate rainfall interception. Its distribution is a function of canopy architecture and is therefore more-or-less radial. Root biomass is important because it is a major stock of carbon and nutrients and is indirectly related to uptake of water and solutes. Its distribution is a function of plant architecture and soil properties and is more-or-less radial. Soil respiration is important as it is a major component of the carbon balance and an indicator of biological activity, a major driver of many soil processes. Being a function of soil biological activity, its distribution depends largely on the distribution of roots and inputs of organic matter such as pruned fronds (patch distribution). Many other parameters are known to vary systematically within the tree unit of oil palm plantations, but the principles examined here apply.

Throughfall data was derived from a previous study (Banabas et al. 2008), carried out at Sangara plantation in Papua New Guinea (148° 12′ E, 8° 44′ S) using 11-year-old palms planted at an equilateral triangular spacing of 9.25 m. Average annual rainfall at the site is 2,417 mm (1979–2005). Sampling was carried out over a one-month period (September 2003), during which a total of 234 mm of rain fell on 11 days. The frequency distribution of rainfall event size during the sampling period was similar to that of the longer term; the proportion of daily rainfall values in the ranges <0.1, 0.1–0.9, 1.0–9.9, 10.0–99.9 and ≥100 mm was 53.3, 0.0, 26.7, 20.0 and 0.0 % in September 2003 and 53.6, 6.1, 22.3, 17.9 and 0.2 % in 2002–2004, with maximum values being 59.6 mm in September 2003 and 105.2 mm in 2002–2004. Throughfall was collected in 48 drums, placed under three trees at 1.0, 1.9, 2.8, 3.7, 4.6 and 5.3 m from the centre of the tree, with the number of drums at each distance being proportional to the area represented by that distance (Fig. 1). The drums at 5.3 m distance were located at the point where three hexagonal tree units meet (the Voronoi vertices). The fronds of adjacent palm canopies overlapped considerably, with the fronds extending to a maximum radial distance (ie vertical projection of frond tips) of 6.0–9.3 m (mean = 7.1 m, n = 80, comprising 4 cardinal points of 20 palms in the field in which throughfall measurements were made,). Quadratic equations were fitted to the plot of throughfall versus radial distance and to the upper and lower 95 % confidence intervals of that relationship. The throughfall was then calculated, using Eqs. 10 and 16, with T = 4.625 m and t i  = 0.455 m. Stemflow was also measured using the same three trees during the same period, so that interception could be calculated (interception = rainfall - throughfall – stemflow). To measure stemflow, the frond bases were removed at a height of about 1.5 m and stemflow was directed into a covered 200-L drum using plastic sheet and gutters. The volume of stemflow collected was recorded for each rainfall event.

Root biomass was measured in Bebere plantation, Papua New Guinea (5° 36′S 150° 14′E) in April–August 2011. The palms were 20 years old, with equilateral spacing of 9.25 m. Half-hexagon sampling grids with H/4 resolution were set up for 4 trees, as described above, and dimensions of the management zones were measured. At each grid point, push-tube core samples were taken at depth increments of 0–0.3, 0.3–0.7, 0.7–1.1, 1.1–1.5 and 1.5–2.0 m. The core diameter was 50 mm to 1.1 m depth and 43 mm from 1.1 to 2.0 m depth. For the grid sampling point that theoretically lies under the centre of the tree, two cores were taken, angled slightly towards the centre of the tree, and the average value from these two cores was used. The fresh soil samples were immediately sieved to 5 mm to remove large roots and then to 2 mm to remove small roots. Roots were hand-picked off the sieves, washed, blotted dry, weighed, oven-dried at 75 °C and then weighed again. The biomass values, expressed as dry matter mass, were summed for the size classes and depths, resulting in one value per sampling grid point. Spatially averaged mean values for the tree unit were calculated for H/4, H/2 and H grid resolutions as described above, by calculating a value for each triangle (mean of the 3 apex values) and summing the values for each triangle, ie. 48, 12 and 3 triangles, respectively for the three resolutions.

Soil respiration was also measured at the Bebere site, in May 2012. In the part of the plantation where measurements were made, empty fruit bunches (a byproduct from the palm oil mill) had been applied sometime in the past and their partially decomposed remains were still visible. Half-hexagon sampling grids with H/4 resolution were set up as described above for 4 trees, and dimensions of the management zones were measured. Respiration was measured using a Licor 8100 portable infrared gas analyser, with 100-mm diameter chambers pushed 20 mm into the soil surface and a monitoring time of 150 s per point. At points where the layer of plant residues lying on the surface was too thick to fit in the chamber (in the frond pile), respiration from the residues was measured and added to the value from the soil surface. In order to measure respiration of the residues, they were sampled by cutting a 0.2 × 0.2 m square down to the soil surface. The residue sample was immediately placed in a 20-L bucket with air-tight lid with air circulation fan, and the respiration rate was determined, converted to the same unit area as the soil surface value, and added to the soil surface value. Spatially averaged mean values for the tree unit were calculated as described for the root biomass. Compared to the spatial variation in soil respiration, temporal variation during the course of a day was minimal. To determine temporal variation, soil respiration was measured at the same 6 points (two in the weeded circle, two in the frond pile and two in the between zones area) 16 times over the course of a day, between 05:10 and 20:30. During this period, mean values of soil temperature across the 6 chambers ranged from a minimum of 26.2 to a maximum of 27.1 °C and mean respiration rate across the chambers ranged from 7.4 to 9.9 μmol CO2 m−2 s−1.

For the root biomass and soil respiration data, interpolation between the grid points was carried out using a regularized spline with tension, to create centimetre-resolution raster surfaces (Mitasova and Hofierka 1993), and assuming that values under the trunk were the same as those at the points immediately adjacent to the trunk.

Results

Throughfall (radial pattern)

Throughfall showed a clear radial pattern, being lowest near the trunk and greatest at the mid-point between stems (Fig. 3). Throughfall collected in individual drums was less than rainfall within 2.5 m of the palm centre, consistent with wide and overlapping petioles in this zone. Rain falling in this zone was directed to throughfall further from the stem (due to fronds bending down towards their tips) or to stemflow. The quadratic equation of best fit for the radial distribution of throughfall was z = −0.0455 + 0.1066 t −0.0097 t 2 (r2 = 0.296). The relationship showed throughfall reaching zero at the edge of the trunk, consistent with reality. Close to the trunk, petioles are wide and overlapping, providing almost-complete shelter from throughfall in non-windy conditions, apart from some splashing. The high variation in throughfall between drums was due to the highly variable pattern of rachises and leaflets overhead. The curve-fitting approach allowed us to quantify the effect of the variability on calculated throughfall and interception. Throughfall was calculated to be 79.3 % of rainfall, with 95 % confidence limits being 62.4 and 96.1 % of rainfall. Measured stemflow was 14 % of rainfall. Interception was thus calculated to be 6.7 % of rainfall, with 95 % confidence limits being −10.2 and 23.6 % of rainfall. According to the relationship between throughfall and radial distance (t), throughfall at a particular point equalled mean throughfall for the whole tree unit at t = 2.97 m (0.321S).

Fig. 3
figure 3

Radial distribution of throughfall in Sangara plantation. Points are values for individual collection drums under 3 palms (each palm having a different symbol), the full line is a quadratic equation fitted to the data, dashed lines show the 95 % confidence band, and the horizontal lines are rainfall (upper) and mean throughfall (lower)

Full size image

Root biomass (grid approach)

Root biomass varied systematically across the tree unit, being greatest near the trunk, decreasing rapidly in the first few metres away from the trunk, and then being fairly uniform over the rest of the area (Fig. 4). Although root biomass was slightly greater under the frond pile than the harvest path, its distribution was essentially radial. Root biomass varied by more than one order of magnitude from point to point within each tree unit, and most of the grid sampling points had lower values than the overall mean. The mean value obtained from the interpolated surface was slightly higher than that calculated directly from the H/4 grid values (Table 1). The largest values and the highest standard deviations were both recorded adjacent to the trunks (Fig. 4).

Fig. 4
figure 4

Map of interpolated root biomass parameters: a mean (kg m−2 to 2-m depth, n = 4), b standard deviation, c fractional deviation of interpolated mean value from overall palm unit mean value, and d region in which fractional deviation of mean value from overall palm unit mean value is <0.2. Points show measurement locations and ‘EFB’ is the target zone for application of empty fruit bunches

Full size image
Table 1 Mean and standard deviation (SD) of root biomass and soil respiration values (n = 4) over the half-hexagon, calculated from the H/4 grid values by interpolation (spline fit, mean of mean and SD values at each point) or directly from the grid values using resolution of H/4, H/2 or H where H is the length of a side of the hexagonal tree unit (see Fig. 1)
Full size table

The lower the resolution of the sampling grid, the higher, and more variable among replicates, the estimate of overall root biomass became (Table 1). This increase in estimated root biomass with decreased grid resolution was due to the increased weighting of the sampling point adjacent to the stem, which was common to all resolutions. It would be ideal if one sample could be taken from a location that represented the overall tree unit mean value. As the distribution of root biomass was essentially radial, a polynomial regression was used to model its radial distribution (5th order, r2 = 0.794) and find this location. Using this approach, the radial distance (t) at which root biomass equalled the overall mean was 1.38 m (0.149S). However, two-dimensional interpolation of root biomass values from the 4 replicates showed that a sample value would fall within 20 % of the overall mean in only a very small region (Fig. 4).

Soil respiration (grid approach)

Soil respiration showed a patchy distribution, being highest: near the trunk; in the frond pile; and where empty fruit bunches had been placed (Fig. 5). Soil respiration varied by an order of magnitude from point to point within each tree unit (Fig. 5). The mean value obtained from the interpolated surface was very close to that calculated directly from the H/4 grid values (Table 1). The largest values and the highest standard deviations were both recorded adjacent to the trunk and in areas where fronds and empty fruit bunches had been applied.

Fig. 5
figure 5

Map of interpolated soil respiration parameters: a mean (μmol CO2 m−2 s−1, n = 4), b standard deviation, c fractional deviation of interpolated mean value from overall palm unit mean value, and d region in which fractional deviation of mean value from overall palm unit mean value is <0.2. Points show measurement locations and ‘EFB’ is the target zone for application of empty fruit bunches

Full size image

The lower the resolution of the sampling grid, the higher the estimate of overall respiration became, with the H-derived value being 1.3 times higher than the H/4-derived value (Table 1). This increase in estimated value was due to the increased weighting at lower resolutions of the sampling points adjacent to the stem and in the frond pile, which were common to all resolutions. Interpolation of soil respiration values from the 4 replicates showed that it would be impossible to predict the location of any point that represented the palm unit mean (Fig. 5), consistent with the patchy distribution of empty fruit bunches.

Discussion

Each of the three approaches for sampling a tree unit has advantages and disadvantages. The patch approach is attractive because the sampling locations are easy to see and sample numbers are small. However, the assumption of within-patch uniformity is unlikely to be justified; this assumption would be worth examining further in studies that rely on patch sampling for scaling up. The radial approach is efficient for parameters known to be radially distributed. It lends itself to quantification of variability, which we demonstrated for throughfall. Finally, the grid approach (hexagon, half-hexagon or elemental triangle, depending on the parameter) is unbiased and universally applicable but it is also potentially the most resource-intensive. One advantage of the grid approach over the patch approach is that it accounts for spatial patterns of variability unrelated to patches visible at the time of sampling. This is especially relevant to replanted plantations in which the existing planting has been off-set from the previous planting, as usually happens. Changes in spatial variability that take place over the course of a crop cycle must be taken into account when interpreting results of any sampling program. When using a grid, the resolution required for a particular parameter at a particular degree of precision in a given situation (eg. stand age) should ideally be determined by initially measuring the parameter using a finer-than-necessary grid over a larger-than-necessary number of replicates. However, we are not aware of any such studies and we did not attempt it here either. The 35-point grid we used showed considerable variation in root biomass and soil respiration and we are not able to say what resolution grid is suitable to attain a particular degree of precision for those parameters. ie. the grid resolution was not fine enough to obtain a ‘true’ picture of spatial variation. For both parameters, means calculated from the H/2 and H/4 grid values were similar to each other and to the interpolated (from spline fit using H/4 grid values) mean value (Table 1), suggesting that H/2 sampling resolution might be adequate for those parameters. A H/3 grid (with 22 sampling points in a half-hexagon grid) may provide a useful compromise between sampling effort and precision.

The grid sampling showed that the largest amount of variation coincided with the largest values. Hence, precision would be improved most efficiently by increasing sampling effort (ie. the number or size of samples and the precision with which sample volume is determined) in the locations where the highest values are expected. It is worth considering this for the quantification of root biomass. To date, most studies of root biomass have increased sample size or number with radial distance. We propose that instead, in studies attempting to quantify total root biomass, sampling effort should be greatest under and near the stem. For example, instead of sampling a 30° triangle under and close to stem, more precise values might be obtained by sampling a 45° triangle in that region. In the case of root biomass it should also be kept in mind that although it had an essentially radial pattern in this study, that is not necessarily the case; for example, Ruer (1967) measured significantly higher root mass under the linear frond pile than elsewhere.

The radial approach we used for calculating throughfall, using Eqs. 10 and 16, allowed us quantify its variability. There have been few quantifications of throughfall variability to date; Muzylo et al. (2009) pointed out that lack of consideration of such uncertainty has been a major drawback for modelling interception. In oil palm systems, spatial distribution of throughfall has a major impact on solute leaching and nutrient cycling processes, as the locations where high throughfall is superimposed on high fertiliser concentrations (due to its non-uniform distribution) are potential hotspots of leaching loss (Banabas et al. 2008). Although there was a clear radial pattern in the throughfall data in this study, the large variability encountered limits its use in hydrological studies. The variability was principally due to differences in the position of rachises and leaflets above each sampling point. Hydrological modelling is usually done on an annual time scale or longer, so throughfall data should be collected for longer than the one-month period used here, to give a more precise long-term picture of throughfall distribution and stemflow. The optimum length of such a study period in palm plantations is the time between appearance of two fronds at the same azimuth (directly above each other). In oil palm, this occurs every 21 fronds, due to its 8/21 phyllotaxis, ie. 21 leaves are produced in 8 complete rotations (Henry 1955; Davis and Mathai 1973). Mature palms produce approximately 20–24 fronds per year (Corley and Tinker 2003), so the optimum monitoring period is in the order of 1 year. Interception and throughfall in oil palm plantations are also known to vary with palm age and rainfall intensity (Squire 1984; Dufrêne 1989; Comte et al. 2012).

If the aim of a sampling exercise is to estimate the mean value of a parameter across the plantation (rather than quantifying tree-scale variation), and if the parameter is distributed radially, then it might be possible to reduce sampling effort per tree by sampling at one radial distance only; the distance where the point value of the parameter equals the mean value for the tree unit. Let us call that distance the reference value of t, or t r . Sampling at t r only would allow sampling effort to be directed to larger scales. By fitting a curve to the radial distribution of throughfall and root biomass in our study, t r could be calculated at 0.321S and 0.149S, respectively. The value of t r for any particular parameter could be expected to differ between planting materials, planting densities and sites. For example, lateral distribution of root biomass is known to differ with soil type (Nelson et al. 2006) and genotype (Nodichao et al. 2011). Given the sampling effort involved in properly accounting for tree-scale variability, it might be worthwhile determining appropriate values of t r for particular situations. Unfortunately though, our results suggest that, for 4 replicate measurements of root biomass, it would not be possible to locate a value of t r that gives a root biomass value within 20 % of the overall tree unit mean.

Soil respiration rate was presumably controlled largely by the magnitude of organic matter inputs. High respiration rates in the locations where pruned fronds and empty fruit bunches had been placed were presumably due to heterotrophic respiration due to the high carbon inputs in these locations (Lamade et al. 1996; Adachi et al. 2006; Law et al. 2009; Goodrick et al. in press). High respiration near the trunk was probably due largely to roots and decomposition of root-derived organic matter, as root biomass is high here, although inputs of dissolved organic matter in stemflow may also be significant.

In this paper we examine data for only three parameters in oil palm plantations, but the principles are the same for other parameters and tree species (in equilateral plantings). The case of fertiliser distribution and soil chemical properties is worth particular mention. Whether spread by machine or by hand, fertiliser distribution generally has a systematic pattern at the tree scale. A grid approach to sampling would seem the most appropriate, because the pattern is unlikely to be radial or related to visible zones. It might be possible to massively increase the number of point-scale measurements that can be made using hand-held remote sensing tools in the field. Gamma ray spectrometry is particularly promising for soil properties related to mineralogy and perhaps potassium fertiliser distribution (Pracilio et al. 2006) whereas visible to mid-infrared spectroscopy is particularly promising for soil properties related to organic matter content (Viscarra Rossel et al. 2006; Kuang et al. 2012). Similarly, soil physical and biological properties and processes have highly variable but systematic patterns within the tree unit. Although we have focussed on systematic variations within the tree unit we also acknowledge that there is variation at the tree-scale that is not related to planting configuration and management in the ways discussed and these variations may also be important for processes.

When using point measurements to estimate field- or landscape-scale values of a parameter, it is important to consider tree-scale variability only if it is as large or larger than field-scale variability. For the parameters we examined, variability within tree units was indeed as large or larger than variability between tree units, confirming findings of others (eg. Anuar et al. 2008; Law et al. 2009). For throughfall this can be seen by comparing individual point measurements in Fig. 3. For root biomass and soil respiration it can be seen by comparing the spatial variation in mean values (Figs. 4a and 5a) with the between-tree standard deviation at any particular location (Figs. 4b and 5b). When designing a sampling program to characterise fields or landscapes it may be most efficient to consider the tree- and field-scale variability together. For example, points on a tree-scale grid need not all be sampled in a particular tree unit but could instead be distributed across the field.

In conclusion, future studies in plantations should account for tree-scale lateral variation using well-defined sampling and calculation techniques, such as those presented here for equilateral triangular planting configuration. For comparative studies it may not be necessary to account for tree-scale spatial variability, but for studies requiring area-based values it is. The tree unit (a hexagon or symmetrical portions thereof) can be delineated in the field using simple techniques. The tree unit can be sampled, either for multiple individual analyses or for preparing representative composite samples, using one of three approaches depending on the parameter in question. A grid approach is desirable for complex or unknown patterns of variability (eg. due to patchy and overlapping patterns of water, plant residue and fertiliser inputs), but sampling resolution should be high in locations where the parameter changes markedly with distance. For radially distributed parameters, samples can be taken in a triangular portion of the tree unit or along radial transects, and spatial averages and variability can be quantified using the procedures presented here. For throughfall studies in oil palm, the sampling period should be at least 1 year in duration. If using a patch or zone sampling approach then the assumption of uniformity within patches might need to be considered. The three approaches defined here form a basis for sampling programs that account for tree-scale variability. However, further studies are warranted to design efficient sampling procedures for given levels of precision for the scale of interest.