Introduction

Classically, the assessment of bioequivalence (BE) relies on the concept of average BE (2). Two drug products, a generic (i.e., the drug product under evaluation) versus the innovator’s are considered to be bioequivalent if the calculated 90% confidence interval (90% CI) for the ratio of the mean measures of bioavailability (AUC, Cmax) lies between the predefined BE limits of 0.80–1.25 (2). Although this definition of BE has the advantage of a priori ensuring the relative risk for the consumers, it also carries the demerit of high producer risk in case of highly variable (HV) drugs (3–5). In other words, as intrasubject variability increases, a higher rejection rate of BE for truly equivalent drugs is observed. Therefore, it becomes too difficult to establish BE unless a large number of subjects is recruited to achieve adequate statistical power.

In order to face off this drawback, an arbitrary widening of BE limits to constant pre-specified values such as 0.75–1.33 or 0.70–1.43 has been suggested (6–8). However, this approach appears less sensitive to detect differences between the means compared with the classic unscaled BE limits when low or moderate variability is encountered (9). An alternative procedure is based on scaled BE limits which are not constant but widen with intrasubject variability, allowing thus HV drugs to be declared bioequivalent (10–13). However, the continuous widening of the scaled BE limits leads to very broad acceptance limits of BE and consequently high consumer risk. To face off this drawback, novel scaled BE limits have been proposed containing an effective constraint criterion. These newly proposed BE limits scaled with intrasubject variability but incorporate also a GMR-dependent criterion, which makes them less permissive as GMR values depart from unity (14). A different approach in the development of GMR-dependent limits has appeared in literature recently. These scaled BE limits (termed BELscE, BELscM, BELscW depending on the type of function used to model the rate of gradual change of the BE limits) were developed to combine the classic (0.80–1.25) and expanded (0.70–1.43) BE limits into a single criterion (1). The gradual expansion, from the classic to the expanded limits, was accomplished by constructing the BE limits to scale with intra-subject variability but until a maximum “plateau” value. In order to further reduce the consumer risk at high GMR values, a GMR-dependent constraint factor was also incorporated. Even though the performance of the new BE limits is improved, the inclusion of the GMR makes them more complicated and potentially can reduce their estimation accuracy.

The objective of the current study is to develop novel scaled BE limits which are levelling-off exclusively as a function of intrasubject variability. Two model functions are used to ensure the gradual change of the BE limits from a starting value towards a predefined plateau value. The performance of the new BE limits is evaluated and compared with the classic (0.80–1.25) and the expanded (0.75–1.33) BE limits.

Theory

The Classic Approach to Bioequivalence

Determination of average BE of two drug products (test versus reference) is usually based on the comparison of the means of a logarithmically transformed metric such as ln(AUC) and ln(Cmax). Bioequivalence is considered if the calculated 90% CI relevant to the difference of the log means falls between specific predefined values for the upper and lower BE limits (15).

Assuming the classic two-treatment, two-period, crossover BE study design, with equal numbers of subjects in each sequence, the upper and lower limits of the 90% CI are given by Eq. (1) (11):

$$ {\text{Upper, Lower limits of the 90\% CI}} = \exp {\left( {\operatorname{Diff} \pm t_{{0.05,N - 2}} s{\sqrt {2 \mathord{\left/ {\vphantom {2 N}} \right. \kern-\nulldelimiterspace} N} }} \right)} $$
(1)

where Diff is the difference between the test and reference means of the logarithmically transformed metric, s is the intrasubject variability (calculated from the mean square error of ANOVA), and N is the number of subjects participating in the BE study. Since upper and lower BE limits are symmetrical [see Eq. (1)], from this point further in the current analysis we will refer only to the upper BE limit.

The major feature of this definition of BE relies on the fact that two constant borderline values (0.80 and 1.25) are assigned for BE limits (Prerequisite 1). Under this condition, extreme geometric mean ratio values, which ensure bioequivalence, converge at unity as intrasubject variability increases (14,16). In other words, when upper and lower BE limits are fixed, the demonstration of BE requires that the means of two products must be closer as variability increases.

Although setting constant the BE limits is conceptually fundamental, however, the 0.80–1.25 limits appear very strict in case of HV drugs i.e., a high producer risk is encountered. On the other hand, the expanded 0.75–1.33 and 0.70–1.43 BE limits suffer from the exactly opposite behavior, namely, they appear to be too permissive even for drugs which are much different; thus the GMR can unacceptably be either too low or high. In order to remedy this demerit of the expanded BE limits, it was suggested to use either the classic 0.80–1.25, or the more liberal (e.g., 0.75–1.33) (7) BE limits only beyond a “switching” variability value (13). However, apart from the fact that in this case two criteria are required, applying an arbitrarily chosen “switching” variability value can lead to unfair treatment of different formulations of the same drug when it is evaluated in separate BE studies (1). The major cause of this attribute is the inherent discontinuity when these two bioequivalence criteria are concomitantly applied.

Scaled BE Limits

Since the cause of failure of the classic unscaled limits is the high producer risk as variability increases, the development of scaled BE limits which incorporate the magnitude of intrasubject variability, would be of great importance (Prerequisite 2).

The use of scaled BE limits reflects the need that the limits should be more liberal as variability increases (in accordance with Prerequisite 2). The basic characteristic of scaled BE limits is their gradual expansion with intrasubject variability (10,11,13).The general form of the upper scaled BE limit is expressed by Eq. (2):

$$ {\text{Upper BE limit }} = {\text{ exp}}{\left( {k{\text{ }} \times {\text{ }}s} \right)} $$
(2)

where k is a proportionality constant.

However, based on the definition of scaled BE limits, it is obvious that these limits show a continuous increase with variability which leads to the violation of the Prerequisite 1. Since, large deviations of geometric mean ratios from unity can be observed, the concomitant application of a secondary constraint criterion on GMR was proposed (8). This secondary criterion suggests that the estimated ratio of geometric means should be constrained in the range 0.80–1.25.

GMR-Dependent Scaled BE Limits

The recently proposed GMR-dependent scaled BE limits (BELscE, BELscM, BELscW) satisfy Prerequisite 2 since their upper values (or symmetrically the lower limits) scale between a predefined basal value (e.g., 1.25) and a levelling-off extreme value (e.g., 1.43). These BE limits do not comprise unique and globally constant values for the upper and lower limits, since they incorporate characteristics (GMR, s) of the study for the definition of the levelling-off extreme value (1).

A demerit of GMR-dependent BE limits is the fact that in order to express a desirable behavior they incorporate two additional variables. The first is intrasubject variability which, according to Prerequisite 2, constitutes a necessary component of a BE limit, while the other variable is the geometric mean ratio. The inclusion of GMR is based on the need that BE limits should be less strict for a study with GMR around unity in comparison to a study exhibiting GMR close to the marginal value of 1.25 (14). In other words, using a GMR-dependent constraint factor ensures a lower consumer risk as the GMR of the study becomes higher.

Novel Scaled BE Limits

Although, the inclusion of GMR in the calculation of BE limits improves their performance in power curves, this additional variable contributes to the complexity and possibly reduces the estimation accuracy of the BE limits.

In order to satisfy both Prerequisites 1 and 2, and construct BE limits not dependent on GMR, an alternative procedure is proposed in this study. The BE limits developed are composed of the following two main elements: a minimum “basal” value of the limit (e.g., 1.25, 1.20 etc.) and an additional quantity (called “BE limit expansion function,” BEef) which is a function of intrasubject variability and a pre-defined extreme value for the upper limit. Mathematically, the new upper BE limit has the form:

$$ {\text{Upper BE limit }} = {\text{ basal BE limit }} + {\text{ BE}}_{{{\text{ef}}}} {\left( {s{\text{, extreme upper limit value}}} \right)} $$
(3)

A variety of different model functions can be used to achieve the desirable behavior of BEef. The specific form of BEef affects the “rate” of gradual change of the BE limit. In this study, two model functions (Sigmoid and Weibull) were considered for the design of the upper BE limit as shown in Eqs. (4) and (5), respectively:

$$ {\text{Upper BE limit }}S = \alpha + \frac{{\beta - \alpha }} {{1 + e^{{ - {\left( {\frac{{\operatorname{CV} - \operatorname{CV} _{0} }} {\gamma }} \right)}}} }} $$
(4)
$$ {\text{Upper BE limit }}W = \alpha + {\left( {\beta - \alpha } \right)}{\left( {1 - e^{{ - (\gamma s)^{2} }} } \right)} $$
(5)

where α is the minimum or “basal” value of the upper BE limit, β is the maximum or “plateau” value of the upper BE limit, and γ is a constant controlling the “rate” of gradual change of the upper BE limit. The terms CV and CV0 represent the coefficient of variation of the study and the coefficient of variation at the inflection point, respectively.

Tables I and II summarize the values for the various parameters of Eqs. (4) and (5) used to design the new BE limits. Using different combinations for α, β, γ, (and CV0 only in case of the Sigmoid model) a variety of different BE limits are defined. The simplest choice for the value of the parameter α, is the value of the classic upper BEL, α = 1.25 (A and B columns of Tables I and II). However, if a more strict criterion is required the value of 1.20 can alternatively be assigned (C and D columns of Tables I and II). Regarding the value of the plateau level, a possible choice is to set β equal to 1.43 (A and C columns of Tables I and II) or to 1.33 (B and D columns of Tables I and II), which correspond to the already adopted values by the regulatory agencies for the upper expanded BE limits (7). Since γ controls the gradual change of BE limit with variability, a variety of γ values were considered, Tables I and II.

Table I A Set of New Scaled BE Limits Considered in the Study: Sigmoid Model Eq. (4)
Full size table
Table II A Set of New Scaled BE Limits Considered in the Study: Weibull Model Eq. (5)
Full size table

Materials and Methods

Extreme GMR Accepted Values Versus Intrasubject Variability

The concept of maximum acceptable difference was initially introduced by Schuirmann (16). Thus, transforming Eq. (1), in the case where the upper limit of the 90% CI falls exactly on the upper preset BE limit, Diff becomes equal to the maximum acceptable difference between the means (11), Diffmax:

$$ {\text{Diff}}_{{{\text{max}}}} = \operatorname{l} {\text{n}}{\left( {{\text{Upper BE limit}}} \right)}-{\left( {t{}_{{0.05{\text{,}}N - 2}}s{\sqrt {2 \mathord{\left/ {\vphantom {2 N}} \right. \kern-\nulldelimiterspace} N} }} \right)} $$
(6)

The maximum acceptable ratio of geometric means, GMRmax, of the two formulations is equal to exp(Diffmax). Plots of the new BE limits (Tables I and II) and extreme GMR values which ensure BE as a function of the coefficient of variation (CV) for various values of N (12, 24, 36…) were constructed.

Simulated BE Trials

Two-treatment, two-period, crossover bioequivalence studies, with equal number of subjects in each sequence, assuming N  =  12, 24, 36 were simulated using the BE limits listed in Tables I and II. Bioequivalence was declared if the 90% CI around the ratio of the estimated geometric means for the two drug products was between preset BE limits; to this end, the two one sided tests procedure was used (16). The average parameter value for the reference formulation was set to 100 arbitrary units and lognormal distribution was assumed. The true CV values considered for the simulations, ranged from 10 to 60%. The standard deviations (σ) of the logarithmically transformed parameters were calculated from the preset CV according to the formula: \( \sigma = {\sqrt {\ln {\left( {1 + \operatorname{CV} ^{2} } \right)}} } \). The true GMR (GMR0) was gradually changed, from the condition of GMR0  =  1.00 to GMR0  =  1.50.

Twenty thousand simulated BE trials were performed under each condition. The percentage of accepted studies was recorded and power curves were constructed by plotting the percentage of acceptance versus the true value of the GMR0. Assuming lognormal distribution of the pharmacokinetic parameters, s was estimated as the square root of the mean square error term of ANOVA for the ln transformed data, while CV was calculated from the relationship: \( \operatorname{CV} = {\sqrt {\exp {\left( {s^{2} } \right)} - 1} } \).

In addition, a non-parametric approach was also used for the statistical evaluation of BE for the specified in Tables I and II scaled BE limits. To this end, the BE criterion was rewritten in a form similar to that presented by Hyslop et al. (17): \(\theta _{{sc}} = {\left( {\mu _{T} - \mu _{R} } \right)}^{2} - {\left[ {\ln {\left( {{\text{Upper}}\;{\text{BE limit}}} \right)}} \right]}^{{\text{2}}} \leqslant 0\)Bootstrap samples were obtained from the original data set of simulated subjects’ response variables with re-sampling stratified by sequences, to create 1999 bootstrap estimates of the metric θ sc. The 95% upper confidence bound of the criterion was determined as the 95th percentile of the distribution of bootstrap estimates of θ sc. BE was declared if the non-parametric bootstrap 95% upper confidence bound of the criterion was less than or equal to zero. Simulations were performed assuming either GMR0  =  1 with N = 24 (CV  =  10, 20, 30, 40 and 60%) and N  =  36 (CV  =  30 and 40%), or GMR0  =  1.25 with N  =  24 (CV  =  30 and 40%). Five hundred simulation runs were performed under each scenario. In parallel, BE was assessed for the original simulated data set using the classical 90% CI approach and the degree of concordance between the two methods was recorded. There was a good concordance of BE acceptance declared by the two methods (the degree of concordance ranged from 95.2 to 100.0%). In all cases, the non-parametric bootstrap approach appears to be somewhat more liberal than the classic approach. Relying on these results and as the bootstrap procedure is computationally intensive and extremely time consuming, the assessment of BE in the present work was based on the classic 90% CI approach which provides a good approximation for the statistical evaluation of the BE. Nevertheless, it is worthy to mention that application of the classic 90% CI approach is correct only asymptotically since the degree of concordance of the two approaches may be lower when N is very small (e.g., N  =  6).

The entire programming work was implemented by developing a computer program in FORTRAN.

Coverage Studies

The estimation accuracy of the scaled methods was assessed by recording the number of times (in %) the GMR0 value fell within the simulated BE limits as GMR0 varied from 1.00 to 1.50. For comparative purposes, the percentage of GMR0 within simulated BE limits was plotted vs. the difference “GMR0 − upper BE limit0”. Simulated BE limits correspond to the scaled BE limits calculated from s and GMR estimates derived from the BE study, while the upper BE limit0 is the true limit calculated from preset σ and GMR0.

Results and Discussion

In order to design the most appropriate BE limits, we first studied the effect of the model parameters on the profiles of extreme GMR versus ANOVA-CV%. In several cases, undesirable properties were observed depending on the parameters’ values of the model functions. The exclusion of the GMR constraint factor (1) from the model may result in undesired properties for the extreme GMR vs. CV plots, namely, non-monotonic curves. This drawback is observed when there is a “high rate” of gradual change of the BE limit with variability. Two characteristic examples are shown in Fig. 1. The first example is a Weibull type BE limit, AW5, which is based on the same equation as the limit BELscW (1), but without the inclusion of the GMR constraint factor. It is worthy to mention that BELscW shows a monotonic decline of the maximum extreme GMR values with CV (1), while AW5 (see Table II) shows the undesired performance presented in Fig. 1. Another example, is the Sigmoid BE limit C1S4 (see Table I); in this case, the GMR vs. CV plots are also non-monotonic, Fig. 1.

Fig. 1
figure 1

Extreme GMR values, which ensure bioequivalence, vs. ANOVA-CV% for the scaled BE limits AW5 and C1S4 (see Tables I and II).

Full size image

However, when there is a smooth change of the BE limit from the “starting” to the “plateau” value, as CV increases, the aforementioned drawback of the extreme GMR vs. CV plots vanishes. Among the various Sigmoid and Weibull models quoted in Tables I and II, some of them (written with italics in Tables I and II) have the desired properties and were selected for further analysis using power curves. Extreme GMR vs. CV plots for four new BE limits (B2S6, D3S8, Table I; BW4, DW4, Table II) are shown in Fig. 2. The GMR acceptance region has a convex shape which is similar to that of the classic unscaled 0.80–1.25 limits and constitutes a desired property for a scaled method, since GMRmax declines (or equivalently GMRmin increases) with ANOVA-CV%. Using a larger number of subjects, the corresponding curves exhibit less steep slopes i.e., they show a more permissive behavior. Obviously, a more strict performance is observed when a smaller number of subjects is recruited. It should be noted that the four new BE limits become more permissive than the classic unscaled 0.80–1.25 BE limit (14) as variability increases. It should be emphasized that the convexity of the GMR versus CV plots ensures that as intrasubject variability increases, the demonstration of BE requires a smaller difference of the means of the two products. In contrast, a simple scaled method, e.g., the simple linear scaled BE limits proposed by Boddy et al. (10), leads to a non-convex shape of GMR versus CV plot [see Fig. 2 of (14)]. This type of plot implies that studies with higher GMR ratios can be accepted as variability increases, a consequence that violates the fundamental concept of bioequivalence.

Fig. 2
figure 2

Extreme GMR values, which ensure bioequivalence, for the novel scaled BE limits as a function of intrasubject variability.

Full size image

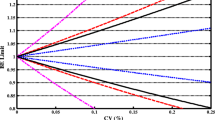
The 15 BE limits, written in italics in Tables I and II, exhibited a desired behavior in extreme GMR vs. CV plots and were subjected in power curves analysis. Four of these 15 BE limits namely, B2S6, D3S8, BW4, and DW4 (indicated with bold in Tables I and II) showed also a satisfactory statistical performance. Figure 3 illustrates the upper BE limits as a function of intrasubject variability (in terms of ANOVA-CV%) of these four new BE limits along with the classic 0.80–1.25 unscaled BE limit (BEL), the extended 0.75–1.33 BE limit (BELw2), and the most well known simple scaled BE limit BELsck1 (10). All new BE limits, in contrast to BEL and BELw2, become wider as variability increases and approach the predefined plateau value of 1.33, Fig. 3A. In the contrary, the upper BE limit of BELsck1 increases continuously as a function of CV, leading to very broad acceptance BE limits, Fig. 3B.

Fig. 3
figure 3

(A) Novel scaled BE limits as a function of intrasubject variability. (B) Graphical representation of one novel scaled BE limit (B2S6) with leveling-off properties in comparison to the most well-known simple scaled BE limit (BELsck1) proposed by Boddy et al. (10).

Full size image

Figure 4 shows the percentage of studies in which BE is declared as a function of GMR0 by applying the four novel BE limits, as well as the classic unscaled BEL, the extended BELw2 limit, and the scaled limit BELsck1. Two-period crossover simulated studies were performed assuming 24 subjects and four levels of ANOVA-CV%: 10, 20, 30, and 40%. At low variability levels two of the novel BE limits (B2S6 and BW4) show similar performance to the 0.80–1.25 criterion, while the other two (D3S8 and DW4), as expected from their design, appear to be less permissive. This performance is desirable for the evaluation of toxic drugs (11). As intra-subject variability increases, all novel BE limits show higher percent acceptance values comparing to the classic BEL. At CV = 30% the new BE limits exhibit much higher statistical power than the classic BEL and at higher variability levels (CV ≥ 40%) they show almost identical behavior with BELw2. Similar results are obtained for N = 12 (data not shown) and N = 36 (data for CV 30 and 40% are shown in Fig. 5). Compared to the recently proposed GMR-dependent BELscW, for CV values ranging from 10 to 30%, the statistical power for the new approaches remains practically unaffected, while at higher variability levels (CV ≥ 40%) the new BE limits appear to be less permissive than BELscW (1). These findings are in full accordance with the theoretical expectations based on the design of the novel BE limits. In contrast to all abovementioned BE limits, the percent acceptance of the BELsck1 increases continuously as variability becomes higher, Figs. 4 and 5. At low CV values, BELsck1 appears very strict, while at high CV levels BELsck1 becomes very liberal. For example, at CV = 40% BE studies with GMR ratio higher than 1.25 can be accepted with substantial probabilities, Figs. 4 and 5.

Fig. 4
figure 4

Acceptance (%) of BE studies by seven procedures at various ratios of the true GMR assuming N = 24.

Full size image
Fig. 5
figure 5

Acceptance (%) of BE studies by seven procedures at various ratios of the true GMR assuming N = 36.

Full size image

The estimation accuracy of three scaled methods (BW4, BELscW, and the scaled BE limit BELsck1 which is based on Eq. (2) with k = 1) at various ratios of the true GMR, assuming N = 24, is presented in comparison to BEL in Fig. 6. Similar results (data not shown) are obtained for N = 12 and 36. All new BE limits (B2S6, D3S8, BW4, DW4) posses almost identical performance; thus, for reasons of clarity, only BW4 is depicted in Fig. 6. It is worthy to mention that although BELscW incorporates two variables (s, GMR), whereas BELsck1 only s, their estimation accuracy is similar at all CV levels. This finding is attributed to the leveling-off properties of the BELscW model function. The percentage of GMR0 within the simulated BE limits shows a sharp decline for the new BE limit BW4, Fig. 6. At all ANOVA-CV% levels, BW4 shows better estimation accuracy than BELscW and BELsck1. Interestingly, this attribute becomes more evident at high CV values. This behavior of the new BE limits is expected, since they are practically not dependent on intrasubject variability at high CVs as they are leveling-off at the predefined plateau value 1.33, see Fig. 3. The more accurate estimation of the new scaled BE limits compared to BELscW is due to the absence of the GMR factor in the model function. On the other hand, the better performance in terms of estimation accuracy of the new scaled BE limits compared to BELsck1 is attributed to the different structure of the model function.

Fig. 6
figure 6

Coverage estimation of three scaled methods in comparison to BEL at various ratios of the true GMR assuming N = 24. X-axis was normalized for comparative purposes.

Full size image

Conclusions

The basic feature of the new BE limits (B2S6, D3S8 and BW4, DW4) is their gradual expansion which combines the performance of the classic BEL at low and moderate variability with the more “permissive” behavior of the expanded BELw2 at high variability values. This new approach allows the application of a single BE criterion, which is continuous and has leveling-off properties. The new BE limits appear to be highly effective at all levels of variation investigated. Furthermore, the estimation accuracy of the new scaled BE limits is improved compared to BELscW, without a significant change in statistical power.