1 Introduction

New federal policies, backed by federal incentive programs such as the Race to the Top Act of (2011) and the Teacher Incentive Fund (TIF) grants, have systematically changed the way in which most U.S. public school teachers are annually evaluated. For the first time in history, most school administrators are required by state-adopted policies (developed in reaction to the aforementioned federal initiatives) to evaluate their teachers based in “significant part” on student growth (Duncan 2009, 2011; Race to the Top Act of 2011).

This is being done most often using student achievement data to measure growth via value-added models (VAMs) or growth models (e.g., the Student Growth Percentiles (SGP) model; Betebenner 2009b), although growth models are not typically considered to be VAMs by methodological purists conducting research in this area. VAMs are designed to measure the amount of “value” that a teacher “adds” to (or detracts from) a student’s growth on large-scale standardized achievement tests over the course of each school year by controlling for students’ prior testing histories. This is also done, sometimes, while controlling for student-level variables (e.g., demographics, English proficiency status, special education status) and school-level variables (e.g., class size, school-level demographics), as available and specified by each model. While growth models are designed to do essentially the same thing in overall purpose, they are not typically as sophisticated in model design, they do not typically use statistically complex controls, and they are accordingly (and in many ways appropriately) typically used for more descriptive versus causal purposes (although this is not always the case).

Regardless of model use, the points are to measure student growth or value added (hereafter, for purposes of this study, referred to as growth) and make inferences about how teachers and their relative levels of effectiveness may have impacted such student growth over time. Currently, 44 states and the District of Columbia have adopted and implemented policies to measure teacher effectiveness based on student growth, all of whom (100 %) are using their large-scale standardized tests in mathematics and reading/language arts as mandated by No Child Left Behind (NCLB; 2002) to calculate this growth over time (Collins and Amrein-Beardsley 2014; see also National Council on Teacher Quality 2013).

However, a majority (i.e., approximately 70 %) of teachers across states are not eligible to receive individual, teacher-level growth scores (Collins 2014; Gabriel and Lester 2013; Harris 2011). This is because all growth models, as currently being used, rely primarily if not solely (at the state level) on the aforementioned large-scale standardized tests to measure growth. This, in effect, makes all teachers who teach in non-tested grades and subject areas ineligible for individual, teacher-level value-added scores.

This typically includes teachers of the primary grades (i.e., K-2), teachers of elementary subject areas that are not typically tested using such large-scale tests (e.g., science, social studies, music, art, physical education, special education, bilingual education, foreign language), and teachers in high schools who teach more specialized subject areas also not often tested using such large-scale tests (e.g., geometry, physics, world history). While there are legitimate reasons why such grade-level and subject area teachers should be excluded from such value-added systems (e.g., testing young children in K-2 might not be appropriate or wise, testing the arts might stifle the discipline meant to unbridle imagination and creativity, the selection biases prevalent when high school students self-select into certain courses), for the purposes of teacher evaluation, especially when high-stakes consequences are attached to growth output (e.g., merit pay, tenure, termination), there does indeed exist an issue with fairness.

The most common approaches to help pacify this problem have been to (1) substitute non-eligible teachers’ growth scores with aggregated school-level growth scores, as based on eligible teachers’ growth scores typically aggregated at the school-level, or (2) use end-of-course exams, commercially available tests (e.g., the Galileo system), or student learning objectives (SLOs) that are teacher-developed and administrator-approved, to hold non-eligible teachers accountable for their students’ growth as not only more individually, comprehensively, and loosely but also more subjectively defined (Gill et al. 2014). While there is some emerging evidence that SLOs might help to evaluate teachers “better” in that SLOs capture more holistic and authentic indicators of student growth (Gill et al. 2014), whether SLOs can serve as valid and useful replacements for the test-based and, hence, “more objective” growth measures has yet to be deliberated, particularly in policy arenas where calls for increased objectivity are seemingly more prevalent (see, for example, Weisberg, Sexton, Mulhern, and Keeling 2009).

In terms of using commercially available tests to increase inclusivity, and thereby fairness, one highly urban, high-needs, elementary school district in the state of Arizona sought to use an alternative achievement test (i.e., the Northwest Evaluation Association’s (NWEA) Measures of Academic Progress for Primary Grades (MAP)) to allow for its primary grade teachers (i.e., K-2) to be equally eligible for individual, teacher-level growth scores (the state of Arizona uses the aforementioned SGP growth model; Betebenner 2009b), as well as the monetary bonuses that were to come along with demonstrated growth. The goal here was to supplement the district’s growth approach, as aligned with the state’s growth approach, with additional test-based data to include more non-eligible teachers in the district’s overall growth system.

Doing this, however, warranted further investigations into (1) whether the different tests to be used were aligned in terms of achievement outcomes and (2) whether the growth estimates derived via the different tests yielded similar output (i.e., concurrent-related evidence of validity). If this district’s K-2 teachers were to be held accountable in ways similar to their grade 3–8 colleagues, researchers needed to investigate whether the new and purportedly fairer and more inclusive system yielded similar information and results from which valid inferences could be made.

2 Purpose of the study

At the request of district administrators, researchers in this study investigated whether the test the district adopted, the NWEA MAP (hereafter referred to as the MAP), again as designed for use in all grades, including early childhood grades (i.e., K-3), was aligned with the large-scale standardized tests being used across the state in grades 3–8, both in terms of achievement outcomes and growth in achievement over time. Researchers sought evidence of concurrent-related evidence of validity to examine these relationships. However, given the district was only using both the MAP and the state’s tests in only two grade levels (i.e., 3–4), researchers had to investigate results only for these grades and then use results to generalize downwards into the grades in which the district only used the MAP (i.e., K-2). This data limitation forced an assumption that the NWEA K-4 tests function similarly across grades K-4.

That being said, researchers defined and operationalized concurrent-related evidence of validity in this study as “the degree of empirical correlation between the test scores and [other, similar] criterion scores” (Messick 1989, p. 7). The output data of the state test and MAP—the other “similar” test to be used by the district—served as the criterion scores of interest here. Neither the state test nor the MAP, however, served as the criterion of choice as either could have very well been superior to the other or equally superior or the inverse. The goal was just to examine the criterion output given the very real differences between both sets of tests.

For example, while the state test is a criterion-referenced, standards-based test, developed by the Pearson Corporation, and it is administered to students via traditional means (i.e., paper and pencil), it is not without issues common to criterion-referenced tests (Linn 1980; Popham 1993; 2011), nor is it without issues prevalent when using criterion-referenced tests to measure student growth over time (see, for example, Betebenner 2009a). Likewise, the computer-adaptive MAP is a norm-referenced test and therefore not as closely aligned with state standards. But it is also developed to measure growth, although critics also have concerns about whether the NWEA’s growth index is indeed the “best-in-class” measure as claimed (NWEA, n.d.). Related, NWEA markets and sells their tests to districts using sometimes questionable statements about their “educational assessment solutions” (NWEA, n.d.). Even though the NWEA holds a non-profit status, NWEA sales (reported at $84 million in 2012) have caused additional concerns. In short, the NWEA, like Pearson, is certainly a company competing for business in today’s era of test- and growth-based accountability (Shaw 2013, March).

Nonetheless, researchers aimed to examine the criterion output given the differences between and among both sets of tests by exploring the following research questions: (1) Were the achievement scores for both test measures correlated? This was important as a necessary precondition for the second research question: (2) Were the growth output derived via both test measures correlated? The assumption was that if both of the grade 3 and 4 test results aligned, particularly in terms of growth output, the empirical correlations between the test scores on achievement and growth in achievement would yield concurrent-related evidence of validity. This evidence would help to validate the district’s use of this test for their intended purposes. Researchers could then support the conclusion that the MAP, if presumably valid in grades 3 and 4, could be used for the lower grades. Again, however, this forced the assumption that results generalized downwards into grades K-2 where only the MAP was to be used, assuming that the NWEA K-4 tests function similarly across grades K-4.

3 Literature review

As now widely recognized, educational policy attention at federal, state, and local levels has, particularly within the past decade, turned most intently to educational reforms based on holding teachers accountable for the learning gains their students make, by using proxy year-to-year growth in student performance on states’ large-scale standardized tests. This was and continues to be triggered by the promises and sometimes exaggerated potentials of such growth models. These promises and potentials (and perils) were most recently debated, for example, in Chetty et al. (2011)) and Adler (2013), as well as in Chetty et al. (2014) and Pivovarova, Broatch, and Amrein-Beardsley (2014).

Regardless, the U.S. Department of Education is still the largest entity promoting accountability policies based on growth models to improve upon the precision with which the nation might better evaluate teacher effectiveness and also hold teachers accountable when their effectiveness is not evidenced or observed. Indeed, it was the U.S. Department of Education (2006) that began to advance growth-based measures and their accompanying educational policies when they first funded their growth model project to inform the reauthorization of the accountability provisions written into NCLB (2002). While before and since their growth model pilot, a plethora of research-based issues were prevalent and have since emerged with greater fervor, the nation is still moving towards adopting growth-based accountability for all, also given the nation’s new tests to be aligned with the Common Core Standards (Duncan 2014).

The research-based issues (in many ways still) of concern include, but are not limited to, issues surrounding whether these models are (1) reliable—or consistently measure teacher effectiveness over time; (2) valid—or appropriately capture what it means to be an effective teacher; (3) biased—or reward/penalize teachers as based on the types of students non-randomly assigned to their classrooms; (4) fair—or can be used to reward/penalize all teachers in similar ways; (5) transparent and useful—or yield visible, comprehensible, and useful data that might help teachers teach better and help students learn more; and (6) used well for their intended purposes, given their research-based limitations and the series of unintended consequences that, also as per the research, sometimes accompany (in)appropriate use. While one can read about these research-based issues in more depth in the academic literature (see, for example, the recent position statement released by the American Statistical 2014; see also Amrein-Beardsley 2014; Baker et al. 2010; Berliner 2014; Haertel 2013; Rothstein 2009), on what researchers specifically focused in terms of the literature for this study were matters related to (1) fairness, (2) reliability, given reliability is a precondition to what was most central to this study, and (3) validity.

3.1 Fairness

Issues of “fairness” arise when a test, or its formative (e.g., informative), or more importantly in this case summative (e.g., summary and sometimes consequential) uses impact some teachers more than others in unfair yet often consequential ways (e.g., merit pay). Because the concept of fairness is a social rather than statistical or psychometric construct, however, its definition depends on what might be agreed upon or considered to be fair (Society for Industrial and Organizational Psychology 2003). Fairness, particularly as researchers defined it here, then, is an indicator of the equitable treatment of those involved in any testing and measurement system, which includes teacher evaluation systems as based on large-scale standardized tests and test-based growth measures. Whereby all teachers are not eligible for equitable treatment in terms of the standardized tests administered, or the growth calculations using standardized test outcomes, or the testing conditions especially when test outcomes are attached to high-stakes (e.g., merit pay, tenure, termination), there exists a need for the equitable treatment of teachers.

As also stated prior, the main issue here is that growth estimates can be produced for only approximately 30 % of all teachers across America’s public schools (Collins 2014; Gabriel and Lester 2013; Harris 2011). The other 70 %, which can include entire campuses of teachers (e.g., early elementary teachers, teachers of non-core subject areas, and high school teachers), cannot altogether be evaluated or held accountable using individual, teacher-level growth data. What VAM-based data provide, rather, are outcome measures for “only a tiny handful [30 %] of teachers” (Baker, Oluwole, and Green 2013, p. 12).

This is one thing that is very important but rarely discussed when those external to the models, metrics, and growth-based accountability debates, including policymakers, dispute growth model use. While as mentioned, districts are beginning to use end-of-course exams, commercially available tests, SLOS, and the like to be more inclusive, this is an approach still in its infantile stages that also needs more attention and empirical work (Gill et al. 2014). In the meantime, this district decided to adopt an alternative, growth-based test and measurement system. While the goal was to increase fairness and inclusivity, the district wanted university-based researchers to examine evidence of validity before they continued to move forward.

3.2 Reliability

“Reliability” represents the extent to which an assessment or measurement tool produces consistent or dependable results, within one assessment, across similar assessments meant to yield similar results (e.g., alternate form reliability), or in the case of teacher-level value added, estimates derived via growth on at least two assessments over time (i.e., intertemporal reliability or consistency). Increasing reliability reduces uncertainty (i.e., less error), and vice versa, although the latter (i.e., more error) is of utmost concern if unreliable measures are to be used for consequential inference or decision-making purposes.

Likewise, without adequate reliability, valid interpretations and inferential uses are difficult to defend. Validity is an essential of any measurement, and reliability is a necessary or qualifying condition for validity. Put differently, if scores are unreliable, it is impossible to make or support valid, authentic, and accurate inferences (Brennan 2006, 2013; Kane 2006, 2013; Messick 1975, 1980, 1995).

In this particular study, researchers did not directly examine the reliability levels of the two tests used (i.e., the MAP and the Arizona Instrument to Measure Standards (AIMS)), with the particular data used at the particular time they conducted this study. Rather, researchers trusted the psychometric properties and reliability statistics provided in each test’s technical manual (see details forthcoming) as indicative of the fact that each test’s levels of reliability were more than sufficient for the tests’ intended and traditional uses (e.g., test and retest). Unfortunately, the data researchers analyzed for this study would not permit analyses of more current forms of value-added reliability over time (i.e., intertemporal reliability or consistency) otherwise.

3.3 Validity

“Validity is not a property of the test. Rather, it is a property of the proposed interpretations and uses of the test scores” (Kane 2013, p. 3). In the same article, Kane continues:

Interpretations and uses that make sense and are supported by appropriate evidence are considered to have high validity (or for short, to be valid), and interpretations or uses that are not adequately supported, or worse, are contradicted by the available evidence are taken to have low validity (or for short, to be invalid). The scores generated by a given test can be given different interpretations, and some of these interpretations may be more plausible than others. (p. 3; see also Messick 1975, 1980, 1989, 1995)

In other words, in order to assess evidence of validity, one must validate an interpretation or use of test scores as well as the plausibility of the claims being made as based on the scores, which in this case includes basic achievement and growth scores. Validation, then, might be thought of as “an evaluation of the coherence and completeness of this interpretation/use argument [IUA] and of the plausibility of [the] inferences and assumptions” that accompany interpretation and use (Kane 2013, p. 1; see also Messick 1975, 1980, 1989, 1995).

Of distinct interest in this study, as mentioned prior, is concurrent-related evidence of validity, or evidence capturing whether the indicators used in an assessment system demonstrate compatibility with other indicators intended to measure the same construct at the same time (i.e., concurrently). Hence, researchers in this study gathered evidence of concurrent-related evidence of validity whereas measures were collected (more or less) at the same time (i.e., concurrently) and examined for similarity (i.e., concurrence).

As per concurrent-related evidence of validity, what is currently known in the literature on growth is that across studies, there seems to be misalignment between growth estimates and other indicators of teacher effectiveness, whereas the correlations being observed among both mathematics and reading/language arts estimates and teacher observational scores, parent or student surveys of teacher quality, and the like are low to moderateFootnote 1 (e.g., .2 ≤ r ≤ .4).

For example, Polikoff and Porter (2014) analyzed the (co)relationships among VAM estimates and observational data, student survey data, and other data pertaining to whether teachers aligned their instruction with state standards, using data taken from 327 grade 4 and grade 8 mathematics and reading/language arts teachers in six school districts, as derived via the Bill & Melinda Gates Foundation’s Measures of Effective Teaching (MET) studies. They concluded that:

[T]here were few if any correlations that large [i.e., greater than r = .3] between any of the indicators of pedagogical quality and the VAM scores. Nor were there many correlations of that magnitude in the main MET study. Simply put, the correlations of value-added with observational measures of pedagogical quality, student survey measures, and instructional alignment were small. (Polikoff and Porter 2014, p. 13)

While these correlations are consistently evidencing themselves across multiple studies as “small” or at best “moderate” (see also Bill and Melinda Gates Foundation 2010, 2013; Corcoran et al. 2011; Grossman et al. 2014, August; Harris 2011; Hill, Kapitula, and Umland 2011; Strunk et al. 2014; Whitehurst, Chingos, and Lindquist 2015), these correlations are also being somewhat arbitrarily classified in terms of strength as there is still no really accepted standardFootnote 2 for such validity coefficients to help others assess how strong a correlation is needed or what “strong enough” might mean for varying purposes. However, one thing on which most, if not all, researchers (including most growth modelers) agree is that these correlations are not yet strong enough to warrant attaching high stakes to growth output (e.g., merit pay, tenure, termination). This is pertinent here in that the district’s explicit need was to attach merit pay to growth output.

Likewise, there also seems to be misalignment between the growth estimates derived from different tests meant to measure the same thing, given tests that are administered at the same time, to the same students, using the same growth models (e.g., .15 ≤ r ≤ .58; Papay 2010; see also Lockwood, McCaffrey, Hamilton, Stecher, Le, and Martinez 2007). This is of interest here, although in this study researchers used different growth models as commensurate with different tests and different growth models (see discussion forthcoming).

In addition, there are studies that demonstrate that if using the same data, the growth model does not really matter much as similar data are yielded almost regardless of the model and model specifications (Briggs and Betebenner 2009; Glazerman and Potamites 2011; Goldhaber and Theobald 2012; Goldschmidt et al. 2012). Researchers did not, however, directly analyze this here as the data researchers used came from two similar albeit different tests with two similar albeit different growth models, complicating things further (see discussion forthcoming).

4 Methods

It was imperative for the district of interest in this study to determine whether including more primary grade teachers in its growth-based teacher evaluation system using the MAP test would yield valid inferences from which summative decisions could be made. Hence, the main purpose of this study was to investigate whether two different tests (i.e., the state and MAP tests), testing the same subject areas (i.e., mathematics and reading/language arts), for the same students in the same grade levels (i.e., grades 3 and 4), taken at the same time (i.e., within the same school year), would yield similar results in terms of achievement and growth output. However, given the district used both the MAP and the state’s tests in only two grade levels (i.e., 3 and 4), researchers had to investigate results only for these grades and then use results to generalize downwards into the grades in which the district only used the MAP test (i.e., K-2). As mentioned, this data limitation forced the assumption that the NWEA K-3 tests function similarly across grades K-4.

4.1 State standardized achievement test

Arizona students are tested yearly in grades 2–10 using the standardized student achievement tests administered by the Arizona Department of Education (ADE)—the AIMS (Arizona Department of Education 2014a and the Stanford Achievement Test, version 10 (SAT-10; Pearson and Inc 2011). AIMS tests are administered in mathematics and reading/language arts in grades 3 through 8 and 10, and SAT-10 tests are administered as part of the AIMS in the same subject areas and solely in grades 2 and 9. Test technicians also integrated SAT-10 items within the AIMS in grades 3 through 8 and 10 as a part of Arizona’s integrated Dual Purpose Assessment (Arizona Department of Education 2012c). This purportedly permits the SAT-10 to serve as a pre-test in grade 2 for the AIMS post-test in grade 3, facilitating growth calculations earlier than grade 3 (the SAT-10 also serves as a pre-test in grade 9 for the AIMS post-test in grade 10).

This state’s testing program yields reliable standardized achievement data for grades 2–10, whereby reliability is demonstrated via strong to very strong Cronbach’s alpha (α) values (i.e., to express tests’ internal consistency) across all tests for grades 2–10 for both mathematics and reading/language arts. More specifically, alpha statistics range from the lowest alpha (α = .78) in grades 6, 7, and 8 reading/language arts to the highest alpha (α = .94) in grades 3 and 7 mathematics (see also Adler 2013, Part 9, p. 259). In addition, correlations between tests’ alternate forms reveal “consistently high [correlations] between tests designed to measures the same or very similar constructs” (Adler 2013, p. 331). More specifically, correlational values range from r = .85 in grade 8 reading/language arts to r = .92 in grade 8 mathematics.

This state’s testing program also yields continuous standardized achievement data for grades 2–10, whereby this also allows for growth calculations for all Arizona students in grades 3–8 and 10. In terms of measuring growth, the ADE adopted the aforementioned SGP package and uses it for Arizona’s A-F School Accountability Letter Grades (Arizona Department of Education 2012a). The state also requires districts to include the same growth scores in their evaluation systems (Arizona Department of Education 2014b; 2014c).

The SGP uses quantile regression methodology to calculate growth percentiles from student scale scores from the aforementioned AIMS and SAT-10 mathematics and reading/language arts tests on a yearly basis for grades 3–8 and 10. Students’ scores on each test are regressed on their prior year scores to calculate growth. Students who score similarly on a prior year test form an academic peer group for current year comparative purposes, and then each student’s growth is compared to the growth of other students in the group (i.e., rank ordered) to establish a percentile ranking for each student within the group (see also Arizona Department of Education 2012b; Betebenner 2009b). Administrators then use SGP values to report on each student’s individual growth over the course of each academic year.

In terms of the reliability, or more specifically intertemporal levels of reliability yielded via the SGP model, very little is known about the SGP model. To the best of the researchers’ knowledge, no external researchers have thus far examined SGP model output reliability in and of itself and no external researchers have thus far examined SGP model output as situated within what we know in general from the research on other VAM-based output. If external researchers have conducted such a study, they have not (yet) published their results in any peer-reviewed publication of which researchers are currently aware.

Given this void in the literature, however, a set of the researchers involved in this study recently conducted such a study, using a larger dataset with 3 years of longitudinal SGP data permitting such analyses. Researchers found that the SGP’s intertemporal levels of consistency are commensurate with those found across other VAMs (see, for example, Di Carlo 2013; Kane and Staiger 2012; Kersting, Chen, and Stigler 2013; Koedel and Betts 2007; Lockwood and McCaffrey 2009; McCaffrey, Sass, Lockwood, and Mihaly 2009; Newton, Darling-Hammond, Haertel, and Thomas 2010; Sass 2008; Schochet and Chiang 2013; Yeh 2013). The SGP’s intertemporal levels of consistency are positive, statistically significant (p < .05), and range from .46 ≤ r ≤ .55. This, in pragmatic terms, is about the same as a flip of a coin; that is, not great, but commensurate with more sophisticated VAMs in their current states (Pivovarova, M., and Amrein-Beardsley, A. (under review). Student Growth Percentiles (SGPs): Testing for reliability and validity).

Otherwise, for purposes of teacher evaluation, ADE includes only data from full academic year (FAY) students in SGP aggregations. That is, evaluations are based only on the students that a teacher was afforded the opportunity to instruct for the majority of the academic year. ADE determines each student’s FAY status using the school attendance data (i.e., entry and exit date) that each district submits yearly to ADE. The designation requires that a student enroll in the first 10 days of school and remain continuously enrolled through statewide test administrations that typically occur every spring.

4.2 The MAP test

The MAP test is part of a computer-adaptive assessment system meant to serve both diagnostic and formative purposes (Northwest Evaluation Association NWEA 2012). The NWEA designed the MAP for students in kindergarten through eleventh grades (Northwest Evaluation Association NWEA 2012) and also aligned it to the Arizona 2010 state standards (Northwest Evaluation Association NWEA 2011a). More recently, the NWEA aligned the MAP to the Common Core Standards (Northwest Evaluation Association NWEA 2013), although some suggest this alignment occurred before the standards were finalized, which may be cause for concern (Anonymous, personal communication, August 29, 2014).

Nonetheless, the test is to be administered three times each academic year, in the fall, winter, and spring. Scores are reported in Rasch Units (RITs), along a theoretically unlimited equal interval scale, although most scores fall between 150 and 250 (Northwest Evaluation Association NWEA 2014a). Using data from the 2011 RIT Scale Norms Study (Northwest Evaluation Association NWEA 2012), the NWEA also establishes target growth and target RIT scores for each student who completes an assessment in the fall or spring. This provides an estimate of typical growth from fall to spring or spring to spring, represented in RIT values (although, researchers only used spring-to-spring scores in this study, to align with the AIMS administration pattern and data underlying SGP calculations). The NWEA then uses the expected growth value and actual performance in the following semester to calculate their growth index value (i.e., actual RIT − expected RIT = growth index). This value also has a theoretically infinite range, based upon the theoretically infinite range of RIT scores (Northwest Evaluation Association NWEA 2014a), ranging from negative to positive with an index of zero representing typical growth. Growth index scores above zero represent higher than expected growth, and growth index scores below zero represent lower than typical growth.

The NWEA has also made publicly available information about the reliability of their tests, as well as their tests’ alignment with state-standardized achievement tests (i.e., another form of concurrent validity). Albeit the forthcoming statistics are a bit outdated, given 2002 was the year in which the state of Arizona adopted its AIMS test, at that time, NWEA researchers determined the MAP’s test-retest reliability for spring-to-spring testing in grades 2–8 to range from .79 ≤ r ≤ .93 (i.e., .84 ≤ r ≤ .91 for reading/language arts and .79 ≤ r ≤ .93 for mathematics) (Northwest Evaluation Association NWEA 2004). They also examined their tests’ alignment with the AIMS tests for grades 3, 5, and 8, with values ranging from .69 ≤ r ≤ .80 (i.e., .69 ≤ r ≤ .80 for reading/language arts and .79 ≤ r ≤ .80 for mathematics) (Northwest Evaluation Association NWEA 2004). Finally, NWEA researchers reported that their tests’ alignment with the SAT-9, which as mentioned prior was incorporated within the AIMS test in grades 2 and 9, ranged from .80 ≤ r ≤ .88 (i.e., .82 ≤ r ≤ .87 for reading/language arts and .80 ≤ r ≤ .88 for mathematics) across the same grade span (Northwest Evaluation Association NWEA 2004). Hence, these tests were also generally determined to be reliable and valid as defined by the extent to which MAP output correlated with AIMS output.

Otherwise, it is important before moving forward to note here that researchers could not use the same methods to compute growth statistics for each set of test scores described above, for three main reasons. First, the district was interested in using the NWEA test results in the same ways as AIMS test results as per their approved growth calculations; thus, it was imperative to compare the accepted output of these two testing systems without additional researcher manipulation. Researchers needed to compare growth output as the district intended to use them—without manipulation or further statistical adjustment when calculating growth. Second, it was not possible to calculate RIT scores and a resultant growth index value using the AIMS test. Because AIMS test scores could not be decomposed based upon individual item difficulty to develop a RIT comparison, this was not possible regardless of desires. Third, and inversely, it was not possible to use the SGP model (used to calculate growth for the AIMS test) with the NWEA data because the sample size was simply not large enough to meet the demands of the SGP model (e.g., approximately 5000 student observations are required; Castellano and Ho 2013).

4.3 Participant sample

Researchers collected achievement and growth data from the state and MAP mathematics and reading/language arts tests from an initial sample including over 3600 students (across grades K-8), with specific Ns for each test and grade-level combination ranging from 1120 to 2675 given variations in testing requirements (e.g., students do not complete state tests before grade 2). Researchers cleaned roster files for the spring 2011 and spring 2012 MAP tests to develop a comprehensive roster connecting each student to his/her teacher at each point in time. In addition, researchers used MAP test rosters to link each student’s MAP identification numbers (district ID) to the state achievement test results. Researchers then combined student records using the state’s Student Accountability Information System ID (SAIS ID) as the primary key for matching data per case. Secondary keys used throughout the merging process included district ID, last name, first name, grade, gender, and ethnicity. The final dataset included state (i.e., AIMS and SAT-10) and MAP test results, with each type of data including the two tested subject areas (mathematics and reading/language arts). All of this yielded over 9000 total data points that researchers used to examine achievement and growth results between these tests.

However, because researchers conducted this study at the request of the district, data for the actual participant sample researchers used they collected out of convenience. This sample, while it included all tested students from the district, ranging from grades K-8, MAP test data were only available for grades K-4. This limited researchers’ participant sample to grades K-4 including 1054 students total, associated with five schools and 38 teachers. Further, growth scores for the state test were limited to grades 3 and 4, at which point the sample decreased further to 420 students, associated with five schools and 15 teachers. Classroom-level sample sizes across grades 3 and 4 were relatively typical and consistent, ranging from 20 students to 46 students, with a mode classroom size of 27 and a mean of 28.

Each student record included a minimum of two and a maximum of four test score observations, depending on the available test data for the student. To be included in a subject-specific analysis, a student would need two growth scores for the subject area, one NWEA growth index observation and one SGP observation, in the same subject area. Thus, a complete student record would have included two NWEA growth index observations, one for mathematics and one for reading/language arts, and two AIMS SGP observations, one for mathematics and one for reading/language arts. As explained previously, each of these observations required a minimum of a current and one prior year score for the subject area to complete the growth index or SGP calculation; thus, the total number of test score observations per student was at least two per subject area per test. For further participant sample statistics, please see Table 1.

Table 1 Descriptive statistics for within-sample test score observations
Full size table

4.4 Data analyses

Researchers calculated descriptive statistics on the test score variables to identify an average level of performance on each test, as well as to determine the variability in scores around the average. Researchers then conducted four sets of Pearson product-moment correlation analyses to explore relationships among achievement and growth measures for the two cohorts that had both tests in common (i.e., grades 3 and 4).

For the growth analyses in grades 3 and 4, researchers examined the relationships among AIMS and MAP growth results. Researchers calculated additional Pearson correlation coefficients (Pearson’s r) for growth result pairings (i.e., MAP growth index and AIMS growth percentiles) for both content areas, mathematics and reading/language arts, and for grades 3 and 4. Researchers used these correlations to draw inferences associated with various aspects of validity, specifically in terms of concurrent-related evidence of validity on growth outcomes.

5 Results

Not surprisingly, researchers observed strong to very strongFootnote 3 positive (i.e., r ≥ .83) correlations between the MAP and AIMS tests at both grades 3 and 4 in the spring 2012. Not surprisingly as well, all correlations among all achievement measures were statistically significant (i.e., p < .01; see Table 2). This serves as support for the strength of the relationships between these tests, in terms of the achievement indicators they generate and the extent to which they similarly capture underlying ability (not independent of student demographic and other extraneous factors, of course).

Table 2 Correlations between the state and MAP tests on achievement—spring 2012
Full size table

Researchers also observed strong to very strong positive correlations at both grades for mathematics and reading/language arts (see Table 3). In reading/language arts, the relationship between the 2011–2012 state test and the 2010–2011 MAP at grade 3 was strong (r = .77, p < .01), and at grade 4 this relationship was also strong (r = .76, p < .01). In mathematics, the same relationship at grade 3 was very strong (r = .86, p < .01), and at grade 4 it was also very strong (r = .86, p < .01).

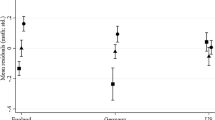
Table 3 Correlations between the state test 2012 and the MAP test 2011 on achievement
Full size table

Contrariwise, correlations among the achievement growth measures were actually negative and positive and small to moderate in magnitude (−.42 ≤ r ≤ +.63) with varying levels of significance (see Table 4). For reading/language arts, the relationships between the MAP growth as per its growth index, and growth on the state test as derived via the SGP, correlations for both grades 3 and 4 were positive, and statistically significant, although moderate (r = .36, p < .01 and r = .28, p < .01, respectively). There was, however, a significant negative correlation between the state and MAP growth in mathematics for grade 3 (r = −.42, p < .01) and also grade 4 (r = −.32, p < .01). The spring 2011 MAP growth scores explained almost none of the variance in the 2012 growth scores as derived via the state test.

Table 4 Correlations among the spring 2012 growth measures
Full size table

While this volatility might not be particularly surprising given the limitations associated with the different growth metrics in use for each data source (i.e., the SGP for the AIMS vs. NWEA’s growth index), including but not limited to the tests and their varying scoring metrics, their traditional as compared to adaptive testing approaches, other dataset limitations, as well as the variability in results for growth calculations, all of which seem to be causing the observed lack of clear, strong alignment between growth outputs; this finding was indeed surprising and unwelcomed by district administrators. Particularly given the high correlations observed in the initial correlational analyses (i.e., achievement correlations sans growth), the district partners were particularly surprised as to how, and why, the growth correlations did not follow suit.

6 Discussion

In line with prior studies on the alignment of multiple measures of students’ subject area proficiency (Bill and Melinda Gates Foundation 2010, 2013; Corcoran et al. 2011; Harris 2011; Hill et al. 2011), and given the specific work completed by the NWEA to align their tests with Arizona state standards (Northwest Evaluation Association NWEA 2011a), it was not surprising that study results were supportive of the alignment of both measures for both subject areas and grade levels on underlying achievement. While correlations indicated strong to very strong alignment between test outcomes from the state tests and the MAP (i.e., .76 < r < .86), what such strong alignment might have foreshadowed in terms of growth did not evidence itself as (especially district administrators) expected. Put simply, the growth results that followed did not align well and in the case of mathematics defied expectations. The lack of alignment was substantial in the case of both mathematics tests, whereas negative correlations yielded opposite indicator growth.

Nowhere in the current literature have researchers observed such negative correlations, although nowhere have researchers read a peer-reviewed, published study in which researchers explicitly examined the concurrent-related evidence of validity among measures used for the youngest of America’s public school students (i.e., in grades K-4). Students in grades 3–8 are almost always those at the foundation of and yielding the data analyzed within similar value-added studies in which researchers have compared estimates derived via various VAMs (see, for example, Ehlert, Koedel, Parsons, and Podgursky 2012; Goldhaber, Gabele, and Walch 2012; Goldhaber and Theobald 2012; Guarino, Reckase, Stacy, and Wooldridge 2015; Ho, Lewis, and Farris 2009; Sass, Semykina, and Harris 2014; Walsh and Isenberg 2015; Wright et al. 2010).

This is an issue of fairness whereby teachers of these students are not typically included in such studies given such data issues (see also Baker et al. 2013; Collins 2014; Gabriel and Lester 2013; Harris 2011). More importantly, though, this study is important not only for its results but also that it brings attention to the fact that more research is certainly needed in this area, hopefully before others attempt to adopt similar measures, like this district did, in the name of fairness. Likewise, results are not to be interpreted to place blame on either measures, but rather to also bring to light what might be a serious issue when measuring something that is so simply conceptualized and labeled as “growth.” Although, many factors could have contributed to these results.

First, the way by which growth is calculated was different for each test (i.e., via using the SGP for the state test and the growth index for the MAP). Both growth systems involve complex and multi-faceted calculations that convert criterion-referenced proficiency scores into normed measures to facilitate growth calculations.

Second, the SGP is only interpretable within the context of an individual academic year and peer group while the MAP norm data are static (Northwest Evaluation Association NWEA 2011b). MAP growth results yield a growth index score, which compares the actual performance of a student to his/her predicted performance, as based upon the norm group (Northwest Evaluation Association NWEA 2014b), not the actual group of students with whom students are grouped (like with the SGP). Doing this with the MAP growth index is quite different, in form and function, from doing this with a growth percentile value.

Third, one of the measures was a paper-and-pencil test, while the other was a computer-based adaptive test, which is also quite different in form and function. Although the paper and computer-based tests should theoretically measure the same knowledge of the students being tested, particularly younger students’ technological skills and abilities (or lack thereof) could also be inherently tested as well. This too may have distorted results.

All things considered, however, the underlying growth systems, if indeed they are both effectively measuring growth, should still have yielded stronger similarities in terms of reading/language arts and at least positive if not positive and moderate-to-strong correlations in terms of mathematics. If growth is the measurement goal of interest, growth should have been at least similar (if not more strongly similar) when observed across similar tests given to similar students at similar times (i.e., concurrent-related evidence of validity) even despite the different tests and ways by which growth was calculated (see a similar discussion in Papay 2010; see also discussion forthcoming). If growth is growth, particularly in the eyes of those measuring it and more importantly in the eyes of those using measurement output for low and high-stakes decision-making purposes, more underlying structure should be evidenced via such correlations.

7 Conclusions

While prior research does evidence that there seems to be misalignment between growth estimates derived from different tests meant to measure the same thing, and administered at the same time to the same students using the same growth model (Papay 2010), researchers did not do this here as the growth models used, as aligned with different tests, differed while all else remained the same. In addition, there are studies that demonstrate that if using the same data, the growth model does not really matter much (Briggs and Betebenner 2009; Glazerman and Potamites 2011; Goldhaber and Theobald 2012; Goldschmidt et al. 2012). But researchers did not examine this either as the data derived were also coming from two similar albeit different growth measures. These realities and real limitations constricted researchers’ capacities to do anything more than conduct a correlational analysis to examine growth on two similar tests, administered at similar times, for the same students, using two different growth measures as linked to two similar tests. What researchers found, all things considered, however, were correlations that were underwhelming for reading/language arts and inverted and hence distorted for mathematics.

The main research-based conclusion, then and given the evidence and limitations, is that growth is difficult to measure, and measuring growth depends largely on the tests and largely on the growth model used to measure test results over time. Measuring growth is not nearly as simple as many, particularly policymakers and in this case education practitioners, might think, and this has serious implications for the validity of the inferences to be so “simply” made using similar growth data.

While noble, whether one wants to be more inclusive or to treat more teachers more fairly to a more common assessment and accountability system, as is increasingly becoming the trend as supported by the U.S. Department of Education (Duncan 2014; Gill et al. 2014), it is certainly unwise for states or school districts to simply take haphazard or commonsense approaches to measure growth. While tempting, this is professionally and (as evidenced in this study) empirically misguided. This was the most important finding demonstrated herein.