Residual Stress Analysis Due to Chemomechanical Coupled Effect, Intrinsic Strain and Creep Deformation During Oxidation

Abstract

Metal oxidation at high temperature is often accompanied with the stress generation both in the metal substrate and the growing oxide scale. In this paper, taking into account the growth strain, intrinsic strain and creep deformation, a new analysis model to characterize the residual stress evolutions during an isothermal oxidation process is developed on the basis of the mechanical-balance and moment-equilibrium equations. In this model, the growth strain and the stress are coupled based on an evolving equation, which reduces to the Clarke’s assumption if the stress influence on the growth strain of the oxide scale is ignored. The curvature describing the bending of the system is expressed. Euler numerical method is adopted to simulate the stress evolution and the comparisons among the present model, Zhang’s creep solution and the experimental results are also performed. Finally, effects of creep constants, substrate thickness and intrinsic strain on the residual stress distribution in the oxide scale/metal substrate are discussed.

Introduction

Metal oxidation at high temperature is often accompanied with the stress generation [1–3]. The existence of stresses has been of much interest for many years and is manifested in several ways [4–6]. However, the exact mechanisms of the stress are not completely understood. Pilling and Bedworth [7] is regarded to be the pioneers to recognize the change of molar volume produced by the metal oxidation as the origin of stresses. They proposed that the mismatch of the oxide and metal led to the generation of stress in the scale. In particular, the sign (compressive or tensile) of the stress in thick oxide scale is predicted perfectly. However, the magnitude order of the stress is often over estimated, typically several tens of GPa compared with less than 1 GPa for the measure. Besides, this model neglects the influence of oxidation time so that the associated strain rate is zero. A more acceptable origin of the stress was offered by Rhines and Wolf [8]. In their model, the stress induced by the oxide formation at the grain boundary of the oxide scale was characterized. They pointed out that the oxide formation parallel to the oxide/substrate interface which causes the oxide scale thickening can not lead to the stress generation. Based on the experimental measurements of the growth strain, Tolpygo et al. [9] found that the growth strain increased parabolically with oxidation time, within the context of Rhines–Wolf model. Besides, little oxide formed at the grain boundary can induce large lateral compressive stress. Clarke [5] proposed that a compressive lateral stress occurs in the oxide scale through the oxide grain boundaries based on a dislocation climb model, and predicted that the lateral growth strain rate increases linearly with the oxide thickening rate in accord with observations at a fixed oxidation temperature, namely, Clarke’s assumption. This assumption has been acknowledged and used in many studies [10–12]. Panicaud et al. [13] proposed a new explanation for the proportional dependence between the growth strain and the thickness of the oxide scale, and developed the viscoplastic stress evolution model. Maharjan et al. took into account the lateral growth strain and creep deformation and respectively developed a deflection stress model [10], and a simplified modeling approach to predict the stress evolution on the basis of the strain compatibility at the oxide/metal interface and the force balance equation [14]. Ruan et al. [11] considered the asymmetric oxidation and gave a theoretical stress analysis model with growth strain and creep strain based on the force and moment balance equation. However, in these above models, the effect of the stress on the growth strain and the intrinsic strain are not considered. Wang et al. [15] considered the coupling between the reaction and stress, and established a reaction–diffusion–stress coupling elastic–plastic model, while the intrinsic strain is not included.

It is reported that the stress can improve the active energy of solids and accelerate the reaction rate [16, 17]. The compressive growth stress was found to decrease the Si oxidation rate [18] and similar phenomena have been observed in the metallic oxidation [19]. The chemical reaction is often described by the growth srain or growth stress as in [10, 11, 14], and the stress effect on the chemical reaction is always neglected. Suo et al. [20] considered the stress effect on the growth strain, while the developed model was based on the strain compatibility at the oxide/metal interface and the force balance equation, and the bending effect was not considered. Creep can lead to the stress relaxation and the stress redistribution in the scale/substrate [12], which shows that the creep plays an essential role in the film or substrate during the high-temperature oxidation. In addition, for some film/substrate systems, the creep may occur even at ambient temperature and lower stress conditions for many solders and polymers. [10–12] developed the simplified models to predict the stress evolution with creep deformation during oxidation and found that the creep deformation has a significant influence upon the stress analysis. Therefore, it is necessary to consider the creep deformation and the stress influence the growth strain rate during high-temperature oxidation.

Up to date, the intrinsic strain is regarded as one of the factors resulting in oxide scale expansion and has been extensively discussed in the thin film growth [21]. The possible origins of intrinsic strains are: (1) dopants; (2) “atomic peening”, which causes compressive stress; (3) microvoids which cause tensile stress; (4) shrinkage which causes tensile stress; (5) grain boundaries; (6) gas entrapment which causes tensile stress and so on. Kobeda and Irene [22] found the intrinsic film stress (or intrinsic stress) during the silicon oxidation by the experimental method. Delph [18] pointed out that most of this volume change takes place normal to the oxidation front, while there exists a small component of expansion in the plane of oxidation, leading to what may be termed as intrinsic. Usually the strain normal to the oxidation front is regarded to be growth strain, which satisfies the relationship $\dot{\varepsilon }_{g} (t) = D_{ox} \dot{h}_{ox} (t)$, i.e., the Clarke assumption [5]. Obviously, intrinsic strain is different from growth strain. In addition, Delph arrived at an intrinsic strain value of approximately 2 × 10⁻³. During the process of the metallic oxidation, compressive stress has been verified to be existent due to the growth of the oxide film. Moreover, the oxidation of metal to form the oxide is often accompanied by volume changes, and these indicate that there exists the intrinsic strain in the metallic oxidation.

The purpose of this paper is to develop a residual stress model considering creep deformations of the metal and the oxide, intrinsic strain and growth strain of the oxide scale where the stress influence on the growth strain is involved. First, the general equations of the stress distribution are derived according to the mechanical-balance and moment-equilibrium equations. Second, numerical simulations of the stress evolution are carried out by adopting the Euler method. Finally, effects of creep constants, substrate thickness and intrinsic strain on the residual stress distribution in the oxide scale/metal substrate are discussed.

The Intrinsic Strain Model for the Stress Evolution

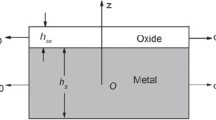
Metal oxidation at high temperature is schematically shown in Fig. 1. The thickness of the oxidation scale is $h_{ox}$ and that of the metal substrate is $h_{s}$. Isothermal oxidation occurs on single surface of the metal and the other surface is protected by the oxide coating as described by Saunders et al. [23] and the oxidation temperature is assumed to be 1000 °C The origin of the system is set at the central of the substrate. Suppose that the mechanical properties of the oxide film and substrate are isotropic.

Fig. 1

A schematic of metal oxidation

For most metals or alloys, the oxidation at high temperature is controlled by the diffusion of the oxygen anions and metal cations in the formed oxide scale. The thickness of the oxide scale is consistent to the parabolic law [5, 24]

$$h_{ox} (t) = \sqrt {k_{p} t}$$

(1)

where $k_{p}$ is the kinetic parabolic constant and $t$ is the elapsed time.

According to the evolution equation [25], the lateral growth strain rate of the oxide is given as in [20]

$$\dot{\varepsilon }_{g} (t) = D_{ox} \dot{h}_{ox} (t) + a\sigma$$

(2)

where $\varepsilon_{g}$ is the growth strain, $D_{ox}$ is the growth parameter, $a$ is the chemo-mechanical coupled coefficient, and $\sigma$ is the stress. It is worth noticing that Eq. (2) provides a direct relation between the growth strain rate and the stress. If the effect of stress on the growth strain vanishes in Eq. (2), the growth strain rate will reduce to Clarke’s assumption [5].

In this section, neglecting the creep deformation and taking into account the thermal expansion in the oxide and metal, and intrinsic strain in the oxide, the total strain in the system is expressed as

$$\begin{array}{ll} {\varepsilon_{ox} (t) = \varepsilon_{ox}^{e} (t) + \alpha_{ox} \Delta T + \varepsilon_{g} (t) + \varepsilon_{ox}^{*} } & {h_{s} /2 < z < h_{s} /2 + h_{ox} } \\ {\varepsilon_{s} (z,t) = \varepsilon_{s}^{e} (z,t) + \alpha_{s} \Delta T} & { - h_{s} /2 < z < h_{s} /2} \\ \end{array}$$

(3)

where $\varepsilon ,$ $\varepsilon_{{}}^{e},$ $\Delta T ,$ $\alpha ,$ $\varepsilon_{{}}^{*}$ are the total strain, elastic strain, the temperature change, thermal expansion coefficient, and intrinsic strain, respectively.

Due to the single surface oxidation, the system will bend and the curvature can be observed. According to the plane assumption, the total strain can be given as

$$\begin{aligned} \varepsilon_{ox} (t) &= \varepsilon_{0} (t) - k(t)\frac{{h_{s} }}{2} \quad h_{s} /2 < z < h_{s} /2 + h_{ox} \\ \varepsilon_{s} (z,t) &= \varepsilon_{0} (t) - k(t)z \quad - h_{s} /2 < z < h_{s} /2 \\ \end{aligned}$$

(4)

where ɛ ₀(t) is the lateral strain at the center of the metal substrate, and $k(t)$ is the curvature of the deformed neutral axis.

Based on the general Hook’s law for the equivalent biaxial stress and Eqs. (3) and (4), the stresses in the system can be given as

$$\begin{array}{ll} \sigma_{ox} (t) = M_{ox} \left[ {\varepsilon_{0} (t) - k(t)\frac{{h_{s} }}{2} - \alpha_{ox} \Delta T - \varepsilon_{g} (t) - \varepsilon_{ox}^{*} } \right] & \quad h_{s} /2 < z < h_{s} /2 + h_{ox} \hfill \\ \sigma_{s} (z,t) = M_{s} [\varepsilon_{0} (t) - k(t)z - \alpha_{s} \Delta T] & \quad - h_{s} /2 < z < h_{s} /2 \hfill \\ \end{array}$$

(5)

where $\sigma$ is the equi-biaxial stress of the system. $M_{ox} = \frac{{E_{ox} }}{{1 - \upsilon_{ox} }},$ $M_{s} = \frac{{E_{s} }}{{1 - \upsilon_{s} }}$ are the biaxial modulus. $E$ and $\upsilon$ are the Young’s modulus and Possion’s ratio, respectively.

Suppose that there is no external force in the system, the mechanical balance equation and moment equilibrium equation can be written as

$$\int_{{ - h_{s} /2}}^{{h_{s} /2}} {\sigma_{s} } dz + \sigma_{ox} h_{ox} = 0$$

$$\int_{{ - h_{s} /2}}^{{h_{s} /2}} {\sigma_{s} } zdz + \sigma_{ox} h_{ox} \left( {\frac{{h_{s} }}{2} + \frac{{h_{ox} }}{2}} \right) = 0$$

(6)

Substituting Eqs. (5) into (6), and given the intrinsic strain $\varepsilon_{ox}^{*}$ and the growth strain in prior,the lateral strain of the central plane in substrate, $\varepsilon_{0}$, and the curvature of the system are solved as follows

$$\varepsilon_{0} (t) = A_{1} \varepsilon_{g} (t) + A_{2} \alpha_{s} \Delta T - A_{3} \alpha_{ox} \Delta T + A_{1} \varepsilon_{ox}^{*}$$

(7)

$$k(t) = - \frac{{6(h_{s} + h_{ox} )}}{{h_{s}^{2} }}\left[ {A_{1} \varepsilon_{g} (t) + (A_{2} - 1)\alpha_{s} \Delta T - A_{3} \alpha_{ox} \Delta T + A_{1} \varepsilon_{ox}^{*} } \right]$$

(8)

where

$$A_{1} = \frac{{h_{s} M_{ox} h_{ox} }}{{h_{s}^{2} M_{s} + 4M_{ox} h_{ox} h_{s} + 3M_{ox} h_{ox}^{2} }}$$

$$A_{2} = \frac{{h_{s}^{2} M_{s} + 3h_{s} M_{ox} h_{ox} + 3M_{ox} h_{ox}^{2} }}{{h_{s}^{2} M_{s} + 4M_{ox} h_{ox} h_{s} + 3M_{ox} h_{ox}^{2} }} = 1 - A_{1}$$

$$A_{3} = - \frac{{h_{s} M_{ox} h_{ox} }}{{h_{s}^{2} M_{s} + 4M_{ox} h_{ox} h_{s} + 3M_{ox} h_{ox}^{2} }} = - A_{1}$$

(9)

The Creep Model for the Stress Evolution

Now, the creep effect in the oxide scale and metal substrate is considered. Similar to the above analysis approach, the total strain of the system in Eq. (3) should add the creep deformation, and Eq. (3) becomes

$$\varepsilon_{ox} (t) = \varepsilon_{ox}^{e} (t) + \alpha_{ox} \Delta T + \varepsilon_{ox}^{cr} (t) + \varepsilon_{g} (t) + \varepsilon_{ox}^{*}$$

$$\varepsilon_{s} (z,t) = \varepsilon_{s}^{e} (z,t) + \varepsilon_{s}^{cr} (z,t) + \alpha_{s} \Delta T$$

(10)

where $\varepsilon_{{}}^{cr}$ is the creep strain of the system. In terms of the Norton’s law, the creep strain is expressed as

$$\dot{\varepsilon }_{ox}^{cr} = J_{ox} \sigma_{ox}^{n}$$

$$\dot{\varepsilon }_{s}^{cr} = J_{s} \sigma_{s}^{m}$$

(11)

where $J$ is the creep coefficient. $m$ and $n$ are the Norton exponents.

Base on Eqs. (4), (10) and the general Hook’s law, the stress of the system becomes

$$\sigma_{ox} (t) = M_{ox} \varepsilon_{ox}^{e} = M_{ox} \left[\varepsilon_{0} (t) - k(t)\frac{{h_{s} }}{2} - \alpha_{ox} \Delta T - \varepsilon_{ox}^{cr} (t) - \varepsilon_{g} (t) - \varepsilon_{ox}^{*} \right]$$

$$\sigma_{s} (z,t) = M_{s} \varepsilon_{s}^{e} = M_{s} [\varepsilon_{0} (t) - k(t)z - \alpha_{s} \Delta T - \varepsilon_{s}^{cr} (t)]$$

(12)

Differentiating Eq. (12) with respect to time yields

$$\dot{\sigma }_{ox} (t) = M_{ox} \left[\dot{\varepsilon }_{0} (t) - \dot{k}(t)\frac{{h_{s} }}{2} - \dot{\varepsilon }_{ox}^{cr} (t) - \dot{\varepsilon }_{g} (t) \right]$$

$$\dot{\sigma }_{s} (z,t) = M_{s} [\dot{\varepsilon }_{0} (t) - \dot{k}(t)z - \dot{\varepsilon }_{s}^{cr} (t)]$$

(13)

For the external oxidation, the substrate thickness is independent on time, differentiating Eq. (6) gives

$$\int_{{ - h_{s} /2}}^{{h_{s} /2}} {\dot{\sigma }_{s} } dz + \dot{\sigma }_{ox} h_{ox} + \sigma_{ox} \dot{h}_{ox} = 0$$

$$\int_{{ - h_{s} /2}}^{{h_{s} /2}} {\dot{\sigma }_{s} } zdz + \frac{1}{2}\dot{\sigma }_{ox} h_{ox} (h_{s} + h_{ox} ) + \sigma_{ox} \dot{h}_{ox} \left(\frac{{h_{s} }}{2} + h_{ox} \right) = 0$$

(14)

Combining Eqs. (2) with (11), then substituting Eqs. (13) into (14) yields

$$\dot{\varepsilon }_{0} (t) = A_{1} \left( {J_{ox} \sigma_{ox}^{n} + D_{ox} \dot{h}_{ox} + a\sigma_{ox} } \right) + \frac{{A_{2} }}{{h_{s} }}\int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s}^{m} } dz + \frac{{6A_{3} }}{{h_{s}^{2} }}\int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s}^{m} } zdz + \frac{{A_{4} }}{{M_{s} h_{s} }}\sigma_{ox} \dot{h}_{ox}$$

$$\dot{k}(t) = - \frac{{6(h_{s} + h_{ox} )A_{1} }}{{h_{s}^{2} }}\left( {J_{ox} \sigma_{ox}^{n} - \int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s}^{m} } dz + D_{ox} \dot{h}_{ox} + a\sigma_{ox} } \right) + B_{1} \sigma_{ox} \dot{h}_{ox} - B_{2} \int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s}^{m} } zdz$$

(15)

where

$$A_{4} = - \frac{{h_{s}^{2} M_{s} + 3M_{ox} h_{ox}^{2} }}{{h_{s}^{2} M_{s} + 4M_{ox} h_{ox} h_{s} + 3M_{ox} h_{ox}^{2} }}$$

$$B_{1} = \frac{{6(h_{s}^{2} M_{s} + 2M_{ox} h_{ox} h_{s} + M_{ox} h_{ox}^{2} )}}{{M_{s} h_{s}^{2} (h_{s}^{2} M_{s} + 4M_{ox} h_{ox} h_{s} + 3M_{ox} h_{ox}^{2} )}}$$

$$B_{2} = \frac{{12(M_{ox} h_{ox} + M_{s} h_{s} )}}{{h_{s} (h_{s}^{2} M_{s} + 4M_{ox} h_{ox} h_{s} + 3M_{ox} h_{ox}^{2} )}}$$

(16)

The stresses in the oxide and the substrate can be calculated by adopting the Euler method, that is

$$\sigma_{ox} (t + \Delta t) = \sigma_{ox} (t) + \dot{\sigma }_{ox} (t + \Delta t) \cdot \Delta t$$

(17)

$$\sigma_{s} (z,t + \Delta t) = \sigma_{s} (z,t) + \dot{\sigma }_{s} (z,t + \Delta t) \cdot \Delta t$$

(18)

The curvature of the system satisfies

$$k(t + \Delta t) = k(t) + \dot{k}(t + \Delta t) \cdot \Delta t$$

(19)

Substitution of Eqs. (13) and (15) into (17) and (18) gives

$$\sigma_{ox} \left| {_{t + \Delta t} } \right. = \sigma_{ox} \left| {_{t} } \right. + M_{ox} \left( {\dot{\varepsilon }_{0} \left| {_{t + \Delta t} } \right. - \dot{k}\left| {_{t + \Delta t} } \right.\frac{{h_{s} }}{2} - \dot{\varepsilon }_{ox}^{cr} \left| {_{t + \Delta t} } \right. - \dot{\varepsilon }_{g} \left| {_{t + \Delta t} } \right.} \right) \cdot \Delta t$$

$$\sigma_{s} \left| {_{t + \Delta t} } \right. = \sigma_{s} \left| {_{t} } \right. + M_{s} (\dot{\varepsilon }_{0} \left| {_{t + \Delta t} } \right. - \dot{k}\left| {_{t + \Delta t} } \right.z - \dot{\varepsilon }_{s}^{cr} \left| {_{t + \Delta t} } \right.) \cdot \Delta t$$

(20)

For convenience, we suppose that the Norton exponents of the system are equal to 1, i.e. $m = n = 1,$ which is also done by Panicaud et al. [6], Suo et al. [20] and Dong et al. [26]. Then Eq. (13) becomes

$$\dot{\sigma }_{ox} (t) = M_{ox} \left[ {\dot{\varepsilon }_{0} (t) - \dot{k}(t)\frac{{h_{s} }}{2} - J_{ox} \sigma_{ox} - \dot{\varepsilon }_{g} (t)} \right]$$

$$\dot{\sigma }_{s} (z,t) = M_{s} [\dot{\varepsilon }_{0} (t) - \dot{k}(t)z - J_{s} \sigma_{s} ]$$

(21)

Combining Eqs. (21) with (14), one obtains

$$\begin{array}{ll} M_{s} \left[ {\dot{\varepsilon }_{0} (t)h_{s} - \int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s} } dz} \right] + \dot{\sigma }_{ox} h_{ox} + \sigma_{ox} \dot{h}_{ox} = 0 \hfill \\ M_{s} \left[ { - \frac{1}{12}\dot{k}(t)h_{s}^{3} - \int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s} } zdz} \right] + \frac{1}{2}\dot{\sigma }_{ox} h_{ox} (h_{s} + h_{ox} ) + \sigma_{ox} \left( {\frac{{h_{s} }}{2} + h_{ox} } \right)\dot{h}_{ox} = 0 \hfill \\ \end{array}$$

(22)

Based on the balance Eq. (6), one has

$$- \int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s} } dz = J_{s} \sigma_{ox} h_{ox}$$

$$- \int_{{ - h_{s} /2}}^{{h_{s} /2}} {J_{s} \sigma_{s} } zdz = \frac{1}{2}J_{s} \sigma_{ox} h_{ox} (h_{s} + h_{ox} )$$

and combining the above equations with Eq. (22) yields

$$M_{s} \dot{\varepsilon }_{0} (t)h_{s} + M_{s} J_{s} \sigma_{ox} h_{ox} + \dot{\sigma }_{ox} h_{ox} + \sigma_{ox} \dot{h}_{ox} = 0$$

(23a)

$$- \frac{1}{6}M_{s} \dot{k}(t)h_{s}^{3} + M_{s} J_{s} \sigma_{ox} h_{ox} (h_{s} + h_{ox} ) + \dot{\sigma }_{ox} h_{ox} (h_{s} + h_{ox} ) + \sigma_{ox} (h_{s} + 2h_{ox} )\dot{h}_{ox} = 0$$

(23b)

$\dot{\varepsilon }_{0} (t)$ and $\dot{k}(t)$ can be given from Eq. (23)

$$\dot{\varepsilon }_{0} (t) = - J_{s} \sigma_{ox} \frac{{h_{ox} }}{{h_{s} }} - \dot{\sigma }_{ox} \frac{{h_{ox} }}{{M_{s} h_{s} }} - \sigma_{ox} \frac{{\dot{h}_{ox} }}{{M_{s} h_{s} }}$$

$$\dot{k}(t) = J_{s} \sigma_{ox} \frac{{6h_{ox} (h_{s} + h_{ox} )}}{{h_{s}^{3} }} + \dot{\sigma }_{ox} \frac{{6h_{ox} (h_{s} + h_{ox} )}}{{M_{s} h_{s}^{3} }} + \sigma_{ox} \frac{{6(h_{s} + 2h_{ox} )\dot{h}_{ox} }}{{M_{s} h_{s}^{3} }}$$

(24)

Combining Eqs. (24) with (13), the stress evolution equations for the oxide scale and the metal substrate are obtained as follows

$$\begin{array}{l} \left[ {\frac{{M_{s} h_{s}^{2} }}{{M_{ox} }} + 4h_{s} h_{ox} + 3h_{ox}^{2} } \right]\dot{\sigma }_{ox} + \bigg[ {2(2h_{s} + 3h_{ox} )\dot{h}_{ox} + M_{s} J_{s} h_{ox} (4h_{s} + 3h_{ox} }) \\ \quad + \,(J_{ox} + a)M_{s} h_{s}^{2} \bigg]\sigma_{ox} = - M_{s} D_{ox} h_{s}^{2} \dot{h}_{ox} \hfill \\ \end{array}$$

$$\begin{array}{ll} \dot{\sigma }_{s} + M_{s} J_{s} \sigma_{s} & = - M_{s} \left[ {J_{s} \sigma_{ox} \frac{{h_{ox} }}{{h_{s} }} + \dot{\sigma }_{ox} \frac{{h_{ox} }}{{M_{s} h_{s} }} + \sigma_{ox} \frac{{\dot{h}_{ox} }}{{M_{s} h_{s} }}} \right] \hfill \\ & \quad - M_{s} z\left[ {J_{s} \sigma_{ox} \frac{{6h_{ox} (h_{s} + h_{ox} )}}{{h_{s}^{3} }} + \dot{\sigma }_{ox} \frac{{6h_{ox} (h_{s} + h_{ox} )}}{{M_{s} h_{s}^{3} }} + \sigma_{ox} \frac{{6(h_{s} + 2h_{ox} )\dot{h}_{ox} }}{{M_{s} h_{s}^{3} }}} \right] \hfill \\ \end{array}$$

(25)

It is noted that if the intrinsic strain and the stress influence on the reaction are omitted, Eq. (25) then reduces to the model of Dong et al. [26].

Numerical Calculation and Discussions

In order to implement the proposed models and compare with the experimental result of Saunders et al. [23] and the creep model of Zhang et al. [27], we suppose that the oxide is alumina scale and the metal substrate is FeCrAlY. Moreover, the effect of the stress on the growth strain rate is neglected in the below simulation since the value of the chemo-mechanical coupled coefficient, $a$, is unknown for FeCrAlY and alumina scale. The sets of the material parameters are the same as in the experiment results of Saunders et al. [23], and $D_{ox}$ is estimated based on the theoretical analysis [13]. They are given in Table 1.

Table 1 Value of some material parameters as in [13, 18, 23]

The relationship between the curvature of the system during oxidation and the oxidation time is shown in Fig. 2. It can be found that the curvature of the elastic model is linear with the oxidation time and dramatically deviates from the experimental data. That of Zhang’s creep model [27] is almost linear and much closer to the experimental data than that of the elastic model at the initial stage of the oxidation. The curvature of the present model considering the intrinsic strain and creep effect can lead to an excellent agreement with the experimental result at longer oxidation time, which indicates that the deformation of the metallic oxidation is controlled by the creep and intrinsic strain and this is also proved in Fig. 3.

Fig. 2

The curvature evolution of the system

Fig. 3

The stress evolution of the oxide

Figure 3 depicts the comparison of the oxide stress among the creep model, present model and experimental result. In the early stage of the oxidation, compressive stress in the oxide scale rapidly increases and reaches the maximum. After the peak, the oxidation stress gradually decreases. These can be observed no matter whether in the creep model or in the present model. Additionally, the creep model can capture the stress relaxation phenomenon at long oxidation time just as the present model. However, it is obvious that the oxidation stress of the creep model is much larger than the experimental data in magnitude, and the present model with intrinsic strain and creep effect is in good agreement with the experimental results. These show that the present model can predict the stress evolution.

The stress evolution in the metal substrate at different locations is exhibited in Fig. 4, where some typical positions are chosen. $z = h_{s} /2$, $z = 0$ and $z = - h_{s} /2$ represent the top surface, middle plane and the bottom surface of the metallic substrate. It can be observed from Fig. 4 that most of the region close to the middle plane and top surface of the substrate is tensile, while the region in the vicinity of the bottom surface is in compressive stress state. Moreover, the tensile is larger than the compressive in magnitude, and this leads to the bending deformation in the metal substrate. It is noted that the middle plane is in the tensile state due to the influence of the creep and intrinsic strain on the stress. At the longer oxidation time, the stress evolution of the different locations is almost not variable with time and reaches the steady state owing to the intrinsic strain and creep effect. It is also found that the stress is bigger at the farther location from the middle plane, and the top surface of the substrate (i.e. the oxide/substrate interface) is most dangerous because it is in the common tensile state and reaches the maximum value among all the planes in the substrate.

Fig. 4

The stress evolution in the metal substrate at different locations

The stress evolution in the oxide scale for different $D_{ox}$ is depicted in Fig. 5. It can be seen that the growth parameter $D_{ox}$ has a significant influence on the stress evolution. The maximum compressive stress increases with increase of $D_{ox}$, while the time at which the maximum stress appears is almost the same. Similar result is observed in [8]. In the later oxidation stage, the stress of the oxidation scale reaches the steady state and decreases in magnitude. Therefore, in order to avoid the oxidation failure, it is a key to reduce the value of $D_{ox}$.

Fig. 5

The stress evolution for different $D_{ox}$

The relationship between the maximum compressive oxide stress and $D_{ox}$ is illustrated in Fig. 6. It can be observed that the maximum compressive stress $\sigma_{ox}$ in magnitude increases with the increasing of $D_{ox}$. Moreover, the maximum compressive stress in the oxide scale varies linearly with $D_{ox}$, which is in agreement with Panicaud et al.’s result [6].

Fig. 6

Maximum compressive oxide stress and $D_{ox}$

In order to investigate the effects of substrate thickness, creep constants, and intrinsic strain on residual stress evolutions in the oxide scale and metal substrate, $h_{s}$, $J_{ox}$, $J_{s}$ and $\varepsilon^{*}$ are varied in the corresponding calculations. It is noted that the stress evolution at the top surface of the substrate is only illustrated, since it represents the common tensile stress state in the substrate and in the most dangerous state.

The influence of the metal substrate thickness on the stress evolution in the oxide scale and metal substrate is depicted in Fig. 7. It is noticed that the oxidation stress becomes smaller for the thinner $h_{s}$, and this is because the system relaxes the stress by a curvature change more easily. The stress decreases significantly with the increase of $h_{s}$ in the metal substrate as shown in Fig. 7b.

Fig. 7

The stress evolution for different $h_{s}$

The stress variations with the creep constant $J_{ox}$ and $J_{s}$ are shown in Figs. 8 and 9. The compressive stress in the oxidation scale increases as $J_{ox}$ decreases, and lower value of $J_{ox}$ in the oxide scale increases the oxide stress. Moreover, the similar results are observed in the metal substrate as shown in Figs. 8b and 9b. It can be seen from Fig. 9 that the compressive stress in the oxide and tensile stress in the substrate decrease obviously with the increase of $J_{s}$. Compared these curves in Figs. 8 and 9, we find that $J_{ox}$ has a stronger influence on the stress variation than $J_{s}$. Therefore, in order to reduce the residual stress generated during oxidation at high temperature, one must increase the creep constant of the oxide or decrease that of the metal substrate.

Fig. 8

The stress evolution for different $J_{ox}$

Fig. 9

The stress evolution for different $J_{s}$

The stress variation with the oxide intrinsic stain $\varepsilon^{*}$ is shown in Fig. 10. It can be seen that the compressive stress in the oxidation scale and the tensile stress in metal substrate decrease as $\varepsilon^{*}$ increases. The intrinsic strain plays a significant role in the oxide stress and metal stress at the initial stage of oxidation, while the stresses in the oxidation scale and metal substrate nearly remain constant in the later oxidation stage, constant whatever $\varepsilon^{*}$ is.

Fig. 10

The stress evolution for different $\varepsilon^{*}$

Conclusions

In this paper, considering the coupled effect between the growth strain and stress, intrinsic strain and creep deformation, a new model to characterize the residual stress evolution during the metal oxidation at high temperature is developed. In this model, the growth strain and the stress in the oxide scale are coupled based on the evolving equation. The curvature describing the deformation of the system is exhibited. The results from the present model are in better agreement with the experimental data than those of the Zhang’s creep model and elastic model for FeCrAlY. Finally, effects of creep constants, substrate thickness and intrinsic strain on the residual stress distribution in the oxide scale/metal substrate are discussed. From the numerical results, it can be concluded that the growth constant, creep constant and the substrate thickness influence the stress evolution in the oxide and substrate, while the intrinsic strain influence the stress at the beginning of the oxidation stage.