1 Introduction

The terahertz frequency range is of great importance to researchers because of the unique features it gives to the communication system, such as fast data transfer speeds, low interrupt risk, low fading, and high reliability (Alharbi et al. 2016; Chowdhury et al. 2020). Various antenna structures, both planar and non-planar, have been investigated for use in the terahertz band, among which structures with higher radiation efficiencies or lower losses are more attractive. Due to the low conduction losses in DRA, which is due to the minimal use of metal in its structure, special attention has recently been paid to the use of DRA in the microwave, terahertz and optical bands as an antenna element (Fakhte and Oraizi 2016; Fumeaux, et al. 2016; Fakhte et al. 2018; Headland et al. 2015; Fakhte and Matekovits 2022). With the advent of graphene in recent years, many terahertz devices have been developed based on it. Electron mobility of graphene at terahertz frequencies leads to interesting properties (Jornet and Akyildiz 2010; Moon and Gaskill 2011; Huang et al. 2012). One of the most important properties is its conductivity control with chemical potential, making it possible to control antenna responses such as operating frequency band and radiation pattern by changing the electrostatic bias voltage (Esquius-Morote et al. 2014; Mehta and Zaghloul 2014; Donelli and Viani 2016). Recently, the use of graphene in hollow cylinder DRA structures has been proposed to create resonant frequency adjustments in both linear and circular polarization (Varshney 2020; Gupta et al. 2021a).

In this paper, for the first time, an approximate formula for obtaining the resonant frequency of graphene-loaded rectangular DRA is presented. Using this formula, it can be seen that by changing the surface impedance of graphene, which is obtained by changing its chemical potential, the resonance frequency of different antenna modes can be changed. This formula is then used to design a dual-band rectangular DRA loaded with graphene. A microstrip line made of silver connected to a trapezoidal matching taper is used to excite the antenna.

The article is organized as follows: Part 2 describes the structure of the antenna. Also, in this section, the theoretical method for obtaining DRA resonant frequency is investigated. In Sect. 3, the simulation results for different values of graphene chemical potential are discussed. Then, the ability to tune the DRA with the help of graphene is explained. Finally, there is a conclusion.

2 Antenna configuration

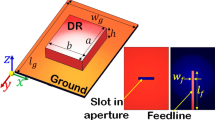
Figure 1 shows the structure of the proposed graphene-loaded DRA. As shown in the Fig. 1, a 0.34 nm thick graphene material with relaxation time \(\tau =1\,ps\) and temperature of T = 300 K is placed on top of a rectangular silicon DRA with permittivity of \({\varepsilon }_{r}=11.9\). The DRA itself is placed on a silicon dioxide (SiO2) substrate with a dielectric constant of \({\varepsilon }_{r}=3.8\) and thickness of \({h}_{sub}=1.6\,\upmu m\). A 50 Ω microstrip line connected to a trapezoidal matching part feeds the antenna. A silver metal plate is placed under the substrate, which plays the role of a ground plane. The ground plane and feed line are considered with silver 0.2\(\mu m\). Also, the electrostatic biasing method of graphene is shown in Fig. 1b, where a DC voltage \({V}_{b}\) is used to tune the conductivity of graphene Gupta et al. 2021a, b; Vishwanath et al. 2022).

Fig. 1
figure 1

Antenna structure, aThe 3D view of proposed graphene-loaded DRA, b the electrostatic biasing mechanism of graphene

Full size image

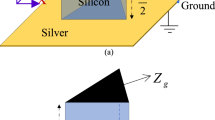
The dielectric waveguide method with two impedance walls is used to obtain a formula for the resonant frequency of graphene-loaded rectangular DRA, as shown in Fig. 2. Figure 2a shows the antenna placed on the ground plane, while in Fig. 2b, based on the image theorem, the ground plane is removed and the height of the antenna is doubled. Some modifications have been made to this model to describe a rectangular DRA loaded with impedance boundary conditions theoretically. The field expressions for the \({TE}_{mnp}^{y}\) modes of the DRA with two impedance walls at \(z=\pm d/2\) can be written as follows:

$$\begin{aligned} & E_{x} = \frac{{j\omega \mu_{0} k_{z} }}{{k_{0}^{2} \varepsilon_{r} - k_{y}^{2} }}H_{0} \sin \left( {k_{x} \left( {x + \frac{a}{2}} \right)} \right)cos(k_{y} y) \\ & \left[ {C_{1} \cos \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right) - C_{2} \sin \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right)} \right] \\ \end{aligned}$$
(1.a)
$$E_{y} = 0$$
(1.b)
$$\begin{aligned} & E_{z} = \; - \;\frac{{j\omega \mu _{0} k_{x} }}{{k_{0}^{2} \varepsilon _{r} - k_{y}^{2} }}H_{0} \cos \left( {k_{x} \left( {x + \frac{a}{2}} \right)} \right)cos(k_{y} y) \\ & \left[ {C_{1} \sin \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right) + C_{2} \cos \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right)} \right] \\ \end{aligned}$$
(1.c)
$$\begin{aligned} & H_{x} = - \frac{{jk_{y} k_{x} }}{{k_{0}^{2} \varepsilon_{r} - k_{y}^{2} }}H_{0} \cos \left( {k_{x} \left( {x + \frac{a}{2}} \right)} \right)sin(k_{y} y) \\ & \left[ {C_{1} \sin \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right) + C_{2} \cos \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right)} \right] \\ \end{aligned}$$
(1.d)
$$\begin{aligned} & H_{y} = H_{0} \sin \left( {k_{x} \left( {x + \frac{a}{2}} \right)} \right)cos(k_{y} y) \\ & \left[ {C_{1} \sin \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right) + C_{2} \cos \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right)} \right] \\ \end{aligned}$$
(1.e)
$$\begin{aligned} & H_{z} = \; - \frac{{jk_{y} k_{z} }}{{k_{0}^{2} \varepsilon _{r} - k_{y}^{2} }}H_{0} \sin \left( {k_{x} \left( {x + \frac{a}{2}} \right)} \right)sin(k_{y} y) \\ & \left[ {C_{1} \cos \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right) + C_{2} \sin \left( {k_{z} \left( {z + \frac{d}{2}} \right)} \right)} \right] \\ \end{aligned}$$
(1.f)
Fig. 2
figure 2

a Graphene-loaded DRA mounted on a metal ground plane, b Its equivalent structure using the image theorem

Full size image

The impedance boundary condition is written as follows (Balanis 2012):

$$\overline{E} = Z_{g} \;\hat{n} \times \overline{H}$$
(2)

where \(\widehat{n}\) is the unit vector perpendicular to the \(z=\pm d/2\) planes, oriented towards the interior of the DRA and \({Z}_{g}={R}_{g}+j{X}_{g}\) is the surface impedance of the graphene, with \({R}_{g}\) and \({X}_{g}\) representing the real and imaginary parts of the surface impedance, respectively. In the following, an approximate formula for obtaining the resonance frequency of the graphene-loaded DRA is obtained.

The conductivity of graphene sheet can be calculated by the well-known Kubo formula (Gusynin et al. 2006) as:

$$\sigma_{s} (\omega ) = \frac{{e^{2} k_{B} T\tau }}{{(1 + j\omega \tau )\pi \hbar^{2} }}\left[ {\frac{{\mu_{c} }}{{k_{B} T}} + 2\ln \left( {e^{{ - \mu_{c} /k_{B} T}} + 1} \right)} \right]$$
(3)

where ω is the angular frequency, \({k}_{B}\) is the Boltzmann constant, ћ is the reduced Plank constant, T is the temperature, and τ is the relaxation time. We assume \(T=300\, K\) and \(\tau =1\, ps\) throughout this work. The chemical potential of graphene, \({\mu }_{c}\), can be tuned by varying its biasing electrostatic voltage. The surface impedance of graphene sheet is calculated as follows:

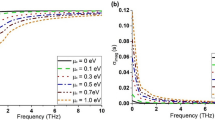
$${Z}_{s}\left(\omega \right)=\frac{1}{{\sigma }_{s}(\omega )}$$
(4)

Figure 3 shows the surface impedance of the graphene with a relaxation time of \(\tau =1 ps\) and a temperature of T = 300 K for different values of chemical potential. As shown, for different values of the chemical potential of graphene, the absolute value of the imaginary part of the surface impedance is much larger than that of the real part, so the real part is neglected in the calculations. This condition is also necessary to satisfy the boundary conditions, because if the real part of the surface impedance is included in the calculations, it can be proved that the \({TE}^{y}\) mode cannot be properly excited in the structure. Therefore, considering that the real part is not zero, but has a very small value compared to the imaginary part, it can be assumed that the quasi \({TE}^{y}\) mode is excited in the antenna.

Fig. 3
figure 3

Surface impedance of graphene for different values of chemical potential, a resistance, b reactance, c the reactance to resistance ratio. The graphene relaxation time and temperature are τ = 1 ps and T = 300 K, respectively

Full size image

By establishing the boundary conditions of the electric and magnetic fields on the walls \(y=\pm b/2\) and \(x=\pm a/2\), it can be seen that the relations extracted to obtain \({k}_{x}\) and \({k}_{y}\) are the same as the DWM method (Kumar Mongia and Ittipiboon 1997), i.e.:

$${k}_{x}=\frac{m\pi }{a}, {k}_{0}=\frac{2\pi {f}_{0}}{c}$$
(5)
$${k}_{y}b=2{tan}^{-1}\left(\frac{\sqrt{{k}_{x}^{2}+{k}_{z}^{2}-{k}_{0}^{2}}}{{k}_{y}}\right)+(n-1)\pi$$
(6)

where c is the speed of light in vacuum and a, b are dimensions of the DRA. Next, to obtain kz, the boundary conditions of the fields should be written on the \(z=\pm d/2\) walls. The boundary condition of the electric and magnetic fields on the \(z=d/2\) wall is written as follows:

$${E}_{x}={Z}_{o}{H}_{y}$$
(7)

By placing \({E}_{x}\) and \({H}_{y}\) from Eqs. (1.a) and (1.e) in Eq. (7) at the boundary \(z=d/2\), the following equation is obtained:

$$\frac{j\omega {\mu }_{0}{k}_{z}}{{\varepsilon}_{r}{k}_{0}^{2}-{k}_{y}^{2}}\left({A}_{1}\mathrm{cos}\left({k}_{z}d\right)-{A}_{2}\mathrm{sin}({k}_{z}d)\right)={Z}_{0}\left({A}_{1}\mathrm{sin}\left({k}_{z}d\right)+{A}_{2}\mathrm{cos}({k}_{z}d)\right)$$
(8)

where \({A}_{1}\) and \({A}_{2}\) are the unknown coefficients of the equation that should be calculated. Also, on the boundary \(z=-d/2\), the boundary condition is \({E}_{x}={-Z}_{o}{H}_{y}\), so by placing the electric and magnetic fields, the following equation is obtained:

$$\frac{j\omega {\mu }_{0}{k}_{z}}{{\varepsilon }_{r}{k}_{0}^{2}-{k}_{y}^{2}}{A}_{1}=-{Z}_{o}{A}_{2}$$
(9)

By solving the two Eqs. (8) and (9), the equation obtained to calculate \({k}_{z}\) is as follows:

$$\mathrm{tan}\left({k}_{z}d\right)=\frac{2j\omega {\mu }_{0}{k}_{z}{Z}_{0}}{({\varepsilon }_{r}{k}_{0}^{2}-{k}_{y}^{2})({Z}_{o}^{2}+{(\frac{\omega {\mu }_{0}{k}_{z}}{{\varepsilon }_{r}{k}_{0}^{2}-{k}_{y}^{2}})}^{2})}$$
(10)

where \(\omega =2\,\pi f\) is the angular frequency, \({\varepsilon }_{r}\) is the permittivity of the DRA and \({Z}_{0}\) is the surface impedance of the graphene layer. Note that Eq. (10) has a real solution for \({k}_{z}\) only if the.

surface impedance \({Z}_{0}\) is considered completely imaginary, i.e., \({Z}_{0}=j{X}_{o}\). By placing an imaginary \({Z}_{0}\) in Eq. (10) we have:

$$\mathrm{tan}\left({k}_{z}d\right)=\frac{240\pi {k}_{z}{X}_{0}}{({\varepsilon }_{r}{k}_{0}^{2}-{k}_{y}^{2})({X}_{o}^{2}-{(\frac{120\pi {k}_{z}{X}_{0}}{{\varepsilon }_{r}{k}_{0}^{2}-{k}_{y}^{2}})}^{2})}$$
(11)

Therefore, by solving Eqs. (5), (6), and (11), the \({TE}_{mnp}^{y}\) mode resonant frequency can be obtained. The following is a design method for graphene-loaded DRA:

  • First, in Fig. 3b, the value of X0 is obtained for the desired design frequency, \({f}_{0}\) and chemical potential, \({\mu }_{c}\). Then, by using Eq. (5), the values of \({k}_{0}\) and \({k}_{x}\) are determined.

  • Then, by solving the Eqs. (6), and (11), the values of b and d are calculated.

3 Results and discussion

In this section, using the design method presented in the previous section, a graphene-loaded DRA at 1.62 THz is designed. The goal is to excite the \({TE}_{111}^{y}\) mode in the DRA. The parameters of graphene are considered as follows: \(\tau =1 ps\), T = 300 K and \({\mu }_{c}=0.5\, eV\). The dielectric material used in the DRA is silicon and its \({\varepsilon }_{r}\) is equal to 11.9. First, the value of X0 at 1.62 THz should be determined, which can be seen from Fig. 3b that the value of X0 at 1.62 is 173 Ω. Then, by solving the Eqs. (6), and (11) and considering the square cross-section for DRA, i.e., a = b, the values calculated for a and d are equal to: \(a=38.8\, \mu m\) and \(d=60\, \mu m\). By inserting the values obtained from this method in the formula available in the literature for the graphene-free DRA (Kumar Mongia and Ittipiboon 1997), the resonance frequency is calculated to be 1.53 THz, which is 0.9 THz lower than the value calculated by the present method. Since the value of X0 is different at other frequencies, to calculate the resonant frequency of the next mode, i.e., \({TE}_{113}^{y}\) mode, for the initial guess, the same X0 as of the \({TE}_{111}^{y}\) mode is used. Therefore, by solving Eqs. (5), (6), and (11), the \({TE}_{113}^{y}\) mode resonant frequency is calculated to be 2.77 THz. Figure 3b shows that the value of X0 at 2.77 THz is about 290 ohms, so considering this value for X0, the resonance frequency of \({TE}_{113}^{y}\) mode is calculated to be 2.72 THz.

To confirm the accuracy of the resonance frequencies obtained from the above method, the antenna structure shown in Fig. 1 is simulated using CST software. To match the input impedance of the DRA to that of the microstrip line, a trapezoidal matching section of dimensions \({L}_{t}=55.8\, \mu m\) and \({W}_{t}=32.8\, \mu m\) is used. Figure 4 shows the simulated reflection coefficient of the antenna for different values of chemical potential. It is obvious that with increasing \({\mu }_{c}\) from 0 to 0.8 eV, the resonant frequencies of both modes shift to higher frequencies. Also, note that for values of chemical potential less than 0.3 eV, the level of the reflection coefficient in the second band is higher than − 10 dB, in which case the antenna works only in the first band and becomes a single band DRA.

Fig. 4
figure 4

Reflection coefficient of the proposed antenna for different values of the chemical potential

Full size image

The results of the proposed theoretical method are compared with the simulation results for different values of chemical potential of graphene in Table 1. As both simulation and theoretical results show, the resonant frequencies of both modes increase with increasing the chemical potential of graphene. Note that \({\mu }_{c}=0\) is approximately equivalent to the problem of DRA without the graphene wall, so the calculated resonant frequency is the same as the resonant frequency calculated by the DWM method (Kumar Mongia and Ittipiboonthis 1997) for isolated DRA. Note that the proposed method accurately follows the resonant frequencies of the \({TE}_{111}^{y}\) and \({TE}_{113}^{y}\) modes of the graphene-loaded DRA for different \({\mu }_{c}\) values, unlike the conventional DWM method, which has fixed resonant frequencies for both modes. The electric field distributions of \({TE}_{111}^{y}\) and \({TE}_{113}^{y}\) modes at frequencies of 1.64–2.77 THz, respectively, for the chemical potential of graphene \({\mu }_{c}=0.3\, eV\) are shown in Fig. 5. This figure shows that these two modes are excited inside the DRA.

Table 1 Comparison between the theoretical and simulated results of the resonance frequencies for different values of the chemical potential
Full size table
Fig. 5
figure 5

Electric field distribution of the graphene-loaded DRA for μ_c = 0.3 eV, a at 1.64 THz for \({TE}_{111}^{y}\)mode, b at 2.77 THz for \({TE}_{113}^{y}\) mode

Full size image

The simulated reflection coefficients of graphene loaded DRA with two different solvers, CST and HFSS, are shown in Fig. 6. Observe that they show a good agreement.

Fig. 6
figure 6

Simulated reflection coefficient of the graphene loaded DRA obtained by two different solvers, CST and HFSS

Full size image

Figure 7 shows the simulated radiation patterns of the proposed graphene-loaded DRA. Note that at the frequencies of 1.64–2.77 THz, where the \({TE}_{111}^{y}\) and \({TE}_{113}^{y}\) modes are excited, respectively, the radiation patterns are broadside. Also, a good agreement between the CST and HFSS results is obtained.

Fig. 7
figure 7

Simulated radiation patterns (gain) of the graphene-loaded DRA, a at 1.64 THz for both XoZ and YoZ planes, b at 2.77 THz for both XoZ and YoZ planes

Full size image

Finally, in Table 2, the theoretical resonant frequencies of \({TE}_{111}^{y}\) and \({TE}_{113}^{y}\) modes calculated by the proposed method are compared with simulated results. Differences between the simulated and theoretical resonant frequencies vary between 0.1 to 4.6%.

Table 2 Comparison between the simulated and calculated results at different frequencies (\({\mu }_{c}=0.5\, eV\))
Full size table

4 Conclusion

In this paper, for the first time, a theoretical method for calculating the resonant frequency of graphene-loaded DRA is presented. The graphene wall is assumed to be an impedance boundary, and the DRA resonant frequency is obtained by applying the impedance boundary conditions for the electric and magnetic fields. Then, using the proposed design formulas, a dual-band graphene-loaded DRA is designed. The proposed antenna is simulated and the resonance frequency results obtained from the theory are in good agreement with the simulation.