1 Introduction

Data transmission using free-space optics (FSO) technology, which capitalizes on the optical frequency spectrum instead of radio frequency, is very beneficial due to its many inherent merits, including no licensing requirements, enhanced security, data transmission with large bandwidth, and fast deployment process. However, the FSO transmission suffers from continuous fluctuations due to variations in pressure and temperature of the atmosphere (Chan 2006; Shapiro and Harney 1980). FSO transmission enabled by dense wavelength-division multiplexing (DWDM) can augment the number of information channels and enhance the information rate of the system for the long-haul transmission network. DWDM transmission allows the multiplexing of multiple information signals having a large channel capacity on a single transmission medium with operating wavelength ranging from 1539 – 1565 nm (C-band) and can offer information transfer rates of the order of Terabits/second in FSO systems (Ciaramella et al. 2009). Passive optical networks (PONs) involve the transmission of information from the core/backbone network to the last-mile user access, i.e., individual homes, offices, buildings, etc., by employing optical fiber cables instead of copper wires (Karp et al. 1988; Ramaswami and Sivarajan 2002). The integration of wavelength-division multiplexed (WDM) transmission in PON systems can offer a high-transmission capacity broadband access network for last-mile users and meet the end subscribers' high bandwidth needs (Manor and Arnon 2003; Hayal et al. 2021; Ansari and Zhang 2013; Zuo and Phillips 2009; Aladeloba et al. 2013). Furthermore, integrating FSO links with PON architectures can offer high data transmission rates to the last-mile subscribers in complex territories, including densely populated urban areas and rough terrains like mountains. In Mandal et al. 2022, proposed a hybrid PON-FSO system with integrated FSO/fiber transmission with enhanced fault protection for long haul communication. 40 Gbps information transmission was achieved with high-tolerance to Rayleigh backscattering. In Singh et al. 2021 proposed a mode-division-multiplexed hybrid PON-FSO architecture for high-information capacity transmission. 40 Gbps transmission at 10 km single mode fiber (SMF) and 1000 m FSO was reliably demonstrated. In Pham et al. 2020, proposed and analysed a WDM-PON architecture incorporating integrated fiber/FSO transmission. The authors reported the performance under four wave mixing effect, background noise, beat noise, atmospheric turbulence, and scattering effects. The authors reported that by the use of amplifiers, the errors in the received bits can be minimized. In Garg et al. 2021 reported a integrated SMF/FSO based PON architecture supporting dual-rate information transmission at 1 Gbps and 10 Gbps. The proposed solution provided a feasible technology for WDM-enabled optical access network for smart cities with high power efficiency and low cost of implementation. In Navas et al. (2016) reported a secure and power efficient integrated fiber/FSO PON transmission by incorporating optical-code division multiplexed transmission technique under the influence of atmospheric turbulence. In Kumari et al. 2021 reported a hybrid mode-time-wavelength-division multiplexed integrated PON-FSO transmission scheme for transporting 40 Gbps upstream and downstream data under the influence of pointing errors and atmospheric turbulences. In Lu et al. 2022 experimentally demonstrated a bi-directional PON-FSO network incorporating PAM-4 signals to achieve 25 km SMF transmission and 500 m FSO transmission. Moreover, the deployment of optical amplifiers (OAs) in PON architecture can enhance the transmission range of the access network (Wilson et al. 2005; Abtahi et al. 2006). Digital-pulse position modulation (DPPM) and on–off keying (OOK) schemes, which modulate photon intensity for data transmission, are the two most important modulation schemes in optical networks. DPPM modulation has a higher power efficiency than OOK schemes and is used for optical fiber networks, satellite communication, terrestrial transmission, and deep-space networks (Phillips et al. 1996).

Although DWDM transmission offers higher information transmission capacity, the user of multiple laser diodes results in inter-channel crosstalk between different wavelength channels, which degrades the transmission performance. In addition, the continuously varying pressure and temperature in the atmosphere result in turbulence losses, which limit the FSO transmission range. This work reports the modeling and numerical analysis of a DWDM-enabled PON-FSO transmission under the effect of inter-channel crosstalk and atmospheric turbulence and investigates the performance of modified OOK/DPPM modulation scheme with adaptive threshold. The remainder of the paper is organized as follows: Sect. 2 reports the proposed DWDM-enabled PON-FSO system design, followed by atmospheric turbulence modeling in Sect. 3. Section 4 discusses the BER analysis of the proposed system, and the results are presented in Sect. 5. The conclusion is drawn in Sect. 6.

2 System design

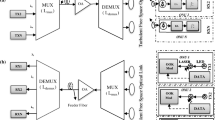
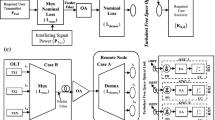
The architecture of the proposed DWDM-enabled PON-FSO system is illustrated in Fig. 1. It has the following units: optical line terminal (OLT), DWDM transmission, optical amplifier (OA), feeder fiber, FSO link, and optical network units (ONUs). The OLT provides the interconnection between the core/backbone network and the PON system. The DWDM technology is used to enhance the information transmission capacity of the PON system by employing multiple carrier wavelengths. The OAs are used to realize a long-reach PON transmission. A feeder fiber of 20 km in length is used in this work.

Fig. 1
figure 1

a Block diagram of the proposed DWDM-enabled PON-FSO system b downstream transmission setup c upstream transmission setup

Full size image

The OLT consists of multi-wavelength users who are multiplexed together to transmit high-speed information in the PON network. The proposed system uses a channel spacing of 0.8 nm for adjacent channels to realize DWDM transmission. Each transmitter unit at the OLT consists of an information source (pseudo-random bit sequence generator) followed by a line encoder (OOK/DPPM). The information is modulated on the optical beam from the laser diode using an optical modulator. Individual modulated signals using distinct wavelengths are multiplexed using multiplexer (MUX). The signal is transmitted towards a feeder fiber of 20 km length which is further amplified using an erbium-doped fiber amplifier (EDFA). At the ONU receiver, individual channels are segregated using de-multiplexer (DEMUX). The data at distinct ONU is transmitted through an FSO link. The signal is retrieved using 3R signal regenerator and analyzed in terms of bit-error rate (BER). An optical band-pass filter (OBPF) is used in the upstream and downstream transmission to remove unwanted signal frequencies.

3 Atmospheric turbulence modeling

Turbulence in the free-space medium results from continuously varying pressure and temperature of the earth's surface and atmosphere. The strength of the atmospheric turbulence can be estimated using the index refraction structure parameter, \({C}_{n}^{2}\) (Andrews et al. 2001). The probability density function (pdf) of Gamma-Gamma turbulence channel can be mathematically represented as (Aladeloba et al. June 2013; Andrews and Phillips 2005; Majumdar 2005; Khalighi et al. 2009):

$$P_{GG} \left( {h_{X} } \right) = \frac{{2\left( {\alpha \beta } \right)^{{\left( {\alpha + \beta } \right)/2}} }}{\left( \alpha \right)\left( \beta \right)}h_{X}^{{\frac{\alpha + \beta }{2} - 1}} K_{ \alpha - \beta } \left( {2\sqrt {\alpha \beta h_{X} } } \right);\quad h_{X} > 0$$
(1)

where \(h_{X}\) is the attenuation due to atmospheric turbulence caused for the information signal (\(h_{sig}\)) and interferer (\(h_{int}\)), \(\alpha\) is the effective number of large-scale eddies of the scattering process, \({\upbeta }\) is the effective number of small-scale eddies of the scattering process, and \(\Gamma \left( \cdot \right)\) is the gamma function (Aladeloba et al. 2013). \({\text{K}}_{{\text{ n}}}\) is the modified Bessel function of the order \(n\) (Aladeloba et al. 2013). The signal and interferer follow distinct paths upstream, as reported in Andrews and Phillips (2005); Majumdar 2005; Khalighi et al. 2009). Aperture averaging is incorporated into the turbulence model to mitigate fading, atmospheric turbulence, and scintillation. The \(\alpha\) and \(\beta\) parameters for plane-wave propagation are given as (Aladeloba et al. 2013):

$$\alpha = \left\{ {\exp \left[ {\frac{{0.49\sigma_{{\text{R}}}^{2} }}{{\left( {1 + 0.65d^{2} + 1.11\sigma_{{\text{R}}}^{12/5} } \right)^{7/6} }} } \right] - 1} \right\}^{ - 1}$$
(2)
$$\beta = \left\{ {\exp \left[ {\frac{{0.51\sigma_{{\text{R}}}^{2} \left( {1 0.69\sigma_{{\text{R}}}^{12/5} } \right)^{ - 5/6} }}{{1 + 0.9d^{2} + 0.62d^{2} \sigma_{{\text{R}}}^{12/5} }} } \right] - 1} \right\}^{ - 1}$$
(3)

where d = \(\sqrt {KD_{RX}^{2} /4l_{fso} }\) is the normalized receiver collector lens (RCL) radius and Rytov variance \({\upsigma }_{{\text{R}}}^{{2}}\) = 1.23 \({\text{C}}_{{\text{n}}}^{2} {\text{K}}^{7/6} l_{fso}^{11/6}\). \({\text{C}}_{{\text{n}}}^{2}\) is the index refraction structure constant (ranging from \(\approx 10^{ - 17} {\text{m}}^{ - 2/3}\) to \(\sim 10^{ - 13} {\text{m}}^{ - 2/3}\)), \(l_{fso}\) is the FSO link length, k = \(2{\uppi }/{\uplambda }\) is the wave number and \({\uplambda }\) is the laser wavelength in nm.

4 General BER analysis

Depending on distinct signal and crosstalk channels for upstream and downstream, the BERs are denoted as (Aladeloba et al. June 2013):

$$\begin{array}{*{20}c} { \overline{{{\text{BER}}}} = \iint\limits_{0}^{ \infty } {BER\left( {h_{sig,} h_{int} } \right)P_{GG,sig} \left( {h_{{{\text{sig}}}} } \right) P_{GG,int} \left( {h_{{\text{int}}} } \right)dh_{sig} dh_{int} }} \\ \end{array}$$
(4)

where \({\text{P}}_{{\text{GG,sig}}} \left( {{\text{h}}_{{{\text{sig}}}} } \right)\) and \({\text{P}}_{{{\text{GG}},{\text{sig}}}} \left( {{\text{h}}_{{{\text{int}}}} } \right)\) are respectively, the signal and interferer GG pdfs (each with different \(\upalpha ,\upbeta , \;{\text{and}}\; \upsigma _{{\text{R}}}^{2} )\) as reported in Aladeloba et al. (2013). The conditional BER can be approximated using Gaussian distribution as (Aladeloba et al. 2013):

$${\text{BER}}\left( {h_{sig} ,h_{int} } \right){ = }\frac{{1}}{{4}}{\text{erfc}}\left( {\frac{{{\text{Q(}}h_{sig} ,h_{int} {)}}}{{\sqrt {2} }}} \right)$$
(5)
$$Q\left( {h_{{sig}} ,h_{{int}} } \right)~ = \frac{{i_{{1,0}} \left( {h_{{sig}} ,h_{{int}} } \right) - {\text{i}}_{{0,1}} \left( {h_{{sig}} ,h_{{int}} } \right)}}{{\sigma _{{1,0}} \left( {h_{{sig}} ,h_{{int}} } \right) + ~\sigma _{{0,1}} \left( {h_{{sig}} ,h_{{int}} ,} \right)}}$$
(6)

where \({\text{i}}_{{d_{sig} }} \left( {h_{sig} } \right) = ad_{sig} RP_{R, sig} \left( {h_{sig} } \right)\) and \({\text{i}}_{{d_{int} }} \left( {h_{int} } \right) = ad_{int} RP_{R, int} \left( {h_{int} } \right)\) are the signal and interferer current for data 1 and 0, respectively (Aladeloba et al. 2013). \(P_{R, sig}\) and \(P_{R, int}\) are the received signal and interferer average powers, respectively. Also \({\text{a}}_{{0}} = {2}/{\text{r}} + {1}\), and \({\text{a}}_{{1}} {\text{ = 2r}}/{\text{r + 1}}\) where \(r\) is the extinction ratio.

4.1 Upstream transmission analysis

The average optical power received by the OLT photodiode for the desired signal and an interferer signal is calculated as (Aladeloba et al. 2013):

$${\text{P}}_{{\text{R,sig}}} \left( {{\text{h}}_{{{\text{sig}}}} } \right) = {\text{GP}}_{{\text{UT,sig}}} {\text{h}}_{{{\text{sig}}}} {\text{L}}_{{{\text{fso}}{\text{.sig }}}} {\text{L}}_{{\text{bs,sig}}} {\text{L}}_{{\text{c,si}}} {\text{L}}_{{{\text{mux}}}} {\text{L}}_{{{\text{fiber}}}} {\text{L}}_{{{\text{demux}}}}$$
(7)
$${\text{P}}_{{\text{R,int}}} \left( {{\text{h}}_{{\text{int}}} } \right) = {\text{GP}}_{{\text{UT,int}}} {\text{h}}_{{{\text{int}} }} {\text{L}}_{{{\text{fso}}{\text{.int }}}} {\text{L}}_{{\text{bs,int}}} {\text{L}}_{{\text{c,int}}} {\text{L}}_{{{\text{mux}}}} {\text{L}}_{{{\text{fiber}}}} {\text{L}}_{{\text{demux }}} {\text{L}}_{{\text{demux,XT}}}$$
(8)

where \({\text{L}}_{{\text{C}}}\) is the coupling loss (Dikmelik and Davidson 2005) and interferer Ldemux,XT refers to the additional loss (above Ldemux) incurred by the interferer when it is connected to the signal photodiode through the demux, G is the gain of the optical amplifier (OA). \({\text{L}}_{{{\text{fiber}}}}\) is the feeder fiber link length (20 km). The loss due to beam divergence may be computed for the FSO connection as (Majumdar 2005; Khalighi et al. 2009):

$$L_{BS} = \left[ {\frac{{D_{RX} }}{{\theta_{lfso} }}} \right]^{2}$$
(9)

where \({\text{L}}_{{{\text{bs}}}}\) is the loss due to beam spreading, \(D_{RX}\) is the diameter of the receiver, and \(\theta\) is the beam divergence angle. The mathematical expression for calculating the coupling loss between the signal and the interferer is (Dikmelik and Davidson Aug. 2005), No = 0.5(NFG − 1)\({\text{ h}}_{{\text{P}}} {\upupsilon }\) Lf Ldemux where G and NF are the OA gain and noise figure, respectively, \({\text{h}}_{{\text{P}}}\) is Planck’s constant,\({\upupsilon }\) is the optical frequency, and Lf is the feeder fiber attenuation. The total OLT thermal noise variance is given as: \(\sigma_{th}^{2} = 2m_{t} R^{2} N_{0}^{2} B_{0} B_{e}\) where \(m_{t}\) is the number of polarization states of amplified-spontaneous-emission (ASE) noise, \(B_{0}\) is the optical bandwidth and \(B_{e}\) is the electrical bandwidth. \(R = \eta q/E\) is the responsivity (in A/W), where q is the electron charge and \(\eta\) is the photodiode quantum efficiency. \(E\) = \({\text{h}}_{{\text{P}}} f_{c}\) where \({\text{h}}_{{\text{P}}}\) is Planck's constant and \({\text{ f}}_{{\text{c}}}\) is the carrier frequency.

4.2 Downstream transmission analysis

The optical power received at the ONU photodiodes for both the intended signal and the interferer can be expressed as (Aladeloba et al. June 2013):

$${\text{P}}_{{\text{dR,sig}}} \left( {{\text{h}}_{{{\text{turb}}}} } \right) = {\text{GP}}_{{\text{dT,sig}}} {\text{h}}_{{{\text{turb}}}} {\text{L}}_{{{\text{mux}}}} {\text{L}}_{{{\text{fiber}}}} {\text{L}}_{{\text{demux }}} {\text{L}}_{{\text{fso }}} {\text{L}}_{{{\text{bs}}}}$$
(10)
$${\text{P}}_{{\text{dR,int}}} \left( {{\text{h}}_{{{\text{turb}}}} } \right){\text{ = GP}}_{{\text{dT,int}}} {\text{h}}_{{{\text{turb}}}} {\text{L}}_{{{\text{mux}}}} {\text{L}}_{{{\text{fiber}}}} {\text{L}}_{{\text{demux,XT }}} {\text{L}}_{{{\text{fso}}}}$$
(11)

where \({\text{ P}}_{{\text{dR,sig}}} {\text{ and}}\) \({\text{ P}}_{{\text{dR,int}}}\) are the OLT transmitter power that can be used for the electric domain noises.

4.3 Error floor using OOK

The proposed approach has been investigated using MATLAB software. Table 1 shows the critical parameters used in the calculations. The power required to maintain a particular BER cannot be calculated using a single formula. By keeping the BER constant and reorganizing the code for calculating the BER, the average power can be calculated to provide the constant BER. The root searching method is used to achieve this (Aladeloba et al. 2013). A BER value above the specified BER threshold and a BER value below the defined BER value can be found by calculating an average power value. Keep dissecting between these two boundaries until an estimated average power is reached that can provide a fixed BER. Then we can use this average power as a starting point for the root-finding search. We analyze the proposed system for weak turbulence (WT) (\({\text{C}}_{{\text{n}}}^{2} = 8.4 \times 10^{ - 15} {\text{m}}^{ - 2/3}\)) and strong turbulence (ST) (\(C_{n}^{2} = 1 \times 10^{ - 13} {\text{m}}^{ - 2/3}\)). The numerical results for the Rytov variance at all turbulence conditions \({\upsigma }_{{\text{R}}}^{{2}} > 1\), we have ST, \({\upsigma }_{{\text{R}}}^{{2}} = 1,\) we have moderate or mild turbulence, and \({\upsigma }_{{\text{R}}}^{{2}} < 1\), we have WT. No turbulence and no interferer (Si), turbulence with no interference (Turbu Si) and turbulence with interferer (Turbu Si, XT) are some of the results of the analysis of interchannel crosstalk with M-ary DPPM. The results of the study of BER for OOK are shown in Fig. 2. Only three occurrences of interchannel crosstalk analysis utilizing the error floor method were analyzed. For example, suppose there is a lot of noise in a signal but no noise in crosstalk. In that case, the error floor is based on the long-term average of the BER, i.e., the same Rytov variance and hence scintillation pdf, but averaging across the numerous outcomes that the scintillation may take from that pdf. This crosstalk power will fluctuate over time due to scintillation (Aladeloba et al. 2012; Yousif and Elsayed 2019; Elsayed and Yousif 2020; Mbah et al. 2014; Elsayed et al. 2018). For a given average (long term, i.e., over different scintillation states) received signal power, the fraction of time that the signal falls below this crosstalk is straightforwardly obtained by integrating the scintillation pdf with an appropriate \({\text{h}}_{{\text{P}}}\) for a limit. This crosstalk power will fluctuate over time due to scintillation. The resultant fraction will be referred to as \(F\). Similarly, when crosstalk is turbulent, but the signal is not, it signifies that the receiver is receiving a set signal power (averaged throughout the data). Due to the scintillation effect, the received crosstalk power will occasionally exceed or fall below the signal power, and for a given average (long-term, i.e., over different scintillation states arising from the same scintillation pdf) received crosstalk power, the fraction of time that is crossed over is directly obtained by integrating the scintillation pdf with an appropriate \({\text{h}}_{{\text{P}}}\). Error floors develop at high-signal-to-noise ratios when using systems that detect directly with constant thresholds and on–off keying and when using systems that vary irradiance. A threshold of responsivity (average signal power and average crosstalk power) will be used when the decision threshold is continuously adjusted to the changing received power signal and crosstalk. Crosstalk data is always retrieved over signal data when the average crosstalk power is greater than the signal's average power (regardless of whether the signal or the crosstalk's turbulence causes this). Because the signal and crosstalk data are uncorrelated, crosstalk can only guess the signal 50% of the time, the BER probability must be 0.5 for scintillation states within this fraction (as determined by the prior integration). Signal wavelength data is always prioritized above data on crosstalk wavelengths when the average signal power is greater than the average power (regardless of circumstance, i.e., whether the signal or the crosstalk's turbulence causes this). Table 2 shows the pdf and error floor expressions for various turbulence channel models (Ghassemlooy et al. 2013). The BER probability for each scintillation state throughout this time interval is thus 0. So, we get an error floor for the average BER of \(0.5 F + 0 \left( {1 - F} \right) = F/2\), where that average is across all states of scintillation for the pdf coming from one Rytov variance and \(F\) is the proportion of time during which the crosstalk is greater than the signal. The error floor will deviate from lower signal powers if we inject a tiny amount of noise into the system (i.e., signal independent thermal noise for simplicity); however, this small quantity of noise may be ignored for sufficiently high signal powers the error floor is kept. Figure 3a as reported in Ref. (Aladeloba et al. 2013) shows the initial error floor that depends on OOK modulation. In addition, this image shows how the average received optical power affects the BER in the following five cases: Results are presented for 1) no interferer and no turbulence (Si); 2) signal with interferer, no turbulence (Si,XT); 3) signal with turbulence, no interferer (turbSi); 4) signal with turbulence, interferer with no turbulence (turbSi,XT); and 5) signal with no turbulence, interferer with turbulence (Si,turbXT) cases. Regarding cases 4 and 5, the BER error floor rises with turbulence strength. To understand turbulence accentuation of crosstalk, consider first the S,turbXT case and note that turbulent crosstalk can sometimes increase with turbulence strength value. These cases have advantages that we will discuss in Sect. 5. In Ref. (Aladeloba et al. 2013), the authors presented five cases for the BER error floor mentioned above. Sections 4 examines the computational complexity and mitigate the atmospheric turbulence. If an optical pulse of peak power \(P_{T}\) is transmitted, it is represented by the digital symbol ‘0’ while the optical pulse transmission of peak power \(\alpha_{e} P_{T}\) represents a digital symbol ‘1’, \(R\) is the photo detector efficiency. For a bit duration of \({\text{T}}_{{\text{b}}}\) with the average bit energy \(E_{b}\), the probability of error is (Ghassemlooy et al. 2013):

$$P_{e - bit - OOK} = Q\left[ {\sqrt {\frac{{E_{b} }}{{ N_{0} }}} } \right]$$
(12)
$$E_{b} = \frac{{E_{P} }}{{2}} = {2} \left( {R_{{P_{T} }} } \right)^{2} T_{b}$$
(13)
Table 1 Key parameters used in the calculations
Full size table
Fig. 2
figure 2

BER probability curve for OOK

Full size image
Table 2 Pdf and error floor expressions for different channel turbulence models
Full size table
Fig. 3
figure 3

a BER versus average received signal optical power (dBm) for WT and ST (no amplifier) with \({\text{C}}_{{{\text{XT}}}} { = }\) 30 dB (Aladeloba et al. June 2013). b Log-normal pdf with E [I] = 1 of log irradiance variance for the proposed system (Ghassemlooy et al. 2013) c BER versus average received signal optical power (dBm) for WT and ST (no amplifier) with \({\text{C}}_{{{\text{XT}}}} { = }\) 30 dB [Proposed]

Full size image

The electrical power spectral densities (PSDs) of OOK–NRZ and OOK-RZ with duty cycle \(\left( {\gamma = 0.5} \right)\) are given as:

$${\text{S}}_{{\text{OOK - NRZ}}} \left( {\text{f}} \right) = \left( {{\text{P}}_{{\text{r}}} {\text{R}}} \right)^{2} {\text{T}}_{{\text{b}}} \left( {\frac{{\sin\uppi {\text{fT}}_{{\text{b}}} }}{{\uppi {\text{fT}}_{{\text{b}}} }}} \right)^{2} \left[ {1 + \frac{1}{{{\text{T}}_{{\text{b}}} }}\updelta \left( {\text{f}} \right)} \right]$$
(14)
$${\text{S}}_{{\text{OOK - RZ}}} \left( {\text{f}} \right)\left( {\text{f}} \right) = \left( {{\text{P}}_{{\text{r}}} {\text{R}}} \right)^{2} {\text{T}}_{{\text{b}}} \left( {\frac{{\sin \left( {\uppi {\text{fT}}_{{\text{b}}} /2} \right)}}{{\uppi {\text{fT}}_{{\text{b}}} /2}}} \right)^{2} \left[ {1 + \frac{1}{{{\text{T}}_{{\text{b}}} }}\mathop \sum \limits_{{{\text{n}} = \infty }}^{\infty } \delta \left( {{\text{f - }}\frac{{\text{n}}}{{{\text{T}}_{{\text{b}}} }}} \right)} \right]$$
(15)

where \(\delta \left( \right)\) is the Dirac delta function (Ghassemlooy et al. 2013).

4.4 Numerical analysis of the error floor in the case of adaptive threshold

In the following, we employ the most generally used notations and offer all values in SI units unless otherwise stated. In the first case, the relationship is as follows (Elsayed et al. 2018):

$${\text{BER}}\left( {P_{{R,sig}} \left( {\text{1}} \right)} \right){\text{ = ~}}\frac{{\text{1}}}{{\text{4}}}{\text{erfc}}\left[ {\frac{{{\text{2(r}} - {\text{1)~R}}P_{{R,~sig}} \left( 1 \right)/~\left( {r + 1} \right)}}{{{\text{2q}}~B_{e} ~R~P_{{R,~sig}} {\text{~}}\left( {\text{1}} \right){\text{ + ~\'o }}_{{{\text{th}}}}^{{\text{2}}} }}} \right]$$
(16)

In the second case,

$${\text{BER = }}\frac{{\text{1}}}{{\text{4}}}\mathop \smallint \limits_{0}^{\infty } {\text{erfc}}\left[ {\left( {\frac{{{\text{2}}\left( {{\text{r'}} - {\text{1}}} \right){\text{~R}} \times P/\left( {r^{\prime} + 1} \right)}}{{{\text{2qB}}_{{\text{e}}} {\text{~R}}{\text{.}}P~ + ~\sigma _{{th}}^{2} }}} \right)} \right]\begin{array}{*{20}c} {{\text{~~~}}} \\ {\text{P}} \\ \end{array} _{{{\text{GG}}}} \left( {\frac{{\text{P}}}{{P_{{R,~sig}} \left( {10} \right)}}} \right){\text{dp}}$$
(17)
$${\text{P}}_{{{\text{GG}}}} \left( {\frac{{\text{P}}}{{P_{R, sig} \left( 1 \right)}}} \right) = \frac{{ 2\left( {\alpha \beta } \right) ^{{\left( {\alpha + \beta } \right)/2}} }}{\Gamma \left( \alpha \right) \Gamma \left( \beta \right)}\left( {\frac{{\text{P}}}{{P_{R, sig} (1)}}} \right)^{{\frac{{\left( {\upalpha +\upbeta } \right)}}{2} - 1}} \times {\text{K}}_{{\upalpha -\upbeta }} \left( {2\sqrt { \upalpha \upbeta \frac{P}{{P_{R, sig} \left( 1 \right)}}} } \right)$$
(18)

Finally, in the last case

$${\text{BER = }}\frac{{1}}{{4}}\mathop \smallint \limits_{0}^{\infty } {\text{erfc}}\left( {\frac{{2\left( {r^{\prime} - 1} \right) R \times \frac{{P\left( {1 - \left( {1/C_{XT} } \right)} \right)}}{r^{\prime} + 1}}}{{2q B_{e} R. P \left( {1 + (1/C_{XT} ) } \right) + \sigma_{th}^{2} }}} \right) \times P_{GG} \left( {\frac{P}{{P_{R, sig} \left( 1 \right)}}} \right)dp$$
(19)

4.5 OOK with an un-optimized detection threshold

The received signal \(\left( {r\prime = \xi I + N} \right)\) is in the low state where \(\xi\) is low and high offset depends on \(r\prime\). N is (PSD noise) and \(I_{s} = \xi I\) is received optical current where N and \(I_{s}\) are independent as written in Ghassemlooy et al. (2013).

$$f\left( {r^{\prime}/s_{o} } \right) = \frac{1}{\xi }f_{1} \left( {\frac{r\prime }{\xi }} \right) \times f_{N} \left( {r\prime } \right) = \mathop \smallint \limits_{0}^{\infty } \frac{1}{{\sqrt {2\pi \sigma_{x} } }}\exp \left( { - \frac{{\left( {In\frac{x}{\xi } + \frac{{\sigma^{2} }}{2}} \right)^{2} }}{{2\sigma^{2} }}} \right) \times \frac{1}{{\sqrt {2\pi \sigma_{y} } }}\exp \left( {\frac{{\left( {r - x} \right)^{2} }}{{2\sigma_{y}^{2} }}} \right)dx$$
(20)

In the high state of Rx i.e. \(\left( {r\prime = \left( {2 + \xi } \right)I + N} \right)\)

$$f\left( {r^{\prime}/s_{1} } \right) = \frac{1}{2 + \xi }f_{1} \left( {\frac{r^{\prime}}{{2 + \xi }}} \right) \times f_{N} \left( {r^{\prime}} \right)$$
(21)

The BER for OOK using a fixed detection threshold \({T}_{th}\) is given as:

$$\begin{aligned} P_{e} = \left( {1 - p_{1} } \right)P_{F} + P_{1} P_{M} = & \frac{{\left( {1 - p_{1} } \right)\exp \left( {\frac{{ - \sigma^{2} }}{8}} \right)}}{{\sqrt {2\pi \sigma } }}\mathop \smallint \limits_{0}^{\infty } \frac{\sqrt \xi }{{x^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}\exp \left( {\frac{{ - In^{2} \frac{x}{\xi }}}{{2\sigma^{2} }}} \right) \times \left( {\frac{{T_{th - x} }}{{\sigma_{y} }}} \right)dx + \frac{{p_{1} \exp \left( { - \frac{{\sigma^{2} }}{8}} \right)}}{{\sqrt {2\pi \sigma } }}\mathop \smallint \limits_{0}^{\infty } \frac{{\sqrt {2 + \xi } }}{{x^{3/2} }} \\ &\quad \times \exp \left( { - \frac{{In^{2} \frac{x}{2 + \xi }}}{{2\sigma^{2} }}} \right)Q\left( {\frac{{X - T_{th} }}{{\sigma_{y} }}} \right)dx = \frac{{\left( {1 - p_{1} } \right)\exp \left( {\frac{{ - \sigma^{2} }}{8}} \right)}}{{\sqrt {2\pi \sigma } }}\mathop \smallint \limits_{0}^{\infty } \frac{\sqrt \xi }{{x^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}\exp \left( {\frac{{ - In^{2} \frac{x}{\xi }}}{{2\sigma^{2} }}} \right) \times Q\sqrt \gamma \left( {T_{th - x} } \right)dx \\ &\quad + \frac{{p_{1} \exp \left( { - \frac{{\sigma^{2} }}{8}} \right)}}{{\sqrt {2\pi \sigma } }}\mathop \smallint \limits_{0}^{\infty } \frac{{\sqrt {2 + \xi } }}{{x^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} \times \exp \left( { - \frac{{In^{2} \frac{x}{2 + \xi }}}{{2\sigma^{2} }}} \right) \times Q\sqrt \gamma \left( {T_{th - x} } \right)dx \\ \end{aligned}$$
(22)

Interchannel crosstalk in a WDM-OOK/DPPM system was considered in Mbah et al. (2014); Elsayed et al. 2018) for a non-turbulent channel. A practical WDM system consists of many wavelengths, and signals in all active wavelengths contribute some crosstalk to signals on other wavelengths. The effects of crosstalk from adjacent wavelengths are typically more severe than crosstalk from different wavelengths further separated from the desired wavelength. Figure 3a shows the BER versus average received optical signal power (dBm) for WT and ST (no amplifier) with \({\text{C}}_{{{\text{XT}}}}\) = 30 dB, as in Ref. (Aladeloba et al. 2013). It can be seen the Fig. 3a (nonamplified case) that crosstalk turbulence accentuates BER floors that rise with turbulence strength. In the WT cases, floors occur at much lower BERs than the range given, using signal-to-crosstalk ratios of 30 dB. Figure 3b shows the log-normal pdf for various log-irradiance variances of \(\upsigma _{{\text{R}}}^{2}\) (Ghassemlooy et al. 2013). The irradiance fluctuates as \(\upsigma _{R}^{2}\) rises, resulting in a highly skewed distribution with tails extending beyond infinity. While in Fig. 3c, we show the three cases for the BER without error floor. As one can see, there is no error floor in case number 3 for Fig. 3c. The illustration in Fig. 3c contains among others, the dependences of BER on average received optical power in the three cases that are the following: 1) Si, 2), TurbSi, and 3) turbSi,XT. At the same time, we chose a much greater value equal to the upper limits. Besides, we used the uniform grid with the increment equal to \({\raise0.7ex\hbox{${\left( {10^{ - 3} - 10^{ - 12} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {10^{ - 3} - 10^{ - 12} } \right)} {200000}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${200000}$}}\).

The results of our computations are shown in Fig. 4. As can be seen, the OOK-modulation case number 3 does not show an error floor compared with Fig. 3a, which is presented in Aladeloba et al. (2013). As a result, it is essential to check the accuracy of the computations. Non-turbulent signal with a turbulent interferer (Si, TurbuXT) at a lower level causes the add/drop of a demux channel, which decreases the power of the turbulent interferer. A reverse threshold crossing is uncommon when the signal power and crosstalk are significant enough to trigger the floor. With a signal-to-crosstalk ratio (Si/Turbulent) of 30 dB, Fig. 4 (a) displays just the first three examples of the BER floor. The error floor is lower in the WT range discovered using signal to crosstalk ratios of 30 dB and 15 dB when the BER is lower. While in Fig. 4b the error floor was attained in all situations but is different in Fig. 2a (Aladeloba et al. June 2013), and a value was computed. ASE-shot noise, signal-ASE beat noise, and signal shot noise are all included in the overall OLT receiver \({\upsigma }_{{{\text{th}}}}^{{2}}\) result, representing the entire variation in OLT receiver noise.

Fig. 4
figure 4

BER versus average received optical signal power (dBm) for turbulence regimes using OOK modulation (with amplifier) and crosstalk a \({\text{C}}_{{{\text{XT}}}}\) = 30 dB, b \({\text{C}}_{{{\text{XT}}}} {\text{ = 15 dB}}\)

Full size image

4.6 Subtleties of the calculations

The most challenging part of these problems is correctly taking integrals on the right-hand side of Eqs. (16) and (17). The following dependencies must be examined to establish the proper integral bounds in these equations:

$${\text{BER}} = \frac{1}{4}\mathop \int \limits_{ 0}^{\infty } erfc\left[ {\left( {\frac{{2 \left( {{\text{r}} - 1} \right) \cdot {\text{R}} \times {\text{P}}/ \left( {{\text{r}} + 1} \right) }}{{2{\text{q}} {\text{B}}_{{\text{e }}} {\text{R}} \cdot {\text{P}} + \upsigma _{{{\text{th}}}}^{2} }}} \right) \times \left[ {\frac{{\text{P}}}{{{\text{P}}_{{\text{R,sig}}} \left( 1 \right)}}} \right]dp} \right]$$
(23)
$${\text{BER}} = \frac{1}{4}\mathop \int \limits_{0}^{\infty } erfc \left[ {\left( {\frac{{2\left( {{\text{r}} - 1} \right) \cdot {\text{R}} \times \frac{{{\text{P}}\left( {1 - \left( {1/{\text{C}}_{{{\text{XT}}}} } \right)} \right)}}{{{\text{r}} + 1}}}}{{2{\text{qB}}_{{\text{e}}} {\text{R}} \cdot {\text{P}} \left( {1 + (1/{\text{C}}_{{{\text{XT}}}} )} \right) + \upsigma _{{{\text{th}}}}^{2} }}} \right) \times {\text{P}}_{{{\text{GG}}}} \left[ {\frac{{\text{P}}}{{{\text{P}}_{{\text{R, sig}}} \left( 1 \right)}}} \right]dP} \right]$$
(24)

Since,

$$\mathop \smallint \limits_{{10^{ - 12} }}^{3} P_{GG} \left( {{\text{h}}_{{\text{X}}} } \right)d{\text{h}}_{{\text{X}}} = 0.9725$$
(25)

performing integrations in the Eqs. (16) and (17) from \({10}^{{ - 12}} {\text{P}}_{{\text{R,sig}}} \left( {1} \right){\text{ to 3}}.{\text{P}}_{{\text{R,sig}}} {(1})\) one can count on the accuracy that does not exceed a few percent. To see how \({\text{h}}_{{\text{X}}}\) influences Gamma-Gamma probability distribution, see Fig. 6a. The value of \({\text{h}}_{{\text{X}}}\) is reduced from 10–12 to 3 in this graph. Figure 6a shows that there are no areas with strong gradients of PGG on this interval. As a result, integrations may be performed on a consistent grid. Figure 4 is based on a range of P values from \({10}^{{ - 12}}\) \({\text{P}}_{{\text{R,sig}}} \left( {1} \right){\text{ to 3}}{\text{.P}}_{{\text{R,sig}}} {(1})\) and \({\text{P}}_{{\text{R,sig}}} {(1})\) with the 72,001-node uniform grid. Calculating the percentage of the maximum variation on a uniform grid with 36,001 nodes helps us determine whether our efforts have been successful. No more than 1% variances can be found in either Case 2 or Case 3. As a result, the selected grid has a sufficient density. When we ran simulations based on data from Manor and Arnon July (2003), and observed that our results for the above three situations closely matched those in Manor and Arnon July (2003) (see Fig. 5). Figure 6b depicts the BER performance for \({\text{C}}_{{\text{n}}}^{{2}}\) at various degrees of air turbulence as a function of average received irradiance (dBm). As the level of turbulence rises, so does the average received irradiance (dBm).

Fig. 5
figure 5

\({\text{Log}}_{10}\) BER versus average received optical signal power (dBm) for turbulence regimes using OOK modulation (with amplifier) with crosstalk much better than Fig. 3a \({\text{C}}_{{{\text{XT}}}}\) = 30 dB, b \({\text{C}}_{{{\text{XT}}}} {\text{ = 15 d}}\) B

Full size image
Fig. 6
figure 6

a pdf versus attenuation due to atmospheric turbulence (\(h_{x} )\), b Bit error rate against average received irradiance (dBm) for various \({\text{C}}_{{\text{n}}}^{{2}}\) (\({\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} {)}\) values

Full size image

4.7 Modified OOK

In the following paragraphs, the experiment is summarized. Using the uniform grid with 20,001 nodes, the lower limit of the integrals may be set close to zero, while the upper limit can be far more prominent than the first integer. The lower and upper boundaries of 10–12 and 10–3, respectively, may be evaluated for accuracy. However, the arbitrary choice of limits can lead to the normalization of the Gamma-Gamma probability density function that does not equal 1 exactly. The normalizing constant A may be entered into the following equation:

$${\text{P}}_{{{\text{GG}}}} \left( {\frac{{\text{P}}}{{{\text{P}}_{{\text{R,sig}}} \left( 1 \right)}}} \right) = A\left[ {\frac{{ 2\left( {\upalpha \upbeta } \right)^{{\left( {\upalpha +\upbeta } \right)/2}} }}{{\Gamma \left( \upalpha \right)\Gamma \left(\upbeta \right)}}\left( {\frac{{\text{P}}}{{{\text{P}}_{{\text{R, sig}}} \left( 1 \right)}}} \right)^{{\frac{{\left( {\upalpha +\upbeta } \right)}}{2} - 1}} \times {\text{K}}_{{\upalpha -\upbeta }} \left( {2\sqrt {\upalpha \upbeta \frac{{\text{P}}}{{{\text{P}}_{{\text{R, sig}}} \left( 1 \right)}}} } \right)} \right]$$
(26)

And A is the normalization constant. Finally, in the last case, the dependence is the following:

$$BER = \frac{1}{4}\int\limits_{0}^{\infty } {{\text{erfc}}\left( {\frac{{{{{2}\left( {\text{r - 1}} \right)R \cdot P\left( {1 - {1 \mathord{\left/ {\vphantom {1 {C_{XT} }}} \right. \kern-\nulldelimiterspace} {C_{XT} }}} \right)} \mathord{\left/ {\vphantom {{{2}\left( {\text{r - 1}} \right)R \cdot P\left( {1 - {1 \mathord{\left/ {\vphantom {1 {C_{XT} }}} \right. \kern-\nulldelimiterspace} {C_{XT} }}} \right)} {\left( {r + 1} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {r + 1} \right)}}}}{{2qB_{e} R \cdot P\left( {1 + {1 \mathord{\left/ {\vphantom {1 {C_{XT} }}} \right. \kern-\nulldelimiterspace} {C_{XT} }}} \right) + \sigma_{th}^{2} }}} \right)p_{GG} \left( {\frac{P}{{P_{R,sig} \left( 1 \right)}}} \right)dP}$$
(27)

Here, one must calculate the value of \(p_{GG} \left( {\frac{P}{{P_{R,sig} \left( 1 \right)}}} \right)\) according to the Eq. (26). For example, the average received optical power (BER) in Fig. 3a of the Ref. (Aladeloba et al. 2013) is the same in both circumstances showing all five cases for the BER floor. We compare our results with Ref. (Aladeloba et al. 2013) for the BER error floor. Calculations may be made assuming that A is equal to 1 and estimating its true value of 10 dBm. The curve shown in Fig. 4 was drawn by using the exact value as in Case 2 and \({\text{C}}_{{\text{n}}}^{{2}} { = 8}{\text{.4e}}^{{ - 15}} {\text{m }}^{{\frac{{ - 2}}{{3}}}}\). \({\text{log}}_{{{10}}} {\text{BER}}\) values in Fig. 5 show that the integration limitations used by Eqs. 16 and 17 are adequate, based on comparisons between the \({\text{log}}_{{{10}}} {\text{BER}}\) values in Cases 1 and 2. Figure 5 shows \({\text{log}}_{{{10}}} {\text{BER}}\) versus average received signal optical power (dBm) for (a) \({\text{C}}_{{{\text{XT}}}}\) = 30 dB, (b) \({\text{C}}_{{{\text{XT}}}}\) = 15 dB for turbulence regimes using OOK modulation (with amplifier) with crosstalk much better than Fig. 4. In Fig. 5, we show four cases that presented the BER error floor in Ref. (Aladeloba et al. June 2013) and mitigate the scintillation.

5 Modeling and analysis of DWDM-enabled PON-FSO system using DPPM

The DWDM-DPPM system is a basic example of a single neighboring interferer. Interchannel crosstalk was accentuated by the analysis, which assigned M bits at the raw data rate \({\text{R}}_{{\text{b}}}\) to a frame, where each block of b bits is mapped to one of M possible symbols (\({\text{s}}_{0}\), \(s_{{1}}\), \(s_{{\text{m}}}\)) where ts = \({\text{MT}}_{{\text{b}}} /{\text{n}}\), where \({\text{T}}_{{\text{b}}} { = 1}/{\text{R}}_{{\text{b}}}\), ts = M/ nRb, where M is the coding level. Each of the four slots in a DPPM frame for M = 2 at 2.5 Gbps binary data rate corresponds to one 2-bit word, so the slot rate of 5 GHz is used to transmit the pulses in those frames. 16-slot example of an OOK-NRZ and equivalent 16-DPPM signal (M = 4) time waveform for M = 4 (Phillips et al. 1996). As the coding level rises, the system bandwidth of optical signals expands, and spacing is required between the optical wavelengths. For systems that incorporate background noise and interference, the average powers of background power Pb and power transmitter \({\text{P}}_{{\text{t}}}\) int., must be taken into account. As a result of integrating across the slot containing just signals, only crosstalk pulses, both signals and crosses, and no signals (i.e., an empty slot), the random variables' means and variances are determined and can be expressed as (Ghassemlooy et al. 2013):

$$\upmu _{{{\text{X}}_{{\text{sig,int}}} }} \left( {{\text{h}}_{{\text{d,}}} {\text{h}}_{{\text{i}}} } \right) = \frac{{{\text{LRqN}}_{{\text{o}}} }}{{{\text{t}}_{{\text{s}}} }} + {\text{Gq}}\left( {{\text{sigRP}}_{{\text{d}}} \left( {{\text{h}}_{{\text{d}}} } \right) + {\text{int}} {\text{R}}_{{\text{i}}} {\text{P}}_{{\text{i}}} \left( {{\text{h}}_{{\text{i}}} } \right)} \right)$$
(28)
$$\'o _{{x_{{sig,int}} }}^{2} \left( {{\text{h}}_{{\text{d}}} ,{\text{h}}_{{\text{i}}} } \right){\text{ = }}\left( {\'o _{{th}}^{2} + \left( {\frac{{\left( {LRq^{2} N_{O} } \right)}}{{t_{s}^{2} }}} \right) + Gq^{2} \left[ {\left( {R + 2R^{2} N_{o} } \right)\frac{{sigP_{d} \left( {h_{d} } \right)}}{{t_{s} }}} \right] + \left( {R_{i} + 2R_{i}^{2} N_{{o,i}} } \right)\frac{{intP_{i} \left( {h_{i} } \right)}}{{t_{s} }}} \right)$$
(29)

At the amplifier output, modifications were made to the means and variances to account for crosstalk–ASE beat noise (Ghassemlooy et al. 2013).

$${\text{ P}}_{{{\text{we}}\left( {\text{l,r}} \right)}} \left( {{\text{h}}_{{\text{d,}}} {\text{h}}_{{\text{i}}} } \right) \ge \mathop \prod \limits_{{\begin{array}{*{20}c} {\text{j = 1}} \\ {\text{j = sig slot}} \\ \end{array} }}^{{\text{n}}} {\text{P}}\left( {{\text{X}}_{{\text{1,int}}} { > }\left( {{\text{X}}_{{\text{j}}} {\text{|h}}_{{\text{d,}}} {\text{h}}_{{\text{i}}} } \right)} \right)$$
(30)

where Xj represents the content of the non-signal slot X0,int.

Figure 7 shows the BER versus average received optical signal power (dBm) for WT and ST (no amplifier) with DPPM crosstalk (a) \({\text{C}}_{{{\text{XT}}}}\) = 30 dB, (b) \({\text{C}}_{{{\text{XT}}}}\) = 15 dB, and (c) \({\text{C}}_{{{\text{XT}}}}\) = 25 dB. There are five distinct types of signals: (1) Si; (2) Si,XT; (3) turbSi; (4) turbSi,XT; and (5) Si,turbXT cases. We achieved in Fig. 7 all five cases presented in Fig. 3a (Aladeloba et al. June 2013) for all BER error floors. The numerical results show in the ST cases the turbS,XT BER floors when \({\text{C}}_{{{\text{XT}}}} =\) 30 dB, while the turbS,XT and S,turbXT both floor when \({\text{C}}_{{{\text{XT}}}} =\) 15 dB and TurbSi,XT floor for \({\text{C}}_{{{\text{XT}}}} =\) 25 dB. As an example, take (Si, TurbuXT), which may increase to 1 value, resulting in crosstalk to become 1 and data 0 to be greater than data 1 for \({\text{h}}_{{{\text{sig}}}} , {\text{h}}_{{{\text{sig}}}}\), which happens when \({\text{h}}_{{{\text{int}}}}\) is more than \({\text{h}}_{{{\text{sig}}}}\). TurbuSi, XT is the only difference between the two situations (saved when the signal attenuation point occurs). The error floor emerges when the interfering \({\text{h}}_{{{\text{int}}}}\) \({\text{h}}_{{{\text{sig}}}}\) is raised by turbulence. With 0.5 Prob (crosstalk Power > Signal Power) as the error floor for the signal, there is perfectly accurate detection of BER crosstalk when there is more crosstalk than signal power. Figure 8 shows power penalty versus (a) interferer demux channel rejection \({\text{L}}_{{\text{demux,i}}}\) at \({\text{l}}_{{{\text{fso}}}} = {\text{1500 meter}}\) (b) crosstalk coupling coefficient (dB) (c) Refractive index structure \({\text{C}}_{{\text{n}}}^{{2}}\). In Fig. 8a, the power penalty for the DPPM system is lower than OOK in weak turbulence for \({\text{C}}_{{\text{n}}}^{{2}} {\text{ = 1e - 17m}}^{{{ - 2}/{3}}}\). It is seen that the DPPM requires lower power than OOK for all values of \({\text{ C}}_{{\text{n}}}^{{2}}\). We achieve lower power penalty with DPPM modulation technique and mitigate the scintillation and fading. To put it another way, for all values of \({\text{C}}_{{\text{n}}}^{{2}}\), the DPPM uses less power than the OOK. Thermal noise has a bigger power penalty than spontaneous beat noise, which has a smaller power penalty. It is more accurate to receive a spontaneous optical signal than a thermally induced one. Figure 9a, b indicate the BER versus average received signal optical power for (a) \({\text{C}}_{{{\text{XT}}}}\) = 30 dB, (b) \({\text{C}}_{{{\text{XT}}}}\) = 15 dB in the WT and ST (with an amplifier) with DPPM crosstalk. Figure 9 shows that the error floor for a non-turbulent signal with a turbulent interferer occurred at a much lower BER (Sig, Turb,XT). FSO connection lengths for both OOK and DPPM systems are shown in Fig. 10, along with no interference and single interference cases. The interferer demux rejection is 30 dB since both the interferer and the signal from the (remote node (RN) are at the same distance. The needed optical power increases when the FSO connection length increases due to attenuation, scattering, beam spreading losses, and scintillation. Because the FSO connection length has augmented, the needed power has also increased. If the power transferred is as high as 0 dBm, the issue of turbulence may be solved. The nonlinear effects that produce interchannel crosstalk are stimulated Raman scattering (SRS) and cross-phase modulation (XPM) (Knisley 1991). Crosstalk in optical networks occurs when the optical power associated with one channel starts appearing in another channel or adjacent channel (Knisley 1991). Figure 10a shows that all scenarios of turbulent flow, from mild to moderate to strong, were covered. When \({\text{C}}_{{\text{n}}}^{2} = 1 \times 10^{ - 13} {\text{m}}^{ - 2/3}\) significant turbulence occurs, the necessary power for \({\text{C}}_{{\text{n}}}^{2} = 1 \times 10^{ - 13} {\text{m}}^{ - 2/3}\) increases. In Fig. 10a, when the \({\text{l}}_{{{\text{fso}}}}\) length increases, the attenuation, scintillation, interchannel crosstalk, fading, and scattering increase. Also, at high \({\text{l}}_{{{\text{fso}}}}\) link length, the losses of beam spreading and the required optical power increase. \({\text{l}}_{{{\text{fso}}}} { = 1300}\) m cannot overcome turbulence. The required optical power for the DPPM system is lower than that for the OOK system in Fig. 10b, the power penalty of DPPM in weak turbulence (WT) is 0.2 smaller than that of OOK. We improve the BER performance, sensitivity, and bandwidth efficiency at the hybrid DPPM/OOK modulations. Also, we achieve a lower power penalty for DPPM compared with OOK modulation. Figure 11a illustrates the needed optical power transmitted (dBm) as a function of FSO link length for a single interferer and no interferer with, \({\text{L}}_{{\text{demux,XT}}} { = }15{\text{ dB}}\). In the first example, the interferer and signal both transmitted power at the same time; in the second case, the interferer and signal both transmitted with high \({\text{C}}_{{{\text{XT}}}}\), obviating the effects of turbulence exacerbated crosstalk, \({\text{L}}_{{\text{demux,XT}}} = 15\;{\text{dB}}\) which is lower demux or impoverished demux. The needed optical power transmitted (dBm) (BER of \(10^{ - 6}\)) as a function of the FSO link length for a single interferer and no interferer, \({\text{L}}_{{\text{demux,XT}}} = 15\;{\text{dB}}\) is shown in Fig. 11b. The necessary optical power increases with increasing \({\text{C}}_{{\text{n}}}^{{2}}\) and transmitting beam divergence. \({\uptheta }_{{{\text{XT}}}}\) for \(>\) 1mrad does not monitor the transmit beam divergence. We believe that the system with \({\uptheta }_{{{\text{XT}}}} <\) 1 mrad would allow for pointing and tracking in the vicinity of 0.12mrad.

Fig. 7
figure 7

BER versus average received signal optical power (dBm) for WT and ST (no amplifier) with DPPM crosstalk a \({\text{C}}_{{{\text{XT}}}}\) = 30 dB, b \({\text{C}}_{{{\text{XT}}}} {\text{ = 15 dB}},{ }\left( {\text{c}} \right){\text{ C}}_{{{\text{XT}}}} = {\text{25 dB}}.\)

Full size image
Fig. 8
figure 8

Power penalty versus a interferer demux channel rejection \({\text{ L}}_{{\text{demux,i}}}\) at \({\text{l}}_{{{\text{fso}}}} {\text{ = 1500 meter}}\) b crosstalk coupling coefficient (dB) c Refractive index structure \({\text{C}}_{{\text{n}}}^{{2}} .\)

Full size image
Fig. 9
figure 9

BER versus average received signal optical power (dBm) for WT and ST (with amplifier) with M-DPPM crosstalk a CXT = 30 dB, b = CXT = 15 dB

Full size image
Fig. 10
figure 10

Required optical power (dBm) verses \({\text{l}}_{{{\text{fso}}}}\) link length (m), for ST and WT at a \({\text{L}}_{{\text{demux,i}}}\) = 30 dBm, \({\text{l}}_{{{\text{fso}}}}\) = 2000 m, b \({\text{l}}_{{{\text{fso}}}}\) = 3000 m, \({\text{L}}_{{\text{demux,i}}}\) = 35 dBm

Full size image
Fig. 11
figure 11

Required optical power (dBm) for ST and WT, at \({\text{L}}_{{\text{demux, i}}}\) = 15 dBm, a \({\text{l}}_{{{\text{fso}}}}\) = 2000 m, b \({\text{L}}_{{{\text{demux}},{\text{i}}}} = ~15~\;{\text{dBm}},\;~{\text{Transmitter}}\;{\text{divergence}}~\;{\text{angle}}~\left( {{\text{mrad}}} \right)~\theta _{{{\text{XT}}}} = 0.2~\;{\text{mrad}}\)

Full size image

Figure 12 shows BER versus average received signal optical power (dBm) for \({\text{C}}_{{{\text{XT}}}}\) = 15 dB using the hybrid modulation schemes to improve the BER floor in Fig. 3c. We analyse the atmospheric turbulence at \({\text{C}}_{{\text{n}}}^{{2}} {\text{ = 1e - 13m}}^{{{ - 2}/{3}}}\) for the ST condition where we mitigate the scintillation and improve the BER performance at TurbuSi, XT and TurbuSi. Also, in the week turbulence, we consider the \({\text{C}}_{{\text{n}}}^{{2}} { = 8}{\text{.4e - 15m}}^{{{ - 2}/{3}}}\) to improve the average power optical power and BER performance. We modified the modulation schemes to improve all BER floors in DWDM-enabled PON-FSO communication systems.

Fig. 12
figure 12

BER versus average received signal optical power (dBm) for WT and ST (no amplifier) using the hybrid modulation schemes and \({\text{C}}_{{{\text{XT}}}}\) = 15 dB

Full size image

The results of Fig. 13 show the impact of interchannel crosstalk on the upstream transmission for both the modified modified OOK and DPPM modulation by evaluating BER versus a required optical power (dBm) within \({\text{l}}_{{{\text{fso}}}} { = 20}\) 00 m with \({\text{L}}_{{\text{demux, XT}}}\) = 30 dB. The numerical results show that the DPPM require less power compared with modified OOK for varying turbulence as shown in Fig. 13.

Fig. 13
figure 13

Required optical power (dBm) for upstream transmission system at target BERs of \({ 10}^{{ - {6}}}\) for varying turbulence levels as a function of the FSO link length for at \({\text{L}}_{{\text{demux, XT}}}\) = 30 dB

Full size image

6 Conclusions

We designed a system model of a DWDM-enabled integrated PON-FSO transmission that can provide higher bandwidth and meet the growing traffic demand. We also analyzed the DWDM-PON-FSO transmission under influence of accentuating interchannel crosstalk, interference, and noise. We calculate the total OLT receiver noise variance as the summation of the signal shot noise, ASE shot noise, beat noise, and ASE-ASE noise variances, which are the main problem of system degradation. We investigated the values of error floor found in turbulence atmospheric with modulation formats such as DPPM, OOK, and adaptive threshold. DPPM systems require lower optical power compared to OOK systems but suffer a small loss in sensitivity as the turbulence strength increases. Further, we obtained values of the BER error floor found in the turbulence atmospheric with hybrid modulation formats such as OOK, and adaptive threshold, and DPPM, schemes. We improve the BER performance and mitigate the scintillation and atmospheric turbulence. Also, we improve the power penalty at the hybrid modulation techniques in the proposed network. We modified the modulation schemes to improve all BER floors in DWDM-enabled PON-FSO communication systems.