1 Introduction

Laser cladding (LC) with superalloy powder is currently receiving increased attention (Gladush and Smurov 2011) due to its aerospace applications. Such powders are used to produce high quality final products. The process window is very narrow, so the precise choice of process conditions is needed. The laser power, the spot size, the timing, the beam scanning speed, the flow velocity, the concentration and size of particles, the physical and chemical properties of powders—are all of great importance. These parameters determine the quality and microstructural properties of the deposited layers. Most studies of microstructure evolution are based on the analysis of experimental data (Dinda et al. 2012; Tian et al. 2014; Simunovica et al. 2014), however, such selection of parameters is extremely difficult and expensive. The task of searching for the optimal regimes of the process to achieve the target parameters of material and products requires a deep understanding of physical processes and phenomena and the development of physical and mathematical models, applying numerical methods.

In LC energy comes to the substrate by two channels: with laser radiation attenuated by powder stream (Niz’ev et al. 2014) and with heated particles (Simunovica et al. 2014; Grishaev et al. 2011). For a self-consistent model of the LC process, it is necessary to take into account the two channels at the free surface (Grishaev et al. 2013).

Nickel-based alloys impurity content is known to affect the final microstructure and melting temperature in LC process (Conde et al. 2002). A movement of dissolved impurities mainly occurs due to the hydrodynamic mixing of tool steel powder in LC (Hea et al. 2011). The rapid phase change kinetics and the role of impurity in this process are not dealt with. The macroscopic temperature and concentration behaviors are only considered. The microstructure evolution of the clad layers is not taken into account.

The multiscale methods are often used (Nie et al. 2014; Cao and Choi 2006; Tan et al. 2011; Tan and Shin 2015) for modeling of the microstructure evolution, where the temperature history calculated at the macro-scale is used to calculate the microstructure at the micro-level. The segregation of Nb and formation of Laves phase, during the solidification of nickel-based superalloy is considered (Nie et al. 2014). The numerical calculations reveal the dependence of microstructure evolution on solidification conditions, particularly on the cooling rate and temperature gradient. An effect of undercooling on the resulting microstructure is investigated by the phase-field method (Cao and Choi 2006) and dendrite growth pattern variation is shown (from dendrite to globular one as undercooling increases). The temperature history is often used in non-self-consistent manner for microscale calculations. Undercooling is specified but not calculated in the above-mentioned papers. In our previous work (Mirzade et al. 2013) we presented the self-consistent 3D model of crystallization in LC in the framework of homogeneous volumetric growth of the crystallites. This model is suitable for the crystallization of a “clean” powder only and does not take into account the effect of impurities on the crystallization of the molten layer.

The aim of the present work is to develop the self-consistent model of crystallization in LC and to study numerically the effect of soluble impurities on the microstructure of the clad layers. The model under consideration includes the nonlinear equations of heat and mass transfer and the kinetic equation for the phase field. Phase change, considered as a nonequilibrium kinetic process, is associated with the nucleation and growth of crystalline nuclei in metastable system. The microscale part of the model uses the surface growth mechanism of the columnar grains. The kinetics of phase transformations is described relying on the model of Kolmogorov–Johnson–Mehl–Avrami (KJMA) [Christian 2002; Belenkii 1980 (in Russian); Skripov and Koverda 1984 (in Russian)], which is used for the conditions of inhomogeneous temperature distribution of the melt pool. The model gives an opportunity to estimate the spatial distribution of crystalline columnar grains in LC.

2 Basic equations

The self-consistent model of LC taking into account the heat transfer, phase change, solute and free surface evolution is as follows:

Continuity equation:

$$\frac{\partial \rho }{\partial t} + \nabla \left( {\rho {\text{u}}} \right) = 0$$
(1)

Heat equation:

$$c\rho \frac{\partial T}{\partial t} + \nabla \left( {c\rho uT} \right) = div\left( {\lambda \nabla T} \right) + \alpha_{l} q\delta \left( \varphi \right) + \rho \left( {1 - f_{l} } \right)\Delta c\frac{\partial T}{\partial t} + \rho L\frac{{\partial f_{l} }}{\partial t}$$
(2)

Momentum equation:

$$\frac{{\partial \rho u_{i} }}{\partial t} + \nabla \left( {\rho {\text{u}}u_{i} } \right) = div\left( {\mu \nabla u_{i} } \right) - S_{D} - \frac{\partial p}{\partial i} + \nabla T\frac{\partial \sigma }{\partial T}\vec{i}$$
(3)

Solute concentration equation:

$$\frac{\partial C}{\partial t} + u\nabla C = div\left( {D\nabla C} \right) + \left( {1 - k_{p} } \right)C\frac{{\partial f_{s} }}{\partial t}$$
(4)

Free boundary evolution:

$$\frac{\partial \varphi }{\partial t} + \nabla \cdot \left( {u\varphi } \right) = F_{p} \left| {\left. {\nabla \varphi } \right|} \right.$$
(5)

Phase change equation:

$$b\left( {x,y,z,t} \right) = 1 - exp\left\{ { - 2\pi \int\limits_{0}^{t} {\tilde{J}\left( {T\left( t \right)} \right)\left( {r^{*} + \int\limits_{\tau }^{t} {G\left( {T\left( {t,\tau } \right)} \right)d\tau } } \right)^{2} dt} } \right\} ,$$
(6)

where ρ is the density, T is the temperature, c is the heat capacity, λ is the heat conductivity, L is the heat latent capacity, α L is the laser power absorption coefficient, u i is the liquid velocity by the coordinate i = x, y, z; μ is the viscosity, C is the solute concentration, D is the diffusivity coefficient, φ is the level set function, Fp is the free boundary speed function, b is the volume fraction of new phase.

The second term in the right-hand side of Eq. (2) is responsible for the absorption of laser radiation. The third and fourth source terms are associated with a phase transition. In Eq. (3) the second term in the right side is used to set the zero velocity in the solid, while the last one is responsible for the thermocapillary Marangoni forces. The last member of the right-hand side of Eq. (4) is responsible for the capture of impurities at the high-speed crystallization (k p is an equilibrium partition coefficient). The speed of movement of the free surface is determined by adding the powder, as well as by hydrodynamic motion of the fluid (Mirzade et al. 2013).

Equation (6) is the KJMA equation for volume fraction of the new phase (2π is the shape factor, r* is the initial nuclei radius, G is the growth rate, \(\tilde{J}\) is the nucleation rate).

Every particle in the cell volume grows with same rate at every instant. The growth rate is defined by:

$$G\left( T \right) = d_{0} \frac{{k_{B} T}}{h}exp\left\{ { - \frac{{E_{a} }}{{k_{B} T}}} \right\}exp\left\{ { - \frac{{\Delta S\Delta T}}{{k_{B} T}}} \right\}$$
(7)

where d 0 is the lattice parameter, E a is the activation energy, \(\Delta S = \frac{{\Delta H}}{{N_{a} T_{m} }}\) is the phase change entropy.

$$\tilde{J}\left( T \right) = N_{0} \frac{{k_{B} T}}{h}exp\left\{ { - \frac{{E_{a} }}{{k_{B} T}}} \right\}exp\left\{ { - \frac{{E_{G} \left( T \right)}}{{k_{B} T}}} \right\}$$
(8)

where N 0 is the sites concentration, E G is the Gibbs energy, which in case of surface nucleation is given by:

$$E_{G} \left( T \right) = \frac{{\pi d_{0} \gamma^{2} T_{m} }}{{\rho L\Delta T}}$$
(9)

where γ is the surface energy, T m is the melting temperature. The solute influence is taken into account by effective supercooling/superheating (Mirzade 2006):

$$\Delta T = T_{m} - m_{e} C - T.$$
(10)

Equations (2) and (6) are coupled by the mass fraction formula:

$${\text{f}}_{\text{l}} = \left( {1 + {\raise0.7ex\hbox{${\uprho_{\text{s}} \left( {1 - {\text{b}}} \right)}$} \!\mathord{\left/ {\vphantom {{\uprho_{\text{s}} \left( {1 - {\text{b}}} \right)} {\uprho_{\text{l}} {\text{b}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\uprho_{\text{l}} {\text{b}}}$}}} \right)^{ - 1}$$
(11)

where ρ s and ρ l are the densities of solid and liquid, respectively.

3 Solution algorithm

The spatially inhomogeneous mesh is used in the calculation. Equations (1)–(6) were approximated by the finite volume method and then solved using the preconditioned bi-conjugate gradients (PbiCG) method by using C++ open class library OpenFoam. The results allow us to calculate the effective coefficient of thermal conductivity (by average melt pool velocity) and the melting temperature. Further, Eqs. (2), (5) and (6) with the effective melting temperature and thermal conductivity were approximated by the method of stabilizing corrections, and solved in parallel by Thomas and Jacobi methods. The latter model uses rather fine mesh to resolve microstructure of clad layer. The self-consistent temperature history of the crystallization process was obtained which allows obtaining the distribution of crystallite sizes by using the population-based approximation of the KJMA equation (Crespo and Pradell 1996). It is possible to calculate the average radius of the particles from the distribution of crystallite sizes. The simplest approach here is to use the total concentration of particles n Σ of all sizes. In the case of surface growth:

$$\hat{R}_{N} = \sqrt[2]{{\frac{1}{{\pi n_{\varSigma } }}}}.$$
(12)

Due to the multimodal distribution of particle sizes, it is important to know what volume is occupied by the particles on average. The average volume-weighted radius can be calculated, knowing the volume fraction is taken by the particles of a certain size:

$$\hat{R}_{V} = \frac{{\mathop \sum \nolimits_{1}^{N} r_{i} b_{i} }}{{\mathop \sum \nolimits_{1}^{N} b_{i} }} = \mathop \sum \limits_{1}^{N} \pi r_{i}^{3} n_{i} .$$
(13)

A peak temperature is used, as a rule, for the normalization of particle sizes for non-isothermal crystallization to calculate the characteristic radius (Farjasa and Roura 2008). Since the peak temperature changes in our case, such normalization is not suitable to compare the radii for different spatial points. In the present work supercooling ∆T = 45 K is used in order to normalize R = R/λ the size of the crystallites:

$$\lambda = \sqrt[3]{{\frac{{G\left( {\Delta T} \right)}}{{J\left( {\Delta T} \right)}}}},$$
(14)

The institute cluster (throughput 3.3 TFlops) is used for the calculation. The time of a single calculation is approximately 24 h.

4 Results

The 3D distribution of temperature and volume fraction of the new phase in the deposited layer is shown in Fig. 1. The processing parameters used are P = 600 W, α L  = 0.45, R = 1.67 mm, F = 10 g/min, α p  = 0.7, d = 4 mm, V = 10 mm/s (α p —powder catchment efficiency). Nickel superalloys contain many impurities for example Inconel 718 (52.5 % Ni, 19.0 % Cr, 18.8 % Fe, 5.2 % Nb, 3.1 % Mo, 0.9 % Ti, 0.5 % Al). Only the redistribution of Cr is studied in the present work as it is an impurity that can have the biggest portion in alloy. The thermal and kinetic parameters of the material are listed in Table 1.

Fig. 1
figure 1

3D Distribution of the temperature field in the melt pool

Full size image
Table 1 The main parameters of the calculation
Full size table

Nickel superalloys have high density and latent heat of melting, so the meltpool is stretched, despite the low scanning speed. There is almost no temperature gradient at the rear of the clad layer due to release of the latent heat of fusion in this area. The phase field distribution permits estimating the depth and width of laser penetration, and the shape of the cladding layer can give the height for LC process parameters.

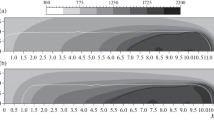
The solute transport is carried out due to the hydrodynamic flow in LC, and diffusion can be neglected. Figure 2a shows the sketch of solute concentration distribution at the initial stage of the LC process. The figure shows that in the area where there are no vortex currents of the melt, the impurity concentration remains at initial value. Due to kinetic phase change nature the melting/crystallization process occurs with superheating/undercooling. The value of undercooling depends on the phase change mechanism, the material properties, and the cooling speed. Figure 2b shows the distribution of concentration at the stage when the deposition process reaches the steady state. It is seen that due to the hydrodynamic flow the solute concentration is almost uniform in the case of well-chosen process parameters.

Fig. 2
figure 2

The distribution of the solute concentration on the initial (top) and final (bottom) stage of the LC process. Red contour is the melting temperature, black contour melt pool boundary (b = 0.5). Arrows show liquid velocity

Full size image

The temperature field and the cladding height come to a steady state by the time of 1500 ms from the beginning of the LC process at the processing parameters under consideration. Figure 3a, b show the melt pool and the temperature field for various solution concentrations under the identical conditions of the LC. It is seen that the melt pool is extended at larger impurity content, and the penetration depth increases slightly. The larger melt pool is obtained in the case of the same heat input, as the increase of solute concentration is expected to reduce the effective melting temperature.

Fig. 3
figure 3

The cladding layer for the different solute concentrations. a CCr = 9 %, Tm* = 1320 K; b CCr = 11 %, Tm* = 1295 K

Full size image

Several sites can be chosen through the melt pool depth for a detailed study of the microstructure of the deposited layers. Figure 4 shows the dynamics of key kinetic variables at three sites through the depth (381 μm above the substrate, at the substrate level and 373 μm under the level of the substrate). The temperature is seen to go near plateau or decrease with time. The supercooling is removed slightly, in other words recalescence does not occur due to the latent heat dissipation into the substrate. The average volume-weighted particle size within the sites under study is also shown. The plateau absence in the lower regions of the clad layer is connected with self-consistent behavior of the process being considered. The latent heat release at crystallization occurs with supercooling increase (temperature lowering) at the sites under the substrate level. At the sites above the substrate the process takes place practically at constant supercooling. The decrease in the effective melting temperature causes a decrease in the rate of growth (from 4 to 3.5 cm/s). This in turn leads to a slow (delayed) metastable process. This creates large undercooling, which results in the increase in the nucleation rate and the reduction in the average size of the crystallites.

Fig. 4
figure 4

Temperature, the volume fraction of the solid phase (top), the nucleation and growth rates of a solid phase (bottom) for two values of the solute concentration. a C = 9 %; b C = 11 %

Full size image

Figure 5 shows the final distribution of volume fraction of particle sizes at the studied sites of the melt pool. It is seen that the distribution of particles has a maximum at small sizes. This is because a large number of particles are nucleated at the final stage of crystallization when the temperature drops sharply. The particles of the smallest radius always take a small amount of space, as the maximum is always distant from the minimum size values.

Fig. 5
figure 5

Final distribution of the volume fraction of particle sizes at the studied sites, the arrows indicate the volume weighted average radius. C = 9 %, Tm* = 1320 K (a, c, e) and C = 11 %, Tm* = 1295 K (b, d, f). The site distance to the substrate and the value of the volume weighted average particle radius is shown

Full size image

The volume fraction distribution occupied by the particles of certain size is different at the sites due to the distance from the surface. Two groups of particles are seen on the clad surface, where the temperature dynamics shows a distinct plateau. The coarse group appears at the onset of the crystallization process and grows at constant supercooling. The fine group of particles is born at the final stage of the crystallization process. Due to the fact that the process on the surface is long, the first group is distant from the second one and the average radius is comparatively large.

The temperature history plateau is shorter at the sites on the substrate level, therefore, two groups of particles are close enough to merge. The average radius is less here than on the surface. In the depth of the substrate, the crystallization process occurs with temperature decrease without isothermal plateau. Only one group of particles is seen and the average particle size is small.

Figure 6 shows the spatial distribution of the average volume-weighted particle size in the cross-section, transverse to the laser beam movement. The area immediately adjacent to the clad surface has a crystallite size less than the area distant from it. This is due to the fact that comparatively more effective heat sink into the substrate leads to rapid cooling, which results in lower particle sizes.

Fig. 6
figure 6

The distribution of the normalized average radius of the crystallites in the transverse cross-section for the two solute concentrations. a CCr = 9 %; b CCr = 11 %

Full size image

The trend for size reduction depending on the depth from the clad surface in our numerical model agrees with the experimental measurements of the microstructure of Al–Si powder deposited on aluminium substrate by laser cladding in paper (Pei and De Hosson 2000). The calculation can be used for estimating and determining the presence (or absence) of microstructure gradients at laser cladding. These are the intermediate results and we are to present a fully self-consistent model in our further work.

5 Summary and conclusions

The self-consistent model of LC involving heat-mass transfer and phase change kinetics is presented to estimate the microstructure evolution in the clad layer. The dynamics of the temperature fields, the impurity distribution and the clad profile are obtained in LC with co-axial nickel superalloy powder injection. Self-consistent heat transfer and phase change kinetics results in qualitatively different temperature behavior at the sites through the depth of the clad layer. This is due to different cooling rates in the regions being considered. The solute transport is carried out due to the hydrodynamic flow of the Ni-based powder, and diffusion can be neglected. A uniform distribution of the solute concentration can be obtained with the proper choice of LC parameters. The solute concentration affects the phase change temperature and the kinetics of the crystallization process, which may lead to changes in the microstructural properties of the deposited layers. The final grain distribution at the various sites of the clad layer has been obtained for different solute concentrations. The microstructural gradients can occur in case of high cladding heights associated with the various cooling rates at the surface and in the depth of the clad layer (due to the heat conduction into the substrate). The results give the opportunity to improve the recommendations for LC of heat-resistant powders, to find the optimal processing conditions from the view point of both the geometric parameters, and the microstructure of the deposited layer.